Complete Solutions to EXAMPLES of chapter TRIANGLES of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | TRIANGLES |
| NCERT GUJARATI | EXAMPLES |
| Number Of Questions | 14 |
| Academic Year | 2023-24 |
AB is a line segment and line l is its perpendicular bisector. If a point P lies on l, show that P is equidistant from A and B.
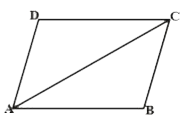
View SolutionIn the given figure, `AB||DC and AD||BC` show that `DeltaABC ~= Delta CDA`.
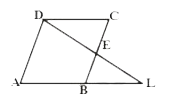
View SolutionIn the given figure, AL || DC, E is mid point of BC. Show that `DeltaEBL ~= DeltaECD`.
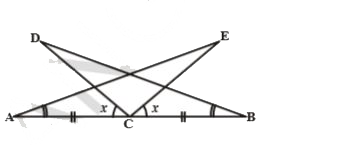
View SolutionUse the information given in the adjoining figure, to prove :
`(i) DeltaDBC ~= DeltaEAC`
`(ii) DC = EC.`
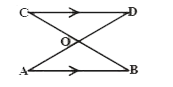
View SolutionLine-segment AB is parallel to another line-segment CD. O is the mid-point of AD.
Show that (i) `DeltaAOB ~= DeltaDOC` (ii) O is also the mid-point of BC.
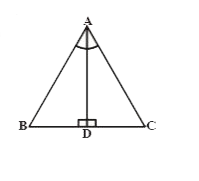
View SolutionIn `DeltaABC`, the bisector AD of A is perpendicular to side BC Show that AB = AC and `DeltaABC` is isosceles.
View SolutionIn the adjacent figure, `AB = BC and AC = CD`. Prove that : `/_ BAD : /_ ADB = 3 : 1.`

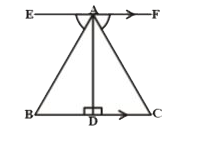
View SolutionIn the given figure, AD is perpendicular to BC and EF || BC, if `/_ EAB = /_ FAC`, show that triangles ABD and ACD are congruent.
Also, find the values of x and y if `AB = 2x + 3, AC = 3y + 1, BD = x and DC = y + 1.`
View SolutionE and F are respectively the mid-points of equal sides AB and AC of `DeltaABC` (see figure)
Show that BF = CE.

View SolutionIn an isosceles triangle ABC with AB = AC, D and E are points on BC such that BE = CD (see figure) Show that AD = AE
View SolutionIn the given figure, `AB||DC and AD||BC` show that `DeltaABC ~= Delta CDA`.

View SolutionAB is a line - segment. P and Q are points on either side of AB such that each of them is equidistant from the points A and B (See Fig ). Show that the line PQ is the perpendicular bisector of AB.
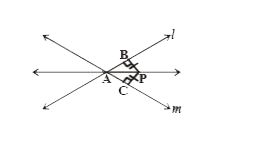
View SolutionP is a point equidistant from two lines l and m intersecting at point A (see figure). Show that the line AP bisects the angle between them.
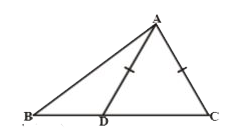
View SolutionD is a point on side BC ΔABC such that AD = AC (see figure). Show that AB > AD.
View Solution
EXAMPLES questions and complete solutions for chapter TRIANGLES of NCERT MATHEMATICS(GUJRATI ENGLISH) of Class 9