Complete Solutions to उदाहरण of chapter त्रिभुज of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | त्रिभुज |
| NCERT HINDI | उदाहरण |
| Number Of Questions | 9 |
| Academic Year | 2023-24 |
आकृति में OA = OB और OD = OC है। दर्शाइए कि
(i) `Delta AOD ~= Delta BOC ` और (ii) AD || BC है।
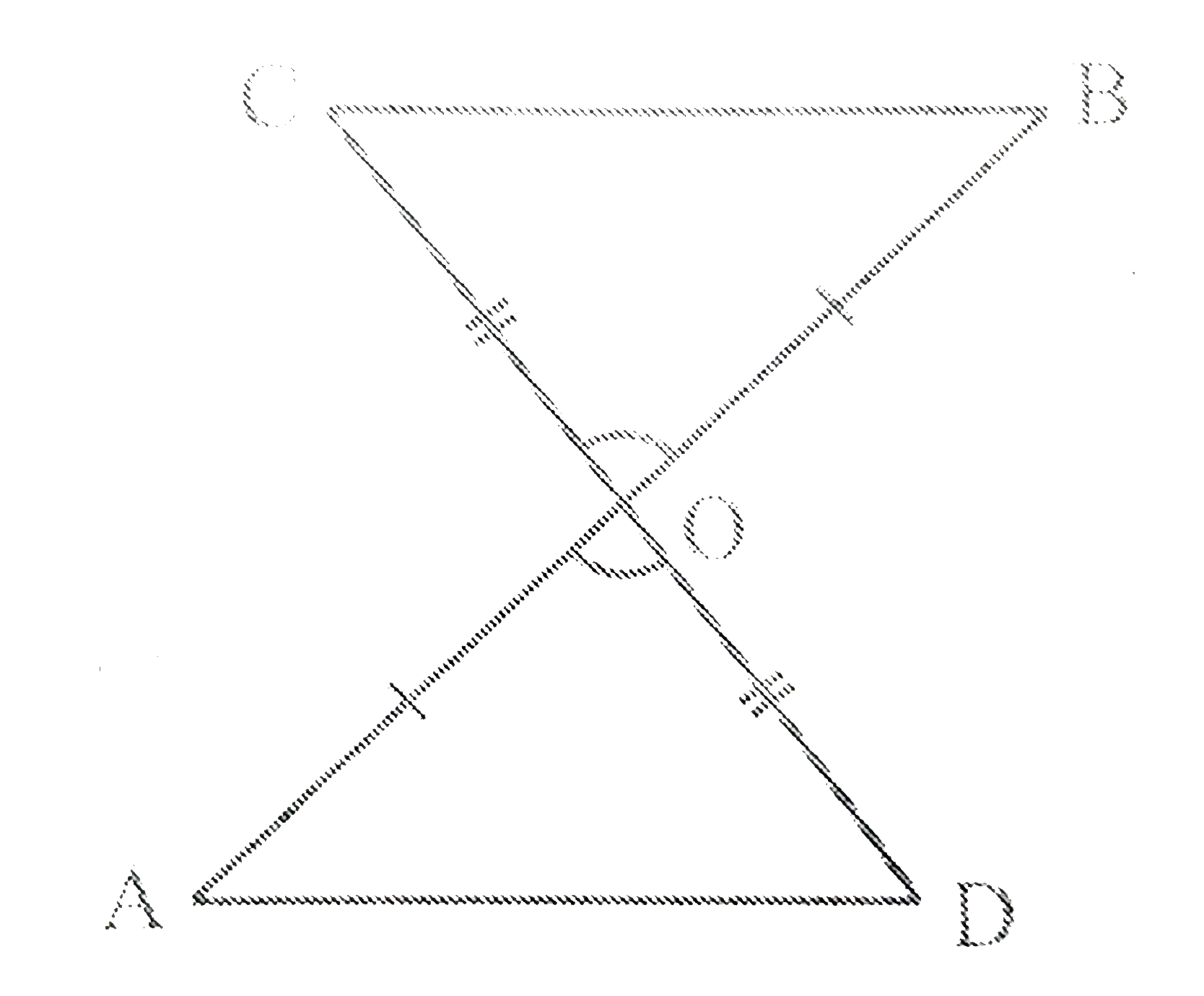
View SolutionAB एक रेखाखंड है और रेखा `l` इसका लम्ब समद्विभाजक है। यदि `l` पर स्थित P कोई बिंदु है, तो दर्शाइए कि P बिंदुओं A और B से समदूरस्थ (equidistant) है।
View Solutionरेखाखंड AB एक अन्य रेखाखंड CD के समांतर है और O रेखाखंड AD का मध्य-बिंदु है। दर्शाइए कि (i) `Delta AOB ~= Delta DOC` (ii) O रेखाखंड BC का भी मध्य-बिंदु है।
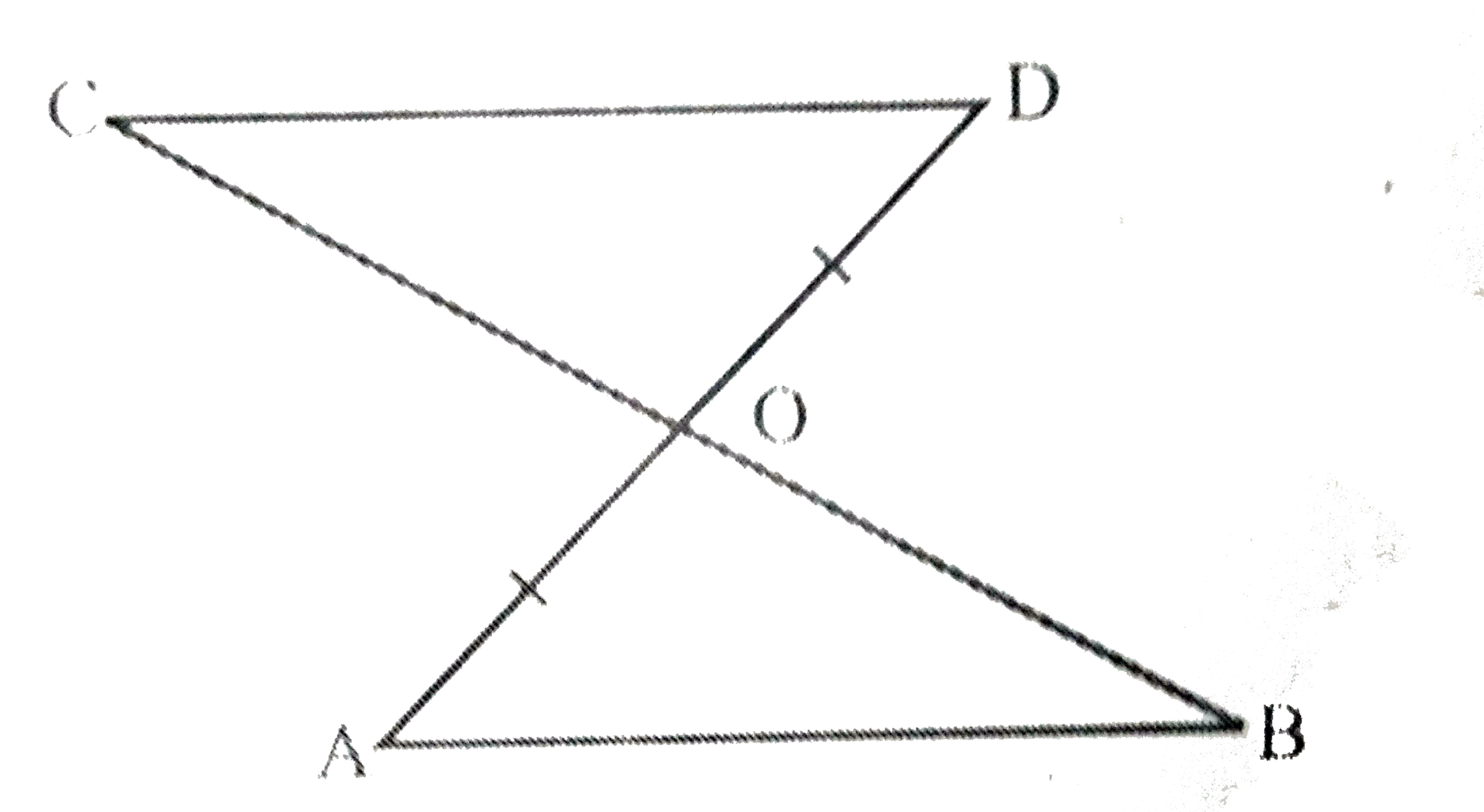
View Solution`Delta ABC` में, `angle A` का समद्विभाजक AD भुजा BC पर लम्ब है। दर्शाइए कि AB = AC है और `Delta ABC` समद्विबाहु है।
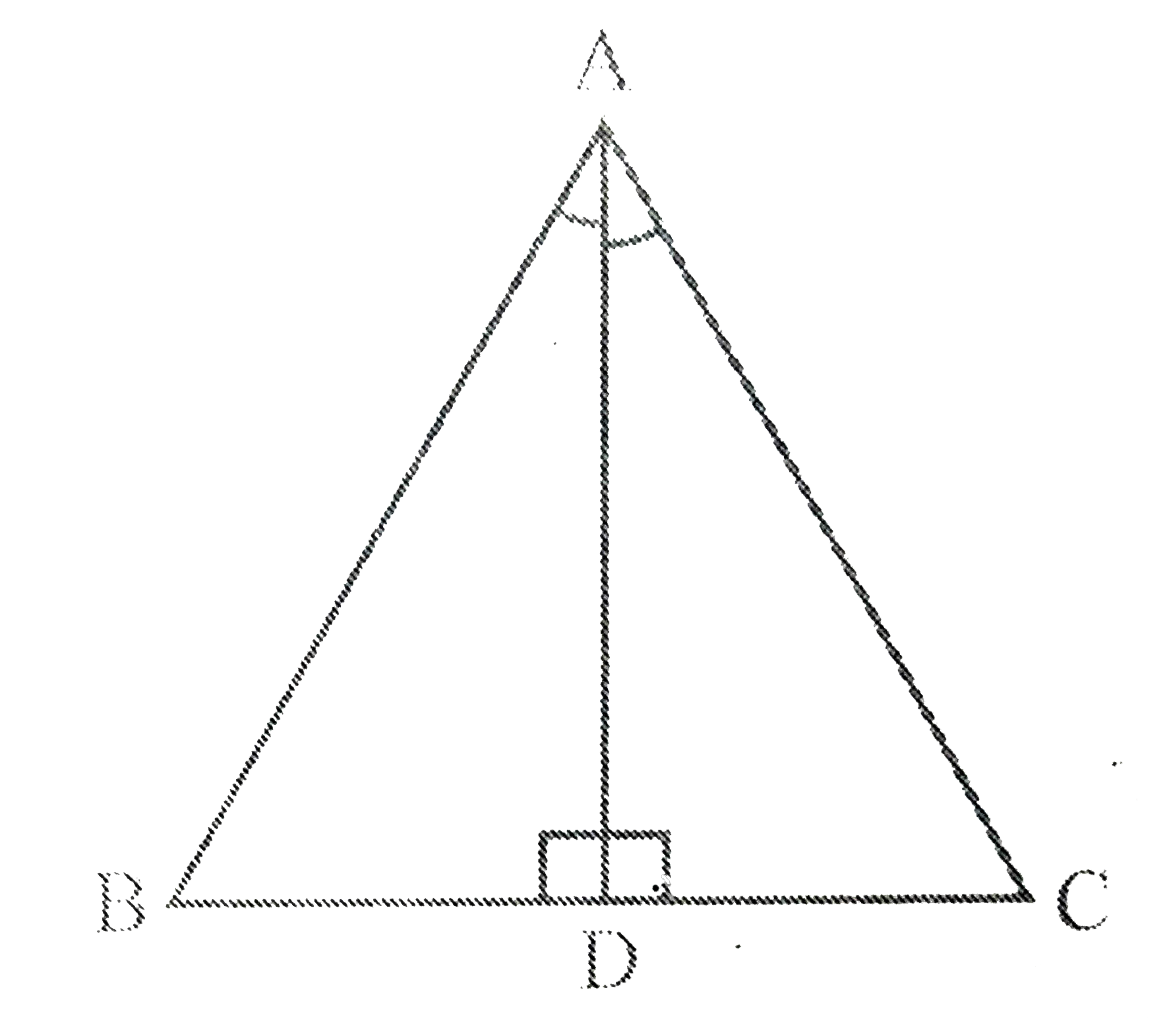
View SolutionE और F क्रमशः त्रिभुज ABC की बराबर भुजाओं AB और AC के मध्य-बिंदु हैं। दर्शाइए कि BF = CE है।
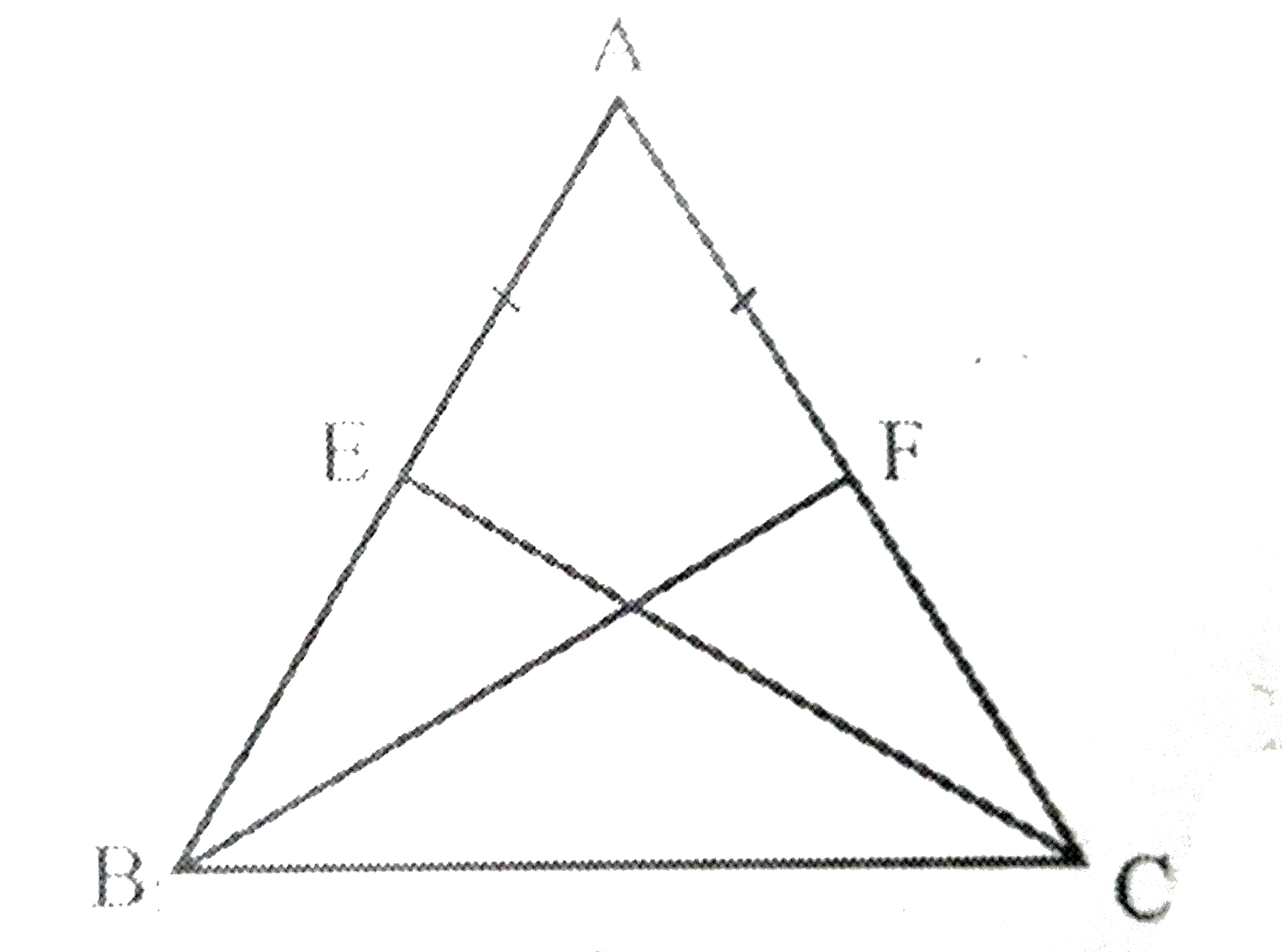
View Solutionएक समद्विबाहु त्रिभुज ABC जिसमें AB = AC है, की भुजा BC पर दो बिंदु D और E इस प्रकार हैं कि BE = CD है। दर्शाइए कि AD = AE है।

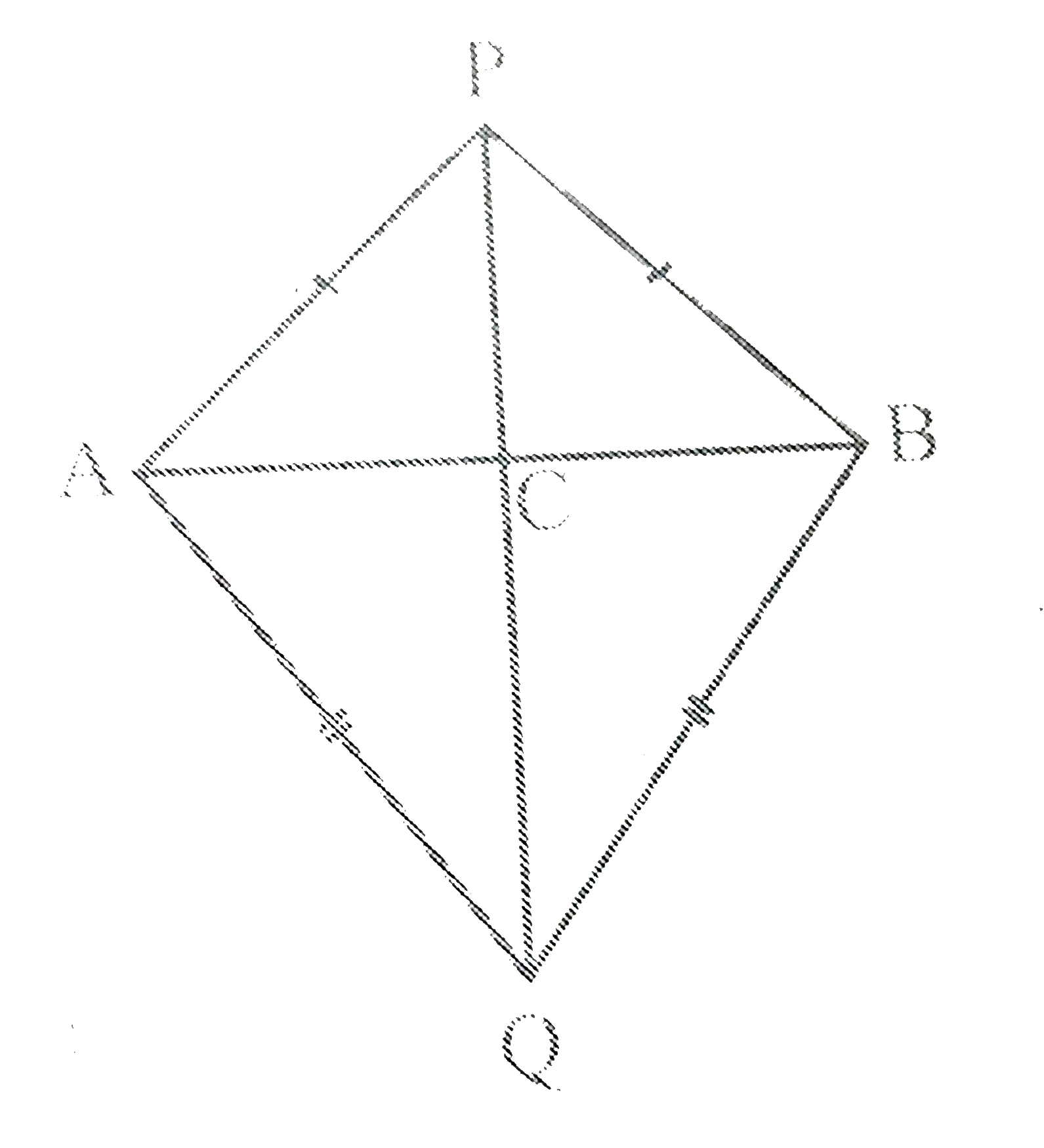
View SolutionAB एक रेखाखंड है तथा बिंदु P और Q इस रेखाखंड AB के विपरीत ओर इस प्रकार स्थित हैं कि इनमें से प्रत्येक A और B से समदूरस्थ है। दर्शाइए कि रेखा PQ रेखाखंड AB का लम्ब समद्विभाजक है।
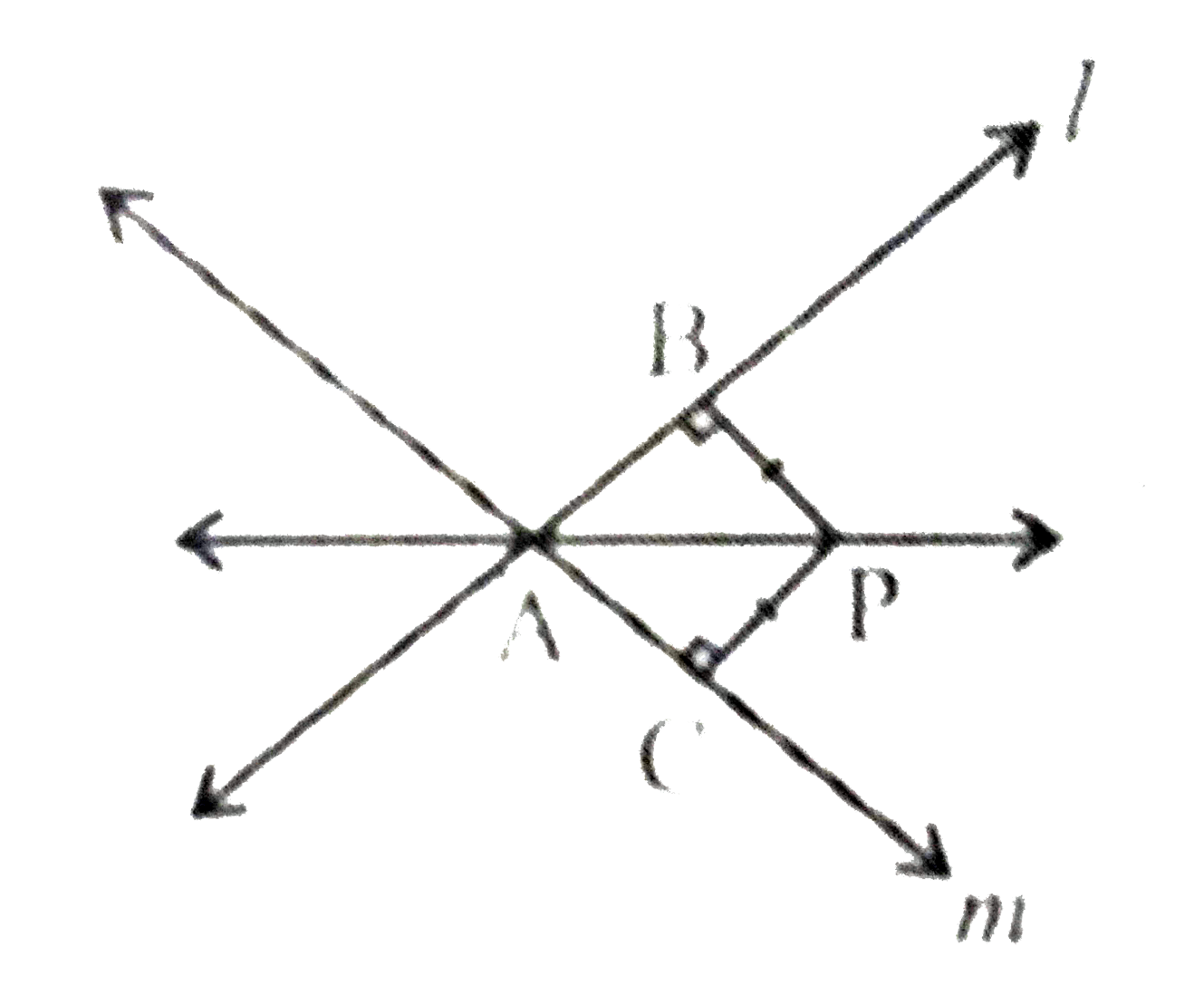
View Solutionबिंदु A पर प्रतिच्छेद करने वाली दो रेखाओं `l ` और m से समदूरस्थ एक बिंदु P है। दर्शाइए कि रेखा AP दोनों रेखाओं के बीच के कोण को समद्विभाजित करती है।
View Solution`Delta ABC` की भुजा BC पर D एक ऐसा बिंदु है कि AD = AC है। दर्शाइए कि `AB gt AD ` है।
View Solution
उदाहरण questions and complete solutions for chapter त्रिभुज of NCERT गणित(HINDI) of Class 9