Complete Solutions to प्रश्नावली 9.3 of chapter समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल |
| NCERT HINDI | प्रश्नावली 9.3 |
| Number Of Questions | 16 |
| Academic Year | 2023-24 |
आकृति में, `Delta ABC ` की एक मध्यिका AD पर स्थित E कोई बिंदु है दर्शाइए कि `ar (ABE)=ar (ACE)` है।
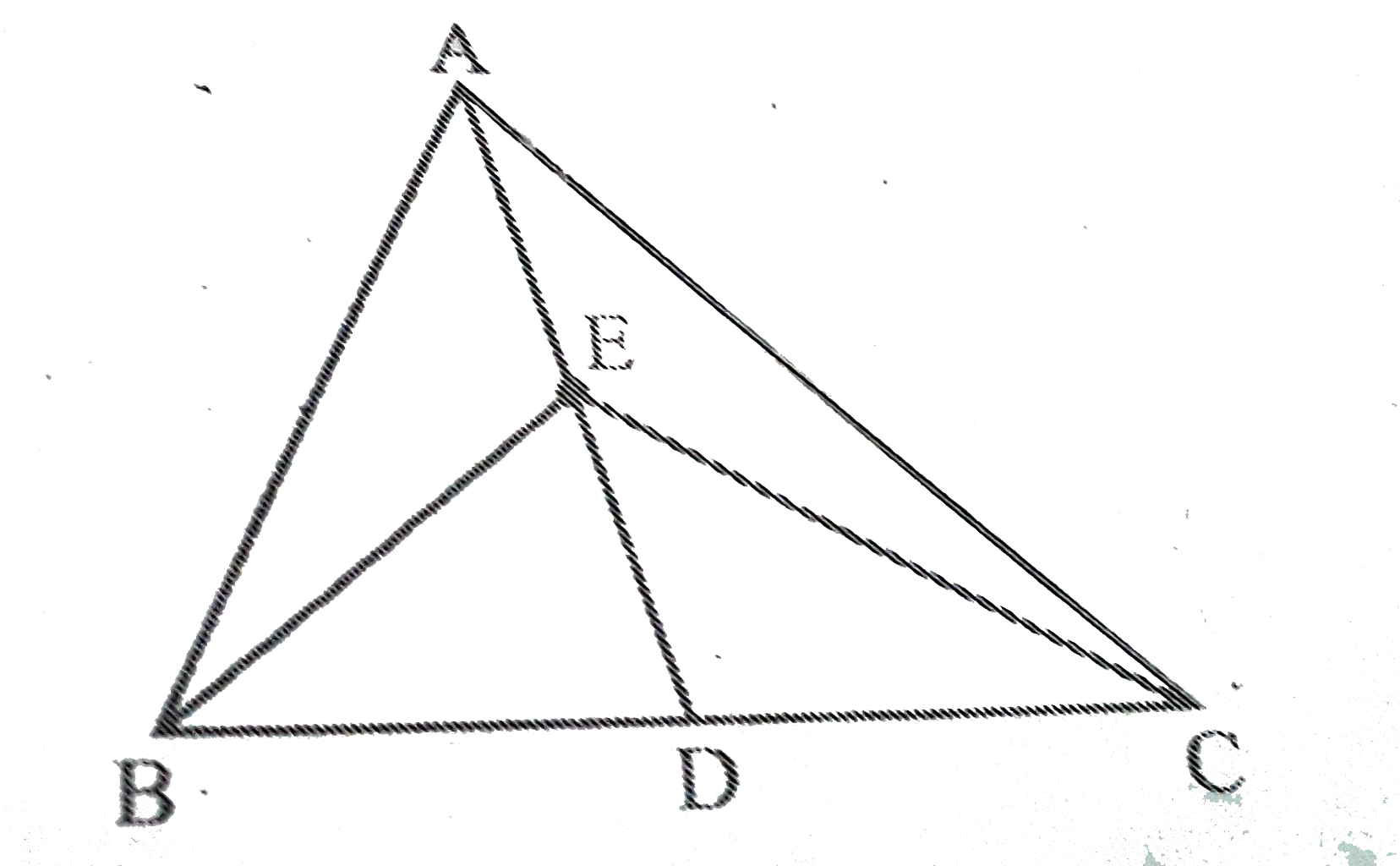
View Solution`Delta ABC` में, E मध्यिका AD का मध्य - बिंदु है । दर्शाइए कि `ar (BED) =(1)/(4) ar (ABC) ` है।
View Solutionदर्शाइए कि समांतर चतुर्भुज के दोनों विकर्ण उसे बराबर क्षेत्रफलो वाले चार त्रिभुजों के बाँटते है ।
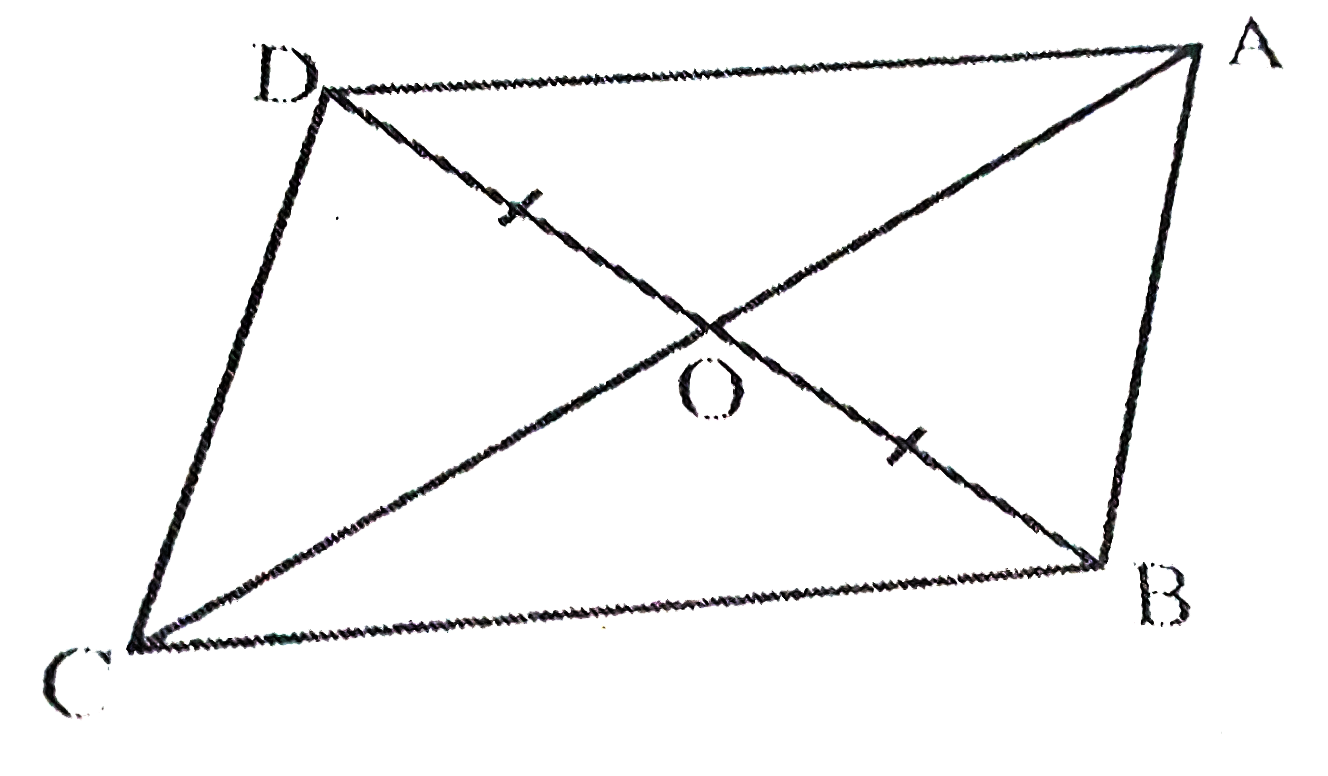
View Solutionआकृति में, ABC और ABD एक ही आधार AB पर बने दो त्रिभुज है यदि रेखाखड़ CD रेखाखड़ AB से बिंदु O पर समद्विभाजित होता है , तो दर्शाइए कि `ar (ABC)=ar (ABD) ` है
View SolutionD, E, और F क्रमश : त्रिभुज ABC की भुजाओ BC, CA और AB के मध्य - बिंदु है । दर्शाइए कि
(i) `BDEF` एक समांतर चतुर्भुज है (ii) `ar (DEF)=(1)/(4) ar (ABC)`
(iii) `ar (BDEF)=(1)/(2)ar(ABC)`
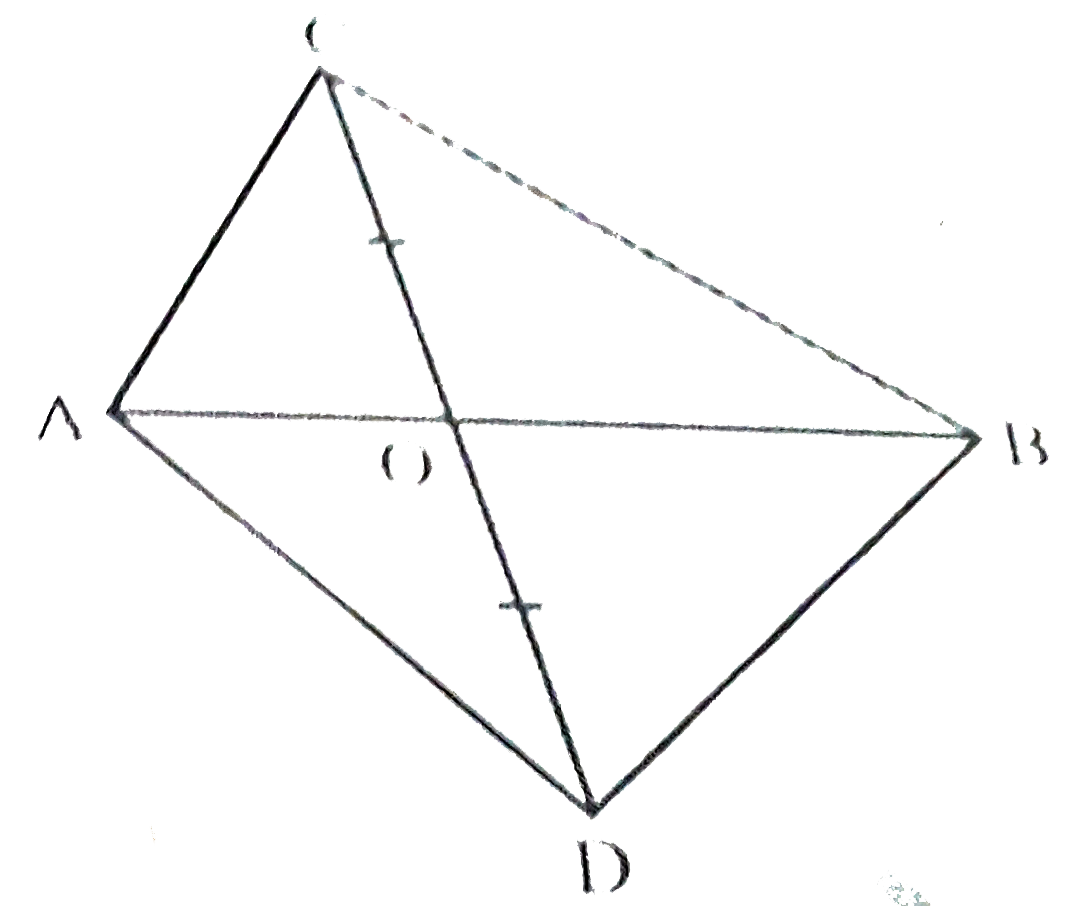
View Solutionआकृति में चतुर्भुज ABCD के विकर्ण AC और BD परस्पर बिंदु O पर इस प्रकार प्रतिच्छेद करते हैं कि `OB =OD` है । यदि `AB =CD` है , तो दर्शाइए कि
(i) `ar (DOC) =ar (AOB)`
(ii) `ar(DCB) = ar(ACB)`
(iii) `DA||CB ` या `ABCD` एक समांतर चतुर्भुज है ।
View Solutionबिंदु D और E क्रमश : `Delta ABC ` की भुजाओ AB और AC पर इस प्रकार स्थित है कि `ar(DBC)=ar (EBC)` है । दर्शाइए कि `DE ।। BC ` है ।
View SolutionXY त्रिभुज ABC कि भुजा BC समांतर एक रेखा है । यदि BE ।। AC और CF ।। AB रेखा XY से क्रमश : E और F पर मिलती है , तो दर्शाइए कि :
`ar (ABE )=ar (ACF)`
View Solutionसमांतर चतुर्भुज ABCD की एक भुजा AB को एक बिंदु P तक बढ़ाया गया है । A से होकर CP के समांतर खींची गई रेखा बढ़ाई गई CB को Q पर मिलती है और फिर समांतर चतुर्भुज PBQR को पूरा किया गया है ( देखिए आक्रति 9.26 )| दर्शाइए कि
`ar (ABCD)=ar(PBQR)` है |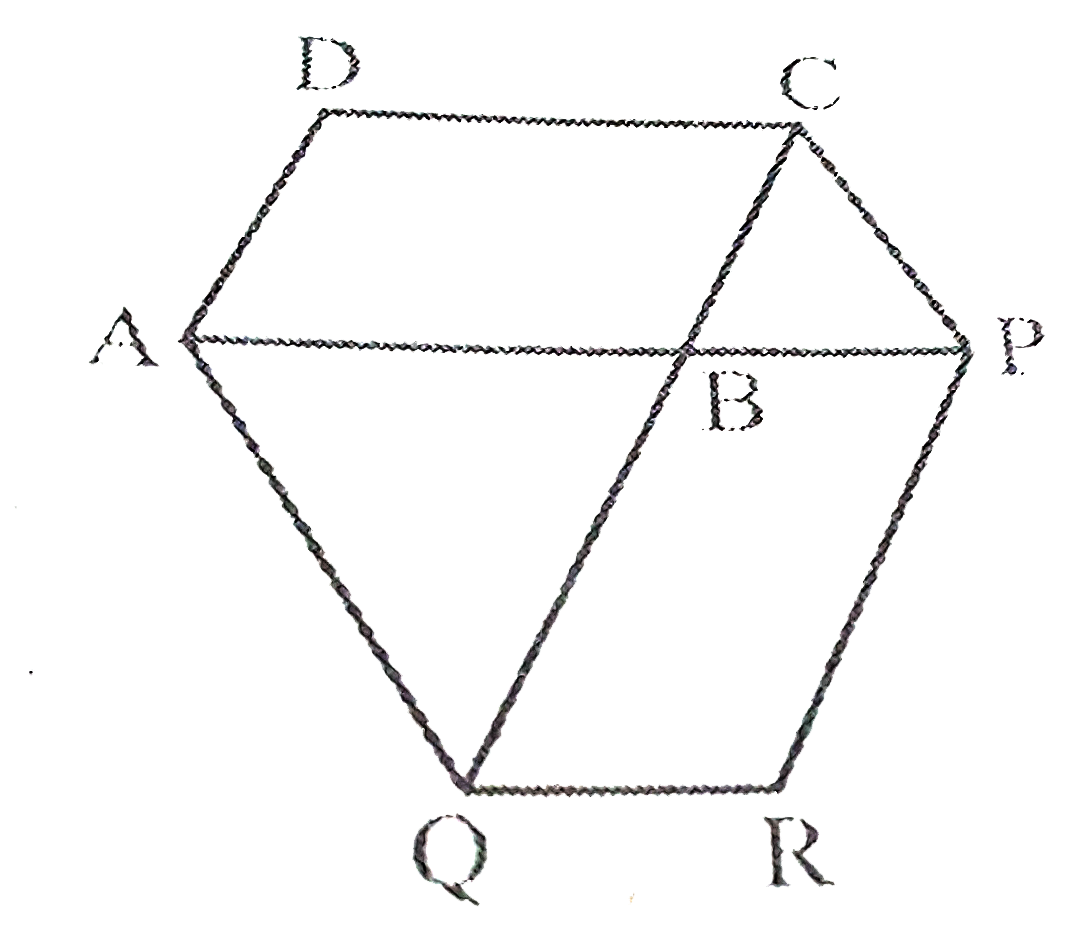
View Solutionएक समलंब ABCD , जिसमें AB ।। DC है , के विकर्ण AC और BD परस्पर O पर प्रतिच्छेद करते है । दर्शाइए कि `ar (AOD) = ar(BOC)` है
View Solutionआकृति में ABCDE एक पंचभुज है । B से होकर AC के समांतर खींची गई रेखा बढ़ाई गई DC को F पर मिलती है दर्शाइए कि
`(i) ar (ACB)=ar(ACF)`
`(ii) ar=(AEDF) =ar(ABCDF)`
View Solutionगाँव के एक निवासी इतवारी के पास एक चतुर्भुजाकार भूखंड था । उस गाँव कि ग्राम पंचायत ने उसके भूखंड के एक कोने से उसका कुछ भाग लेने का निर्णय लिया ताकि वहाँ एक स्वास्थ्य केंद्र का निर्माण कराया जा सके । इतवारी इस प्रस्ताव को इस प्रतिबन्ध के साथ स्वीकार कर लेता है कि उसे इस भाग के बदले उसी भूखंड के भूखंड के संलग्न एक भाग ऐसा दे दिया जाए कि उसका भूखंड त्रिभुजाकार हो जाए । स्पष्ट कीजिए कि इस प्रस्ताव को किस प्रकार कार्यान्वित किया जा सकता है ।
View Solution`ABCD` एक समलंब है , जिसमें `AB ।। DC` है ` AC` के समांतर एक रेखा `AB` को `X` पर और `BC` को `Y` पर प्रतिच्छेद करती है सिद्ध कीजिए कि `ar(ADX)=ar(ACY)` है।
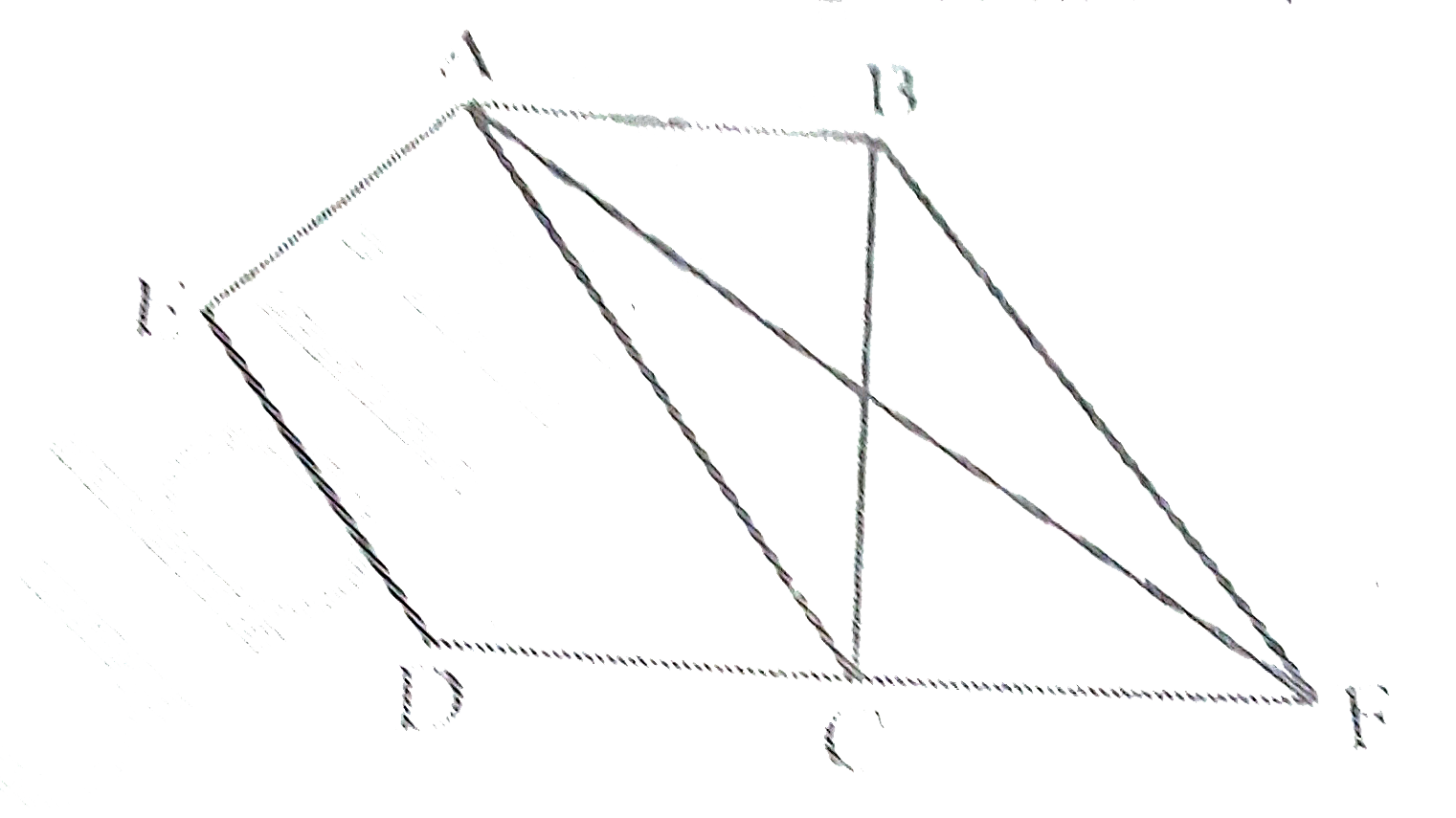
View Solutionआकृति में, `AP ।। BQ ।।CR` है । सिद्ध कीजिए कि `ar (AQC)=ar(PBR)`है ।

View Solutionचतुर्भुज ACBD के विकर्ण AC और BD परस्पर बिंदु O पर इस प्रकार प्रतिच्छेद करते है कि `ar(AOD)=ar(BOC)` है सिद्ध कीजिए कि ABCD एक समलंब है
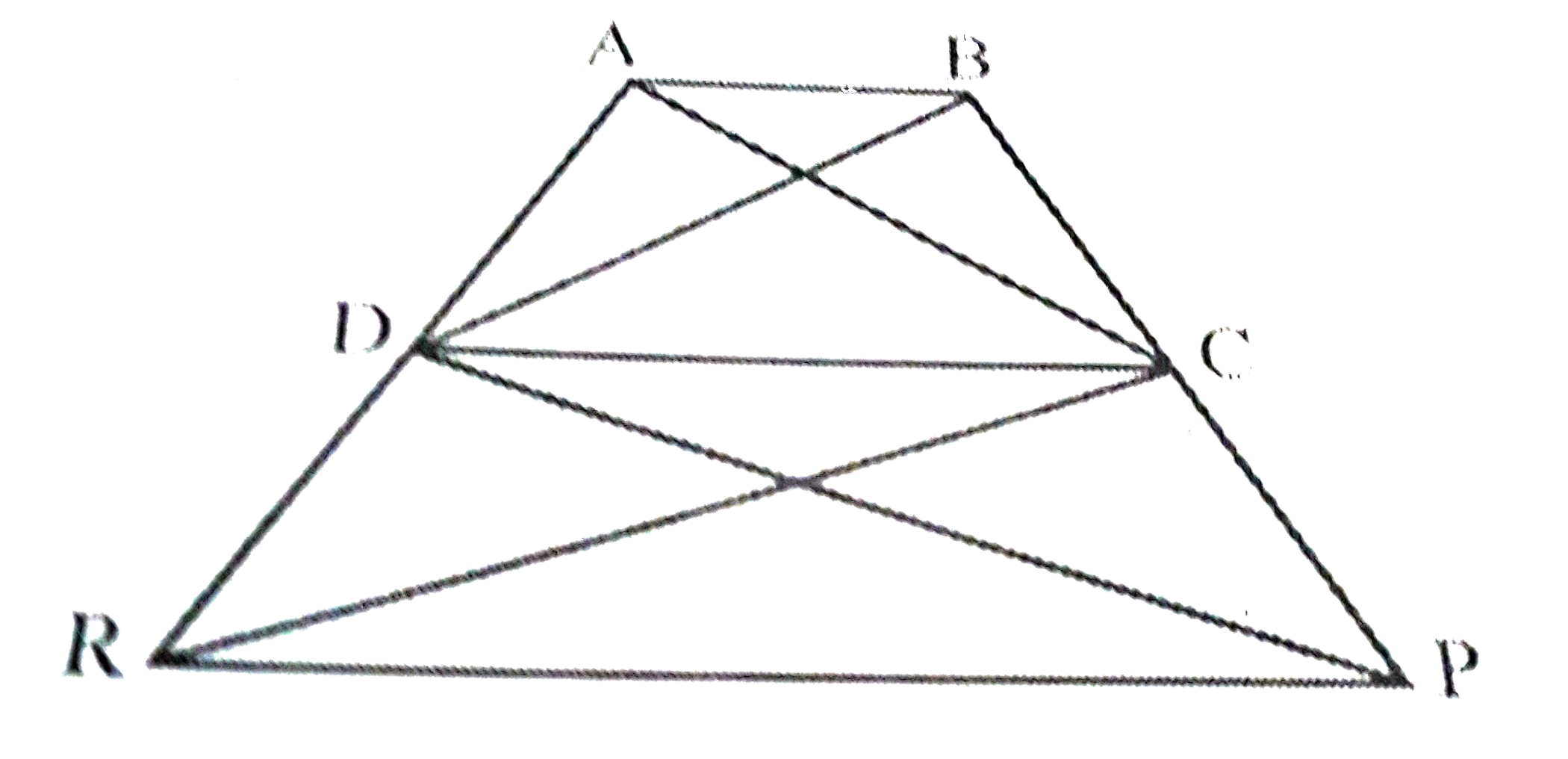
View Solutionआकृति में `ar(DRC)=ar(DPC)` है और `ar(BDP)=ar(ARC)` है । दर्शाइए की दोनों चतुर्भुज ABCD और DCPR समलंब है ।
View Solution
प्रश्नावली 9.3 questions and complete solutions for chapter समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल of NCERT गणित(HINDI) of Class 9