Complete Solutions to एनo सीo ईo आरo टीo प्रश्न प्रश्नावली 1.2 of chapter संख्या पद्धति of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | संख्या पद्धति |
| MADHUR GUPTA | एनo सीo ईo आरo टीo प्रश्न प्रश्नावली 1.2 |
| Number Of Questions | 4 |
| Academic Year | 2023-24 |
नीचे दिए गए कथन सत्य हैं या असत्य हैं ? कारण के साथ होने उत्तर दीजिए ।
(i) प्रत्येक अपरिमेय संख्या एक वास्तविक संख्या होती है
(ii) संख्या रेखा का प्रत्येक बिंदु `sqrt(m)` के रूप में होता है, जहाँ m एक प्राकृत संख्या है।
(iii) प्रत्येक वास्तविक संख्या का एक अपरिमेय संख्या होती है ।
View Solutionक्या सभी धनात्मक पूर्णांकों के वर्गमूल अपरिमेय होते हैं यदि नहीं , तो एक ऐसी संख्या के वर्गमूल का उदाहरण दीजिए जो एक परिमेय संख्या है ।
View Solutionदिखाइए कि संख्या रेखा पर `sqrt(5)` को किस प्रकार निरूपित किया जा सकता है।
View Solutionकक्षा के लिए क्रियाकलाप (वर्गमूल सर्पिल कि रचना) कागज कि एक बड़ी शीट लीजिए और नीचे दी गई विधि से "वर्गमूल सर्पिल" (square sheet spiral) कि रचना कीजिए । सबसे पहले एक बिंदु O लीजिए और एकक लम्बाई का रेखाखण्ड (line segment) `OP_(1)` खींचिए । एकक लम्बाई वाले `OP_(1)` पर लम्ब रेखाखण्ड `P_(1)P_(2)` खींचिए (देखिए आकृति) । अब `OP_(2)`पर लम्ब रेखाखण्ड `P_(2)P_(3)` खींचिए । तब `OP_(3)` पर लम्ब `P_(3)P_(4)` रेखाखण्ड खींचिए । इस प्रक्रिया को जारी रखते हुए `OP_(n-1)`पर एकक लम्बाई वाला लम्ब रेखाखण्ड खींचकर आप रेखाखण्ड `P_(n-1)P_(n)` प्राप्त कर सकते हैं । इस प्रकार आप बिंदु `O, P_(1),P_(2),P_(3),".....",P_(n),"...."` प्राप्त कर लेंगे और उन्हें मिलाकर `sqrt(2),sqrt(3),sqrt(4),"...."` को दर्शाने वाला एक सुंदर सर्पिल प्राप्त कर लेंगे ।
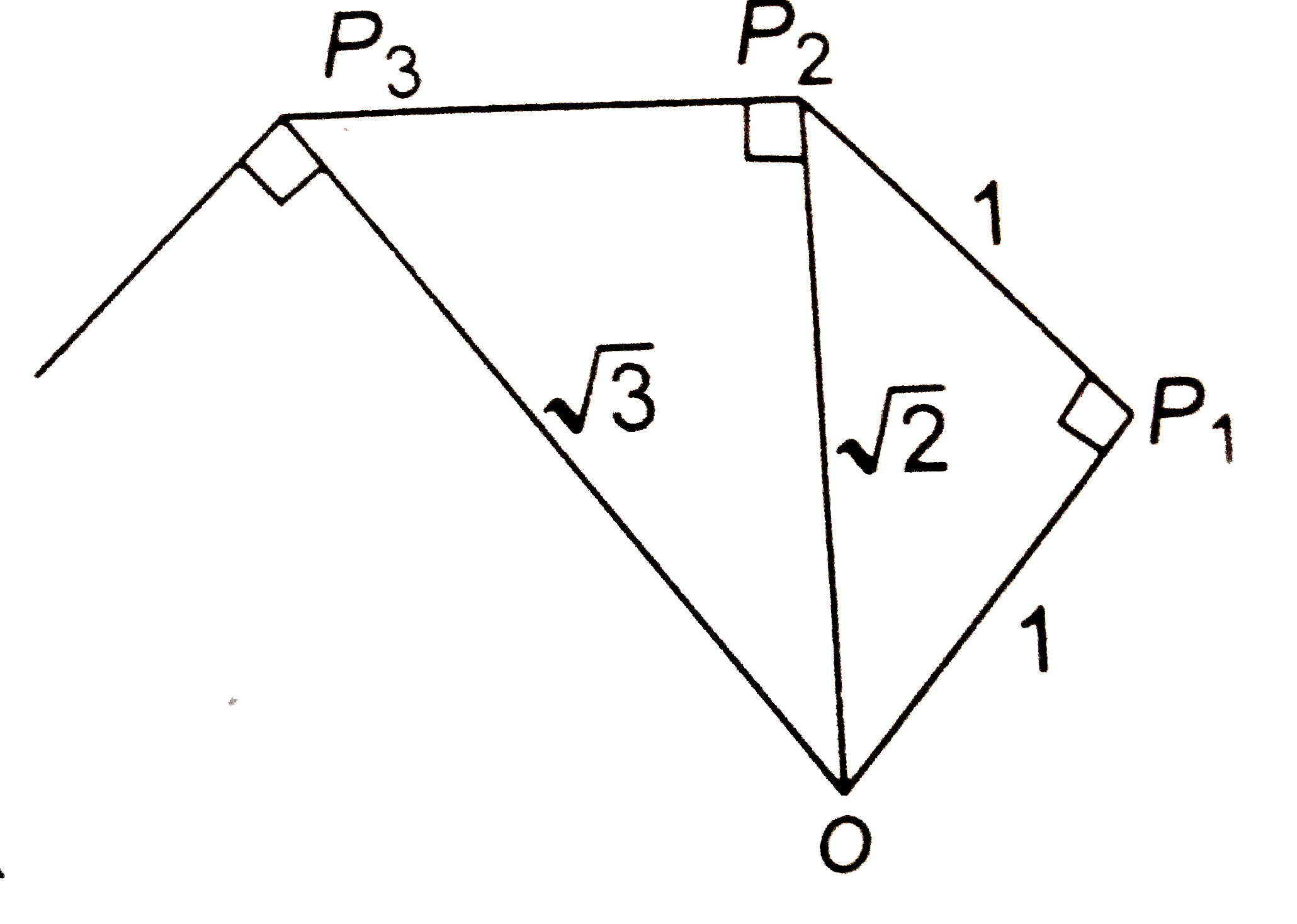
View Solution
एनo सीo ईo आरo टीo प्रश्न प्रश्नावली 1.2 questions and complete solutions for chapter संख्या पद्धति of NAGEEN MATHS (HINDI) of Class 9
All Exercises from MADHUR GUPTA Class 9 MATHS संख्या पद्धति
- उदाहरण
- एनo सीo ईo आरo टीo प्रश्न प्रश्नावली 1.1
- एनo सीo ईo आरo टीo प्रश्न प्रश्नावली 1.2
- एनo सीo ईo आरo टीo प्रश्न प्रश्नावली 1.3
- एनo सीo ईo आरo टीo प्रश्न प्रश्नावली 1.4
- एनo सीo ईo आरo टीo प्रश्न प्रश्नावली 1.5
- एनo सीo ईo आरo टीo प्रश्न प्रश्नावली 1.6
- प्रश्नावली 1A
- प्रश्नावली 1B
- प्रश्नावली 1C
- प्रश्नावली 1D
- प्रश्नावली 1E
- विविध प्रश्नावली (अतिलघु उत्तरीय प्रश्न)
- विविध प्रश्नावली (लघु उत्तरीय प्रश्न)
- साधित उदाहरण