Complete Solutions to EXERCISE of chapter LINES AND ANGLES of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | LINES AND ANGLES |
| PSEB | EXERCISE |
| Number Of Questions | 18 |
| Academic Year | 2023-24 |
In Fig.
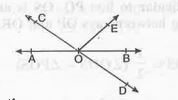 , lines AB and CD intersect at O. If `angleAOC+angleBOE=70^@` and `angleBOD = 40^@`, find `angleBOE` and reflex `angleCOE`.
, lines AB and CD intersect at O. If `angleAOC+angleBOE=70^@` and `angleBOD = 40^@`, find `angleBOE` and reflex `angleCOE`.
View SolutionIn Fig.
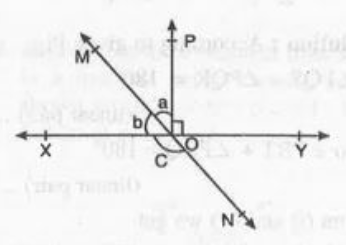 , lines XY and MN intersect at O. If `anglePOY = 90^@` and `a : b = 2 : 3`, find C.
, lines XY and MN intersect at O. If `anglePOY = 90^@` and `a : b = 2 : 3`, find C.
View SolutionIn Fig. 6.15, `angle PQR = angle PRQ`, then prove that `angle PQS = angle PRT`.

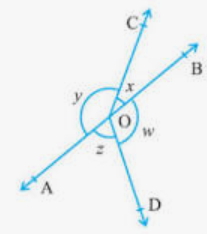
View SolutionIn Fig. 6.16, if` x + y = w + z`, then prove that AOB is a line.
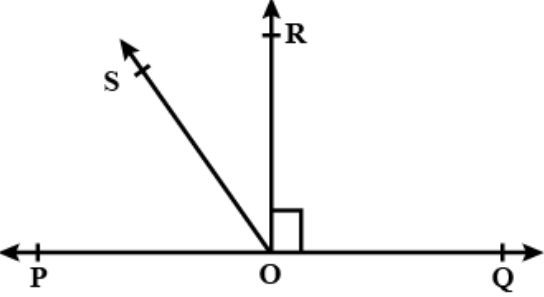
View SolutionIn Fig. 6.17, POQ is a line. Ray OR is perpendicular to line PQ. OS is another ray lying between rays OP and OR. Prove that `angle ROS=1/2 (angle QOS-angle POS)`.
View SolutionIn fig.
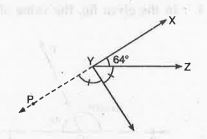 `angleXYZ = 64^@` and XY is produced to point P. If ray YQ bisect `angleZYP` then the value of `angleXYQ` is :
`angleXYZ = 64^@` and XY is produced to point P. If ray YQ bisect `angleZYP` then the value of `angleXYQ` is :
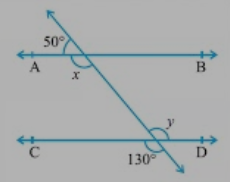
View SolutionIn Fig. 6.28, find the values of x and y and then show that `AB|| CD`.
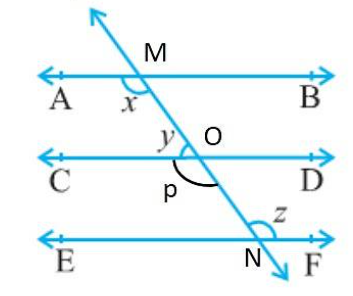
View SolutionIn Fig. 6.29, if AB || CD, CD || EF and y : z = 3 : 7, find x.
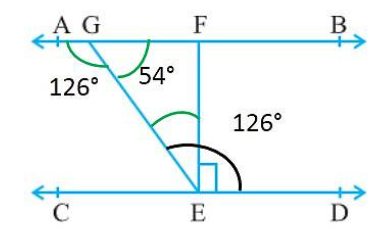
View SolutionIn Fig. 6.30, if AB || CD, `EF bot CD` and `angle GED = 126^@`, find `angle AGE, angle GEF` and `angle FGE`.
View SolutionIn Fig. 6.31, if PQ || ST, `angle PQR = 110^@` and `angle RST = 130^@`, find `angle QRS`. [Hint : Draw a line parallel to ST through point R.]

View SolutionIn Fig. 6.32, if AB || CD, `angle APQ = 50^@` and `angle PRD = 127^@`, find x and y.
View SolutionIn Fig. 6.33, PQ and RS are two mirrors placed parallel to each other. An incident ray AB strikes the mirror PQ at B, the reflected ray moves along the path BC and strikes the mirror RS at C and again reflects back along CD. Prove that AB || CD.

View SolutionIn the given fig.
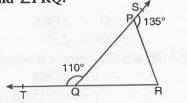 , sides QP and RQ of `DeltaPQR` aer produced to points S and T respectively. If `angleSPR = 135^@` and `anglePQT = 110^@`, find `anglePRQ`.
, sides QP and RQ of `DeltaPQR` aer produced to points S and T respectively. If `angleSPR = 135^@` and `anglePQT = 110^@`, find `anglePRQ`.
View SolutionIn the given fig.
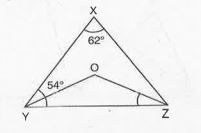 `angleX = 62^@`, `angleXYZ = 54^@`. If YO and ZO are the bisectors of `angleXYZ` and `angleXZY` respectively of `DeltaXYZ`, find `angleOZY` and `angleYOZ`.
`angleX = 62^@`, `angleXYZ = 54^@`. If YO and ZO are the bisectors of `angleXYZ` and `angleXZY` respectively of `DeltaXYZ`, find `angleOZY` and `angleYOZ`.
View SolutionIn Fig. 6.41, if AB || DE, `angle BAC = 35^@` and `angle CDE = 53^@`, find `angle DCE`.

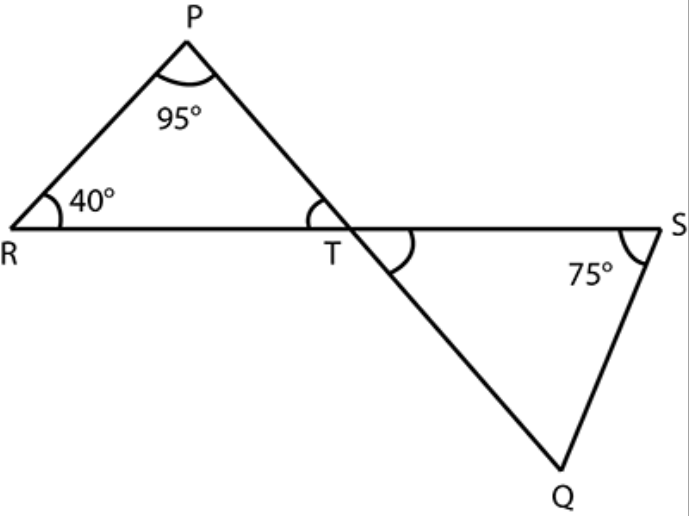
View SolutionIn Fig. 6.42, if lines PQ and RS intersect at point T, such that `angle PRT = 40^@, angle RPT = 95^@ and angle TSQ = 75^@`, find `angle SQT`.
View SolutionIn Fig. 6.43, if `PQ bot PS`, PQ || SR, `angle SQR = 28^@` and `angle QRT = 65^@`, then find the values of x and y.
View SolutionIn Fig. 6.44, the side QR of `triangle PQR` is produced to a point S. If the bisectors of `angle PQR` and `angle PRS` meet at point T, then prove that `angle QTR =1/2 angle QPR`.
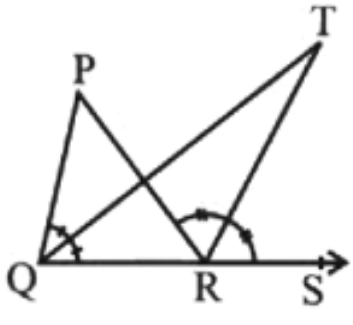
View Solution
EXERCISE questions and complete solutions for chapter LINES AND ANGLES of PSEB of Class 9