Complete Solutions to EXERCISE of chapter CIRCLES of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | CIRCLES |
| PSEB | EXERCISE |
| Number Of Questions | 45 |
| Academic Year | 2023-24 |
The centre of a circle lies in .............. of the circle.
00:42View SolutionA point, whose distance from the centre of a circle is greater than its radius lies in .................. Of the circle.
01:11View SolutionThe longest chord of a circle is a ........... of the circle.
01:11View SolutionAn arc is a ........... When its ends are the ends of a diameter.
01:13View SolutionSegment of a circle is the region between an arc and ........... of the circle.
01:22View SolutionA circle divides the plane, on which it lies, in ............. parts.
00:56View Solution(True/ False) Line segment joining the centre to any point on the circle is a radius of the circle.
01:46View Solution(True/ False) A circle has only finite number of equal chords.
01:34View Solution(True/ False) If a circle is divided into three equal arcs each is a major arc.
01:28View Solution(True/ False) A chord, which is twice as long as its radius is a diameter of the circle.
01:34View Solution(True/ False) Sector is the region between the chord and its corresponding arc.
02:15View Solution(True/ False) A circle is a plane figure.
01:33View SolutionRecall that two circles are congruent if they have the same radii. Prove that equal chords of congruent circles subtend equal angles at their centres.
01:46View SolutionProve that if chords of congruent circlessubtend equal angles at their centres, then the chords are equal.
05:03View SolutionDraw different pairs of circles. How many points does each pair have in common ? What is the maximum number of common points ?
03:02View SolutionSuppose you are given a circle. Give a construction to find its centre.
03:16View SolutionIf two circles intersect at two points, prove that their centres lie on the perpendicular bisector of the common chord.
05:49View SolutionTwo circles of radii 5 cm and 3 cm intersect at two points and the distance between their centres is 4 cm. Find the length of the common chord.
03:35View SolutionIf two equal chords of a circle intersect within the circle, prove that the segments of one chord are equal to corresponding segments of the other chord.
05:00View SolutionIf two equal chords of a circle intersect within the circle, prove that the line joining the point of intersection to the centre makes equal angles with the chord.
01:56View SolutionIf a line intersects two concentric circles (circles with the same centre) with centre O at A, B, C and D, prove that AB = CD
03:53View SolutionThree girls Reshma, Salma and Mandip are standing on a circle of radius 5 m drawn in a park. Reshma throws a ball to Salma, Salma to Mandip, Mandip to Reshma. If the distance between Reshma and Salma and between Salma and Mandip is 6 m each, what is the distance between Reshma and Mandip ?
04:04View SolutionA circular park of radius 20 m is situated in a colony. Three boys Ankur, Syed and David are sitting at equal distance on its boundary each having a toy telephone in his hands to talk each other. Find the length of the string of each phone.
04:32View SolutionIn the given figure, A,B and C are three points on a circle with centre O such that `angle BOC = 30^@` and `angle AOB = 60^@`. If D is a point on the circle other than the arc ABC, find `angle ADC`.
04:40View SolutionA chord of a circle is equal to the radius of the circle. Find the angle subtended by the chord on a point on the minor arc and also at a point on the major arc.
02:59View SolutionIn the given figure, `angle PQR = 100^@`, where P, Q and R are points on a circle with centre O. Find `angle OPR`.
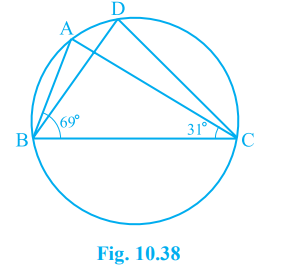
06:41View SolutionIn Fig. 10.38, `angle ABC = 69^@`, `angle ACB = 31^@`, find `angle BDC`.
 02:01View Solution
02:01View SolutionIn fig.
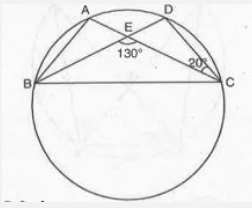 , A, B, C, D are four points on a circle. AC and BD intersect at a point E such that `/_BEC = 130^@` and `/_ECD = 20^@`. Find `/_BAC`.05:57View Solution
, A, B, C, D are four points on a circle. AC and BD intersect at a point E such that `/_BEC = 130^@` and `/_ECD = 20^@`. Find `/_BAC`.05:57View SolutionABCD is a cyclic quadrilateral whose diagonals intersect at a point E. `/_DBC = 70^@`, `/_BAC is 30^@`, find `/_BCD`. Futher, if AB = BC, find `/_ECD`.
03:56View SolutionIf diagonals of a cyclic quadrilateral are diameters of the circle through the vertices of the quadrilateral, prove that it is a rectangle.
03:35View SolutionIf the non-parallel sides of a trapezium are equal, prove that it is cyclic.
03:56View SolutionTwo circles intersect at two points B and C. Through B, two line segments ABD and PBQ are drawn to intersect the circles at A, D, P, Q respectively (see fig.
 ). Prove that `/_ACP = /_QCD`.01:36View Solution
). Prove that `/_ACP = /_QCD`.01:36View SolutionIf circles are drawn taking two sides of a triangle as diameters, prove that the point of intersection of these circles lie on the third side.
04:18View SolutionABC and ADC are two right triangles with common hypotenuse AC. Prove that `/_CAD = `/_CBD`.
05:40View SolutionProve that a cyclic parallelogram is a rectangle.
03:19View SolutionProve that the line of centres of two intersecting circles subtends equal angles at the two points of intersection.
01:42View SolutionTwo chords AB and CD of lengths 5 cm and 11 cm respectively of a circle are parallel to each other and are on opposite sides of its centre. If the distance between AB and CD is 6 cm, find the radius of the circle.
10:55View SolutionThe lengths of two parallel chords of a circle are 6 cm and 8 cm. If the smaller chord is at a distance of 4 cm from the centre, what is the distance of the other chord from the centre ?
04:10View SolutionLet vertex of an angle ABC be located outside a circle and let the sides of the angle intersect chords AD and CE with the circle. Prove that `/_ABC` is equal to half the difference of the angles subtended by the chords AC and DE at the centre.
07:22View SolutionProve that the circle drawn with any side of a rhombus as diameter, passes through the point of intersection of its diagonals.
02:19View SolutionABCD is a parallelogram. The circle through A, B and C intersect CD (produced if necessary) at E. Prove that AE = AD.
05:49View SolutionAC and BD are chords of a circle which bisect each other. Prove that (i) AC and BD are diameters, (ii) ABCD is a rectangle.
06:53View SolutionBisectors of angles A, B and C of a triangle ABC intersect its circumcircle at D, E and F respectively. Prove that angles of the triangle are `90^@-A/2,90^@-B/2` and `90^@-C/2` respectively.
07:51View SolutionTwo congruent circles intersect each other at points A and B. Through A any line segment PAQ is drawn so that P, Q lie on the two circles. Prove that BP = BQ.
03:23View SolutionIn any triangle ABC, if the angle bisector of `/_A` and perpendicular bisector of BC intersect, prove that they intersect on the circumcircle of the triangle ABC.
13:05View Solution
EXERCISE questions and complete solutions for chapter CIRCLES of PSEB of Class 9
