Complete Solutions to प्रश्नावली 28.1 of chapter समतल आकृतियों का क्षेत्रफल of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | समतल आकृतियों का क्षेत्रफल |
| S CHAND | प्रश्नावली 28.1 |
| Number Of Questions | 35 |
| Academic Year | 2023-24 |
एक त्रिभुज का क्षेत्रफल ज्ञात करें, जिसके आधार का माप 10.5 सेमी और संगत ऊँचाई का माप 12.5 सेमी हो ।
View Solutionएक त्रिभुजाकार खेत का आधार, इसके शीर्षलम्ब का तीन गुना है यदि खेत को 58 रुपए प्रति हेक्टेयर की दर से बोने का खर्च 783 रुपए हो, तो इसकी आधार और ऊंचाई ज्ञात करें ।
View Solutionएक समकोण त्रिभुज का क्षेत्रफल ज्ञात करें, जिसके परिवृत्त की त्रिज्या का माप 8 सेमी और कर्ण पर खींचे गए शीर्षलम्ब का माप 6 सेमी है।
View Solutionएक समबाहु त्रिभुज की ऊँचाई 9 सेमी है । इसका क्षेत्रफल दशमलव के दो शुद्ध स्थानों तक ज्ञात करें। (`sqrt(3)=1.732` लें।)
View Solutionएक समबाहु त्रिभुज का क्षेत्रफल ज्ञात करें, जिसकी एक भुजा की माप 8 सेमी है । इसका शीर्षलम्ब क्या होगा?
View Solutionएक समबाहु त्रिभुज का परिमाप 12 मी है, तो इसका क्षेत्रफल और ऊँचाई ज्ञात करें ।
View Solutionएक समबाहु त्रिभुज की भुजा 9 सेमी है, तो इसका क्षेत्रफल और ऊँचाई ज्ञात करें।
View Solutionएक समबाहु त्रिभुज का क्षेत्रफल `36sqrt(3)"सेमी"^(2)` है, तो इसका परिमाप ज्ञात करें ।
View Solutionएक समबाहु त्रिभुज का क्षेत्रफल `81sqrt(3)"सेमी"^(2)` है, तो इसकी ऊँचाई ज्ञात करें ।
View Solutionएक समबाहु त्रिभुज का परिमाप, इसके क्षेत्रफल का `sqrt(3)` गुना है, तो इसके प्रत्येक भुजा की लम्बाई ज्ञात करें।
View Solutionएक समबाहु त्रिभुज के अभ्यान्तर में स्थित एक बिन्दु से, इसकी तीन भुजाओं, जिनकी लम्बाइयाँ 10 मी, 12 मी और 18 मी हे, पर लम्ब खीचें गए हैं । इस त्रिभुज का क्षेत्रफल ज्ञात करें ।
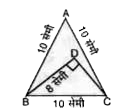
View Solutionदिए गए आकृति में, `DeltaABC` एक समबाहु त्रिभुज है, जिसके भुजा की लम्बाई 10 सेमी है और `DeltaABC` D पर समकोण है, और BD = 8 सेमी है, तो छायांकित भाग का क्षेत्रफल ज्ञात करें । (`sqrt(3)` = 1.732 लें।)
View Solutionएक त्रिभुज की भुजाएँ 15 सेमी, 14 सेमी तथा 13 सेमी हैं, तो इस त्रिभुज का क्षेत्रफल ज्ञात करें ।
View Solutionएक त्रिभुज, जिसकी भुजाएँ 18 सेमी. 24 सेमी और 30 सेमी लम्बी हैं, का क्षेत्रफल ज्ञात करें । साथ ही त्रिभुज की सबसे छोटी भुजा के संगत शीर्षलम्ब की लम्बाई भी ज्ञात करें ।
View Solutionएक त्रिभुज की भुजाएँ 10 सेमी, 24 सेमी और 26 सेमी हैं । इसका क्षेत्रफल और सबसे लम्बा शीर्षलम्ब ज्ञात करें ।
View Solutionएक त्रिभुज की भुजाओं की लम्बाईयां `3:4:5` के अनुपात में हैं और इसका परिमाप 144 सेमी है त्रिभुज का क्षेत्रफल तथा बड़ी की संगत ऊंचाई ज्ञात कीजिए।
View Solutionएक त्रिभुज का परिमाप 300 मी है और इसकी भुजाएँ 5 : 12 : 13 के अनुपात में हैं । इसका क्षेत्रफल ज्ञात करें ।
View Solutionकिसी त्रिभुजाकार मैदान की दो भुजाएं क्रमशः 85 मी एवं 154 मी है तथा इसकी परिमाप 324 मी है। (i) मैदान का क्षेत्रफल ज्ञात करें एवं (ii) सम्मुख शीर्ष से 154 मी लंबी भुजा पर डाले गए शीर्षलंब की लंबाई ज्ञात करें।
View Solutionएक त्रिभुजाकार खेत की भुजाएँ 165 सेमी, 143 सेमी और 154 सेमी हैं । इसे 12 पैसे प्रति वर्ग मी जर की दर से जोतने का खर्च निकालें ।
View Solutionएक समद्विबाहु त्रिभुज का क्षेत्रफल निकालें, जिसके बराबर भुजाओं में से एक का माप 'b' और तीसरी भजा का माप 'a' है।
View Solutionएक समद्विबाहु त्रिभुज का आधार 12.4 मी लम्बा है और इसकी बराबर भुजाओं में से प्रत्येक का माप 16.3 मी है, तो इसका क्षेत्रफल ज्ञात करें ।
View Solutionएक समद्विबाहु त्रिभुज जिसकी बराबर भुजाओं में से प्रत्येक की लम्बाई 13 सेमी है और आधार 24 सेमी है, का क्षेत्रफल ज्ञात करें ।
View Solutionएक समद्विबाहु त्रिभुज के आधार का माप 24 सेमी और इसका क्षेत्रफल 192 वर्ग सेमी है तो इसका परिमाप ज्ञात करें ।
View Solutionएक समद्विबाहु त्रिभुज का क्षेत्रफल 60 वर्ग सेमी० है। यदि इसकी दोनों बराबर भुजाओं की लम्बाई 13 सेमी० हो, तो इसके आधार की लम्बाई ज्ञात कीजिए।
View Solutionएक समद्विबाहु त्रिभुज का क्षेत्रफल ज्ञात करें, जिसकी बराबर भुजाओं में से प्रत्येक का माप 13 सेमी और आधार का माप 20 सेमी है । अपने उत्तर दशमलव के एक शुद्ध स्थानों तक ज्ञात करें ।
View Solutionएक समद्विबाहु त्रिभुज के आधार का माप 80 सेमी है और इसका क्षेत्रफल `360 "सेमी"^(2)` है, तो त्रिभुज का परिमाप निकालें ।
View Solutionएक समद्विबाहु त्रिभुजा का परिमाप 42 सेमी. है तथा समान भुजाओं का माप आधार का 3/2 गुना हो, तो त्रिभुज की प्रत्येक भुजा की लम्बाई , क्षेत्रफल एवं ऊँचाई ज्ञात कीजिये |
View Solutionएक समद्विबाहु त्रिभुज के प्रत्येक भुजाओं का माप इसकी ऊँचाई से 2 सेमी अधिक है और त्रिभुज के आधार का माप 12 सेमी है, तो त्रिभुज का क्षेत्रफल ज्ञात करें ।
View Solutionएक समकोण त्रिभुज, जिसका कर्ण 25 सेमी और आधार 7 सेमी है, का क्षेत्रफल ज्ञात करें।
View Solutionएक समकोण त्रिभुज का परिमाप 40 सेमी है। इसका कर्ण 17 सेमी है । समकोण आविष्ट करने वाली भुजाएँ ज्ञात करें । त्रिभुज का क्षेत्रफल भी ज्ञात करें ।
View Solutionएक समकोण त्रिभुज का परिमाप 60 सेमी है । इसका कर्ण 26 सेमी है। अन्य दो भुजाएँ और त्रिभुज का क्षेत्रफल ज्ञात करें।
View Solutionएक समकोण त्रिभुज में, समकोण आविष्ट करने वाली दो भुजाओं की लम्बाइयों का अन्तर 2 सेमी है। यदि त्रिभुज का क्षेत्रफल 24 सेमी हो, तो त्रिभुज का परिमाप ज्ञात करें ।
View Solutionएक समद्विबाहु समकोण त्रिभुज की बराबर भुजाओं में से प्रत्येक का माप 10 सेमी है तो इसका क्षेत्रफल और परिमाप ज्ञात करें । ( `sqrt(2)` = 1.414 लें)
View Solutionएक समकोण त्रिभुज का परिमाप 60 सेमी० है यदि इसके कर्ण की लम्बाई 25 सेमी० हो, तो त्रिभुज का क्षेत्रफल ज्ञात कीजिए।
View Solutionएक समकोण त्रिभुज का क्षेत्रफल `600 "सेमी"^(2)` है। यदि त्रिभुज का आधार इसके शीर्षलम्ब से 10 सेमी अधिक है, तो त्रिभुज की विमाएँ ज्ञात करें।
View Solution
प्रश्नावली 28.1 questions and complete solutions for chapter समतल आकृतियों का क्षेत्रफल of S CHAND of Class 9