Complete Solutions to उदहारण of chapter वृत्त , वृत्त का त्रिज्यखण्ड तथा वृत्तखण्ड का क्षेत्रफल of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | वृत्त , वृत्त का त्रिज्यखण्ड तथा वृत्तखण्ड का क्षेत्रफल |
| S CHAND | उदहारण |
| Number Of Questions | 48 |
| Academic Year | 2023-24 |
यदि एक वृत का व्यास 21 सेमी है तो उसकी परिधि तथा क्षेत्रफल निकालें ।
View Solutionएक वृत्ताकार पार्क की त्रिज्या 4.5 मी है। उसका क्षेत्रफल तथा परिधि ज्ञात करें | `(pi = (22)/(7))`
View Solutionएक वृत्ताकार पार्क की त्रिज्या 4.5 मी है। उसका क्षेत्रफल तथा परिधि ज्ञात करें
View Solutionएक वृत्ताकार पार्क की त्रिज्या 4.5 मी है। उसका क्षेत्रफल तथा परिधि ज्ञात करें
View Solutionयदि एक अर्धवृत्ताकार का चाँदे का व्यास 14 सेमी. है, तो इसकी परिधि ज्ञात कीजिए |
View Solutionएक घोड़े को 70 मी x52 मी के एक आयताकार खेत में चरने के लिए रखा गया और उसे 21 मी लम्बी रस्सी से खेत के एक कोने में बाँध दिया गया । बताइए यह घोड़ा खेत के कितने हिस्से में घास चर सकता है?
View Solutionएक वृत्ताकार खेत को 1.50 रु. प्रति वर्ग मीटर की दर से जोतने पर 5775 रु. खर्च होता है। 8.50 रु. प्रति मी. की दर से खेत के चारों ओर तार लगाने का खर्च ज्ञात कीजिए।
View Solutionएक तार जब वर्ग के आकार में मोड़ा जाता है तब वह 121 वर्ग सेमी का क्षेत्र परिबद्ध करता है । यदि तार को वृत्त के आकार में मोड़ा जाए तो वृत्त का क्षेत्रफल ज्ञात कीजिए।
View Solutionएक तार को मोड़कर 28 सेमी त्रिज्या का एक वृत्त बनाया गया । इसी तार को दोबारा मोड़कर एक वर्ग बनाया गया तो वर्ग की भुजा की लम्बाई ज्ञात करें ।
View Solutionदो वृत्त एक दूसरे को बाह्य रुप से स्पर्श करते हैं । यदि उनके क्षेत्रफलों का योग 130 `pi` सेमी`""^(2)` है और उनके केन्द्रों के बीच की दूरी 14 सेमी है तो दोनों वृत्तों की त्रिज्याएँ ज्ञात करें।
View Solutionदो वृत्त एक दूसरे को आन्तरिक स्पर्श करते हैं । यदि उनके क्षेत्रफलों का योग `116pi` वर्ग सेमी तथा उनके केन्द्रों के बीच की दूरी 6 सेमी हो, तो दोनों वृत्तों की त्रिज्याएँ ज्ञात करें।
View Solutionदो वृत्तों की त्रिज्याओं का योग 140 सेमी है और उनकी परिधियों का अन्तर 88 सेमी है तो वृत्तों का व्यास ज्ञात करें।
View Solutionगाड़ी का एक पहिया प्रति सेकेण्ड चार चक्कर लगाता है । यदि पहिया का व्यास 84 सेमी हो, तो चाल ज्ञात करें।
View Solutionएक वृत्ताकार मैदान का क्षेत्रफल 88,704 वर्ग मी. है । इसमें 4.5 किमी/घंटे की चाल से 10 चक्कर लगाने पर कितना समय लगेगा।
View Solutionएक समषट्भुज जिसकी प्रत्येक भुजा 72 सेमी है, का क्षेत्रफल तथा इसके अंदर बने वृत्त के क्षेत्रफल का अंतर ज्ञात करें `(pi = (22)/(7)
View Solutionएक वलय का क्षेत्रफल निकालिए जिसकी बाह्य और आन्तरिक त्रिज्याएँ क्रमश: 20 सेमी और 15 सेमी हों।
View Solution42 m व्यास वाले एक वृत्ताकार पार्क के बाहर चारों तरफ 3.5 m चौड़ा पथ है | 4 रु ० प्रति ` m ^2 ` की दर से पथ बनाने का खर्च ज्ञात करे |
View Solutionएक r त्रिज्या के वृत्ताकार क्षेत्र के चारों ओर h चौड़ाई के समान पथ का क्षेत्रफल `pi h(2r+h)` होता है । सिद्ध कीजिए ।
View Solutionएक पार्क `120" मी."xx100"मी."` माप के आयत के रूप में हे | पार्क के मध्य में एक वृत्ताकार घास का मैदान है | घास के मैदान को छोड़कर शेष पार्क का क्षेत्रफल `8700" मी."^(2)` है | वृत्ताकार घास के मैदान की त्रिज्या ज्ञात कीजिये | `(pi=22//7)`
View Solutionएक कागज, आयत ABCD के आकार का है, जहाँ AB = 22 सेमी तथा BC = 14 सेमी । यदि BC व्यास वाले अर्धवृत्ताकार को हटा दिया जाय, तो शेष बचे हुए भाग का क्षेत्रफल ज्ञात करें।
View Solution4 सेमी भुजा के एक वर्ग के प्रत्येक कोने से एक वर्ग के प्रत्येक कोने से एक सेमी त्रिज्या वाले वृत्त का एक चतुर्थाश काटा गया है तथा बीच में 2 सेमी व्यास का एक वृत्त भी काटा गया है, जैसे की आकृति में दिखाया गया है। वर्ग के शेष भाग का क्षेत्रफल ज्ञात कीजिए।
View Solutionकिसी वर्ग के चारों कोनों पर चार बराबर त्रिज्या वाले वृत्त इस प्रकार खींचे है कि प्रत्येक वृत्त दूसरे दो वृत्तों को स्पर्श करता है । यदि वर्ग की प्रत्येक भुजा 140 सेमी. हो तो वृत्त की परिधि के बीच परिबद्ध स्थान का क्षेत्रफल बताइए? यह मानते हुए कि `pi=227`
View Solutionदिए गए आकृति में छायांकित क्षेत्र का क्षेत्रफल ज्ञात करें, जहाँ AB = 12 सेमी तथा BC = 5 सेमी । `(pi = 3.14 "का उपयोग करें"।)`
View Solutionएक वृत्ताकार खेत का परिमाप 660 मी. है। इस खेत पर वर्ग के आकार का एक भूखण्ड, इस प्रकार चिन्हित किया गया है कि इसके शीर्ष वृत्ताकार खेत की परिधि पर स्थित हों । वर्गाकार भूखण्ड का क्षेत्रफल ज्ञात करें
View Solutionआयताकार मैदान की छोटी भुजाओ को व्यास मानकर दो अर्धवृत्त उसकी चोहोती भुजा में जोड़े गए है यदि आयत की भुजाएं 36 मीटर व 24.5 मीटर हो तो मैदान का क्षेत्रफल ज्ञात कीजिए `(pi=(22)/(7))`
View Solutionएक वर्गाकार पानी के टैंक की प्रत्येक भुजा 40 मी है । इसके चारों तरफ चार अर्धवृत्ताकार घास के मैदान हैं। इन घास के मैदानों को 1.25 रु. प्रति मी' की दर से साफ कराने का खर्च ज्ञात करें।
View Solutionआकृति में, छायांकित भाग का क्षेत्रफल ज्ञात करें।
View Solutionएक समबाहु त्रिभुज की प्रत्येक भुजा 24 सेमी है । त्रिभुज के अन्दर इसकी भुजाओं को स्पर्श करते हुए एक अन्तः वृत्त बना हुआ है । त्रिभुज के शेष बचे हुए भाग का क्षेत्रफल ज्ञात करें |
View Solutionएक 14 मी चौड़ा दौड़ का मैदान इस प्रकार बनाया गया है कि इसमें दो समान्तर आयतीय भाग हैं जिनमें प्रत्येक की लम्बाई 150 मीटर है तथा ये दो अर्धवृत्ताकार, सिरों से दोनों ओर जुड़े हुए हैं । यदि इन अद्धवृत्ताकार सिरों की आन्तरिक त्रिज्या 28 मी हो तो पथ का क्षेत्रफल ज्ञात करें।
View Solution14 सेमी त्रिज्या वाले वृत्त का एक चतुर्थाश ABCP है। इसमें AC को व्यास लेकर एक अर्धवृत्त खींचा गया है । आकृति में, दर्शाए गए छायांकित भाग का क्षेत्रफल ज्ञात करें ।
View Solutionएक फूलो की क्यारी ABCD है यदि OA = 21 मी तथा OC=14 मी तो क्यारी का क्षेत्रफल ज्ञात कीजिए ।
View Solutionआकृति में, 7 सेमी त्रिज्या के एक वृत्त के चतुर्थाश ABDCA को निरूपित करता है जिसका केन्द्र A है । छायांकित भाग के क्षेत्रफल की गणना करें। `[pi = (22)/(7) ]`
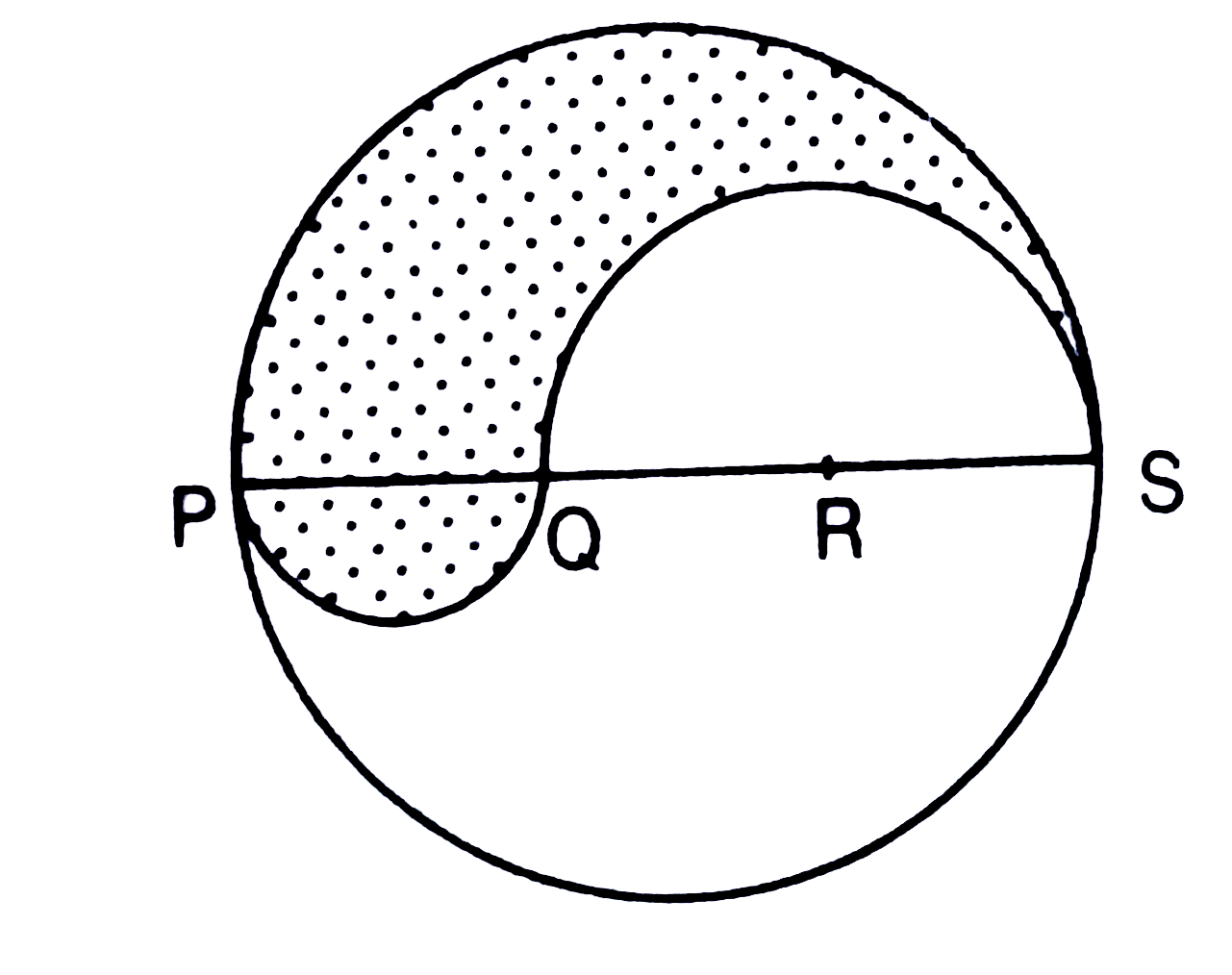
View Solutionएक 6 सेमी. त्रिज्या के वृत्त का व्यास PQRS इस प्रकार है कि PQ, QR और RS बराबर हैं | चित्र के अनुसार PQ और QS को व्यास मानकर अर्धवृत्त खींचे गये हैं | छायांकित भाग का परिमाप तथा क्षेत्रफल ज्ञात कीजिये |
View Solutionएक वृत्त के त्रिज्यखण्ड का क्षेत्रफल और परिमाप ज्ञात कीजिए जिसके केन्द्रीय कोण `60^(@)` तथा त्रिज्या 21 सेमी है।
View Solution42 सेमी त्रिज्या के वृत्त से एक त्रिज्यखण्ड काट लिया गया है । यदि इस त्रिज्यखण्ड का कोण `120^(@)` हो, तो इसके चाप की लम्बाई तथा क्षेत्रफल ज्ञात करें।
View Solutionदी गई आकृति में दो संकेन्द्रीय वृत्तों की त्रिज्याएँ 7 सेमी तथा 3.5 सेमी है। छायांकित भाग का क्षेत्रफल ज्ञात करें |`[pi = (22)/(7) ]`

View Solutionएक वृत्त की त्रिज्या 14 सेमी है तथा इसके त्रिज्यखण्ड का क्षेत्रफल 102.7 सेमी है। त्रिज्यखण्ड का केन्द्रीय कोण ज्ञात करें।
View Solutionएक वृत्त की त्रिज्या 5.6 सेमी है। यदि इसके त्रिज्यखण्ड का परिमाप 27.2 सेमी हो, तो त्रिज्यखण्ड का क्षेत्रफल ज्ञात करें ।
View Solutionएक लोलक (Pendulum) `60^(@)` के कोण तक घूमकर 8.8 सेमी की लम्बाई का एक चाप बनाता है। लोलक की लम्बाई ज्ञात करें।
View Solutionएक घड़ी की मिनट की सूई 10 सेमी लम्बी है। मिनट की सूई द्वारा 9:00 पूर्वाहन से 9.35 पूर्वाहन के मध्य पड़ी के तल पर बनाए गए त्रिज्यखण्ड का क्षेत्रफल ज्ञात कीजिए।
View Solutionएक घड़ी की मिनट की सूई की लम्बाई 14 सेमी है। इस मिनट की सूई द्वारा । मिनट में तय किए गए क्षेत्रफल को ज्ञात करें। `[pi = (22)/(7) "लें ।"]`
View Solutionएक समबाहु त्रिभुज का क्षेत्रफल 100`sqrt(3)` `c m^2` की भुजा की आधी लम्बाई को त्रिज्या मानकर वृत्त खींचे गए हैं जैसा कि आकृति में दिखाया गया है । त्रिभुज का वह क्षेत्रफल ज्ञात कीजिए जो वृत्तों में शामिल न हो। (`sqrt(3)` = 1.732 "तथा" `pi` = 3.14 "लीजिए।")
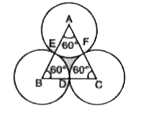
View Solutionएक त्रिभुजाकार खेत जिसकी भुजाएँ 20 मी. 34 मी तथा 42 मी हैं, के तीनों कोने में 7 मी लम्बी रस्सी से तीन घोड़े को बाँध दिया गया है। उस क्षेत्र का क्षेत्रफल ज्ञात करें जिसे घोड़े द्वारा चराया जा सकता है। उस भाग का क्षेत्रफल ज्ञात करें जो घोड़े द्वारा नही चराया गया है।
View Solution21 सेमी त्रिज्या के वृत्त में, एक चाप, केन्द्र पर `60^(@)` का कोण बनाता है (i) चाप की लम्बाई (ii) त्रिज्यखण्ड का क्षेत्रफल (ii) लघु वृत्तखण्ड का क्षेत्रफल तथा (iv) दीर्घ वृत्तखण्ड का क्षेत्रफल, ज्ञात करें।
View Solution10 सेमी की त्रिज्या वाले वृत्त की जीवा AB वृत्त के केन्द्र पर समकोण बनाती है। दीर्घ वृत्तखण्ड और लघु वृत्तखण्ड के क्षेत्रफल ज्ञात कीजिए। (`pi=3.14` लीजिए)
View Solutionएक 10 सेमी. त्रिज्या के वृत्त में एक जीवा केन्द्र पर समकोण बनाती है | ज्ञात कीजिए:
दीर्घ वृत्तखण्ड का क्षेत्रफल
View Solutionएक वृत्त का व्यास 16 सेमी है। इसकी एक जीवा PQ केन्द्र पर `60^(@)` का कोण बनाती है। इस प्रकार निर्मित दीर्घ वृत्तखण्ड का क्षेत्रफल ज्ञात कीजिए।
View Solutionएक वृत्त की त्रिज्या 15 सेमी है। इसकी एक जीवा केन्द्र पर `60^(@)` का कोण बनाती है। लघुवत्तखण्ड तथा दीर्घ वृत्तखण्ड का क्षेत्रफल ज्ञात करेंi`pi=3.14`, तथा `sqrt3` = 1.731
View Solution
उदहारण questions and complete solutions for chapter वृत्त , वृत्त का त्रिज्यखण्ड तथा वृत्तखण्ड का क्षेत्रफल of S CHAND of Class 9