Complete Solutions to QUESTION BANK of chapter New Numbers of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | New Numbers |
| V PUBLICATION | QUESTION BANK |
| Number Of Questions | 52 |
| Academic Year | 2023-24 |
In the picture, the square on the hypotenuse of the top most right triangle Is drawn. Calculate the area and the length of a side of the square.
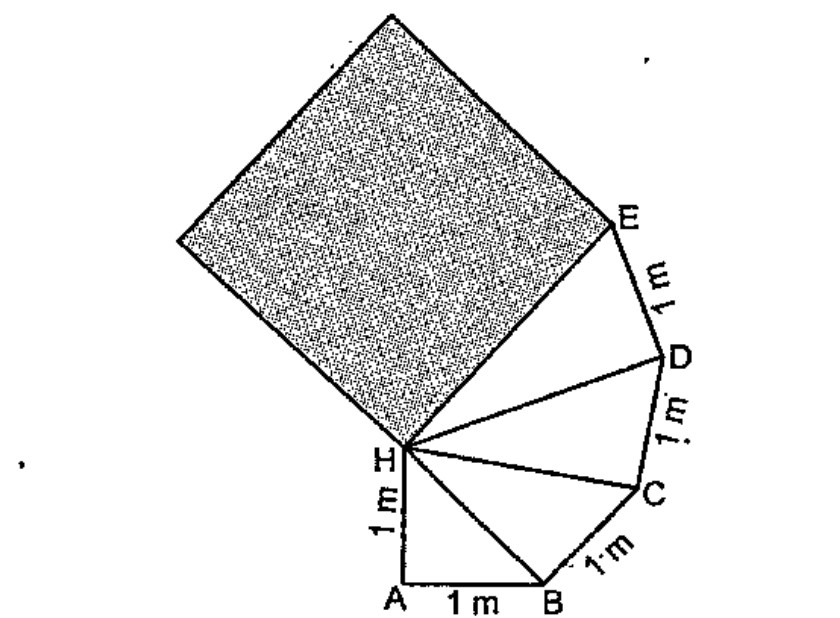 .06:49View Solution
.06:49View SolutionA square is drawn on the altitude of an equilateral triangle of side 2 metres.
a) What is the area of the square?
b) What is the altituđe of the triangle03:01View SolutionWe have seen In Class 8 that any odd number can be written as the difference of two perfect squares. Using this, draw squares of areas 7 and 11 square cențimetres.
05:22View SolutionExplain fwo different methods of drawing a square of area 13 centimetres:
07:29View SolutionFind three fractions larger than `sqrt2` and less than `sqrt3`.
04:11View Solutiona) Draw the square ABCD of àrea 9 square centimetres.
b) Draw the diagonal AC of the square. Draw a square with AC as side.
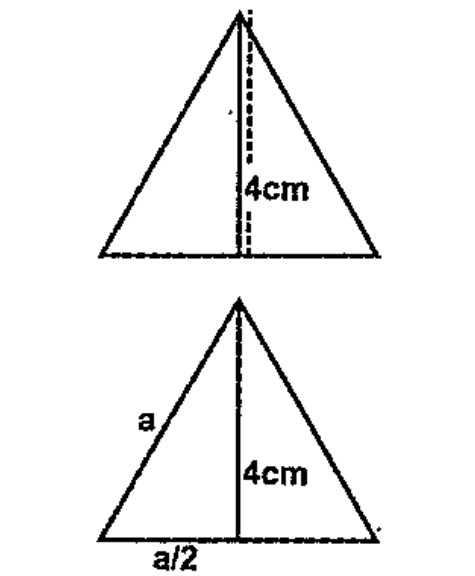
c) How mưch is the area of this new square? Calculate its perimeter also, :04:25View SolutionA square is drawn on the altitude of an equilateral triangle of side 4 cm.
a) What is the altitude of the triangle?
b) What is the area and perimeter of the square?03:08View SolutionDraw a square of area 19 sq.cm
03:16View SolutionThe hypotenuse of a right triangle is `1 1/2` meters and another side is `1/2` meter. Calculate its perimeter correct to a centimeter.
03:43View SolutionThe picture shows an equilateral triangle cut into halves by a line through a vertex.
What is the perimeter of a part?
 .03:16View Solution
.03:16View SolutionCalculate the perimeter of the triangle shown below.
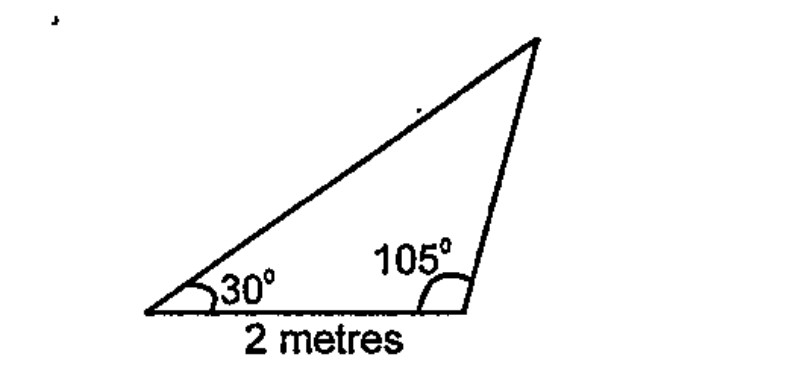 .05:59View Solution
.05:59View SolutionWe have seen how we can draw a series of right triangles as in the picture.
How mulch more is the perimeter of the `10^th` triangle than the perimeter of the ninth triangle?
 .07:02View Solution
.07:02View SolutionWhat is the hypotenuse of the right triangle with perpendicular sides `sqrt2`centimeteres and `sqrt3` centimeters? How much larger than the hypotenuse is the sum of the perpendicular sides?
01:56View SolutionSimplify
a)`sqrt18` + `sqrt50` b) `sqrt 2`+ `sqrt 32`+`sqrt512`
c) `sqrt48` -`sqrt27`06:51View SolutionA rhombus with one side-3 meters and one angle `60^@`is given in the picture. Find the sum of the length of its diagonals
08:03View SolutionIn the figure, a side of the triangle is 12 centimetres and the angle at its ends are are 45∘ and 60∘
i) Find the length of the other two sides of the triangle.
ii) Find the perimeter of this triangle.05:40View SolutionOf four equal equilateral triangles, two are cut vertically into halves and two whole are put together to make a rectangle:
If a side of the triangle ls 1 metre, what is the area and the perimeter of the rectangle?05:03View SolutionA square and equiIateral triangle of sides twice as long we cut and the pieces are rearranged to form a trapezium, as shown below.
If a side of the square is 2 centimetres, what are the perimeter and area of the trapezium?
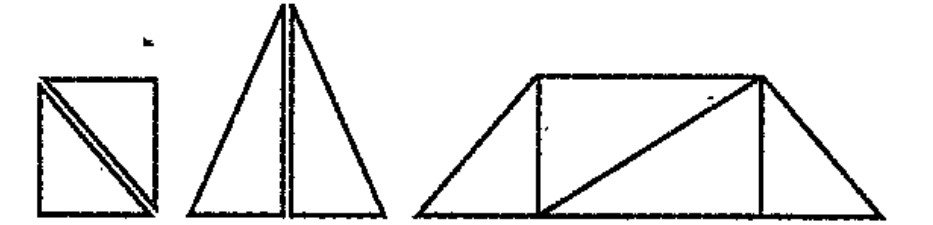 .09:22View Solution
.09:22View SolutionCalculate the perimeter and area of the triangle in the picture.
09:00View SolutionFrom the pairs of numbers given below, pick out those whose product is a natural number or a fraction.
i) `sqrt3`, `sqrt12`
ii) `sqrt3`, `sqrt1.2`
iii) `sqrt5`,`sqrt8`
iv) `sqrt0.5`,`sqrt8`04:51View SolutionCompute the perimeter of the quadrilateral with measures as given in the figure, correct to centimetres.
03:07View SolutionThe hypotenuse of a right triangle is 1 1/2 metres and another side is1/2metre. Calculate its perimeter correct to a centimetre.
03:43View SolutionArea of a square is 3 square metres.
a) Find țhe length of a side.
b) What is the perimeter?01:09View SolutionSimplify
a) `sqrt24` `sqrt6` b)`sqrt7` `sqrt4` `sqrt8` c) `sqrt21` `sqrt15` `sqrt35` d) `sqrt242` `sqrt12` `sqrt6`05:54View SolutionCalculate the length of the sides of the equilateral triangle on the right correct to a millimeter.
 .04:20View Solution
.04:20View SolutionProve that `(sqrt2+1)(sqrt2-1)=1`. Use this to compute `frac(1)sqrt(2-1)`.Correct two decimal places.
02:35View SolutionCompute `frac(1)(sqrt2+1)` correct two decimal places.
02:10View SolutionSimplify
`(sqrt3-sqrt2)(sqrt3+sqrt2)`
Using this compute
`1/(sqrt3-sqrt2)` and `1/(sqrt3+sqrt2)`.04:08View SolutionProve that sqrtx2 \2\3=2 \sqrtx\2\3 and sqrtx3 \3\8=3 \sqrtx3\8Can you:find other numbers like this?
04:12View SolutionAll black triangles in the picture are equilateral.
What is the ratio of sides of the outer and inner squares?
 .05:11View Solution
.05:11View SolutionUsing `sqrt3`= 1.73, find `sqrt3/4` correct to three decimals.
03:01View SolutionUsing `sqrt10` = 3.162, compute `1/sqrt10` correct to three decimals.
02:36View SolutionUsing `sqrt6`= 2.449, calculate `sqrt(2/3)`+`sqrt(3/2)` correct to three decimals.
03:30View SolutionCompute √12 - √3 upto two decimals.
01:45View SolutionGiven `sqrt2` = 1.414, find the approximate value of `3/sqrt2` to three decimal places.
02:14View SolutionUsing sqrtx2 \approx 1.414, \sqrtx3=1.732 . Calculate the value of the following
01:29View SolutionIn the picture A B C is an equilateral triangle. BC=5cm. Find the area of triangle BCD.
02:45View SolutionIn the figure, angle B=`120circ`, angle A=`15^circ`, A B=10 centimeters. Also distance from A to BC is AP.
a) Write the angle measures of triangleA P B.
b) Find the lengths of AP, PB.
c) Calculate the area of triangle A B C.07:18View Solutiona) `sqrt3` `sqrt3`=
b) What is the product of(`sqrt3`+`sqrt2` and`sqrt3`-`sqrt2`)
c)What is the reciprocal of `sqrt3`+`sqrt2` ?03:46View SolutionIn the figure, angle A=`30^circ`,angle B=`90^circ`, A C=16cm
(a) What is the length of BC?
b) What is the length of AB ?03:57View Solutiona)`sqrt7``sqrt7`=
b) `sqrt7`+`sqrt7`=02:14View Solutiona) Find the area and perimeter of the rectangle in the figure.
b) What is the iength of A C ?04:42View Solution(sqrtx3+sqrtx2)(\sqrt{3}-sqrtx2)=(sqrtx3)^2-(sqrtx2)^2=3-2=1Using this, find the aproximate values of 1(sqrtx3+sqrtx2) "and 1(sqrtx3-sqrtx2) correct to two décimal: places.(sqrtx3 \approx 1.732, sqrtx2 \approx 1.414)
02:49View SolutionIn the figure, angle B=angle AC D=90^circ
a) What is the length of AC?
b) Find the length of AD.
c) How much more is the perimeter of triangle ACD than the perimefer of triangle ABC?01:32View SolutionCompute the following (14+`sqrt3`)(14-`sqrt3`)
01:37View SolutionFind the value of √243 + √300
02:11View SolutionIf √3 =1.732 and √5 =2.236, compute √5 +√3 correct two decimal places:
01:20View SolutionCalculate.the perimeter and area of the triangle in the picture.
09:00View SolutionCompute √12 - √3 upto two decimals.
01:45View SolutionIn the figure, angle B=120 ∘ angle A=15 ∘ , AB=10 centimetres. Also distance from A to BC is AP.
a) Write the angle measures of triangle APB.
b) Find the lengths of AP, PB.
c) Calculate the area of triangle A B C.07:18View SolutionThe pictures shows a tangram of 7 pieces made by cutting a square of side 4 centimetres. Calculate the length of the sides of each piece.
04:42View SolutionDraw an equilateral triangle with side sqrtx10 centimetres.
01:37View Solution
QUESTION BANK questions and complete solutions for chapter New Numbers of V PUBLICATION of Class 9