Complete Solutions to EXERCISE of chapter CIRCLES of Class 9 book with complete answers and questions
| Class 9 | MATHS |
| Chapter | CIRCLES |
| VGS PUBLICATION-BRILLIANT | EXERCISE |
| Number Of Questions | 78 |
| Academic Year | 2023-24 |
What measure of the circles make them congruent?
02:01View SolutionName the following parts from the given figure where 'O' is a centre of the circle. ` bar AO` ,
01:51View SolutionName the following parts from the adjacent figure where ‘O’ is the centre of the circle
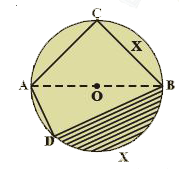
`(i) bar(AO) (ii) bar(AB) (iii) frown(BC) (iv) bar(AC) (v) frown(DCB) (vi) frown (ACB) (vi) bar(AD)` (viii) shadedregion02:37View SolutionName the following parts from the adjacent figure where ‘O’ is the centre of the circle

`(i) bar(AO) (ii) bar(AB) (iii) frown(BC) (iv) bar(AC) (v) frown(DCB) (vi) frown (ACB) (vi) bar(AD)` (viii) shadedregion02:37View SolutionName the following parts from the adjacent figure where ‘O’ is the centre of the circle

`(i) bar(AO) (ii) bar(AB) (iii) frown(BC) (iv) bar(AC) (v) frown(DCB) (vi) frown (ACB) (vi) bar(AD)` (viii) shadedregion02:37View SolutionName the following parts from the adjacent figure where ‘O’ is the centre of the circle

`(i) bar(AO) (ii) bar(AB) (iii) frown(BC) (iv) bar(AC) (v) frown(DCB) (vi) frown (ACB) (vi) bar(AD)` (viii) shadedregion02:37View SolutionName the following parts from the adjacent figure where ‘O’ is the centre of the circle

`(i) bar(AO) (ii) bar(AB) (iii) frown(BC) (iv) bar(AC) (v) frown(DCB) (vi) frown (ACB) (vi) bar(AD)` (viii) shadedregion02:37View SolutionName the following parts from the adjacent figure where ‘O’ is the centre of the circle

`(i) bar(AO) (ii) bar(AB) (iii) frown(BC) (iv) bar(AC) (v) frown(DCB) (vi) frown (ACB) (vi) bar(AD)` (viii) shadedregion02:37View SolutionState true or false .
A circle divides the plane on which it lies into three parts.02:26View SolutionState true or false .
The region enclosed by a chord and the minor arc is minor segment01:13View SolutionState true or false .
The region enclosed by a chord and the major arc is major segment01:31View SolutionState true or false .
A diameter divides the circle into two unequal parts.01:22View SolutionState true or false .
A sector is the area enclosed by two radii and a chord01:43View SolutionState true or false .
The longest of all chords of a circle is called a diameter.01:29View SolutionState true or false .
The mid point of any diameter of a circle is the centre.01:09View Solutionif three points are collinear , how many circles can be drawn through these points? Now, try to draw a circle passing through these three points.
02:41View SolutionConstruct a circumcircle of the triangle ABC where AB = 5cm, `angleB = 75^@` and BC = 7 cm.
04:52View SolutionDraw the following triangles and construct circumcircles for them : In `DeltaABC`, AB = 6 cm, BC = 7 cm and `angleA = 60^@`.
03:32View SolutionDraw the following triangles and construct circumcircles for them: In `DeltaPQR` , PQ = 5 cm , QR = 6 cm and RP= 8.2cm.
04:38View SolutionDraw the following triangles and construct circumcircles for them: In `DeltaXYZ , XY = 4.8 cm `angleX = 60^@` and `angleY = 70^@`.
04:10View SolutionDraw two circles passing through A, B where AB = 5.4cm.
02:24View SolutionIf two circles intersect at two points , then prove that their centres lie on the perpendicular bisector of the common chord.
06:00View SolutionIn the adjacent figure, AB is a chord of circle with centre O. CD is the diameter perpendicualr to AB. Show that AD = BD.
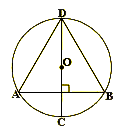 04:59View Solution
04:59View SolutionLet ‘O’ be the centre of a circle, PQ is a diameter, then prove that `angle PRQ = 90^@` (OR) Prove that angle in a semi-circle is right angle.
03:41View SolutionIn the figure, 'O' is the centre of the circle.
`angleAOB = 100^(@)` find `angleADB`.
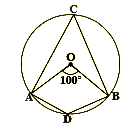 02:09View Solution
02:09View SolutionDraw a circle with any radius and then draw two chords equidistant from the centre.
02:08View SolutionGiven that the vertices A, B, C of a quadrilateral ABCD lie on a circle. Also `angleA + angleC = 180^@` , then prove that the vertex D also lie on the same circle.
01:54View SolutionIf a parallelogram is cyclic, then it is a rectangle. Justify.
02:23View SolutionProve that a cyclic rhombus is a square
01:29View SolutionFor each of the following, draw a circle and inscribe the figure given. If a polygon of the given type can’t be inscribed , write not possible : Rectangle.
02:07View SolutionFor each of the following, draw a circle and inscribe the figure given. If a polygon of the given type can’t be inscribed , write not possible :Trapezium.
02:20View SolutionFor each of the following, draw a circle and inscribe the figure given. If a polygon of the given type can’t be inscribed , write not possible : Obtuse triangle.
02:05View SolutionFor each of the following, draw a circle and inscribe the figure given. If a polygon of the given type can’t be inscribed , write not possible : Rectangle.
02:07View SolutionFor each of the following, draw a circle and inscribe the figure given. If a polygon of the given type can’t be inscribed , write not possible : Acute isosceles triangle .
02:23View SolutionFor each of the following, draw a circle and inscribe the figure given. If a polygon of the given type can’t be inscribed , write not possible : A quadrilateral PQRS with `bar PR` as diameter.
02:13View SolutionDefine a 'Circle '.
01:51View SolutionDefine the terms: Arc
01:16View SolutionDefine the terms: Chord
01:11View SolutionDefine a 'Sector'.
01:37View SolutionDefine the terms: Minor segment
01:59View SolutionDefine the terms: Major segment
01:41View SolutionDefine a ‘Cyclic Quadrilateral’ .
01:58View SolutionDefine a 'Circumcircle'.
01:58View SolutionState the converse of the following theorem. "Equal chords of a circle subtend equal angles at the centre".
04:05View SolutionState the converse of the following theorem. "The perpendicular from the centre of a circle to a chord bisects the chord".
03:51View SolutionDefine 'Concentric Circle'.
01:18View SolutionABCD is a cyclic quadrilateral. If `angleA - angleC = 20^@`, find `angleC`.
02:20View SolutionIf ABCD is a cyclic rhombus, find `angleB`.
02:05View SolutionABCD is a cyclic parallelogram and AC = 9 cm, find BD.
02:58View SolutionState the converse of the following theorem. "The pairs of opposite angles of a cyclic quadrilateral are supplementary".
04:14View SolutionProve that angle subtended by semicircle is `90^@`.
02:04View SolutionThe point which is at equidistant from the circumference of a circle is called
02:33View SolutionIf AC and AD are at equidistant from ‘O' then
01:40View SolutionArea enclosed by two radii and the arc between them is called
01:26View SolutionAngle in the same segment of the circle ……………
01:53View SolutionAngle in a minor segment is ……….
04:49View SolutionA diameter divides the circle into two
01:53View SolutionLet 'O' be the centre of a circle. The distance of chord AB from O is greater than the distance of chord CD from ‘O' then
01:51View SolutionIn the figure, if `angleC = 60^@` then y =
02:20View SolutionNumber of points required to describe a circle is
01:37View SolutionNumber of circles that can be drawn through a given point is
02:01View SolutionNumber of circles that can be drawn through two non-collinear points is
01:52View Solution_____________number of circles can be draw through 3 non-collinear points.
01:12View SolutionIf a quadrilateral is cyclic then it is a
04:58View SolutionAngle subtended by an arc at its centre is `‘x^@’` then, angle subtended by it at any other point on the circle is
05:50View SolutionThe perpendicular from the centre of a circle to a chord
01:55View SolutionThe measure of the angle in a semicircle is
01:32View SolutionAngle in the same segment of the circle ……………
01:53View SolutionThe circle that passes through the vertices of a triangle is called its
01:46View SolutionABCD is a cyclic quadrilateral then `angleA+angleC` = ……….
01:21View SolutionIf the sum of the pairs of opposite angles of a quadrilateral is `180^@`, then the quadrilateral is
02:19View SolutionWhich part of a circle divides it into two semicircles?
01:38View SolutionConcentric circles have
01:59View SolutionNumber of points required to describe a circle is
01:37View SolutionCyclic rhombus is a ……..
03:46View SolutionA cyclic parallelogram is a
03:06View SolutionAngle in a semi -circle at the centre is …….
02:01View Solution_____________number of circles can be draw through 3 non-collinear points.
01:12View Solution
EXERCISE questions and complete solutions for chapter CIRCLES of VGS PUBLICATION-BRILLIANT of Class 9
