समांतर श्रेढ़ियाँ कक्षा 10 गणित
भूमिका
बच्चों जैसा कि अध्याय के नाम से स्पष्ट है कि जिस श्रेढ़ी के क्रमशः अवयवों मे समान अंतर हो ऐसे अवयवों से बनी श्रेढ़ी, समांतर श्रेढ़ी कहलाएगी। समांतर श्रेढ़ी के प्रत्येक पद में एक निश्चित संख्या जोड़ने पर हमें अगला पद प्राप्त होता है। इस अध्याय में हम अनुक्रम तथा श्रेढ़ी के बारे मे विस्तार से जानने का प्रयास करेंगे।
आइये जानते है अनुक्रम तथा श्रेढ़ी को और करीब से....
प्रकृति में हम अपने आस-पास ऐसे अनेक वस्तुओं को देखते है जिनमे एक विशेष प्रतिरूप (Pattern) होता है। उदाहरण के लिए सूरजमुखी के फूल की पंखुड़ियां, मकई के भुट्टे पर दाने, मधुकोष में छिद्र, खेल का स्टेडियम इत्यादि।

सबसे अच्छा उदाहरण कहे तो, आप सभी ने क्रिकेट स्टेडियम देखा होगा
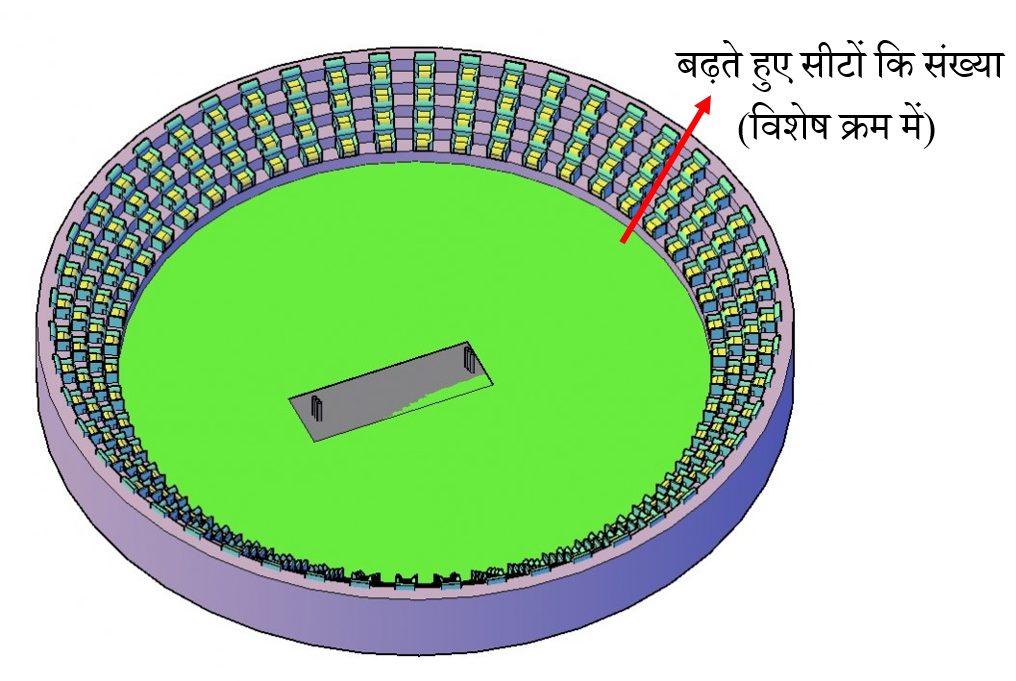
किसी वृत्ताकार स्टेडियम मे नीचे से ऊपर की ओर सीटों की संख्या देखे, आप देख पाएंगे की वे बढ़ती जा रही है, हर लाइन अपने नीचे वाली लाइन से ज्यादा सीट वाली होती है। चूँकि यहाँ नीचे से ऊपर जाने पर वृत का आकार बढ़ता हुआ दिखाई दे रहा है। इस अध्याय मे हम इसी प्रकार के विशेष क्रम के बारे मे पढ़ेंगे, जिन्हे हम अनुक्रम कहते है।
- इसी प्रकार से हम गणित में संख्याओं के ऐसे विभिन्न संग्रह को देख सकते हैं जो एक विशेष क्रम (Pattern) में हो।
यदि हम प्राकृत संख्याओ को देखे तो 1, 2, 3, 4, 5..... ये एक विशेष क्रम का पालन कर रहा है, इसमे प्रत्येक संख्या के बाद एक अधिक होता हुआ दिखाई दे रहा है।
आइये इसे हम कुछ उदाहरणों के माध्यम से समझते है :
उदाहरण -
(i){12,23,34,45,...,nn+1} जहाँ n कोई प्राकृतिक संख्या है।
यहाँ देखिए अंश मे जो भी संख्या प्राप्त होती है हर मे सदैव एक अधिक प्राप्त हो रहा है ।
(ii){1,3,5,7,9,11,13,15,17....(2n−1)}जहाँ n कोई प्राकृतिक संख्या है।
(iii){2,4,6,8,10,12...(2n)}जहाँ n कोई प्राकृतिक संख्या है।
उदाहरण (i) में यदि हम देखे तो हमने ऐसे परिमेय संख्याओं का संग्रह किया है जिनका अंश क्रमागत प्राकृतिक संख्याए है तथा हर अंश से एक अधिक है।
उदाहरण (ii) में देखे तो हमने n क्रमागत विषम प्राकृतिक संख्याओं का संग्रह किया है ,हम देखते है कि किन्ही दो विषम संख्याओं के बीच 2 का अंतर है।
उदाहरण (iii) में हमने n क्रमागत सम प्राकृतिक संख्याओं का संग्रह किया है, यहाँ भी किन्ही दो क्रमागत सम संख्याओं के बीच 2 का अंतर है।
इस प्रकार संख्याओं के ऐसे विभिन्न पैटर्न देखे जा सकते है जो एक विशेष नियम का पालन करते हो।
- इस अध्याय में सर्वप्रथम हम अनुक्रम को परिभाषित करेंगे और कुछ अनुक्रमों के पदों को लिखने के तरीकों को समझेंगे इसके पश्चात हम अपना ध्यान एक विशेष प्रकार के अनुक्रम कि ओंर केंद्रित करेंगे जिसे हम समान्तर श्रेढ़ी के रूप में परिभाषित करेंगे। इसके पश्चात हम किसी समांतर श्रेढ़ी का n वाँ पद तथा श्रेढ़ी के n पदों के योग को ज्ञात करने के सूत्रों का अध्ययन करेंगे।
1. अनुक्रम
बच्चों अनुक्रम (sequence) को समझने का प्रयास करते हैं, यह दो शब्दों "अनु" व "क्रम" से मिलकर बना है । यदि कोई क्रम विशेष नियम का अनुसरण करते हुए बनाया जाए अनुक्रम कहलाएगा।
बच्चों यहाँ अनुसरण का तात्पर्य समझते है , अनुसरण से तात्पर्य "के अनुसार" कह सकते हैं । जैसे कि आपके गणित के अध्यापक ने आपको कोई गणित की विधि समझाई , अब आगे आप उनके अनुसार बताई गई नियम का पालन करेंगे तथा आप यदि इस विधि को किसी अन्य को समझाते है तो वह आपके अनुसार नियमों का पालन करेगा और सवाल हल करेगा ।
इस उदाहरण में हम देख सकते हैं कि एक विशेष नियम का पालन हो रहा है और प्रत्येक व्यक्ति अपने से पहले व्यक्ति के अनुसार (का अनुसरण करते हुए ) कार्य कर रहा है , अतः हम कह सकते है
ऐसे वस्तुओं अथवा संख्याओं का समूह जिनका प्रत्येक पद अपने पूर्व के पद का अनुसरण करता हो ,अनुक्रम कहलाता है।
अथवा
एक अनुक्रम किसी विशेष नियम का पालन करने वाले संख्याओं का समूह होता है तथा उस नियम को पालन करने वाली संख्याएं अनुक्रम के पद कहलाते हैं।
उदाहरण -
(i) सम संख्याये - 2,4,6,8,10,12....
(ii) विषम संख्याये - 3,5,7,9,11....
(iii) 2,1,4,3,6,5..... इस उदाहरण को ध्यान से देखे इसे चित्र से समझते है
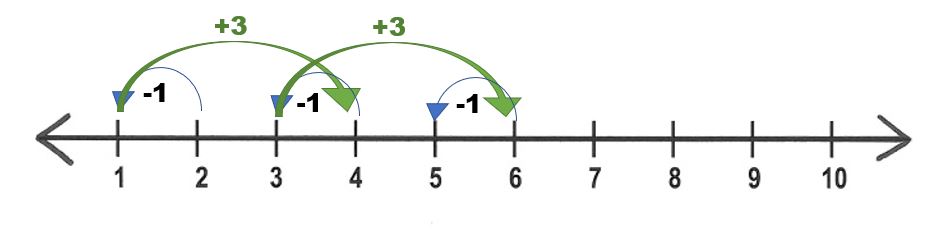
इसमे प्रथम पद 2 के बाद 1 आया अर्थात 1 कम हुआ , परन्तु इसके आगे 4 मिला जो की 1 से 3 अधिक है । 4 के आगे 3 प्राप्त हुआ अतः पुनः 1 कम हुआ तथा 3 के आगे 6 मिला अतः पुनः 3 जोड़ा गया ।
उदाहरण (iii) भी अनुक्रम का एक उदाहरण है चूँकि यहाँ आप देख सकते है एक विशेष नियम का पालन हुआ पहले 1 कम होता है फिर 3 बढ़ता है इसी प्रकार यहाँ क्रम आगे बढ़ रहा है ।
बच्चों यहाँ अनुक्रम हमने समझ लिया। आपने श्रेढ़ी के बारे मे सुना होगा , ध्यान रखे श्रेढ़ी भी एक प्रकार का अनुक्रम ही है जिसमे प्रत्येक पद अपने पूर्व के पद में एक निश्चित संख्या जोड़ने पर प्राप्त होती है।
उदाहरण 1
निम्न से परिभाषित अनुक्रमों के पहले तीन पदों को लिखिए :
an=3n+2
दिया है :an=3n+2
इसमें n=1,2, और 3 रखने पर हम पाते है कि
a1=3×1+2=3+2=5,
a2=3×2+2=6+2=8
a3=3×3+2=9+2=11
अंत : an=3n+2 सूत्र से परिभाषित अनुक्रम के पहले तीन पद क्रमश : 5 8 और 11 है
उदाहरण 2
अनुक्रम an=n(n−3)n+4 का 18 वां पद ज्ञात कीजिए ।
दिया है
an=n(n−3)n+4
इसमें n का मान 18 रखने पर
a18=18×(18−3)18+4
=18×1522=13511
2. समांतर श्रेढ़ी
एक ऐसा अनुक्रम जिसके किन्ही दो क्रमागत पदों के बीच अंतर सदैव एक समान होता है, इस प्रकार जो श्रेढ़ी मिलती है, समांतर श्रेढ़ी (Arithmetic Progression AP) कहलाती है।
आइए इसे संख्या रेखा पर समझने का प्रयास करे -
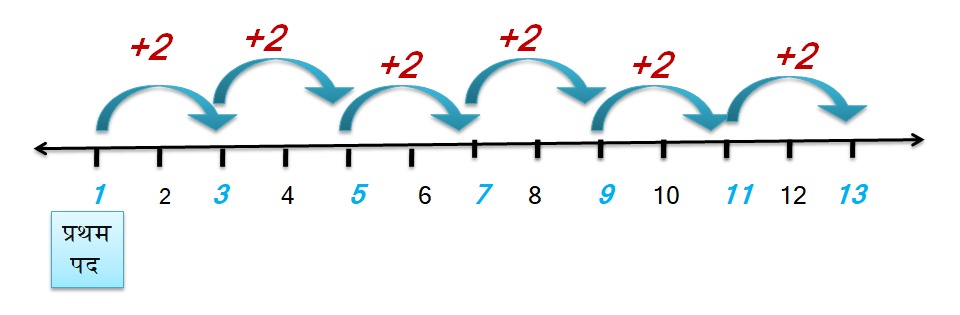
यहाँ आप देख सकते हैं संख्या रेखा पर यदि प्रथम पद (a=1) को लें तथा क्रमशः 2 बढ़ाते जाएं तब अनुक्रम 1,3,5,7,9... प्राप्त होगा। यहाँ पदों के बीच का अंतर देखे तो एक समान अंतर (d=2) दिखाई देता है, अतः इस प्रकार के अनुक्रम को समांतर श्रेढ़ी कहते हैं।
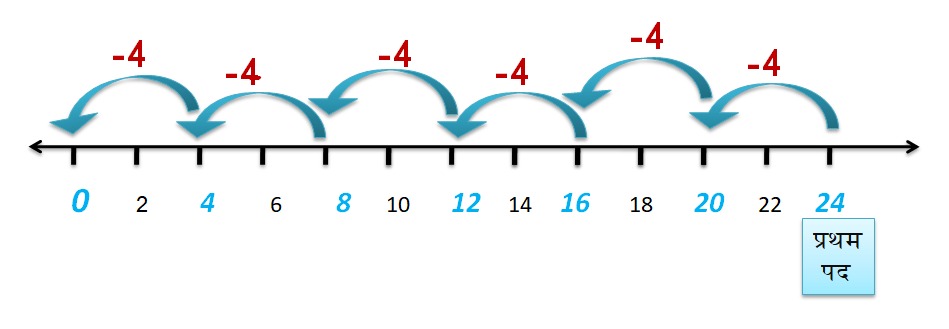
इसी प्रकार यदि संख्या रेखा पर कोई पद 24 को लें तथा क्रमशः 4 घटाते जाए तब अनुक्रम 24,20,16,12,8,4,0,.. प्राप्त होगा। यहाँ पदों के बीच का अंतर देखें तो एक समान अंतर (d=−4) दिखाई देता है, अतः यह भी एक समांतर श्रेढ़ी है। (a= प्रथम पद d=सार्व अन्तर )
( यहाँ से हम देख सकते हैं कि समांतर श्रेढ़ी संख्या रेखा पर आगे व पीछे जा सकती है। )
उदाहरण -
3nजहाँ n एक प्राकृतिक संख्या है अर्थात {3,6,9,12,15,18,21.......}
इस श्रेढ़ी में यदि हम देखें तो इसके किन्ही दो पदों के बीच अंतर सदैव 3 के बराबर है, अर्थात यह एक समांतर श्रेढ़ी है। किसी समांतर श्रेढ़ी के पदों के बीच के एक समान अंतर को सार्व अंतर कहते है 3,6,9,12,.....,3+(n−1)3 क्रमशः समांतर श्रेढ़ी के प्रथम ,द्वितीय ,तृतीय पद....... ,n वां पद कहलाते हैं।
अब हम किसी समांतर श्रेढ़ी के व्यापक रूप को जानेंगे :
माना कोई समांतर श्रेढ़ी है जिसका प्रथम पद a तथा सार्व अंतर d है तो समांतर श्रेढ़ी का व्यापक रूप निम्न प्रकार प्रदर्शित करेंगे
a,a+d,a+2d,a+3d.....a+(n−1)d
जहाँ n=1,2,3,4,5...
उदाहरण 3
संख्याओं की निम्नलिखित सूचियों में से कौन-कौन से A.P. नहीं है ? यदि इनमे कोई A.P. है तो उसके अगले दो पद लिखिए ।
(i) 4, 10, 16, 22, ….
(ii) 1,-1,-3,-5, . . .
(iii) -2,2,-2,2,-2, . . . .
(iv) 1,1,1,2,2,2,3,3,3, . . . .
.(i) 4, 10, 16, 22, ….
दी गयी श्रेढ़ी का प्रथम पद (a)=4
जैसे की हमने ऊपर परिभाषा में जाना कि किसी समांतर श्रेढ़ी के किन्ही दो क्रमागत पदों बीच अंतर एक समान रहता है ,यदि इस श्रेढ़ी के द्वितीय (a2) तथा प्रथम पद (a1) के बीच अंतर
a2−a1 = 10−4=6
इसी प्रकार तृतीय (a3) तथा द्वितीय पदों (a2) के बीच अंतर
a3−a2=16−10=6
चतुर्थ (a4) तथा तृतीय पदों (a3) के बीच अंतर
a4−a3=22−16=6
चूँकि क्रमागत पदों के बीच अंतर सदैव एक समान है अतः यह समांतर है।
अतः आगे के दो पद 6 जोड़कर निकाल सकते हैं
a5=22+6=28
a6=28+6=34
आगे के दो पद 28 और 34 प्राप्त हुए।
(ii) 1,-1,-3,-5, . . .
यहाँ
d=−1−1=−2
d=−3−(−1)=−3+1=−2
d=−5−(−3)=−5+3=−2
यहाँ सार्व अंतर -2 है । अतः दी गयी श्रेणी स. श्रे. में है ।
अगले दो पद=
−5+(−2)=−7 तथा −7+(−2)=−9 है |
(iii) −2,2,−2,2,−2,...
यहाँ
d=2−(−2)=4
d=−2−(2)=−4
d=2−(−2)=4
यहाँ d का मान सामान नहीं है । अतः स. श्रे. में नहीं है |
(iv) 1,1,1,2,2,2,3,3,3, . . .
यहाँ d=1−1=0
d=1−1=0,
d=2−1=1
यहाँ d का मान समान नहीं है । अतः दी गयी श्रेणी स. श्रे. में नहीं है ।
3. समांतर श्रेढ़ी का `n` वां पद
माना कोई समांतर श्रेढ़ी जिसका प्रथम पद a तथा सार्व अंतर d का व्यापक रूप निम्न प्रकार है :
a,a+d,a+2d,a+3d,........a+(n−1)d
जहाँ n=1,2,3....n
इस श्रेढ़ी का प्रथम पद T1=a
द्वितीय पद T2=a+d
तृतीय पद T3=a+2d
इसी प्रकार व्यापक रूप में श्रेढ़ी का n वां पद निम्न प्रकार परिभाषित होगा :
Tn=a+(n−1)d
an को समांतर श्रेढ़ी (AP) का व्यापक पद भी कहते हैं।
आइए इसे उदाहरण से समझते है
यदि 4,8,12,16,20,24,28,32... समांतर श्रेढ़ी में है तब देख सकते हैं इसका 6वाँ पद 24 है
सूत्र के अनुसार
a=4
d=8−4=12−8=4 तथा
n=6 लेना होगा
चूँकि श्रेढ़ी का n वाँ पद
Tn=a+(n−1)d
श्रेढ़ी का 6वाँ पद
T6=4+(6−1)×4
=4+20
=24
इसप्रकार हमने सूत्र की सहायता से 6वाँ पद ज्ञात किया।
OMR (One Minute Revision)
a,a+d,a+2d,a+3d......a+(n−1)d
जहाँ n=1,2,3,4,5...
an=a+(n−1)d
an को समांतर श्रेढ़ी (AP) का व्यापक पद भी कहते हैं।
a प्रथम पद है
d सार्वान्तर है
n पद का क्रमांक है
उदाहरण 4
समांतर श्रेढ़ी 9,13,17,21,25,...., का 12 वाँ, 24 वाँ तथा n वाँ पद ज्ञात कीजिए।
यहाँ
a = प्रथम पद = 9
d = सार्वान्तर = 4
[ चूँकि 13−9=4,17−13=4,21−17=4,........]
हम जानते है कि समांतर श्रेढ़ी का n वाँ पद
an=a+(n−1)d
अतः 12 वाँ पद a12=a+(12−1)d
⇒a+11d=9+11×4=53
इसी प्रकार a24=a+(24−1)d
⇒a+23d=9+23×4=101
तथा an=a+(n−1)d
⇒9+(n−1)×4=4n+5
अत: a12=53
a24=101
और an=4n+5 है।
उदाहरण 5
अनुक्रम −1,3,7,11,..... का कौन सा पद 95 है ?
स्पष्ट है कि दिए गए अनुक्रम के किन्ही भी दो क्रमागत पदों का अन्तर समान है अतः दिया गया अनुक्रम एक समांतर श्रेढ़ी है ।
यहाँ ,
a= प्रथम पद = -1 तथा d = सार्व अंतर = 4
मान लीजिए कि दिए गए अनुक्रम का n वाँ पद 95 है अर्थात
an=95
⇒a+(n−1)d=95
⇒−1+(n−1)×4=95
⇒−1+4n−4=95
⇒4n−5=95
⇒4n=100⇒n=25
अत: दिए गए अनुक्रम का 25 वाँ पद 95 है।
उदाहरण 6
एक A.P. का pवाँ पद 1q तथा qवाँ पद 1p हैं , तो इसका (pq) वाँ पद ज्ञात करें ।
A.P. का n वाँ पद जिसका प्रथम पद a तथा सार्व - अंतर d हैं , होता हैं
an=a+(n−1)d
दिया हैं ,
ap=1q
∴1q=a+(p−1)d...(i)
और aq=1p
∴1p=a+(q−1)d ...(ii)
(ii) को (i) से घटाने पर हमें मिलता हैं ,
1q−1p=(p−q)d
या (p−q)pq=(p−q)d
∴d=1pq ...(iii)
समी (i) में d=1pq रखने पर ,
1q=a+(p−1)⋅1pq
∴a=1pq .....(iv)
अब apq=1pq+(pq−1).1pq=1
अतः A.P. का (pq) वाँ पद 1 हैं ।
उदाहरण 7
A.P. ज्ञात करे यदि उसके 7 वाँ और 13 वाँ पद क्रमशः 34 और 64 हैं ।
A.P. का n वाँ पद जिसका प्रथम पद a तथा सार्व - अंतर d हैं निम्नलिखित सूत्र से प्राप्त होता हैं ,
tn=a+(n−1)d
दिया हैं , t7=34
∴34=a+6d ....(i)
तथा t13=64
∴64=a+12d ...(ii)
समी (i) को (ii) से घटाने पर ,
30=6d ∴d=5
समी (i) में d=5 रखने पर
34=a+30 ∴a=4
अतः अभीष्ट A.P. है :
4,9,14,19,24....
4. समांतर श्रेढ़ी के `n` पदों का योग
माना कोई समांतर श्रेढ़ी जिसका प्रथम पद a तथा सार्व अंतर d का व्यापक रूप निम्न प्रकार है :
a,a+d,a+2d,a+3d,....a+(n−1)d
जहाँ n=1,2,3....n
इस A.P.का n वाँ पद a+(n−1)d है।
माना S इस A.P. के प्रथम n पदों के योग को व्यक्त करता है। तब Sn=a+(a+d)+(a+2d)+...+[a+(n−1)d]....(i)
पदों को विपरीत क्रम में लिखने पर हमें प्राप्त होता है:
Sn=[a+(n−1)d]+[a+(n−2)d]+...+(a+d)+a....(ii)
अब (i) और (ii) को पदों के अनुसार जोड़ने पर, हमें प्राप्त होता है :
2Sn=[2a+(n−1)d]+[2a+(n−1)d]+⋯+[2a+(n−1)d]+[2a+(n−1)d]] n बार
2Sn=n[2a+(n−1)d]
( चूँकि इसमें n पद हैं)
Sn=n2[2a+(n−1)d
अतः किसी समांतर श्रेढ़ी (AP) के प्रथम n पदों का योग का सूत्र निम्न है :
Sn=n2[2a+(n−1)d]
यदि किसी A.P का अंतिम पद l है तो पदों का योग :
S=n2(a+l)
आइए इसे उदाहरण से समझते है
यदि 1,2,3,4,5,6,7,8,9,10..... समांतर श्रेढ़ी मे है तब 7 पदों तक का योग कीजिए
1 + 2 + 3 + 4 + 5 + 6 + 7 = 28
अब इसे सूत्र केअनुसार हल करते हैं
सूत्र के अनुसार a=1, d=2−1=3−2=1 तथा n=7 होगा
चूँकि n पदों का योगफल
Sn=n2[2a+(n−1)d]
अतः 7 पदों का योगफल
S7=72[2×1+(7−1)×1]
⇒S7=72[2+6]
=72[8]=28
यहाँ से सही मान प्राप्त हुआ ।
टिप्पणी -
किसी AP का n वां पद प्रथम n पदों के योग तथा प्रथम n−1 पदों के योग के अंतर के बराबर होता है
अर्थात an=Sn−Sn−1
OMR (One Minute Revision)
S=n2[2a+(n−1)d
S=n2(a+l)
अर्थात
an=Sn−Sn−1
उदाहरण 8
समांतर श्रेढ़ी 1,4,7,10,.., के 20 पदों का योगफल ज्ञात कीजिए।
मान लीजिए दी गई समांतर श्रेढ़ी का प्रथम पद a तथा सार्व अन्तर d है ।
स्पष्ट है कि : a=1 तथा d=3
हमे दी गई श्रेढ़ी के 20 पदों का योगफल ज्ञात करना है।
सूत्र sn=n2{2a+(n−1)d} में
a=1 , d=3 तथा n=20 रखने पर
अभीष्ट योगफल
=S20=202{2×1+(20−1)×3}
=10×59=590
उदाहरण 9
यदि एक समांतर श्रेढ़ी का n वाँ पद an=3−5n है तो उसके n पदों का योगफल ज्ञात कीजिए।
दिया है,
अत: an=3−5n
∴a1=3−5×1=3−5=−2
दिया गया अनुक्रम एक समांतर श्रेढ़ी है जिसका प्रथम पद a=a1=−2 तथा अंतिम पद l=an=3−5n
a तथा l का मान सूत्र sn=n2(a+l) में रखने पर अभीष्ट योगफल
sn=n2{−2+3−5n}
=n2(1−5n)
उदाहरण 10
1 और 200 के बीच की सभी संख्याओं का योग ज्ञात करें जो 3 और 7 का अपवर्त्य हैं ।
3 और 7 दोनों से विभाज्य संख्याएँ वे ही होगी जो 3 और 7 के ल0 स0 अर्थात् 21 से भी विभाज्य होंगी ।
अर्थात् 21,42,63,.......,189
अब 1 और 200 के बीच 21 से विभाज्य प्रथम एंव अंतिम संख्यायें क्रमशः 21 और 189 हैं ।
यहाँ
a = 21
d = 21
an=189
∴189=21+(n−1)21
n=9
अब 3 और 7 से विभाज्य 1 और 200 के बीच के सभी पूर्णांकों का योग =n2[a+an]
=92[21+189]
=92×210
=945
उदाहरण 11
6 से विभाज्य होने वाली 100 से कम प्राकृत संख्याओं का योग ज्ञात कीजिए ।
6 से विभाज्य 100 से कम की सबसे छोटी संख्या एंव सबसे बड़ी संख्याएँ क्रमशः 6 और 96 हैं । अतः 6 से विभाज्य प्राकृत संख्याये
6,12,18,24, ..., 96 हैं ।
स्पष्टतः ये संख्याये A.P. में हैं ।
यहाँ a = 6 , d = 6 , tn=96
अब tn=96
⇒a+(n−1)d=96
⇒6+(n−1)6=96
⇒6n=96∴n=16
अब n पदों का योग
Sn=n2[2a+(n−1)d]
अभीष्ट योग ,
S16=162[2×6+(16−1)6]
=8×102=816
उदाहरण 12
A.P. 24,21,18 , .... के कितने पदों का योग 78 हैं ? दो उत्तरों का कारण बताइये ।
a=24,d=21−24=−3,Sn=78
हम जानते हैं कि
Sn=n2[2a+(n−1)d]
78=n2[48+(n−1)(−3)]
=n2[51−3n]
या , 3n2−51n+156=0
या , n2−17n+52=0
या , (n−4)(n−13)=0
∴ n=4 या , n=13
n के दोनों मान ग्राह्रा हैं ।
यहाँ 4 पदों का योग = 13 पदों का योग = 78
दो उत्तरों की व्याख्या :
दो उत्तर संभव हैं क्योंकि 5 वें से 13वें पद का योग शून्य हैं । यहाँ a≥0 और d≤0 और इसलिए शुरु से 13 पदों में कुछ पद धनात्मक और कुछ ऋणात्मक होंगे ।
उदाहरण 13
यदि किसी A.P. के प्रथम n , 2n, 3n पदों के योग क्रमशः S1,S2 और S3 हो , तो दिखाएँ कि S3=3(S2−S1)
A.P. के n पदों का योग
Sn=n2[2a+(n−1)d]
जहाँ a = प्रथम पद , d = सार्व अन्तर
अब S1=n पदों का योग
S1=n2[2a+(n−1)d]
S2=2n पदों का योग
S2=n2[2a+(2n−1)] ...(ii)
S3=3n पदों का योग
S3=3n2[2a+(3n−)d] ...(iii)
समी (i) को (ii) से घटाने पर हम पाते हैं ,
S2−S1=2n2[2a+(2n−1)d]−n2[2a+(n−1)d]
=n2[2a+(3n−1)d]
∴3(S2−S1)=3n2[2a+(3n−1)d]
3(S2−S1)=S3 [ समी (iii) से ]
सारांश
a,a+d,a+2d,a+3d......a+(n−1)d
जहाँ n=1,2,3,4,5...
an=a+(n−1)d
an को समांतर श्रेढ़ी (AP) का व्यापक पद भी कहते हैं।
a प्रथम पद है
d सार्वान्तर है
n पद का क्रमांक है
S=n2[2a+(n−1)d
S=n2(a+l)
अर्थात an=Sn−Sn−1