वृत्त कक्षा 10 गणित

Table Of Contents

भूमिका

बच्चों, अध्याय के शीर्षक के अनुसार इस अध्याय में हम वृत्त के बारे में अध्ययन करेंगे। आपने पिछली कक्षा में वृत्त के बारे में पढ़ा होगा, इस कक्षा में और अच्छे से जानने का प्रयास करते है।
आप अपने दैनिक जीवन में, बहुत सी ऐसी वस्तुओं के संपर्क में अवश्य आए होंगे जिनके आकार गोल हों, जैसे - किसी गाड़ी का पहिया, चूड़ियाँ, घड़ियों के डायल, सिक्के, चाबी के गुच्छे, कमीज के बटन आदि।

आइए बच्चों वृत्त को समझते हैं और करीब से...

बच्चों! आइए कक्षा 9 का पुनरावलोकन करते है।
जैसा की हम जानते है, वृत्त किसी नियत बिंदु के चारों ओर समान दूरी पर स्थित बिंदुओं का समूह होता है।
इसे एक उदाहरण से समझते है, जैसा की आपने चूड़ियाँ देखी होगी, चूड़ी वृत्त का एक अच्छा उदाहरण है। यदि चूड़ी का केंद्र ले तब हम देख पाएंगे की उसका केंद्र उसके सतहों से समान दूरी पर है।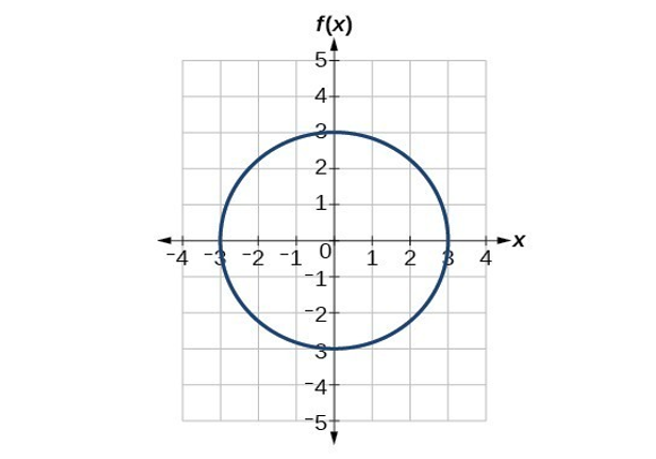
ocr_image

यह देखने के लिए एक ग्राफ पेपर ले और चूड़ी को मूलबिंदु के पास ले जाए और अब x - अक्ष के धनात्मक व ऋणात्मक दिशा में समान मान (उदाहरण $+ 3 व - 3$ ) उसके सतह (परिधि) पर लाने का प्रयास करे। इससे आप देखेंगे की y - अक्ष में भी आप वही मान प्राप्त करेंगे जो x - अक्ष में प्राप्त हुआ था, तथा चूड़ी का केंद्र मूलबिंदु (0, 0) पर मिलेगा। इससे हम कह सकते हैं चूड़ी के सतह, मूल बिंदु (केंद्र) से समान दूरी पर है, अतः परिभाषा के अनुसार यह वृत्त है।

इसी प्रकार आपने ध्यान दिया होगा कि घड़ी में सेकेंड की सुई घड़ी के डायल के ऊपर जल्दी-जल्दी चक्कर लगाती हैं तथा इसका एक सिरा एक गोल पथ में चलता है। सेकेंड की सुई के सिरे से बनता हुआ पथ एक वृत्त (circle) है। वृत्त में कुछ भाग ( त्रिज्या, व्यास, वृत्तखण्ड आदि) होते है, जिनसे वृत्त का निर्माण होगा यहाँ हमने केंद्र को समझा जो चूड़ी के सतह से समान दूरी पर है, यहाँ जिस समान दूरी की बात कर रहे हैं वह वृत्त की त्रिज्या कहलाती हैं । यहाँ जो चूड़ी की चारों तरफ सतह हैं विभिन्न बिंदुओं से मिलकर बना हैं परिधि कहलाता है, तथा चूड़ी का अर्थात परिधि का एक छोटा भाग, चाप कहलाता है। इसी प्रकार अन्य भागों के लिए कुछ परिभाषाये हैं आइए इसे नीचे देखते है।

वृत्त व वृत्त से संबंधित पद

वृत्त (circle)

एक तल पर उन सभी बिंदुओं का समूह, जो तल के एक स्थिर बिंदु से, एक स्थिर दूरी पर स्थित हों, वृत्त कहलाता है।

नीचे दिए गए आकृति में आप देख सकते हैं की हमने एक काला बिंदु लिया हैं वह स्थिर बिंदु हैं तथा तीन लाल बिंदु हैं जो काले बिंदु से एक निश्चित दूरी पर स्थित हैं अर्थात ये तीनों बिंदुओं की दूरी बराबर हो, तो इन सभी बिंदुओं का समूह वृत्त कहलाता हैं|

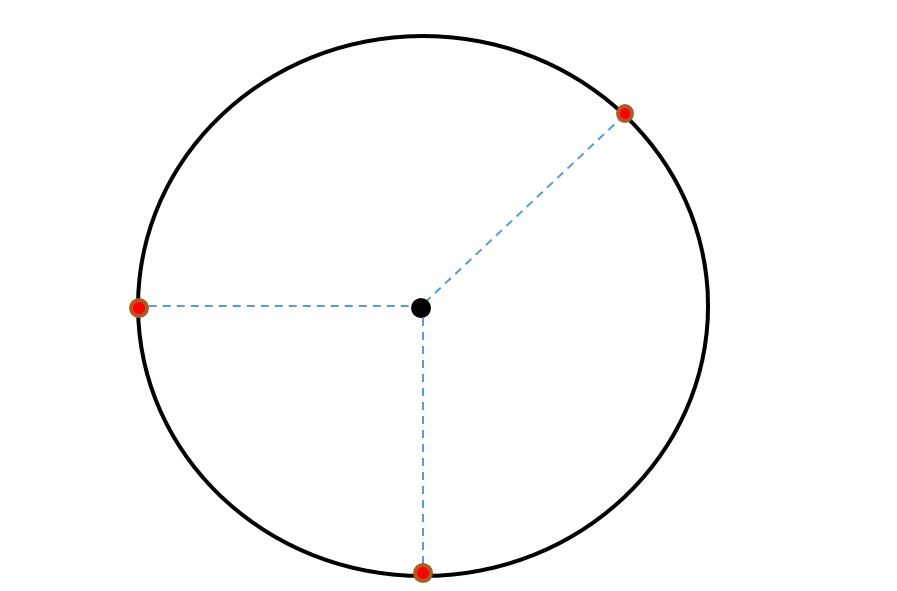
ocr_image

केन्द्र (centre)

स्थिर बिंदु को वृत्त का केन्द्र (centre) कहते हैं या एक निश्चित बिंदु जहां से बिंदुओं का समूह निश्चित दूरी पर होता है, वृत्त का केंद्र कहलाता है।

त्रिज्या (Radius)

केंद्र को वृत्त के किसी बिंदु से मिलाने वाला रेखाखंड, वृत्त की त्रिज्या कहलाती हैं | लंबाई

O P

वृत्त की त्रिज्या हैं तथा

O

वृत्त का केन्द्र है|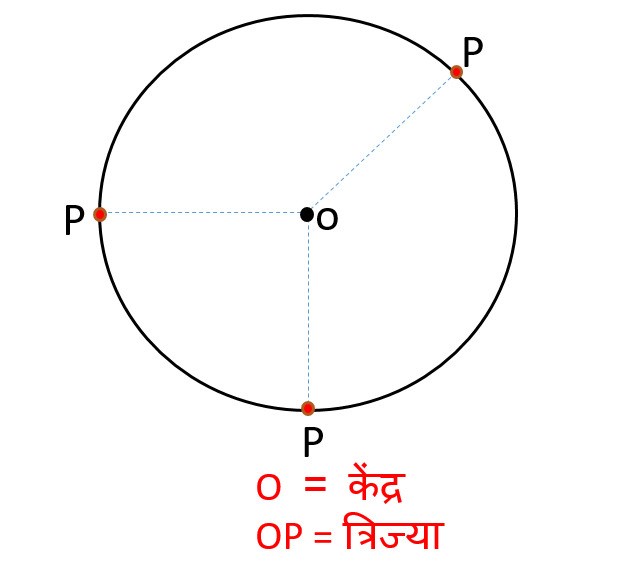

ocr_image

अभ्यंतर, वृत्त तथा बहिर्भाग

वृत्त का तल, जिस पर वह स्थित है, तीन भागों में विभाजित करता हैं -

(i) वृत्त के अन्दर का भाग, जिसे अभ्यंतर (interior) भी कहते हैं|
(ii) वृत्त|
(iii) वृत्त के बाहर का भाग, जिसे बहिर्भाग (exterior) भी कहते हैं|
वृत्त तथा इसका अभ्यंतर मिलकर वृत्तीय क्षेत्र (circular region) बनाते है|

ocr_image

जीवा

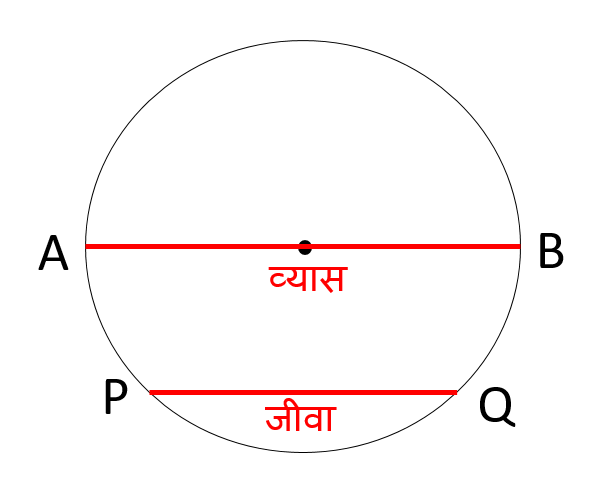
वृत्त के अंदर किन्हीं 2 बिंदुओं को मिलाने वाले रेखाखंड को जीवा कहते हैं आकृति में PQ वृत्त की जीवा हैं|

व्यास

जीवा, जो वृत्त के केंद्र से होकर जाती हैं वृत्त का व्यास कहलाती हैं| व्यास वृत्त की सबसे लम्बी जीवा होती हैं तथा वृत्त में सभी व्यासों की लम्बाई समान होती हैं| व्यास, त्रिज्या का दुगना होता हैं। वृत्त का व्यास

= 2 \times

त्रिज्या
आकृति में

A B

वृत्त का व्यास हैं|

ocr_image

चाप (arc)

दो बिंदुओं के बीच के वृत्त के भाग को एक चाप (arc) कहते हैं। आकृति में, बिंदुओं P तथा Q के बीच के वृत्त के भागों को देखिए। आप पाएंगे कि दोनों भागों में से एक बड़ा हैं तथा एक छोटा हैं बड़े भाग को दीर्घचाप तथा छोटे भाग को लघु चाप कहते हैं|

ocr_image

अर्धवृत्त (semicircle)

जो पूरा गोला होता हैं उसका आधा अर्धवृत्त कहलाता हैं । दूसरे शब्दों में कहा जाए तो किसी वृत्त में बीच के बिंदु को मिलाते हुए जो सीधी रेखा उस वृत्त को 2 भागो में बांट देगी, दो अलग अलग भाग अर्धवृत्त होंगे पूरा मिलाने पर वह सिर्फ वृत्त होगा।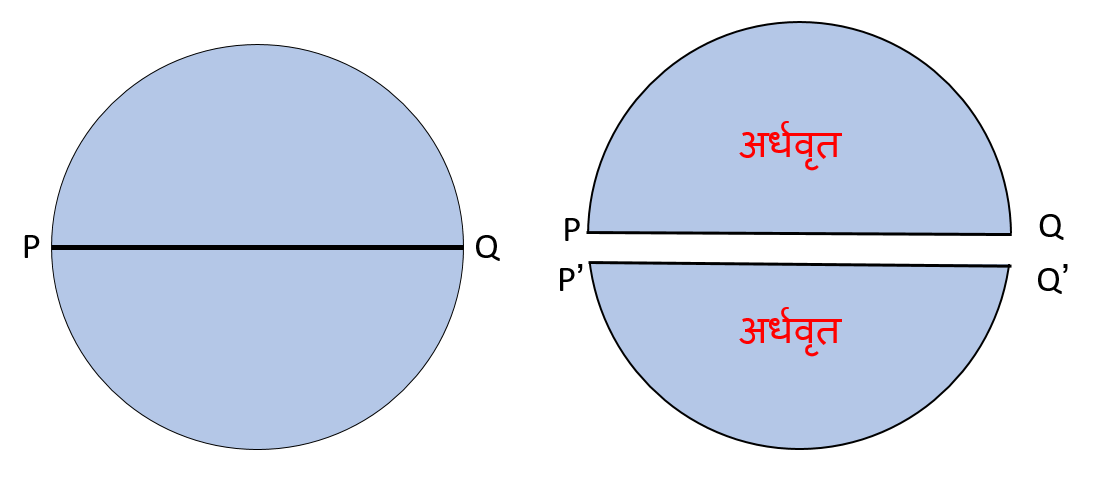

ocr_image

परिधि (circumference)

संपूर्ण वृत्त की लम्बाई को उसकी परिधि (circumference) कहते हैं। या वृत्त का एक चक्कर लगाने में जो दूरी तय की जायेगी उस माप को परिधि कहते हैं। परिधि से केंद्र की दूरी हर स्थिति में एक समान ही होती है।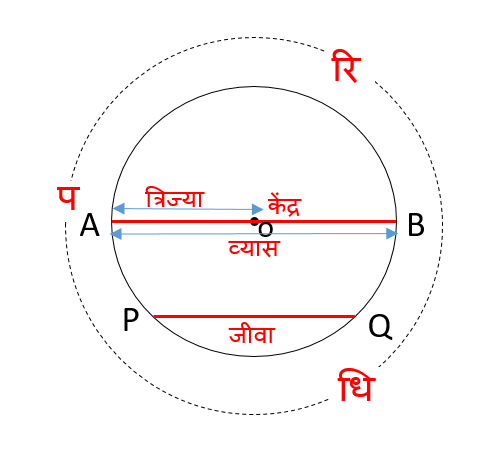

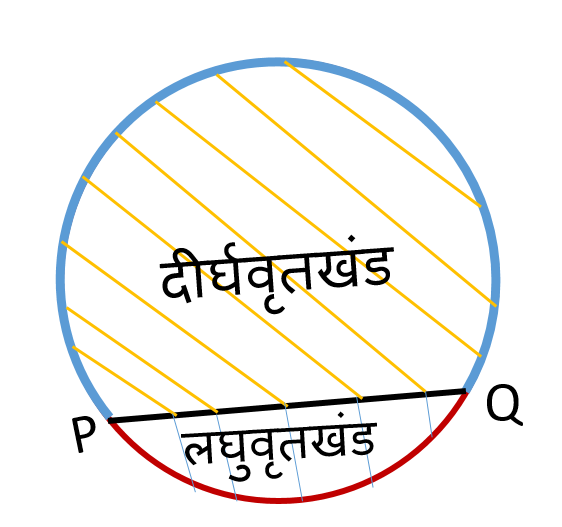
ocr_image

वृत्तखंड

वृत्त की प्रत्येक जीवा तथा चाप वृत्त को दो भागों में विभाजित करती हैं। प्रत्येक भाग को वृत्तखंड कहते है। आप पाएंगे कि दो प्रकार के वृत्तखंड होते हैं -

(i) दीर्घ वृत्तखंड (ii) लघु वृत्तखंड

ocr_image

त्रिज्यखंड (sector)

केन्द्र को एक चाप के सिरों से मिलाने वाली त्रिज्याओं एवं चाप के बीच के क्षेत्र को त्रिज्यखंड (sector) कहते हैं। आकृति में, क्षेत्र OPQ लघु त्रिज्यखंड तथा शेष वृत्तीय क्षेत्र दीर्घ त्रिज्यखंड है। जब दोनों चाप बराबर हो जाते हैं, अर्थात् प्रत्येक अर्धवृत्त होता है, तो दोनों वृत्तखंड तथा दोनों त्रिज्यखंड एक समान हो जाते हैं और प्रत्येक को अर्धवृत्तीय क्षेत्र कहते हैं।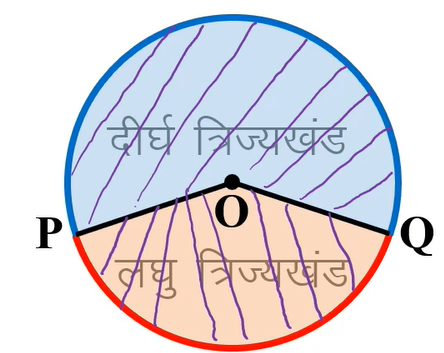

ocr_image

OMR (One Minute Revision)

वृत्तों से संबंधित महत्वपूर्ण परिभाषाये

परिधि (Circumstance)
किसी नियत बिंदु (केंद्र) के चारों ओर समान दूरी पर स्थित बिंदुओं का समूह परिधि कहलाता है।

केंद्र (Center)
वृत्त पर स्थित नियत बिंदु जो परिधि के प्रत्येक बिंदु से समान दूरी पर हो केंद्र कहलाता है।

त्रिज्या (Radius)
केंद्र से परिधि को जोड़ने वाला रेखाखण्ड त्रिज्या कहलाता हैं ।

व्यास (Diameter)
परिधि के किसी एक बिंदु से परिधि के किसी दूसरे बिंदु को जोड़ने वाला रेखाखण्ड जो केंद्र से होकर जाता हैं , व्यास कहलाता हैं । व्यास की लंबाई किसी एक वृत्त के लिए सदैव समान होगी तथा त्रिज्या के दोगुनी होगी।

जीवा (Chord)
परिधि के किसी एक बिंदु से परिधि के किसी दूसरे बिंदु को जोड़ने वाला रेखाखण्ड जीवा कहलाता हैं परन्तु आवश्यक नहीं हैं की केंद्र से होकर जाता हो , किसी एक वृत्त में विभिन्न प्रकार की जीवाये होती हैं (व्यास वृत्त की सबसे बड़ी जीवा होती है)।

चाप (Arc)
परिधि का एक भाग चाप कहलाता है, यदि परिधि में कोई दो बिंदु लिए जाए तो हमें 2 भाग प्राप्त होंगे, छोटा भाग लघु चाप तथा बड़ा भाग दीर्घ चाप कहलाता हैं ,अब यदि दोनों भाग बराबर हो जाए तो वे दोनों अर्धवृत्त कहलाते है।

त्रिज्यखण्ड (Sector)
किन्ही दो त्रिज्याओ व एक चाप से घिरा क्षेत्र त्रिज्यखण्ड कहलाता हैं ।

वृत्तखण्ड (Segment)
किसी जीवा व चाप के मध्य घिरा क्षेत्र वृत्तखण्ड कहलाता हैं ।

उदाहरण 1

उस वृत्त की त्रिज्या ज्ञात कीजिये जिसकी परिधि, 36 सेमी. व 20 सेमी. व्यास वाले दो वृत्तों की परिधि के योग के बराबर है

माना वृत्त की त्रिज्या = R सेमी
तथा माना दिए गए दो वृत्तो की त्रिज्याएँ क्रमशः $r_{1}$ तथा $r_{2}$ हैं
अर्थात $r_{1} = \frac{36}{2} = 18$ सेमी.
एवं $r_{2} = \frac{20}{2} = 10$ सेमी.

प्रश्न अनुसार
$2 π R = 2 π r_{1} + 2 π r_{2}$
$2 π R = 2 π (r_{1} + r_{2})$
$R = 18 + 10$
$R = 28$ सेमी.

Learn more

वृत्त की स्पर्श रेखा

वृत्त की स्पर्श रेखा से संबंधित महत्वपूर्ण तथ्य

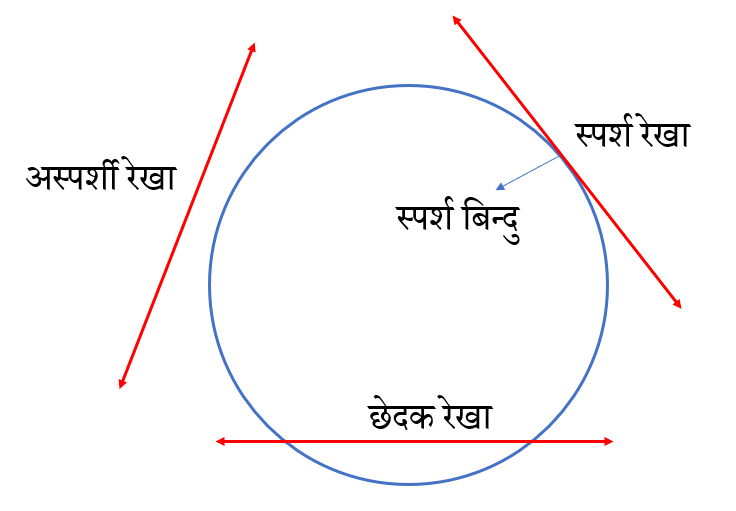
जैसा की चित्र में दर्शाया गया है, एक वृत्त पर निम्न प्रकार से रेखा खींची जा सकती हैं

छेदक रेखा (Secant)

किसी वृत्त को दो भिन्न बिंदुओं पर प्रतिच्छेद करने वाली रेखा, छेदक रेखा कहलाती हैं ।

अस्पर्श रेखा

वह रेखा जो वृत्त को किसी भी बिंदु पर प्रतिच्छेद नहीं करती हैं अर्थात रेखा और वृत्त में कोई उभयनिष्ठ बिंदु नहीं होता हैं, अस्पर्शी रेखा कहलाती हैं

स्पर्श रेखा (Tangent)

किसी वृत्त की स्पर्श रेखा वृत्त को केवल एक बिंदु पर स्पर्श करती हैं ।

इसके अतिरिक्त वृत्त और एक रेखा में अन्य कोई संबंध स्थापित नहीं हो सकता।

छेदक रेखा और स्पर्श रेखा-

यहां, यदि छेदक रेखा को केंद्र से दूर करते जाए तो एक स्थिति ऐसी आएगी जहाँ वह एक स्पर्श रेखा बन जाएगा। अब चूँकि छेदक रेखा दो बिंदुओं को प्रतिच्छेद करती है, जिससे एक जीवा प्राप्त होती है। इस स्थिति में हम कह सकते हैं की स्पर्श रेखा, छेदक रेखा की विशेष स्थिति है, जब संगत जीवा के दोनों सिरे संपाती हो जाते है।

स्पर्श बिन्दु-

स्पर्श रेखा वृत्त को एक बिंदु पर स्पर्श करती है, वृत्त के जिस बिंदु पर स्पर्श रेखा वृत्त को स्पर्श करती हैं स्पर्श बिन्दु कहलाता है।
चूँकि वृत्त की परिधि पर अनंत बिंदुओं के स्थित होने के कारण वृत्त से अनंत स्पर्श रेखाएं गुजर सकती है।

प्रमेय-1

वृत्त की स्पर्श रेखा स्पर्श बिंदु से होकर जाने वाली त्रिज्या पर लंब होती है।

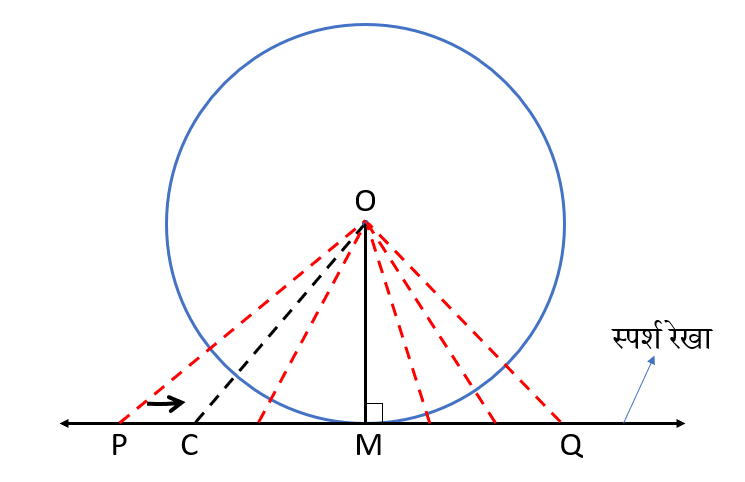
माना,
किसी वृत्त पर कोई स्पर्श रेखा PQ, हैं तथा M स्पर्श बिंदु है
अब यदि केंद्र बिंदु से स्पर्श रेखा के बिंदु P को मिलाए तब एक रेखाखण्ड मिलेगा, इसी प्रकार P से M की ओर आने पर केंद्र से स्पर्श रेखा की दूरी क्रमशः कम होती जाएगी तथा M से Q की ओर जाने पर पुनः दूरी बढ़ती जाएगी। ऐसा इसलिए होता हैं चूँकि M वृत्त पर स्थित हैं तथा स्पर्श रेखा के अन्य बिंदु वृत्त से बाहर है।
इस प्रकार M को छोड़ कर स्पर्श रेखा पर स्थित किसी अन्य बिंदु को यदि हम C से दर्शाये तब

O C > O M

अतः हम कह सकते हैं की OM, केंद्र से स्पर्श रेखा की न्यूनतम दूरी हैं साथ ही हमें ज्ञात हैं की किसी बिंदु से किसी रेखा की न्यूनतम दूरी उस रेखा पर बिंदु से लम्बवत दूरी के बराबर होता है।

अतः $O M ⊥ P Q$

इस प्रकार हम कह सकते हैं कि वृत्त की स्पर्श रेखा, स्पर्श बिंदु से होकर जाने वाली त्रिज्या पर लंब होती है।

एक बिंदु से एक वृत्त पर स्पर्श रेखाओ की संख्या

बच्चों, यहां हम देखेंगे कि एक बिंदु से एक वृत्त पर कितने प्रकार से स्पर्श रेखाएं खींची जा सकती हैं उससे पहले यह देखते हैं कि किसी वृत्त के सापेक्ष किसी बिंदु की कितनी स्थितियाँ हो सकती है।
यदि कोई बिंदु P मान लें तो उस बिंदु की वृत्त के सापेक्ष निम्न तीन संभव स्थितियाँ हो सकती है,

1. बिंदु P वृत्त के अंदर स्थित हो,
2. बिंदु P वृत्त पर स्थित हो, तथा
3. बिंदु P वृत्त के बाहर स्थित हो।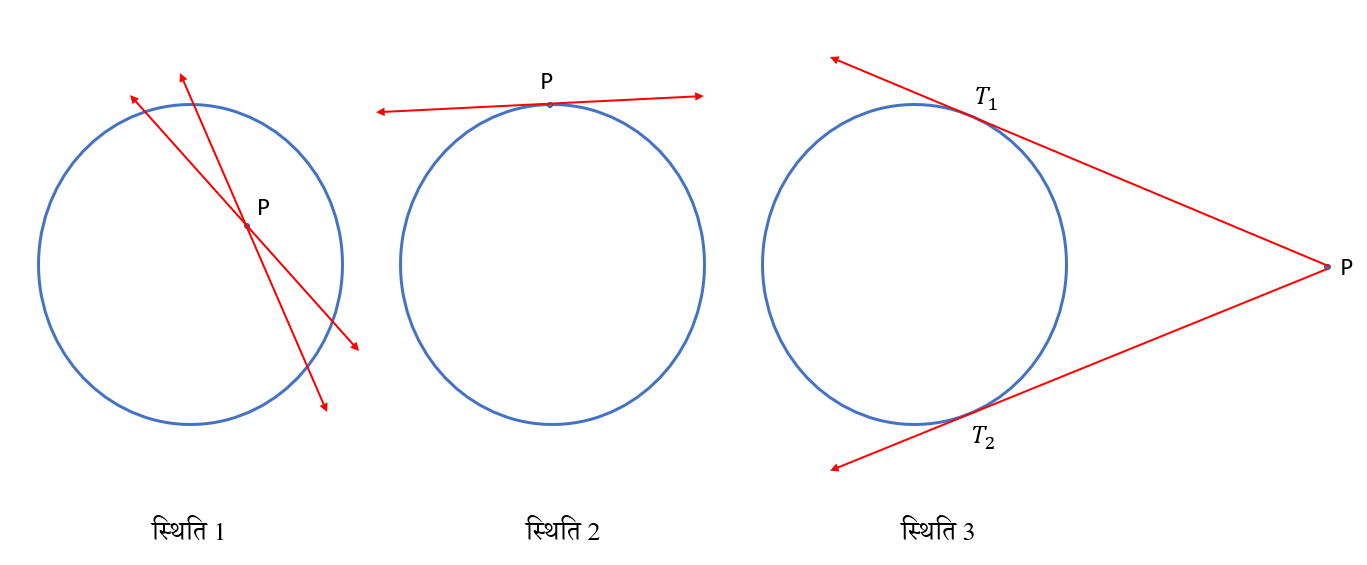

ocr_image

अब यदि वृत्त के अंदर स्थित बिंदु को देखे तो इससे होकर जाने वाली कोई भी रेखा स्पर्श रेखा नहीं होगी, इसी प्रकार वृत्त पर स्थित बिंदु देखें तो इससे होकर जाने वाली एक और केवल एक रेखा स्पर्श रेखा होगी तथा वृत्त के बाहर स्थित बिंदु की बात करें तो इससे होकर जाने वाली दो और केवल दो स्पर्श रेखाएं प्राप्त होगी।
स्थिति 3 के अनुसार बिंदु P से होकर जाने वाली दो रेखाएं वृत्त की स्पर्श रेखाएं है, अतः दो स्पर्श बिंदु ( $T_{1}$ व $T_{2}$ ) भी प्राप्त होंगे। इस प्रकार बिंदु P से क्रमशः $T_{1}$ व $T_{2}$ की दूरी $P T_{1}$ व $P T_{2}$ होगी , ये दोनों दूरियाँ स्पर्श रेखाओ की लंबाई है।

प्रमेय-2

बाह्य बिंदु से वृत्त पर खींची गई स्पर्श रेखाओं की लंबाइयाँ बराबर होती है।

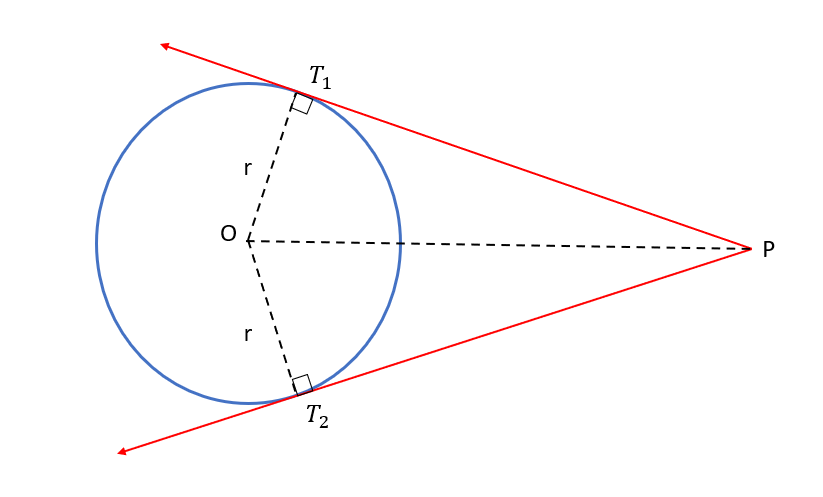
माना,
बिंदु P, वृत्त का बाह्य बिंदु हैं तथा इससे होकर जाने वाले रेखाओ में से दो रेखाएं ऐसी हैं जो वृत्त की स्पर्श रेखाएं है।

माना, स्पर्श रेखाओ की लंबाई क्रमशः

P T_{1}

व

P T_{2}

है,
जहाँ

T_{1}

व

T_{2}

स्पर्श बिंदु है।

अब यदि बिंदु P तथा स्पर्श बिंदु

T_{1}

व

T_{2}

को केंद्र O से मिलाए, तब हमें दो त्रिभुज

△ P O T_{1}

व

△ P O T_{2}

प्राप्त होंगे

अतः

△ P O T_{1}

व

△ P O T_{2}

में

O T_{1} = O T_{2} = r

(वृत्त की त्रिज्या)

O P = O P

(उभयनिष्ठ भुजा)

∠ P T_{1} O = ∠ P T_{2} O = 90^{\circ}

(वृत्त की त्रिज्या, स्पर्श रेखा पर लंब होती है)

अतः

△ P O T_{1} ≅ △ P O T_{2}

अतः

P T_{1} = P T_{2}

इस प्रकार हम कह सकते हैं की बाह्य बिंदु से वृत्त पर खींची गई स्पर्श रेखाओं की लंबाइयाँ बराबर होती है।

ध्यान दें - यहाँ OP,

∠ T_{1} P T_{2}

का कोण अर्द्धक रेखा हैं अतः

∠ T_{1} P O = ∠ T_{2} P O

तथा
त्रिभुजों

△ P O T_{1}

व

△ P O T_{2}

में पाइथागोरस प्रमेय का उपयोग किया जा सकता हैं चूँकि

∠ P T_{1} O = ∠ P T_{2} O = 90^{\circ}

OMR (One Minute Revision)

वृत्त की स्पर्श रेखा स्पर्श बिंदु से होकर जाने वाली त्रिज्या पर लंब होती है।

वह रेखा जो त्रिज्या के छोर बिंदु से होकर जाती हैं और इस पर लंब है, वृत्त की स्पर्श रेखा होती है।

किसी बाह्य बिंदु से वृत्त पर खींची गई दो स्पर्श रेखाओं की लंबाइयाँ बराबर होती हैं।

संकेन्द्रीय वृत्त

संकेन्द्रीय वृत्त - एक ही बिंदु को केंद्र मानकर बनाये गए वृत्त, संकेन्द्रीय वृत्त कहलाते हैं अर्थात वे वृत्त जिनके केंद्र उभयनिष्ठ होते हैं, संकेन्द्रीय वृत्त कहलाते हैं

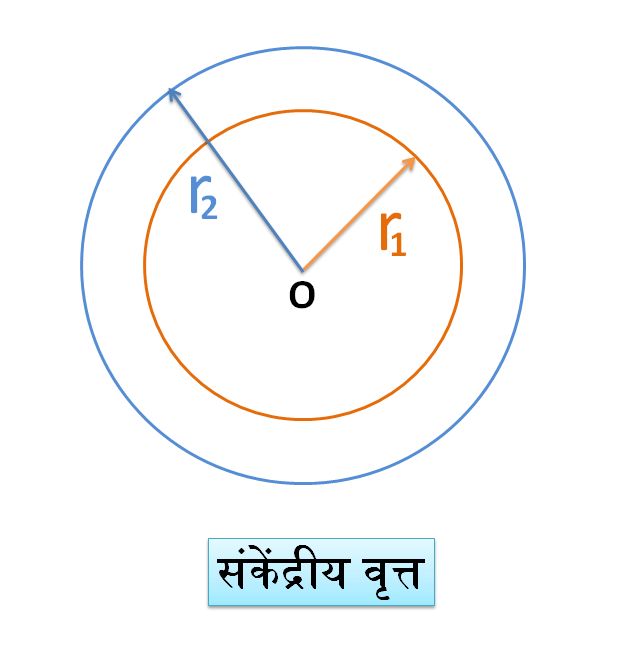
ocr_image

दो सकेंद्रीय वृत्तों में बड़े वृत्त की जीवा जो छोटे वृत्त को स्पर्श करती है, स्पर्श बिंदु पर समद्विभाजित होती है।

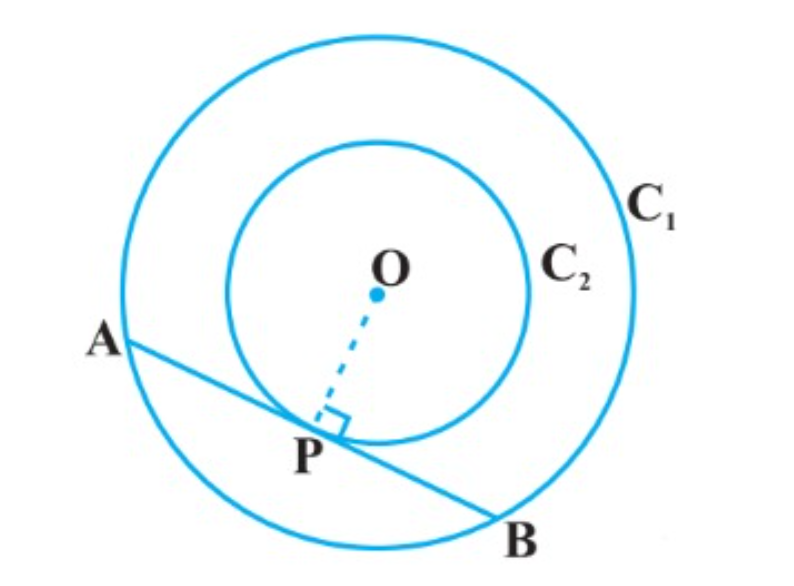
ocr_image

अतः चित्रानुसार

A P = B P

किसी बाह्य बिंदु से किसी वृत्त पर खींची गई स्पर्श रेखाओं के बीच का कोण, स्पर्श बिंदुओं को मिलाने वाले रेखाखंड द्वारा केंद्र पर अंतरित कोण का संपूरक होता है।

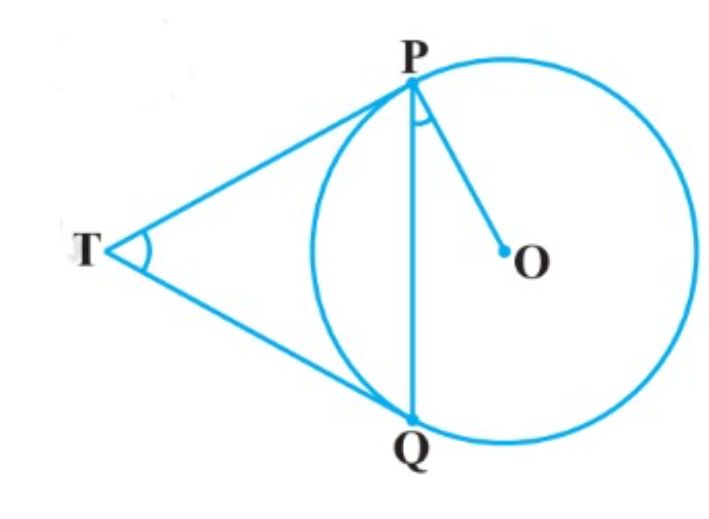
ocr_image

अतः चित्रानुसार

∠ P T Q + ∠ P O Q = 180^{\circ}

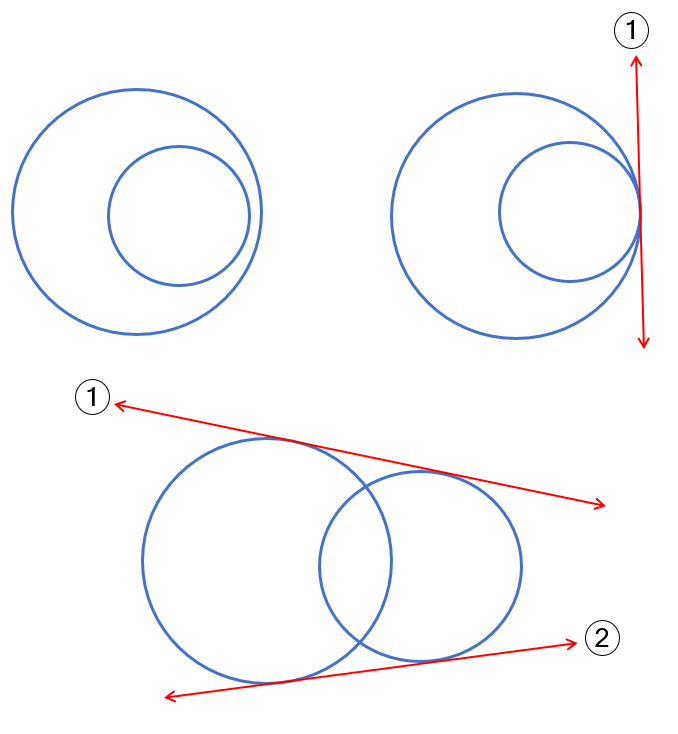
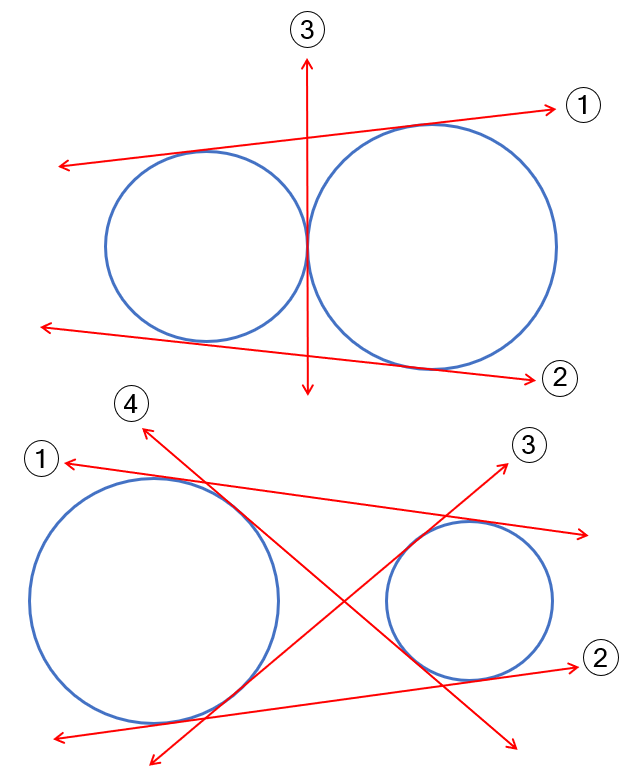
दो वृत्तों की उभयनिष्ठ स्पर्श रेखाएँ

दो वृत्तों की विभिन्न स्थितियो में निम्न प्रकार से उभयनिष्ठ स्पर्श रेखाएं प्राप्त हो सकती हैं -

उदाहरण 1

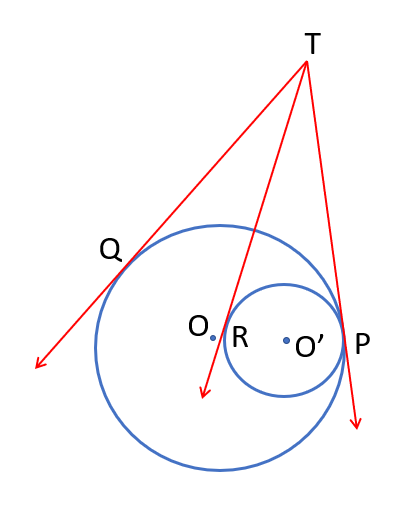
दो वृत्त जिसके केंन्द्र O और O' है, एक -दूसरे को अन्तः बिंदु P पर स्पर्श करते है। उभयनिष्ठ स्पर्श रेखा PT के बिंदु T से वृत्तों पर रेखाएं क्रमशः TQ और TR खींची जाती है।
सिद्ध कीजिए कि
रेखाखण्ड TR = रेखाखण्ड TQ

प्रश्न से-

हम जानते हैं कि,
बाह्य बिंदु से वृत्त पर खींची गयी दोनों स्पर्श रेखाएं लम्बाई में बराबर होती हैं [प्रमेय-2]

∴

केंन्द्र O वाले वृत्त के लिए :

T P = T Q ... . (1)

तथा केंन्द्र O' वाले वृत्त के लिए :

T P = T R ... . (2)

अतः (1) और (2) से,

T R = T Q

यही सिद्ध करना था।

Learn more

उदाहरण 2

चित्र में, यदि O वृत्त का केंन्द्र हैं तथा यदि $∠ B O C = 110^{\circ}$ और AB तथा AC वृत्त की स्पर्श रेखाएं है, तो $∠ O A B$ की माप ज्ञात कीजिए।

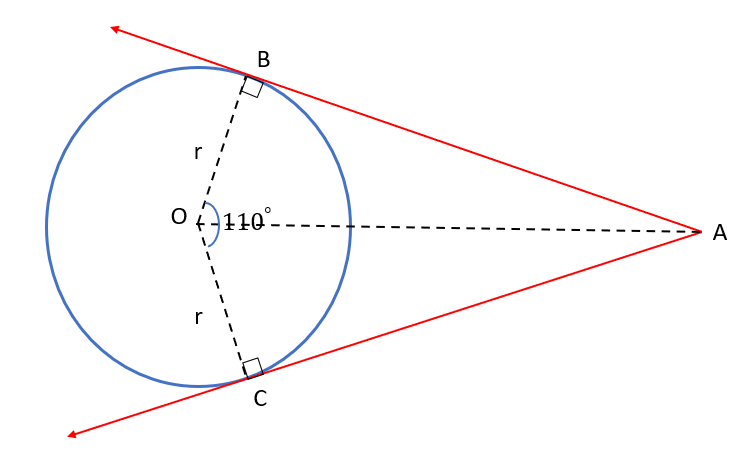
चूँकि हमें ज्ञात है
बाह्य बिंदु से वृत्त पर खींची गयी दोनों स्पर्श रेखाएं लम्बाई में बराबर होती हैं [प्रमेय-2]
$A B = A C$
अतः $∠ A O B = ∠ A O C = α$ (समान भुजाओ के सम्मुख कोण)

अतः $2 α = ∠ B O C = 110^{\circ}$

$∴ ∠ A O B = \frac{1}{2} ∠ B O C$

$∠ A O B = \frac{1}{2} \times 110^{\circ}$

$= 55^{\circ}$

तथा $∠ A B O = 90^{\circ}$
तब $∠ O A B = 180^{\circ} - (55^{\circ} + 90^{\circ})$

$= 180^{\circ} - 145^{\circ}$ $= 35^{\circ}$

अतः $∠ O A B = 35^{\circ}$

Learn more

उदाहरण 3

5 सेमी. त्रिज्या के एक वृत्त की 8 सेमी. लम्बी एक जीवा PQ है। P और Q पर स्पर्श रेखाएं परस्पर एक बिंदु T पर प्रतिच्छेद करती है। TP की लम्बाई ज्ञात कीजिए।

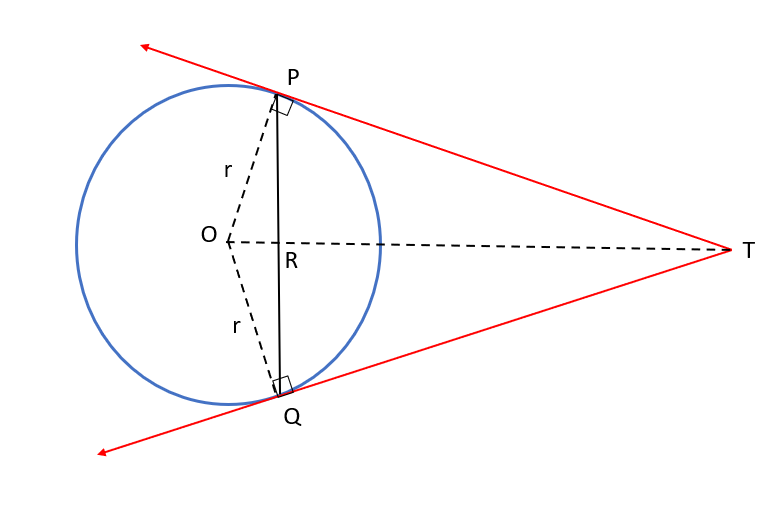
सर्वप्रथम OT को मिलाया,
माना OT, PQ को बिंदु R पर काटती है
अतः

Δ T P Q

समद्विबाहु त्रिभुज हैं (चूँकि

T P = T Q

)
और

T O, ∠ P T Q

का अर्द्धक है।

इसलिए

O T ⊥ P Q

तब

O T

P Q

का अर्द्धक है
(चूँकि

O R

, केंद्र से जीवा

P Q

पर लम्ब हैं (

O R ⊥ P Q

) अतः PQ को समद्विभाजित करेगी।)

अतः

\frac{P Q}{2} = P R

= R Q

= \frac{8}{2} = 4

सेमी.

चूँकि

△ P O R

समकोण त्रिभुज हैं जहाँ

∠ P R O

समकोण हैं
अतः

O P^{2} = O R^{2} + P R^{2}

∴ O R = \sqrt{O P^{2} - P R^{2}}

= \sqrt{{(5)}^{2} - {(4)}^{2}}

= 3

सेमी.

∠ T P R + ∠ R P O

= ∠ T P O = 90^{\circ}

....(1)

तथा

∠ T P R + ∠ P T R = 90^{\circ}

....(2) (

△ T P R

में )

अतः

△ T P R

व

△ P R O

में

∠ R P O = ∠ P T R

(समी. (1) व (2) से)

तथा

∠ P R T = ∠ P R O = 90^{\circ}

∴ Δ T R P ≅ Δ P R O,

(AA समरूपता से)

अतः

\frac{T P}{P O} = \frac{R P}{R O}

\frac{T P}{5} = \frac{4}{3}

अतः

T P = \frac{20}{3}

सेमी.

Learn more

महत्वपूर्ण बिन्दु

त्रिज्या (Radius)
केंद्र से परिधि को जोड़ने वाला रेखाखण्ड त्रिज्या कहलाता हैं ।

चाप (Arc)
परिधि का एक भाग चाप कहलाता है, यदि परिधि में कोई दो बिंदु लिया जाए तो हमें 2 भाग प्राप्त होगा छोटा भाग लघु चाप तथा बड़ा भाग दीर्घ चाप कहलाता हैं ,अब यदि दोनों भाग बराबर हो जाए तो वे दोनों अर्धवृत्त कहलाते है।

छेदक रेखा (Secant)
किसी वृत्त को दो भिन्न बिंदुओं में प्रतिच्छेद करने वाली रेखा, छेदक रेखा कहलाती हैं ।

स्पर्श रेखा (Tangent)
किसी वृत्त की स्पर्श रेखा वृत्त को केवल एक बिंदु पर स्पर्श करती हैं ।

स्पर्श बिंदु (Point of contact)
स्पर्श रेखा वृत्त को जिस बिंदु पर स्पर्श करती है, स्पर्श बिंदु कहलाती हैं ।

वृत्तखण्ड (Segment)
किसी जीवा व चाप के मध्य घिरा क्षेत्र वृत्तखण्ड कहलाता हैं ।

वृत्त की स्पर्श रेखा स्पर्श बिंदु से होकर जाने वाली त्रिज्या पर लंब होती है।

Home
Ask Doubt
Profile