निर्देशांक ज्यामिति कक्षा 10 गणित
भूमिका
बच्चों, कक्षा 9 मे आपने निर्देशांक ज्यामिति के बारे में पढ़ा था, निर्देशांक ज्यामिति गणित की वह शाखा है जिसमें समतल पर बिन्दुओं की स्थिति को दो संख्याओं के जोड़े से परिभाषित किया जाता है। जिन संख्याओं के जोड़ों से उस बिंदु की स्थिति को परिभाषित किया जाता है वे दो बिंदु निर्देशांक कहलाते हैं। इस युग्म मे x निर्देशांक तथा y निर्देशांक या नियामक होता है, जहाँ x निर्देशांक (भुज) बिन्दु की Y−अक्ष से लम्बवत दूरी तथा y निर्देशांक (कोटि) बिन्दु की X−अक्ष से लम्बवत दूरी को कहते है तथा इसे (x,y) द्वारा दर्शाया जाता है। इस अध्याय मे हम दो बिन्दुओ के बीच की दूरी, एक रेखा के मध्य-बिंदु का पता लगाना, दो बिन्दुओ को जोड़ने वाली रेखाखण्ड का किसी अन्य बिन्दु के सापेक्ष विभाजन, तीन बिन्दुओ के मध्य (त्रिभुज) के क्षेत्रफल आदि के बारे मे बात करेंगे।
आइए बच्चों निर्देशांक ज्यामिति को समझते है और करीब से...
बच्चों! आपने इससे पूर्व की कक्षाओं में निर्देशांक ज्यामिति के बारे मे पढ़ा हैं। आइये जो हमने पढ़ा था उसे पुनः याद कर लेते है -
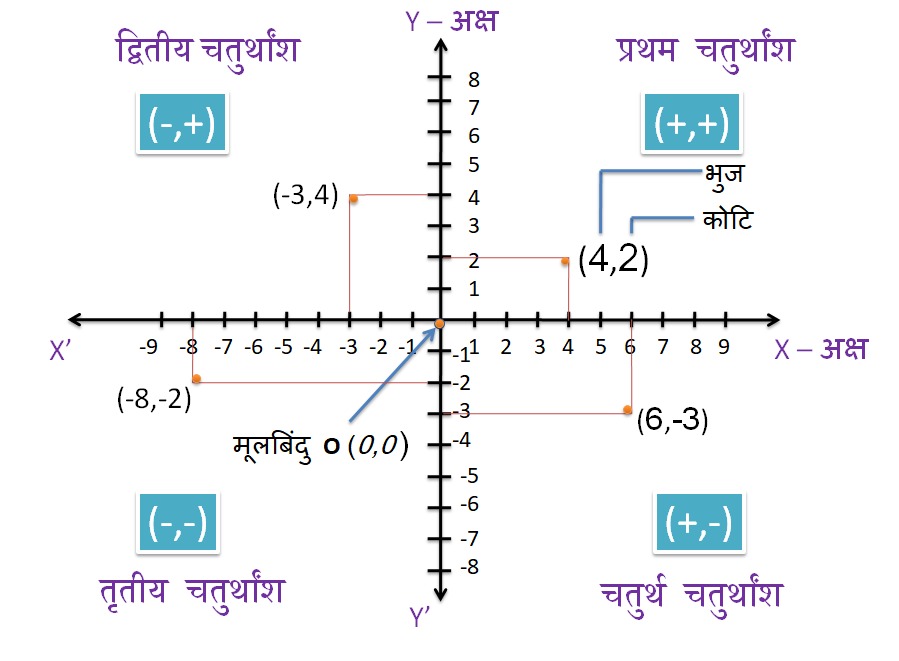
(i) पहले चतुर्थांश में, x और y दोनों निर्देशांक धनात्मक होते है।
(ii) दूसरे चतुर्थांश में, x निर्देशांक ऋणात्मक व y निर्देशांक धनात्मक होता है।
(iii) तीसरे चतुर्थांश में, x और y दोनों निर्देशांक ऋणात्मक होते है।
(iv) चौथे चतुर्थांश में, x निर्देशांक धनात्मक व y निर्देशांक ऋणात्मक होता है।
निर्देशांक ज्यामिति के कुछ मूलभूत बिंदुओं का परिचय हमने ऊपर देखा, इसके अतिरिक्त पिछली कक्षाओं में हमने मुख्य रूप से दो लम्ब अक्षों (X व Y) के माध्यम से बनने वाले निर्देशांक समतल पर स्थित किसी बिंदु की स्थिति तथा किसी क्रमित युग्म का समतल पर निरूपण करना देखा था,
आइए इससे आगे इस अध्याय मे हम दो बिन्दुओ के बीच की दूरी, एक रेखा के मध्य-बिंदु का पता लगाना, दो बिन्दुओ को जोड़ने वाली रेखाखण्ड का किसी अन्य बिन्दु के सापेक्ष विभाजन, तीन बिन्दुओ के मध्य (त्रिभुज) के क्षेत्रफल आदि देखेंगे।
1. दो बिंदुओ के बीच की दूरी
किन्ही दो बिंदुओं के बीच दूरी सदैव धनात्मक या शून्य (जब दो बिंदु सम्पाती हों ) होती है। यदि किसी समतल पर कोई दो बिंदु A तथा B दिए हो तो A से B की दूरी या B से A की दूरी एक समान अर्थ रखते है।
यहां हम विभिन्न परिस्थितियों में दो बिंदुओ के बीच दूरी ज्ञात करना सीखते हैं
सबसे पहले हम दो ऐसे बिंदुओं के मध्य दूरी ज्ञात करना सीखते है जो एक ही क्षैतिज या ऊर्ध्वाधर तल पर स्थित है :
माना कोई दो बिंदु A(1,2) तथा B(4,2) दिए है, जिनके मध्य की हमें दूरी ज्ञात करनी है।
ध्यान से देखने पर हम पाते है कि दोनों ही बिंदुओं की कोटि अर्थात y नियामक एक समान है अर्थात दोनों बिन्दुओ के लिए y=2 है, अतः दोनों ही बिन्दुओ की x अक्ष से दूरी 2 होगी। इसका आशय यह है कि यह दोनों बिंदु किसी एक क्षैतिज रेखा पर स्थित है, इन दोनों बिंदुओं को मिलाने वाली रेखा का आलेख नीचे प्रदर्शित है
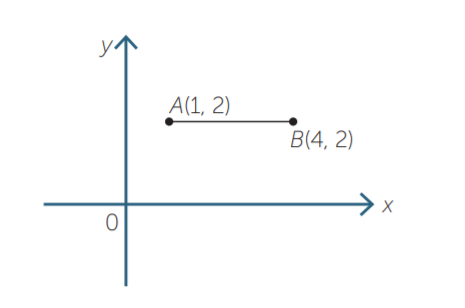
किसी क्षैतिज रेखा पर स्थित किन्ही दो बिंदुओं की दूरी सदैव उनके x निर्देशांकों के अंतर के बराबर होती है।
अर्थात ऊपर रेखाखंड की दूरी AB=4−1=3 इकाई है।
माना यदि बिंदु A(1,−2) तथा B(1,3) है। चूँकि दोनों बिंदुओं के x निर्देशांक (भुज) एक समान है अर्थात इन बिन्दुओ की y अक्ष से लम्बवत दूरी समान होगी अतः यह दोनों बिंदु एक ही ऊर्ध्वाधर रेखा पर स्थित होंगे। इनको मिलाने वाली रेखा का आलेख निम्न चित्र में प्रदर्शित है।
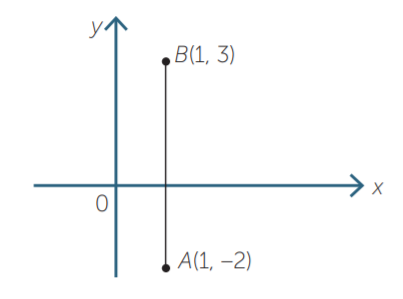
किसी ऊर्ध्वाधर रेखा पर स्थित बिंदुओं के मध्य दूरी उनके y निर्देशांकों के अंतर के बराबर होती है।
अर्थात दूरी AB=3−(−2)=5
ऊपर हमने ऐसे दो स्थितियों की व्याख्या की जिसमे या तो दोनों बिंदु किसी एक क्षैतिज रेखा पर स्थित थे या किसी किसी ऊर्ध्वाधर रेखा पर।
परन्तु यदि हमें ऐसे दो बिंदुओं के बीच दूरी ज्ञात करनी हो जो न तो क्षैतिज और न ही किसी एक ऊर्ध्वाधर रेखा पर स्थित हो, तो उसके लिए हम पाइथागोरस प्रमेय का प्रयोग करते है।
माना कोई दो बिंदु P(x1,y1) तथा Q(x2,y2)है। इन बिंदुओं से क्रमशः क्षैतिज तथा ऊर्ध्वाधर रेखा पर स्थित बिंदु X(x2,y1) है।
नीचे चित्र में इनका निरूपण देख सकते है :
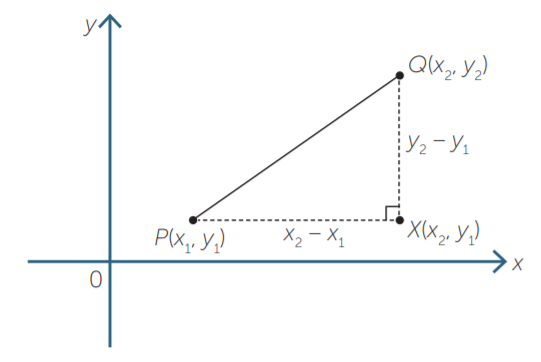
समकोण त्रिभुज ΔPQX में
PX=x2−x1या x1−x2
QX=y2−y1 या y1−y2
पाइथागोरस प्रमेय से
(PQ)2=(PX)2+(QX)2
PQ=√(x2−x1)2+(y2−y1)2
जो कि किसी दो बिंदुओं के बीच दूरी ज्ञात करने के लिए व्यापक सूत्र है।
इस सूत्र की उत्पत्ति हम निम्न उदहारण से समझ सकते हैं
माना, कोई दो बिंदु इस प्रकार है A(1,2) तथा B(4,6), तब AB की दूरी हमें ज्ञात करनी है।
सबसे पहले यदि हम ऐसे बिंदु को ज्ञात करने का प्रयास करे जो बिंदु A(1,2) से गुजरने वाले क्षैतिज रेखा पर स्थित हो अर्थात उस बिंदु का y निर्देशांक या कोटि 2 हो इसी प्रकार वह बिंदु B(4,6) से गुजरने वाली ऊर्ध्वाधर रेखा पर स्थित हो अर्थात बिंदु का x निर्देशांक या भुज 4 हो। अतः इस प्रकार इस नए बिंदु C के निर्देशांक (4,2) होंगे।
नीचे दिए चित्र में इनका निरूपण देख सकते है :
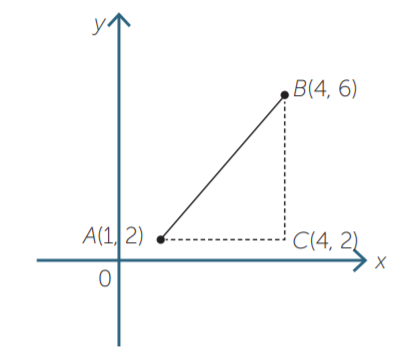
इस प्रकार हम देख सकते है हमे एक ΔABC एक समकोण त्रिभुज प्राप्त हो गया।
चूँकि हमें AB की दूरी की माप करनी है जो कि समकोण त्रिभुज का कर्ण है।
यहाँ AC की माप =4−1=3
BC की माप =6−2=4
अब पाइथागोरस प्रमेय से हम जानते है कि
(AB)2=(AC)2+(BC)2
AB=√(AC)2+(BC)2
AB=√32+42
AB=√9+16
=√25
=5
अर्थात बिंदु A तथा B के मध्य की दूरी 5 इकाई है।
:
PO=√(x−0)2+(y−0)2
:
PO=√x2+y2
OMR (One Minute Revision)
दूरी सूत्र
दो बिंदुओं P(x1,y1) और Q(x2,y2)के बीच दूरी ज्ञात करने के लिए व्यापक सूत्र :
PQ=√(x2−x1)2+(y2−y1)2
मध्य बिंदु सूत्र
दो बिंदुओं A(x1,y1) तथा B(x2,y2) को जोड़ने वाले रेखाखण्ड AB को समद्विभाजित करने वाले अर्थात मध्य बिंदु P(x,y) के निर्देशांक है -
(x,y)≡(x2+x12,y2+y12)
उदाहरण 1
निम्नलिखित बिन्दु किस चतुर्थाश में स्थित हैं?
(i)(5,−4)
(ii)(−3,−2)
(iii)(4,3)
(iv)(−5,2)
(v)(0,−3)
प्रथम चतुर्थांश =(+,+)
द्वितीय चतुर्थांश=(−,+)
तृतीय चतुर्थांश=(−,−)
चतुर्थ चतुर्थांश=(+,−)
(i) माना कि A≡(5,−4)
चूंकि A का x - नियामक धनात्मक और y - नियामक ऋणात्मक है |
अतः बिन्दु A चतुर्थ चतुर्थांश में स्थित है |
(ii) माना कि B≡(−3,−2)
चूंकि B के दोनों नियामक ऋणात्मक है अतः B तृतीय चतुर्थांश में है।
(iii) माना कि C≡(4,3)
चूंकि C के दोनों नियामक धनात्मक है अतः C प्रथम चतुर्थांश में है |
(iv) माना कि D≡(−5,2)
चूंकि D का x - नियामक ऋणात्मक और y - नियामक धनात्मक है |
∴D द्वितीय चतुर्थांश में है|
(v) माना कि E≡(0,−3)
यहाँ E का x -नियामक शून्य और y - नियामक ऋणात्मक है |
अतः E, y - अक्ष पर इसके ऋणात्मक दिशा में है |
उदाहरण 2
दो बिन्दु P(2,3) और Q(4,2) के बीच की दूरी ज्ञात करें।
माना,
P(x1,y1)≡P(2,3)
तथा
Q(x2,y2)≡Q(4,2)
अतः दूरी के सूत्र के अनुसार
दो बिन्दुओ के बीच की दूरी =
√(x2−x1)2+(y2−y1)2
अतः
PQ=√(4−2)2+(2−3)2
PQ=√22+(−1)2
PQ=√4+1
PQ=√5 इकाई
उदाहरण 3
सिद्ध कीजिये की बिंदु A(1,2),B(5,4),C(3,8) तथा D(−1,6) एक वर्ग के शीर्ष हैं।
वर्ग की विशेषताएं
प्रश्नानुसार
AB=√(5−1)2+(4−2)2
=√42+22
=√20
=2√5 इकाई
BC=√(3−5)2+(8−4)2
=√4+16=√20
=2√5 इकाई
CD=√(−1−3)2+(6−8)2
=√(−4)2+(−2)2
=√20=2√5 इकाई
तथा
DA=√(1+1)2+(2−6)2
=√20=2√5 इकाई
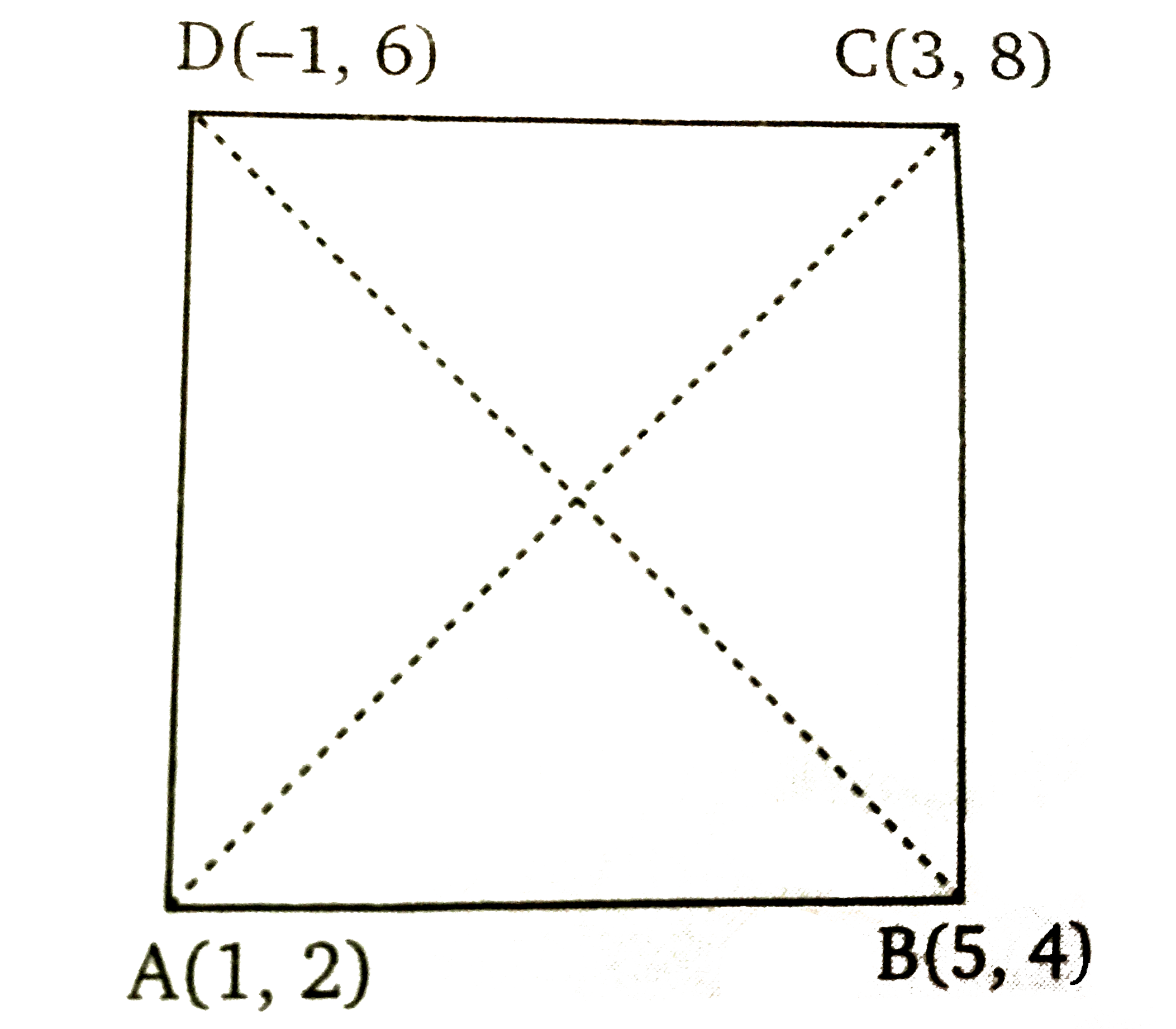
इसलिए
AB=BC=CD=DA
विकर्ण AC
=√(3−1)2+(8−2)2
=√22+62
=√4+36
=√40
=2√10 इकाई
विकर्ण BD
=√(−1−5)2+(6−4)2
=√(−6)2+(2)2
=√36+4
=√40
=2√10 इकाई
∴ विकर्ण AC= विकर्ण BD
अतः ABCD एक ऐसा चतुर्भुज है जिसकी सभी भुजाएँ एवं विकर्ण बराबर है|अतः ABCD एक वर्ग है|
उदाहरण 4
X−अक्ष पर एक बिंदु ज्ञात कीजिये जो A(2,−5) तथा B(−2,9) से समान दुरी पर हो
माना बिंदु का भुज x है| तब
P≡P(x,0)
बिंदु p, बिंदु A(2,−5) तथा B(−2,9) से समान दुरी पर है, तब
PA=PB
⇒√(x−2)2+(0+5)2
=√(x+2)2+(0−9)2
दोनों पक्षों का वर्ग करने पर
(x−2)2+25=(x+2)2+81
x2−4x+4+25
=x2+4x+4+81
−8x=56
x=−7
अतः (−7,0) अभीष्ट बिंदु है।
2. विभाजन सूत्र
यहाँ विभाजन से तात्पर्य किसी एक पूर्ण भाग वाले किसी भी प्रकार के वस्तु, या किसी विशेष लंबाई, मोटाई आदि को उसके बराबर या भिन्न भागों मे अलग करने से है।
इस भाग मे हम किसी लंबाई के विभाजन की बात करेंगे, इसे इस प्रकार समझा जा सकता हैं कि एक लकड़ी को कही से भी पकड़ कर उसे वहाँ से तोड़ दें, तो आपको लकड़ी दो समान या असमान भागों मे मिलेगी।
इसी प्रकार किसी लकड़ी को दो जगह से पकड़े अब इन दोनों जगहों से तोड़े तो आपको लकड़ी के तीन टुकड़े प्राप्त होंगे।
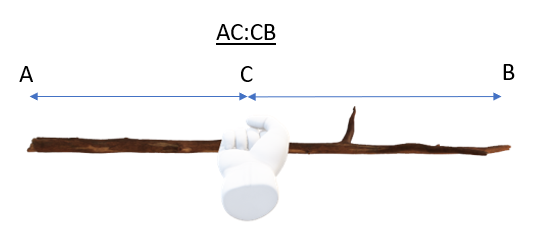
अतः यहाँ से आप समझ सकते है की एक स्थान से पकड़ने पर अर्थात एक बिन्दु के सापेक्ष विभाजन करने पर लकड़ी के दो भाग मिल रहे है अर्थात लकड़ी दो समान या असमान अनुपात मे बट रही है।
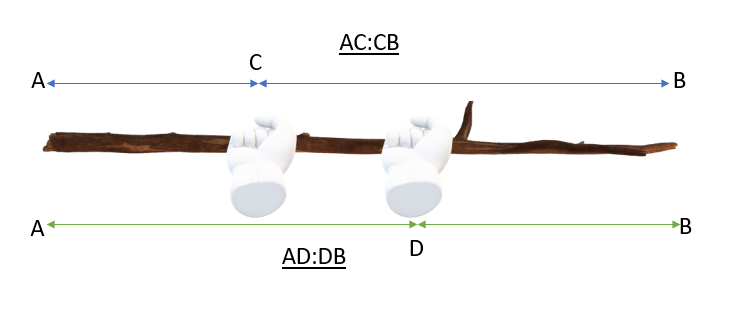
इसी प्रकार दो स्थान से पकड़ने पर अर्थात लकड़ी के तीन भाग मिल रहे है
अर्थात प्रत्येक बिन्दु के सापेक्ष लकड़ी के सिरों से दो-दो अनुपात मिलेंगे।
गणितीय व्याख्या
माना, कोई दो बिंदु A(x1,y1) तथा B(x2,y2) है
बिंदु A तथा B को मिलाने वाली रेखा पर माना कोई बिंदु P(x,y) इस प्रकार है कि वह रेखा को m:n के रूप में अन्तः विभाजित करता है।
अर्थात
(PA):(PB)=m:n
⇒PAPB=mn
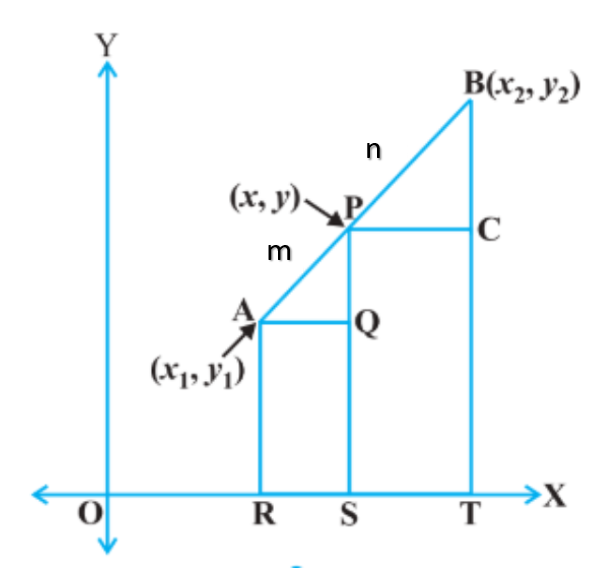
अब हम बिंदुओं A,P तथा B से X− अक्ष पर क्रमशः लम्ब R,S तथा T खींचते है और X−अक्ष के समांतर AQ और PC खींचते है।
अब ΔPAQ और ΔBPC में
∠PAQ=∠BPC
( संगत कोण)
चूँकि रेखाखण्ड AB पर AQ, व PC समान कोण बना रहे चूँकि दोनों ही X−अक्ष के समांतर है।
∠PQA=∠BCP
(प्रत्येक समकोण)
अतः AA समरूपता से
ΔPAQ~ΔBPC
अतः
PAPB=AQPC=PQBC.....(1)
अब बच्चों आगे आप सभी बिन्दु A(x1,y1), P(x,y) तथा B(x2,y2) के निर्देशांकों पर ध्यान दें
अब चित्र मे देखें -
क्षैतिज रेखाओ व x नियामकों पर ध्यान दें
AQ=RS=OS−OR=x−x1
PC=ST=OT−OS=x2−x
ऊर्ध्वाधर रेखाओ व y नियामकों पर ध्यान दें
PQ=PS−QS=PS−AR=y−y1
BC=BT−CT=BT−PS=y2−y
इन मानो को समीकरण (1) में रखने पर
mn=x−x1x2−x=y−y1y2−y
⇒mn=x−x1x2−x
लेकर हल करने पर
(वज्र गुना करने पर )
mx2−mx=nx−nx1
mx2+nx1=mx+nx
x=mx2+nx1m+n
इसी प्रकार
⇒mn=y−y1y2−y
लेकर हल करने पर
y=my2+ny1m+n
प्राप्त होता है।
अतः इस प्रकार दो बिंदुओं A(x1,y1) तथा B(x2,y2) को जोड़ने वाले रेखाखण्ड AB को m:n के अनुपात में आंतरिक रूप से विभाजित करने वाले बिंदु P(x,y) के निर्देशांक है
(x,y)
=(mx2+nx1m+n,my2+ny1m+n)
विशेष स्थिति -
अर्थात m:n=1:1
(x,y)=(x2+x12,y2+y12)
G=(x1+x2+x33,y1+y2+y33)
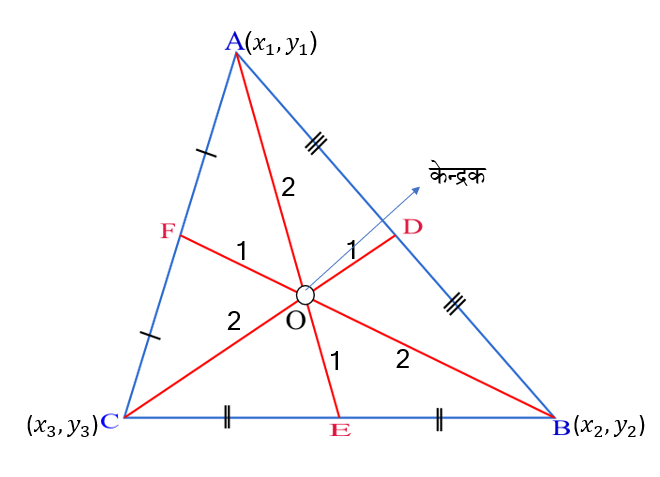
यहाँ ध्यान दें, चूँकि त्रिभुज का केन्द्रक त्रिभुज की तीनों मध्यिकाओ के मिलान बिन्दु पर प्राप्त होता है, तथा मध्यिकाये वे रेखाए होती है जो प्रत्येक त्रिभुज के शीर्ष से उसके सम्मुख भुजा के मध्य बिन्दु पर जाकर मिलती है तथा केन्द्रक द्वारा 2:1 के अनुपात मे होती है। अतः इस गुण का प्रयोग करके विभाजन सूत्र के प्रयोग से केन्द्रक ज्ञात किया जा सकता है।(उदाहरण 6 देंखे।)
I≡(X,Y)
X=ax1+bx2+cx3a+b+c,
Y=ay1+by2+cy3a+b+c
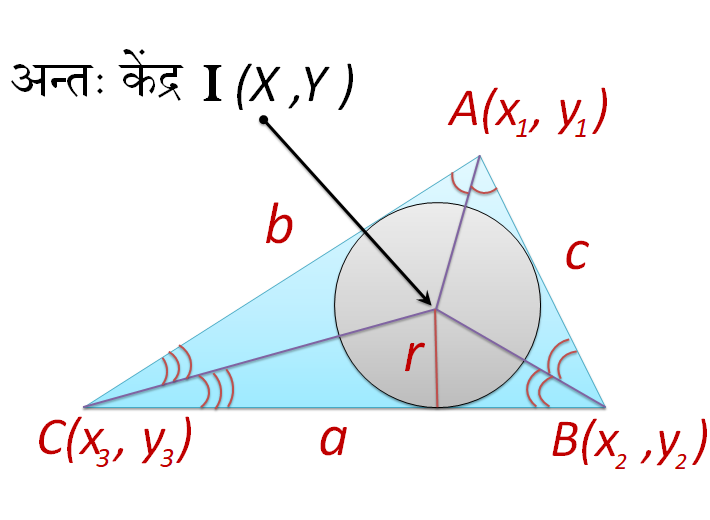
यहाँ ध्यान दे, त्रिभुज के अंत:केंद्र को त्रिभुज के अंत: कोण समद्विभाजक के प्रतिच्छेद बिंदु के रूप में परिभाषित किया जाता है।चूँकि त्रिभुज मे तीन कोण होते है, और प्रत्येक कोण के लिए उसे समद्विभाजित करने वाली एक अद्वितीय रेखा होती है, यही रेखाए अंत: कोणों के कोण समद्विभाजक कहलाते है। चूंकि किसी त्रिभुज में तीन अंत: कोण होते हैं, इसलिए तीन अंत: समद्विभाजक अवश्य होंगे, इस प्रकार सभी तीन अंत: समद्विभाजक का प्रतिच्छेद बिंदु त्रिभुज का अंत: केंद्र कहलाता है। यहाँ इस बिन्दु को केंद्र मान कर एक अद्वितीय वृत्त खिचा जा सकता है जो त्रिभुज की तीनों भुजाओ को आंतरिक रूप से स्पर्श करती है, अन्तः वृत्त कहलाता है। अन्तः केंद्र समद्विभाजक रेखाओ को विशेष अनुपात मे बांटती है, इस प्रकार विभाजन सूत्र की सहायता से इसका मान ज्ञात किया जा सकता है।
OMR (One Minute Revision)
विभाजन सूत्र
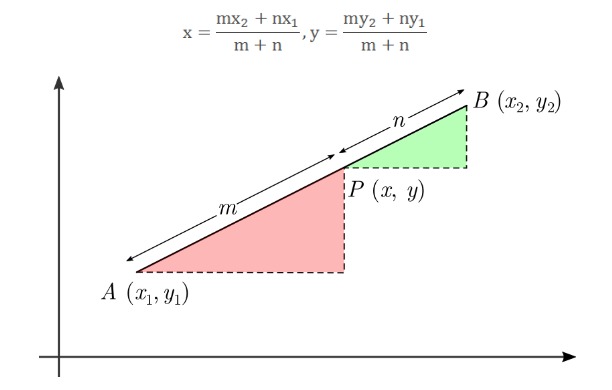
- दो बिंदुओं A(x1,y1) तथा B(x2,y2) को जोड़ने वाले रेखाखण्ड AB को m:n के अनुपात में आंतरिक रूप से विभाजित करने वाले बिंदु P(x,y) के निर्देशांक है -
(x,y)=(mx2+nx1m+n,my2+ny1m+n)
- दो बिंदुओं A(x1,y1) तथा B(x2,y2) को जोड़ने वाले रेखाखण्ड AB को m:n के अनुपात में बाह्य रूप से विभाजित करने वाले बिंदु P(x,y) के निर्देशांक है -
(x,y)=(mx2−nx1m−n,my2−ny1m−n)
उदाहरण 5
बिंदु (6, 3) और (-4, 5) को मिलाने वाली रेखाखण्ड को 3:2 अनुपात में अन्तः विभाजित करने वाले बिंदु के निर्देशांक ज्ञात कीजिए।
मान लीजिये, P(x,y) अभीष्ट बिंदु है, जो दिए गए बिन्दुओ से बनने वाले रेखाखण्ड को आंतरिक रूप से 3:2 विभाजित करती है,
विभाजन सूत्र
x=mx2+nx1m+n
y=my2+ny1m+n
के प्रयोग से
x=3×(−4)+2×63+2,
y=3×5+2×33+2
⇒x=0,y=215
अतः बिंदु P के निर्देशांक (0,215) हैं।
उदाहरण 6
यदि A(x1,y1),B(x2,y2) और C(x3,y3) ΔABC के शीर्ष है, तो त्रिभुज के केन्द्रक का निर्देशांक ज्ञात करे।
यहाँ ΔABC में
A(x1,y1)≡(4,2)
B(x2,y2)≡(6,5)
C(x3,y3)≡(1,4)
यदि A(x1,y1),B(x2,y2) और C(x3,y3) त्रिभुज ABC के शीर्ष हैं, तो इस त्रिभुज के केन्द्रक के निर्देशांक-
(x1+x2+x33,y1+y2+y33)
(4+6+13,2+5+43)
(113,113)
उदाहरण 7
यदि बिंदु P,A(−2,−2) व B(2,−4) को मिलाने वाले रेखाखण्ड को इस प्रकार विभाजित करता है की APPB=34 तब P के निर्देशांक ज्ञात कीजिए।
दिया है-
बिन्दु A(−2,−2) व B(2,−4)
APPB=34
इसलिए
बिन्दु P रेखा AB को 3:4 के अनुपात में विभाजित करती है|
हम जानते हैं दो बिंदुओं A(x1,y1) तथा B(x2,y2) को जोड़ने वाले रेखाखण्ड AB को m:n के अनुपात में आंतरिक रूप से विभाजित करने वाले बिंदु P(x,y) के निर्देशांक है -
(mx2+nx1m+n,my2+ny1m+n)
अब P के निर्देशांक
(3×2+4×(−2)3+4,3×(−4)+4×(−2)3+4)
(6−87,−12−87)
(−27,−207)
3. त्रिभुज का क्षेत्रफल
जैसा की बच्चों आपको पहले से ज्ञात है, त्रिभुज का क्षेत्रफल विभिन्न परिस्थितियों में विभिन्न तरीके से ज्ञात किया जा सकता हैं
इस सूत्र का प्रयोग हम तब कर सकते है जब हमें किसी त्रिभुज की आधार तथा उसके शीर्ष से डाले गए लम्ब के माप ज्ञात हो।
हीरोन के सूत्र से =
√s(s−a)(s−b)(s−c)
जहाँ s=परिमाप/2
a,b,c=
त्रिभुज के भुजाओ की माप
आइये नीचे दिए चित्र में देखते है,
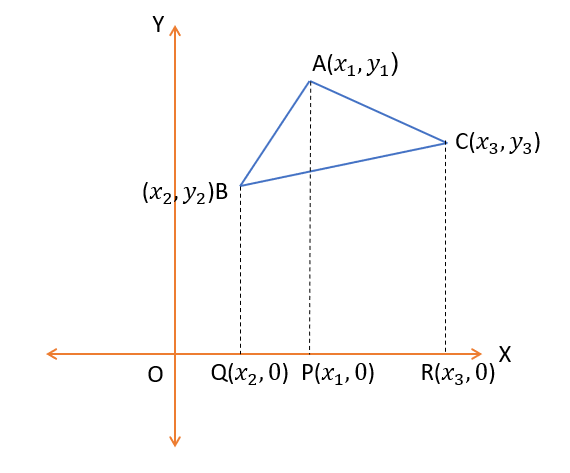
माना XY तल पर कोई तीन बिंदु A(x1,y1), B(x2,y2) तथा C(x3,y3) है, तथा इन्हे आपस में मिलाने से एक त्रिभुज ΔABC बनता है।
अब हम त्रिभुज के तीनों शीर्षों A,B तथा C से x अक्ष पर लंब क्रमशः P(x1,0), Q(x2,0) तथा R(x3,0) डालते है।
इस प्रकार हम देखते है, हमें तीन समलम्ब ABQP, APRCतथा BQRC प्राप्त होते है।
त्रिभुज ABC का क्षेत्रफल = क्षेत्रफल ABQP+ क्षेत्रफल APRC− क्षेत्रफल BQRC
जैसा कि हम जानते है कि समलम्ब का क्षेत्रफल =12× समांतर भुजाओं का योग × उनके बीच की दूरी
क्षेत्रफल ABQP
=12×(AP+BQ)×(PQ)
⇒12×(y1+y2)×(x1−x2)
क्षेत्रफल APRC
=12×(AP+RC)×(PR)
⇒12×(y1+y3)×(x3−x1)
क्षेत्रफल BQRC
=12×(BQ+CR)×(QR)
⇒12×(y2+y3)×(x3−x2)
अतः त्रिभुज ABC का क्षेत्रफल
=12×(y1+y2)×(x1−x2)
+12×(y1+y3)×(x3−x1)
−12×(y2+y3)×(x3−x2)
⇒12[x1(y2−y3)+x2(y3−y1)+x3(y1−y2)]
अतः ΔABC का क्षेत्रफल
=∣12[x1(y2−y3)+x2(y3−y1)+x3(y1−y2)]∣
(यहाँ ध्यान दें, चूँकि यहाँ हम त्रिभुज का क्षेत्रफल निकाल रहे है, तथा क्षेत्रफल का मान सदैव धनात्मक होता है इसलिए इसके सूत्र का उपयोग मापांक मे करेंगे ताकि मान हमेशा धनात्मक प्राप्त हो।)
[NOTE - यदि किसी त्रिभुज का क्षेत्रफल निकालने पर मान शून्य प्राप्त हो तो इससे तात्पर्य है की तीनों बिंदु के मध्य कोई भी क्षेत्रफल नहीं है अर्थात तीनों बिन्दु एक ही रेखा पर स्थित है अतः संरेखी है। ]
OMR (One Minute Revision)
ΔABC का क्षेत्रफल
=∣12[x1(y2−y3)+x2(y3−y1)+x3(y1−y2)]∣
उदाहरण 8
उस त्रिभुज का क्षेत्रफल ज्ञात कीजिये जिसके शीर्ष क्रमश: (2,3),(4,5) और (6,2) है।
माना त्रिभुज के शीर्ष ,
A≡(2,3)
B≡(4,5)
C≡(6,2)
ΔABC का क्षेत्रफल
=12[x1(y2−y3)+x2(y3−y1)+x3(y1−y2)]
=∣12[2(5−2)+(4)(2−3)+6(3−5)]∣
=∣∣∣12[6−4−12]∣∣∣
=∣∣∣−102∣∣∣=5
अतः ΔABC का क्षेत्रफल
= 5 वर्ग इकाई
उदाहरण 9
बिंदुओं P(−1.5,3),Q(6,−2) और R(−3,4) से बनने वाले त्रिभुज का क्षेत्रफल ज्ञात कीजिये।
दिए हुए बिंदुओं
P(x1,y1)≡(−1.5,3),
Q(x2,y2)≡(6,−2) तथा
R(x3,y3)≡(−3,4) से बनने वाले त्रिभुज का क्षेत्रफल
=12[x1(y2−y3)+x2(y3−y1)+x3(y1−y2)]
=12[−1.5(−2−4)+6(4−3)+(−3)(3+2)]
=12[9+6−15]=0
चूँकि त्रिभुज का क्षेत्रफल शून्य कभी नहीं होता हैं।
अतः ये बिंदु संरेखी हैं।
उदाहरण 10
सिद्ध कीजिये की बिंदु A(3,0),B(4,5),C(−1,4) तथा D(−2,−1) क्रम से लेने पर एक समचतुर्भुज के शीर्ष है| समचतुर्भुज का क्षेत्रफल भी ज्ञात कीजिये|
समचतुर्भुज की विशेषताएं
यहाँ AC का मध्य-बिंदु
(3−12,0+42)
अर्थात
(1 ,2 )
तथा BD का मध्य-बिंदु
(4−22,5−12)
अर्थात
(1 ,2 )
विकर्ण AC व BD के समान मध्य बिंदु है|
क्योंकि,
AB=√(4−3)2+(5−0)2
=√12+52
=√1+25
=√26
तथा
BC=√(4+1)2+(5−4)2
=√52+12
=√25+1
=√26
तथा
CD=√((−1)−(−2))2+(4+1)2
=√12+52
=√1+25
=√26
तथा
AD=√(3+2)2+(0+1)2
=√52+12
=√25+1
=√26
अतः ABCD की सभी भुजाएँ बराबर है|
अतः AB=BC=CD=AD
यह समचतृर्भुज की (1) शर्त पूरी करता हैं
अब
AC=√(3+1)2+(0+4)2
=√42+(−4)2
=√16+16
=√32
=4√2
और
BD=√(4+2)2+(5+1)2
=√62+62
=√72
=6√2
∴AC≠BD
यह समचतृर्भुज की (2) शर्त पूरी करता हैं
अब समचतुर्भुज ABCD का क्षेत्रफल
=12× (विकर्णों का गुणनफल)
=12(AC×BD)
=(12×4√2×6√2)
=24 वर्ग इकाई
उदाहरण 11
k का वह मान ज्ञात कीजिये जिसके लिए बिंदु (−5,1),(1,k) तथा (4,−2) संरेख है।
यहाँ A(−5,1),B(1,k) तथा C(4,−2)
∴ x1=−5,y1=1,
x2= 1,y2=k,
x3= 4,y3=−2
चूंकि दिए गए बिंदु संरेख है|
∴ΔABC का क्षेत्रफल =0
∴12[x1(y2−y3)+x2(y3−y1)+x3(y1−y2)]=0
x1(y2−y3)+x2(y3−y1)+x3(y1−y2)=0
(−5)⋅(k+2)+1(−2−1)+4(1−k)=0
−5k−10−2−1+4+4k=0
−5k−10−3+4−4k=0
−9k−9=0
9k=−9
k=−1
महत्वपूर्ण बिंदु
- दो बिंदुओं A(x1,y1) तथा B(x2,y2) को जोड़ने वाले रेखाखण्ड AB को m:n के अनुपात में आंतरिक रूप से विभाजित करने वाले बिंदु P(x,y) के निर्देशांक है -
(x,y)≡(mx2+nx1m+n,my2+ny1m+n) - दो बिंदुओं A(x1,y1) तथा B(x2,y2) को जोड़ने वाले रेखाखण्ड AB को m:n के अनुपात में बाह्य रूप से विभाजित करने वाले बिंदु P(x,y) के निर्देशांक है -
(x,y)≡(mx2−nx1m−n,my2−ny1m−n)
कार्तीय तल
किसी बिंदु को भिन्न भिन्न चतुर्थांशों में निम्न प्रकार दर्शाया जाता है-

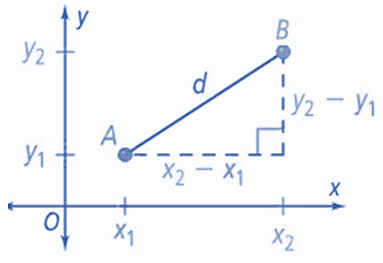
दूरी सूत्र
दो बिंदुओं के बीच दूरी ज्ञात करने के लिए व्यापक सूत्र :
PQ=√(x2−x1)2+(y2−y1)2
मध्य बिंदु सूत्र
दो बिंदुओं A(x1,y1) तथा B(x2,y2) को जोड़ने वाले रेखाखण्ड AB को समद्विभाजित करने वाले अर्थात मध्य बिंदु P(x,y) के निर्देशांक है -
(x,y)≡(x2+x12,y2+y12)
विभाजन सूत्र
त्रिभुज का केन्द्रक
यदि किसी त्रिभुज के शीर्षों के निर्देशांक
A(x1,y1), B(x2,y2), C(x3,y3)
हों तो त्रिभुज के केन्द्रक के निर्देशांक
G≡(x1+x2+x33,y1+y2+y33)

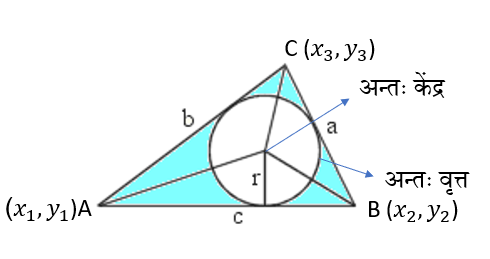
त्रिभुज का अन्तः केंद्र
यदि किसी त्रिभुज के शीर्षों के निर्देशांक A(x1,y1), B(x2,y2), C(x3,y3) तथा भुजाओ का मान BC=a, CA=b, तथा AB=c हो, तो त्रिभुज का अन्तः केन्द्र के निर्देशांक
I≡(ax1+bx2+cx3a+b+c,ay1+by2+cy3a+b+c)
त्रिभुज का क्षेत्रफल
यदि किसी त्रिभुज के शीर्षों के निर्देशांक
A(x1,y1), B(x2,y2), C(x3,y3)
हों तो ΔABC का क्षेत्रफल
=12[x1(y2−y3)+x2(y3−y1)+x3(y1−y2)]

| त्रिभुज के प्रकार | गुण |
|---|---|
| समबाहु त्रिभुज | एक समबाहु त्रिभुज की तीनों भुजाएं समान होती हैं |
| समद्विबाहु त्रिभुज | समद्विबाहु त्रिभुज की कोई दो भुजाएं समान होती हैं |
| विषमबाहु त्रिभुज | एक विषमबाहु त्रिभुज की तीनों भुजाएं असमान होती हैं |
| समकोण त्रिभुज | समकोण त्रिभुज की दो भुजाओं की लम्बाइयों के वर्गों का योग कर्ण की लम्बाई के वर्ग के बराबर होता है। |
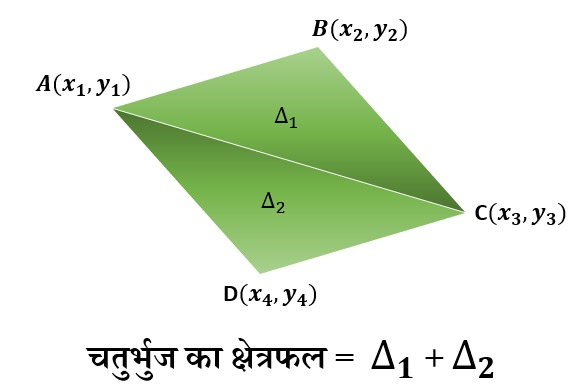
चतुर्भुज के क्षेत्रफल को ज्ञात करने के लिए हम दो विपरीत कोनों को जोड़कर, इसे दो त्रिभुजों में विभाजित करेंगे और उन त्रिभुजों का अलग-अलग क्षेत्रफल ज्ञात करके उन्हें जोड़ देते हैं।

| चतर्भुज के प्रकार | गुण |
|---|---|
| समचतुर्भुज | एक समचतुर्भुज की सभी भुजाएं समान होती हैं लेकिन विकर्ण असमान होते हैं |
| समांतर चतुर्भुज | एक समांतर चतुर्भुज की सम्मुख भुजाएं समान होती हैं, लेकिन विकर्ण असमान होते हैं |
| आयत | एक आयत की विपरीत भुजाएँ समान होती हैं और दो विकर्ण भी समान होते हैं |
| वर्ग | एक वर्ग की सभी भुजाएं समान होती हैं और विकर्ण भी समान होते हैं |

