त्रिकोणमिति का परिचय कक्षा 10 गणित

भूमिका

बच्चों! आइए सबसे पहले त्रिकोणमिति (Trigonometry) शब्द को समझने का प्रयास करते है, अंग्रेजी शब्द "Trigonometry" की व्युत्पत्ति ग्रीक शब्दों "tri" ( जिसका अर्थ है तीन ), "gon" ( जिसका अर्थ है भुजा) और "metron" ( जिसका अर्थ है माप ) से हुई है। अतः त्रिकोणमिति से तात्पर्य त्रिभुजों की माप से है, जैसे कि त्रिभुज भुजा तथा भुजाओ के मध्य के कोण से मिलकर बनता है, अतः त्रिभुज की माप हम उसके भुजाओ की लंबाई तथा कोण का मान ज्ञात करके करते है। अतः त्रिकोणमिति में त्रिभुज की भुजाओं और कोणों के बीच के संबंधों का अध्ययन किया जाता है तथा इनकी सहायता से त्रिभुज का माप ज्ञात किया जाता है।
प्राचीन काल में त्रिकोणमिति पर किए गए कार्य का उल्लेख मिस्र और बेबीलॉन में मिलता है। प्राचीन काल के खगोलविद् त्रिकोणमिति का प्रयोग पृथ्वी से तारों और ग्रहों की दूरियाँ मापने में करते थे। आज भी इंजीनियरिंग और भौतिक विज्ञान में प्रयुक्त अधिकांश प्रौद्योगिकीय उन्नत विधियाँ त्रिकोणमितीय संकल्पनाओं पर आधारित हैं।
इस अध्याय में हम एक समकोण त्रिभुज की भुजाओं के अनुपातों का उसके न्यून कोणों के सापेक्ष अध्ययन करेंगे जिन्हें कोणों के त्रिकोणमितीय अनुपात कहते हैं।

आइए बच्चों त्रिकोणमिति को समझते है और करीब से...

जैसे कि हमने ऊपर समझा कि त्रिकोणमिति से तात्पर्य त्रिभुज के भुजाओ व कोणों की माप की सहायता से त्रिभुज की माप करने से है।
मुख्यतः हम यहाँ समकोण त्रिभुज का अध्ययन करेंगे, जैसे कि आपने पिछले अध्याय मे समकोण त्रिभुज के बारे मे पढ़ा है तथा उसके भुजाओ मे से लंब, कर्ण व आधार का चयन करना सीखा है, साथ ही पाइथागोरस प्रमेय देखा है जिसके अनुसार किसी समकोण त्रिभुज में, सबसे बड़ी भुजा (कर्ण) का वर्ग अन्य दो भुजाओं के वर्गों के योग के बराबर होता है।
इस प्रमेय के अनेकों अनुप्रयोग हैं जैसे कि यदि कोई बिन्दु किसी ऊंचाई पर स्थित है, तब किसी अन्य बिन्दु से उसकी क्षैतिज दूरी (आधार) तथा ऊर्ध्वाधर दूरी (लंब / ऊंचाई) ज्ञात हैं तब दोनों बिन्दुओ की तिर्यक दूरी (कर्ण) ज्ञात किया जा सकता है।

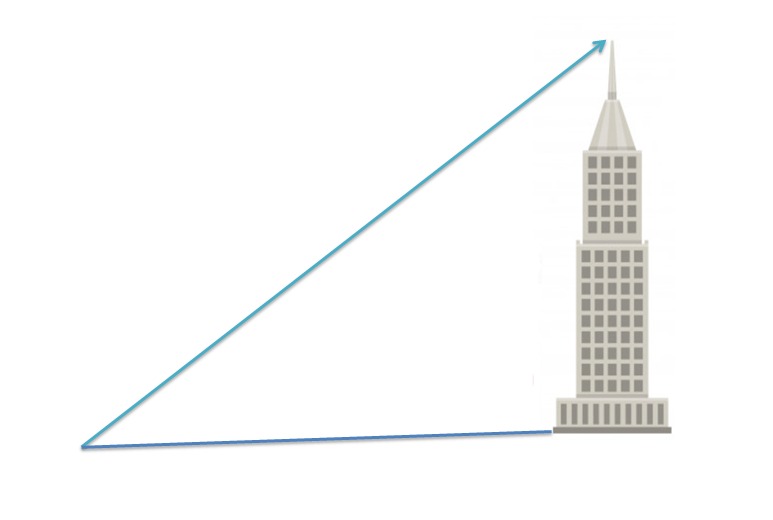
उदाहरण के लिए किसी उड़ते हुए पतंग के डोर की लंबाई इस प्रकार प्राप्त की जा सकती है।

ocr_image

यहाँ हम समझ सकते हैं कि यदि लंब, कर्ण या आधार मे से कोई दो मान दिए हो तो तीसरा मान ज्ञात किया जा सकता है परन्तु

क्या हो यदि केवल कोई एक मान ज्ञात हो?
तब क्या आप पाइथागोरस प्रमेय से अन्य माप प्राप्त कर सकते है?

तो ऐसा संभव नहीं है चूँकि पाइथागोरस प्रमेय से कोई एक भुजा का मान ज्ञात करने के लिए अन्य दो भुजाओ के मान ज्ञात होने आवश्यक है।

अब यदि केवल क्षैतिज दूरी (आधार) या ऊर्ध्वाधर दूरी (लंब) या तिर्यक दूरी (कर्ण) ज्ञात हो तब हम त्रिभुज के अन्य माप की ओर देख सकते हैं जैसे कि आंतरिक कोण की माप ।
अब जैसा कि आप जानते हैं कि समकोण त्रिभुज मे एक समकोण तथा अन्य न्यून कोण होते हैं, तो यदि केवल एक भुजा तथा किसी न्यूनकोण की जानकारी ज्ञात हो तब उस न्यूनकोण (वह कोण जिनका मान

90^{\circ}

से कम है।) के सापेक्ष समकोण त्रिभुज के भुजाओ के अनुपात मे संबंध देखेंगे जिन्हे कोणों के त्रिकोणमितीय अनुपात कहा जाता है तथा इससे अन्य मान ज्ञात करेंगे। त्रिकोणमितीय अनुपातों के आपस मे संबंध प्राप्त होते हैं जिन्हे हम सर्वसमिका कहते है।

दैनिक जीवन मे त्रिकोणमिति का उपयोग विभिन्न प्रकार से किया जा सकता है, जैसे कि किसी मीनार अथवा किसी पहाड़ की ऊचाई ज्ञात करना, किसी ऊंची वस्तु की किसी बिन्दु से क्षैतिज दूरी ज्ञात होने पर उसकी ऊंचाई ज्ञात करना या इसका विपरीत भी संभव है।
(आपके मन मे एक सवाल उठ रहा होगा कि किसी ऊंची चोटी का जमीन से कोण कैसे ज्ञात होगा यदि दूरियाँ ज्ञात न हो, तो इस स्थिति मे "clinometer (क्लाइनो मीटर )" का उपयोग किया जाता है, जिससे ऊर्ध्वाधर कोण ज्ञात किया जाता है।)

1. त्रिकोणमितीय अनुपात

बच्चों! कल्पना करें, आप एक पतंग उड़ा रहे हैं और आप जिस बिन्दु पर खड़े हैं वह बिन्दु A है तथा पतंग आकाश मे जिस बिन्दु पर है वह बिन्दु C है, इस प्रकार AC डोर की लंबाई हुई और यह डोर क्षैतिज से कोई कोण बनाती है मान लेते है यह बिन्दु A, के लिए $∠ A$ है। अब पतंग से नीचे की ओर ऊर्ध्वाधर नीचे जमीन मे लंब डाले तो एक समकोण प्राप्त होगा, मान लेते है यह बिन्दु B है।
अब यहाँ नीचे आप चित्र मे देख सकते है की एक समकोण त्रिभुज ( $△ A B C$ ) प्राप्त हो रहा है, त्रिकोणमिति मे हम इसी प्रकार के समकोण त्रिभुज की कल्पना करके विभिन्न मान ज्ञात करते है

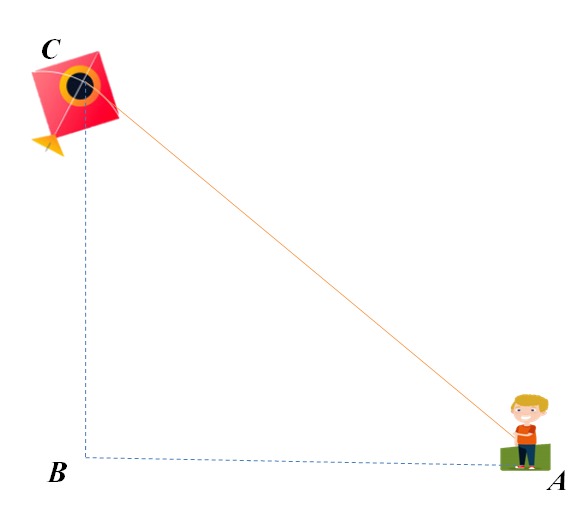
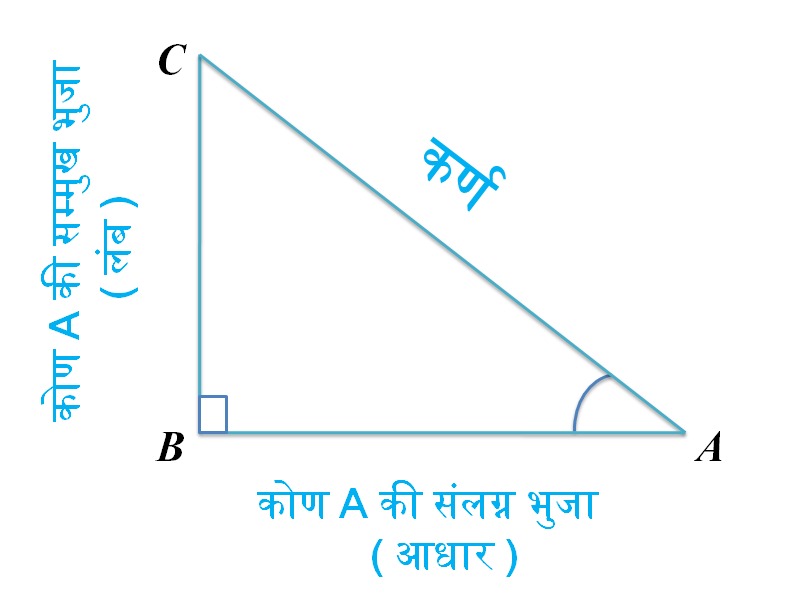
उपरोक्त चित्र में एक त्रिभुज

Δ A B C

दिया गया है जिसका कोण

∠ B

समकोण है। इस प्रकार हम देख सकते है समकोण त्रिभुज के अन्य दो कोण

∠ A

तथा

∠ C

न्यून कोण है। यदि हम न्यून कोण

∠ A

के सापेक्ष बात करें तो, $∠ A$ की सम्मुख भुजा (BC) को हम समकोण त्रिभुज की ऊंचाई (height) या लंब बोलते है, $∠ A$ से संलग्न भुजा (AB) समकोण त्रिभुज का आधार (base) होगा तथा समकोण की सम्मुख भुजा (AC) सदैव कर्ण (hypotenuse) कहलाती है।

यहाँ पर ध्यान देने योग्य बात यह है कि यदि हम

∠ A

के अतिरिक्त यदि

∠ C

के सापेक्ष देखे तो आधार तथा लम्ब की स्थिति आपस में बदल जायगी। अर्थात कोण

∠ C

के सापेक्ष लम्ब

A B

और आधार

B C

होगा।
अब यदि हम बात करें भुजाओं में अनुपात की तो हम देख सकते है समकोण त्रिभुज

Δ A B C

में न्यून कोण

∠ A

के सापेक्ष भुजाओं के निम्नलिखित 6 अनुपात संभव होंगे :

$(i) . \frac{B C}{A C} = \frac{height}{hypotenuse} =$ लंब / कर्ण

$(i i) . \frac{A B}{A C} = \frac{base}{hypotenuse} =$ आधार/कर्ण

$(i i i) . \frac{B C}{A B} = \frac{height}{base} =$ लंब/आधार

इसीप्रकार अन्य तीन हम इन्ही तीन अनुपातों का व्युत्क्रम ले लेते है।

$(i v) . \frac{A C}{B C} = \frac{hypotenuse}{height} =$ कर्ण / लंब

$(v) . \frac{A C}{A B} = \frac{hypotenuse}{base} =$ कर्ण / आधार

$(v i) . \frac{A B}{B C} = \frac{base}{height} =$ आधार / लंब

अब हम इन अनुपातों को निम्न प्रकार से परिभाषित करते है -

∠ A

का sine

= \frac{B C}{A C}

∠ A

का cosine

= \frac{A B}{A C}

∠ A

का tangent

= \frac{B C}{A B}

∠ A

का cotangent

= \frac{A B}{B C}

∠ A

का secant

= \frac{A C}{A B}

∠ A

का cosecant

= \frac{A C}{B C}

उपरोक्त परिभाषित अनुपातों को हम संक्षेप में क्रमशः

sin A

cos A

tan A

cot A

sec A

और

cos e c A

पढ़ते है।
इस प्रकार हम देख सकते है कि

cos e c A = \frac{1}{sin A}

sec A = \frac{1}{cos A}

cot A = \frac{1}{tan A}

tan A = \frac{sin A}{cos A}

cot A = \frac{cos A}{sin A}

उदाहरण 1

यदि $tan A = \frac{4}{3}$ , तो कोण $A$ के अन्य त्रिकोणमितीय अनुपात ज्ञात कीजिए।

इस प्रश्न में हमें एक त्रिकोणमिति अनुपात $tan A = \frac{4}{3}$ दे दिया गया है और हमें अन्य पांच त्रिकोणमिति अनुपात ज्ञात करना है। ऐसे प्रश्नो को हल करने के लिए सबसे पहले तो एक त्रिभुज बना ले जिसका एक कोण $∠ A$ न्यूनकोण हो।

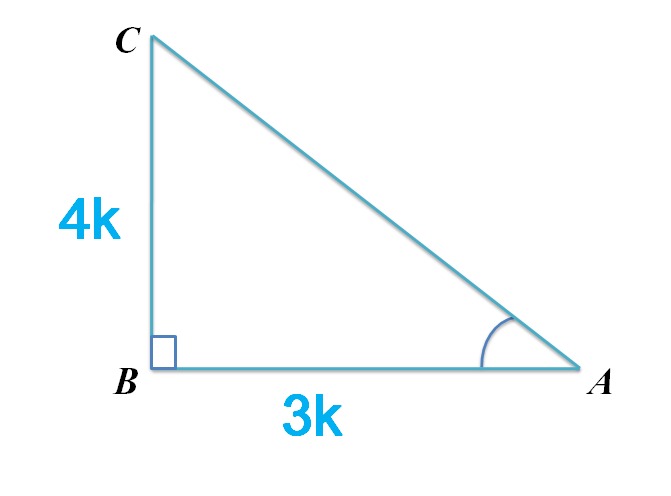
माना,

A B C

एक समकोण त्रिभुज है।

हम जानते है की,

∠ A

\Rightarrow

tan A = \frac{B C}{A B}

\Rightarrow

tan A = \frac{4}{3}

अतः माना,

B C = 4 k,

A B = 3 k

जहाँ

k

एक धनात्मक आनुपातिक गुणांक है।

पाइथागोरस प्रमेय से हम जानते हैं कि,

A C^{2} = A B^{2} + B C^{2}

A C^{2} = {(3 k)}^{2} + {(4 k)}^{2} = 25 k^{2}

अतः वर्गमूल लेने पर

A C = 5 k

(चूंकि लंबाई सदैव धनात्मक होता है अतः

A C

का धनात्मक मान लिया गया।)

अतः हमें तीनो भुजाओ की माप मिल गयी, अब हम बड़ी ही आसानी से अन्य त्रिकोणमितीय अनुपात ज्ञात कर सकते है।

sin A = \frac{B C}{A C} = \frac{4 k}{5 k} = \frac{4}{5}

cos A = \frac{A B}{A C} = \frac{3 k}{5 k} = \frac{3}{5}

बचे हुए अन्य तीन अनुपात हम उपरोक्त तीन के व्युत्क्रम करके ज्ञात कर सकते है -

cot A

= \frac{1}{tan A} = \frac{3}{4}

cos e c A

= \frac{1}{sin A} = \frac{5}{4}

sec A

= \frac{1}{cos A} = \frac{5}{3}

Learn more

OMR (One Minute Revision)

त्रिकोणमितीय अनुपात

(i) sin θ =

(i i) cos θ =

(i i i) tan θ =

(i v) cos e c θ =

(v) sec θ =

(v i) cot θ =

2. विशिष्ट कोणों के त्रिकोणमितीय अनुपात

जैसे की हम जानते है समकोण त्रिभुज मे एक समकोण तथा अन्य न्यून कोण प्राप्त होते है, यहाँ कुछ महत्वपूर्ण न्यूनकोण के त्रिकोणमितीय अनुपात देख लेते है -

$45^{\circ}$ के त्रिकोणमितिय अनुपात

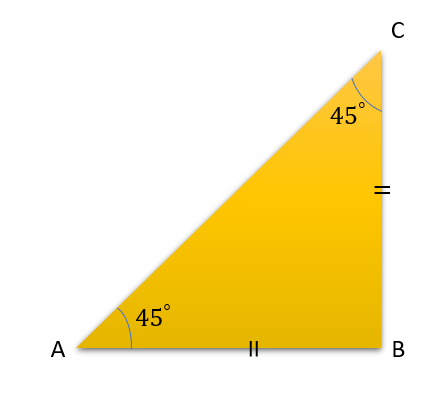
माना एक त्रिभुज

Δ A B C

है जिसका कोण

∠ B

समकोण है तथा

∠ A = 45^{\circ}

है, इस प्रकार की स्थिति में हम देख सकते है कि त्रिभुज का दूसरा न्यून कोण (

∠ C

) भी

45^{\circ}

का होगा, तथा जैसा की हम जानते है त्रिभुज मे समान कोणों के सम्मुख भुजाओ के मान समान होते है अर्थात यह त्रिभुज एक समद्विबाहु त्रिभुज होगा।
चूँकि हमे त्रिकोणमिति अनुपात की गणना करनी है इसलिए,

माना

A B = B C = a

पाइथागोरस प्रमेय से

{(A C)}^{2} = {(A B)}^{2} + {(B C)}^{2}

{(A C)}^{2} = a^{2} + a^{2} = 2 a^{2}

A C = \sqrt{2 a^{2}} = a \sqrt{2}

sin 45^{\circ} = \frac{B C}{A C} = \frac{a}{a \sqrt{2}} = \frac{1}{\sqrt{2}}

{cos 45}^{\circ} = \frac{A B}{A C} = \frac{a}{a \sqrt{2}} = \frac{1}{\sqrt{2}}

{tan 45}^{\circ} = \frac{B C}{A B} = \frac{a}{a} = 1

इसी प्रकार अन्य त्रिकोणमिति अनुपात

{cot 45}^{\circ} = 1

{sec 45}^{\circ} = \sqrt{2}

cos e c 45^{\circ} = \sqrt{2}

$30^{\circ}$ व $60^{\circ}$ के त्रिकोणमितिय अनुपात

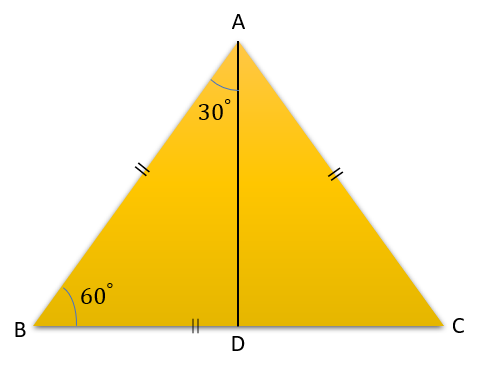
माना,
एक समबाहु त्रिभुज ABC है। कोण

∠ A

से भुजा

B C

पर लम्ब

A D

की रचना की गयी है।

अब

Δ A B D

व

Δ A D C

में

A B = A C

(समबाहु त्रिभुज की भुजाएं है)

A D = A D

(उभयनिष्ठ भुजाएं)

∠ A D B = ∠ A D C

(प्रत्येक समकोण )

अतः

Δ A B D

≅

Δ A D C

अतः हम कह सकते है कि

B D = D C = a

(माना)
तथा

∠ B A D = ∠ D A C = 30^{\circ}

चूँकि

Δ A B C

एक समबाहु त्रिभुज है
अतः

A B = A C = B C = 2 a

समकोण त्रिभुज

A D B

में
पाइथागोरस प्रमेय से

{(A B)}^{2} = {(A D)}^{2} + {(B D)}^{2}

{(2 a)}^{2} = {(A D)}^{2} + {(a)}^{2}

{(A D)}^{2} = 4 a^{2} - a^{2}

= 3 a^{2}

A D = a \sqrt{3}

चूँकि

Δ A D B

समकोण त्रिभुज है, साथ ही हमने इसकी भुजाओं की गणना भी कर ली है अतः अब हम त्रिकोणमिति अनुपातों की गणना कर सकते है।

अब

Δ A D B

में
न्यूनकोण

∠ B = 60^{\circ}

के सापेक्ष सभी त्रिकोणमिति अनुपात के मान निम्न प्रकार प्राप्त
होते है:

sin 60^{\circ} = \frac{A D}{A B}

= \frac{a \sqrt{3}}{2 a} = \frac{\sqrt{3}}{2}

{cos 60}^{\circ} = \frac{B D}{A B}

= \frac{a}{2 a} = \frac{1}{2}

{tan 60}^{\circ} = \frac{sin 60^{\circ}}{{cos 60}^{\circ}}

= \frac{\frac{\sqrt{3}}{2}}{\frac{1}{2}} = \sqrt{3}

{cot 60}^{\circ} = \frac{1}{{tan 60}^{\circ}}

= \frac{1}{\sqrt{3}}

{sec 60}^{\circ} = \frac{1}{{cos 60}^{\circ}} = 2

cos e c 60^{\circ} = \frac{1}{sin 60^{\circ}}

= \frac{2}{\sqrt{3}}

अब न्यूनकोण

∠ B A D = 30^{\circ}

के सापेक्ष त्रिकोणमिति अनुपात निम्न प्रकार प्राप्त होते है :

{sin 30}^{\circ} = \frac{B D}{A B}

= \frac{a}{2 a} = \frac{1}{2}

{cos 30}^{\circ} = \frac{A D}{A B} = \frac{a \sqrt{3}}{2 a} = \frac{\sqrt{3}}{2}

{tan 30}^{\circ} = \frac{sin 30^{\circ}}{{cos 30}^{\circ}}

= \frac{\frac{1}{2}}{\frac{\sqrt{3}}{2}} = \frac{1}{\sqrt{3}}

{cot 30}^{\circ} = \frac{1}{{tan 30}^{\circ}}

= \sqrt{3}

{sec 30}^{\circ} = \frac{1}{{cos 30}^{\circ}}

= \frac{2}{\sqrt{3}}

cos e c 30^{\circ} = \frac{1}{sin 30^{\circ}} = 2

$0^{\circ}$ व $90^{\circ}$ के त्रिकोणमितिय अनुपात

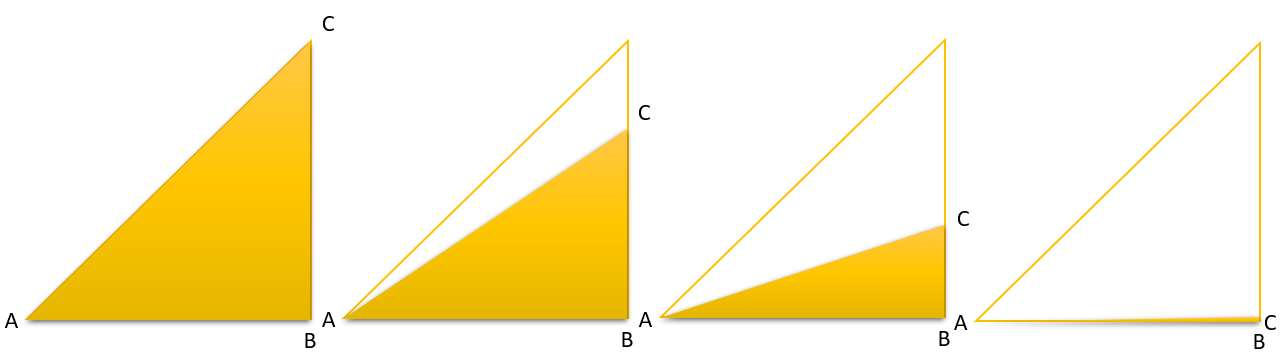
ऊपर दिए गए चित्र में देखते है...

बांये क्रम से पहले चित्र में

Δ A B C

को देखिये,
न्यून कोण

∠ A

के सापेक्ष त्रिभुज

Δ A B C

की ऊंचाई (लंब)

B C

, आधार

A B

तथा कर्ण

A C

है।

यदि अब हम त्रिभुज के शीर्ष

C

को शीर्ष

B

की ओंर लेकर चले तो त्रिभुज की ऊंचाई घटती जाती है, कर्ण

A C

आधार

A B

के सम्पाती हो जाता है अर्थात

A B = A C

, साथ ही साथ न्यून कोण

∠ A

का मान भी घटता जाता है।

अंततः जब शीर्ष $C$ शीर्ष $B$ पर पहुँच जायेगा तब त्रिभुज की ऊंचाई $B C = 0$ हो जाएगी तथा न्यून कोण $∠ A = 0^{\circ}$ हो जायेगा, जैसा की दांये क्रम के चित्र में देख सकते है।

अब हम न्यून कोण

∠ A = 0^{\circ}

के सापेक्ष त्रिकोणमिति अनुपातों की गणना करते है।

sin 0^{\circ} = \frac{B C}{A C}

= \frac{0}{A C} = 0

{cos 0}^{\circ} = \frac{A B}{A C}

= 1 (∴ A B = A C)

{tan 0}^{\circ} = \frac{sin 0^{\circ}}{{cos 0}^{\circ}}

= \frac{0}{1} = 0

{cot 0}^{\circ} = \frac{1}{{tan 0}^{\circ}}

= \frac{1}{0} =

अपरिभाषित

{sec 0}^{\circ} = \frac{1}{{cos 0}^{\circ}} = 1

cos e c 0^{\circ} = \frac{1}{sin 0^{\circ}}

= \frac{1}{0} =

अपरिभाषित

ऊपर बताये गए स्थिति में यदि थोड़ा सा परिवर्तन करे, मतलब अब हम यदि शीर्ष

A

को शीर्ष

B

की ओंर लेकर बढ़ाए तो आइये नीचे दिए गए चित्र से समझते है।

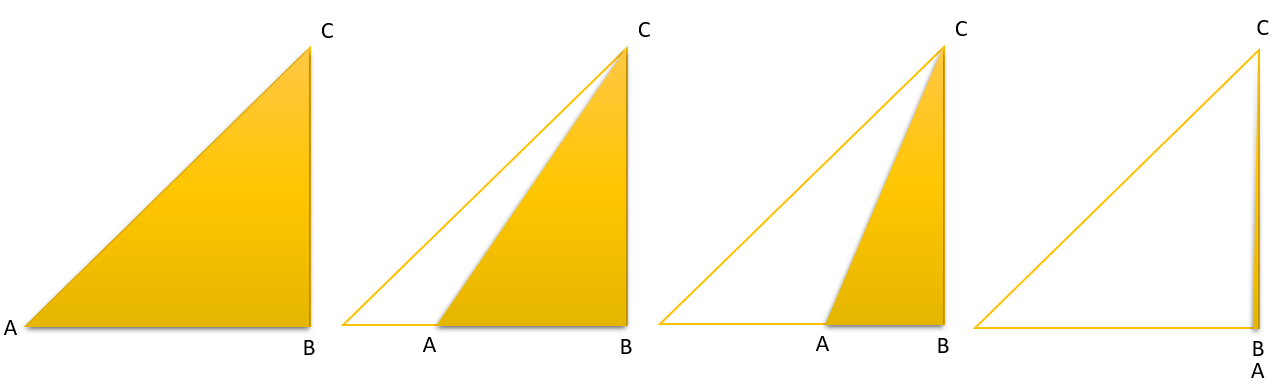
ocr_image

अगर हम ध्यान से देखे तो हम समझ सकते है कि जैसे ही शीर्ष

A

शीर्ष

B

की ओंर बढ़ता है आधार

A B

घटता जायेगा अर्थात अंततः

A B = 0

(लगभग) हो जायेगा, कर्ण

A C

, लम्ब

A B

के लगभग सम्पाती हो जायेगा साथ ही साथ न्यून कोण

∠ A

का बढ़ता जायेगा और अंततः

∠ A = 90^{\circ}

(लगभग)

अब हम

∠ A = 90^{\circ}

के लिए सभी त्रिकोणमिति अनुपातों की गणना कर सकते है।

sin 90^{\circ} = \frac{B C}{A C} = 1

(चूँकि

B C = A C)

{cos 90}^{\circ} = \frac{A B}{A C} = \frac{0}{1} = 0

{tan 90}^{\circ} = \frac{sin 90^{\circ}}{{cos 90}^{\circ}} = \frac{1}{0} =

अपरिभाषित

{cot 90}^{\circ} = 0

{sec 90}^{\circ} =

अपरिभाषित

cos e c 90^{\circ} = 1

अपरिभाषित (Note defined) को हम

\infty

से भी निरूपित कर सकते है।

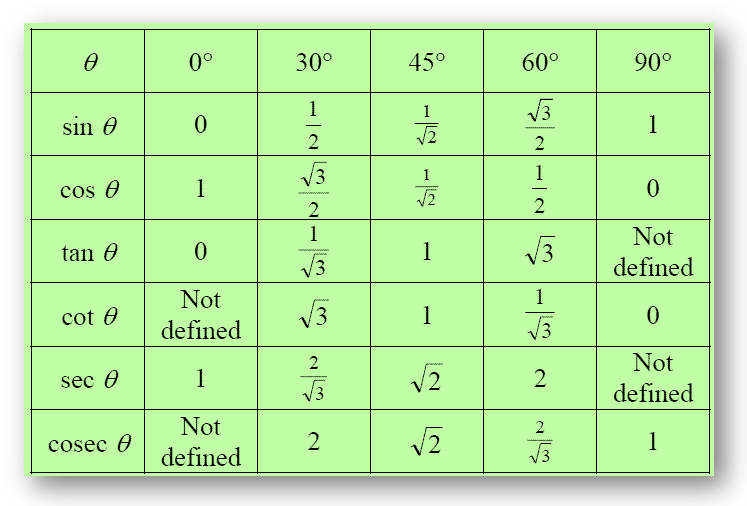
त्रिकोणमिति अनुपातों के यह मान बहुत ही महत्वपूर्ण है, इनके मान नीचे एक सारणी के रूप में एक साथ दिखाया गया है -
ocr_image

उदाहरण 2

${cos 60}^{\circ} {cos 30}^{\circ} + {sin 60}^{\circ} {sin 30}^{\circ}$ को सरलतम रूप में परिकलित कीजिए।

${cos 60}^{\circ} {cos 30}^{\circ}$ $+ {sin 60}^{\circ} {sin 30}^{\circ}$

$= \frac{1}{2} \times \frac{\sqrt{3}}{2}$ $+ \frac{\sqrt{3}}{2} \times \frac{1}{2}$

$= \frac{\sqrt{3}}{4} + \frac{\sqrt{3}}{4}$

$= 2 (\frac{\sqrt{3}}{4}) = \frac{\sqrt{3}}{2}$

Learn more

उदाहरण 3

सिद्ध करें कि,
$2 {sin 30}^{\circ} \cdot {cos 30}^{\circ}$ = $\frac{2 {tan 30}^{\circ}}{1 + {tan}^{2} 30^{\circ}}$

$L H S =$ $2 {sin 30}^{\circ} {cos 30}^{\circ}$

$= 2 \times \frac{1}{2} \times \frac{\sqrt{3}}{2}$ $= \frac{\sqrt{3}}{2}$ ....(i)

$R H S =$ $\frac{2 {tan 30}^{\circ}}{1 + {tan}^{2} 30^{\circ}}$

$= \frac{2 \cdot \frac{1}{\sqrt{3}}}{1 + {(\frac{1}{\sqrt{3}})}^{2}}$

$= \frac{\frac{2}{\sqrt{3}}}{1 + \frac{1}{3}}$

$= \frac{\frac{2}{\sqrt{3}}}{\frac{4}{3}} = \frac{2}{\sqrt{3}} \times \frac{3}{4}$

$= \frac{\sqrt{3}}{2}$ ....(ii)

समी. (i) और (ii) से हम पाते है,

$2 {sin 30}^{\circ} \cdot {cos 30}^{\circ}$ $= \frac{2 {tan 30}^{\circ}}{1 + {tan}^{2} 30^{\circ}}$

Learn more

उदाहरण 4

${tan}^{2} 30^{\circ} + {tan}^{2} 45^{\circ} + {tan}^{2} 60^{\circ}$ का मान ज्ञात करें।

${tan}^{2} 30^{\circ} + {tan}^{2} 45^{\circ} + {tan}^{2} 60^{\circ}$

$= {(\frac{1}{\sqrt{3}})}^{2} + 1^{2} + {(\sqrt{3})}^{2}$

$= \frac{1}{3} + 1 + 3$

$= \frac{1}{3} + 4$

$= \frac{1 + 12}{3}$

$= \frac{13}{3}$

Learn more

3. पूरक कोणों के त्रिकोणमितीय अनुपात

पूरक कोणों से हमारा तात्पर्य ऐसे कोणों के युग्म से है जिनका योग $90^{\circ}$ के बराबर हो। जैसे कि हम जानते है कि समकोण त्रिभुज मे एक कोण सदैव $90^{\circ}$ का होता है तथा कुल योग $180^{\circ}$ होती है अतः अन्य दो कोणों का योग $90^{\circ}$ होगा, आशय है की समकोण त्रिभुज मे स्थित न्यूनकोण एक दूसरे के पूरक कोण होते है।

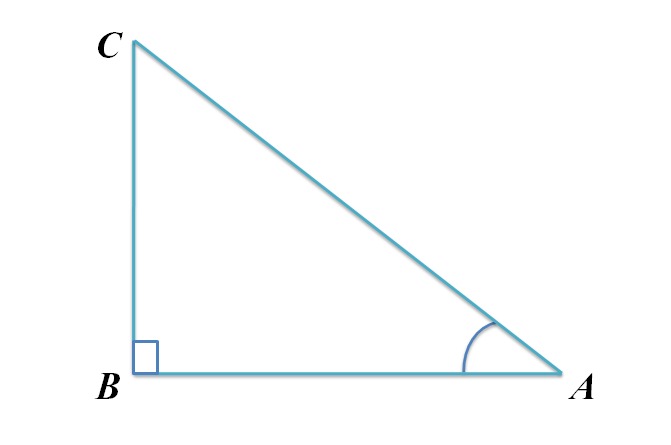
अब चित्र से

Δ A B C

में
कोण

∠ A

तथा

∠ C

ऐसे दो कोण है जिनका योग निश्चित रूप से

90^{\circ}

के बराबर होगा।
अतः

∠ C = 90^{\circ} - ∠ A

अब हम यदि न्यून कोण

∠ C

के सापेक्ष त्रिकोणमिति अनुपात को देखे तो,

sin (C) = \frac{A B}{A C}

अतः

sin (90 - A) = \frac{A B}{A C}

चूँकि

cos A = \frac{A B}{A C}

अतः

sin (90 - A) = \frac{A B}{A C}

= cos A

अतः

sin (90 - A) = cos A

इसी प्रकार

cos (90 - A) = \frac{B C}{A C} = sin A

tan (90 - A) = \frac{A B}{B C} = cot A

cot (90 - A) = \frac{B C}{A B} = tan A

sec (90 - A) = \frac{A C}{B C} = cos e c A

cos e c (90 - A) = \frac{A C}{A B} = sec A

उदाहरण 5

निम्न लिखित के मान ज्ञात कीजिये
$\frac{{tan 54}^{\circ}}{{cot 36}^{\circ}}$

$\frac{{tan 54}^{\circ}}{{cot 36}^{\circ}}$ $= \frac{tan (90^{\circ} - 36^{\circ})}{{cot 36}^{\circ}}$

[चूँकि $tan (90^{\circ} - θ) = cot θ$ ]

$= \frac{{cot 36}^{\circ}}{{cot 36}^{\circ}} = 1$

Learn more

उदाहरण 6

${sin 67}^{\circ} + {cos 75}^{\circ}$ को $0^{\circ}$ और $45^{\circ}$ के बीच के त्रिकोणमितीय अनुपातों के पदों में व्यक्त करें।

${sin 67}^{\circ} + {cos 75}^{\circ}$

$= sin (90^{\circ} - 23^{\circ}) + cos (90^{\circ} - 15^{\circ})$

$= {cos 23}^{\circ} + {sin 15}^{\circ}$

Learn more

उदाहरण 7

यदि $tan 2 A = cot (A - 18^{\circ})$ , जहाँ 2A एक न्यूनकोण है, तब A का मान ज्ञात करें।

दिया हुआ है,

$tan 2 A = cot (A - 18^{\circ})$ ....(i)

चूंकि $tan θ = cot (90^{\circ} - θ)$

माना $θ = 2 A$

अतः $tan 2 A$ $= cot (90^{\circ} - 2 A)$ ....(ii)

समीकरण (i) व (ii) से

$cot (90^{\circ} - 2 A)$ $= cot (A - 18^{\circ})$

$\Rightarrow 90^{\circ} - 2 A = A - 18^{\circ}$

$\Rightarrow 3 A = 108^{\circ}$

$\Rightarrow A = 36^{\circ}$

Learn more

OMR (One Minute Revision)

sine का पूरक

sin (90 - A) = cos A

cos (90 - A) = sin A

sec का पूरक

sec (90 - A) = cos e c A

cos e c (90 - A) = sec A

tangent का पूरक

tan (90 - A) = cot A

cot (90 - A) = tan A

4. त्रिकोणमितीय सर्वसमिकायें

बच्चों यहाँ हम सबसे पहले सर्वसमिका शब्द का मतलब देख लेते है, जैसे की आपने पहले समीकरण पढे हुए है जिसमे स्थित चर कुछ विशेष मान के ही सत्य होते है उदाहरण के लिए -
$x + y = 5$
यहाँ यदि हम धनात्मक संख्याओ की बात करे तो $5$ , 3 व 2 तथा 1 व 4 को जोड़ने पर प्राप्त होता है इसके अलावा अन्य किसी प्रकार से 5 प्राप्त नहीं होगा।

इसके विपरीत सर्वसमिका वह है जो चरों के सभी मानों के लिए सही हो, चूँकि सर्वसमिका हमे सिद्ध करके प्राप्त होती है।
उदाहरण -
${(x + y)}^{2} = x^{2} + y^{2} + 2 x y$
यहाँ हम $x$ , $y$ के कोई भी मान रखें यह सभी को संतुष्ट करेगा । अतः यह सर्वसमिका है ।

यहाँ हम त्रिकोणमितीय अनुपातों से सम्बंधित सर्वसमिकाओं को पढ़ेंगे

Δ A B C

में पाइथागोरस प्रमेय से

{(A C)}^{2} = {(A B)}^{2} + {(B C)}^{2}

......(i)

यदि

△ A B C

मे

∠ A

के सापेक्ष देखें तो, AC = कर्ण, BC = लंब, तथा AB = आधार
समीकरण

(i)

के दोनों पक्षों में

{(A C)}^{2}

से भाग देने पर

1 = {(\frac{A B}{A C})}^{2} + {(\frac{B C}{A C})}^{2}

\Rightarrow 1 = {(cos A)}^{2} + {(sin A)}^{2}

= {cos}^{2} A + {sin}^{2} A

अर्थात

${sin}^{2} A + {cos}^{2} A = 1$

समीकरण

(i)

के दोनों पक्षों में

{(A B)}^{2}

से भाग देने पर

{(\frac{A C}{A B})}^{2} = {(\frac{A B}{A B})}^{2} + {(\frac{B C}{A B})}^{2}

${sec}^{2} A = 1 + {tan}^{2} A$

अर्थात

${sec}^{2} A - {tan}^{2} A = 1$

समीकरण

(i)

के दोनों पक्षों में

{(B C)}^{2}

से भाग देने पर

{(\frac{A C}{B C})}^{2} = {(\frac{A B}{B C})}^{2} + {(\frac{B C}{B C})}^{2}

$cos e c^{2} A = {cot}^{2} A + 1$

अर्थात

$cos e c^{2} A - {cot}^{2} A = 1$

उदाहरण 8

$Δ A B C$ में जिसका कोण C समकोण है जिसमे $A B = 29$ इकाई, $B C = 21$ इकाई और $∠ A B C = θ,$ तो निम्नलिखित के मान ज्ञात कीजिए:
(i) ${cos}^{2} θ + {sin}^{2} θ$
(ii) ${cos}^{2} θ - {sin}^{2} θ$

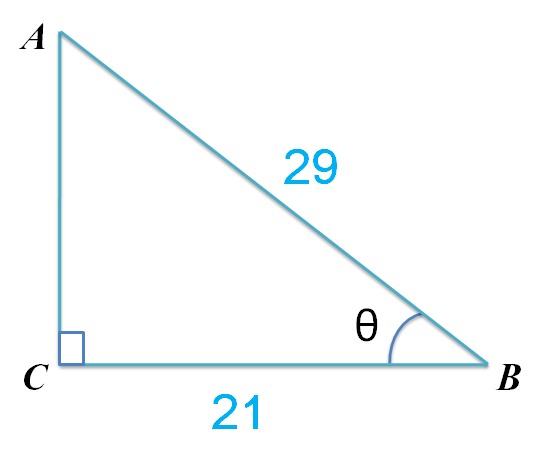
Δ A B C

में, पाइथागोरस प्रमेय से

A B^{2} = A C^{2} + B C^{2}

A C^{2} = A B^{2} - B C^{2}

A C = \sqrt{A B^{2} - B C^{2}}

A C = \sqrt{{(29)}^{2} - {(21)}^{2}}

= \sqrt{841 - 441}

= \sqrt{400} = 20

(चूंकि लंबाई सदैव धनात्मक होता है अतः

A C

का धनात्मक मान लिया गया।)

चूँकि

sin θ = \frac{A C}{A B} = \frac{20}{29}

cos θ = \frac{B C}{A B} = \frac{21}{29}

तब
(i)

{cos}^{2} θ + {sin}^{2} θ

= {(\frac{21}{29})}^{2} + {(\frac{20}{29})}^{2}

= \frac{441 + 400}{841}

= \frac{841}{841} = 1

अथवा
सर्वसमिका के उपयोग से

चूँकि

{cos}^{2} θ + {sin}^{2} θ = 1

अतः मान 1 प्राप्त होगा।

(ii)

{cos}^{2} θ - {sin}^{2} θ

= {(\frac{21}{29})}^{2} - {(\frac{20}{29})}^{2}

= \frac{441 - 400}{841} = \frac{41}{841}

Learn more

उदाहरण 9

$9 {sec}^{2} A - 9 {tan}^{2} A$ का मान ज्ञात करें।

दिया है,
$9 {sec}^{2} A - 9 {tan}^{2} A$

$= 9 \times ({sec}^{2} A - {tan}^{2} A)$

{sec}^{2} A = 1 + {tan}^{2} A

{sec}^{2} A - {tan}^{2} A = 1

अतः

9 \times ({sec}^{2} A - {tan}^{2} A)

= 9 \times 1 = 9

Learn more

उदाहरण 10

सर्वसमिका को सिद्ध कीजिए
${sec}^{4} θ - {sec}^{2} θ = {tan}^{4} θ + {tan}^{2} θ$

$L . H . S .$ $= {sec}^{4} θ - {sec}^{2} θ$

= {sec}^{2} θ ({sec}^{2} θ - 1)

{sec}^{2} θ = 1 + {tan}^{2} θ

{sec}^{2} θ - 1 = {tan}^{2} θ

L . H . S .

= {sec}^{2} θ ({sec}^{2} θ - 1)

= (1 + {tan}^{2} θ) {tan}^{2} θ

= {tan}^{2} θ + {tan}^{4} θ

= {tan}^{4} θ + {tan}^{2} θ = R . H . S .

Learn more

OMR (One Minute Revision)

${sin}^{2} A + {cos}^{2} A = 1$
या $1 - {sin}^{2} A = {cos}^{2} A$
या $1 - {cos}^{2} A = {sin}^{2} A$

${sec}^{2} A - {tan}^{2} A = 1$
या $1 + {tan}^{2} A = {sec}^{2} A$

$cos e c^{2} A - {cot}^{2} A = 1$
या $1 + {cot}^{2} A = cos e c^{2} A$

सारांश

आइए इस अध्याय के कुछ महत्वपूर्ण बिन्दु देख लेते है -

किसी समकोण त्रिभुज $Δ A B C$ के लिए त्रिकोणमिति अनुपात निम्न है

$sin A = \frac{B C}{A C}$

$cos A = \frac{A B}{A C}$

$tan A = \frac{B C}{A B}$

$cot A = \frac{A B}{B C}$

$sec A = \frac{A C}{A B}$

$cos e c A = \frac{A C}{B C}$

विशिष्ट कोणों के लिए त्रिकोणमिति अनुपात की सारणी

पूरक कोणों के लिए त्रिकोणमिति अनुपात

$sin (90 - A) = \frac{A B}{A C} = cos A$

$cos (90 - A) = \frac{B C}{A C} = sin A$

$tan (90 - A) = \frac{A B}{B C} = cot A$

$sec (90 - A) = \frac{A C}{B C} = cos e c A$

$cos e c (90 - A) = \frac{A C}{A B} = sec A$

$cot (90 - A) = \frac{B C}{A B} = tan A$

त्रिकोणमिति सर्वसमिकाएँ

${cos}^{2} A + {sin}^{2} A = 1$

${sec}^{2} A - {tan}^{2} A = 1$

$cos e c^{2} A - {cot}^{2} A = 1$

Home
Ask Doubt
Profile