दो चर वाले रैखिक समीकरण युग्म कक्षा 10 गणित
भूमिका
वह समीकरण जिनमे दो चर (अज्ञात) राशियाँ होती है तथा जो एक रेखा को प्रदर्शित करते है, दो चरों वाले रैखिक समीकरण कहलाते है। दो चरों वाले रैखिक समीकरण को ax+by+c=0 के रूप मे व्यक्त करते है, यहाँ x तथा y चर पद है तथा a व b क्रमशः उनके गुणांक है , यहाँ c अचर पद है। जहाँ a≠0 व b≠0 होना आवश्यक है।
इस अध्याय मे हम दो चर वाले रैखिक समीकरण उनके आलेख तथा दो चर वाले रैखिक समीकरण के युग्म, एक युग्म का हल व हलों कि संख्या, दो चर वाले रैखिक समीकरण युग्म का ज्यामितीय अर्थ, रैखिक समीकरण युग्म को हल करने का बीजीय तरीका तथा दो चरों के रैखिक समीकरणो के युग्म में बदले जा सकने वाले समीकरण आदि बिन्दुओ पर चर्चा करेंगे।
आइये जानते है, 2 चरों वाले रैखिक समीकरण को और करीब से ...
बच्चो, आपने पिछली कक्षा मे एक चर का रैखिक समीकरण के बारे मे पढ़ा है, जिसमे हमारे पास एक चर राशि होती थी इसी प्रकार इस अध्याय मे हम 2 चरों वाले रैखिक समीकरण की बात करेंगे । अब यहाँ आपने कुछ पदों के नाम देखे जैसे कि चर, रैखिक समीकरण आदि तो आइए इन्हे संक्षेप मे देख लेते है। बात करें यदि चर राशि की तो चर वे अज्ञात राशि होती है, जो समय के साथ परिवर्तित होती है तथा जिन्हे हम सामान्यतः अंग्रेजी के अक्षर x, y, z, t आदि से प्रदर्शित करते हैं। साथ ही बच्चों यहाँ हम रैखिक समीकरण की बात करें तो रैखिक समीकरण इस प्रकार का समीकरण होता है जिसमे चर की अधिकतम घात 1 होती है तथा इन समीकरणों के चर पदों मे भिन्न - भिन्न मान रखने पर यह एक रेखा को प्रदर्शित करता है।
आप रोज़ अपने चारों तरफ कुछ इस तरह की स्थिति जरूर देखते होंगे जैसे मान लो कि आप पेन खरीदने दुकान पर जाते हो और दुकान वाले भैया से कहते हो कि भैया मुझे 2 काले और 4 नीले पेन दे दो, वो आपको पेन दे देते है फिर आप उनसे पूछते हो कि कितने रुपए देने हैं, तब वो आपसे कहते हैं 26 रुपए। अब आपका दोस्त जाता है और कहता है की मुझे 3 काले और 3 नीले पेन दे दो, फिर वो पूछता है कि कितने रूपए देने है तो दुकान वाले भैया कहते है कि 25 रूपए। अब अगर मैं आपसे ये पूछूं कि 1 काला और 1 नीला पेन कितने का था ? तो आपको थोड़ा टाइम लगेगा और बताने मे भी मुश्किल होगी, अब देखिये इसी समस्या को हल करने के लिए हम इन स्थितियों को समीकरणों के रूप में लिखते हैं। यदि हम काले पेन का मूल्य x तथा नीले पेन का मूल्य y से प्रदर्शित करे तो पहला समीकरण 2x+4y=26.....(i) प्राप्त होगा। यहाँ हम देख सकते है की 2 काले पेन का मूल्य इस प्रकार 2x रुपए तथा 4 नीले पेन का मूल्य 4y रुपए होगा इसलिए कुल मूल्य 2x+4y रुपए होगा तथा जिसे हम दिए गए कुल मूल्य 26 रुपए के बराबर लिख सकते हैं जो की हमने दुकानदार को दिया था। इसी प्रकार आप अपने दोस्त द्वारा किये गए लेन - देन को भी समीकरण 3x+3y=25....(ii) के रूप मे लिख सकते हैं।
अब यहाँ समीकरण (i) व (ii) को देखें तो यहाँ दो चरों x व y के पद है तथा एक अचर पद है साथ ही x व y पदों के गुणांक अचर पद हैं यदि यहाँ x व y के गुणांको को क्रमशः a व b तथा अचर पद को c से दर्शाये तब हमे यह ax+by=c या ax+by+c=0 रूप का समीकरण दिखेगा। यहाँ उदाहरण के अनुसार पहला रूप प्राप्त होगा, परन्तु दोनों ही रूप सही हैं इसे दो चरों का रैखिक समीकरण का व्यापक रूप कहते हैं, जिसे हम आगे देखेंगे।
बच्चों इस अध्याय में हम दो चरों वाले रैखिक समीकरण , उनके हल की विधियों (आलेखीय तथा बीजीय) तथा हलो की संख्या के बारे में बात करेंगे।
1. दो चर वाले रैखिक समीकरण
जैसे की हमने पहले उदाहरण द्वारा दो चर वाले रैखिक समीकरण को समझा, अब यहाँ यदि हम दो चरों वाले रैखिक समीकरण के व्यापक रूप को देखे तो, हमे प्राप्त होगा समीकरण
ax+by+c=0, जहाँ a , b ,c ∈R और a≠0,b≠0 , के रुप के समीकरण को दो चर x और y वाले रैखिक समीकरण कहते हैं ।
उदाहरण
(i) 9x−4y+8=0
(ii) x+√5y+3=0
(iii) 57x+39y−1=0
हम प्रायः a और b के शून्येतर होने (शून्य के बराबर न हो) की शर्त को a2+b2≠0 के रुप में प्रदर्शित करते है ।
दो चर वाले रैखिक समीकरण के हल -
आइये इसे हम एक उदाहरण के माध्यम से समझते है
माना x+y=5 एक दो चरों x तथा y के लिए रैखिक समीकरण दिया है
अब हम x तथा y के उन मानों को ज्ञात करने का प्रयत्न करते है जो इस समीकरण को संतुष्ट करे :
x=1, y=5−x⇒y=4
x=1,y=4
x=2, y=5−x⇒y=3
x=2,y=3
x=0, y=5−x⇒y=5
x=0,y=5
इस प्रकार हम देखते है कि x के भिन्न -भिन्न मानों के लिए y के भिन्न -भिन्न मान मिलते है अतः हम यहाँ से ये निष्कर्ष निकाल सकते है कि :
(1) समीकरण x+y=5 के वास्तविक संख्याओं के समुच्चय R पर अनेक हल प्राप्त होंगे।
(2) समीकरण x+y=5 के प्राकृतिक संख्याओं के समुच्चय N पर सीमित हल प्राप्त होंगे।
ऐसा हम क्यों कह रहे है ? तो आप देख सकते है R:(−∞,∞) तथा N:{1,2,3.....} होता है x व y के भिन्न-भिन्न मान यदि N से ली जाए तो कुछ सीमित हल प्राप्त हो रहे है तथा यदि R से लिया जाए तो अनेक हल मिलेंगे ।
इस प्रकार हमने देखा की दो चर वाले रैखिक समीकरण के वास्तविक संख्याओं के समुच्चय R पर अद्वितीय हल प्राप्त करना असंभव है इसलिए इन समीकरणों के अद्वितीय हल प्राप्त करने के लिए हमे दो रैखिक समीकरण युग्म आवश्यक होते है। अगर इसे व्यापक रूप में परिभाषित करें तो हम कह सकते है कि किसी रैखिक समीकरण में जितने चर होते है उन समीकरणों के अद्वितीय हल प्राप्त करने के लिए उतने ही भिन्न-भिन्न रैखिक समीकरण आवश्यक होते है।
2. दो चर वाले रैखिक समीकरण युग्म
अब बच्चों यहाँ युग्म से तात्पर्य जोड़े से है यहाँ हम रैखिक समीकरणों के जोड़े लेते है अर्थात दो चर वाले दो रैखिक समीकरणों को एक साथ लेने पर उसे दो चर वाला रैखिक समीकरण युग्म कहते हैं।
उदाहरण
(i) 12x+3y=8
5x−4y=0
(ii) 13x+15y=5
37x−12y=0
दो चर xऔर y में रैखिक समीकरण युग्म का व्यापक (general) रुप है :
a1x+b1y+c1=0
और a2x+b2y+c2=0
जहाँ a1,b1,c1,a2,b2,c2 वास्तविक संख्यायें हैं।
अर्थात् a1और b1 में कम - से - कम एक शून्येत्तर (शून्य के बराबर न हो) है तथा a2 और b2 में भी कम - से - कम एक शून्येत्तर है ।
दो चरों में दो या अधिक रैखिक समीकरणों को साथ - साथ लेने पर बना निकाय (System) रैखिक - समीकरण निकाय कहलाता है ।
OMR (One Minute Revision)
रैखिक समीकरण युग्म का सबसे व्यापक रूप निम्न है:
a1x+b1y+c1=0
a2x+b2y+c2=0
जहाँ a1,a2,b1,b2 ऐसी वास्तविक संख्याएं है की a21+b21≠0, a22+b22≠0 है।
3. रैखिक समीकरण ax + by + c = 0 का आलेख
यहाँ हम रैखिक समीकरण के आलेखीय निरूपण की बात करेंगे, अब यदि हम कहे यहाँ आलेखीय निरूपण से क्या तात्पर्य है, तो यहाँ हम दिए गए समीकरण को आलेख अर्थात चित्र रूप मे दर्शाते है। जो हम समीकरण मे दिए गए चर पदों के भिन्न-2 मान (यहाँ हम पूर्णांक मान का उपयोग करते है) रखकर किसी ग्राफ पेपर पर प्राप्त कर सकते है। जैसा की बच्चों आपको याद होगा की रैखिक समीकरण के कोई 2 हल (बिन्दुओ) चुनकर उनको ग्राफ मे आलेखित करते है, तत्पश्चात उन बिन्दुओ को मिलाकर समीकरण का ग्राफ (आलेख) प्राप्त होता है।
आइए मानक रैखिक समीकरण (ax+by+c=0) के सहायता से इसे समझते है -
दत्त रैखिक समीकरण है,
ax+by+c=0....(i)
स्थिति I. जब c≠0
समीकरण (i) से,
y=−c−axb ....(ii)
(i) में y=0 रखने पर हम पाते हैं कि x =−ca
∴ रेखा (i), x - अक्ष को बिंदु A(−ca,0) पर काटती है ।
पुनः (i) में x = 0 रखने पर , हम पाते हैं कि y=−cb
अतः रेखा (i), y - अक्ष को बिंदु B(0,−cb) पर काटती है ।
अब A और B को मिलाते हैं तथा इसे दोनों तरफ बढ़ा देते हैं।
रेखा AB ही रैखिक समीकरण ax+by+c=0 का आलेख होगा।
उदाहरण:
x+y=4......(i)
(i) में y=0 रखने पर हम पाते हैं कि x=4
∴ रेखा (i), x− अक्ष को बिंदु (4,0) पर काटती है।
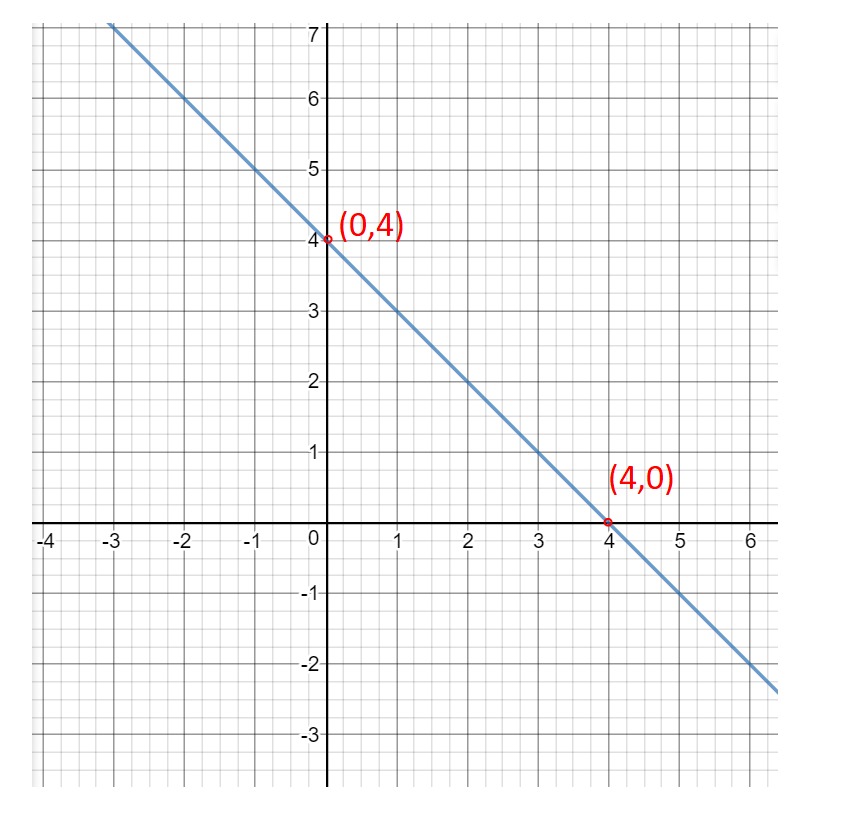
पुनः (i) में x = 0 रखने पर , हम पाते हैं कि y = 4
अतः रेखा (i), y - अक्ष को बिंदु B(0,4) पर काटती है।
स्थिति II. जब c=0
इस स्थिति में समीकरण ax+by=0 के रुप का होगा।
हम x के दो उपयुक्त मान x1 और x2 लेकर y के संगत मान y1 और y2 ज्ञात करते हैं ।
इस तरह हम दो बिंदुएँ A(x1,y1) और B(x2,y2) प्राप्त कर लेते हैं।
A(x1,y1) और B(x2,y2) को मिलाने वाली रेखा ही ax+by=0 का आलेख होगा ।
उदाहरण:
x−y=0
जब x=3, तब y=3
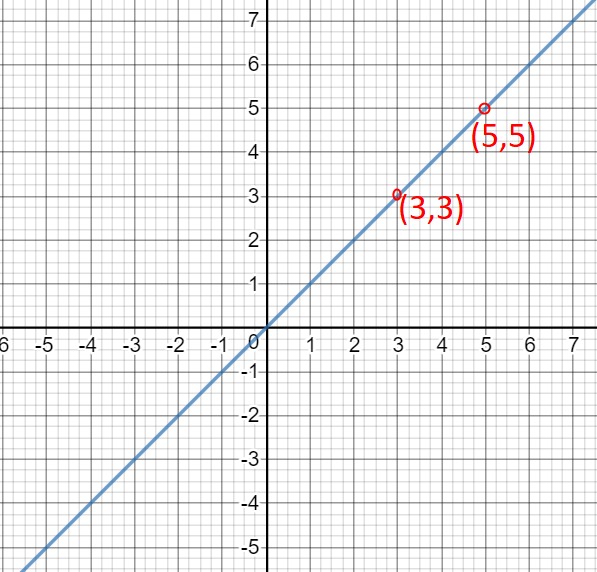
जब x=5 तब y=5 इस प्रकार आलेख प्राप्त कर सकते है जो मूल बिंदु (0,0) से होकर जाता है।
समीकरण का प्रत्येक हल उसको निरूपित करने वाली रेखा पर स्थित एक बिंदु होता है
तात्पर्य है कि रेखा पर जितने भी बिन्दु मिलेंगे वह रेखा को संतुष्ट करेंगे अर्थात बिन्दु के निर्देशांक रेखा के समीकरण को संतुष्ट करेंगे।
आइए इसे समीकरण (i) के उदाहरण से समझते हैं
हमने समीकरण x+y=4 के लिए आलेख देखा, यहाँ हमने दो बिन्दु (0,4) व (4,0) दर्शाया है जो रेखा पर स्थित है।
आइए यहाँ हम जाँच करते हैं कि ये समीकरण को संतुष्ट करते हैं अथवा नहीं?
यदि संतुष्ट करते है अतः ये रैखिक समीकरण के हल होंगे -
पहले बिन्दु (4,0) के लिए x=4,y=0
x+y=4+0=4 संतुष्ट करता है तथा
बिन्दु (0,4) के लिए x=0, y=4
x+y=0+4=4 भी संतुष्ट करता है।
अतः हम कह सकते है की रेखा पर स्थित बिन्दु रेखा के रैखिक समीकरण के हल होते हैं।
उदाहरण 1
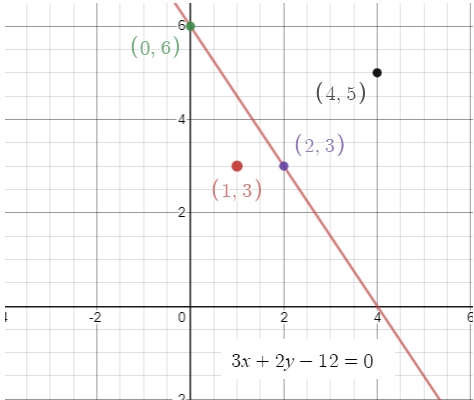
जांच कर देखें कि निम्न बिंदुओं में कौन समीकरण 3x+2y−12=0 के आलेख पर स्थित है?
(i) A(0,6) (ii) B(2,3) (iii) C(4,5) (iv) D(1,3)
दिया गया समीकरण है: 3x+2y−12=0
(i) जब x=0,y=6
3x+2y−12
⇒3×0+2×6−12
⇒0+12−12=0
⇒0=0
अतः बिंदु A(0,6) रेखा (i) के आलेख पर स्थित है।
(ii) जब x=2,y=3
3x+2y−12
⇒3×2+2×3−12
⇒6+6−12=0
⇒0=0
अतः बिंदु B(2,3) रेखा (i) के आलेख पर है।
(iii) जब x=4,y=5
3x+2y−12
⇒3×4+2×5−12
⇒12+10−12
⇒10≠0
अतः बिंदु C(4,5) रेखा (i) के आलेख पर नहीं है।
(iv) जब x=1,y=3
3x+2y−12
⇒3×1+2×3−12
⇒3+6−12
⇒−3≠0
अतः बिंदु D(1,3) रेखा (i) के आलेख पर नहीं है।
4. रैखिक समीकरण के एक युग्म का हल
यदि हमे रैखिक समीकरणों का एक युग्म दिया गया है तब उनके हल से क्या तात्पर्य है यह समझते हैं -
जैसा कि हमने पहले उदाहरण में आपके व आपके दोस्त द्वारा पेन (काला तथा नीला) खरीदने से प्राप्त दो समीकरणों (समीकरण युग्म) को देखा था। अब उन समीकरणों में हमारे पास दो अज्ञात राशियाँ (x तथा y) थीं, जो कि क्रमशः काले व नीले पेन के मूल्यों को दर्शाता था। अब इन्ही मूल्यों (x तथा y) का मान ज्ञात करना हमारा हल होगा , जहाँ x तथा y दोनों ही समीकरणों के लिए समान है इसलिए इसका मान दोनों समीकरणों को संतुष्ट करेगा ।
a1x+b1y+c1=0
a2x+b2y+c2=0,
चरों x और y वाला रैखिक समीकरणों का एक युग्म है
x और y के मानों के वे युग्म जो दोनों समीकरणों को संतुष्ट करते है , दिये गये रैखिक समीकरण युग्मों का हल कहलाता है ।
उदाहरण :
2x+y=5...(i)
2x−y=3...(ii)
x=2,y=1 इन दोनों समीकरणों को संतुष्ट करते हैं , इस प्रकार मानों का युग्म (2,1) दिए गये समीकरण युग्म का एक हल कहलाता है ।
समीकरण युग्मों के भिन्न प्रकार के हल होते है , जिनके बारे मे हम आगे देखेंगे ।
5. दो चर वाले रैखिक समीकरण युग्म का ज्यामितीय अर्थ
अब यदि हम रैखिक समीकरणों को ज्यामितीय रूप में देखें तब हम जानते हैं कि एक तल में यदि दो रेखाएँ दी हो तो निम्न तीन स्थतियों में से केवल एक ही संभावना हो सकती है
(i) दोनों रेखाएँ एक दूसरे को केवल एक बिन्दु पर प्रतिच्छेद करती है।
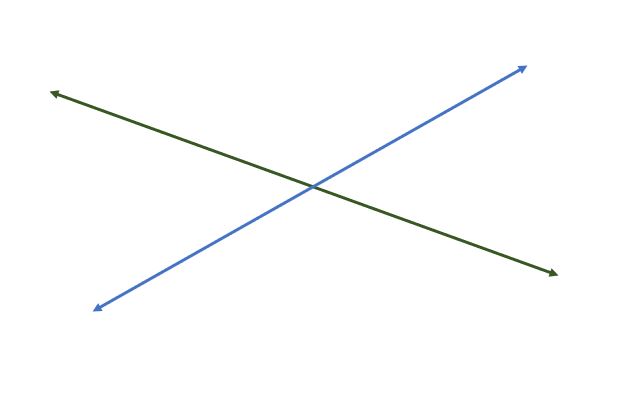
चूँकि 2 रेखाए एक ही बिन्दु पर मिल सकती है, अर्थात एक ही उभयनिष्ट बिन्दु प्राप्त होता है इसलिए केवल एक (अद्वितीय) हल प्राप्त होगा ।
(ii) दोनों रेखाएँ प्रतिच्छेद नहीं करती अर्थात वे एक दूसरे के समान्तर है।
चूँकि समांतर रेखाओ मे कोई भी उभयनिष्ट बिन्दु नहीं प्राप्त होता चूँकि वे कभी नहीं मिल सकती ।अतः कोई हल प्राप्त नहीं होगा ।
(iii) दोनों रेखाएँ संपाती हैं।
चूँकि संपाती रेखाएं एक - दूसरे पर आरोपित होता है अतः अनंत बिन्दु उभयनिष्ट होंगे (चूँकि रेखा कि सीमा नहीं होती तथा उसमे अनंत बिंदुए होती है ) , अतः अनंत हल प्राप्त होंगे।
इसे हम चित्र में देख के समझ सकते है, जैसा कि हमने रेखाओं के एक तल मे होने की बात कही थी यहाँ उदाहरण के लिए एक किताब का पृष्ट लेकर उस पर रेखाएं अंकित करके देखिए । आप देख सकते है, केवल इन्ही दिए गए 3 प्रकार से आप 2 रेखाओ (रेखायुग्म) मे संबंध प्रदर्शित कर सकते है ।
NOTE - यदि 2 रेखाए समांतर नहीं है तो वे अवश्य रूप से एक- दूसरे को प्रतिच्छेद करेंगे, संभव है कि पृष्ट मे सीमित स्थान होने के कारण असमांतर रेखाए प्रतिच्छेद करती हुई न दिखाई दे परंतु आगे बढ़ाने पर अवश्य प्रतिच्छेद करेंगी।
OMR (One Minute Revision)
दो चरों में एक रैखिक समीकरण युग्म का ग्राफ दो रेखाएँ निरूपित करता है|
उदाहरण 2
दो रेल पटरियाँ समीकरणों x+2y−4=0 और 2x+4y−12=0 द्वारा निरूपित की गई है। इस स्थिति को आलेखीय रूप में व्यक्त कीजिए।
दोनों पटरियों को निम्न रैखिक समीकरणों द्वारा निरूपित किया जाता है।
x+2y−4=0 ...(i )
2x+4y−12=0 ... (ii )
उपयुक्त रैखिक समीकरण युग्म को आलेखीय रूप से निरूपित करने के लिए हमें प्रत्येक समीकरण को निरूपित करने वाली रेखा पर दो बिंदुओं की आवश्यकता होगी।अतः हम प्रत्येक समीकरण के दो बिन्दु प्राप्त करते हैं।
दिया है ,
x+2y−4=0
इसमें y=0 रखने पर,
x+0−4=0
⇒x=4
पुनः x=0 रखने पर,
0+2y−4=0
⇒y=2
अतः समीकरण x+2y−4=0 के दो हल =x=0,y=2
और x=4,y=0 है।
दिया है, 2x+4y−12=0
इसमें x=0 रखने पर,
0+4y−12=0
⇒y=3
पुनः y=0 रखने पर,
2x+0×12=0
⇒x=6
इस प्रकार समीकरण 2x+4y−12=0 के दो हल x=0,y=3 और x=6,y=0 प्राप्त होते हैं।
अब हम बिंदुओं A(4,0) तथा B(0,2) को ग्राफ पेपर पर आलेखित करते है और समीकरण (i) के द्वारा निरूपित रेखा का आलेख ( ग्राफ ) प्राप्त करने के लिए इन बिंदुओं से गुजरने वाली रेखा खींचते है। समीकरण (ii) के द्वारा निरूपित रेखा के ग्राफ को प्राप्त करने के लिए बिंदुओं P(0,3) और Q(6,0) को आलेख पेपर पर आलेखित करते है तथा इन बिंदुओं से गुजरें वाली रेखा खींचते है।
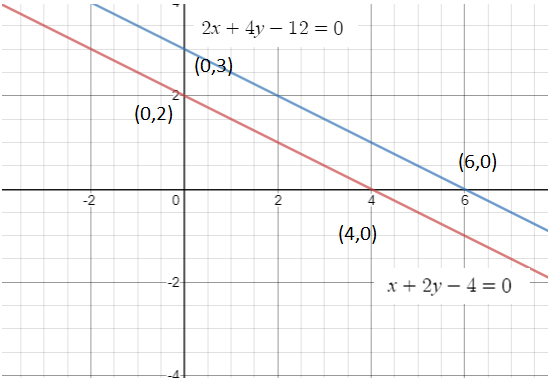
हम देखते है कि दोनों रेखाएँ समांतर है अर्थात रेखाएँ कभी भी प्रतिच्छेद नहीं करती है।
6. रैखिक समीकरण युग्म के हलों कि संख्या
अब यहाँ हम बात करेंगे रैखिक समीकरण युग्म के हलों की संख्या के बारे में, जो कि निर्भर करता है रेखा युग्मों की स्थिति पर, जैसा कि हमने तल पर रेखायुग्म की तीन स्थितियों कि बात कही थी । हम समझ सकते हैं कि यदि रेखाएँ प्रतिच्छेद करती हैं तो एक बिन्दु दोनों ही रेखाओं पर स्थित होगा तथा यदि संपाती अर्थात एक-दूसरे पर स्थित होगा , तब अनंत बिंदुए दोनों पर उभयनिष्ट होगी । इसके अलावा समांतर होने पर कोई भी बिन्दु दोनों पर स्थित नहीं होंगे , यहाँ हम कह सकते हैं कि उभयनिष्ट बिन्दुओं की संख्या ही रैखिक समीकरण युग्म के हलों की संख्या होगी ।
रैखिक समीकरण युग्म संगत या अविरोधी (consistent) कहलाता है यदि इसका हल संभव है, अर्थात या तो दोनों रेखाएँ केवल एक बिंदु पर प्रतिच्छेद करें या फिर दोनों संपाती हों
और यदि हल संभव नहीं है , अर्थात दोनों रेखाएँ एक दूसरे के समांतर है तब यह असंगत या विरोधी (inconsistent) समीकरण युग्म कहलाता है ।
समीकरण युग्म a1x+b1y=c1 "औऱ" a2x+b2y=c2 का
(i) अद्वितीय हल(केवल एक ) होगा यदि और केवल यदि a1a2≠b1b2
(ii) कोई हल नहीं होगा यदि और केवल यदि a1a2=b1b2≠c1c2
(iii) अनन्त हल होंगे यदि और केवल यदि a1a2=b1b2=c1c2
OMR (One Minute Revision)
रैखिक समीकरण युग्म
a1x+b1y+c1=0
a2x+b2y+c2=0
के लिए
| प्रतिबंध | हलों की संख्या | प्रकार |
|---|---|---|
| a1a2≠b1b2 | एक अद्वितीय हल | संगत |
| a1a2=b1b2=c1c2 | अनंत हल | संगत |
| a1a2=b1b2≠c1c2 | कोई हल नहीं | असंगत |
उदाहरण 3
k का मान ज्ञात करें जिसके लिये निम्नलिखित समीकरण निकाय का कोई हल न हो।
4x−y−9=0
8x−2y−k=0
दी गई समीकरणें हैं,
3x+y=1
(2k−1)x+(k−1)y=2k+1
कोई हल न होने के लिए,
a1a2=b1b2≠c1c2
a1b2=b1a2
3(k−1)=2k−1
3k−3=2k−1
⇒k=2
और
b1c2≠b2c1
1−1≠12k+1
⇒k≠−2
अतः दिए गए समीकरण निकाय का कोई हल न होने के लिए,
k=2,k≠−2
उदाहरण 4
a और b के किन मानों के लिए निम्नलिखित रैखिक समी युग्म के अनंत (अनेक) हल होंगें?
2x+3y=7
a(x+y)−b(x−y)=3a+b−2
दिए गए समीकरण निकाय है
2x+3y−7=0 …….(i)
और a(x+y)−b(x−y)=3a+b−2
या (a−b)x+(a+b)y=3a+b−2…….(ii)
यहां a1=2,b1=3,c1=−7
और a2=a−b,b2=a+b,c2=−(3a+b−2)
दिए गए समीकरण निकाय के अनन्त (अनेक) हल होने के लिए
2a−b=3a+b=−7−(3a+b−2)
(i) और (ii) से
2a+2b=3a−3b
⇒a−5b=0…….(A)
(ii) और (iii) से
9a+3b−6=7a+7b
⇒2a−4b=6
⇒a−2b=3…….(B)
अब (A) − (B) ⇒−3b=−3
⇒b=1
(A) में b का मान रखने पर हम पाते हैं कि a=5
अतः दिए गए समीकरण युग्म के अनेक हलों के लिए a=5,b=1
उदाहरण 5
k के किस मान के लिए, निम्न समीकरण निकाय का है-
x+2y=5
3x+ky−15=0
(i) एक अद्वितीय हल
(ii ) कोई हल नहीं
यहाँ दी गई समीकरणें हैं-
x+2y=5
3x+ky−15=0
(i ) अद्वितीय हल के लिए,
a1a2≠b1b2
13≠2k
⇒ k≠6
कोई हल नहीं होने के लिए,
a1a2=b1b2≠c1c2
13=2k≠515
13=2k और 2k≠(13)
k=6 और k≠6
जो कि सम्भव नहीं है।
अतः k का कोई मान नहीं है, जिसके लिए दिए गये समीकरण निकाय का कोई हल न हो।
7. रैखिक समीकरण युग्म को हल करने का बीजीय तरीका
अब तक हमने दो चर वाले रैखिक समीकरण युग्म को हल करने की ग्राफीय-विधि के बारे में सीखा और उनसे सम्बन्धित प्रश्नों को हल किया है किन्तु यह विधि हल के अपूर्णांक होने पर उपयुक्त (सुविधाजनक) नहीं होती है। उदाहरण के लिए 2 रेखाएं यदि आपस मे प्रतिच्छेद करती है तथा उनका प्रतिच्छेदन बिन्दु के x तथा y के नियामक यदि अपूर्णांक संख्या है तब ग्राफ पेपर मे उन्हे अंकित करना जटिल है , साथ ही गलती की संभावना भी अधिक होगी ।
इन स्थितियों में हम शुद्ध वांछित हल नहीं प्राप्त कर सकते हैं। इसलिए अब हम दो चर वाले रैखिक-समीकरण निकाय को हल करने के बीजीय विधि के बारे में चर्चा करेंगे।
रैखिक-समीकरण निकाय को हल करने की मुख्य निम्नलिखित `3` बीजीय विधियां हैं :
(1) प्रतिस्थापन विधि
(2) विलोपन विधि
(3) बज्र-गुणन विधि
(1) प्रतिस्थापन विधि :
जैसा कि इस विधि के नाम से स्पष्ट है कि इसमे एक चर राशि का दूसरे चर के पदों मे प्रतिस्थापन किया जाता है, उदाहरण के लिए यदि हम थैले में कुछ गेंदों की बात करते हैं मान लेते है थैले-1 मे 10 तथा थैले-2 में 20 गेंदे हैं, जिसमे लाल (R) व हरी (G) गेंद सम्मिलित हैं जो कि ज्ञात नहीं है। यदि दोनों थैले में समान लाल गेंदे हों तथा दूसरे थैले में पहले से 3 गुने हरे गेंद है तब
R+G=10.......(i) तथा
R+3G=20........(ii) प्राप्त होगा ।
∴ हम पहले थैले के लिए कह सकते है कि
R=10−G......(iii)
तथा दूसरे थैले मे लाल गेंद का मान हरे गेंद के पदों मे लिख सकते है , अतः समीकरण (iii) का मान समीकरण (ii) मे रखने पर
∴ 10−G+3G=20
⇒ G=5
अतः मान समी. (i) मे रखने पर R=5
अर्थात यदि समीकरण ax+by=c के रूप मे हो तब यहाँ से हम दिए गए समीकरणों में किसी एक अज्ञात राशि (माना y) को दूसरी अज्ञात राशि (माना x) के पदों में व्यक्त किया जाता है और तब इसका मान दूसरे समीकरण में रखा जाता है। इस प्रकार हम एक चर x वाला रैखिक समीकरण प्राप्त करते हैं जिसे आसानी से हल किया जा सकता है। इस चर x का मान ज्ञात कर, दूसरे चर y के मान भी x के पदों में व्यक्त y के व्यंजक से प्राप्त कर लिया जाता है।
उदाहरण 6
प्रतिस्थापन विधि का उपयोग करके निम्न समीकरण युग्मों को हल करो :
2xa+yb=2
xa−yb=4
दिया गया समीकरण युग्म है :
2xa+yb=2......(i)
xa−yb=4.......(ii)
प्रतिस्थापन विधि के अनुसार सर्वप्रथम एक समीकरण को लेकर किसी एक चर को दूसरे चर के पदों मे लिखेंगे तथा दूसरे समीकरण मे मान प्रतिस्थापित करके हल ज्ञात करेंगे
समीकरण (i ) से
yb=2−2xa
⇒y=2b(1−xa) .....(iii)
समीकरण (ii ) में y=2b(1−xb) प्रतिस्थापित करने पर
xa−2bb(1−xa)=4
⇒xa−2+2xa=4
⇒3x=6a
⇒x=2a
x का यह मान समीकरण (iii ) में प्रतिस्थापित करने पर
y=2b(1−2aa)=2b(1−2)
⇒y=−2b
अतः x=2a,y=−2b समीकरण युग्म का अभीष्ट हल है।
(2) विलोपन विधि
बच्चों विलोपन का सामान्य अर्थ समझे तो इसका अर्थ होता है गायब करना, इस विधि के अनुसार किसी एक चर को गायब कर दिया जाता है जिससे दूसरा चर आसानी से ज्ञात हो जाता है । यहाँ यदि पूर्व (प्रतिस्थापन विधि का) उदाहरण ले तब दो समीकरण इस प्रकार है
R+G=10....(i)
R+3G=20....(ii)
यहाँ समी- (ii) - समी- (i) करने पर R का विलोपन हो जाता है
इस प्रकार 2G=10 ⇒ G=5 तथा R=5 समीकरण (i) से ।
इसे हम नीचे दिए गए चित्र से समझ सकते है - 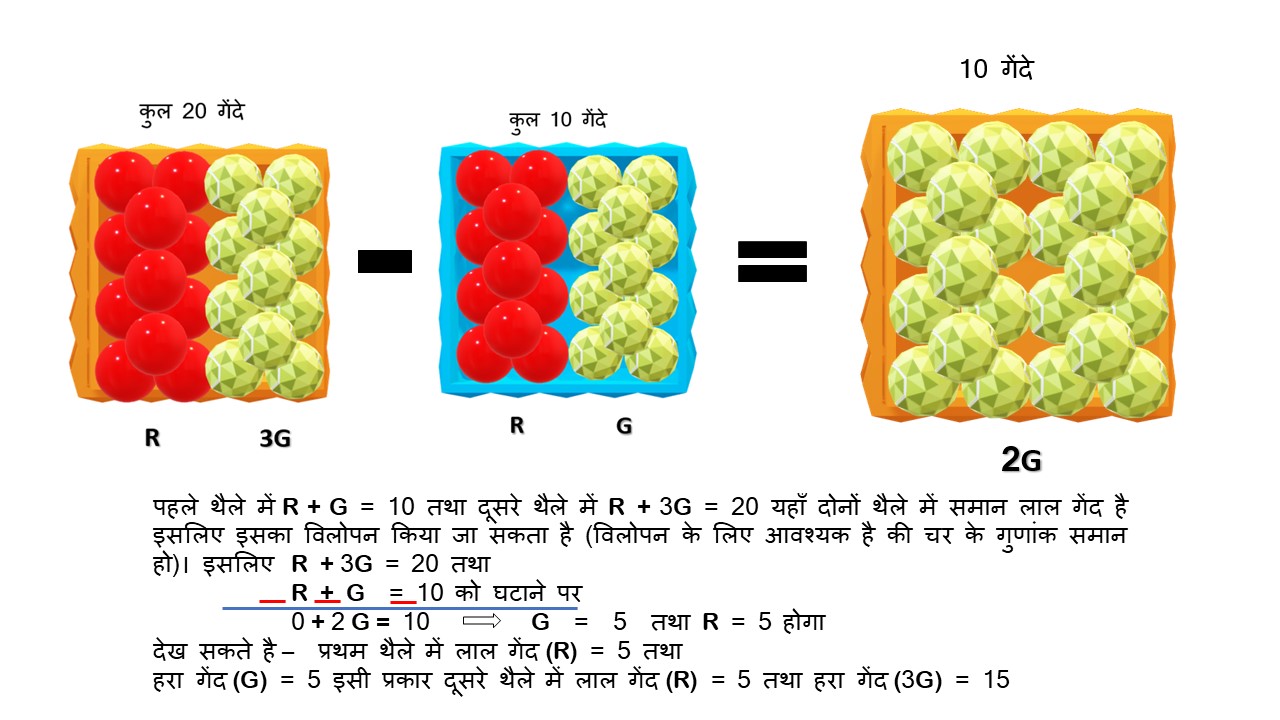
यदि दो चर x और y में से एक को दिए समीकरणों से विलोपित कर दिया जाए तब इस प्रकार प्राप्त समीकरण को हल कर हम दूसरे चर का मान ज्ञात कर लेते हैं ।
मान लें , दिए हुए रैखिक समीकरण युग्म हैं :
a1x+b1y+c1=0 ..(i)
और a2x+b2y+c2=0 ...(ii)
(1) चरों x और y में किसी एक को विलोपित करते हैं । इसके लिए यदि y को विलोपित करना है , तब समीकरण (i) को b2 से तथा (ii) को b1 से गुणा कर (दोनों समीकरणों में y के गुणांकों को समान बना कर घटा लेते हैं । इससे x का मान ज्ञात हो जायेगा ।
(2) अब x के इस मान को समीकरण (i) या (ii) में रखकर y का मान प्राप्त कर लेते हैं ।
(3) जाँच कर देख लेते हैं कि x और y के प्राप्त मान दिए गये समीकरणों को संतुष्ट करते हैं ।
उदाहरण 7
निम्न रैखिक समीकरण युग्मों का विलोपन विधि से हल करो :
3x+2y=11
2x+3y=4
दिया गया समीकरण युग्म निम्न है :
3x+2y=11 ... (i)
2x+3y=4 ...(ii)
विलोपन विधि के अनुसार किसी एक चर का विलोपन करेंगे, यदि y को विलोपित करना चाहे तब , हम दोनों समीकरणों में चर y के गुणांक समान करने के लिए हम देखते है कि समीकरण (i ) और (ii ) में y के गुणांक क्रमशः 2 तथा 3 है जिनका लघुत्तम समापवर्तक 6 है। अतः दोनों समीकरणों में y का गुणांक 6 के बराबर बनाने के लिए प्रथम समीकरण को 3 से तथा दूसरे को 2 से गुणा करते है, तो हमें निम्न समीकरण युग्म प्राप्त होता है :
9x+6y=33 ...(iii)
4x+6y=8 ...(iv)
समीकरण (iii ) में (iv ) को घटाने पर
9x+6y=33 −4x+−6y=−8 ––––––––––––––––––––– 5x=25
5x=25⇒x=5
x का यह मान समीकरण (i ) में प्रतिस्थापित करने पर
3×5+2y=11
⇒2y=−4
⇒y=−2
अतः x = 5 , y = -2 दिये गये समीकरण युग्म का अभीष्ट हल है।
उदाहरण 8
विलोपन विधि का उपयोग करके निम्न समीकरण युग्म को हल करो :
x10+y5+1=15
x8+y6=15
दिये गये समीकरण युग्म को निम्न रूप में लिखते है :
x10+y5=14 ...(i)
x8+y6=15 ...(ii)
विलोपन विधि के अनुसार किसी एक चर का विलोपन करेंगे, अतः x के गुणांक बराबर करने के लिए समीकरण (i ) को 14 तथा (ii ) को 15 से गुणा करके निम्न समीकरण युग्म प्राप्त करते है :
x40+y20=144
x40+y30=155
इसी समीकरण युग्म को सरल करके निम्न रूप में लिखा जा सकता है :
x40+y20=72 ...(iii)
x40+y30=3 ...(iv)
समीकरण (iii ) में से (iv ) को घटाने पर
x40+y20=72 −x40+−y30=−3 –––––––––––––––––––––y20−y30=72−3
⇒3y−2y60=7−62
⇒y60=12
⇒y=30
y का यह मान समीकरण (i ) में प्रतिस्थापित करने पर
x10+305=14
⇒x10=14−6
⇒x10=8
⇒x=80
अतः x=80,y=30 उपर्युक्त समीकरण युग्म का हल है ।
(3) वज्र - गुणन - विधि :
अगर हम बात करे प्रतिस्थापन तथा विलोपन विधि की तो ये तब तक उपयुक्त होती है जब तक रैखिक समीकरण निकाय के अद्वितीय हल हो लेकिन अनंत तथा कोई हल प्राप्त न होने की स्थिति में ये प्रयोग में नहीं आती इसके लिए हम वज्र गुणन विधि का प्रयोग करते है।
आइये इस विधि को समझते है।
माना कि दिए गए रैखिक समीकरण युग्म है: ,
a1x+b1y+c1=0 ...(i)
तथा a2x+b2y+c2 = 0 ...(ii)
समीकरण (i) को b2 से तथा समीकरण (ii) को b1 से गुणा करने पर ,
a1b2x+b1b2y+c1b2=0 ....(iii)
तथा a2b1x+b1b2y+b1c2 = 0 ...(iv)
समीकरण (iii) − समीकरण (iv) करने पर
⇒(a1b2−a2b1)x+c1b2−b1c2=0
(a1b2−a2b1)x=b1c2−b2c1
⇒x=b1c2−b2c1a1b2−a2b1 ...(v)
समीकरण (i) को a2 से और समीकरण (ii) को a1 से गुणा करने पर ,
a1a2x+a2b1y+a2c1=0 ...(vi)
तथा a1a2x+a1b2y+a1c2=0 ...(vii)
समीकरण (vi) - समीकरण (vii) करने पर
⇒(a2b1−a1b2)y+a2c1−a1c2=0
⇒(a2b1−a1b2)y=−(a2c1−a1c2)
⇒y=−(a2c1−a1c2a2b1−a1b2) ...(viii)
(v) और (viii) , से हम पाते हैं ,
x=b1c2−b2c1a1b2−a2b1
तथा y=−a1c2−a2c1a1b2−a2b1
या xb1c2−b2c1=1a1b2−a2b1....(ix)
तथा y−(a1c2−a2c1)=1a1b2−a2b1.....(ix)
(ix) और (x) से , xb1c2−b2c1=y−(a1c2−a2c1)=1a1b2−a2b1 ......(ξ)
यहाँ पहले और दूसरे समीकरण में गुणांक निम्नलिखित हैं

xb1c2−b2c1=yc1a2−c2a1=1a1b2−a2b1
Note : वज्र - गुणन विधि प्रयोग करने के पहले समीकरणों के दायें पक्ष को शून्य बना लें ।
उदाहरण 9
वज्र गुणन विधि का उपयोग करते हुए निम्न रैखिक समीकरण युग्मों को हल करों :
x+y=7
5x+12y=7
दिये गये समीकरणों को इसप्रकार लिखते है कि दोनों समीकरणों के दायीं और शून्य हो ।
x+y−7=0 ...(i)
5x+12y−7=0 ...(ii)
वज्र गुणन विधि का उपयोग करने पर
⇒x−7+84=y−35+7=112−5
⇒x77=y−28=17
⇒x77=17 और y−28=17
⇒x=777=11 तथा
y=−287=−4
अतः x = 11 तथा y = - 4 समीकरण युग्म का अभीष्ट हल है।
उदाहरण 10
निम्नलिखित रैखिक समीकरण युग्म को वज्र - गुणन विधि से करें।
4x−7y+28=0
5y−7x+9=0
दी गई समीकरणें इस प्रकार लिखी जा सकती हैं,
4x−7y+28=0 …(1)
−7x+5y+9=0 ....(ii)

x(−7)×9−5×28=y(−7)×28−4×9=14×5−(−7)(−7)
x−63−140=y−196−36=120−49
x−203=y−232=1−29
यहाँ x=−203−29=7
y=−232−29=8
यहाँ x = 7 व y = 8 अभीष्ट हल हैं।
8. दो चरों के रैखिक समीकरणो के युग्म में बदले जा सकने वाले समीकरण (एक चर के दूसरे चर से प्रतिस्थापन द्वारा)
यहाँ हम ऐसे समीकरणों के युग्मों के विषय में बात करेंगे जो रैखिक नहीं है परंतु कुछ उपयुक्त प्रतिस्थापनों द्वारा इन्हे रैखिक समीकरणों के रूप में बदला जा सकता है। आइये इसे कुछ उदाहरणों से समझते है....
उदाहरण 11
निम्न समीकरणों के युग्म को रैखिक समीकरणों के युग्म में बदल कर हल करो:
8v−3u=5uv
6v−5u=−2uv
दोनों समीकरणों को देखने से स्पष्ट है उपर्युक्त दोनों समीकरण u और v में रैखिक (एकघातीय) समीकरण नहीं है परन्तु इन्हें रैखिक समीकरणों के रूप में ( उचित प्रतिस्थापन द्वारा) बदला जा सकता है। यदि हम दोनों में से किसी भी एक समीकरण u = 0 रखें तो v = 0 प्राप्त होता है। अतः स्पष्ट है कि u = 0 , v = 0 समीकरण का एक हल होगा।
अन्य हल ज्ञात करने के लिए मान लेते है कि u≠0 तथा v≠0 है। चूँकि u≠0 तथा v≠0 है, तो uv≠0 होगा। दोनों समीकरणों को uv से विभाजित करने पर
8u−3v=5...(i)
6u−5v=−2...(ii)
उपर्युक्त समीकरणों में 1u=x तथा 1v=y प्रतिस्थापित करने पर
8x−3y=5...(iii)
6x−5y=−2...(iv)
समीकरण (iii ) को 3 से व (iv ) को 4 से गुणा करके घटाने पर
24x−9y=152−4x−20+y=−8+¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯ 11y=23⇒y=2311
समीकरण (iii ) में y=2311 प्रतिस्थापित करने पर
8x−3×2311=5
⇒8x=5+6911=12411
⇒x=12411×8=3122
अतः x=3122 और y=2311
∴1u=3122 और 1v=2311
⇒u=2231 और v=1123
अतः दिये गये समीकरण के युग्म के निम्न दो हल होंगे :
(i)u=0,v=0
(ii)u=2231,v=1123
उदाहरण 12
यदि 8 आदमी व 12 लड़के एक काम को 10 दिन में पूरा करते है जबकि 6 आदमी व 8 लड़के उसी काम को 14 दिन में पूरा करते है, तो बताओं एक आदमी अकेला उस काम को कितने दिन में व एक लड़का अकेला उसे कितने दिन में पूरा कर सकता है।
माना एक आदमी अकेला उस कार्य को x दिनों में व लड़का उसी कार्य को अकेला y दिनों में पूरा कर सकता है।
एक आदमी द्वारा एक दिन में किया गया कार्य =1x भाग
एक लड़के द्वारा एक दिन में किया गया कार्य =1y भाग
अतः 8 आदमियों द्वारा एक दिन में किया गया कार्य =8x भाग
12 लड़कों द्वारा एक दिन में किया गया कार्य =12y भाग
चूँकि 8 आदमी व 12 लड़के उस कार्य को 10 दिनों में पूरा करते है।
∴10(8x+12y)=1 ...(i)
दिया है की 6 आदमी व 8 लड़के उस कार्य को 14 दिन में पूरा करते है।
∴14(6x+8y)=1... (ii)
समीकरण (i ) व (ii ) में 1x=u तथा 1y=v प्रतिस्थापित करने पर
80u+120v−1=0
84u+112v−1=0
वज्र गुणन विधि का उपयोग करने पर
u−120+112=−v−84+80=180×112−120×84
⇒u−8=v−4=1−1120
⇒u−8=1−1120 तथा
v−4=1−1120
⇒u=−8−1120 तथा
v=−4−1120
⇒u=1140 तथा v=1280
⇒1x=1140 तथा
1y=1280
[u और v के मान रखने पर]
⇒x=140 तथा y=280
अतः एक आदमी उस कार्य को अकेला 140 दिन में पूरा कर सकता है तथा एक लड़का 280 दिन में पूरा कर सकता है।
सारांश
इस अध्याय में, आपने निम्न तथ्यों का अध्यन किया है:
1. रैखिक समीकरण युग्म का सबसे व्यापक रूप है:
a1x+b1y+c1=0
a2x+b2y+c2=0
जहाँ a1,a2,b1,b2 ऐसी वास्तविक संख्याएं है की a21+b21≠0,a22+b22≠0 है|
2. किसी रैखिक समीकरण युग्म को ग्राफ़िय रूप में निरूपित किया जा सकता है और हल किया जा सकता है|
(i) ग्राफ़िय विधि द्वारा
(ii) बीजगणितीय विधि द्वारा
(i) ग्राफ़िय विधि:
दो चरों में एक रैखिक समीकरण युग्म का ग्राफ दो रेखाएँ निरूपित करता है|
(a) यदि रेखाएँ एक बिंदु पर प्रतिच्छेद करती है, तो वह बिंदु दोनों समीकरण का अद्वितीय हल होता है| इस स्थिति में, समीकरण युग्म संगत होता है|
(b) यदि रेखाएँ सम्पाती है, तो उसके अपरिमित रूप से अनेक हल होते है- रेखा पर स्थित प्रत्येक बिंदु हल होता है| इस स्थिति में, समीकरण युग्म आश्रित (संगत) होता है|
(c) यदि रेखाएँ समान्तर है, तो समीकरण युग्म का कोई हल नहीं होता है| इस स्थिति में समीकरण युग्म असंगत होता है|
(ii). बीजगणितीय विधि: हमने एक रैखिक समीकरण युग्म के हल ज्ञात करने के लिए निम्न विधियाँ की चर्चा की है:
(a) प्रतिस्थापन विधि
(b) विलोपन विधि
(c) वज्र-गुणन विधि
3. यदि दिए गए रैखिक समीकरण a1x+b1y+c1=0 और a2x+b2y+c2=0 एक रैखिक समीकरण युग्म को प्रदर्शित करते है, तो निम्न स्थितियाँ उत्पन्न हो सकती है:
(i) a1a2≠b1b2; इस स्थिति में, रैखिक समीकरण युग्म संगत होता है,और हम ऐसे समीकरण युग्मों के अद्वितीय हल प्राप्त करते है|
(ii) a1a2=b1b2=c1c2: इस स्थिति में, रैखिक समीकरण युग्म आश्रित (संगत) होता है,इस स्थिति में समीकरण युग्मो के अनंत हल प्राप्त होते है |
(iii) a1a2=b1b2≠c1c2: इस स्थिति में, रैखिक समीकरण युग्म असंगत होता है,अर्थात इस स्थिति में समीकरण युग्मो का कोई हल प्राप्त नहीं होता है|
4.हमने ऐसे समीकरणों को भी हल किया , जो प्रारम्भ में रैखिक नहीं हों, परन्तु हम उन्हें परिवर्तित कर एक रैखिक समीकरण युग्म में बदल सकते है|