बहुपद कक्षा 10 गणित
भूमिका
कक्षा-IX में हमने एक चर वाले बहुपद और उनके घात के बारे में पढ़ा है, यहाँ हम बहुपद की परिभाषा एवं उसके घात के बारे में पुनः स्मरण करेंगे। इस अध्याय मे हम बहुपद व उसके विभिन्न रूपों को देखेंगे तथा बहुपदीय समीकरणों के हल (शून्यक) के बारे मे पढ़ेंगे साथ ही बहुपदो के लिए विभाजन एल्गोरिथम का अध्ययन करेंगे।
आइये जानते है, बहुपदों को और करीब से ...
बहुपद एक विशेष प्रकार का बीजीय व्यंजक है, निम्नांकित व्यंजक से बहुपदों को समझने का प्रयास करते है -
- p(x)=5x2+2x−3
यहाँ p(x), एक चर का बीजीय व्यंजक है और यहाँ p(x) के प्रत्येक पद में x की घात अऋणात्मक पूर्णांक है ।
- इसमें एक ध्यान देने योग्य बात यह है कि किसी भी बहुपद में चर की घात सदैव एक अऋणात्मक पूर्णांक होनी चाहिए। किसी बहुपद में चर की सबसे बड़ी घात बहुपद की घात कहलाती है।
आइये इन्हे हम कुछ उदाहरणों के माध्यम से समझने का प्रयास करते है
- 4x+2 चर x में घात 1 का बहुपद है।
- 2y2−3y+4 चर y में घात 2 का बहुपद है।
- 5x3−4x2+x−√2 चर x में घात 3 का बहुपद है।
- 7u6−(32)u4+4u2−8 चर u में घात 6 का बहुपद है।
व्यंजक 1x−1,√x+2,1x2+2x+3
इत्यादि बहुपद नहीं है,
क्योकि x के पद यदि हर मे होंगे तो अंश मे जाकर वे ऋणात्मक घात वाले हो जाएंगे तथा यदि वर्गमूल या घनमूल मे होंगे तो घात पूर्णांक संख्या नहीं होगी। जबकि यह आवश्यक है की चर की घात अऋणात्मक पूर्णांक संख्या हो, इसलिए ऊपर के कुछ व्यंजक बहुपद नहीं है।
अधिकतम घात 1 के बहुपद को रैखिक बहुपद कहते हैं।
- उदाहरण -
2x−3,√3x+5,y+√2,x−211,3z+4,(23)u+1
इत्यादि सभी रैखिक बहुपद है। क्योकि इनकी अधिकतम घात 1 है।
अधिकतम घात 2 वाले बहुपद को द्विघात बहुपद कहते हैं।
- उदाहरण -
2x2+3x−25,u3−2u2+5,√5v2−(23)v,4z2+17
उक्त द्विघात बहुपदों के कुछ उदाहरण हैं (जिनके गुणांक वास्तविक संख्याएं है।)
ax2+bx+c होगा , जहां a,b,c वास्तविक संख्याएं हैं और a≠0 है।
घात 3 का बहुपद त्रिघात बहुपद कहलाता है।
- उदाहरण -
2−x3, 3x3−2x2+x−1
ax3+bx2+cx+d, जहां a,b,c,d वास्तविक संख्याएं हैं और a≠0 है।
बच्चों यहाँ हमने रैखिक, द्विघात व त्रिघात बहुपदों का व्यापक रूप देखा है अतः इसी प्रकार हमे बहुपद का व्यापक रूप भी ज्ञात हो जाएगा।
बहुपद का व्यापक रूप
यदि P(x) , n घात का बहुपद है तो P(x) का व्यापक रूप :
P(x)=a0+a1.x1+a2.x2+a3.x3.........+an−1.xn−1+an.xn
चूँकि बहुपद P(x), n घात का बहुपद है अतः n, चर x का सबसे बड़ा घात होगा तथा यहाँ n∈N जहाँ N= धनात्मक पूर्णांक संख्याओ का समुच्चय है।
1. बहुपद के शून्यक
माना, x में कोई बहुपद p(x)=x2−3x−4 है
और k कोई वास्तविक संख्या है तो p(x) में x को k से प्रतिस्थापित करने पर प्राप्त मान x=k पर मान कहलाता है और इसे p(k) से निरूपित करते हैं।
उदाहरण के लिए x=1 तो
p(1)=12−3(1)−4
p(1)=1−3−4
∴P(1)=−6
इस प्रकार हमे x के भिन्न मानो के लिए P(x) के भिन्न मान प्राप्त होंगे ।
यहाँ x के जिस मान के लिए p(x)=0 प्राप्त हो वह मान बहुपद का शून्यक होता हैं । अतः
p(x)=x2−3x−4
p(x)=x2−4x+x−4 (गुणनखंड विधि)
p(x)=x(x−4)+1(x−4)
p(x)=(x−4)(x+1)
हम पाते हैं: x=−1,4 रखने पर p(x) का मान 0 प्राप्त होगा l
अर्थात p(−1)=0 और
p(4)=0 है
इसलिए −1 और 4 द्विघात बहुपद x2−3x−4 के शून्यक होंगे।
अधिक व्यापक रूप में एक वास्तविक संख्या k बहुपद p(x) का शून्यक कहलाती है यदि p(k)=0 है।
रैखिक (एक घातीय) बहुपद में शून्यक की अधिकतम संख्या 1 होती है
उदाहरण के लिए P(x)=ax+b है तथा माना P(k)=0
अतः x=k, P(x) का शून्यक है
तब ak+b=0
∴k=−ba
यहाँ देख सकते है k का केवल एक मान प्राप्त हुआ ।
इसी प्रकार द्विघातीय , त्रिघातीय आदि बहुपदों के लिए अधिकतम शून्यको की संख्या क्रमशः 2 , 3 प्राप्त होती है ।
अतः हम कह सकते है n घात के बहुपद के लिए अधिकतम शून्यको की संख्या n होगी।
2. बहुपद के शून्यको का ज्यामितीय अर्थ
एक घातीय बहुपद के शून्यक का ज्यामितीय अर्थ :
हम जानते हैं कि एक -घातीय बहुपद का आलेख एक सरल रेखा होती है और बहुपद का आलेख x -अक्ष को जिस बिंदु पर प्रतिच्छेद (स्पर्श) करता है, उस बिंदु का x -नियामक ही बहुपद का शून्यक होता है ।
उदाहरण के लिए
(i) मान लिया कि p(x)=2x−4
अब p(x)=0⇒2x−4=0
⇒2x=4⇒x=2
अब, हम y=p(x) अर्थात y=2x−4 का आलेख खींचते हैं।
आलेख के लिए
हम x के दो उचित मान लेकर उनके संगत y के दो मानों की गणना करते हैं ।
x=0 ⇒ y=−4
x=1 ⇒ y=−2
x=2 ⇒ y=0
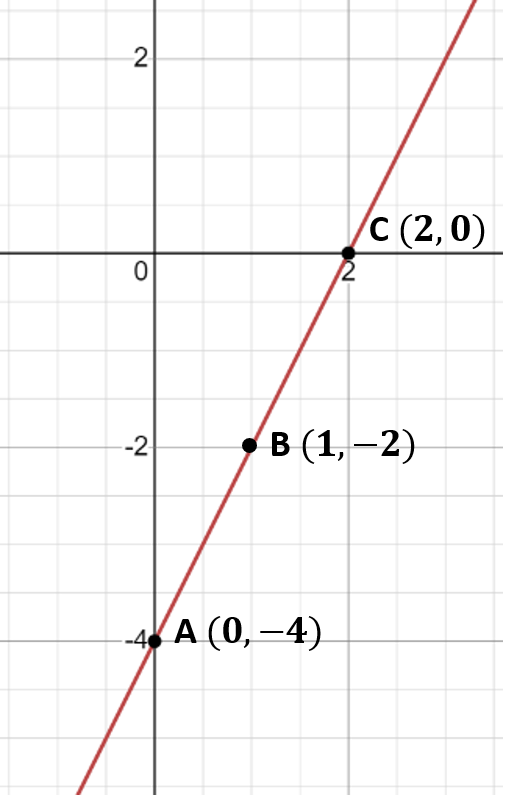
y=2x−4 का आलेख एक सरल रेखा होगी जो बिंदुओं (0,−4) और (1,−2) को जोड़ती है ।
y=2x−4 का आलेख x -अक्ष को बिंदु C(2,0) पर प्रतिच्छेद करता है ।
C का x -नियामक 2 है जो बहुपद 2x−4 का शून्यक है ।
इसी प्रकार
द्विघातीय बहुपद के शून्यक का ज्यामितीय अर्थ :
मान लिया कि p(x)=x2−4x+3 एक द्विघातीय बहुपद है।
y=x2−4x+3, का आलेख खींचने के लिये हम x के कुछ उपयुक्त मानों (... −2,−1, 0,1,2, ..) को लेकर संगत y के मान ज्ञात करते हैं ।
हम x -अक्ष और y -अक्ष पर उचित स्केल लेकर बिंदुओं (−1,8),(0,3),(1,0),(2,−1),(3,0),(4,3),(5,8) को अंकित करते हैं और स्वतंत्र हस्त से इनको मिलाते हैं।
(यहाँ निर्देशांकों को (x , y) से निरूपित करते है )
इस तरह से प्राप्त आलेख ही y=x2−4x+3 का आलेख होगा।

y=x2−4x+3 का आलेख x -अक्ष को (1,0) और (3,0) पर प्रतिच्छेद (स्पर्श) करता है , अर्थात x के मान 1 व 3 के लिए y का मान शून्य मिल रहा हैं। बिंदुओं के x -नियामक जहाँ आलेख x -अक्ष को काटती है 1 तथा 3 हैं ।
यह बहुपद p(x)=x2−4x+3 के शून्यक हैं क्योंकि p(1)=0 और p(3)=0
इस तरह जिन बिंदुओं पर द्विघातीय बहुपद का आलेख x -अक्ष को प्रतिच्छेद करता है उनके x -नियामक ही उस द्विघातीय बहुपद के शून्यक होते हैं ।
वास्तव में किसी द्विघात बहुपद ax2+bx+c,a≠0 के लिए संगत समीकरण y=ax2+bx+c के ग्राफ का आकार या तो ऊपर की ओर खुला
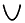 अथवा नीचे की ओर खुला
अथवा नीचे की ओर खुला 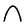 का होगा,
का होगा, जो इस पर निर्भर करेगा कि a>0 है या a<0 है।
(इन वक्रों को परवलय कहते हैं।)
इस प्रकार हम कह सकते है
बहुपद की ज्यामितीय आकृति x अक्ष को जितने बिन्दु पर काटेगी (स्पर्श करेगी) , बहुपद के शून्यक की संख्या उतनी ही प्राप्त होगी ।
अतः व्यापक रूप में, घात n के दिए गए बहुपद p(x) के लिए y=p(x) का ग्राफ x- अक्ष को अधिकतम n बिंदुओं पर प्रतिच्छेद करता है। अतः घात n के किसी बहुपद के अधिकतम n शून्यक हो सकते हैं।
OMR (One Minute Revision)
- बहुपद के शून्यक उन बिंदुओं के x- निर्देशांक है जिन पर y=p(x) का आलेख (GRAPH) x-अक्ष को प्रतिच्छेद करता है।
- बहुपद के अधिकतम शून्यक उत्तने हो सकते है जितनी बहुपद की घात है।
उदाहरण 1
नीचे दी गई आकृति में, ग्राफों को देखिए। प्रत्येक आकृति y=p(x), जहां p(x) एक बहुपद है, का ग्राफ है। ग्राफों से प्रत्येक के लिए p(x) के शून्यकों की संख्या ज्ञात कीजिए।
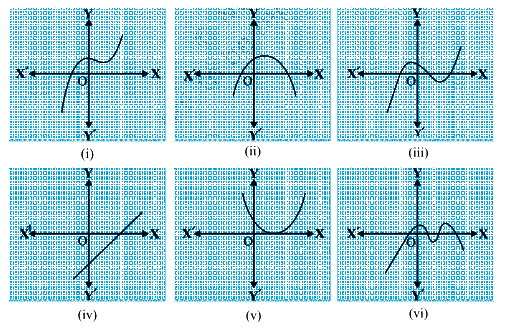
(i) शून्यकों की संख्या 1 है, क्योंकि ग्राफ x- अक्ष को केवल एक बिंदु पर प्रतिच्छेद करता है।
(ii) शून्यकों की संख्या 2 है, क्योंकि ग्राफ x- अक्ष को दो बिंदुओं पर प्रतिच्छेद करता है।
(iii) शून्यकों की संख्या 3 है, क्योंकि ग्राफ x- अक्ष को 3 बिंदुओं पर प्रतिच्छेद करता है।
(iv) शून्यकों की संख्या 1 है, क्योंकि ग्राफ x- अक्ष को केवल एक बिंदु पर प्रतिच्छेद करता है।
(v) शून्यकों की संख्या 1 है, क्योंकि ग्राफ x- अक्ष को केवल एक बिंदु पर प्रतिच्छेद करता है।
(vi) शून्यकों की संख्या 4 है, क्योंकि ग्राफ x- अक्ष को 4 बिंदुओं पर प्रतिच्छेद करता है।
उदाहरण 2
सत्यापित कीजिए की दिखाए गए मान संगत बहुपद के शून्यक है:
p(x)=3x2−1
−1√3,2√3
p(x)=3x2−1
∴p(−1√3)=3(−1√3)2−1
p(−1√3)=3(13)−1=1−1=0
तथा p(2√3)=3(2√3)2−1
p(2√3)=3×43−1=4−1=3≠0
अतः −1√3 दिए गए बहुपद का शून्यक है तथा 2√3 इसका शून्यक नहीं है।
उदाहरण 3
यदि x−2,x5−3x4−ax3+3ax2+2ax+4 का गुणनखण्ड़ है तो a का मान ज्ञात करे।
x−2=0⇒x=2
अतः x−2 का शून्यक 2 है ।
माना कि,
p(x)=x5−3x4−ax3+3ax2+2ax+4
चूँकि x−2, p(x) का गुणनखण्ड़ है,
∴ गुणनखण्ड़ प्रमेय से, p(2)=0
∴(2)5−3(2)4−a(2)3+3a(2)2+2a(2)+4=0
या 32−48−8a+12a+4a+4=0
या −12+8a=0
या, 8a=12
∴a=128=32
3. किसी बहुपद के शून्यकों और गुणांकों में संबंध
हम जानते हैं कि रैखिक बहुपद ax+b का शून्यक −ba होता है ।
अब हम किसी द्विघाती बहुपद के शून्यको और उसके गुणांकों के संबंध के विषय में जानेंगे
यदि द्विघात बहुपद
p(x)=ax2+bx+c,a≠0
के शून्यक α,β हो, तो
x−α और x−β,p(x) के गुणनखंड होते है ।
अतः ax2+bx+c=k(x−α)(x−β), जहां k एक अचर है
=k[x2−(α+β)x+αβ]
=kx2−k(α+β)x+kαβ
α,β,γ यूनानी भाषा के अक्षर है जिन्हें क्रमश: अल्फ़ा, बीटा, गामा द्वारा उच्चारित किया जाता है ।
दोनों ओर (L.H.S तथा R.H.S) के x2,x के गुणांकों तथा अचर पदों कि तुलना करने पर, हम पाते है:
a=k,b=−k(α+β) और c=kαβ
इससे प्राप्त होता है:
α+β=−ba
αβ=ca
अर्थात शून्यको का योग =α+β=−ba =−Coefficient of xCoefficient of x2 (Coefficient = गुणांक)
शून्यको का गुणनफल = αβ=ca =ConstantCoefficient of x2 (Constant = अचर पद )
इसी प्रकार त्रिघातीय बहुपद
ax3+bx2+cx+d के लिए
यदि α,β,γ इसके शून्यक है तो
α+β+γ=−ba
αβ+βγ+γα=ca
और αβγ=−da
प्राप्त होता है ।
OMR (One Minute Revision)
α और β हो, तो
α+β=−ba,αβ=ca
α+β+γ=−ba
αβ+βγ+γα=ca
और αβγ=−da
उदाहरण 4
द्विघात बहुपद x2+7x+10 के शून्यक ज्ञात कीजिए और शून्यको तथा गुणांकों के बीच के संबंध की सत्यता की जॉंच कीजिए ।
यहाँ द्विघात बहुपद x2+7x+10 दिया है,
:
अतः x2+7x+10
= x2+5x+2x+10 = x2+5x+2x+10
x(x+5)+2(x+5)
= (x+2)(x+5)
इसलिए x2+7x+10 का मान शून्य है जब
x+2=0 है या x+5=0 है ,
अर्थात जब x=−2 या x=−5 हो।
इसलिए x2+7x+10 के शून्यक -2 और -5 है । अब आइये जांच कर लेते है चूँकि
शून्यको का योग =−Coefficient of xCoefficient of x2 (Coefficient=गुणांक)
अतः ⇒−2+(−5)=(−7)1
−7=−7
शून्यको का गुणनफल =constantCoefficient of x2 (Constant =अचर पद )
(−2)×(−5)=101
10=10
उदाहरण 5
एक द्विघात बहुपद ज्ञात कीजिए जिसका शून्यांकों का योग और गुणनफल है।
−14,14
मान लिया कि द्विघात बहुपद के शून्यांक alpha" और "beta है।
दिया हुआ है, α+β=−14 और <br> αβ=14
−ba=−14
तुलना करने पर →a=4, b=1
और
ca=14
तुलना करने पर→a=4, c=1
अब, α,β शून्यकों वाला एक द्विघात बहुपद है :
x2−(α+β)x+αβ
या, x2−(−14)x+14
या, x2+14x+14
या इसे द्विघात बहुपद के मानक रूप ax2+bx+c में लिखने पर
→a=4, b=1, c=1
⇒4x2+x+1
उदाहरण 6
यदि द्विघात बहुपद x2+5x+4 के शून्यांक α और β हो, तो α3+β3 के मान ज्ञात करें।
दिया है,
द्विघात बहुपद x2+5x+4 के शून्यांक α और β है
∴ α+β=−coefficient of xcoefficient of x2
α+β=−51=−5
तथा α⋅β=Constantcoefficient of x2=41=4
α3+β3=(α+β)3−3αβ(α+β)
=(−5)3−3×4(−5)=−125+60=−65
उदाहरण 7
यदि द्विघात बहुपद x2−5x+4, के शून्यांक α और β हो, तो एक द्विघात बहुपद को ज्ञात करें जिसके शून्यांक α+1β और β+1α है।
चूँकि द्विघात बहुपद x2−5x+4 के शून्यांक α और β है,
∴ α+β=5 तथा αβ=4
माना,
α'=α+1β और β'=β+1α
अब, α'+β'=α+1β+β+1α
=α+β+1β+1α
=α+β+α+βαβ=5+54
=254=−ba
तुलना करने पर →a=4, b=−25
और
α'β'=(α+1β)(β+1α)
=(αβ+1β)(αβ+1α)
=(αβ+1)2αβ=(4+1)24=254=ca
तुलना करने पर →a=4, c=25
अब, α' और β' शून्यांक वाला एक द्विघात बहुपद है :
x2−(α'+β')x+α'β'
या, x2−254x+254
या इसे द्विघात बहुपद के मानक रूप ax2+bx+c में लिखने पर
→a=4,b=−25, c=25
4x2−25x+25
उदाहरण 8
एक त्रिघाती बहुपद ज्ञात करें जिसके शुन्यकों के योग, दो-दो शुन्यकों को लेकर गुणा करने पर गुणनफलों का योग, इसके तीनों शुन्यकों का गुणनफल क्रमश: 2,-7 और -14 है।
माना कि त्रिघाती बहुपद ax3+bx2+cx+d है।
तथा माना α,β,γ बहुपद ax3+bx2+cx+d के शून्यक है |
तब α+β+γ=−ba
⇒2=−ba
αβ+βγ+γα=ca
⇒−7=ca
αβγ=−da
⇒ −14=−da
⇒ax3+bx2+cx+d
=a(x3+bax2+cax+da)
ba,ca,da के मान रखने पर, हम पाते है कि
a(x3−2x2−7x+14)
इस तरह α,β,γ शून्यक वाला त्रिघाती बहुपद x3−2x2−7x+14 है।
नोट : यहाँ α,β,γ शून्यक वाले सभी त्रिघाती बहुपदों का रूप
a(x3−2x2−7x+14) होगा जहाँ a∈R,a≠0
इसे निम्न प्रकार से भी हल कर सकते है -
x3−(α+β+γ)x2+(αβ+βγ+γα)x−αβγ
⇒ x3−2x2+(−7x)−(−14)
⇒ x3−2x2−7x+14
4. बहुपदो के लिए विभाजन एल्गोरिथ्म
पिछ्ले अध्याय में हमने किन्ही दो अऋणात्मक पूर्णांकों के लिए यूक्लिड की विभाजन एल्गोरिथ्म तथा उसके अनुप्रयोगों को पढ़ा था इस अध्याय में हम किन्ही दो बहुपदों के लिए इस एल्गोरिथ्म को जानेंगे।
यदि p(x) और g(x) कोई दो बहुपद है, जहाँ g(x)≠0 तो हम ऐसे दो बहुपद q(x) और r(x) प्राप्त कर सकते है कि p(x)=g(x)×q(x)+r(x)
जहाँ r(x)=0 है
अथवा r(x) के चर की घात < g(x) के चर की घात
(चूँकि r(x) = शेषफल तथा g(x) = भाजक है व शेषफल के चर की घात, भाजक के चर की घात से कम आने पर आगे भाग नहीं जाएगा।)
यहाँ आप ध्यान से देखे तो उक्त समीकरण
⇒ भाज्य = भाजक × भागफल + शेषफल के रूप मे दिखाई देता है।
ऊपर प्राप्त निष्कर्ष बहुपदों के लिए विभाजन एल्गोरिथ्म कहलाता है।
विभाजन एल्गोरिथ्म विधि के चरण:
चरण 1: भागफल का पहला पद प्राप्त करने के लिए, उच्चतम घात वाले पद को भाजक के उच्चतम घात वाले पद से भाग दीजिए।
चरण 2: अब भागफल का दूसरा पद ज्ञात करने के लिए, नए भाज्य के उच्चतम घात वाले पद को भाजक के उच्चतम घात वाले पद से भाग कीजिए।
चरण 3: भाग देने की प्रक्रिया तब तक जारी रहती हैं जब तक शेषफल की घात भाजक की घात से कम ना हो जाए।
OMR (One Minute Revision)
p(x)=g(x)q(x)+r(x) हो,
जहाँ r(x)=0 या
घात r(x) < घात g(x) है।
उदाहरण 9
2x2+3x+1 को x+2 से भाग दीजिए।
भाज्य =2x2+3x+1 तथा
भाजक =x+2 दिया है
अतः हल करने पर
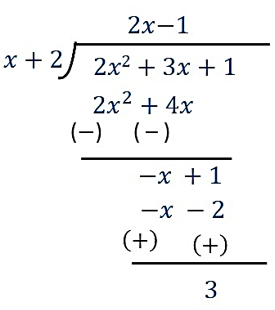
चरण 1: भागफल का पहला पद प्राप्त करने के लिए, उच्चतम घात वाले पद ( अर्थात् 2x2) को भाजक के उच्चतम घात वाले पद ( अर्थात् x) से भाग दीजिए। भागफल 2x प्राप्त होगा तब, भाग देने की प्रक्रिया कीजिए। यहाँ शेषफल −x+1 है।
चरण 2: अब भागफल का दूसरा पद ज्ञात करने के लिए, नए भाज्य के उच्चतम घात वाले पद (अर्थात् −x) को भाजक के उच्चतम घात वाले पद ( अर्थात् x) से भाग कीजिए। इससे भागफल −1 मिला है।
चरण 3: अब शेष बचे 3 मे x की घात (0) भाजक के x की घात (1) से कम है। इसलिए हम भाग देने की क्रिया को आगे और नहीं कर सकते हैं।
ध्यान दीजिए की जब शेषफल या तो शून्य हो जाए या इसकी घात भाजक की घात से कम हो जाए, तो हम भाग देने की प्रक्रिया को रोक देते है। इसलिए यहाँ भागफल 2x−1 है तथा शेषफल 3 है । इसके अतिरिक्त
विभाजन एल्गोरिथ्म की सत्यता की जाँच
(2x−1)(x+2)+3
=2x2+3x−2+3
=2x2+3x+1
अतः भाज्य = भाजक × भागफल + शेषफल के लिए
2x2+3x+1=(x+2)(2x−1)+3
उचित हल प्राप्त हुआ ।
उदाहरण 10
3x2−x3−3x+5 को x−1−x2 से भाग दीजिये और विभाजन एल्गोरिथ्म की सत्यता की जाँच कीजिये।
ध्यान दीजिए कि दिए हुए बहुपद मानक रूप में नहीं है । भाग करने के लिए हम सर्वप्रथम भाज्य और भाजक दोनों को उनकी घातो के घटते क्रम में लिखते है ।
इसलिए
भाज्य =−x3+3x2−3x+5 तथा
भाजक =−x2+x−1 है ।
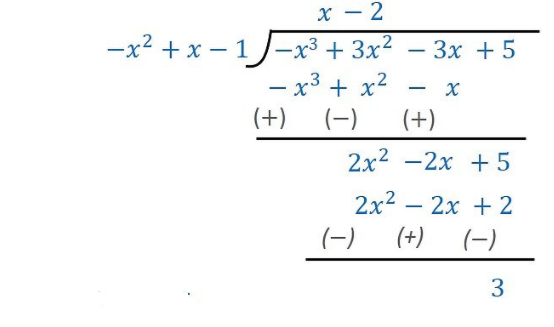
हम यहाँ रुकते है , क्योकि 3 मे x की घात 0 है ,जो कि −x2+x−1 मे x की घात से 2 कम है।
इसलिए भाग की क्रिया करके शेषफल 3 तथा भागफल x−2 प्राप्त होता है। अब
विभाजन एल्गोरिथ्म की सत्यता की जाँच
भाजक × भागफल + शेषफल
=(−x2+x−1)(x−2)+3
=−x3+x2−x+2x2−2x+2+3
=−x3+3x2−3x+5
= भाज्य
अतः विभाजन एल्गोरिथ्म सत्यापित हो गया ।
उदाहरण 11
x3−3x2+x+2 को बहुपद g(x), से भाग देने पर भागफल और शेष क्रमश: x-2 और -2x+4 है | g(x) ज्ञात करें |
माना,
p(x)=x3−3x2+x+2m
q(x)=x−2 तथा
r(x)=−2x+4
प्रश्नानुसार,
p(x) भाज्य है g(x) भाजक, q(x) भागफल तथा r(x) शेष है।
अतः विभाजन एल्गोरिथ्म से हम पाते है कि
p(x)=q(x)×g(x)+r(x)
⇒ q(x)g(x)=p(x)−r(x)
⇒ g(x)=p(x)−r(x)q(x)
=x3−3x2+x+2−(−2x+4)x−2
=x3−3x2+3x−2x−2
इस तरह g(x) ज्ञात करने के लिए हमें x3−3x2+3x−2 को (x-2) से भाग देना होगा |
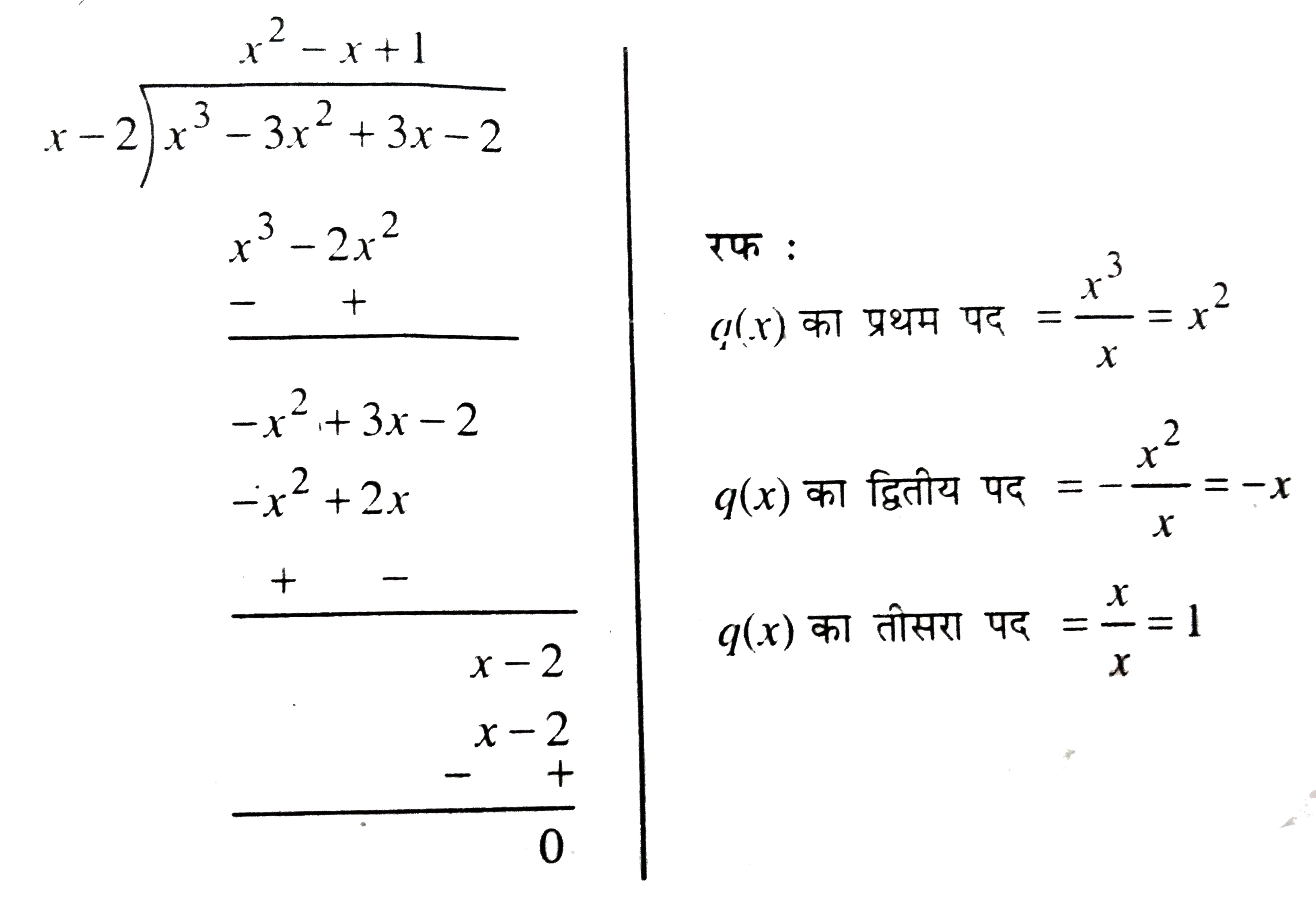
अतः g(x)=x2−x+1
उदाहरण 12
बहुपद p(x),q(x),g(x)[g(x)≠0],r(x)के उदाहरण दें जो भाग एल्गोरिदम को संतुष्ट करते है और
p(x) का घात = q(x) का घात
विभाजन एल्गोरिथ्म से,
p(x)=g(x)×q(x)+r(x)
चूँकि घात p(x)=घात q(x)
अतः g(x) अवश्य एक अचर है तथा r(x) अवश्य एक बहुपद है जिसका घात p(x) या q(x) के घात से कम है।
विशेष स्थिति में हम r(x) को एक अचर मानते है
मान लें
p(x)=4x2+2
और g(x)=2
तब, p(x)g(x)=4x2+22
अतः हल करने पर भागफल q(x)=2x2+1,
तथा शेषफल r(x)=0
जहाँ p(x) की घात = q(x) की घात = 2
उदाहरण 13
दिया गया बहुपद के सभी शून्यांक को ज्ञात करें यदि दी गई संख्या उनके शून्यक है |
x3+2x2−x−2,−2
दत्त बहुपद
p(x)=x3+2x2−x−2
चूँकि -2 बहुपद p(x) का एक शून्यक है
अतः x+2 बहुपद p(x) का एक गुणनखंड होगा।
अब हम p(x) को (x+2) से विभाजित करते है।
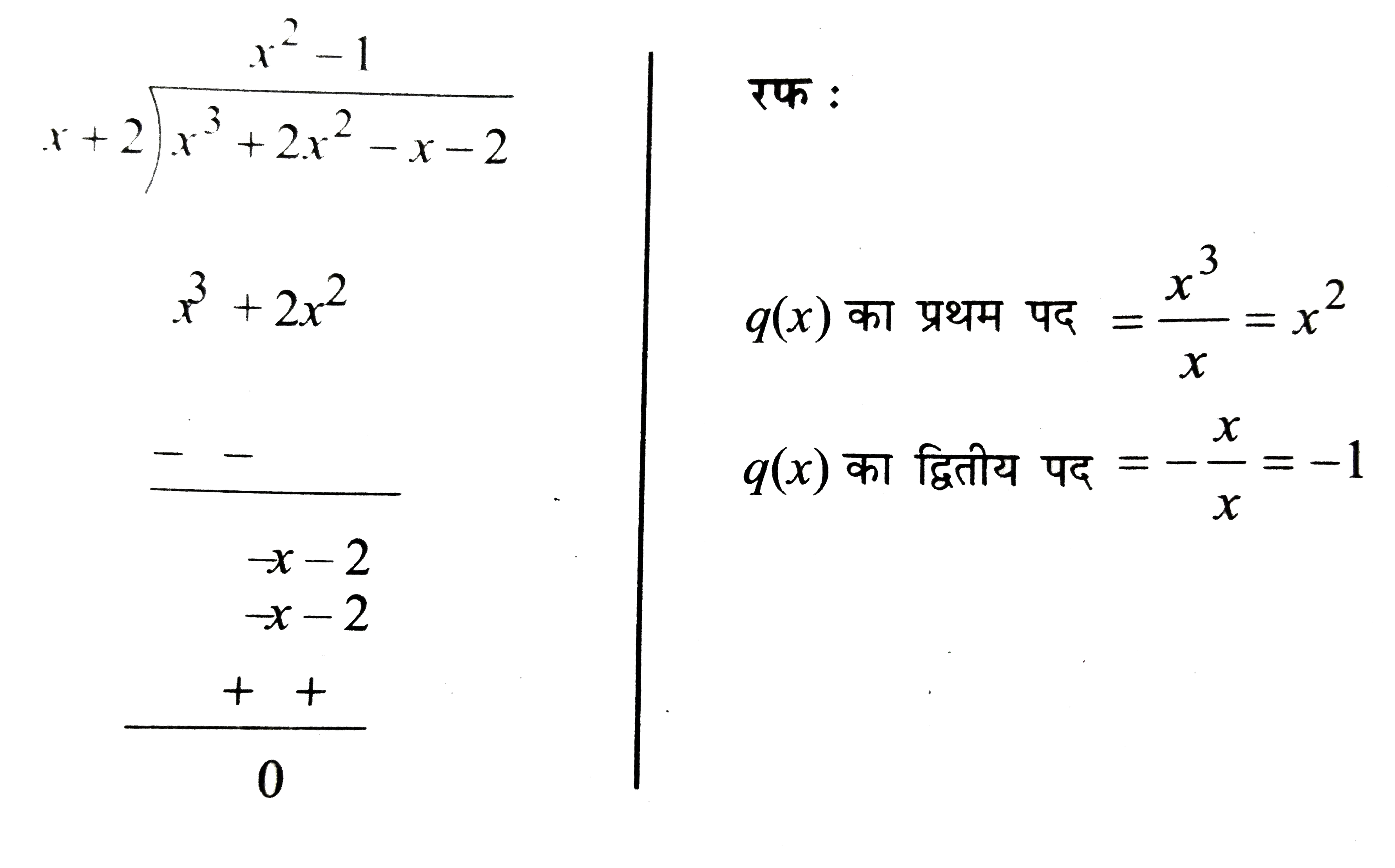
विभाजन एल्गोरिथ्म से,
p(x)=g(x)q(x)+r(x)
∴ x3+2x2−x−2
=(x+2)(x2−1)+0
=(x+2)(x2−1)
भागफल q(x) के शून्यांक अर्थात (x2−1) के शून्यांक 1,−1 है।
[ x2−1=0
⇒x2=1
⇒x=±1 ]
अतः -2 के अतिरिक्त p(x) के शून्यक 1,−1 है।
सारांश
इस अध्याय में हमने निम्न तथ्यों के बारे में पढ़ा और जाना :
p(x)=g(x)q(x)+r(x),
जहाँ r(x)=0 है या घात r(x)<घात g (x) है।