प्रायिकता कक्षा 10 गणित

बच्चों! पिछले कक्षा $9$ में हमने घटनाओं की प्रायोगिक प्रायिकताओं के बारे में अध्ययन किया हैं, जो वास्तविक प्रयोगों के परिणामों पर आधारित थी। यहाँ हम किसी घटना की सैद्धांतिक प्रायिकता (परंपरागत प्रायिकता या Classical Probability) के बारे में अध्ययन करेंगे तथा सैद्धांतिक प्रायिकता की सरल अवधारणा के अनुप्रयोग भी जानेंगे।

हमने पिछली कक्षा में प्रायिकता की प्रारंभिक जानकारी ली है। प्रायिकता किसी भी घटना के घटित होने की संभावना का बोध कराता है तथा किसी घटना की प्रयोगात्मक या आनुभविक (Experimental or Empirical) प्रायिकता की परिभाषा सीखा है, किसी घटना (Event) $E$ के घटने की आनुभविक (प्रायोगिक) प्रायिकता (empirical Probability) निम्न प्रकार से परिभाषित की जाती है:

$P\left(E\right)=$
अभिप्रयोगों की संख्या जिनमें घटना घटी है / अभिप्रयोगों की कुल संख्या

चित्त (Head) : 448
पट (Tail) : 552

किसी घटना $E$ की सैद्धांतिक प्रायिकता (theoretical probability) [जिसे परंपरागत प्रायिकता (classical probability) भी कहा जाता है।] $P\left(E\right)$ निम्नलिखित रूप में परिभाषित की जाती है:

$P\left(E\right)=$
$E$ के अनुकूल परिणामों की संख्या / कुल संभव परिणामों की संख्या

तीन थैलों में रखे 10 नारंगी, 10 हरे एवं 10 लाल गेंदों को एक बड़े थैलों में मिश्रित कर रखा जाता है। यदि इनमें से एक गेंद यादृच्छ निकाला जाए (बिना थैला के अंदर देखे), तो निम्न की प्रायिकता क्या होगी:
(i) गेंद नारंगी हो, (ii) गेंद हरा हो, (iii) गेंद लाल हो।

चूंकि थैले के अंदर देखे बिना यादृच्छया एक गेंद निकाला जाता है, इसलिए कोई भी एक गेंद निकल सकता है।
माना कि
$E_1$ नारंगी गेंद के निकलने की घटना है।
$E_2$ हरे गेंद के निकलने की घटना है।
$E_3$ लाल रंग के गेंद के निकलने की घटना है।

कुल गेंद $=10+10+10=30$

बड़े थैले में रखे $30$ गेंदों में $10$ नारंगी, $10$ हरे एवं $10$ लाल गेंद है।
इसलिए कुल संभावित परिणामों की संख्या $=30$

(i) घटना $E_1$ के अनुकूल परिणामों की संख्या $=10$
$\therefore$ नारंगी रंग एक गेंद के निकलने की प्रायिकता

$P\left(E_1\right)=\frac{10}{30}=\frac{1}{3}$

(ii) इसी प्रकार हरे रंग के गेंद के निकलने की प्रायिकता

$P\left(E_2\right)=\frac{10}{30}=\frac{1}{3}$

(iii) लाल रंग के गेंद के निकलने की प्रायिकता

$P\left(E_3\right)=\frac{10}{30}=\frac{1}{3}$

यहाँ $P\left(E_1\right)+P\left(E_2\right)+P\left(E_3\right)=1$

एक पासा एक बार फेंका जाता है। निम्नलिखित को प्राप्त करने की प्रायिकता ज्ञात कीजिए:
(i) एक सम अभाज्य संख्या
(ii) 3 का गुणज।

जब एक पासा फेंका जाता है, तब 1, 2, 3, 4, 5 या 6 में से कोई एक संख्या प्राप्त होती हैं।

$\therefore$ कुल संभावित परिणामों की संख्या $=6$

माना कि $E_1$ एक सम अभाज्य संख्या आने की घटना है तथा $3$ का गुणज आने की प्रायिकता $E_2$ हैं।

(i) अभाज्य संख्याएँ 2, 3, 5 है।

इनमें से मात्र एक संख्या $2$ ही सम अभाज्य संख्या है।

$\therefore$ सम अभाज्य संख्या आने के अनुकूल परिणामों की संख्या $=1$

अतः $P\left(E_1\right)=\frac{1}{6}$

अतः $P\left(E_2\right)=\frac{2}{6}=\frac{1}{3}$

एक पासा एक बार फेंका जाता है। (i) 4 से बड़ी संख्या प्राप्त करने की प्रायिकता क्या है?
(ii) 4 से छोटी या उसके बराबर संख्या प्राप्त होने की प्रायिकता क्या है?

जब एक पासा फेंका जाता है, तब 1, 2, 3, 4, 5 या 6 में से कोई एक संख्या प्राप्त होती हैं।

$\therefore$ कुल संभावित परिणामों की संख्या $=6$

(i) माना $4$ से बड़ी संख्या प्राप्त करने की घटना $E$ है।

चूंकि 5 और 6, 4 से बड़े हैं।

अतः $E$ के अनुकूल परिणामों की संख्या $2$ है।

$\therefore P\left(E\right)=\frac{2}{6}=\frac{1}{3}$

$\therefore P\left(F\right)=\frac{4}{6}=\frac{2}{3}$

किसी प्रयोग की वह घटना जिसका केवल एक ही परिणाम हो प्रारंभिक घटना (elementary event) कहलाती है। उदाहरण 1 में घटनाएँ $E_1$, $E_2$ और $E_3$ प्रारंभिक घटनाएँ हैं।

यहाँ $P\left(E_1\right)+P\left(E_2\right)+P\left(E_3\right)$$=\frac{1}{3}+\frac{1}{3}+\frac{1}{3}=1$

उदाहरण $3$ में दी हुई घटना $E$ और $F$ प्रारंभिक घटनाएँ नहीं हैं, क्योंकि घटना $E$ के $2$ परिणाम हैं तथा घटना $F$ के $4$ परिणाम हैं।

किसी प्रयोग की सभी प्रारंभिक घटनाओं की प्रायिकताओं का योग 1 है। यह व्यापक रूप में भी सत्य है।

$P\left(E_1\right)+P\left(E_2\right)+P\left(E_3\right).......P\left(E_n\right)=1$

पूरक घटनाएँ: घटना E नहीं को निरूपित करने वाली घटना $\overline{E}$, घटना $E$ की पूरक (complement) घटना कहलाती है। हम यह भी कहते हैं कि $E$ और $\overline{E}$ परस्पर पूरक घटनाएँ हैं।
व्यापक रूप में, किसी घटना $E$ के लिए यह सत्य है कि

$P\left(\overline{E}\right)=1–P\left(E\right)$

$=1-\frac{2}{3}$
$=\frac{1}{3}$

0$\le$P(E)$\le$1

(i) $20$ बल्बों के एक समूह में $4$ बल्ब खराब हैं। इस समूह में से एक बल्ब यादृच्छया निकाला जाता हैं। इसकी क्या प्रायिकता है कि बल्ब खराब होगा ?
(ii) मान लीजिए $\left(i\right)$ में निकाला गया बल्ब खराब नहीं है और न ही इसे दुबारा बल्बों के साथ मिलाया जाता है। अब शेष बल्बों में से एक बल्ब यादृच्छया निकाला जाता है। इसकी क्या प्रायिकता है कि यह बल्ब खराब नहीं होगा ?

(i) मान लीजिए कि $E_1$ खराब बल्ब निकालने की घटना है।
चूँकि कुल बल्बों की संख्या $20$ है।
अतः कुल संभव परिणामों की संख्या $=20$

अब एक खराब बल्ब निकालने का अर्थ होगा चार खराब बल्बों में से एक खराब बल्ब निकालना।
$\therefore E_1$ के अनुकूल परिणामों की संख्या $=4$
$\therefore$ एक खराब बल्ब निकालने की प्रायिकता

$P\left(E_1\right)=\frac{4}{20}<br>=\frac{1}{5}$

$P\left(E_2\right)$$=\frac{15}{19}$

यदि $3$ छात्रों के समूह में $2$ छात्रों के जन्मदिन समान नहीं होने की प्रायिकता $0.992$ है। दोनों छात्रों के जन्मदिन एक-ही होने की क्या प्रायिकता है ?

प्रश्न के अनुसार,

$3$ छात्रों के समूह में से दो छात्रों के जन्मदिन समान नहीं होने की प्रायिकता

$P\left(\overline{E}\right)=$ $0.992$

$P\left(E\right)=1-0.992=0.008=\frac{8}{1000}$

एक बक्से में $5$ लाल, $4$ हरे और $7$ सफेद गेंद है। बक्से से एक गेंद यादृच्छया रूप से निकाला जाता है। निकाले गये गेंद की (i) सफेद होने, (ii) न लाल, न सफेद होने की प्रायिकता ज्ञात करें।

लाल गेंदों की संख्या $=5$
हरे गेंदों की संख्या $=4$
सफेद गेंदों की संख्या $=7$
कुल गेंदों की संख्या $=5+4+7=16$
(i) $P$ (सफेद गेंद) $=\frac{7}{16}$

(ii) गेंदों की संख्या जो लाल या सफेद है $=5+7=12$
$\therefore P$ ( न लाल गेंद न सफेद गेंद ) $=1-P$ (लाल या सफेद गेंद) $=1-\frac{12}{16}$$=1-\frac{3}{4}=\frac{1}{4}$

दूसरी विधि : $P$ (न लाल गेंद न सफेद गेंद) $=P$ (हरा गेंद) $=\frac{4}{16}=\frac{1}{4}$

एक थैले में $6$ लाल और कुछ नीली गेंद है। यदि थैले से नीली गेंद निकालने की प्रायिकता लाल गेंद निकालने की प्रायिकता की दुगनी ( double ) है, तो थैले में नीली गेंदों की संख्या ज्ञात कीजिए।

थैले में लाल गेंदों की संख्या $=6$

मान लीजिए कि थैले में नीली गेंदों की संख्या $=x$

$\therefore$ थैले में कुल गेंदों की संख्या $=(6+x)$

$P$ (लाल गेंद)$=\frac{6}{6+x}$

$P$ (नीली गेंद) $=\frac{x}{6+x}$

प्रश्नानुसार, $P$ (नीली गेंद) $=2\times P$ (लाल गेंद)

$\frac{x}{6+x}=2\left(\frac{6}{6+x}\right)$

$\Rightarrow x=12$

एक लापता हेलीकॉप्टर के बारे में सुचना मिलती है की वह चित्र में दिखाई गयीं आयातकार क्षेत्र में कही गिर गया है। इसकी चित्र में दिखाई गयी झील में गिरने की क्या प्रायिकता है?

हेलीकॉप्टर का आयताकार क्षेत्र में कहीं भी गिरना समप्रायिक है।
मान लीजिए झील में हेलीकॉप्टर के गिरने की घटना $E$ है।

पुरे क्षेत्र का क्षेत्रफल जहाँ हेलीकॉप्टर गिर सकता है

$=(9\times 4.5)k{m}^2=40.5k{m}^2$

यदि एक पासे को आकृति में दर्शाए आयताकार क्षेत्र में यादृच्छया रूप से गिराते हैं। इसकी क्या प्रायिकता है कि वह पासा $1m$ व्यास वाले वृत्त के अंदर गिरेगा?

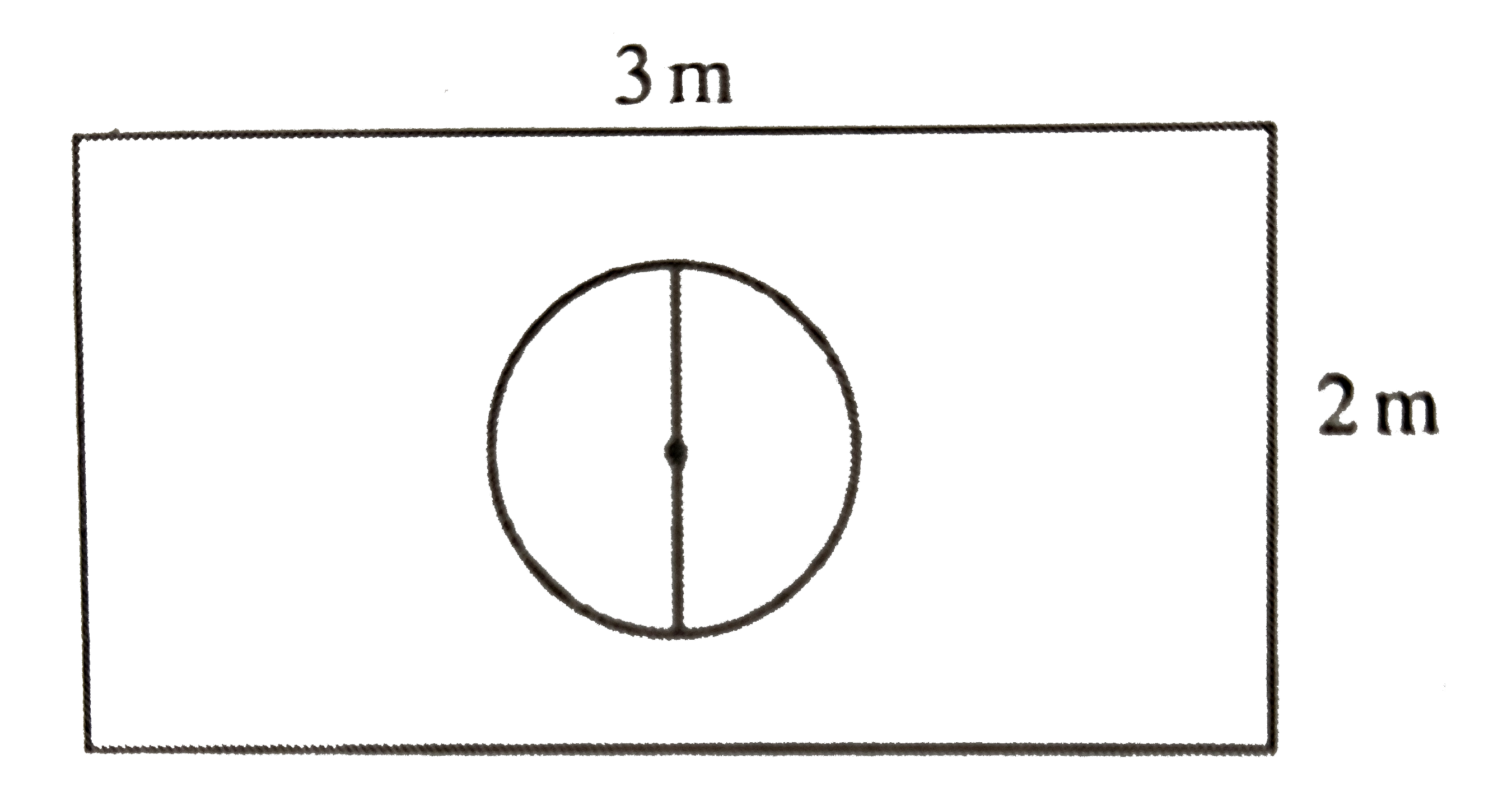
मान लीजिए कि $E$ वृत्त में पासा के गिरने की घटना है।

पासा के गिरने पर, कुल संभावित परिणामों को निरूपित करने वाले क्षेत्र का क्षेत्रफल,
आयत का क्षेत्रफल $=$ लम्बाई $\times$ चौड़ाई $=3\times 2=6m^2$

$E$ के अनुकूल परिणामों वाला क्षेत्र का क्षेत्रफल,
वृत्त का क्षेत्रफल $=\pi \times r^2=\pi \times {\left(\frac{1}{2}\right)}^2<br><br>=\frac{\pi }{4}{m}^2$

(चूंकि व्यास $=1m\Rightarrow$ त्रिज्या $r=\frac{1}{2}$)

$\therefore$ वृत्त के अंदर पासा के गिरने की प्रायिकता

$P\left(E\right)=$
वृत्त का क्षेत्रफल / आयत का क्षेत्रफल
$=\frac{\frac{\pi }{4}}{6}=\frac{\pi }{24}$

दो पासे को एक साथ फेंके जाते है। निम्नलिखित सारणी को पूर्ण कीजिए:

माना की दो पासे को फेंकने पर योग 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 आने की घटना क्रमशः $E_1$, $E_2$, $E_3$, $E_4$, $E_5$, $E_6$, $E_7$, $E_8$, $E_9$, $E_{10}$, $E_{11}$

हम जानते है कि किसी पासा के छः फलकों 1, 2, 3, 4, 5, 6 संख्या अंकित होते हैं।

दो पासों को फेंकने पर, सभी संभव परिणामों की संख्या $=6\times 6=36$

(1,1), (1,2), (1,3), (1,4), (1,5), (1,6)

(2,1), (2,2), (2,3), (2,4), (2,5), (2,6)

(3,1), (3,2), (3,3), (3,4), (3,5), (3,6)

(4,1), (4,2), (4,3), (4,4), (4,5), (4,6)

(5,1), (5,2), (5,3), (5,4), (5,5), (5,6)

(6,1), (6,2), (6,3), (6,4), (6,5), (6,6)

दोनो पासों की संख्याओं का योग $=12$
अनुकूल परिणामों की संख्या $=1\left\{(6,6)\right\}$
$\therefore P\left(E_{11}\right)=\frac{1}{36}$

अतः सारणी:

ताश की गड्डी से संबंधित प्रश्नों को हल करने के लिए हमें सभी प्रकार के ताश के पत्तों के बारे में पता होना चाहिए।

$J$, $Q$, और $K$ को तस्वीर (चेहरे) (Face) या वस्त्र (Coat) वाले पत्ते भी कहते हैं।

इस प्रकार, प्रत्येक समूह में तीन - तीन (फेस कार्ड) चेहरे वाले पत्ते होते हैं।

अतः कुल चेहरे वाले पत्तों की संख्या $=3+3+3+3=12$

अत: बिना चेहरे वाले पत्तों की संख्या $=52-12=40$

$52$ पत्तों की अच्छी प्रकार से फेंटी गई एक ताश की गड्डी में से काला पान की तीन तस्वीर वाली पत्तियाँ निकाल ली जाती है। तब शेष पत्तियों में से एक पत्ती यादृच्छया निकाली जाती है। निम्नलिखित को प्राप्त करने की प्रायिकता ज्ञात करें
(i) काले तस्वीर की पत्ती (ii) एक बेगम (iii) एक काली पत्ती

कुल पत्तियों की संख्या $=52$ ($26$ काले $+26$ लाल)
तब काले पान की तीन तस्वीर वाली पत्तियों को निकालने पर,
शेष पत्तियों की संख्या $=52-3$$=49$

(i) अब काले तस्वीर वाली शेष पत्तियों में चिड़ी के बादशाह, बेगम और गुलाम होंगे।
$\therefore$ शेष तस्वीर वाले काली पत्तियों की संख्या $=3$
$\therefore P$ (एक काली तस्वीर वाली पत्ती) $=\frac{3}{49}$

(ii ) $P$ (एक बेगम) $=\frac{3}{49}$

[चूंकि काला पान के बेगम को छोड़कर शेष बेगमों की संख्या = 3]

(iii) $P$ (एक काली पत्ती) $=\frac{23}{49}$
[चूंकि तीन काली पत्तियाँ निकाली जा चुकी हैं $(26-3=23)$]

ताश के $52$ पत्तों की गड्डी को अच्छी तरह फेंटने के बाद एक पत्ता निकाला जाता है। निम्नलिखित के निकलने कि प्रायिकता ज्ञात करें: (i) लाल पान का एक बादशाह (ii) एक काला पान (iii) काले रंग की बेगम (iv) एक तस्वीर वाला लाल पत्ता

माना की
$E_1$ लाल पान के बादशाह निकलने की घटना है।
$E_2$ काला पान के निकलने की घटना है।
$E_3$ काले रंग के बेगम को निकलने की घटना है।
$E_4$ तस्वीर वाले लाल पत्ते के निकलने की घटना है।

पत्तों की कुल संख्या $=52$
अतः कुल संभव परिणामों की संख्या $=52$

(i) लाल पान के बादशाह की संख्या $1$ है
अतः $E_1$ के अनुकूल परिणामों की संख्या $=1$

$\therefore$$P\left(E_1\right)=\frac{1}{52}$

(ii) काले पान की पत्तों की संख्या $13$ है
अतः $E_2$ के अनुकूल परिणामों की संख्या $=13$

$\therefore P\left(E_2\right)=\frac{13}{52}=\frac{1}{4}$

(iii) काले रंग की बेगम की संख्या $2$ है (काला पान और चिड़ी का बेगम)
अतः $E_3$ के अनुकूल परिणामों की संख्या $=2$

$\therefore P\left(E_3\right)=\frac{2}{52}=\frac{1}{26}$

(iv) तस्वीर वाले पत्ते बादशाह, बेगम और गुलाम है। लाल पान एवं ईंट के बादशाह, बेगम एवं गुलाम की संख्या $6$ है।
अतः $E_4$ के अनुकूल संभव परिणामों की संख्या $=6$

$\therefore P\left(E_4\right)=\frac{6}{52}=\frac{3}{26}$

ताश के चार पत्तों लाल पान का गुलाम, बेगम, बादशाह तथा इक्का को पलट कर अच्छी तरह फेंटा जाता है इनमें से यादृच्छया एक पत्ता निकाला जाता है।
(i) इसकी क्या प्रायिकता है की पत्ता बादशाह है?
(ii) यदि बेगम निकलती है और अलग रख दिया जाता है एक अन्य पत्ता निकाला जाता है। इसकी क्या प्रायिकता है दूसरा निकाला गया पत्ता (a) एक इक्का है ? (b) एक बेगम है ?

(i) माना की $E_1$ बादशाह के निकलने की घटना है।
जब $4$ पत्तों में से एक पत्ता निकाला जाता है, तो कुल संभव परिणामों की संख्या $=4$
और $E_1$ के अनुकूल परिणामों की संख्या $=1$
$\therefore$ एक बादशाह के निकलने की प्रायिकता $P\left(E_1\right)=\frac{1}{4}$

(ii) जब बेगम निकाल कर अलग रख दी जाती है, तो बचे पत्तों की संख्या $=3$
$\therefore$ कुल संभव परिणामों की संख्या $=3$

(a) माना की $E_2$ निकाले गए दूसरे पत्ते के इक्का होने की घटना है।
तब $E_2$ के अनुकूल परिणामों की संख्या $=1$
$\therefore$ बेगम के निकालने एवं उसे अलग रखने के बाद इक्का के निकलने की प्रायिकता $P\left(E_2\right)=\frac{1}{3}$

(b) माना की $E_3$ निकाले गए दूसरे पत्ते के बेगम होने के घटना है
तब, $E_3$ के अनुकूल परिणामों की संख्या $=0$
[चूंकि शेष तीन पत्तों में बेगम का पत्ता नहीं है]
$\therefore$ बेगम के निकलने एवं उसे अलग रखे जाने के बाद बेगम के निकलने की प्रायिकता $P\left(E_3\right)=\frac{0}{3}=0$

इस अध्याय में हमने निम्नलिखित तथ्यों का अध्ययन किया है: