त्रिकोणमिति के कुछ अनुप्रयोग कक्षा 10 गणित
भूमिका
हमने पिछले अध्याय में त्रिकोणमिति का परिचय तथा त्रिकोणमितीय अनुपातों को समझा था, अब हम त्रिकोणमितीय अनुपातों के दैनिक जीवन में अनुप्रयोग देखेंगे अर्थात समझने का प्रयास करेंगे कि त्रिकोणमितीय अनुपात का प्रयोग कर हम किस प्रकार से समस्याओं का हल प्राप्त कर सकते हैं। इस अध्याय मे हम मुख्यतः ऊँचाई एवं दूरी से संबंधित अनुप्रयोग देखेंगे।
आइए बच्चों त्रिकोणमिति के अनुप्रयोगों को समझते है और करीब से...
पिछले अध्याय में आपने त्रिकोणमितीय अनुपातों के बारे में अध्ययन किया है, इस अध्याय में आप कुछ उन विधियों के बारे में अध्ययन करेंगे जिनमें त्रिकोणमिति का प्रयोग आपके आस-पास के दैनिक जीवन से जुड़ा होता है।
जैसे कि हमने पिछले अध्याय में समझा था कि त्रिकोणमिति, त्रिभुजों की माप करने की एक विधि है जिसमे हम सामान्यतः समकोण त्रिभुज का उपयोग करते हैं। जैसा कि हम जानते हैं समकोण त्रिभुज में एक समकोण तथा दो न्यून कोण होते हैं साथ ही भुजाओ की बात करें तो इसमे कर्ण, आधार तथा लंब होते हैं।
अब सोचिए दैनिक जीवन में हमें समकोण त्रिभुज की स्थिति कहाँ - कहाँ प्राप्त हो रही है?
आइए कुछ उदाहरण देखते है
पतंग उड़ाते हुए किसी बच्चे की कल्पना कीजिए, यदि पतंग, बच्चे, तथा पतंग के नीचे के जमीन पर एक बिन्दु लें तो ये समकोण त्रिभुज के 3 शीर्ष हो गए।
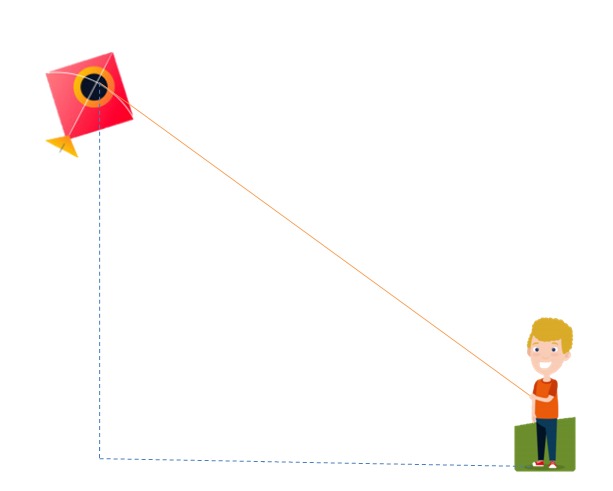
इसी प्रकार यदि कोई व्यक्ति किसी छत मे खड़ा है व नीचे जानवर को देख रहा हो तब भी एक व्यक्ति, जानवर तथा व्यक्ति के नीचे का बिन्दु मिलकर समकोण त्रिभुज बनाते है।
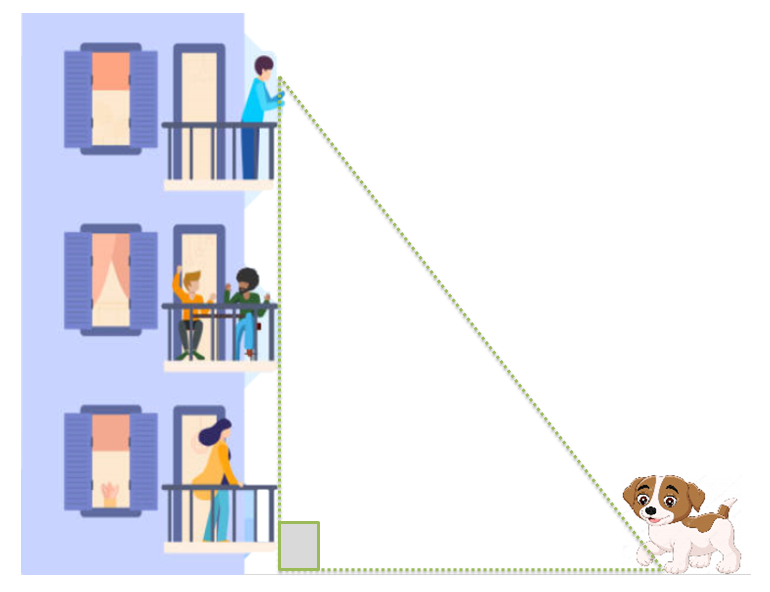
आपको दैनिक जीवन मे इस प्रकार की जितनी भी स्थितियाँ दिखाई दे रही हो, उनको हम त्रिकोणमितीय अनुपातों की सहायता से ज्ञात कर सकते हैं। जैसे कि पतंग की ऊँचाई, व्यक्ति से उस जानवर की दूरी, यहाँ तक आप हिमालय पर्वत की ऊँचाई भी निकाल सकते हैं।
ऊँचाई एवं दूरियाँ
जैसे कि हमने ऊपर कुछ उदाहरण देखे जहाँ समकोण त्रिभुज प्राप्त होगा, इन स्थितियो में हमें जो न्यून कोण प्राप्त होते हैं वे दो प्रकार के होते हैं, आइए इन्हे देखते हैं - 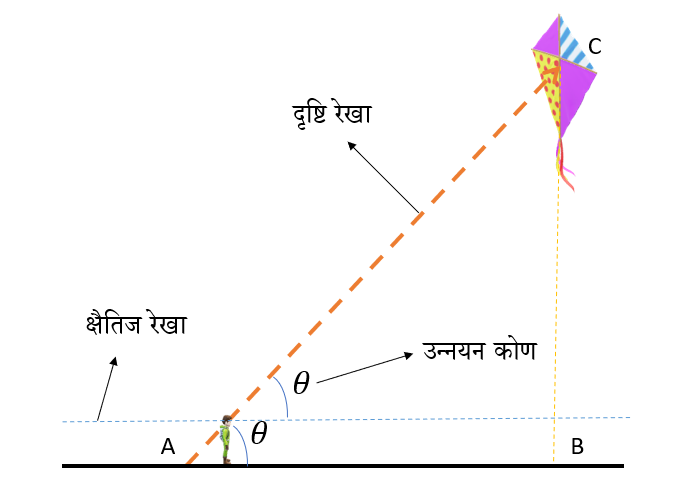
उन्नयन कोण
ऊपर चित्र मे देखिए एक लड़का पतंग उड़ा रहा और वह पतंग को देख रहा है, इस प्रकार जो बच्चे की आँख से पतंग की ओर रेखा जा रही है (AC) दृष्टि रेखा कहलाती है तथा उसके आँख से जमीन के समांतर वाली रेखा (AB) क्षैतिज रेखा कहलाएगी।
अब आप देखिए क्षैतिज रेखा के सापेक्ष दृष्टि रेखा एक कोण (∠BAC) बनाती है इसे हम उन्नयन कोण कहते है।
यहाँ उन्नयन का शाब्दिक अर्थ समझें तो इससे तात्पर्य अपने आँखों (नयन) को ऊपर (ऊंचा) करने से है और यहाँ भी हम देख सकते हैं कि आँखों को ऊपर करने से बना कोण उन्नयन कोण है।
ध्यान दें: चूंकि क्षैतिज रेखा जमीन के समांतर है अतः दृष्टि रेखा जमीन पर भी θ कोण (संगत कोण से) अर्थात उन्नयन कोण बनाती है।
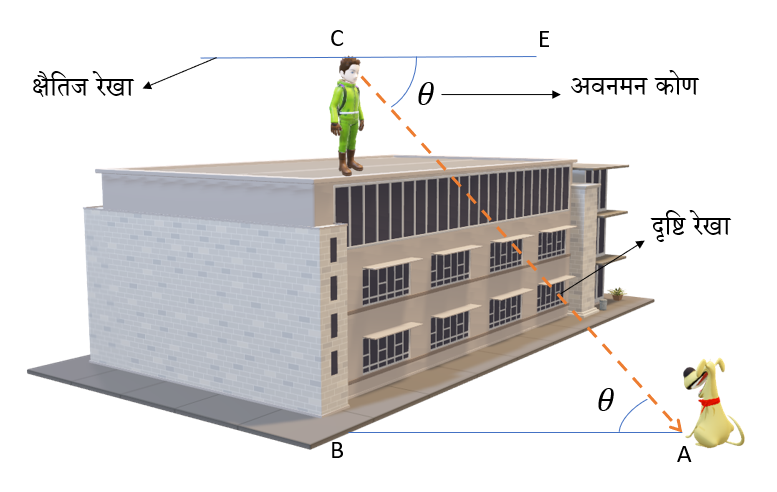
अवनमन कोण
ऊपर चित्र मे देखिए एक लड़का छत में खड़ा है तथा एक कुत्ता नीचे जमीन पर है जिसे वह लड़का देख रहा है, इस प्रकार जो बच्चे की आँख से कुत्ते की ओर रेखा जा रही है (CA) दृष्टि रेखा कहलाएगी तथा उसके आँख से जमीन के समांतर वाली रेखा (CE) क्षैतिज रेखा कहलाएगी।
अब आप देखिए क्षैतिज रेखा के सापेक्ष दृष्टि रेखा एक कोण (∠ECA) बनाती है इसे हम अवनमन कोण कहते हैं।
यहाँ अवनमन का शाब्दिक अर्थ समझे तो इससे तात्पर्य झुकने से है, जैसे कि किसी को प्रणाम (नमन) करते समय हम झुकते है और यहाँ भी हम देख सकते हैं कि आँखों को नीचे झुकाने से बना कोण अवनमन कोण है।
ध्यान दें: चूंकि क्षैतिज रेखा जमीन के समांतर है अतः दृष्टि रेखा जमीन पर भी θ कोण (एकांतर कोण) अर्थात अवनमन कोण बनाती है।
उदाहरण 1
धरती पर एक मीनार ऊर्ध्वाधर खड़ी है, धरती के एक बिन्दु से, जो मीनार के पाद-बिन्दु से 15 मीटर दूर है , मीनार के शिखर का उन्नयन कोण 60∘ है। मीनार की ऊँचाई ज्ञात कीजिए।
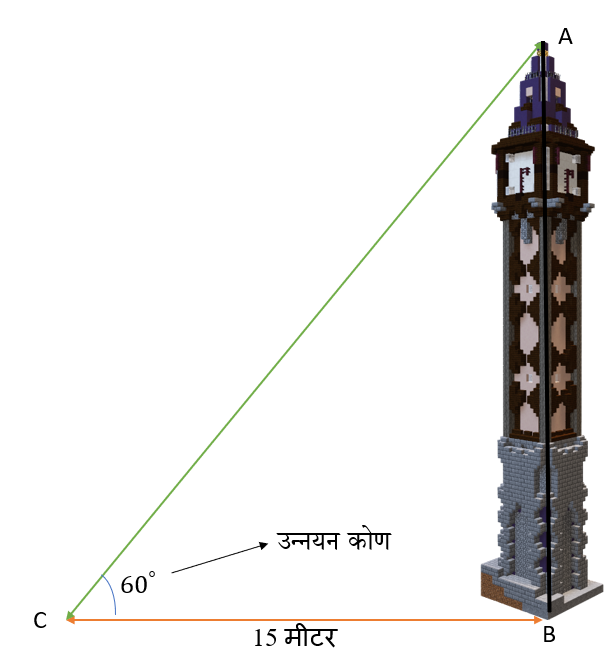
माना AB एक मीनार है तथा मीनार के पाद - बिन्दु B से C तक की दूरी अर्थात
BC=15 मीटर
बिन्दु C से मीनार के शिखर का उन्नयन कोण अर्थात ∠ACB=60∘ है ।
दिया है,
∠ABC=90∘
अब tan60∘=ABBC
√3=AB15
या AB=15√3
अतः मीनार की ऊँचाई 15√3 मीटर है।
उदाहरण 2
1.5 मीटर लम्बा एक प्रेक्षक एक चिमनी से 28.5 मीटर की दुरी पर हैं । उसकी आँखों से चिमनी के शिखर का उन्नयन कोण 45∘ है। चिमनी की ऊँचाई बताइए।
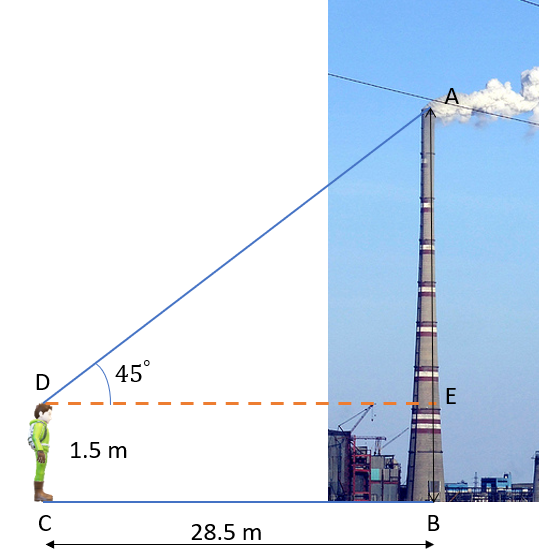
माना AB चिमनी है , CD प्रेक्षक है और ∠ADE उन्नयन कोण है ।
ADE एक समकोण त्रिभुज है,
जिसमें ∠E=90∘
ऊँचाई AB=AE+EB
तथा DE=CB=28.5 मीटर
अब tan45∘=AEDE
1=AE28.5 या AE=28.5 मीटर
अतः चिमनी की ऊँचाई
=(AE+EB)
=(AE+CD)
[चित्र से EB=CD]
=(28.5+1.5)=30 मीटर
उदाहरण 3
7 मीटर ऊँचे भवन के शिखर से एक टॉवर के शिखर का अवनमन कोण 45∘ तथा उसके पाद से उन्नयन कोण 60∘ है। टॉवर की ऊँचाई ज्ञात कीजिए।
समकोण त्रिभुज AMC में
AMh−7=cot45∘=1
⇒ AM=h−7
समकोण त्रिभुज BDC में
BDh=cot60∘=1√3
⇒ BD=h√3
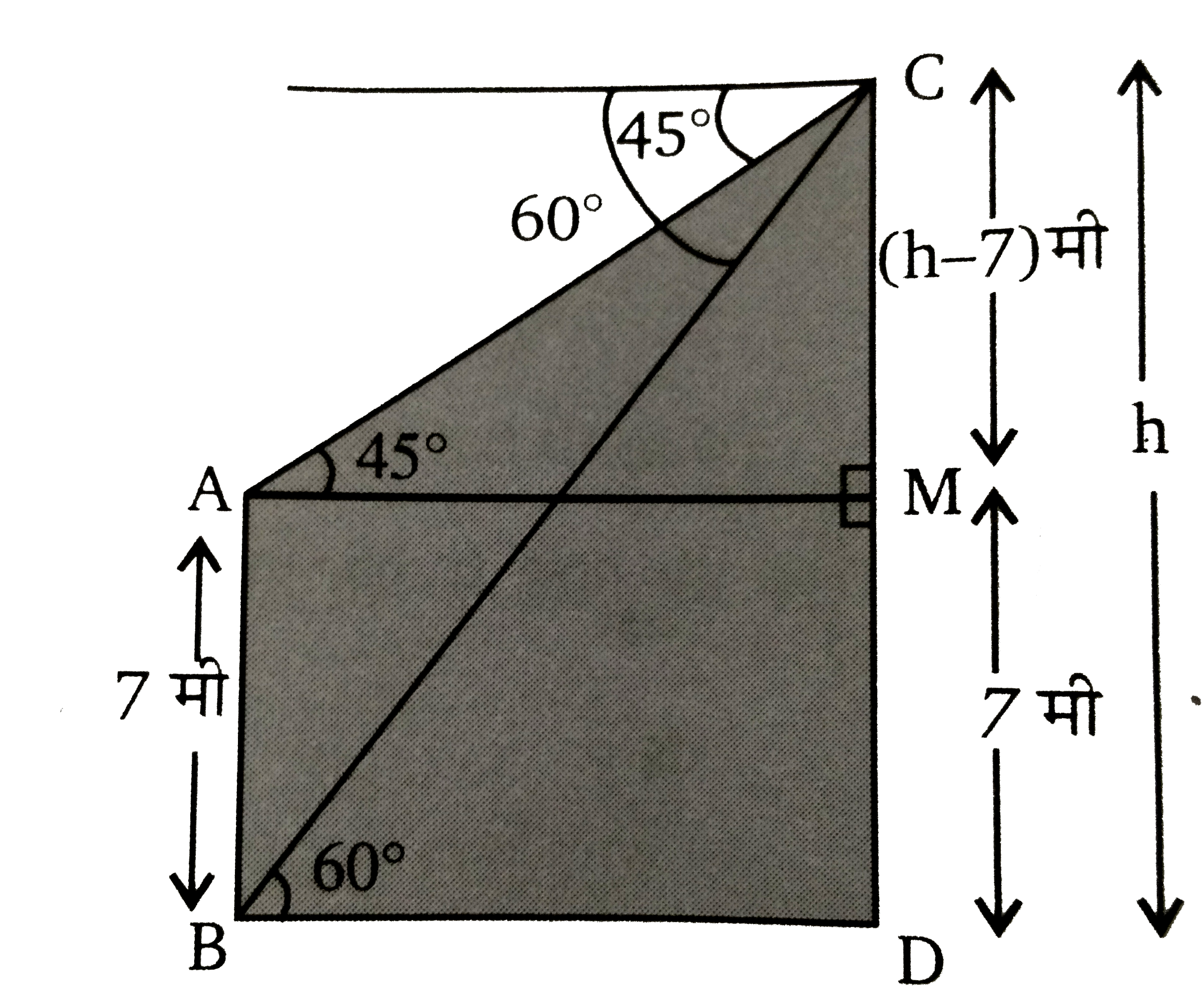
लेकिन AM=BD [ चित्र से ]
⇒ h−7=h√3
⇒ h√3−7√3=h
⇒ h√3−h=7√3
⇒ h(√3−1)=7√3
⇒ h=7√3√3−1
हर का परिमेयकरण करने पर-
⇒ h=(7√3√3−1)(√3+1√3+1)
=21+7√33−1
=21+7×1.7322
=16.56 मीटर
उदाहरण 4
एक लम्बा वृक्ष नदी के किनारे पर ऊर्ध्वाधर खड़ा है। दूसरे किनारे पर वृक्ष के ठीक सम्मुख बिंदु पर वृक्ष की चोटी का उन्नयन कोण 60∘ है। उसी किनारे पर इस बिंदु से 20 मीटर पीछे,वृक्ष की चोटी का उन्नयन कोण 30∘ है।वृक्ष की ऊँचाई व नदी की चौड़ाई ज्ञात कीजिए।
माना पेड़ AB की ऊँचाई h है
दूसरे किनारे पर वृक्ष के सम्मुख O बिंदु है।
नदी की चौड़ाई OB=d
बिंदु O से 20 मीटर पीछे एक बिंदु C है।
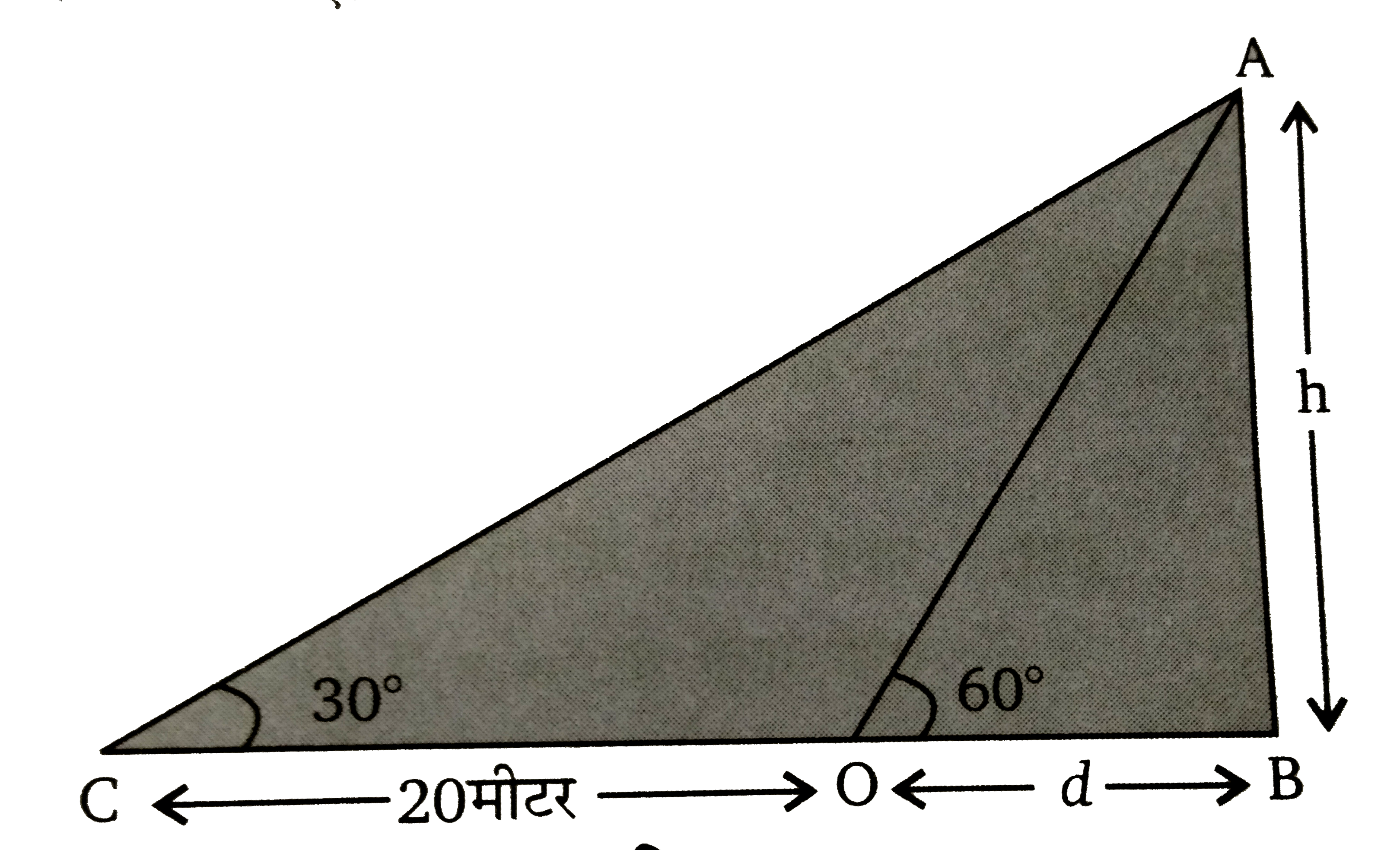
तब AB=h OB=d
∠BOA=60∘ तथा
∠BCA=30∘
ΔABO से
tan60∘=ABOB
⇒ √3=hd
∴ h=√3⋅d ...(1)
ΔABC में tan30∘=ABCB
⇒1√3=h20+d
⇒h=20+d√3 ...(2)
समीकरण (1) व (2) से,
√3⋅d=20+d√3
⇒√3×√3×d=20+d
⇒ 3d−d=20
⇒ 2d=20
⇒ d=10 मीटर उत्तर
तथा h=√3×d
=√3×10
=10√3 मीटर
=10×1.732 मीटर
=17.32 मीटर उत्तर
उदाहरण 5
एक पेड़ 30 मीटर ऊँचा है जो बीच में कही से टूट जाता है| टूटा हुआ भाग तल से 30∘ का कोण बनाता वह ऊँचाई ज्ञात कीजिए जहाँ से पेड़ टूटा है।
माना PQ एक पेड़ है|
अब PQ=30 मीटर
माना पेड़ बिंदु R से टूटकर तल से बिंदु S पर मिलता है
इसलिए RQ=RS
तथा ∠RSP=30∘
यदि RP=x
तब RS=QR=30−x
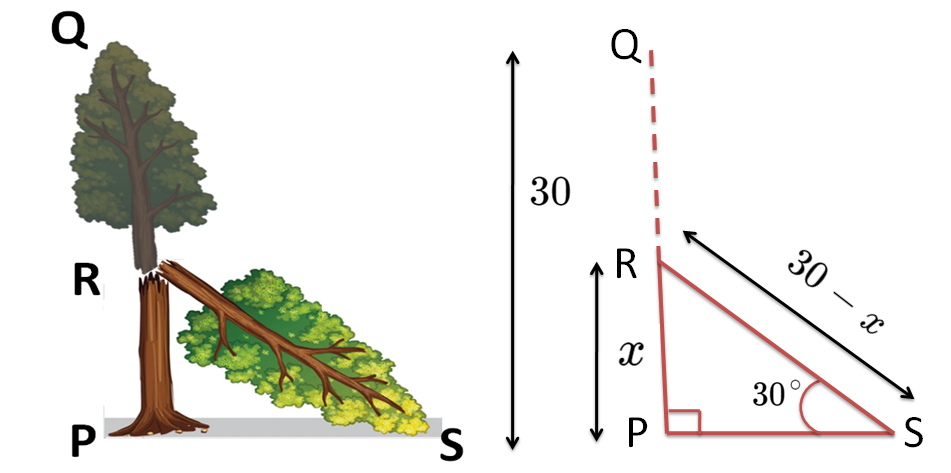
अब समकोण त्रिभुज RSP में,
RPRS=sin30∘
⇒ x30−x=12
⇒ 2x=30−x
⇒ 2x+x=30
⇒ 3x=30
⇒ x=10 मीटर
उदाहरण 6
100 मीटर ऊँचे प्रकाश स्तम्भ से दो जहाजों के अवनमन कोण 30∘ व 45∘ है। यदि एक जहाज, दूसरे के बिलकुल पीछे है तो दोनों जहाजों के बीच की दुरी ज्ञात कीजिए।
माना PQ प्रकाश स्तम्भ है तथा A व B दो जहाज है| PR बिंदु P से एक क्षैतिज रेखा है| बिंदु P पर A व B के अवनमन कोण क्रमशः∠RPA=45∘ व ∠RPB=30∘ है अब ΔPQA में,

tan45∘=PQQA
⇒ 1=PQQA
⇒ PQ=QA=100 मीटर
अब ΔPQB में
tan30∘=PQQB
⇒ 1√3=100QB
⇒ QB=100√3 मीटर
इसलिए AB=QB−QA
=100√3−100
=100(√3−1)
=100(1.732−1)
=100×0.732=73.2
अतः दो जहाजों के बीच की अभीष्ट दुरी 73.2 मीटर है।
उदाहरण 7
एक व्यक्ति एक जहाज पर खड़ा है, जो समुंद्री तल से 8 मीटर ऊपर है। एक पहाड़ी की चोटी से इसका उन्नयन कोण 60∘ तथा पहाड़ की तली से अवनमन कोण 30∘ है| जहाज से पहाड़ की दूरी तथा पहाड़ की ऊँचाई ज्ञात कीजिए।
माना व्यक्ति पहाड़ी से x मीटर की दुरी पर है तथा
पहाड़ी की ऊँचाई h+8 मीटर है जोकि हमें ज्ञात करनी है|
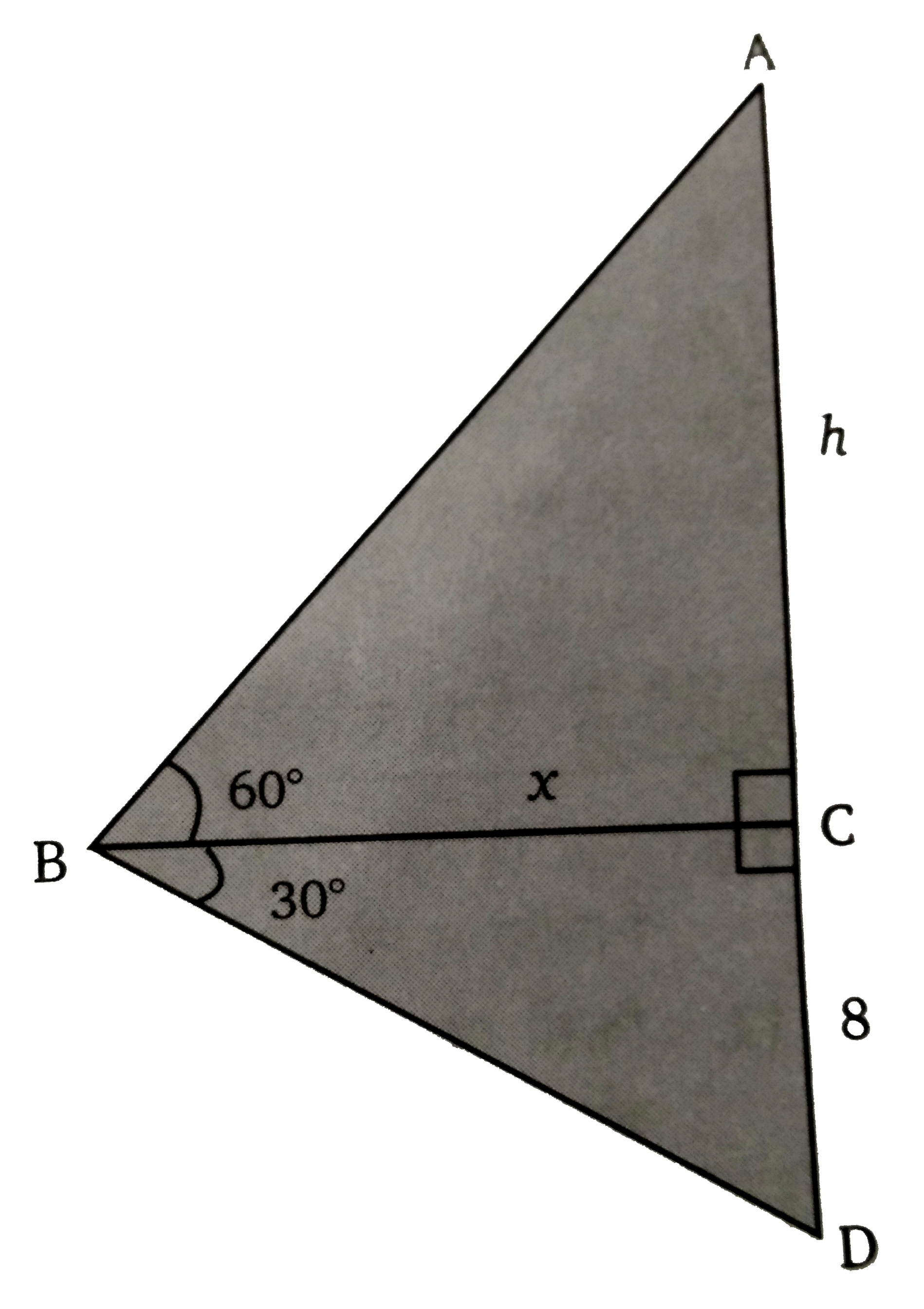
समकोण त्रिभुज ACB में,
tan60∘=hx
⇒ √3=hx
⇒ h=√3⋅x ...(1)
पुनः समकोण त्रिभुज BCD में,
tan30∘=8x
⇒ 1√3=8x
⇒ x=8√3 ...(2)
समीकरण (1) व (2) से
h=√3×8√3
h=8×3=24 मीटर
∴ पहाड़ी की अभीष्ट ऊँचाई
=h+8
=24+8=32 मीटर
तथा जहाज की पहाड़ी से दुरी
=x=8√3 मीटर
उदाहरण 8
एक झील से h मीटर ऊँचाई पर बादलों का उन्नयन कोण α है तथा झील में उसकी परछाई का अवनमन कोण β है। सिद्ध कीजिए कि बादलों की ऊँचाई h(tanβ+tanα)tanβ−tanα है।
माना झील से h मीटर ऊपर बिंदु O है तथा बिंदु A बादलों को तथा बिंदु B उसकी परछाई को प्रदर्शित करते है|
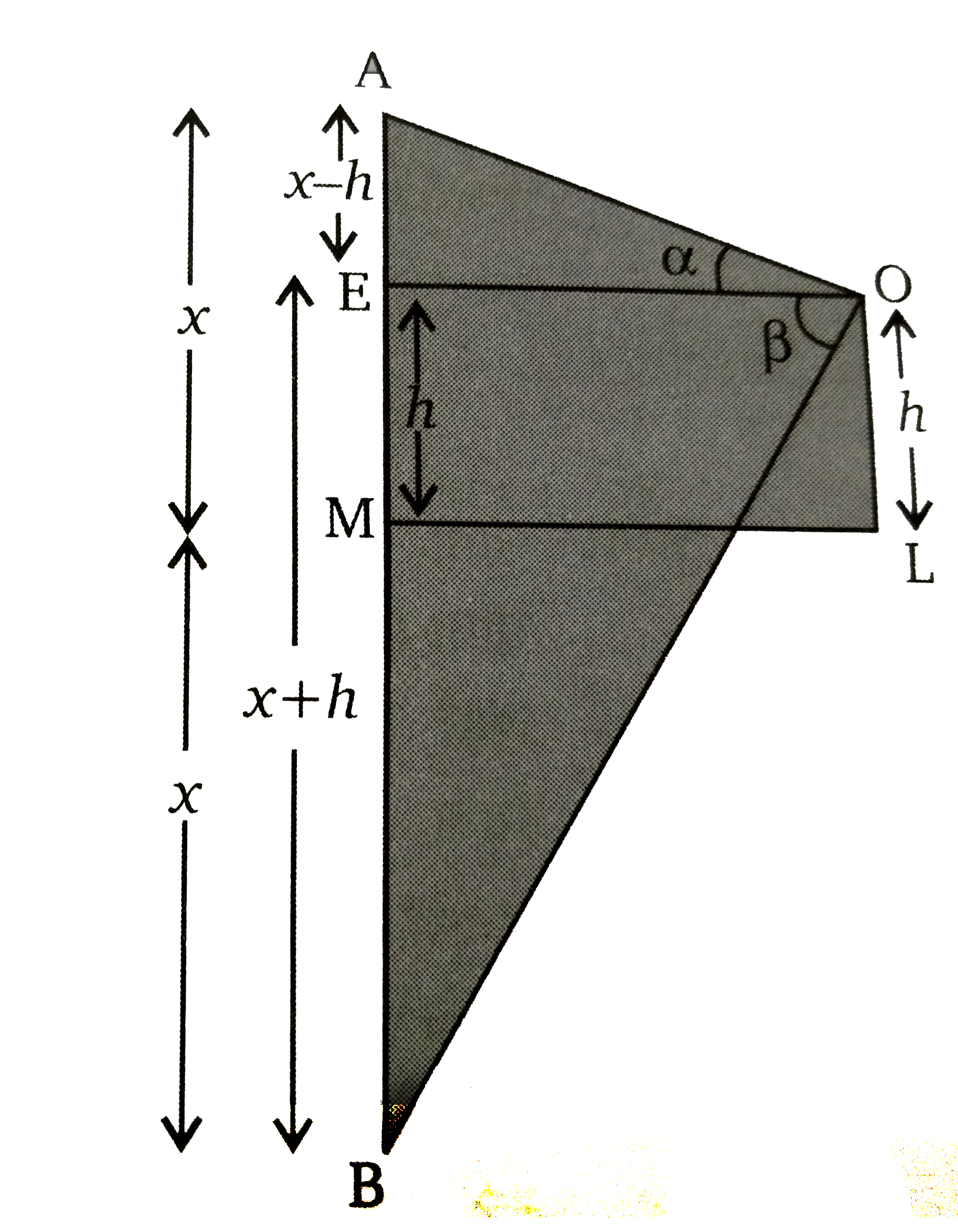
तब OL=h
∠AOE=α,
∠BOE=β
माना झील से ऊपर बादलों की ऊँचाई x मीटर है तब बादल की परछाई भी x मीटर गहराई में होगी।
तब AE=x−h,
BE=x+h
अब समकोण त्रिभुज OEA में
OEAE=cotα
⇒OE=AEcotα
=(x−h)cotα ...(1)
तथा समकोण ΔOEB में
OEEB=cotβ
⇒ OE=EBcotβ
=(x+h)cotβ ...(2)
समीकरण (1) व (2) से
(x−h)cotα=(x+h)cotβ
⇒ x−htanα=x+htanβ
⇒ xtanβ−htanβ
=xtanα+htanα
⇒ x(tanβ−tanα)
=h(tanα+tanβ)
⇒ x=h(tanβ+tanα)tanβ−tanα
सिद्ध हुआ।
उदाहरण 9
गली के एक मकान की खिड़की जिसकी ऊँचाई तल से 15 मीटर है से गली की विपरीत दिशा में सामने बने मकान के शीर्ष व पाद के उन्नयन व अवनमन कोण क्रमशः 30∘ व 45∘ है। सिद्ध कीजिए कि विपरीत दिशा में बने मकान की ऊँचाई 23.66 मीटर है। (√3=1.732)
माना खिड़की बिंदु P पर है अर्थात
AP=15 मीटर
BC विपरीत दिशा में एक घर है|

माना BC=h मीटर तब
QC=BC−BQ=BC−AP
=(h−15) मीटर
(∵BQ=AP)
अब ΔPQB में,
tan45∘=QBPQ
⇒ 1=15PQ
PQ=15 मीटर
अब ΔPQC में
tan30∘=QCPQ
⇒ 1√3=h−1515
h के लिए हल करने पर,
h=15+5√3
=15+5×1.732
=23.66
उदाहरण 10
एक लड़का जिसकी आंखों का स्तर सतह से 1.3 मीटर है। हवा के रूख की ओर सतह से कुछ ऊँचाई पर क्षैतिज रूप में उड़ रहे एक गुब्बारे को देखता है। उसकी आंखों से किसी क्षण गुब्बारे का उन्नयन कोण 60∘ है, 2 सेकण्ड बाद उन्नयन कोण 30∘ हो जाता है। यदि हवा की चाल 29√3मीटर/सेकण्ड है तो सतह से गुब्बारे की ऊँचाई ज्ञात कीजिए।
माना AM क्षैतिज मैदान है तथा लड़के की स्थिति AB तथा गुब्बारे की स्थितियाँ C व D है|
यहाँ ∠CBN=60∘
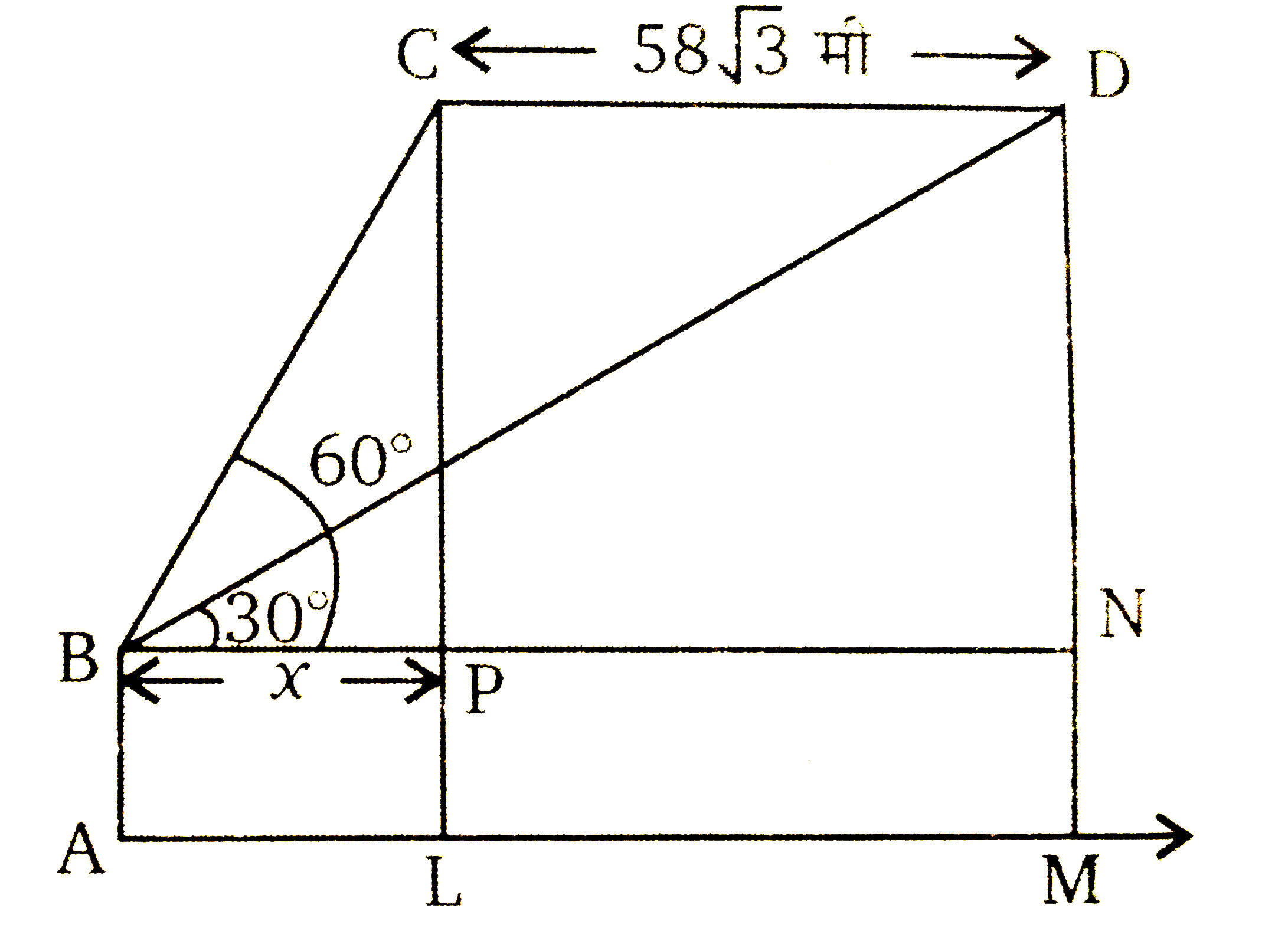
∠DBN=30∘
2 सेकण्ड में गुब्बारे द्वारा तय की गयी दुरी
=चाल × समय
CD=29√3×2=58√3 मीटर
CD=58√3 मीटर
यदि BP=x मीटर
BN=BP+PN=BP+CD
=x+58√3
DN=CP
अब ΔBND में,tan30∘=DNBN
⇒1√3=DNx+58√3
⇒DN=(x+58√3√3) मीटर
......(1)
आगे ΔBPC में
tan60∘=CPBP⇒√3=CPx
⇒CP=x√3
अब DN=CP ...(2)
⇒x+58√3√3=x√3
⇒nx=29√3
तब समीकरण (2) से,
CP=29√3×√3=87 मीटर
अतः सतह से गुब्बारे की ऊँचाई
=CL=CP+PL
[∵PL=AB=1.3]
=CP+AB=87+1.3
=88.3 मीटर
सारांश
इस अध्याय में, आपने निम्नलिखित तथ्यों का अध्ययन किया है:
(i) दृष्टि-रेखा प्रेक्षक की आँख से प्रेक्षक द्वारा देखी गई वस्तु के बिंदु को मिलाने वाली रेखा होती है।
(ii) क्षैतिज-रेखा प्रेक्षक की आँख से जमीन के समांतर वाली रेखा होती है।
(iii) देखी गई वस्तु का उन्नयन कोण दृष्टि-रेखा और क्षैतिज रेखा से बना कोण होता है यह क्षैतिज स्तर से ऊपर होता है अर्थात् वह स्थिति जब किसी वस्तु को देखने के लिए हमें अपने सिर को ऊपर उठाना होता है।
(iv) देखी गई वस्तु का अवनमन कोण दृष्टि-रेखा और क्षैतिज रेखा से बना कोण होता है जब दृष्टि-रेखा क्षैतिज स्तर से नीचे होती है अर्थात् वह स्थिति जब किसी वस्तु को देखने के लिए हमें अपने सिर को झुकाना पड़ता है।
(v) त्रिकोणमितीय अनुपातों की सहायता से किसी वस्तु की ऊँचाई, लंबाई या दो सुदूर वस्तुओं के बीच की दूरी ज्ञात की जा सकती है।