पृष्ठीय क्षेत्रफल और आयतन कक्षा 10 गणित
भूमिका
बच्चों! जैसा की आपने पिछले कक्षा 9 मे पृष्ठीय क्षेत्रफल व आयतन का अध्ययन किया हैं तथा भिन्न-भिन्न ठोसों के लिए इनके सूत्र भी देखें थे। अब आगे इस अध्याय मे हम भिन्न ठोसों का आपस में संयोजन देखेंगे तथा ठोसों को आपस मे जोड़कर उनके संगत पृष्ठीय क्षेत्रफल तथा आयतनों को आपस मे जोड़कर नए ठोस के लिए मान ज्ञात करेंगे।
साथ ही किसी ठोस का किसी अन्य ठोस मे अथवा अन्य ठोस के छोटे-छोटे भागों मे रूपांतरण, शंकु का छिन्नक आदि का अध्ययन इस अध्याय मे करेंगे।
आइए बच्चों पृष्ठीय क्षेत्रफल और आयतन को समझते है और करीब से...
आइए कक्षा 9 के पृष्ठीय क्षेत्रफल तथा आयतन के महत्वपूर्ण सूत्रो का पुनरावलोकन कर लेते है 


ठोसों के संयोजन का पृष्ठीय क्षेत्रफल
ऊपर हमने भिन्न-भिन्न ठोसों के पृष्ठीय क्षेत्रफल देखे, अब यहाँ दो ठोसों को लेकर उनके सम्पूर्ण पृष्ठीय क्षेत्रफल देखते है। यहाँ हमे कुछ बाते भी ध्यान देनी होती है, जैसे की संयोजन करने पर कौन सा भाग बाहर पृष्ठ मे है तथा कौन सा भाग छुपा हुआ है। इसके लिए आइए दैनिक जीवन से ही एक उदाहरण देख लेते है -
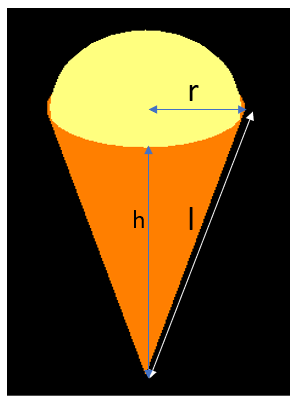
आपने ice-cream तो अवश्य रूप से खाई होगी उसका नीचे का भाग शंकु तथा ऊपर का भाग अर्धगोले का होता है। हमने शंकु व अर्धगोले के वक्र तथा सम्पूर्ण पृष्ठीय क्षेत्रफल का सूत्र देखा हुआ है, परन्तु यहाँ हमे समझना होगा की कौन से सूत्र का प्रयोग उचित होगा।
अगर यहाँ आप ध्यान दें तो देख सकते है की शंकु का ऊपरी तल तथा अर्धगोले का निचला तल संयोजन करने पर छिप गया है। जिसके कारण प्राप्त नए ठोस का सम्पूर्ण पृष्ठीय क्षेत्रफल मे वह भाग सम्मिलित नहीं होगा। अतः
ice-cream का सम्पूर्ण पृष्ठीय क्षेत्रफल = शंकु का वक्र पृष्ठीय क्षेत्रफल + अर्धगोले का वक्र पृष्ठीय क्षेत्रफल
ice-cream का सम्पूर्ण पृष्ठीय क्षेत्रफल =πrl+2πr2
जिन ठोसों का आपस मे संयोजन संभव हो उनका सम्पूर्ण पृष्ठीय क्षेत्रफल निकाल सकते है।
इसी प्रकार ठोसों का वियोजन भी किया जा सकता है
नीचे चित्र मे एक a कोर वाला एक घन है जिससे r त्रिज्या का एक अर्धगोला बाहर निकाल दिया गया। अब आप इसका सम्पूर्ण पृष्ठीय क्षेत्रफल निकालना चाहे तो आप देख सकते है की घन के जिस फलक से अर्धगोले को निकाला गया है, वहाँ अर्धगोले का तल जितना भाग पृष्ठीय क्षेत्रफल से कम हो रहा है परन्तु साथ ही वह अर्धगोले का वक्र चूँकि घन के अंदर है अतः अर्धगोले का वक्रपृष्ठ प्राप्त नए ठोस के सम्पूर्ण वक्रपृष्ठ मे जुड़ जाएगा।
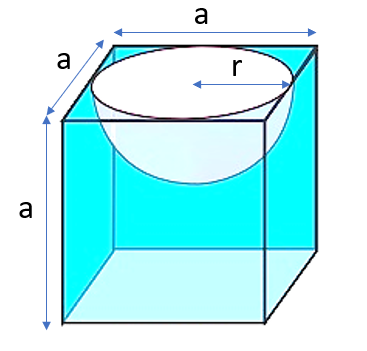
ऊपर दिए गए ठोस का सम्पूर्ण पृष्ठीय क्षेत्रफल
= घन का सम्पूर्ण पृष्ठीय क्षेत्रफल − अर्धगोले के तल का क्षेत्रफल + अर्धगोले का वक्र पृष्ठीय क्षेत्रफल
ऊपर दिए गए ठोस का सम्पूर्ण पृष्ठीय क्षेत्रफल =6a2−πr2+2πr2
आइए इससे संबंधित कुछ उदाहरण देख लेते है -
उदाहरण 1
दी गई आकृति में दर्शाया गया सजावट के लिए उपयोग होने वाला ब्लॉक दो ठोसों से मिलकर बना है। इनमे से एक घन है और दूसरा अर्ध गोला है। इस ब्लॉक का आधार 5 सेमी कोर या किनारे वाला एक घन है और उसके ऊपर लगे हुए अर्ध गोले का व्यास 4.2 सेमी है। इस ब्लॉक का सम्पूर्ण पृष्ठीय क्षेत्रफल ज्ञात कीजिए। ( π=227 लीजिए )
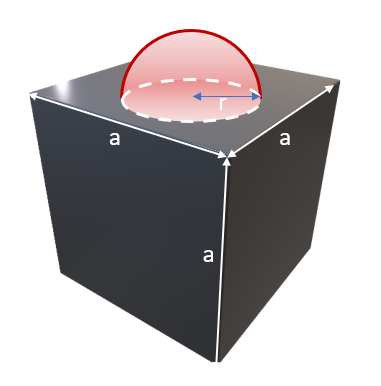
माना,
घन का किनारा =a=5cm
अर्धगोले का त्रिज्या =r=
घन का सम्पूर्ण पृष्ठीय क्षेत्रफल
=6×(a)2=6×(5)2cm2=150cm2
ब्लॉक का सम्पूर्ण पृष्ठीय क्षेत्रफल
= (घन का सम्पूर्ण पृष्ठीय क्षेत्रफल) − (अर्धगोला के आधार का क्षेत्रफल) + (अर्धगोले के वक्रपृष्ठ का क्षेत्रफल)
=(150−πr2+2πr2)cm2
=(150+πr2)cm2
=(150+227×2.1×2.1)cm2
=(150+69350)cm2
=(150+13.86)cm2=163.86cm2
उदाहरण 2
एक लकड़ी के गोले जिसकी त्रिज्या 6√3 सेमी है, से सबसे बड़ा घन बनाया गया है। घन का सम्पूर्ण पृष्ठ ज्ञात कीजिए।
यहाँ पर घन का विकर्ण, गोले का व्यास होगा।
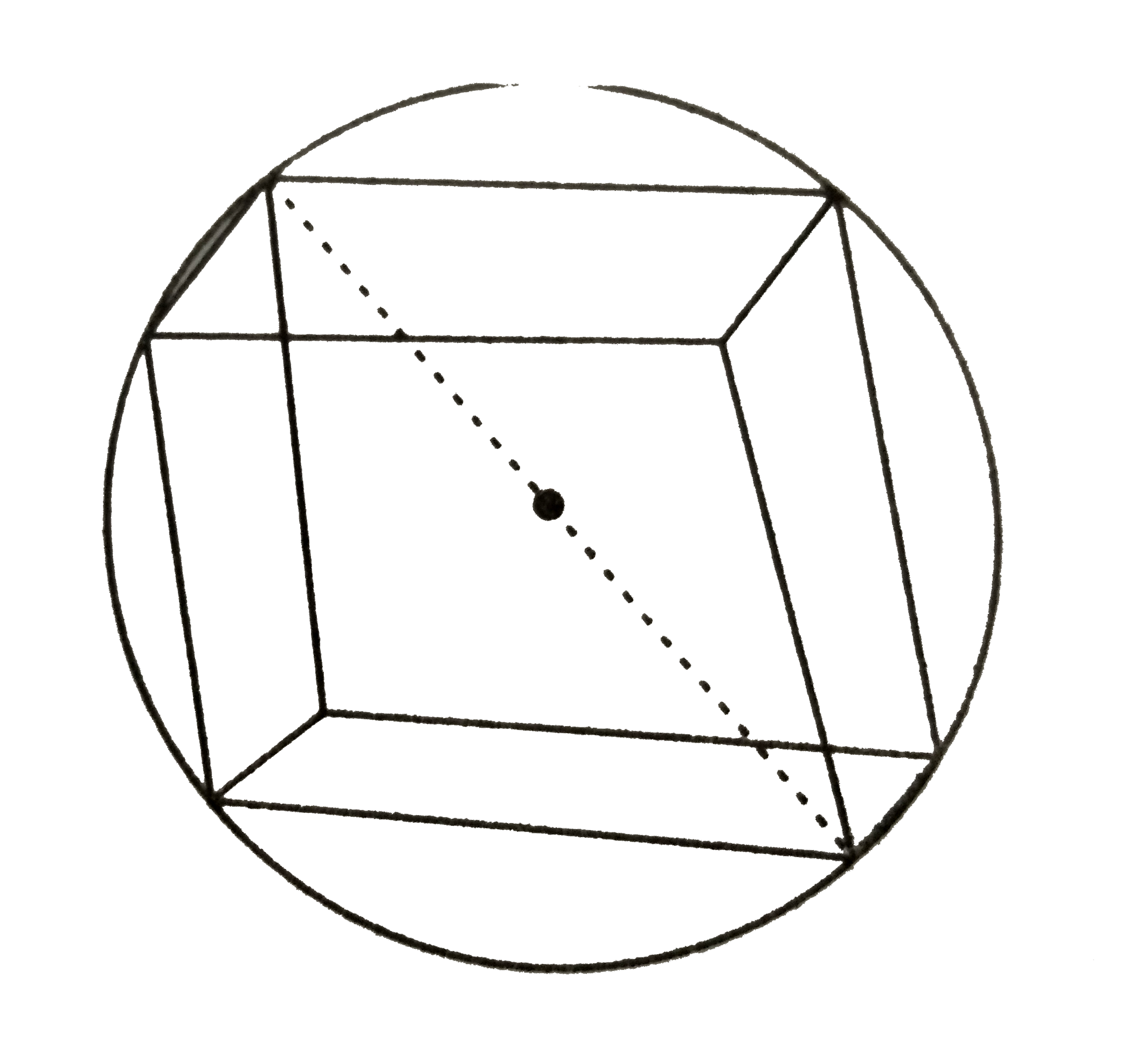
गोले का व्यास = घन का विकर्ण
⇒2×त्रिज्या =√3a
⇒2×6√3=√3a
⇒12√3=√3a
⇒a=12 सेमी
∴ घन का सम्पूर्ण पृष्ठ
=6a2=6(122) सेमी 2=864 सेमी 2
उदाहरण 3
एक धातु के घन जिसकी कोर 2.5 सेमी है, को पिघलाकर एक आयताकार ठोस बनाया जाता है। जिसका आधार 1.25 सेमी ×0.25 सेमी है। यह मानते हूए कि पिघलाने में कोई हानि नहीं है, ठोस की ऊंचाई ज्ञात कीजिए। सम्पूर्ण पृष्ट में वृद्धि भी ज्ञात कीजिए।
माना,
घन का एक कोर =a=2.5 सेमी
घन का आयतन =a3=2.53 सेमी 3
आयताकार ठोस के आधार की लम्बाई =1.25 सेमी
आयताकार ठोस के आधार की चौड़ाई =0.25 सेमी
यहाँ, घन का आयतन = आयताकार ठोस का आयतन
⇒2.53= लम्बाई×चौड़ाई×ऊँचाई
आयताकार ठोस की ऊंचाई =
=2.531.25×0.25
=2.5×2.5×2.51.25×0.25
=50 सेमी
सम्पूर्ण पृष्ठ में वृद्धि = आयताकार ठोस का सम्पूर्ण पृष्ठ − घन का सम्पूर्ण पृष्ठ
घन का सम्पूर्ण पृष्ठ =6×a2=6×(2.5)2=37.5 सेमी 2
ठोस का सम्पूर्ण पृष्ठ =2( लम्बाई ×चौड़ाई+ चौड़ाई × ऊंचाई + ऊंचाई ×लम्बाई )
=2(1.25×0.25+0.25×50+50×1.25)
=2(0.312+12.5+62.5)
=2(75.31)
=150.62
∴ सम्पूर्ण पृष्ठ में वृद्धि
=150.62−37.50=113.12 सेमी 2
ठोसों के संयोजन का आयतन
बच्चों जैसे की आपने ऊपर ठोसों के संयोजन का वक्र पृष्ठीय क्षेत्रफल देखा उसी प्रकार आयतन को भी समझ सकते है। इसके लिए पुनः ice-cream का उदाहरण देख लेते है

ठोसों के संयोजन मे आयतन निकालने के लिए, पृष्ठीय क्षेत्रफल का संयोजन के समान कुछ भागों के छिप जाने से कोई अंतर नहीं आता है इसमे भिन्न ठोसों के आयतनों को जोड़ा जाता है।
अतः
ice-cream का आयतन = शंकु का आयतन + अर्धगोले का आयतन
ice-cream का आयतन =13πr2h+23πr3
जिन ठोसों का आपस मे संयोजन संभव हो उनका आयतन ज्ञात किया जा सकता है।
इसी प्रकार ठोसों का वियोजन भी किया जा सकता है, पुनः पूर्व उदाहरण देखते है -

ऊपर दिए गए ठोस का आयतन
= घन का आयतन − अर्धगोले का आयतन
ऊपर दिए गए ठोस का आयतन =a3−23πr3
यहाँ आप देख सकते है कि अर्धगोले का तल एक वृत्त है, जिसका व्यास घन के कोर (a) के बराबर होगा तथा वृत्त कि त्रिज्या r है।
अतः 2r=a⇒r=a2
ठोस का आयतन =a3−23πr3
=a3−23π(a2)3
=a3(1−23×8π)
=a3(1−224π)
=a3(1−112π)
आइए इससे संबंधित कुछ उदाहरण देख लेते है -
उदाहरण 4
कोई तंबू एक बेलन के आकार का है जिस पर एक शंकु अध्यारोपित है यदि बेलनाकार भाग की ऊंचाई और व्यास क्रमश: 2.1m और 4m है तथा शंकु की तिर्यक ऊंचाई 2.8m है, तो इस तंबू को बनाने में प्रयुक्त कैनवास (Canvas) का क्षेत्रफल ज्ञात करे। साथ ही, 500 रुपए प्रति वर्ग मीटर की दर से प्रयुक्त कैनवास का लागत ज्ञात करे।
( ध्यान दीजिये कि तंबू के आधार को कैनवास से नहीं ढका जाता है )। (टेंट के आधार पर कैनवास नहीं बिछाना है)।
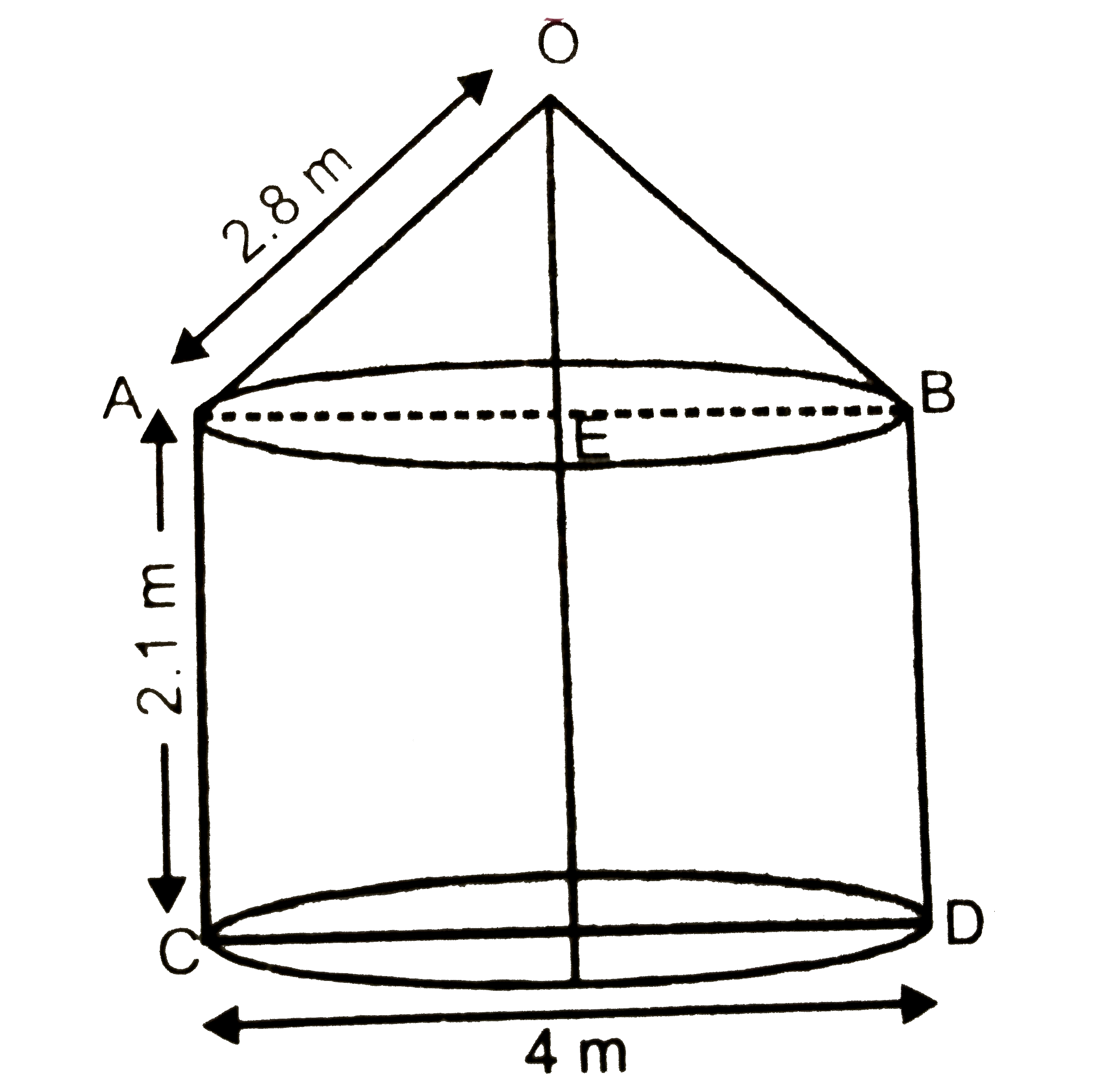
बेलनाकार तंबू की ऊंचाई h=2.1m
बेलनाकार तंबू का व्यास =4m
∴ तंबू की त्रिज्या r=42=2m
शंकु की तिर्यक ऊंचाई l=2.8m
कैनवास का कुल क्षेत्रफल =?
कैनवास की लागत 500m2 की दर से =?
तंबू के बेलनाकार भाग के वक्रपृष्ठ का क्षेत्रफल =2πrh
=2×227×2×2.1m2=26.4m2
शंकुकार सिरे के वक्रपृष्ठ का क्षेत्रफल =πrl
=227×2×2.8=17.6m2
तंबू में प्रयुक्त कैनवास का क्षेत्रफल
= बेलनाकार भाग के वक्रपृष्ठ का क्षेत्रफल + शंकु भाग के वक्र पृष्ठ का क्षेत्रफल
=26.4+17.6=44m2
500 रुo प्रति वर्ग मीटर के कैनवास का लागत
=44×500=22000 रुo
उदाहरण 5
संलग्न चित्र में एक ठोस एक बेलन के रूप में है जिसके एक ओर एक शंकु और दूसरे सिरे पर अर्धगोला बना है। दिया है, उभयनिष्ट त्रिज्या =3.5 सेमी, बेलन की ऊंचाई =6.5 सेमी और कुल ऊंचाई =12.8 सेमी है। ठोस का आयतन लगभग सेमी 3 में ज्ञात कीजिए।

दिया है,
अर्धगोले की त्रिज्या 3.5 सेमी =72 सेमी
बेलन की ऊंचाई =6.5 सेमी =132 सेमी
कुल ऊंचाई =12.8 सेमी
∴ शंकु की ऊंचाई =(12.8−3.5−6.5) सेमी
=2.8 सेमी =145सेमी
बेलन की त्रिज्या =72सेमी = शंकु की त्रिज्या
अर्धगोले का आयतन =23πr3=23π(72)3 सेमी 3
बेलन का आयतन =πr2h=π(72)2(132) सेमी 3
शंकु की ऊंचाई =13πr2h=13π(72)2(145) सेमी 3
∴ दिए ठोस का आयतन =
अर्धगोले का आयतन + बेलन का आयतन + शंकु की ऊंचाई
=23π×(72)3+π×(72)2×132+13π×(72)2×145 सेमी 3
=π(72)2(23×72+132+13×145) सेमी 3
=227×494(73+132+1415) सेमी 3
=772×70+195+2830 सेमी 3
=77×29360 सेमी 3
=376 सेमी 3 लगभग
उदाहरण 6
6 सेमी त्रिज्या और 8 सेमी ऊंचाई का एक शंक्वाकार बर्तन पानी से पूर्णतया भरा है। एक गोला पानी में डुबोया जाता है तथा इसका आकार इस प्रकार है कि डूबते समय यह बर्तन की दीवारों को स्पर्श करता है। पानी का कितना भाग बाहर गिरेगा?
दिया हैं,
शंक्वाकार बर्तन की त्रिज्या =6 सेमी
शंक्वाकार बर्तन की ऊंचाई =8 सेमी
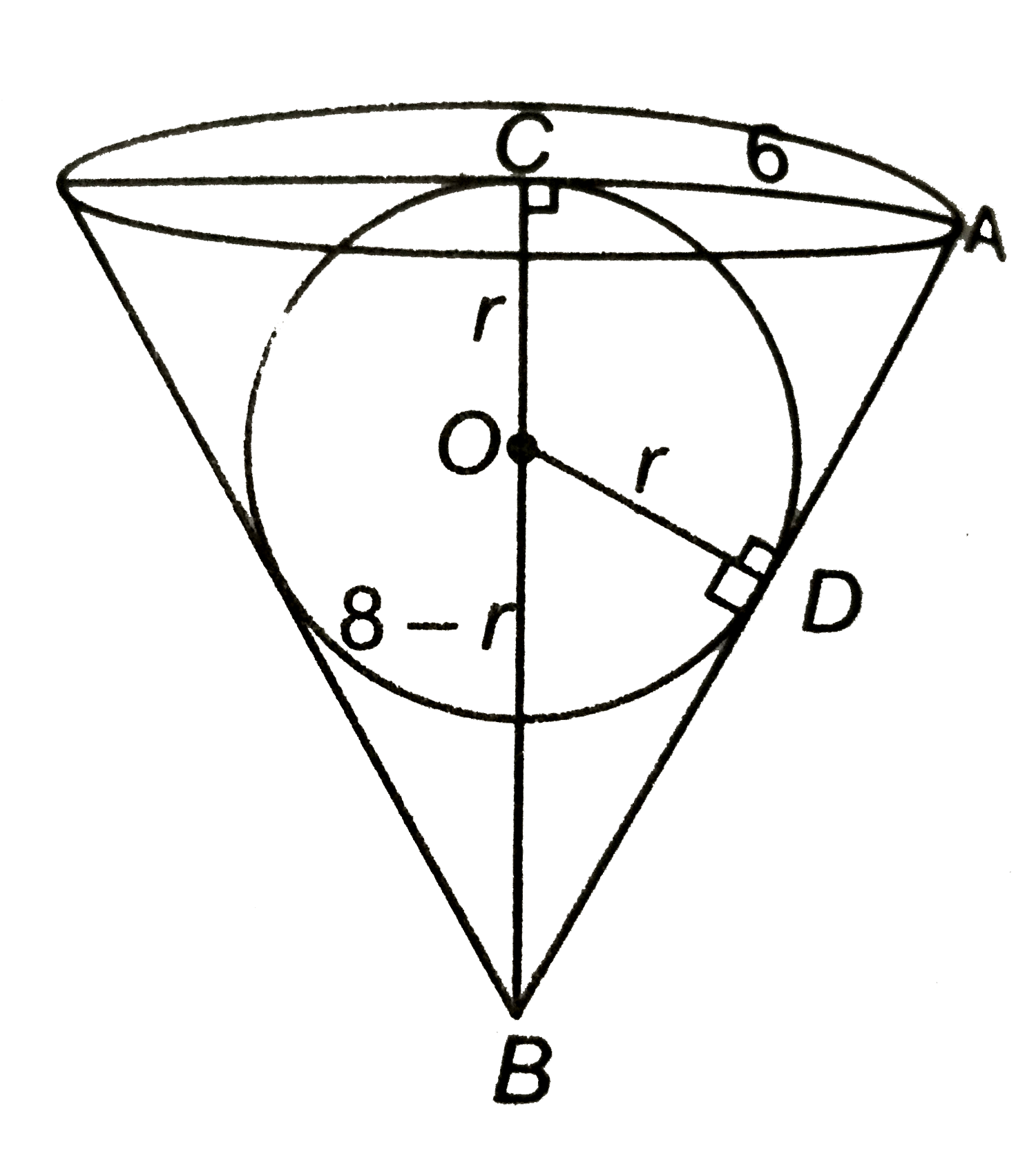
पाइथागोरस प्रमेय से, (ΔABC में)
AB2=AC2+BC2
=62+82
=36+64=100
∴AB=10 सेमी
∵ AB गोले की स्पर्श रेखा है
∴OD⊥AB
∴ΔACB~ΔODB
⇒ACOD=CBDB=ABOB
⇒6r=108−r
⇒48−6r=10r
⇒16r=48⇒r=3 सेमी
अब बर्तन में पानी का आयतन=13π(6)2×8
गोले के कारण पानी बाहर गिरता है
∴ बाहर गिरे पानी का आयतन = गोले का आयतन =43π(3)3
∴ बाहर गिरे पानी का भाग
=43π(3)313π(6)2×8=38
अतः पानी का 38 भाग बाहर गिरेगा।
उदाहरण 7
दो लम्ब वृतीय बेलनों की त्रिज्याओं में 2:3 तथा ऊंचाईयों में 5:4 का अनुपात है। इनके वक्र पृष्ठों का अनुपात तथा इनके आयतनों का अनुपात भी ज्ञात कीजिए।
माना, दो बेलनों की त्रिज्याएँ क्रमश: 2r और 3r तथा इसकी ऊँचाइयाँ क्रमश: 5h और 4h है।
वक्र पृष्ठों का अनुपात =
=2π×2r×5h2π×3r×4h
अर्थात S1S2=56 या S1:S2=5:6
आयतनों का अनुपात =
=π×(2r)2×5hπ×(3r)2×4h
अर्थात V1V2=59 या V1:V2=5:9
एक ठोस का एक आकार से दूसरे आकार मे रूपांतरण
बच्चों! आपने देखा होगा धातु को हम विभिन्न रूपों मे ढाल सकते है, कोई घनाकार ठोस है उसे बेलनाकार बनाने के लिए पिघलाकर ढाला जा सकता है परन्तु आयतन मे कोई परिवर्तन नहीं आएगा। इसे समझने के लिए समान आयतन का एक शंकु और एक बेलनाकार बर्तन लें तथा शंकु मे पानी लेकर बेलनाकार बर्तन मे डाले। क्या पानी मे कोई कमी या वृद्धि हुई? पानी मे कोई कमी या वृद्धि नहीं आएगी, चूँकि बर्तनों के आयतन आपस मे समान है।
इस प्रकार यदि दो ठोसों के आयतन तुलनीय है तब तुलना करके उनकी अन्य विमायें (ऊँचाई, चौड़ाई, त्रिज्या आदि) भी ज्ञात की जा सकती है, यदि कुछ विमायें ज्ञात हो।
आइए इसे कुछ उदाहरणों से समझने का प्रयास करते है -
उदाहरण 8
एक खोखले गोले का अंत: एवं बाह्य त्रिज्याएँ क्रमश: 3cm और 5cm है गोले को पिघलाकर 223cm ऊँचे एक ठोस बेलन के रूप में बनाया जाता है। बेलन का व्यास तथा सम्पूर्ण पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
गोले की बाह्य त्रिज्या R=5cm
गोले की अंत: त्रिज्या r=3cm
खोखले गोले में धातु का आयतन
=43π(R3−r3)
=43π×{(5)3−(3)3}cm3
=(392π3)cm3
माना, ठोस बेलन की त्रिज्या =r' cm
दिया है, ठोस बेलन की ऊँचाई =223=83cm
∴ ठोस बेलन का आयतन =πr'2h
=(πr'2×83)cm3
=(8πr'23)cm3
अब, बेलन का आयतन = खोखले गोले का आयतन
∴8πr'23=392π3
⇒r'2=49
⇒r'=7
अत: निर्मित बेलन का व्यास
=(2×7)cm=14cm
बेलन का वक्र पृष्ठीय क्षेत्रफल =2πr'h
=(2×227×7×83)cm2
=3523cm2
=11713cm2
उदाहरण 9
10.5 सेमी त्रिज्या के ठोस धातु के गोले को पिघलाकर 3.5 सेमी त्रिज्या और 3 सेमी ऊंचाई के शंकु बनाये गए है। इस प्रकार बने शंकुओं की संख्या ज्ञात कीजिए।
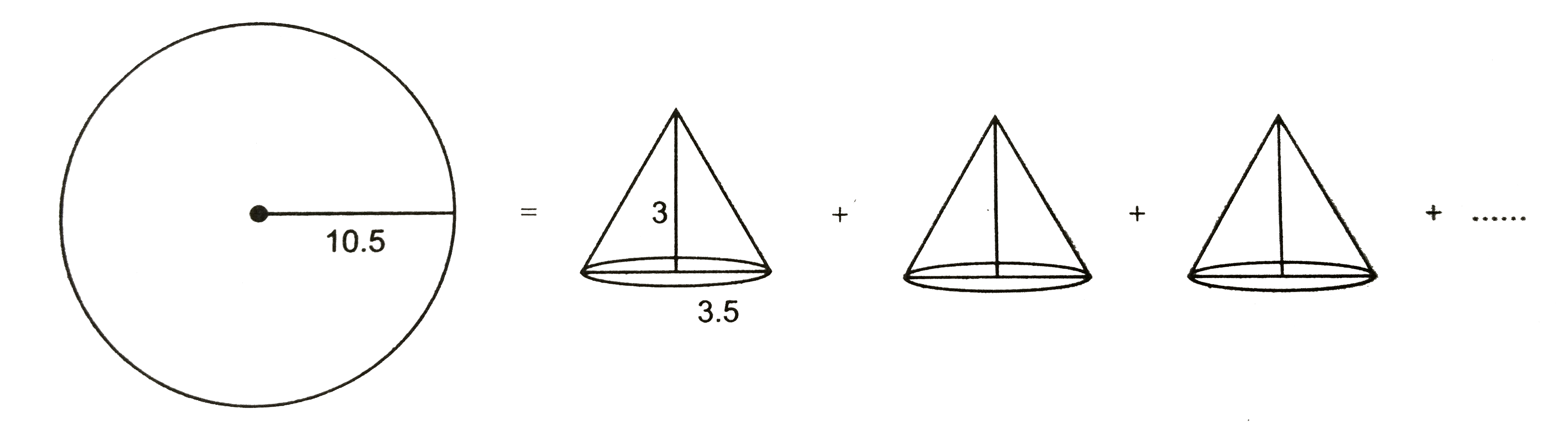
माना, गोले से n शंकु बनाये जाते है
∴n शंकुओं के आयतनों का योग = गोले का आयतन
n[13π(3.5)2×3]=43π(10.5)3
⇒n=4×10.5×10.5×10.53.5×3.5×3=126
अतः बनाये गए शंकुओं की संख्या =126
उदाहरण 10
24 सेमी ऊंचे और आधार त्रिज्या 7 सेमी वाले बेलन में से समान ऊंचाई और समान आधार का शंकु काटकर पृथक कर दिया गया है। शेष ठोस का सम्पूर्ण पृष्ठ और आयतन ज्ञात कीजिए।

यहाँ, त्रिज्या r=7 सेमी
ऊंचाई h=24 सेमी
शेष ठोस आकृति का आयतन = बेलन का आयतन − शंकु का आयतन
=πr2h−13πr2h
=23πr2h
=23×227×7×7×24
=2464 घन सेमी
अब l2=h2+r2=242+72
⇒l=25 सेमी
∴ शेष आकृति का सम्पूर्ण पृष्ठ = बेलन का वक्र पृष्ठ + शंकु का वक्र पृष्ठ + शिखर का क्षेत्रफल
=2πrh+πrl+πr2
=πr(2h+l+r)
=227×7(2×24+25+7)
=22×80
=1760 वर्ग सेमी
उदाहरण 11
22 मी ×20 मी की आयताकार छत से वर्षा का पानी एक बेलनाकार बर्तन में ईकठ्ठा किया गया है। इस बर्तन के आधार का व्यास 2 मीटर और ऊंचाई 3.5 मीटर है। ज्ञात कीजिए कि कितने सेमी वर्षा हुई थी?
माना, h मीटर वर्षा हुई थी
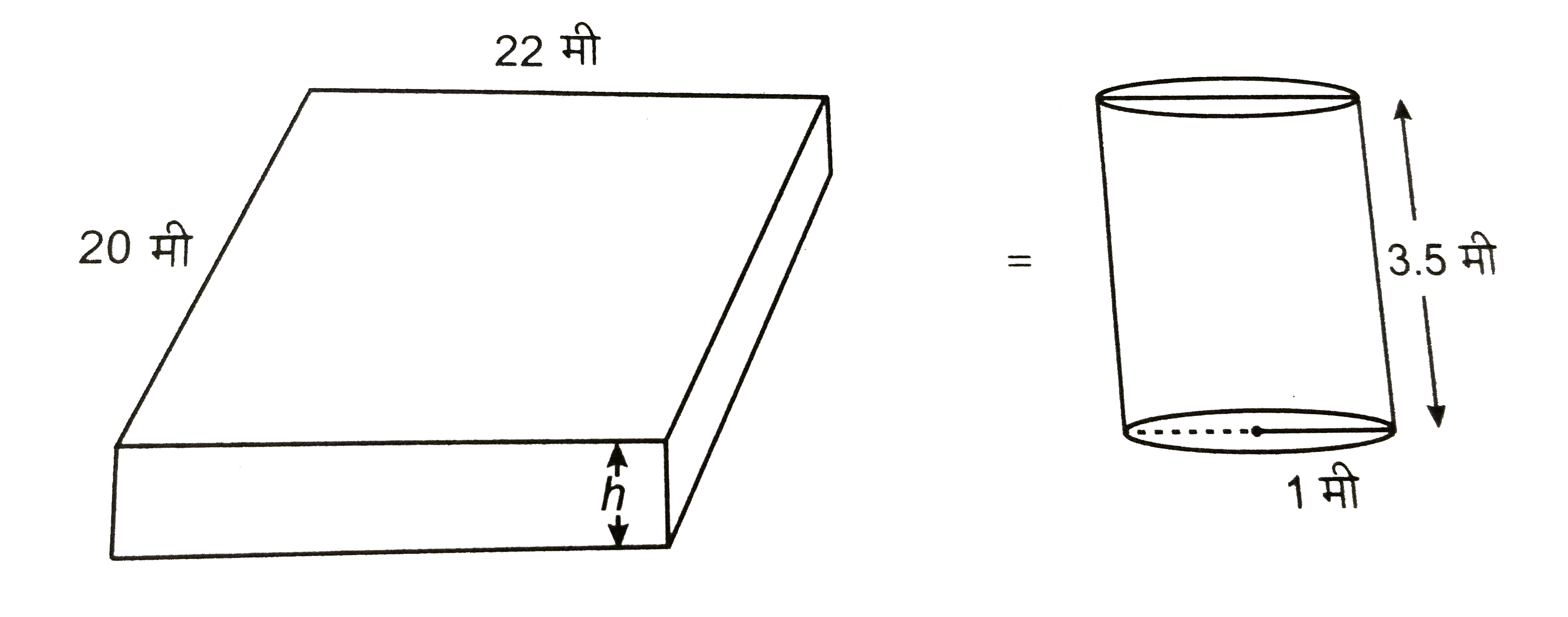
∴ छत पर वर्षा के पानी का आयतन =22×20×h मी 3
बेलनाकार बर्तन की त्रिज्या r=22=1 मी
ऊंचाई H=3.5 मीटर
∴ बर्तन का आयतन =πr2H
=227×1×3.5=11 घन मीटर
प्रश्नानुसार,
छत मे एकत्रित पानी का आयतन = बेलनाकार बर्तन मे एकत्रित पानी का आयतन
⇒22×20×h=11
⇒h=1122×20 मी
⇒h=11×10022×20 सेमी
⇒h=2.5 सेमी
शंकु का छिन्नक
यदि कोई शंकु अपने आधार पर खड़ा है तब उस शंकु को उसके आधार तल के समांतर किसी समतल से काट दिया जाए तो प्राप्त निचला भाग उस शंकु का छिन्नक कहलाता है।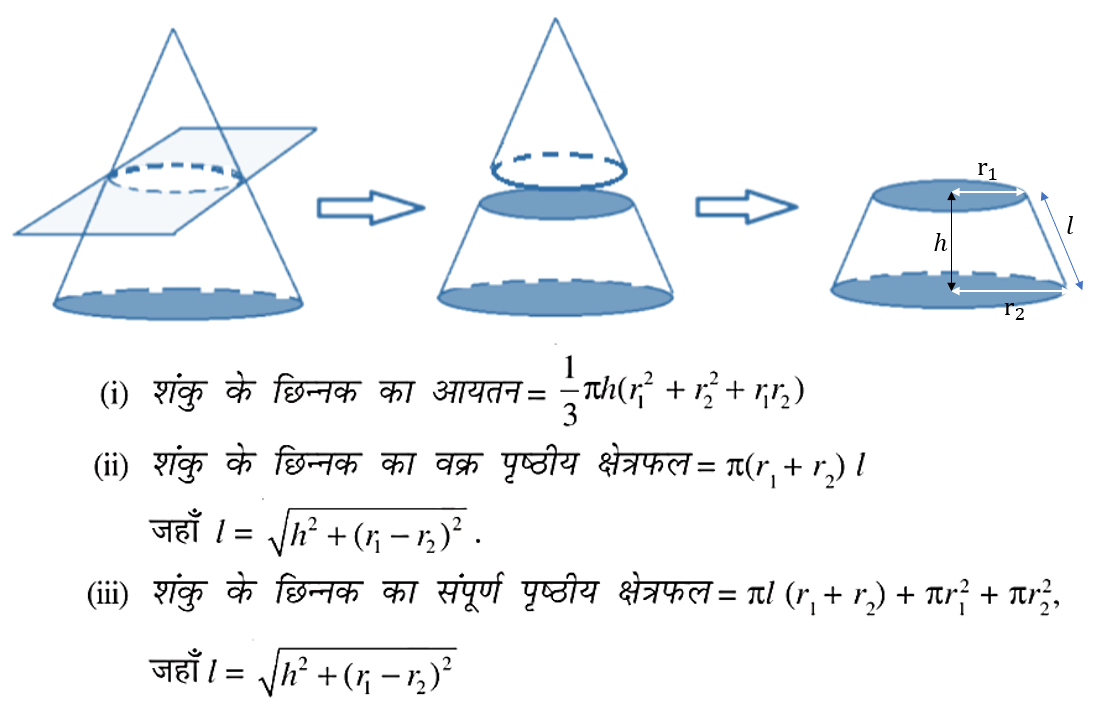
यहाँ
h= छिन्नक की ऊर्ध्वाधर ऊँचाई
l= छिन्नक की तिर्यक ऊँचाई तथा
r1 व r2 छिन्नक के दोनों वृत्तीय सिरों की त्रिज्याएँ है।
उदाहरण 12
एक बाल्टी एक छिन्नक के आकर का है जिसकी धारिता 12308.8cm3 पानी रखने की है बाल्टी के सिरे और पेंदी की त्रिज्याएँ क्रमश: 20cm और 12cm है, तो बाल्टी की ऊँचाई और इसके बनने में लगे धातु के चादर का क्षेत्रफल ज्ञात करे।
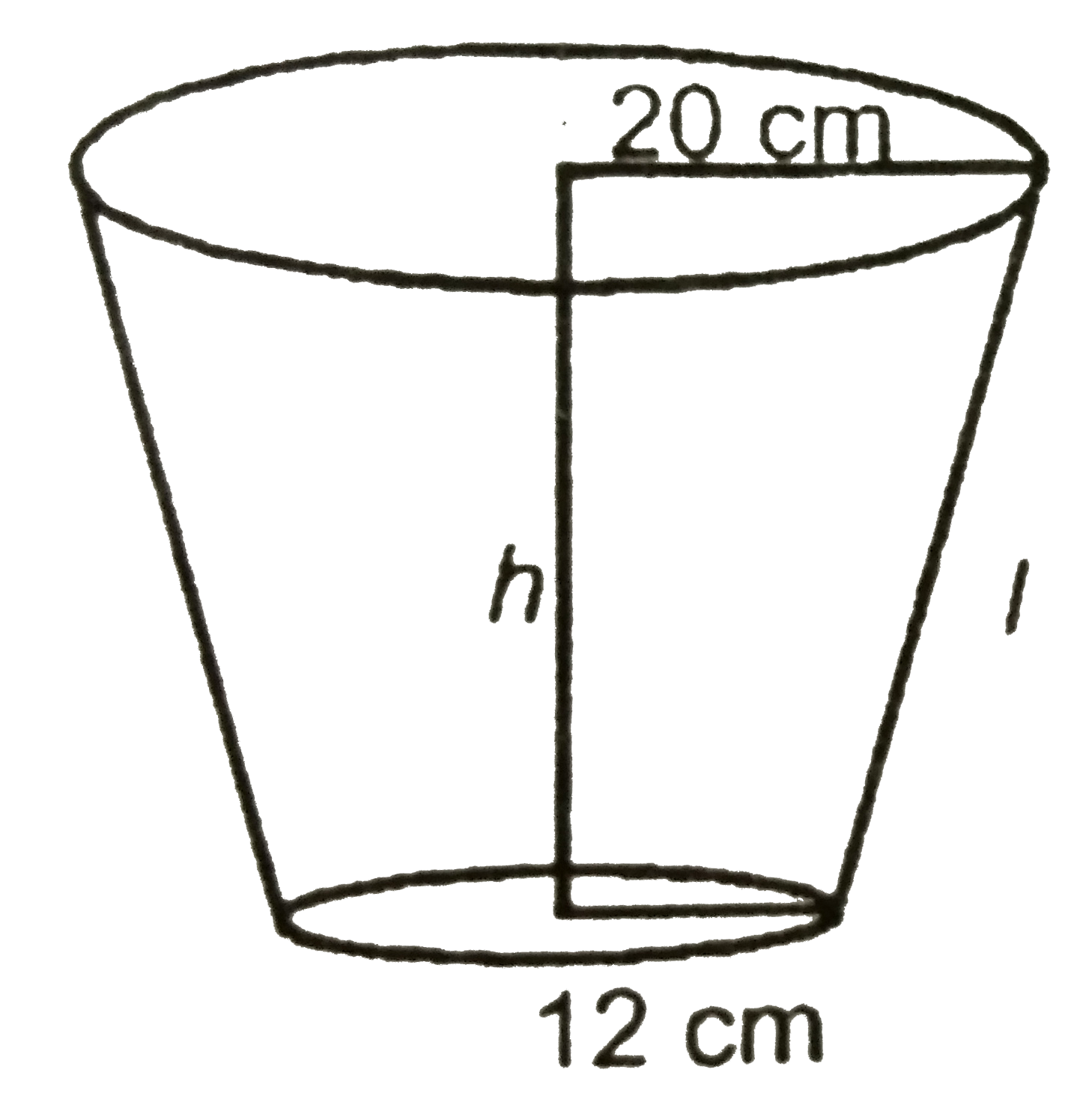
छिन्नक के सिरे की त्रिज्या R=20cm
छिन्नक के पेंदी की त्रिज्या r=12cm
छिन्नक का आयतन (धारिता) =12308.8cm3
माना, बाल्टी की ऊँचाई =hcm
∴13πh(R2+r2+rR)=12308.8
⇒13×227×h[(20)2+(12)2+20×12]=12308.8
⇒784h=12308.8×3227
⇒h=⎛⎝12308.8×3227×784⎞⎠=15cm
यदि बाल्टी की तिर्यक ऊँचाई l है तब
l=√h2+(R−r)2
=√(15)2+(20−12)2cm
=√(15)2+(8)2cm
=√225+64cm=√289cm=17cm
अब, प्रयुक्त धातु के चादर का क्षेत्रफल = वक्र पृष्ट का क्षेत्रफल + पेंदी का क्षेत्रफल
=πl(R+r)+πr2 वर्ग इकाई
=227×17×(20+12)+227×12×12cm2
=[227×(17×32)+227×144]cm2
=[227×(544+144)]cm2
=(227×688)cm2
=2162.28cm2
उदाहरण 13
एक बाल्टी के ऊपरी सिरे का व्यास 32 सेमी और नीचे के सिरे का व्यास 20 सेमी है। बाल्टी की धारिता लीटर में ज्ञात कीजिए। यदि यह 21 सेमी गहरी है, इसमे प्रयुक्त टीन की शीट का मूल्य भी ज्ञात कीजिए। यदि इसकी दर रु 1.50 प्रति वर्ग डेमी है।
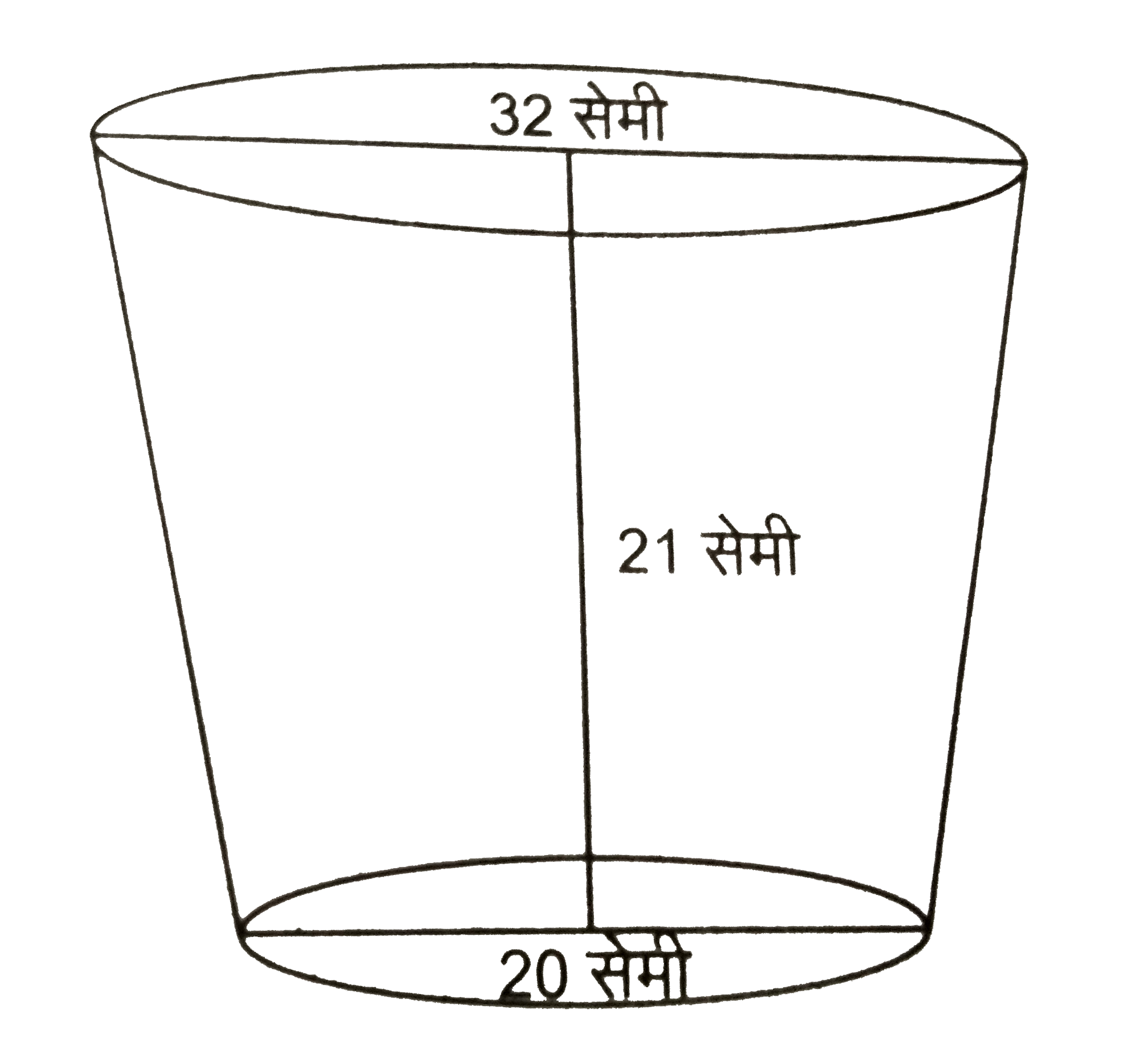
यहाँ, ऊपरी सिरे का व्यास =32cm
∴ त्रिज्या R=16 सेमी
निचली सिरे का व्यास =20 सेमी
∴ त्रिज्या r=10 सेमी
बाल्टी की ऊंचाई h=21 सेमी
बाल्टी का आयतन =πh3(R2+r2+Rr)
=227×13×21(162+102+16×10)
=22(256+100+160)
=22×516=11352 सेमी 3
=113521000 ली =11.352 ली
बाल्टी की तिर्यक ऊंचाई l के लिए
l2=h2+(R−r)2
=212+(16−10)2
=441+36=477
l=√477=21.84 सेमी
अब बाल्टी का सम्पूर्ण पृष्ठ =πl(R+r)+πr2
=227×21.84×(16+10)+227×102
=227×(21.84×26+100)
=227×667.84
=2098.92 सेमी 2=20.99 डेमी 2
रु 1.50 प्रति वर्ग डेमी को दर से शीट का मूल्य
=20.99×1.50 =31.485 रु
उदाहरण 14
एक शंकु के छिन्नक के सिरों की त्रिज्याएँ 3 सेमी और 4 सेमी तथा इसकी ऊंचाई 5 सेमी है। इसका आयतन ज्ञात कीजिए।
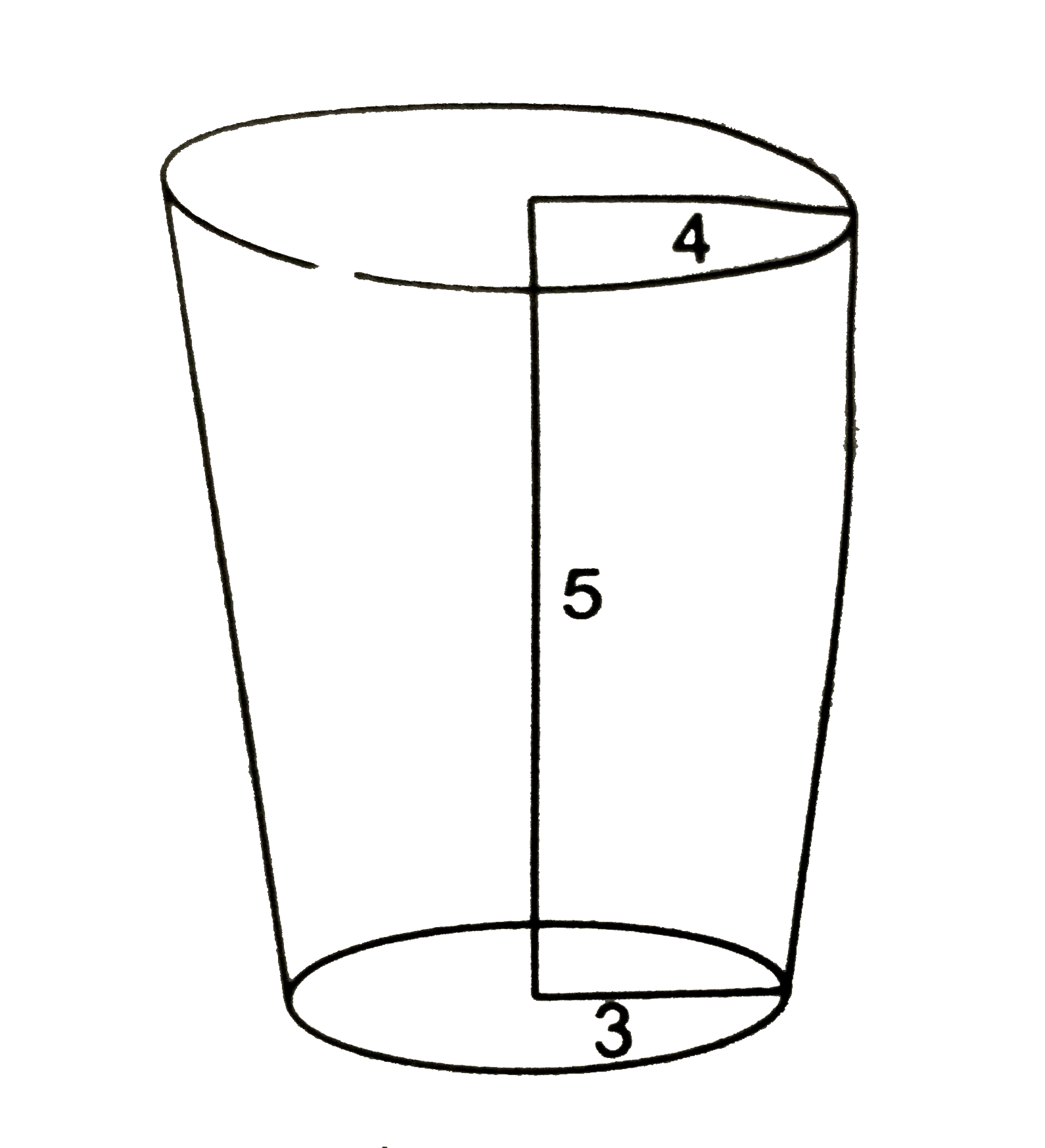
यहाँ r=3 सेमी, R=4 सेमी और h=5 सेमी
शंकु के छिन्नक का आयतन
=13πh(R2+r2+Rr)
=13×227×5(42+32+4×3)
=13×1107(16+9+12)
=11021×37=407021 सेमी 3
उदाहरण 15
एक लम्ब वृत्तीय शंकु की ऊंचाई को आधार के समान्तर दो समतलों द्वारा समत्रिभाजीत किया गया है दिखाइए कि तीनों भागों के आयतनों का अनुपात शीर्ष से 1:7:19 है।
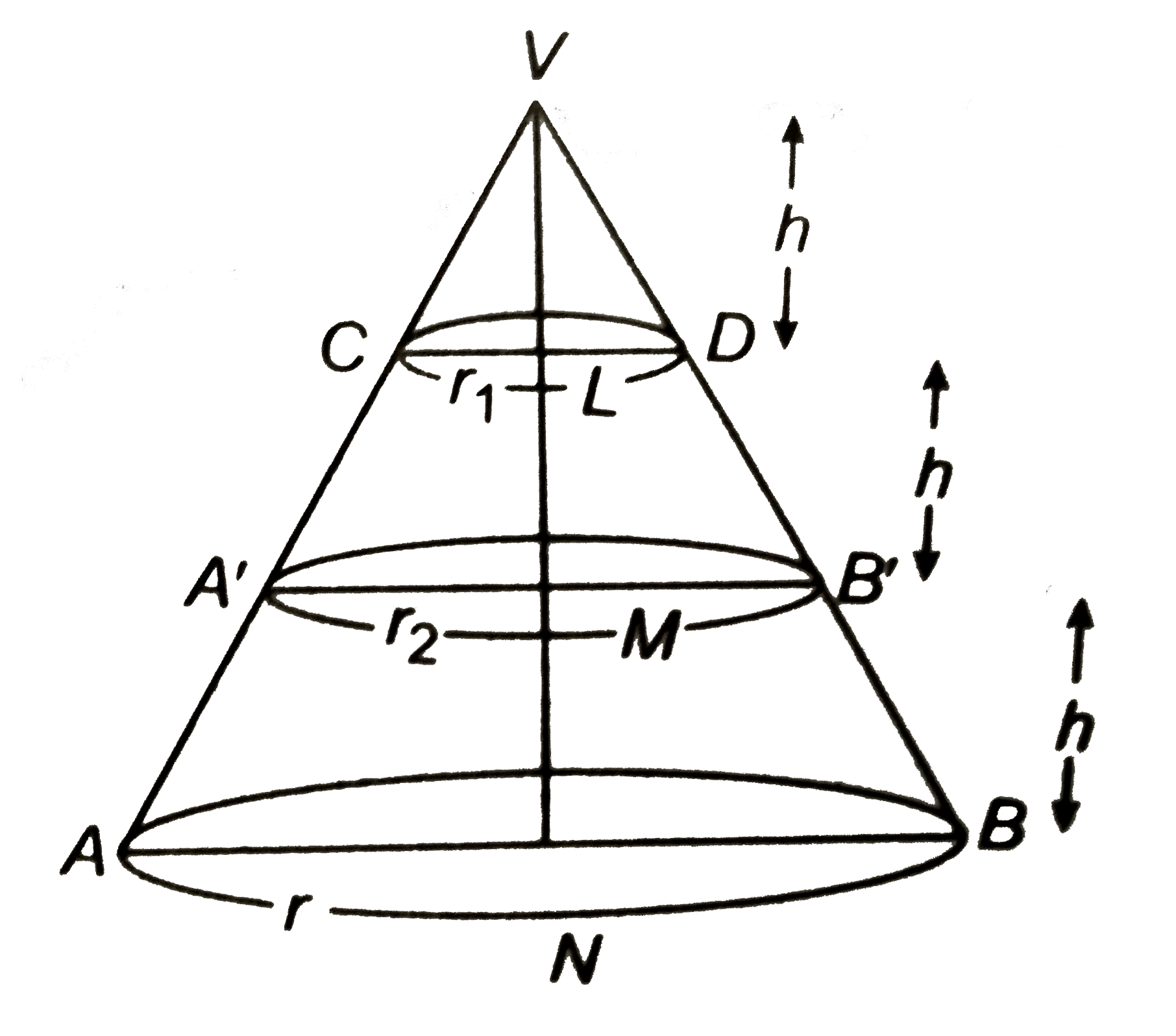
∴ ऊंचाई को समत्रिभाजित किया गया है, अतः आधारभूत प्रमेय से शंकुओं VCD,VA'B' और VAB के आधार की त्रिज्याओ में अनुपात 1:2:3 होगा।
(∵CL:A'M:AN=r1:r2:r=1:2:3)
माना शंकु का आयतन VCD=V=13πr21h
∴ शंकु VA'B' का आयतन =13πr22(2h)
=13π(2r1)2(2h)
=8×13πr21h=8V
और शंकु VAB का आयतन =13πr2(3h)
=13π(3r1)2(3h)
=27×13πr21h=27V
∴3 भागों के आयतनों का अनुपात
=(VCD) का आयतन : (CDB'A') का आयतन : (A'B'BA) का आयतन
=V:(8V−V):(27V−8V)=1:7:19
महत्वपूर्ण सूत्र



