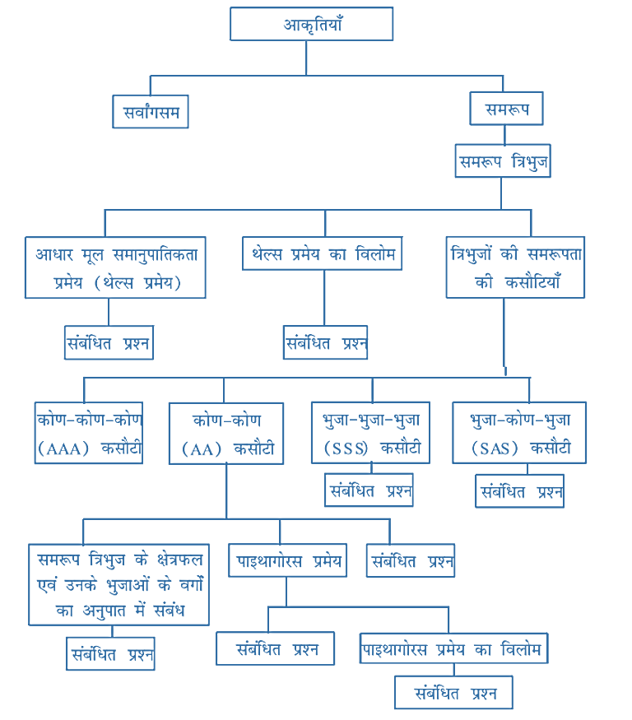
त्रिभुज कक्षा 10 गणित
भूमिका
बच्चों आपने पहले विभिन्न ज्यामितीय आकृतियों के बारे मे पढ़ा होगा , जिनमे से एक त्रिभुज (Triangle) होता है।
"त्रिभुज शब्द दो शब्दों =त्रि (तीन) + भुज (भुजा)" से मिलकर बना होता है , अर्थात त्रिभुज से तात्पर्य तीन भुजाओ के समूह से है ।
किसी तीन प्रतिच्छेदी रेखाओ द्वारा बनी बंद आकृति को त्रिभुज कहते हैं, यहाँ 3 भुजाये होती है , प्रत्येक भुजा अन्य दो भुजाओ को मिलती है जिससे 3 शीर्ष प्राप्त होते है तथा इन शीर्षों मे 3 आंतरिक कोण प्राप्त होते है , जिनका कुल योग 180∘ होता हैं ।
अतः हम कह सकते है , त्रिभुज (Triangle), तीन शीर्षों और तीन भुजाओं (side) वाला एक बहुभुज (Polygon) होता है, यह ज्यामिति की मूल आकृतियों में से एक है।
शीर्षों A, B, और C वाले त्रिभुज को ΔABC लिखा जाता है।
अब यूक्लिडियन ज्यामिति के अनुसार देखें तो कोई भी तीन असंरेखीय बिन्दु ( उन बिन्दुओ का समूह जो एक रेखा पर स्थित न हो ) , एक अद्वितीय त्रिभुज ( केवल एक ही प्रकार का त्रिभुज ) का निर्धारण करते हैं और साथ ही, एक अद्वितीय तल (यानी एक द्वि-विमीय यूक्लिडियन समतल) का भी, इस प्रकार इस अध्याय मे हम त्रिभुज के बारे मे विस्तार से अध्ययन करेंगे।
आइए बच्चों त्रिभुज को समझते है और करीब से...
बच्चों आपने पहले विभिन्न ज्यामितीय आकृतियों के बारे मे पढ़ा होगा , जिनमे से एक त्रिभुज (Triangle) होता है। आइये जो हमने पढ़ा था उसे पुनः याद कर लेते है -
हम जानते हैं कि
12× आधार ×ऊँचाई
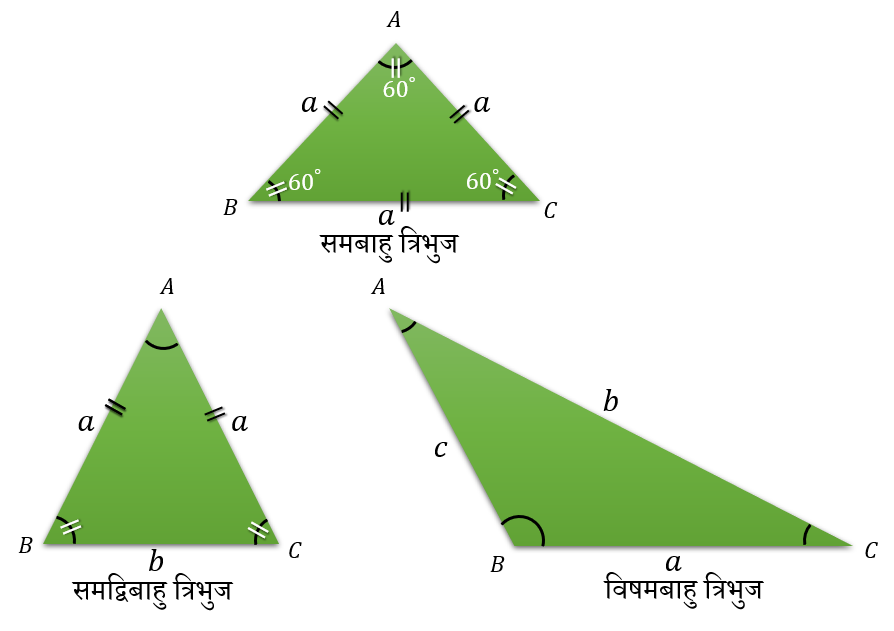
भुजाओं के आधार पर त्रिभुज 3 प्रकार के होते हैं।
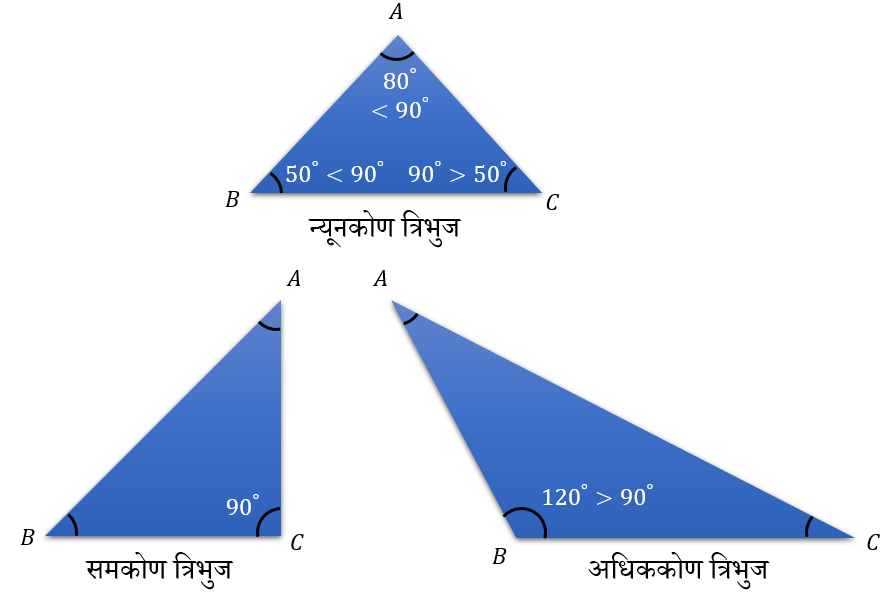
कोण के आधार पर भी त्रिभुज 3 प्रकार के होते हैं।
भुजाओं के आधार पर त्रिभुज के प्रकार:
त्रिभुजों की परिभाषा और सूत्र नीचे दिए गए हैं
परिमाप=3× भुजा
क्षेत्रफल =√34a2
परिमाप=2A+B
(सूत्र में त्रिभुज की बराबर भुजाओं की माप A और B तीसरी भुजा है।)
क्षेत्रफल = 12×आधार× ऊँचाई
परिमाप =AB+BC+AC
क्षेत्रफल =12× आधार× ऊँचाई
• यदि त्रिभुज की तीनों भुजाएँ दी गई है और उपरोक्त किसी सूत्र की मदद से क्षेत्रफल निकालना संभव नहीं लग रहा, तो हीरोन के सूत्र से किसी भी प्रकार के त्रिभुज का क्षेत्रफल जात किया जा सकता है।
त्रिभुजों का क्षेत्रफल =√s(s−a)(s−b)(s−c)
जहाँ s=परिमाप/2
कोण के आधार पर भी त्रिभुज 3 प्रकार के होते हैं।
बच्चों ! जैसे की हमने त्रिभुज के बारे मे पढ़ा, साथ ही बच्चों आपने पिछली कक्षाओ मे दो त्रिभुजों की सर्वांगसमता का अध्ययन किया था, आइये एक बार यहाँ उन्हें पुनः स्मरण करते है,
यहाँ सर्वांगसम शब्द को देखे तो "सर्वांगसम = सर्व + अंग + सम" से मिलकर बनता है अर्थात
जिस आकृति के सभी अंग समान हो तब उस आकृति को सर्वांगसम कहते है ।
दो त्रिभुज सर्वांगसम (Congruent) होते हैं, यदि
आइए इसे एक उदाहरण से समझते है
इसके लिए आप कॉपी का एक पेज ले तथा इसके 2 सम्मुख कोरों (विकर्ण) को लेकर उसे काटे, आप देखेंगे आपको 2 त्रिभुज प्राप्त होंगे ये दोनों त्रिभुज बिल्कुल समान दिखाई देंगे तथा एक-दूसरे को पूरा ढक लेंगे। ये त्रिभुज आपस मे सर्वांगसम त्रिभुज होंगे ।
अब बच्चों आगे इस अध्याय में हम ऐसे ज्यमितियो का अध्ययन करेंगे जिनके आकार तो समान होंगे लेकिन उनके संगत भुजाओं के माप भिन्न होंगे, ऐसी आकृतियों को हम समरूप आकृतियों के रूप में परिभाषित करते है।
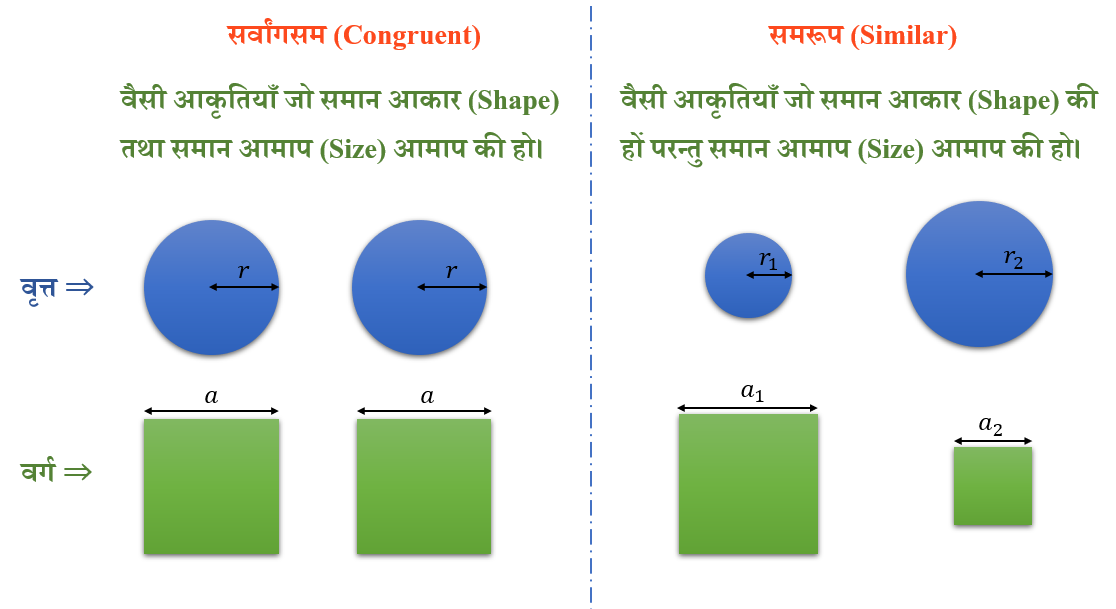
1. समरूप आकृतियाँ
यहाँ समरूप शब्द दो शब्द "सम + रूप" से मिलकर बना है ,
यदि दो ज्यामितीय वस्तुओं का स्वरूप समान हो तो उन्हें समरूप (similar) कहा जाता है, इनके माप समान होना आवश्यक नहीं है दूसरे शब्दों में, यदि दूसरी आकृति की सभी लम्बाइयों को समान अनुपात में घटाकर या बढ़ाकर पहली आकृति प्राप्त की जा सकती है तो, ये दोनो आकृतियाँ परस्पर समरूप हैं। किन्ही दो समरूप बहुभुजों की संगत भुजाये समानुपाती होतीं हैं और संगत कोणों के मान समान होते हैं।
अब बच्चों यहाँ कुछ समरूप आकृतियों के उदाहरण देख लेते है -
उदाहरण- सभी वृत्त समरूप होते है, चूँकि वृत्त का आकार छोटा हो या बड़ा ये एक समान ही दिखाई देंगे । 
इसी प्रकार सभी वर्ग समरूप होते है। 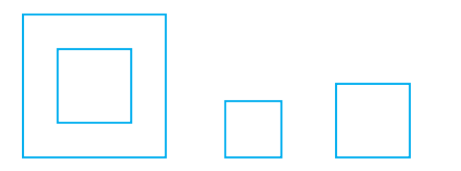
सभी समबाहु त्रिभुज समरूप होते है । 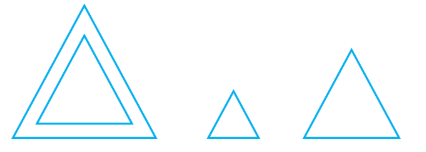
अधिक व्यापक रूप में हम कह सकते है कि सभी समान n - भुजाओं वाले बहुभुज समरूप होंगे यदि
(i) उनके संगत कोण बराबर हों तथा
(ii) उनकी संगत भुजाये समानुपाती ( एक ही अनुपात मे ) हो
टिप्पणी - प्रायः हमारे मन में सर्वांगसमता व समरूपता को लेकर संदेह उत्पन्न हो जाता है, दो सर्वांगसम आकृतियों की संगत भुजाएं समान तथा संगत कोण समान होते है लेकिन दो आकृतियों के समरूप होने के लिए उनके संगत भुजाओ का बराबर होना आवश्यक नहीं है अर्थात भुजाओं में अनुपात एक समान होता है। इस प्रकार हम कह सकते है कि दो आकृतियां जो सर्वांगसम है समरूप होंगी यह सदैव सत्य है, परन्तु कोई समरूप आकृति का सर्वांगसम होना आवश्यक नहीं है।
OMR (One Minute Revision)

उदाहरण 1
बतायें कि निम्नाकित चतुर्भुज समरूप है या नहीं ।
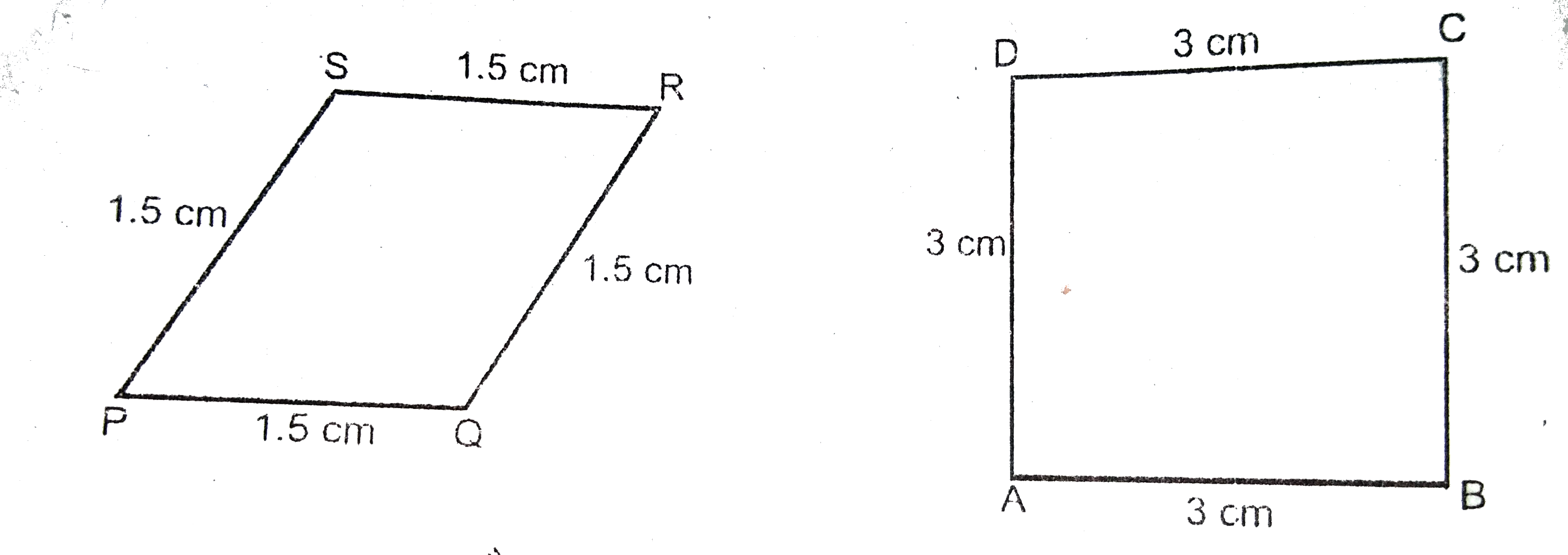
यहाँ चतुर्भुज PQRS और ABCD इस प्रकार है कि
(i) उनकी भुजाओं की संख्या समान है ।
(ii) उनकी भुजाएँ समानुपाती है ,
PQAB=QRBC=RSCD=SPDA
=1.53=12
किन्तु ∠P≠∠A
∠Q≠∠B
चुकि समरूप के लिए
अतः चतुर्भुज PQRS और चतुर्भुज ABCD समरूप नहीं है ।
2. त्रिभुज की समरूपता
जैसे की हमने समरूप आकृतियों के बारे मे पहले पढ़ा था, यदि दूसरी आकृति की सभी लम्बाइयों को समान अनुपात में घटाकर या बढ़ाकर पहली आकृति प्राप्त की जा सकती है तो, ये दोनो आकृतियाँ परस्पर समरूप हैं। आइए इसकी जाँच करते है -
उदाहरण के लिए
माना यदि △ABC व △DEF समरूप है तथा उनके भुजाओ की लम्बाइयाँ इकाई मे AB, BC व CA क्रमशः 3 , 4 व 5 तथा DE, EF व FD क्रमशः 6 , 8 व 10 है, यहाँ देख सकते है की इनकी संगत भुजाओ का अनुपात समान है
चूँकि
ABDE=BCEF=CAFD=12
तब △DEF के भुजाओ के मान को 12 से गुणा करने पर लम्बाइयाँ 3 , 4 व 5 प्राप्त होगी
इसी प्रकार △ABC के भुजाओ के मान को 2 से गुणा करने पर लम्बाइयाँ 6 , 8 व 10 प्राप्त होगी।
अर्थात त्रिभुज ABC व DEF आपस मे समरूपता के शर्त को पूर्ण कर रहे है।
अतः हम कह सकते है, दो त्रिभुज समरूप (Similiar) होते हैं यदि एक त्रिभुज के प्रत्येक कोण का मान, दूसरे त्रिभुज के संगत (तत्स्थानिक) कोणों के मान के बराबर होता है तथा समरूप त्रिभुजों में संगत भुजाओं की लंबाइयाँ समान अनुपात में होती हैं और यह गुण त्रिभुजों में समरूपता स्थापित करने के लिए पर्याप्त है।
यदि त्रिभुज ABC तथा त्रिभुज DEF समरूप है तो इसे △ABC~△DEF से दर्शाते है , संकेत "~" समरूप को प्रकट करता है।
गुण-
प्रमेय - 1 आधारभूत समानुपातिक प्रमेय (थेल्स प्रमेय)
यदि किसी त्रिभुज में एक भुजा के समान्तर रेखा खींची जाए जो अन्य दो भुजाओं को भिन्न-भिन्न बिंदुओं पर प्रतिच्छेद करती हो, तो ये अन्य दो भुजाएँ एक ही अनुपात में विभाजित हो जाती हैं।
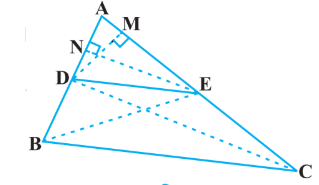
दिया है,
एक त्रिभुज ΔABC है, जिसमें भुजा BC के समांतर खींची गई एक रेखा अन्य दो भुजाओं AB और AC को क्रमश: D और E पर काटती हैं।
हमें सिद्ध करना है कि,
ADDB=AEEC
रचना-
(i) चित्र में B और E तथा C और D को मिलाएँ
(ii) फिर DM⊥AC एवं EN⊥AB खीचें।
अब Δ ADE का क्षेत्रफल =
12 आधार × ऊँचाई
=12×AD×EN
अतः
ar(ADE)=12AD×EN
इसी प्रकार
चूँकि BD भुजा को आगे बढ़ाने पर बिन्दु N मे शीर्ष E द्वारा लंब आ रहा है इस प्रकार EN, △BDE के लिए भी लंब होगा तथा DB आधार
ar(BDE)=12DB×EN
△ADE मे ही पुनः यदि लंब DM को ले तब आधार AE होगा
अतः
ar(ADE)=12AE×DM
जैसे पहले △BDE के लिए देखा था उसी प्रकार
ar(DEC)=12EC×DM
तब
ar(ADE)ar(BDE)=
=12AD×EN12DB×EN
=ADDB.....(1)
तथा
ar(ADE)ar(DEC)=
=12AE×DM12EC×DM
=AEEC....(2)
ध्यान दीजिये कि
/_\ВDE और ΔDEC एक ही आधार DE तथा समान्तर रेखाओ BC और DE के बीच बने दो त्रिभुज हैं, अतः उनका क्षेत्रफल बराबर होगा
अतः
ar(BDE)=ar(DEC)....(3)
इसलिए (1),(2) और (3), से हमें प्राप्त होता है:
ADDB=AEEC
इति सिद्धम
प्रमेय - 2 (थेल्स प्रमेय का विलोम)
यदि एक रेखा किसी त्रिभुज की दो भुजाओं को एक ही अनुपात में विभाजित करे तो वह तीसरी भुजा के समांतर होती है।अर्थात यदि ADDB=AEEC हो
तब DE∣∣BC
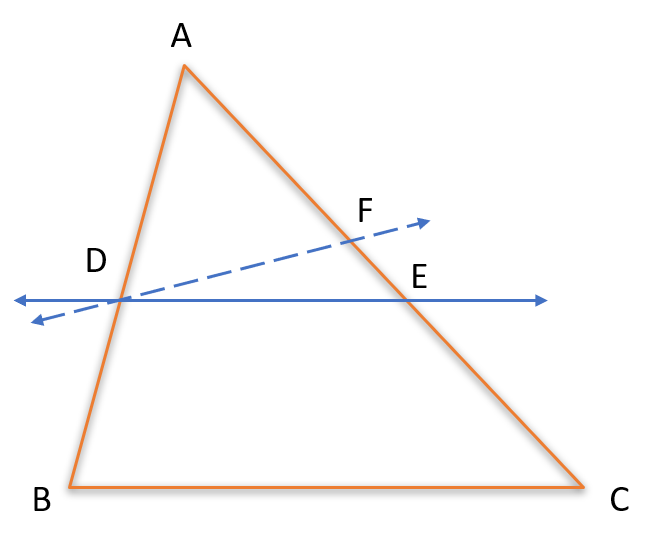
चित्र के अनुसार रेखा DE, AB व AC को क्रमशः D व E मे प्रतिच्छेद करता है तथा AB व AC को समान अनुपात मे विभाजित कर रहा है तो
हमें सिद्ध करना है कि,
इस प्रमेय के अनुसार DE, BC के समान्तर होगा।
(थेल्स प्रमेय की तरह इसे भी हल किया जा सकता है,)
अब यहां चित्र में BC के समांतर एक रेखा DF खींचते हैं अब आधारभूत समानुपातिक प्रमेय से =
ADDB=AFFC...(1)
तथा हमे दिया गया हैं कि
ADDB=AEEC....(2)
समीकरण 1 तथा 2 से
AFFC=AEEC
दोनों तरफ 1 जोड़ने पर
AFFC+1=AEEC+1
AF+FCFC=AE+ECEC
ACFC=ACEC
FC=EC
अतः F तथा E सम्पाती बिंदु हैं अतः DF तथा DE एक ही रेखा हैं
चुकि DF, BC के समांतर हैं इसलिए DE भी , BC के समांतर हैं
इसी सिद्धम
OMR (One Minute Revision)
उदाहरण 2
दी गई आकृति में यदि DE∣∣BC और AD=4x−3,AE=8x−7,BD=3x−1 और CE=5x−3 तो x का मान ज्ञात करें ।
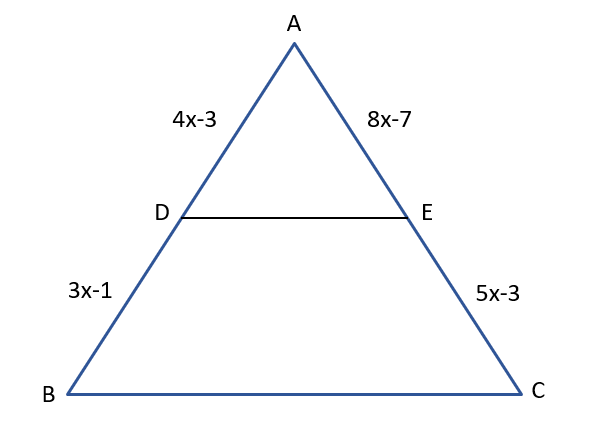
ΔABC में, DE∣∣BC
⇒ADDB=AEEC
(आधारभूत समानुपातिक प्रमेय से)
⇒4x−33x−1=8x−75x−3
⇒(4x−3)(5x−3)
=(8x−7)(3x−1)
⇒20x2−27x+9
=24x2−29x+7
⇒4x2−2x−2=0
⇒2x2−x−1=0
⇒2x2−2x+x−1=0
⇒2x(x−1)+1(x−1)=0
⇒(x−1)(2x+1)=0
⇒x=1
या x=−12
किन्तु जब
x=−12
⇒AD=4x−3
=−5
(संभव नहीं है चूँकि लंबाई ऋणात्मक नहीं हो सकती)
अतः x=1 इकाई प्राप्त होगा
उदाहरण 3
दी गई आकृति में EF||AB||CD है तो सिद्ध कीजिए कि
AEED=BFFC
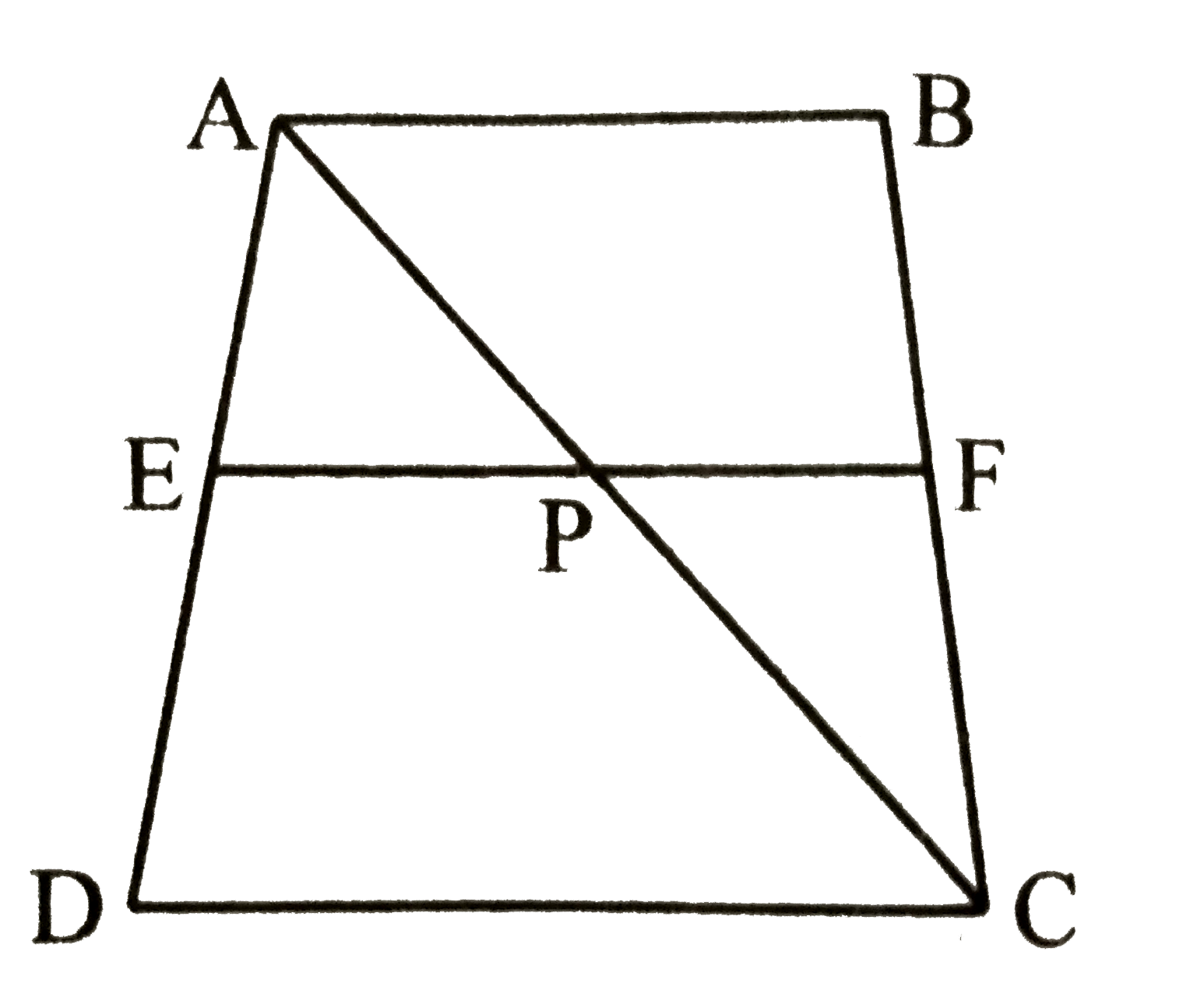
दिया है,
EF।।AB।।DC
⇒ EF।।DC
अब
△ ABC में,
EP।।DC
तब थेल्स प्रमेय से,
AEED=APPC
पुनः यहाँ
EF।।AB।।DC
⇒FP।।AB
तब थेल्स प्रमेय से,
BFFC=APPC
समी० (1) तथा (2) से स्पष्ट है कि,
AEED=BFFC
उदाहरण 4
दी गई आकृति में DE।।BC तथा ADDB=35 है यदि AC =4.8 सेमी है तो AE ज्ञात कीजिए ।
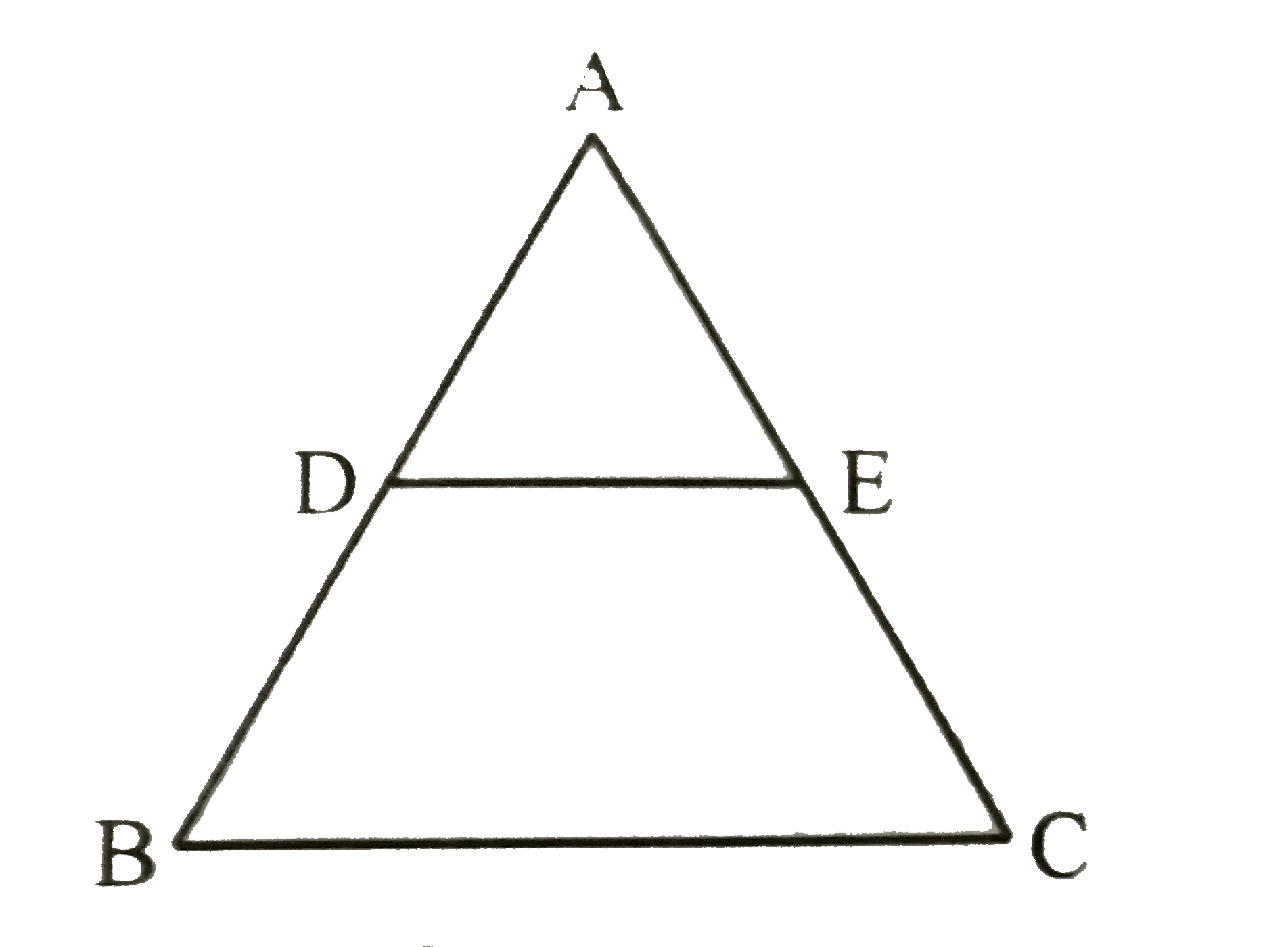
माना कि,
AE=x
तब, EC=AC−AE
=4.8−x
अब △ABC में,
DE।।BC
तब आधारभूत समानुपातिकता प्रमेय से,
ADDB=AEEC
⇒35=x4.8−x
अब x के लिए हल करने पर,
x=1.8
⇒AE=1.8 सेमी
3. त्रिभुजों की समरूपता के लिये कसौटियाँ
माना, कोई दो त्रिभुज ΔABC और ΔDEF दिए गए है इनके समरूपता की जाँच के लिए हम निम्न प्रमेयों का ज्ञान होना आवश्यक है, आइये देखते है।
प्रमेय - 3
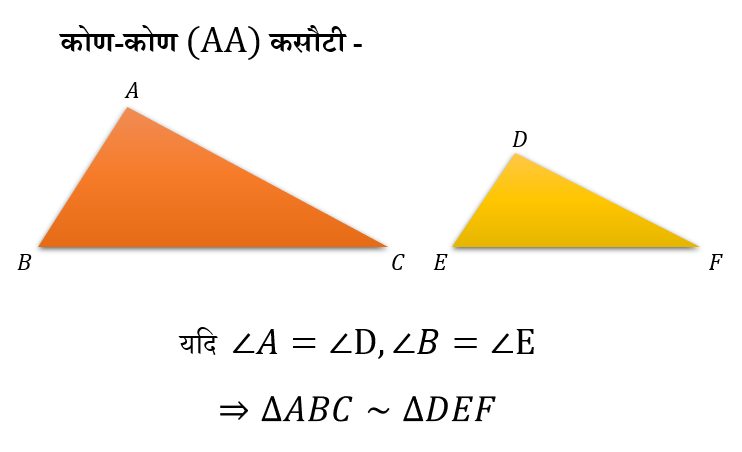
यदि दो त्रिभुजों में, संगत कोण बराबर हों, तो उनकी संगत भुजाएँ एक ही अनुपात में (समानुपाती) होती हैं और इसीलिए ये त्रिभुज समरूप होते हैं।
उपरोक्त कसौटी को दो त्रिभुजों की समरूपता की AAA ( कोण-कोण-कोण) कसौटी कहा जाता है।
माना त्रिभुज ΔABC
और ΔDEF में
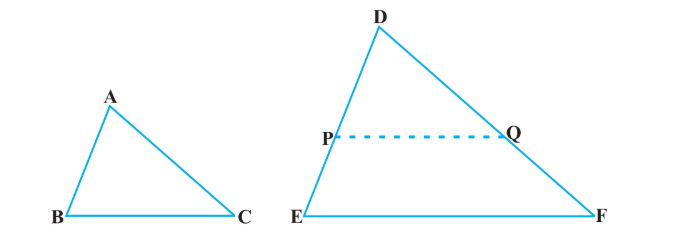
दिया है-
∠A=∠D
∠B=∠E
∠C=∠F
सिद्ध करना है कि -
ABDE=BCEF=ACDF
रचना -
भुजा DE व DF मे क्रमशः बिन्दु P व Q इस प्रकार लेंगे की
DP=AB और DQ=AC तथा P और Q को मिलाये
अतः ΔABC
और ΔDPQ में
DP=AB
( रचना से )
∠A=∠D
(दिया है)
DQ=AC
(रचना से )
अत
ΔABC≅ΔDPQ,
(SAS सर्वांगसमता से)
∠B=∠P
तथा
∠B=∠E दिया है
इस प्रकार ∠P=∠E
अतः PQ ॥ EF प्राप्त होता है।
चूँकि किसी एक रेखाखण्ड पर अन्य दो रेखाए यदि समान कोण बनाती है तो वे रेखाए आपस मे समान्तर होती है
चूँकि
PQ ॥ EF
अतः
DPPE=DQQF
(थेल्स प्रमेय से)
इस प्रकार
DPDE=DQDF होगा
चूँकि समान आनुपातिक भुजाये है
चूँकि DP=AB
और DQ=AC
(रचना से )
अतः मान रखने पर
ABDE=ACDF
इसी प्रकार
ABDE=BCEF
और इसीलिए
ABDE=BCEF=ACDF
चूँकि दिया है त्रिभुजों के संगत कोण बराबर है तथा प्राप्त हुआ की संगत भुजाये समानुपातिक है, अर्थात दोनों त्रिभुज समरूप है।
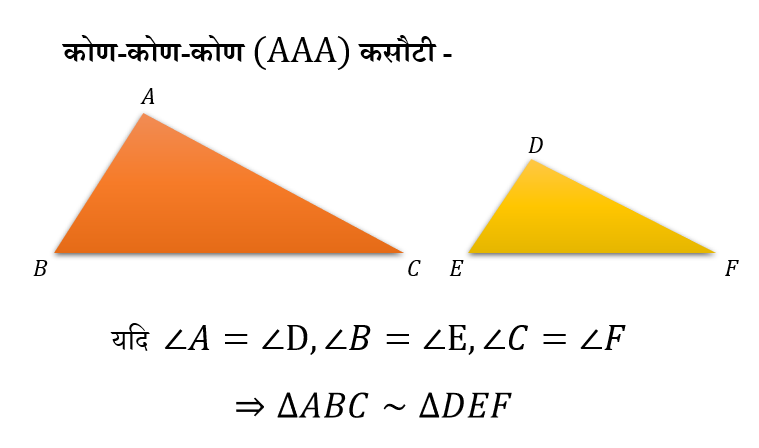
प्रमेय - 4
यदि दो त्रिभुजों में एक त्रिभुज की भुजाएँ दूसरे त्रिभुज की भुजाओं के समानुपाती (अर्थात एक ही अनुपात में) हों, तो इनके संगत कोण बराबर होते हैं और इसीलिए दोनों त्रिभुज समरूप होते हैं।
उपरोक्त कसौटी को दो त्रिभुजों की समरूपता की SSS ( भुजा-भुजा-भुजा) कसौटी कहा जाता है।

दिया हैं
दो त्रिभुज ABC और DEF इस प्रकार है कि:
ABDE=BCEF=CAFD
सिद्ध करना हैं कि
इनके संगत कोण भी बराबर होंगे
रचना:
△DEF में DP=AB और DQ=AC काटिए तथाP और Q को मिलाइए।और PQ∣∣EF है
चुकि
DPPE =DQQF
(थेल्स प्रमेय से)
तब
∠P=∠E
∠Q=∠F
DPDE=DQDF=PQEF
DPDE=DQDF=BCEF
BC=PQ
△ABC≅△DPQ
अतः सर्वांगसमता से
∠B=∠E
∠C=∠F
∠A=∠D
इति सिद्धम
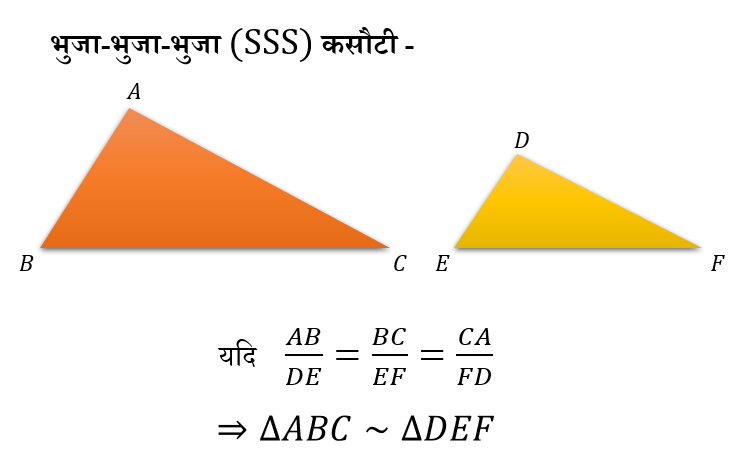
प्रमेय - 5
यदि एक त्रिभुज का एक कोण दूसरे त्रिभुज के एक कोण के बराबर हो तथा इन कोणों को अंतर्गत करने वाली भुजाएँ समानुपाती हों, तो दोनों त्रिभुज समरूप होते हैं।
इस कसौटी को दो त्रिभुजों की समरूपता की SAS ( भुजा-कोण-भुजा) कसौटी कहा जाता है।

माना दो त्रिभुज ABC और DEF इस प्रकार है कि:
ABDE=ACDF
तथा ∠A=∠D
सिद्ध करना हैं कि -
ΔABC~ΔDEF
रचना - भुजा DE व DF मे क्रमशः बिन्दु P व Q इस प्रकार लेंगे की
DP=AB और DQ=AC तथा P और Q को मिलाये
AB=DP
(रचना से )
AC=DQ
(रचना से )
∠A=∠D
(दिया है)
अतः
ΔABC≅ΔDPQ
अत:
∠A=∠D
∠B=∠P
∠C=∠Q होगा ।
चूँकि
ABDE=ACDF
(दिया है)
चूँकि AB=DP
तथा AC=DQ
⇒DPDE=DQDF
(समानुपातिक भुजाये)
=> PQ ॥ EF
(थेल्स प्रमेय से)
अत:
∠E=∠P
∠F=∠Q है।
अतः
∠B=∠E
व ∠F=∠Cहोगा
तथा ∠A=∠D (दिया है)
अतः ΔABC तथा ΔDEF आपस मे समान कोणीय त्रिभुज है, चूँकि संगत कोण आपस मे समान है।
इसलिए
ΔABC ~ΔDEF
OMR (One Minute Revision)



उदाहरण 5
निम्न आकृति में यदि PQ||RS है, तो सिद्ध कीजिए कि ΔPOQ~ΔSOR है ।
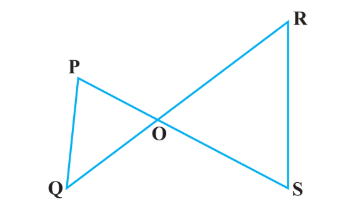
PQ ∣∣ RS
(दिया है)
अतः
∠P=∠S (एकांतर कोण )
∠Q=∠R
(एकांतर कोण )
∠POQ=∠SOR
(शीर्षाभिमुख कोण )
∴ΔPOQ~ΔSOR
(A A A समरूपता से)
उदाहरण 6
दी गई आकृतियों में ∠E ज्ञात कीजिए ।
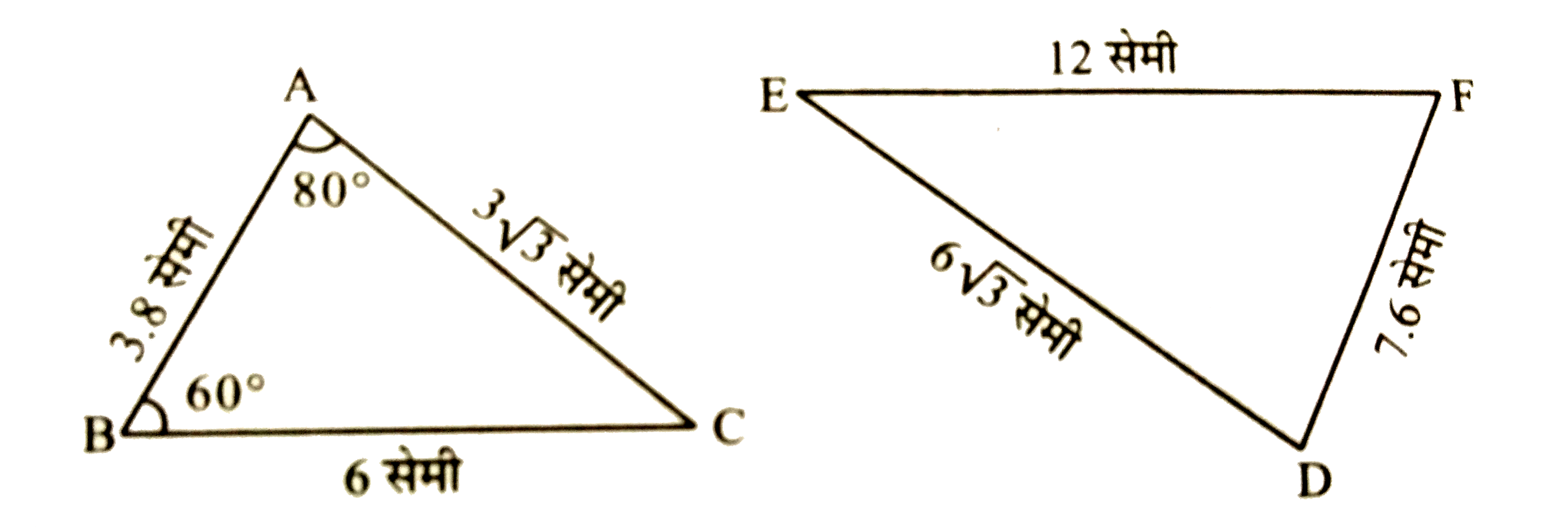
ऊपर दिए गए त्रिभुज में,
ABDF=BCFE=CAED=12
तब SSS- द्वारा,
△ABC~△DEF
तब त्रिभुजों की समरूपता से,
∠A=∠D
∠B=∠F
∠C=∠E
⇒∠D=80∘
∠F=60∘
⇒∠E=40∘
उदाहरण 7
6 मीटर ऊँचा एक ऊर्ध्वाधर स्तम्भ जमीन पर 4 मीटर लम्बी छाया बनाता है और ठीक उसी प्रकार मीनार 28 मीटर लम्बी छाया बनाता है | मीनार की ऊँचाई ज्ञात कीजिए
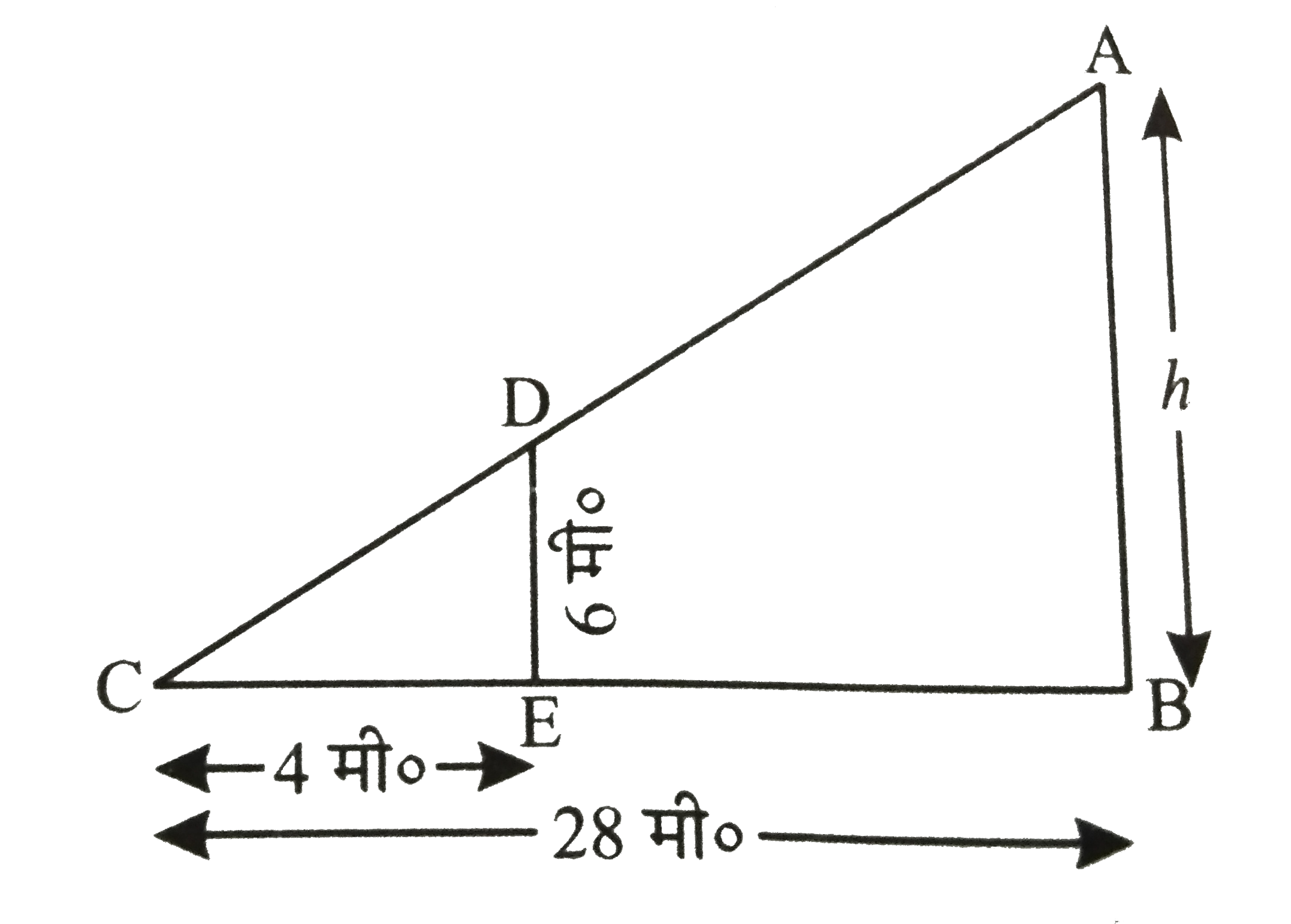
ऊर्ध्वाधर स्तम्भ की ऊँचाई
DE = 6 मीटर
जमीन पर 4 मीटर छाया बनती है |
माना, कि, मीनार की ऊँचाई h है |
मीनार की छाया की ऊँचाई = 28 मीटर
अब △ABC
तथा △DEC से,
∠ABC=∠DEC
(प्रत्येक =90∘)
∠C=∠C
तब समरूपता की AA-कसौटी द्वारा,
△ABC~△DEC
इसलिए,
ABDE=BCEC
⇒h6=284
अर्थात h = 42 मीटर,
यही मीनार की अभीष्ट ऊँचाई है |
उदाहरण 8
दी गई आकृति में, △ABC तथा △AMP क्रमशः Bतथा M पर समकोण है तो सिद्ध कीजिए कि,
(i) △ABC~△AMP
(ii) CAPA=BCMP
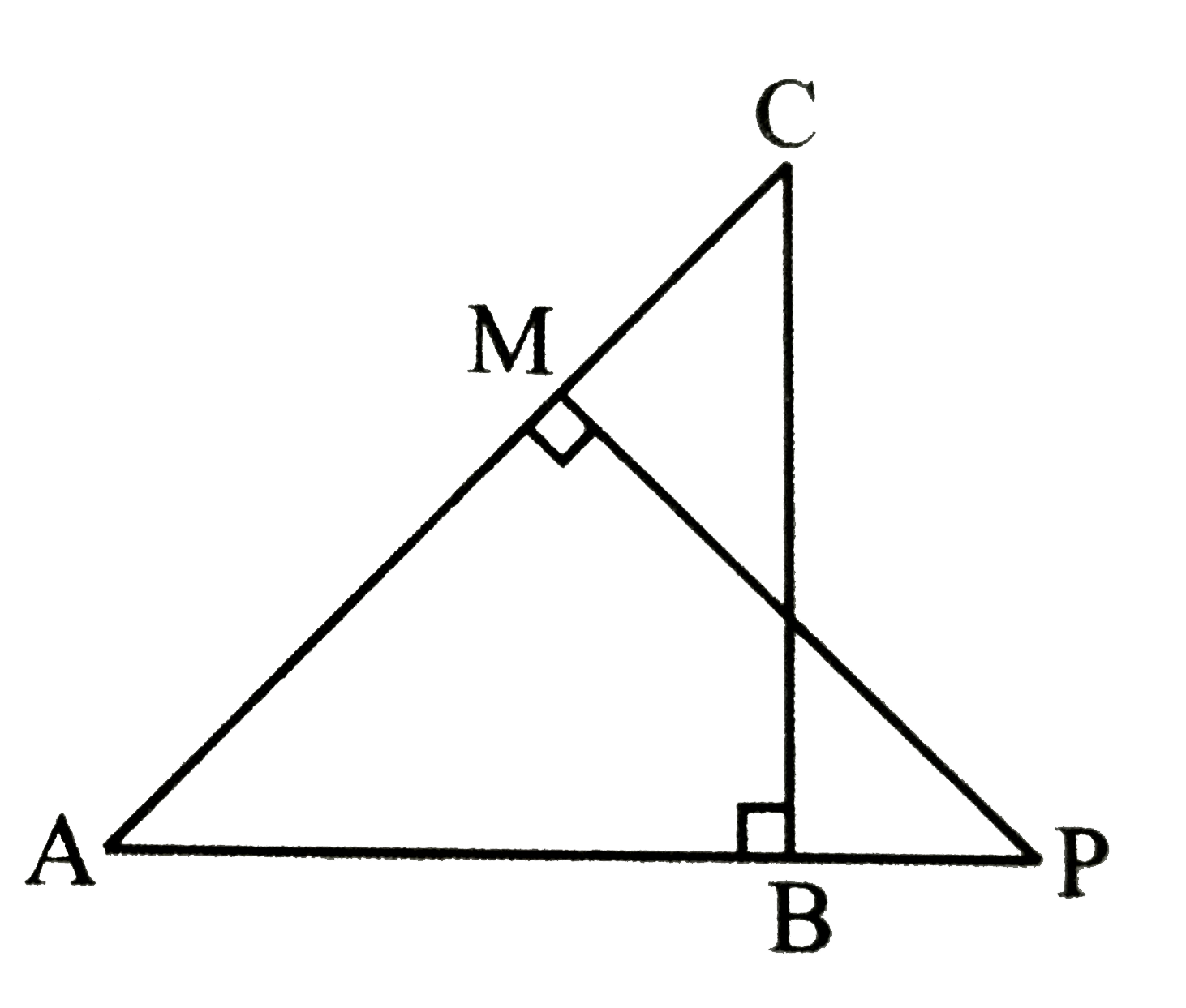
यहाँ दो त्रिभुज ABC तथा AMP है तथा
∠B=90∘ और
∠M=90∘
हमे सिद्ध करना है कि
(i) △ABC~△AMP
(ii)CAPA=BCMP
(i) △ABC
तथा △AMP में,
∠ABC=∠AMP=90∘
∠A=∠A
इसलिए समरूपता की कसौटी द्वारा,
△ABC ~△AMP
(ii) चूँकि
△ABC ~△AMP है
तब आधारभूत समानुपातिक प्रमेय द्वारा,
CAPA=BCMP
4. समरूप त्रिभुजों के क्षेत्रफल
इस भाग में हम समरूप त्रिभुजों के क्षेत्रफल व उनके संगत भुजाओं के अनुपातों के बीच सम्बन्ध का अध्ययन करेंगे।
प्रमेय - 6
दो समरूप त्रिभुजों के क्षेत्रफलों का अनुपात इनकी संगत भुजाओं के अनुपात के वर्ग के बराबर होता है।
हमें दो त्रिभुज ΔABC और ΔPQR ऐसे दिए हैं कि ΔABC ~ΔPQR है
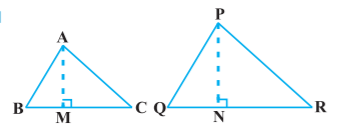
हमें सिद्ध करना है कि
ar(ABC)ar(PQR)
=(ABPQ)2
=(BCQR)2
=(CARP)2
दोनों त्रिभुजों के क्षेत्रफल ज्ञात करने के लिए, हम इनके क्रमश: शीर्षलंब AM और PN खींचते हैं।
अब
ar(ABC)
=12BC×AM
तथा
ar(PQR)
=12QR×PN
अतः
ar(ABC)ar(PQR)
=12×BC×AM12×QR×PN
=BC×AMQR×PN......(1)
अब
/_\АВМ
और ΔPQN में
∠B=∠Q
(क्योंकि ΔABC ~ΔPQR है )
और ∠M=∠N,
(प्रत्येक 90∘ का है )
अतः
ΔABM~ΔPQN
(AA समरूपता कसौटी)
इसलिए
AMPN=ABPQ....(2)
साथ ही
ΔABC~ ΔPQR
इसलिए
ABPQ=BCQR=CARP.....(3)
चूँकि
ar(ABC)ar(PQR)
=BCQR×AMPN
अतः समीकरण (1)और (3) से
ar(ABC)ar(PQR)
=ABPQ×AMPN
=ABPQ×ABPQ
(समीकरण (2) से)
=(ABPQ)2
अब समीकरण (3) के प्रयोग से हमें प्राप्त होता है
ar(ABC)ar(PQR)
=(ABPQ)2
=(BCQR)2
=(CARP)2
इति सिद्धम
OMR (One Minute Revision)

ar(ABC)ar(PQR)
=(ABPQ)2
=(BCQR)2
=(CARP)2
उदाहरण 9
सिद्ध कीजिए कि एक वर्ग की भुजा पर बने समबाहु त्रिभुज का क्षेत्रफल उस वर्ग की विकर्ण पर बने त्रिभुज के क्षेत्रफल से आधा होता है |
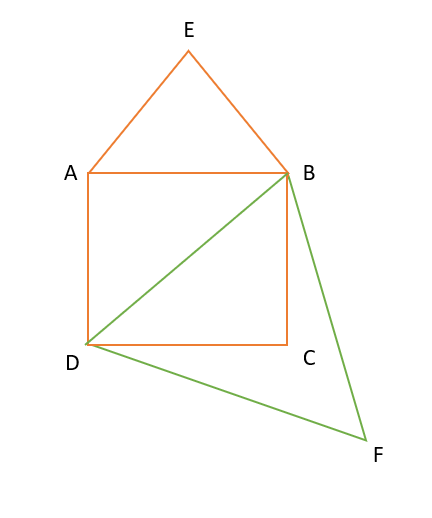
माना कि, ABCD एक वर्ग है तथा समबाहु त्रिभुज ABE तथा BDF क्रमशः भुजा AB तथा विकर्ण BD पर बने है |
हमे सिद्ध करना है कि,
(△ABE) का क्षेत्रफल
=12×(△BDF) का क्षेत्रफल
चूँकि
त्रिभुज ABE तथा BDF समबाहु है इसलिए उनके कोण भी बराबर होंगे |
( प्रत्येक =60∘)
तथा
△ABE~ △BDF
⇒ar(△ABE)ar(△BDF)
=(AB)2(BD)2
∵ABCD एक वर्ग है इसिलए विकर्ण
=√2× भुजा
⇒BD=√2AB
इसलिए,
ar(△ABE)ar(△BDF)
=(AB)2(√2⋅AB)2
=12
उदाहरण 10
दो समरूप त्रिभुजों के क्षेत्रफलों का अनुपात 16:25 है । त्रिभुजों की संगत भुजाओं का अनुपात ज्ञात कीजिए ।
माना, दो त्रिभुज ABC तथा त्रिभुज PQR हैं ।
चूँकि
areaΔABCareaΔPQR
=(ABPQ)2
=(BCQR)2
=(CARP)2
इस प्रकार
1625
=(ABPQ)2
=(BCQR)2
=(CARP)2
वर्ग मूल लेने पर
ABPQ=BCQR =CARP
=45
अतः भुजाओं में अनुपात
=4:5
उदाहरण 11
दिये गये चित्र में , DE∣∣BC तथा AD:DB=7:5 है तो
ar(△DEF)ar(△CFB) ज्ञात कीजिए।
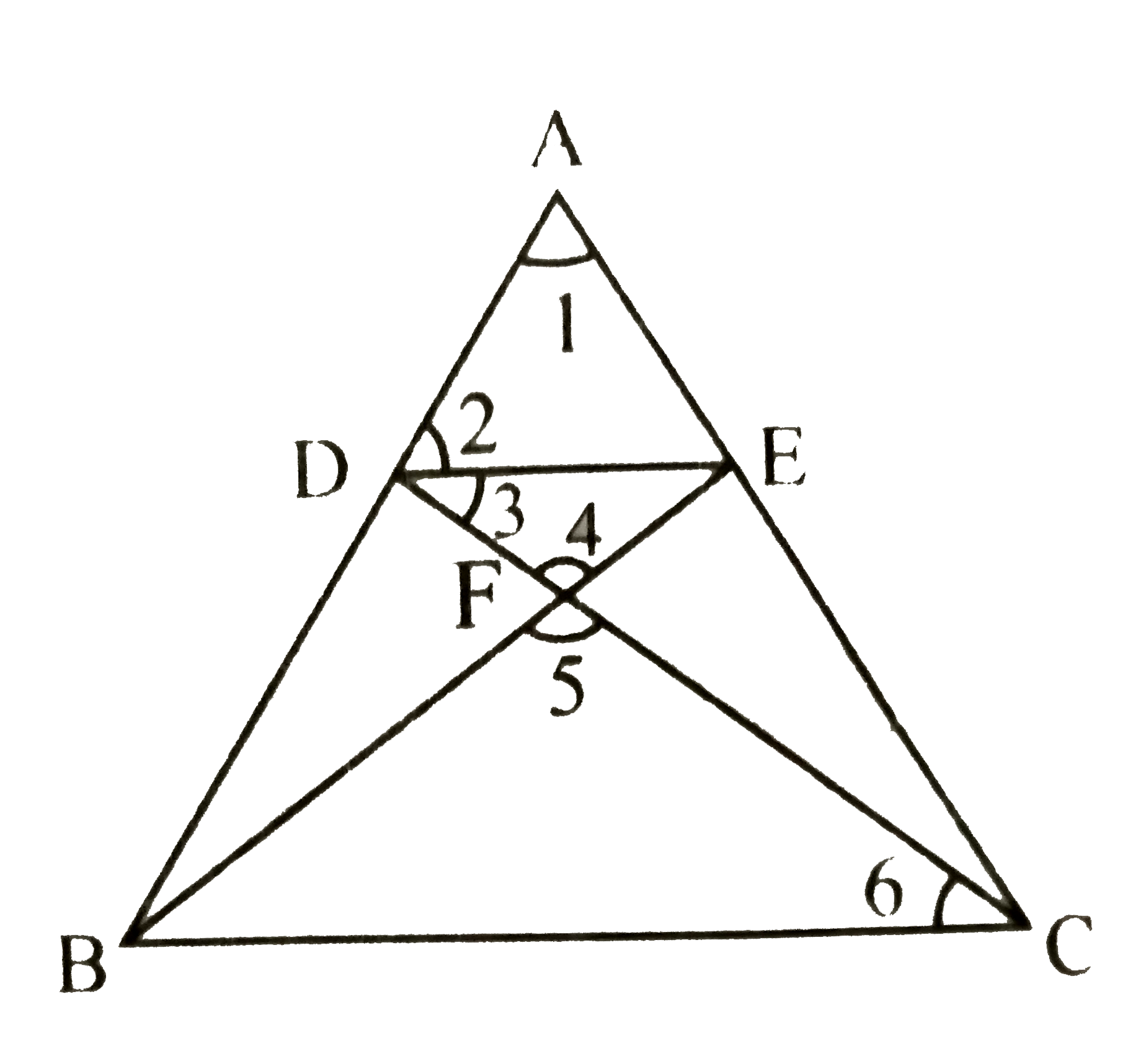
माना कि
AD=7k,<br>BD=5k
तब
AB=7k+5k=12k
△ADE तथा △ABC में
∠1(उभयनिष्ठ कोण )
∠2=∠ABC
⇒△ADE ~△ABC
(AA-समरूपता)
⇒ADAB=AEAC=DEBC
⇒7k12k=DEBC
ऐसे ही △DFE तथा △CFB में,
ar(△DEF)ar(△CFB)
=DE2BC2
=(712)2
=49144
5. पाइथागोरस प्रमेय
पाइथागोरस प्रमेय या बौधायन प्रमेय यूक्लिडीय ज्यामिति में किसी समकोण त्रिभुज के तीनों भुजाओं के बीच एक सम्बन्ध बताने वाला प्रमेय है,
इस प्रमेय के अनुसार "समकोण त्रिभुज की दो भुजाओं की लम्बाइयों के वर्गों का योग कर्ण की लम्बाई के वर्ग के बराबर होता है।"
इस भाग में हम त्रिभुज की समरूपता की अवधारणा का प्रयोग करके इसे सिद्ध करेंगे।
इससे पहले त्रिभुज की समरूपता से संबंधित एक प्रमेय समकोण त्रिभुज मे देखते है -
प्रमेय - 7
यदि किसी समकोण त्रिभुज के समकोण वाले शीर्ष से कर्ण पर लंब डाला जाए तो इस लंब के दोनों और बने त्रिभुज संपूर्ण त्रिभुज के समरूप होते हैं तथा परस्पर भी समरूप होते हैं।
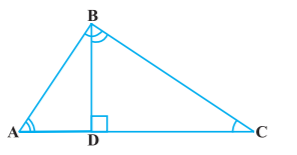
माना एक समकोण त्रिभुज ΔABC जिसका कोण В समकोण है।
मान लीजिए BD, कर्ण AC पर लंब है
अब ΔADB
और ΔABC में
∠A=∠A
(उभयनिष्ठ कोण)
और ∠ADB=∠ABC
(समकोण)
अतः
ΔADB ~ΔABC......(1)
(AA समरूपता से)
इसी प्रकार
ΔBDC ~ΔABC.......(2)
समीकरण (1) व (2) से
लम्ब BD के दोनों ओर के त्रिभुज संपूर्ण त्रिभुज ABC के समरूप हैं।
इसलिए
ΔADB ~ΔBDC
प्रमेय - 8 (पाइथागोरस प्रमेय)
एक समकोण त्रिभुज में कर्ण का वर्ग शेष दो भुजाओं के वर्गों के योग के बराबर होता है।
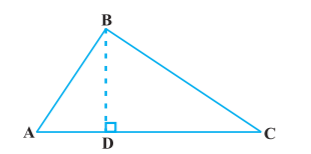
हमें एक समकोण त्रिभुज ABC दिया है जिसका ∠B समकोण है।
हमें सिद्ध करना है कि -
AC2=AB2+BC2
आइए BD bot "АС" खीचें
अभी ऊपर जो हमने समकोण त्रिभुज मे समरूपता का प्रमेय (प्रमेय - 7) देखा था उसके अनुसार
ΔADB ~ΔABC
( प्रमेय 7 से )
अतः
ADAB=ABAC
(भुजाएँ समानुपाती हैं )
[देखते है यहाँ हमने संगत भुजाओ का चुनाव किस प्रकार किया,
चित्र मे देखे तो ∠B व ∠D क्रमशः △ABC तथा △ADB के समकोण है अतः समकोण से जुड़े हुए भुजा, मान लेते है लंब क्रमशः AB व AD है तथा कर्ण क्रमशः AC व AB है ]
अतः हल करने पर
AD⋅AC=AB2.....(1)
साथ ही
ΔBDC ~ΔABC
(प्रमेय 7 से )
अत:
CDBC=BCAC
(भुजाएँ समानुपाती हैं)
या
CD⋅AC=BC2......(2)
समी. (1) और (2) को जोड़ने पर
AD⋅AC+CD⋅AC=AB2+BC2
या
AC(AD+CD)=AB2+BC2
या
AC⋅AC=AB2+BC2
या
AC2=AB2+BC2
अतः △ABC मे देख सकते है की कर्ण (AC) का वर्ग, लंब व आधार (माना AB व BC) के वर्गों के योग के बराबर होता है।
प्रमेय - 9
यदि किसी त्रिभुज की एक भुजा का वर्ग अन्य दो भुजाओं के वर्गों के योग के बराबर हो तो पहली भुजा का सम्मुख कोण समकोण होता है।
दिया हैं :
(AC)2=(AB)2+(BC)2
सिद्ध करना हैं
∠B=90∘
रचना :
हम एक △PQR की रचना करते हैं जिसमें ∠Q=90∘ औरPQ=AB औरQR=BC
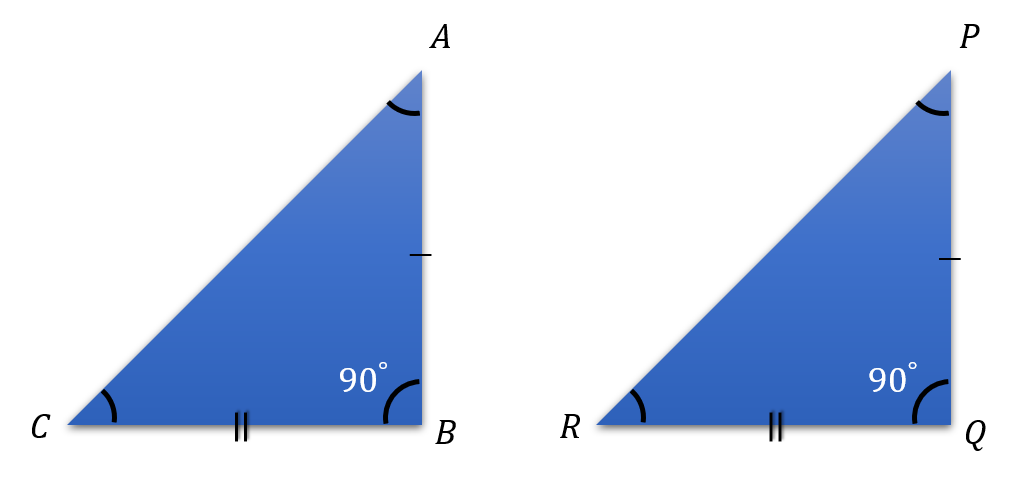
△POR से हमें प्राप्त है:
(PR)2=(PQ)2+(QR)2.....(i)
(पाइथागोरस प्रमेय)
(AC)2=(AB)2+(BC)2.....(ii)
(दिया हैं )
अतः AC=PR
[(1) और (2) से]
अब △ABC और △PQR में
AB=PQ (रचना से)
BC=QR(रचना से)
AC=PR
(ऊपर सिद्ध किया है)
△ABC≅△PQR
(SSS सर्वांगसमता)
इसलिए ∠B=∠Q
परन्तु ∠Q=90∘
( रचना से)
अतः ∠B=90∘
OMR (One Minute Revision)
उदाहरण 12
एक सीढ़ी किसी दिवार पर इस प्रकार टिकी हुई है कि इसका निचला सिरा दिवार से 2.5 मीटर की दूरी पर है तथा इसका ऊपरी सिरा भूमि से 6 मीटर की ऊँचाई पर बनी एक खिड़की तक पहुँचता है । सीढ़ी की लम्बाई ज्ञात कीजिए ।
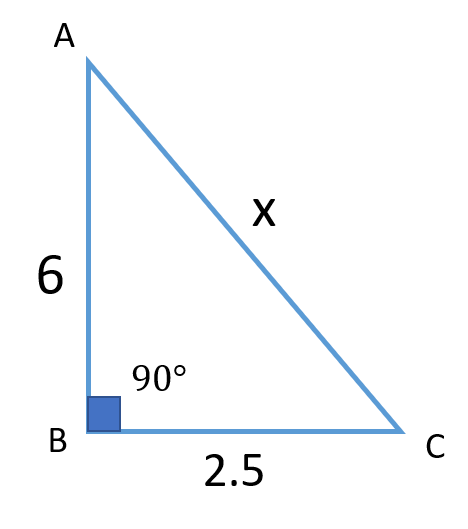
माना AC सीढ़ी है तथा AB दिवार है जिसमें A खिड़की है,
क्योंकि BC=2.5 मी.
और AB = 6 मी . है
यहाँ AB दीवार है (चूँकि भूमि से लम्बवत है)
अतः कोण B समकोण होगा, इस प्रकार AC कर्ण होगा
ΔABC में ,
AC2=BC2+AB2
[ पाइथागोरस प्रमेय से ]
AC2=(2.5)2+(6)2
=6.25+36
=42.25
अतः AC2=42.25
तब AC=6.5
(वर्गमूल लेने पर)
अतः सीढ़ी की लम्बाई
=6.5 मी. है ।
उदाहरण 13
नीचे कुछ त्रिभुजों की भुजाएँ दी गई है | निकालिये कि कौन-सा त्रिभुज समकोण त्रिभुज है |
(i) 8 सेमी, 15 सेमी, 17 सेमी
(ii) (2a-1) सेमी, 2√2a सेमी, (2a+1) सेमी
माना कि,
a=8,
b=15
c=17
तब,
a2+b2
=82+152
=64+225=289
=(17)2
=(c)2
⇒a2+b2=c2
तब
पाइथागोरस प्रमेय द्वारा, दिया गया त्रिभुज समकोण त्रिभुज है |
(ii) माना कि
p=(2a−1)
q=2√2a तथा
r=2a+1
स्पष्ट्तः
p2+q2
=(2a−1)2+(2√2a)2
=4a2+1−4a+4×2a
=4a2+4a+1
=(2a+1)2=r2
⇒p2+q2=r2
अतः दिया गया त्रिभुज समकोण त्रिभुज है |
उदाहरण 14
यदि एक △ABC की भुजाओं CA तथा CB के मध्य बिंदु क्रमशः P तथा Q है, तथा त्रिभुज C पर समकोण है | तो सिद्ध कीजिए कि
(i) 4AQ2=4AC2+BC2
(ii) 4BP2=4BC2+AC2

△AQC में, पाइथागोरस प्रमेय द्वारा,
AQ2=AC2+QC2
⇒4AQ2=4AC2+4QC2
⇒4AQ2=4AC2+(2QC)2
⇒4AQ2=4AC2+BC2
(चूंकि BC=2QC)
(ii) समकोण △BPC में पाइथागोरस प्रमेय का प्रयोग करने पर,
BP2=BC2+CP2
⇒4BP2=4BC2+4CP2
⇒4BP2=4BC2+(2CP)2
=4BC2+AC2
(चूंकि 2CP=AC)
महत्वपूर्ण बिंदु
इस अध्याय में हमने निम्नलिखित बिंदुओं का अध्ययन किया :
सारांश






ar(ABC)ar(PQR)
=(ABPQ)2
=(BCQR)2
=(CARP)2