TEXTBOOK CORNER EXERCISE 12.1 from OSWAAL PUBLICATION MATHS (KANNADA ENGLISH) SOME APPLICATION OF TRIGONOMETRY for Class 10
| Class 10 | MATHS |
| Chapter | SOME APPLICATION OF TRIGONOMETRY |
| OSWAAL PUBLICATION MATHS (KANNADA ENGLISH) | TEXTBOOK CORNER EXERCISE 12.1 |
| Medium | English |
| Academic Year | 2023-2024 |
Question 3
A contractor plans to install two slides for the children to the play in a park. For the children below the age of 5 years, she prefers to have slide whose top is at a height of 1.5m, and is inclined at an angle of 30∘ to the ground, whereas for elder children, she wants to have a steep slide at a height of 3m, and inclined at an angle of 60∘ to the ground. What should be the length of the slide in each case ? View SolutionQuestion 10
Two poles of equal heights are standing opposite each other on either side of the road, which is 80 m wide. From a point between them on the road, the angles of elevation of the top of the poles are 60∘and30∘, respectively. Find the height of the poles and the distances of the point from the poles.View SolutionQuestion 11
A TV tower stands vertically on a bank of a canal. From a point on the other bank directly opposite the tower, the angle of elevation of the top of the tower is 60∘. From another point 20 m away from this point on the line joining this point to the foot of the tower, the angle of elevation of the top of the tower is 30∘ (see figure below). find the height of the tower and the width of the canal.
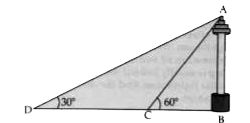 .View Solution
.View SolutionQuestion 14
A 1.2 m tall girl spots a balloon moving with the wind in a horizontal line at a height of 88.2 m from the ground. The angle of elevation of the balloon from the eyes of the girl at any instant is 60∘. After some time, the angle of elevation reduces to 30∘ (see figure below). find the distance travelled by the balloon during the interval.View SolutionQuestion 15
A straight highway leads to the foot of a tower. A man standing at the top of the tower observes a car at an angle of depression of30∘, which is approaching the foot of the tower with a uniform speed. Six seconds later , the angle of depression of the car is found to be 60^(@)'.Find the time taken to reach the foot of the tower from this point. View Solution