CIRCLES for Class 10 MATHS
Introduction
To bachho aaj hum padhenge circles ke baare mei aur hum circles se related sari baato ko janege jaise ki circle ka circumference, radius, diameter, minor sector, major sector etc. basically circle se related sari baato ko.
To sabse pehle aap btaye circle hota kya hai ? Aapne ye sabhi figures apne daily life mein dekhe honge. 
Ye sabhi circle ke examples h. So, What is Circle ? To chalo hum ek fixed point consider karte hai fixed point ke around equal distance par jo points hai unke locus ko hum circle bolte hai (see all the figures carefully). English mein ese define kiya jata hai as a A circle is the locus of points equidistant from the given point. 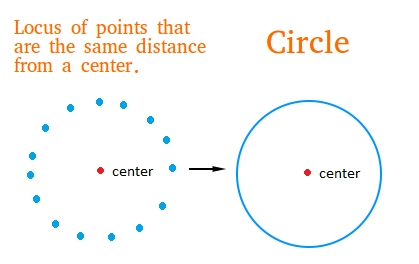
Points ki es fixed point se jo equal distance hai ushe hum Radius ( r ) of the circle khte hai. 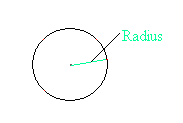
Aur es fixed point ko hum center of circle khte hai. Ek line segment jo circle ke two different points ko join krne se bnta h, ushe Chord khte hai.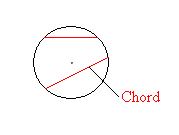
Agar ye chord center se pass hoti hai to eshe Diameter ( d ) khte hai. Diameter basically circle ko do equal parts mei divide karti hai.
Note→Diameter is double of radius that is d=2r. 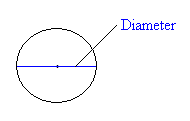
Ab hum janenge Secant ke baare mein secant ek aesi line hai jo circle ko two points pe intersect karti hai. Kya apko secant aur chord ke beech ka difference pta hai Secant basically circle ke beech nhi rhta it is extended beyond the loci.
Difference between secant and chord.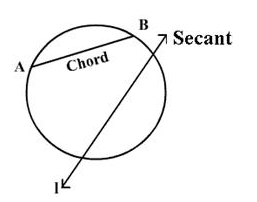
Tangent ko agar hum define kare to tangent ek line hai jo circle ko exactly ek point pe touch karti hai.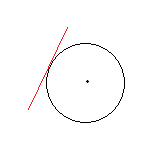
Ab humne circle ki basic information to jaan li ab hum es chapter ko detail
mein padhte hai.
Tangent to a Circle
To abhi tak humne pdha ki circle basically kya hai points ka collection in a plane at a constant distance(radius) from a fixed point(center). Aur humne bahut sari terms bhi padhi hai like chord, segment, etc. To ab hum examine karte hai kuch different situations ko with circle and line in a plane.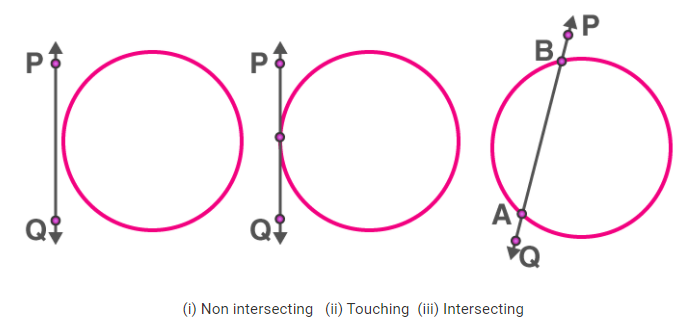
Ab es figure mein (i)st case mein PQ line aur circle ka koi common point nahi hai. Es case mein PQ ek non-intersecting line hai with respect to the circle. (ii)nd case mein PQ line circle ko sirf ek point pe touch kar rahi hai in this case line is called the tangent to a circle. (iii)rd case mein hmare pass do common points hai A aur B to line PQ circle ko do points pe intersect kar rahi hai. In this case we call line PQ secant of the circle.
Tangent to a Circle
Ab humne yeh to jaan liya ki tangent kya hota hai to chalo abh hum tangent ki kuch property ko samjhte hai ek example consider karte hai aap apne aas pass dekho kya apne kabhi koi bicycle ya cart ko chalte hue dekha hai ?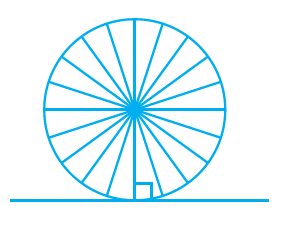
Agar aap wheel ko dhyan se dekhenge to aapne dekha hoga ki wheel ke sare spokes along radii hote hai. Ab wheel ka position note karo with respect to its movement on the ground. Kya aapko koi tangent dikh rha hai khi ? In fact, the wheel moves along a line which is a tangent to the circle representing the wheel. Balki wheel ko har ek position pe note karo, the radius through the point of contact with the ground appears to be at right angles to the tangent. Ab hum tangent ki es property ko prove karenge through a theorem.
Theorem 1
The tangent at any point of a circle is perpendicular to the radius through the point of contact.
We are given a circle with centre O and a tangent XY to the circle at a point P. We need to prove that OP is perpendicular to XY.
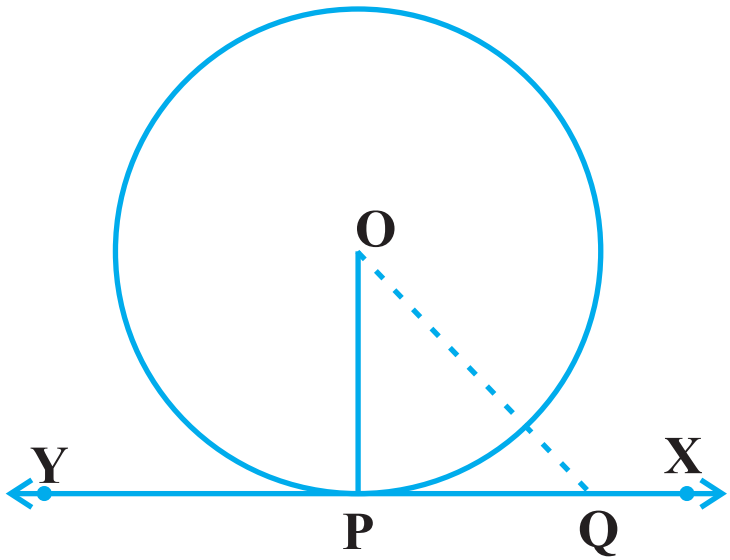
Take a point Q on XY other than P and join OQ
If Q lies inside the circle, XY will become a secant and not a tangent to the circle. So, The point Q must lie outside the circle.
Therefore, OQ is longer than the radius OP of the circle. That is, OQ>OP
Since this happens for every point on the line XY except the point P, OP is the shortest of all the distances of the point O to the points of XY.And we know that in a triangle, perpendicular is the shortest distance So OP is perpendicular to XY.
Note: 1. By above theorem, we can say at any point on a circle there can be one and only one tangent.
2. The line containing the radius through the point of contact is also sometimes called the ‘normal’ to the circle at the point.
Remarks :
To es theorem se humne ye conclude kiya
1. ki tangent kisi bhi point pe ho circle ke radius ke perpendicular hoga through the point of contact.
2. ki ek point se keval ek hi tangent form hoga.
3.Ek line jo tangent ke bhi perpendicular ho ushe normal khte hai.
Example 1
Find the length of the tangent drawn from a point whose distance from the centre of a circle is 25 cm. Given that the radius of the circle is 7 cm.
Let P be the given point, O be the centre of the circle and PT be the length of tangent from P. Then, OP=25 cm and OT=7 cm.
Since tangent to a circle is always perpendicular to the radius through the point of contact.
∴∠OTP=90∘
In right triangle OTP, we have
OP2=OT2+PT2
⇒252=72+PT2
⇒PT2=252−72=(25−7)(25+7)=576
⇒PT=24cm.
Hence, length of tangent from P=24 cm. 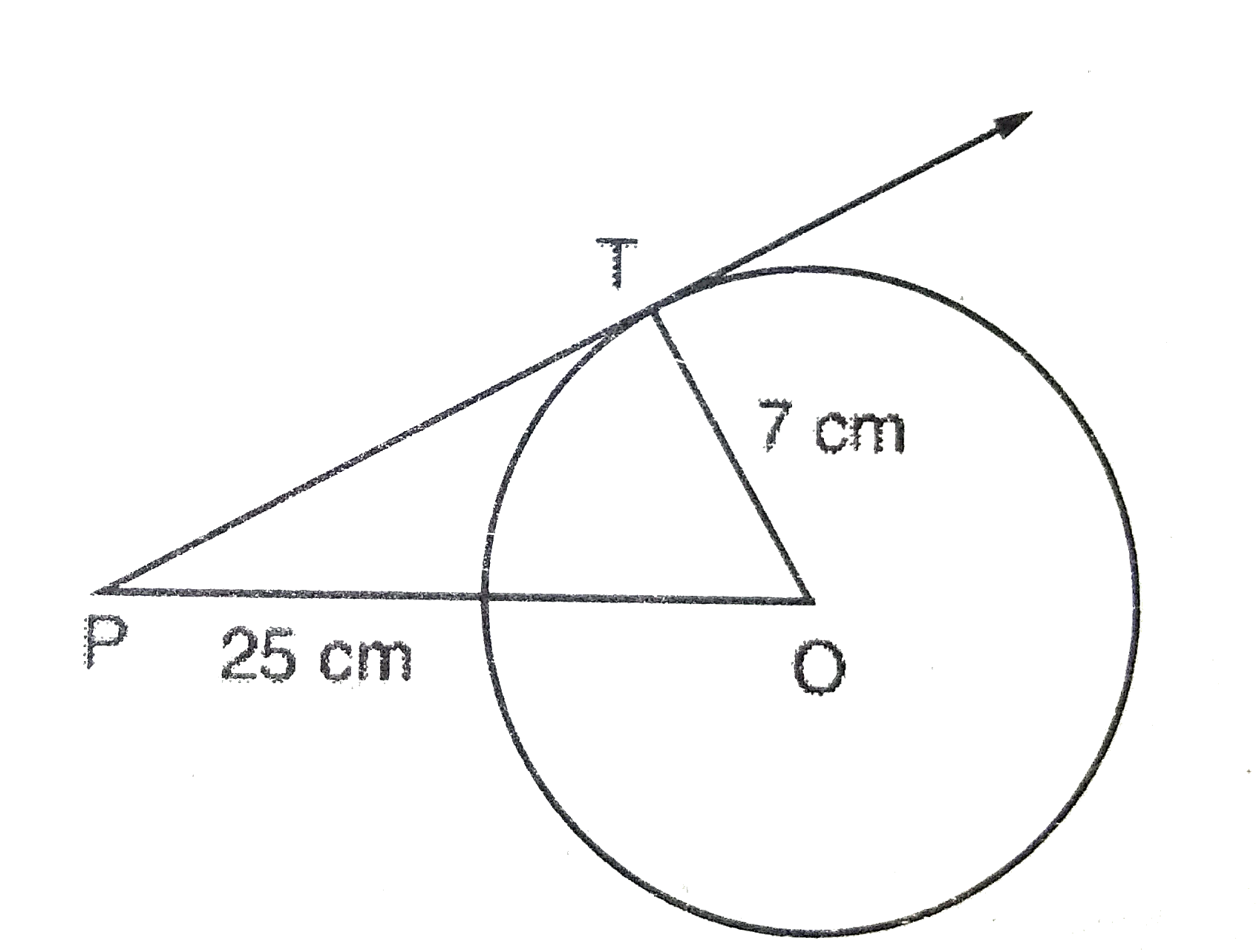
Number of Tangents from a Point on a Circle
Ab hum padhne vale hai about number of tangents from a point, on a circle i.e. kisi ek point se kitne number of tangents form ho sakte hai. So, we have to find out. To iske liye hmare pass teen cases bante hai.
Case I : When point is inside the circle. In that case, There is no tangent to a circle passing through a point lying inside the circle. that means ki agar point circle ke andr hoga to koi tangent form nahi hoga. Es case mein tangent draw krna possible hi nahi hai kyuki agar hum us point se tangent draw karte hai to vo circle ko do points pe intersect karegi to vo secant ho gya, tangent sirf ek hi point pe cut karti hai.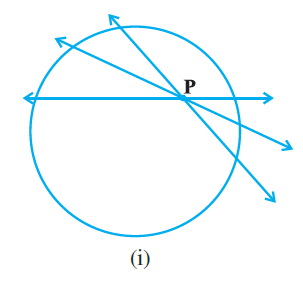
Case II :When point is at circle. In that case, There is one and only one tangent to a circle passing through a point lying on the circle. That means ki agar point circle ke upar hota hai to keval ek hi tangent possible hai. 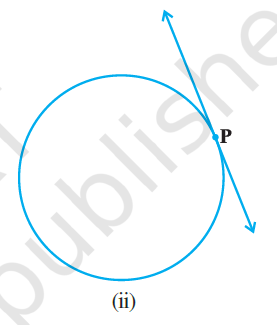
Case III : Point circle ke bhar ho (outside the circle). In that case There are exactly two tangents to a circle through a point lying outside the circle. In Fig. T1 and T2 are points of contact of tangents PT1 and PT2 respectively. 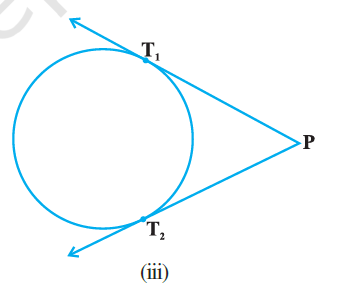
Point P se circle ke point of contact ka distance length of the tangent khlata hai.
Theorem 2
The lengths of tangents drawn from an external point to a circle are equal.
We are given a circle with centre O, a point P lying outside the circle and two tangents PQ, PR on the circle from P. We are required to prove that PQ=PR. 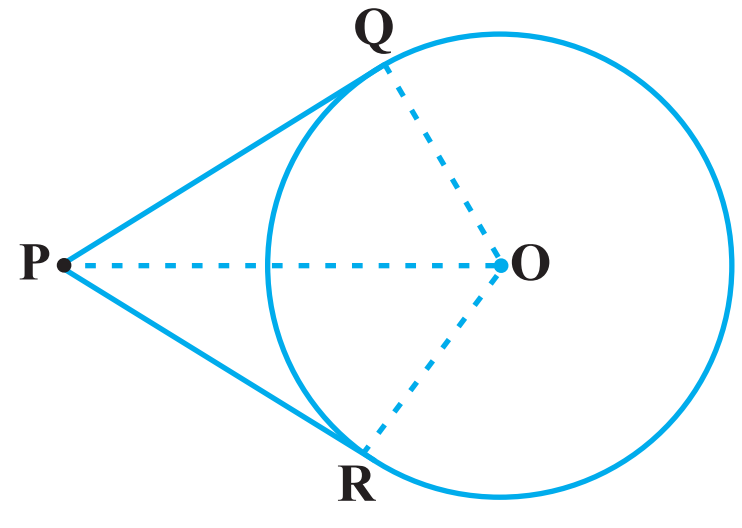
For this, we join OP, OQ and OR. Then ∠OQP and ∠ORP are right angles, because these are angles between the radii and tangents, and according to Theorem 10.1 they are right angles. Now in right triangles OQP and ORP,
OQ=OR (Radii of the same circle)
OP=OP (Common)
Therefore, ΔOQP≅ΔORP (RHS)
This gives PQ=PR (CPCT)
NOTE: ∠OPQ=∠OPR. Therefore, OP is the angle bisector of ∠QPR, i.e., the centre lies on the bisector of the angle between the two tangents.
Remarks :
1. Ye theorem Pythagoras theorem se bhi prove ki ja sakti thi
PQ2=OP2−OQ2=OP2−OR2=PR2 (As OQ=OR)
which gives PQ=PR
2. ∠OPQ=∠OPR To, OP angle bisector hai ∠QPR ka, i.e. the center lies on the bisector of the angle between the two tangents.
Example 2
Prove that the segment joining the points of contact of two parallel tangents passes through the centre.
Let PAQ and RBS be two parallel tangents to a circle with centre O.
Join OA and OB. Draw OC∣∣PQ.
Now, PA∣∣CO 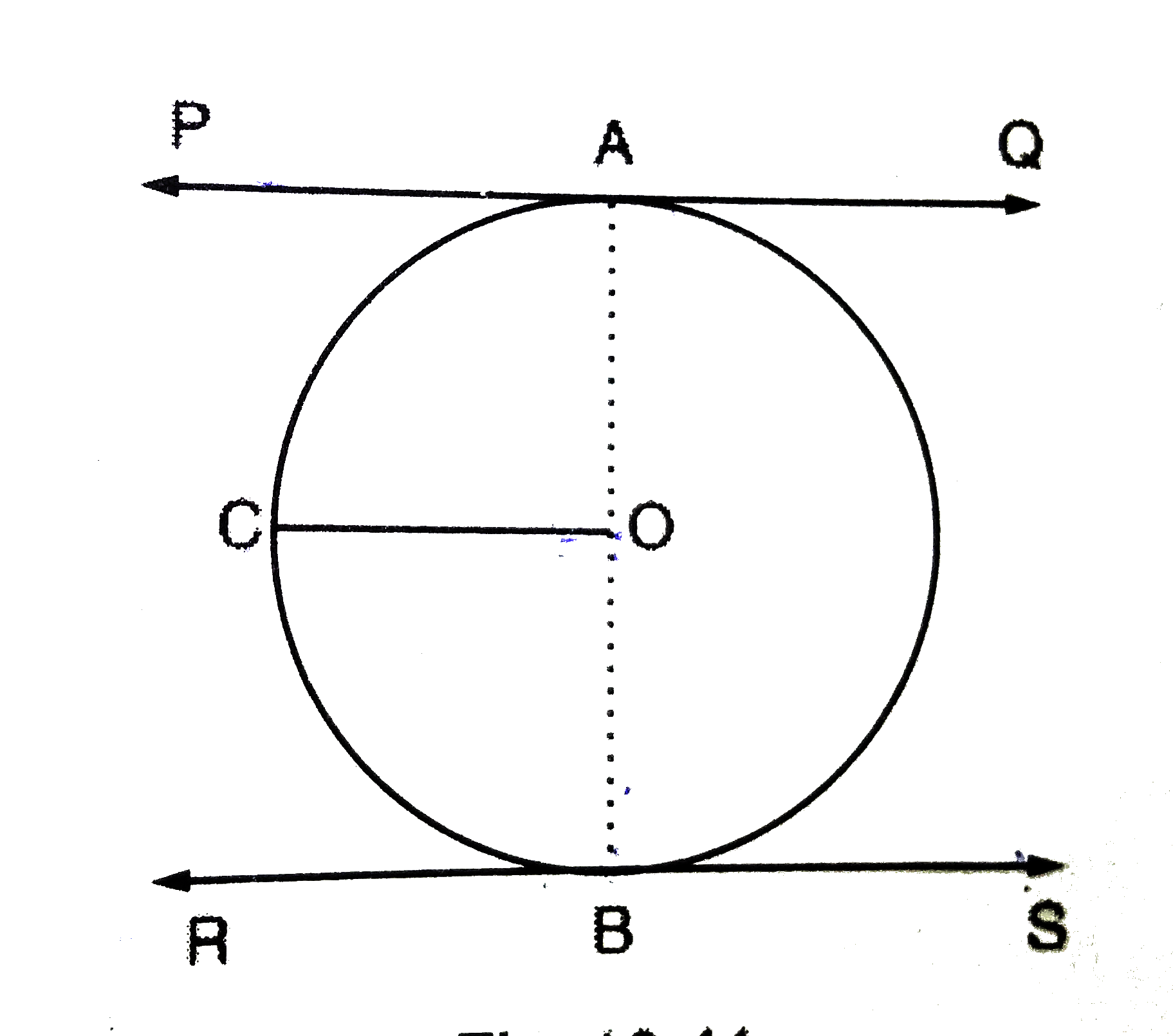
⇒∠PAO+∠COA=180∘ [Sum of the angles on the same sides of a transversal is 180∘]
⇒90∘+∠COA=180∘[∵∠PAO= angle between a tangent and radius =90∘]
⇒∠COA=90∘
Similarly, ∠COB=90∘
∴∠COA+∠COB=90∘+90∘=180∘
Hence, AOB is a straight line passing through O.
Example 3
Two tangents TP and TQ are drawn to a circle with centre O from an external point T. Prove that ∠PTQ=2∠OPQ
Bachho hmein ek circle given h with centre O, and an external point T given h and circle ki two tangents TP and TQ given h , where P, Q are the points of contact (see fig.).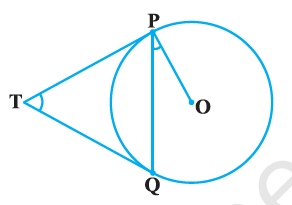
We need to prove that
∠PTQ = 2 ∠OPQ
Let ∠PTQ=θ
Now, by Theorem 2, TP=TQ. So, TPQ is an isosceles triangle.
Therefore, ∠TPQ = ∠TQP = 12(180∘−θ) = 90∘ - 12θ
Also, by Theorem 1 ∠OPT=90∘
So, ∠OPQ = ∠OPT - ∠TPQ = 90∘−(90∘−12θ)
12 θ = 12∠PTQ
This gives ∠PTQ = 2∠OPQ
Example 4
PQ is a chord of length 8 cm to a circle of radius 5 cm. The tangents at P and Q intersect at a point T. Find the length of the tangent TP.
According to question,
OT is the perpendicular bisector of chord PQ.
Let TR = y 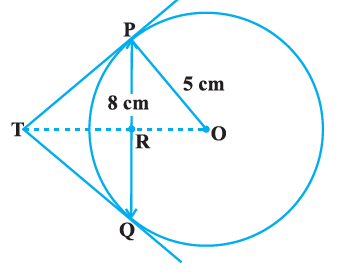
In right angled ΔPRO
PO2=(PR)2+RO2
(5)2=(4)2+RO2
(RO)2=25−16
(RO)2=25−16
(RO)2=9, RO=3cm
Right angle ΔTPO and ΔTRP
(TO)2=PT2+OP2.............(i)
PT2=TR2+PR2...............(ii)
Put the value of PT2 in equation (i)
TO2=TR2+PR2+OP2
(y+3)2=y2+(4)2+(5)2
y2+9+6y=y2+16+25
9+6y=41, 6y=32
y=3216=163cm
In right angle ΔTRP
PT2=TR2+PR2
PT2=(163)2+(4)2
PT2=2569+16
PT2=TR2+PR2
PT2=2569+16
PT2=256+1449
PT=√4009
PT=203
Example 5
A triangle ABC is drawn to circumscribe a circle of radius 4 cm such that the segments BD and DC into which BC is divided by the point of contact D are of lengths 8 cm and 6 cm respectively. Find the sides AB and AC.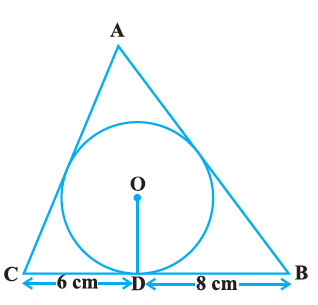
Let the circle touches AB and AC at E and F respectively. Let AF=xcm
We know that the tangents drawn from same external point to the circle are equal. Therefore,
CF=CD=6cm [Tangents drawn from point C]
BE=BD=8cm [Tangents drawn from point B]
AE=AF=x [Tangents drawn from point A] 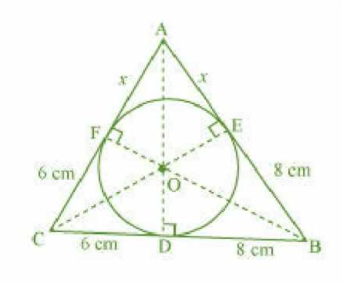
AB=AE+EB=x+8
BC=BD+DC=8+6=14
CA=CF+FA=6+x
In △ABC,
2s=AB+BC+CA=x+8+14+6+x=28+2x
∴s=14+x
Area of △ABC
=√s(s−a)(s−b)(s−c)
=√{14+x}{(14+x)−14}{(14+x)−(8+x)}{(14+x)−(6+x)}
=√(14+x)(x)(6)(8)
=√48x(14+x) cm2
=4√3(14x+x2) cm2
Area of △OBC = 12×OD×BC=12×4×14=28cm2
Area of △OCA = 12×OF×AC=12×4×(6+x)=12+2x cm2
Area of △OAB = 12×OE×AB=12×4×(8+x)=16+2x cm2
Area of △ABC = Area of △OBC + Area of △OCA + Area of △OAB
⇒ 4√3(14x+x2) = 28+(12+2x)+(16+2x)
⇒ 4√3(14x+x2) = 56+4x
⇒ √3(14x+x2) = 14+x
⇒ 3(14x+x2)=(14+x)2
⇒ 42x+3x2=196+x2+28x
⇒ 2x2+14x−196=0
⇒x2+7x−98=0
⇒x2+14x−7x−98=0
⇒x(x+14)−7(x+14)=0
⇒(x+14)(x−7)=0
⇒x+14=0 or x−7=0
Therefore, x=−14 or 7
But the side of triangle can't be negative, x≠−14. Therefore, x=7
Hence, AB=x+8=7+8=15cm and CA=6+x=6+7=13cm
Summary
1. A line that intersects the circle at only one point is called tangent.
2. The tangent to a circle is perpendicular to the radius through the point of contact.
3. The lengths of the two tangents from an external point to a circle are equal.
Let's Revise
To bachcho ab hum Circles chapter ka revision karenge.
- A circle is a locus of a point which moves in such a way that the distance from that point is always fixed.
- Ek circle aur ek line jo same plane mein hai, uske liye three possibilities ho sakti hai
(i) wo non- intersecting hongi yani circle aur line ek dusre ko intersect nhi karengi
(ii) unke beech mein single common point ho yani line circle ko ek point pe touch karey
(iii) unkey beech two common points ho saktey hai mtlb line cirle ko intersect kar rhi ho.
- Tangent :
- Secant :
- Tangent ko special case of secant ki tarh dekha jaa sakta hai jab uske corresponding chords ke dono end points coincide karey.
- Ek given secant ke liye maximum do parallel tangent ho saktey hai jo diametrically opposite points ko touch kartey ho.
- The tangent at any point of a circle is perpendicular to the radius through the point of contact.
- Wo line jo point of contact ke through radius ko contain karti hai ussey kabhi kabhi us point pe normal to the circle bhi kaha jaata hai.
- Number of Tangents from a given Point on a Circle :
(i) Agar koi point circle ke andar (inside) hai tab uss point ke liye koi tangent nhi hoga.
(ii) Agar koi point circle ke upar lie kar rha hai tab circle ke us point se sirf ek tangent pass karega.
(iii) Agar koi point circle ke bahar (outside) hai tab us point se circle par exactly do tangents pass karenge.
- The length of the segment of the tangent from a external point and the point of contact with the circle is called the length of the tangent from that point to the circle.
- Ek external points se jo circle par tangents draw kartey hai unki length equal hoti hai.