COORDINATE GEOMETRY for Class 10 MATHS
Introduction
To bachcho Coordinate Geometry ko shuru karne se pehle hum thoda Cartesian System ko revise karenge. Ab tak cartesian system mei humne ye pdha hai ki cartesian system do number lines se bana hai x - axis yani horizontal line aur y - axis yani vertical line inhi dono perpendicular lines ko coordinate axis kahte hai.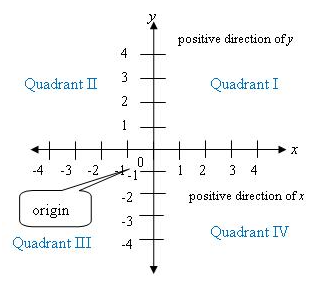
- In dono lines ka intersection point origin kehlata hai known as the center or the origin of the coordinate plane. Its coordinate are(0, 0).
- Coordinate plane mei kisi bhi point ko ordered pair ki form mein represent kiya jata hai by (a, b) where a is the x - coordinate and b is the y - coordinate.
- kisi bhi point ka distance y - axis se is called its x - coordinate aur abscissa and the distance from x - axis is called y - coordinate or ordinate.
- Cartesian plane 4 quadrants mei divided hai I, II, III and IV.
- In Cartesian plane quadrant Ist is (+, +), IInd is (-, +), IIIrd is (-, -) and IV is (+, -).
Basic Concepts
To ab dekho agar hume ek coordinate (4,2) cartesian plane pe represent karna hai to hum kse karenge 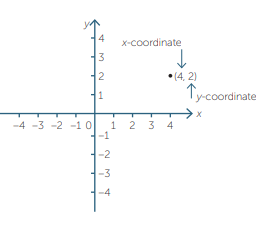
like this and the coordinates of the origin is (0,0). Ek baar agar do points ke coordinates pta lag gye to do points ke beech ka distance nikalna asan ho jata hai. Distance hamesha positive hota hai ya zero agar points coincide kare to A to B ka distance same hota as B to A. So we first find the distance between two points that
are either vertically or horizontally aligned.
So, let's suppose hmare pass do points hai A(1,2) and
B(4,2) let's plot it on coordinate plane 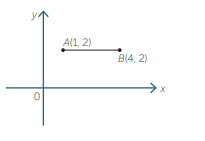
To AB ke beech ka distance kya hua ? Distance nikalne ke liye hum B ke x-coordinate ko A ke x-coordinate se subtract karenge i.e., 4−1=3. So, AB=3 that means it is horizontally inclined.
Ab hum ek aur example lete hai, let's say A(1,–2) and
B(1,3) 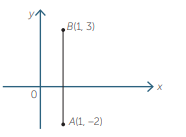
So, difference between AB=5. To ye distance hume kisse mila y-coordinate se so that means it is vertically inclined aur isse pehle humne distance nikala tha x-coordinate se.
To ab issi concept se hum distance formula samjhenge.
DISTANCE BETWEEN TWO POINTS
The distance between any two points A(x1,y1) and B(x2,y2) is given by the formula
AB=√(x2−x1)2+(y2−y1)2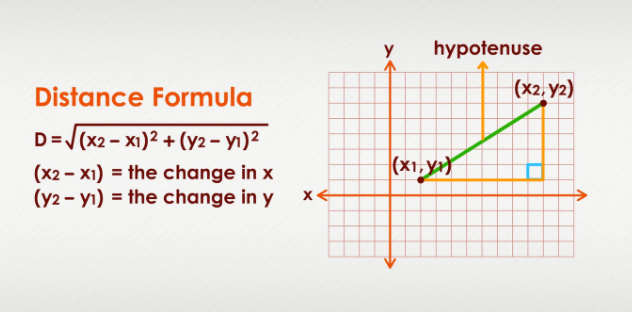
( Distance Formula )
Let X'OX and YOY' be the x - axis and y - axis respectively.
Then, O is the origin.
Let A(x1,y1) and B(x2,y2) be the given points.
Draw AL⊥OX, BM⊥OX and AN⊥BM.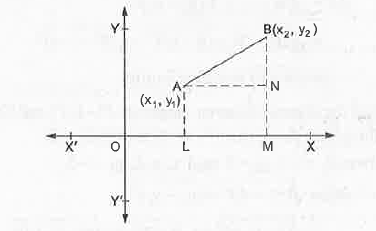
Now, OL=x1, OM=x2, AL=y1 and BM=y2.
∴ AN=LM=(OM−OL) = (x2−x1),
BN=(BM−NM)=(BM−AL)=(y2−y1)[becauseNM=AL].
From right △ANB, by Pythagoras' theorem, we have:
(AB)2 = (AN2 + BN2)
AB2=(x2−x1)2+(y2−y1)2
AB=√(x2−x1)2+(y2−y1)2
Hence, the distance between the points A(x1,y1) and B(x2,y2) is given by
AB=√(x2−x1)2+(y2−y1)2
Note
The distance of the point P(x,y) from the origin O(0,0) is given by
OP=√(x−0)2+(y−0)2, i.e., OP=√x2+y2.
Example 1
Find the distance the points A(7, 13) and B(10, 9).
The given point are A(7, 13) and B(10, 9).
Then, x1=7,y1=13andx2=10,y2=9
∴AB=√(x2−x1)2+(y2−y1)2
=√(10−7)2+(9−13)2=√32+(−4)2
=√9+16=√25=5units.
SECTION FORMULA
The coordinates of the point P(x,y) which divides the line segment joining A(x1,y1), B(x2,y2) internally in the ratio m:n are given by
x=mx2+nx1m+n, y=my2+ny1m+n
( Section formula )
Let X'OX and YOY' be the coordinate axes.
Let A(x1,y1) and B(x2,y2) be the end points of the given line segment AB.
Let P(x,y) be the point which divides AB in the ratio m:n.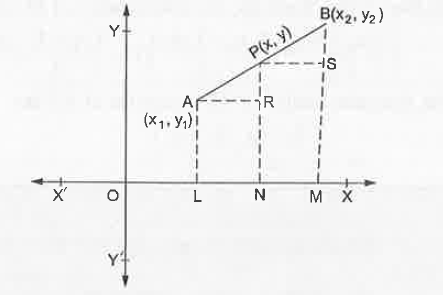
Then, APPB=mn
→ Draw AL⊥OX; BM⊥OX; PN⊥OX;
AR⊥PN and PS⊥BM.
→ Now, AR=LN=ON−OL=x−x1
→ PS=NM=OM−ON=x2−x
→ PR=PN−RN=PN−AL=y−y1
→ BS=BM−SM=BM−PN=y2−y .
Clearly, △ARP and △PSB are similar and, therefore, their sides are proportional.
∴ APPB = ARPS = PRBS
⇒mn=x−x1x2−x=y−y1y2−y
⇒mn=x−x1x2−x,
and mn=y−y1y2−y
⇒ mx2−mx=nx−nx1 and my2−my=ny−ny1
⇒(m+n)x=(mx2+nx1) and (m+n)y=(my2+ny1)
⇒x=mx2+nx1m+n, y=my2+ny1m+n
Hence, the coordinates of P are (mx2+nx1m+n,my2+ny1m+n).
MIDPOINT FORMULA
The coordinates of the midpoint M of a line segment AB with end points A(x1,y1) and B(x2,y2) are
M(x1+x22,y1+y22)
Let M be the midpoint of the line segment joining the points A(x1,y1) and B(x2,y2)
Then, M divides AB in the ratio 1:1.
So, by the section formula, the coordinates of M are
(1.x2+1.x11+1,1.y2+1.y11+1) i.e., (x1+x22,y1+y22)
Hence, the coordinates of the midpoint of AB are
(x1+x22,y1+y22).
Example 2
Find the coordinates of the point which divides the line segment joining the points A(4,−3) and B(9,7) in the ratio 3:2.
The end of points AB are A(4,−3) and B(9,7)
∴(x1=4,y1=−3)and(x2=9,y2=7)
Also, m=3 and n=2. 
Let the required point by P(x, y).
By the section formula, we have
x=(mx2+nx1m+n),y=(my2+my1m+n)
⇒x=(3×9+2×4)(3+2),y=[3×7+2×(−3)](3+2)
⇒x=7,y=3.
Hence, the required point is P(7,3).
Example 3
In what ratio does the point P(2,−5) divide the line segment joining A(−3,5) and B(4,−9)?
Let the required ratio be k:1.
Then, by the section formula, the coordinates of P are
P(4k−3k+1,−9k+5k+1)
∴4k−3k+1=2
and −9k+5k+1=−5 [because P(2,−5) is given]
⇒4k−3=2k+2 and −9k+5=−5k−5
⇒ 2k=5
and 4k=10
⇒k=52 in each case.
So, the required ratio is 52:1, which is 5:2.
Hence, P divides AB in the ratio 5:2.
AREA OF A TRIANGLE
The area of a ΔABC with vertices A(x1,y1), B(x2,y2) and C(x3,y3) is given by
Area of ΔABC = 12[x1(y2−y3)+x2(y3−y1)+x3(y1−y2)]
We know area of a triangle when its base and corresponding height (altitude) is given by:
Area of a triangle =12× base × altitude
Let A(x1,y1), B(x2,y2) and C(x3,y3) be the vertices of the given △ABC

∴ area of △ABC
= area of trapezium ABQP + area of trapezium APRC – area of trapezium BQRC
Since, area of a trapezium =12 (sum of parallel sides)(distance between them)
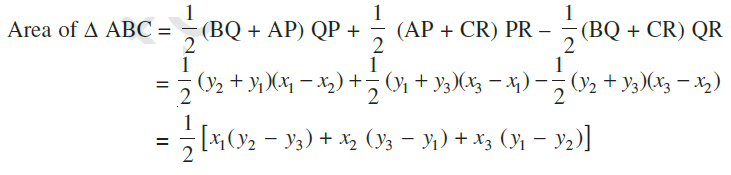
∴ Area of ΔABC=12[x1(y2−y3)+x2(y3−y1)+x3(y1−y2)]
CONDITION OF COLLINEARITY OF THREE POINTS
Let the given points be A(x1,y1), B(x2,y2) and C(x3,y3).
Then, A,B and C are collinear
⇒ area of △ABC = 0
⇒12[x1(y2−y3)+x2(y3−y1)+x3(y1−y2)] = 0
⇒x1(y2−y3)+x2(y3−y1)+x3(y1−y2) = 0
Example 4
Prove that the points (−3, 0), (1, −3) and (4, 1) are the vertices of an isosceles right-angled triangle. Find the area of this triangle.
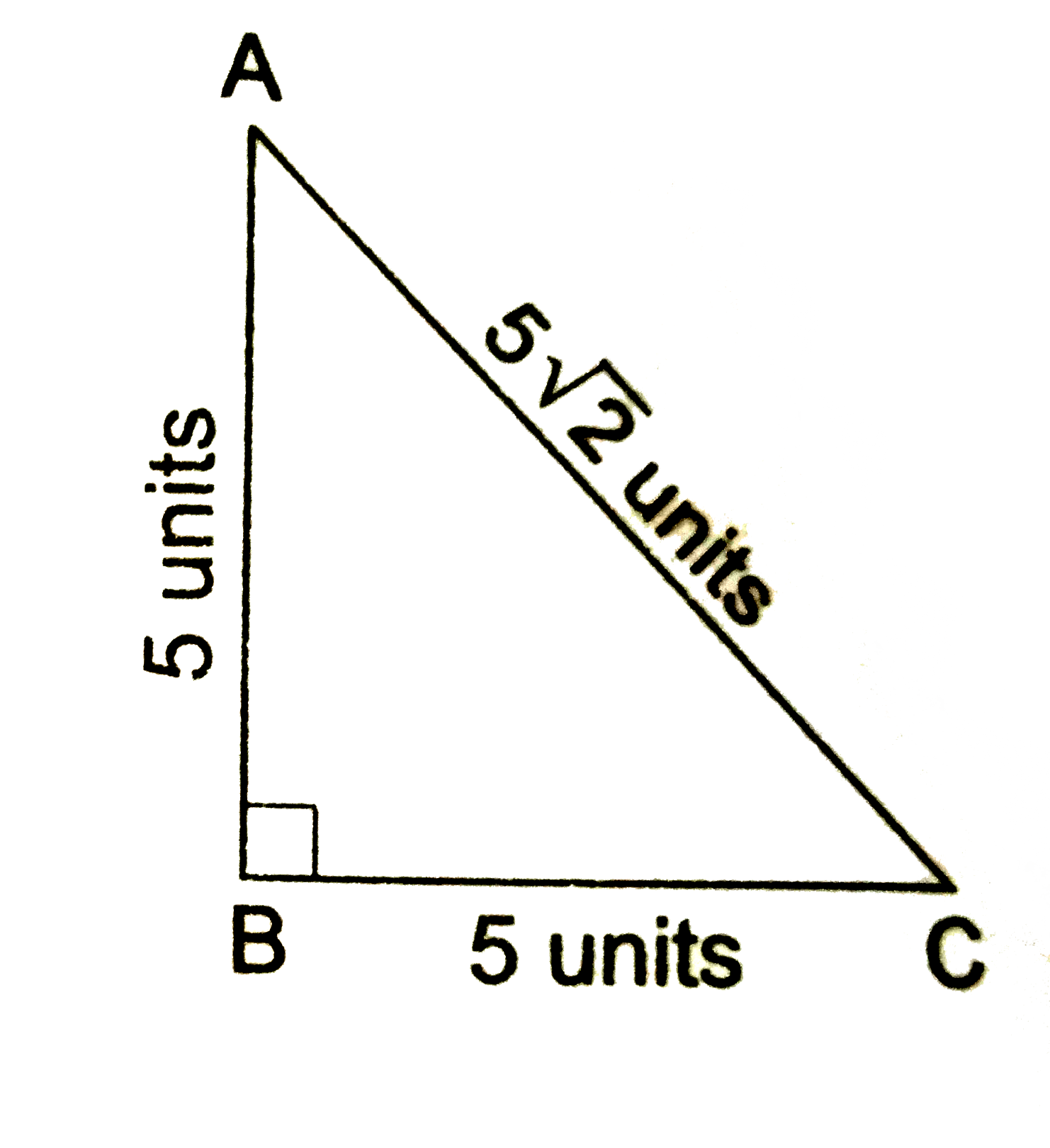
Let A(−3,0),B(1,−3) and C(4,1) be the given points. Then,
AB=√[1−(−3)]2+(−3−0)2=√42+(−3)2=√25=5 units,
BC=√(4−1)2+[1−(−3)]2=√32+42=√25=5 units
andAC=√[4−(−3)]2+(1−0)2=√72+12=√50=5√2 units.
Thus, AB=BC=5 units.
∴ΔABC is isosceles.
Also, (AB2+BC2)=(52+52)=50 and
AC2=(5√2)2=50.
Thus, AB2+BC2=AC2
This shows that ΔABC is right-angled at B.
In ΔABC, we have
base =BC=5 units and height =AB=5 units.
∴ area of ΔABC=(12×base×height)=(12×5×5) sq units
=12.5 sq units.
Summary
1. The distance between P(x1,y1) and Q(x2,y2) is
√(x2−x1)2+(y2−y1)2
2. The distance of a point P(x,y) from the origin is √x2+y2
3. The coordinates of the point P(x,y) which divides the line segment joining A(x1,y1), B(x2,y2) internally in the ratio m:n are given by
x=mx2+nx1m+n , y=my2+ny1m+n
4. The mid-point of the line segment joining the points P(x1,y1) and Q(x2,y2) is
(x1+x22,y1+y22)
5. The area of the triangle formed by the points (x1,y1),(x2,y2) and (x3,y3) is the numerical value of the expression 12[x1(y2−y3)+x2(y3−y1)+x3(y1−y2)]
Let's Revise
- Ek numbers ka pair jise hum graph par represent kar saktey hai usey coordinates kahtey hai. Usually hum kisi bhi 2−D object ke presence ko hum X−Y graph se represent kartey hai aur X-axis aur Y-axis ko coordinate axis kaha jata hai. Ye axis jis point par ek dusre ko cut karti hai use centre of coordinate axis ya origin (0,0) kaha jata hai.
- Kisi bhi point ka distance Y-axis se abscissa ya x-coordinate kahlata hai. Aur kisi bhi point ka distance X-axis se ordinate ya y-coordinate kahlata hai.
- Distance Formula:
→DAB=√(x2−x1)2+(y2−y1)2.
Kisi bhi do points ke beech ka distance humesha +ve hota hai lekin agar wo points coincide kar rhey ho to unke beech ka distance 0 hoga.
- Section Formula:
→ P(x,y)=(mx2+nx1m+n,my2+ny1m+n)
Agar hume P ke coordinates given hai aur humse ye pucha gya ki P, AB ko kis ratio mein divide karega ? Tab hum ratio ko K:1 maan lenge aur iss ratio ko section formula mein substitute karne par hume ratio ki actual value mil jayegi.
- Midpoint:
The coordinates of the midpoint(P) of line segment joining A(x1,y1) and B(x2,y2) is given by
→ P(x,y)=(x1+x22,y1+y22)
- Area of Triangle:
Area of ΔABC=12[x1(y2−y3)+x2(y3−y1)+x3(y1−y2)].
- Centroid of Triangle:
→ P(x,y)=(x1+x2+x33,y1+y2+y33).
- Conditions of Collinearity:
(i) Collinear points se form honey waley triangle ka area zero hota hai.
(ii) AB+BC=AC.
AB, BC, and AC can be calculated using the distance formula.