PAIR OF LINEAR EQUATIONS IN TWO VARIABLES for Class 10 MATHS
Introduction
To bachho jaisa ki humne ab tak padh rkha hai What is Linear ? Jab bhi kisi polynomial ki degree agar 1 hoti hai yani ki 'x' ki highest power agar 1 hai to wo polynomial kya kehlayega linear. Humne Class IX mei linear equation in two variable ke baare mei thoda sa pdha tha lekin ab hum Pair of Linear Equations in Two Variables ko solve karne ke methods ke baare mei padhenge. Jo equation ax+b=0, where a≠0, ki form mei hoti hai usse hum linear equation in one variable khte hai, jha a aur b real numbers hai, aur x ek variable hai. Linear equation in two variables asi equations hoti hai jinme do variables ho x aur y, ye equations ax+by+c=0 ki form mei hoti hai, where a, b and c are real numbers and a≠0 and b≠0, es equation ke baare mei aur detailing mei hum ess chapter mei padhenge.
Linear Equation in Two Variables :
An equation in two variables with the degree of the variables 1, is called a linear equation in two variables. For example : (i) 5x+2y=60 (ii) 3x+y=35
(iii) 2x+0y=7
are linear equations in two variables x and y where the degree of the variables x and y is 1.
Let's Learn
The term linear is derived from the idea that the graph of a linear equation represents a straight line.
* Note → That the degree of a Linear Equation is always 1.
Note :
To ab apne ye to dekh liya ki linear equation kya hoti hai ab hum dekhenge ki kis trha ki equation ko linear equation nhi kahte.
(i) 2x + 5y=7 ye equation linear equation nahi hai, ku kuki yha x aur y ki degree kya hai −1. lekin proper substitution se hum es equation ko convert kar sakte hai linear equation mei.
By, substituting m for 1x and n for 1y to equation kya bn jaygi 2m+5n=7, which is a linear equation.
(ii) 3m2+5n2=10 ye equation ek linear equation nahi hai, ku kuki yha m aur n ki degree kya hai 2, aur es equation ko hum linear equation mei convert bhi nahi kar sakte isliye ye equation hmari linear equation nhi hai.
General Form of a Linear Equation in Two Variables :
Two linear equations in the same two variables are called a pair of linear equations in two variables. The most general form of a pair of linear equations is
a1x+b1y+c1=0
a2x+b2y+c2=0
where a1,a2,b1,b2,c1,c2 are real numbers, such that (a21+b21≠0),(a22+b22≠0) as the coefficients of variables should not be zero.
Note :
Solution of linear equation in two variables ka mtlb hai ki equation ke variables ki aisi values ho jinki wajh se equation LHS=RHS ho jaye. Linear equation ka ek solution bhi ho sakta hai, infinite solutions bhi ho sakte hai aur aisa bhi ho sakta hai ki ki linear equation ka solution hi na ho.
Example 1
Show that x=5,y=2 is a solution of the system of linear equation
2x+3y=16,x−2y=1
The given equations are
2x+3y=16 … (i)
x−2y=1 … (ii)
Putting x=5andy=2 in (i), we get
LHS =(2×5+3×2)=16 = RHS.
Putting x=5andy=2 in (ii), we get
LHS =(5−2×2)=1= RHS
Thus, x=5andy=2 satisfy both (i) and (ii).
Hence, x=5,y=2 is a solution of the given system equations.
Let's Learn
A pair of linear equations in two variables can be represented, and solved, by the:
(i) Graphical Method
(ii) Algebraic Method
Do you know, how linear equations look like geometrically?
Kya aapko pata hai Geometrical representation kya hota hai do linear equations ka ?
Geometrical yani graphical representation do linear variables ka straight line hota hai. kya aapko pata hai wo kese banayi jati hai linear equation ko straight lines se represent kiya jata hai inki possibilities hai
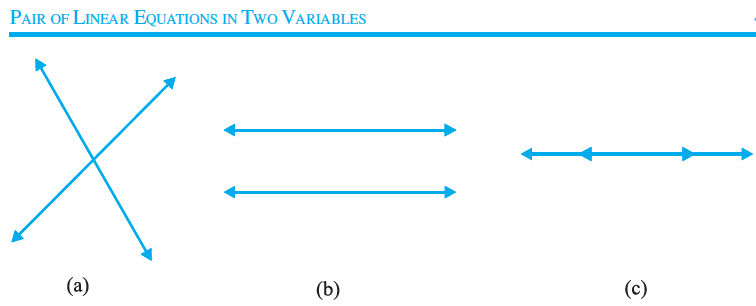
(i) ya to dono lines intersect karengi ek point pe.
(ii) ya to dono lines intersect nahi karegi yani ki parallel rahengi.
(iii) dono lines coincident hongi.
Types of Solution
enn equations ke teen trha ke solutions possible hai
(i) Unique solution
(ii) Infinitely many solutions
(iii) No solution
Example 2
The coach of a cricket team buys 3 bats and 6 balls for Rs.3900. Later, he buys another bat and 3 more balls of the same king for Rs.1300. Represent this situation algebraically and geometrically.
Let the price of a bat be Rs x and that of a ball be Rs y.
It is given that 3 bats and 6 balls are bought for Rs.3900.
∴ 3x+6y=3900
It is also given that one bat and 3 balls of the same king cost Rs. 1300.
∴ x+3y=1300
Algebraic Representation: The algebraic representation of the given situation is
(3x+6y=3900 .........(i)),(x+3y=1300..........(ii))
Graphical Representation: In order to obtain the equivalent graphical representation, we find two points on the representing each equation. That is, we find two solutions of each equation.
We have, 3x+6y=3900
When y=0, we have 3x+0=3900⇒x=39003=1300
When x=0, we have 0+6y=3900⇒y=39006=650
Thus, two solutions of equation (i) are : 
We have, x+3y=1300
When y=100, we have x+300=1300⇒x=1000
When x=100, we have 100+3y=1300⇒3y=1200⇒y=400
Thus, two solutions of equation (ii) are:


Now, we plot the points A(1300,0) and B(0,650) and draw the line AB passing through these two points to represent equation 3x+6y=3900 as shown in Fig. 3.5. To represent the equation x+3y=1300, we plot points the points P(1000,100) and Q(100,400) and the line passing through these points is as shown in Fig.
We observe the two lines representing the two equations are intersecting at the point A(1300,0).
Graphical Method of Solution of a Pair of Linear Equations
Graphical method mei hamara system do tarah ka hota hai Consistent aur Inconsistent
(A) Consistent: Agar do linear equations ke pass kam se kam ek solution hai to system consistent kehlata hai.
(i) Consistent equations with unique solution: Agar do equations ka graph ek point pe intersect krta hai at a unique point then the system is called consistent with unique solution.
For example :
x+2y=4
7x+4y=18 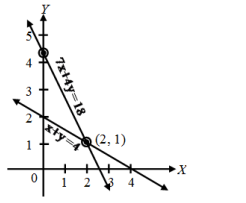
Ess graph ki equation ki lines intersect kar rahi hai ek dusre ko at a unique point (2, 1) i.e. , x = 2, y = 1. to, equation kya hui consistent with unique solution.
(ii) Consistent equations with infinitely many solutions : Agar do equation ki graphical lines coincide karti hai to system consistent kehlata hai with infinitely many solutions.
For example : 2x+4y=9,
3x+6y=272 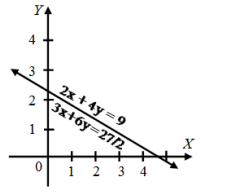
(B) Inconsistent Equation : Agar simultaneous linear equations ke koi solutions nhi hai, to system inconsistent kehlata hai.
(i) No Solution : agar do equation ka solution nhi hota hai to yeh equations nature mei parallel rahengi.
For example : 4x+2y=10
6x+3y=6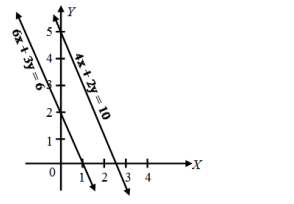
Graphical representation
mein in dono equations ki lines parallel hai, that's why there is no solution and therefore system is inconsistent.
Example 3
Show graphically that the system of equations 2x+4y=103x+6y=12 has no solution.
Graph of 2x+4y=10 :
We have, 2x+4y=10⇒4y=10−2x⇒y=5−x2
When x=1, we have y=5−12=2
When x=3, we have y=5−32=1
Thus, we have the following table : 
Plot the points A(1,2) and B(3,1) on a graph paper. Join A and B and extend it on both sides to obtain the graph of 2x+4y=10 as shown in Fig.
Graph of 3x+6y=12 :
We have, 3x+6y=12⇒6y=12−3x⇒y=4−x2
When x=2, we have y=4−22=1
When x=0, we have y=4−02=2
Thus, we have the following table :

Plot the points C(2,1) and D(0,2) on the same graph paper. Join C and D and extend it on both sides to obtain the graph of 3x+6y=12 as shown in Fig.
We find the lines represented by equations 2x+4y=10 and 3x+6y=12 are parallel. So, the two lines have no common point. Hence, the given system of equations has no solution.
Example 4
Solve graphically the system of equations
x+y=33x−2y=4
Graph of the equation x+y=3 :
x+y=3⇒y=3−x
When x=1, we have y=3−1=2
When x=2, we have y=3−2=1
Thus, we have the following table : 
Plotting the points A(1,2) and B(2,1) and drawing a line joining them, we get the graph of the equation x+y=3 as shown in Fig.
Graph of the equation 3x−2y=4 :
We have, 3x−2y=4⇒2y=3x−4⇒y=3x−42
When x=0, we have y=3×0−42=−2
When x=4, we have y=3×4−42=4
Thus, we have the following table :

Plotting the point C(0,−2) and D(4,4) on the same graph paper and drawing a line joining them, we obtain the graph of the equation 3x−2=4.
Clearly, the two lines intersect at point P(2,1).
Hence, x=2, y=1 is the solution of the given system.
Algebraic Methods of Solving a Pair of Linear Equations
Kahi, baar humme graphical method se accurate answer nahi milta. Graph paper se coordinates padhte hue galtiyo ke chances jada rahte hai. To jada precise result ke liye hum algebraic method ka use karte hai to obtain accurate answer.
Solving System of Equations By Substitution Method
→ Ess method mei sabse pehle hum variable (y) ki value nikalte hai dusre variable (x) ki terms mei. Aur dusri equation, ek linear equation bn jati hai in terms of x aur x ke liye solve ki ja sakti hai.
→Ab secondly hum x ki value first equation mei put karke y ka value nikal sakte hai.
→ Ye method linear equations ke system ko solve karne ke liye use kiya jata hai and this is called method of elimination by substitution.
→ 'Elimination', isliye kuki hum second equation se y ko 'eliminate' karte hai aur 'Substitution' isliye kuki hum 'y' ki value ko substitute karte hai second equation mei.
Working rule :
Let the two equations be
a1x+b1y+c1=0 ................(1)
a2x+b2y+c2=0 ................(2)
Step I. Sabse pehle ek variable ki value nikalenge, let's say y, in terms of x (1)st equation se.
Step II. y ka value jo (1)st equation se aya hai usse (2)nd mei substitute kar denge ab ye equation sirf ek variable mei form ho jayegi x.
Step III. Ab (2)nd equation solve karenge x ki value ke liye.
Step IV. Ab (2)nd equation se jo x ka value aya hai usse hum (1)st equation mei substitute kar denge for the value of y.So ess tarah se hume solution mil gya i.e. the value of x and y.
Remark : Verification is a must to check the answer.
Example 5
Solve the following system of equations by using the method of substitution
2x+3y=93x+4y=5
The given system of equations is
2x+3y=9........(i)3x+4y=5..........(ii)
From equation (i), we get
3y=9−2x⇒y=9−2x3
Substituting y=9−2x3 in equation (ii), we get
3x+4(9−2x3)=5
⇒9x+36−8x3=5
⇒x+36=15
⇒x=−21
putting x=−21 in y=9−2x3, we get
y=9+423=17
Hence, the solution of the given system of equations is x=−21,y=17.
Example 6
The path of a train A is given by the equation x+2y−4=0 and the path of another train B is given by the equation 2x+4y−12=0. Will the rails cross each other ?
The pair of linear equations formed were: x+2y−4=0 ...(1)
2x+4y−12=0 ...(2)
We express x in terms of y from Equation (1) to get
x=4−2y
Now, we substitute this value of x in Equation (2) to get
2(4−2y)+4y–12=0
i.e., 8–12=0
i.e., −4=0
which is a false statement.
Therefore, the equations do not have a common solution. So, the two rails will not cross each other.
Example 7
In a two digit number, the ten's digit is three times the unit's digit. When the number is decreased by 54, the digit are reversed. Find the number.
Let the digit in the unit's place be x and digit in the ten's place be y. Then,
Number =10y+x
According to the given condition, we have
y=3x ...(i)
Number obtained by reversing the digits =10x+y
If the number is decreased by 54, the digits are reversed.
Number −54= Number obtained by reversing the digits.
∴10y+x−54=10x+y
implies 9x-9y= -54 implies x-y= -6"
"...(ii)
Putting y=3x in equation (ii), we get
x−3x=−6⇒x=3
Putting x=3 in y=3x, we get y=9
Hence, the number =10y+x=10×9+3=93.
Solving Systems of Equations By Elimination Method
Step I. Let the two equations be
a1x+b1y+c1=0 ................(1)
a2x+b2y+c2=0 ................(2)
Step II. Dono equations ko kisi factor se multiply karenge taki dono equations ke koi ek variable k co-efficients equal ban jaye eliminate karne ke liye.
Step III. Dono equations ko Add ya Subtract karenge jo hme Step II mei mili hai.
Step IV. Dono equations ko ek variable mei obtain karenge jo hme Step III mei mili hai.
Step V. Jo value hume Step IV mei mili hai usse kisi bhi equation mei substitute karke dusre variable ki value nikalenge.
Example 8
Use elimination method to find all possible solutions of the following pair of linear equations :
2x+3y=8
4x+6y=7
2x+3y=8......... (1)
4x+6y=7.......... (2)
Step 1 : Multiply Equation (1) by 2 and Equation (2) by 1 to make the coefficients of x equal. Then we get the equations as :
4x+6y=16......... (3)
4x+6y=7......... (4)
Step 2 : Subtracting Equation (4) from Equation (3), (4x−4x)+(6y−6y)=16−7
i.e., 0=9, which is a false statement.
Therefore, the pair of equations has no solution.
Example 9
A and B each have certain number of oranges. A says to B ''if you give me 10 of your oranges, I will have twice the number of oranges left with you.'' B replies, ''if you give me 10 of your oranges, I will have the same number of oranges as left with you.'' Find the number of oranges with A and B separately.
Suppose A has x oranges and B has y oranges.
According to the given conditions, we have
x+10=2(y−10)⇒x−2y+30=0 ...(i)y+10=x−10⇒x−y−20=0 ...(ii)
Subtracting equation (ii) from equation (i), we get
−y+50=0⇒y=50
Putting y=50 in equation (i), we get x=70
Hence, A has 70 oranges and B has 50 oranges.
Cross - Multiplication Method
The system of two linear equations
a1x+b1y+c1=0,a2x+b2y+c2=0,
where a1a2≠b1b2, has a unique solution, given by
x=(b1c2−b2c1)(a1b2−a2b1),y=(c1a2−c2a1)(a1b2−a2b1).
PROOF : The given equations are
a1x+b1y+c1=0 ...(i)
a2x+b2y+c2=0 ...(ii)
Multiplying (i) by b2, (ii) by b1 and subtracting, we get
(a1b2−a2b1)x=(b1c2−b2c1)
⇒x=(b1c2−b2c1)(a1b2−a2b1) [∵a1a2≠b1b2⇒(a1b2−a2b1)≠0]
Multiplying (ii) by a1, (i) by a2 and subtracting, we get (a1b2−a2b1)y=(c1a2−c2a1)
⇒y=(c1a2−c2a1)(a1b2−a2b1) [∵(a1b2−a2b1)≠0]
Hence, a unique solution exists, which is given by
x=(b1c2−b2c1)(a1b2−a2b1),y=(c1a2−c2a1)(a1b2−a2b1)
or, xb1c2−b2c1=ya2c1−a1c2=1a1b2−a2b1
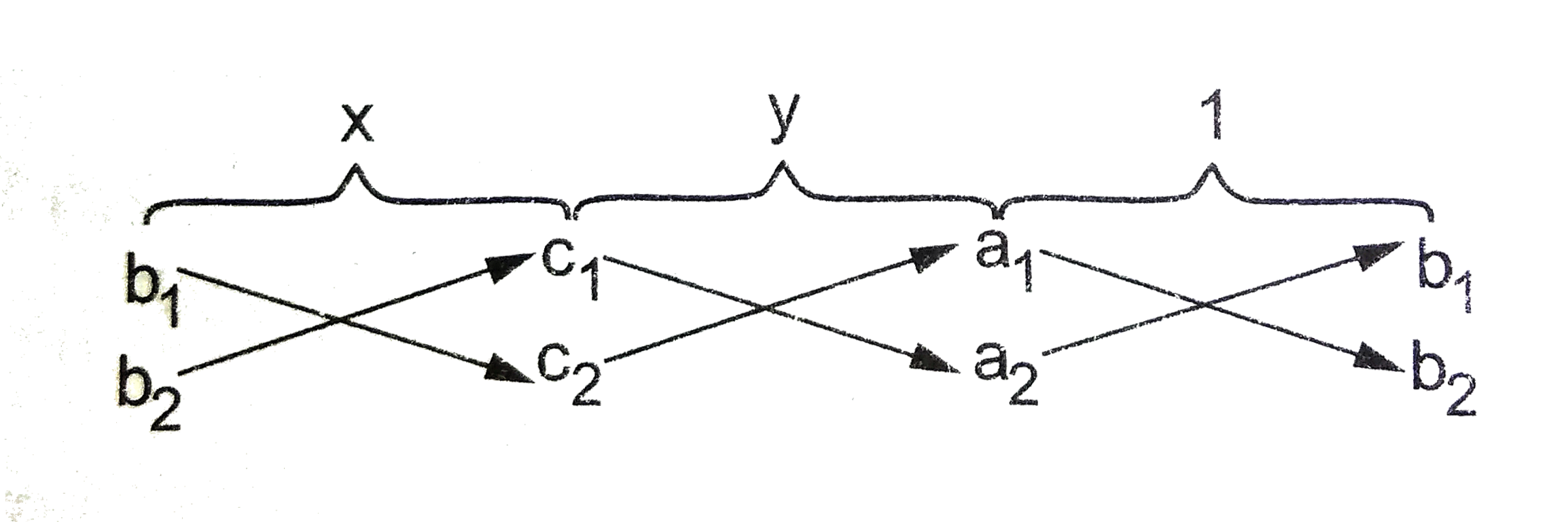
This diagram can be used to remember formula. Numbers with downward arrows are multiplied first and then the product of numbers with upwards arrows is subtracted.
Conditions for Solivability (or Consistency)
From the above proof now we will find some relation between coefficient of both equation
Case 1 : When a1b2−a2b1≠0 i.e., a1a2≠b1b2
If a1b2−a2b1≠0, then we have
x=b1c2−b2c1a1b2−a2b1 and y=c1a2−c2a1a1b2−a2b1
It follows from this that the system of equations a1x+b1y+c1=0 and a2x+b2y+c2=0 is consistent with unique solution, if
a1a2≠b1b2
Case 2 : When a1b2−a2b1=0 i.e., a1a2=b1b2
Let a1a2=b1b2=k. Then, a1=ka2 and b1=kb2
Putting a1=ka2 and b1=kb2 , we get
k(a2x+b2y)+c1=0
From equation, we have
a2x+b2y=−c2
Putting a2x+b2y=−c2 in equation we get
−kc2+c1=0⇒c1=kc2
Thus, we have
a1=ka2,b1=kb2 and c1=kc2
Subtracting the values fo a1,b1,c1 in equation (i), we obtain
k(a2x+b2y+c2)=0a2x+b2y+c2=0
Clearly, every solution of first of these two equations is a solution of the other and vice-versa.
Thus, in this case, the system has infinitely many solutions.
It follows from this that the system of equations a1x+b1y+c1=0 and a2x+b2y+c2=0 is consistent with infinitely many solutions, if
a1a2=b1b2=c1c2.
Case 3 : When a1a2=b1b2≠c1c2
In this case, Let a1a2=b1b2=k. Then, a1=ka2 and b1=kb2
Putting a1=ka2 and b1=kb2, we get
k(a2x+b2y)+c1=0
From equation, we have
a2x+b2y=−c2
Putting a2x+b2y=−c2 in equation we get
−kc2+c1=0⇒c1=kc2 which contradict our assumption, therefore the given system of equations is inconsistent i.e., it has no solution.
Example 10
Solve 4x−7y+28=0,5y−7x+9=0.
The given equations are
4x−7y+28=0 …(i)
−7x+5y+9=0 …(ii)
By cross multiplication, we have
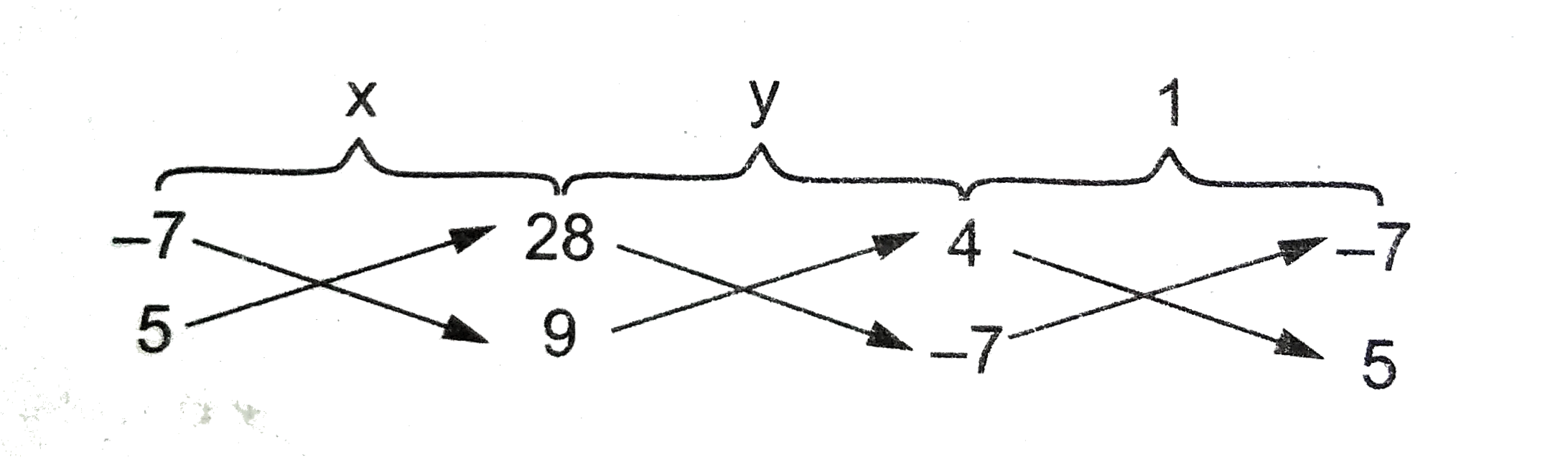
∴x{(−7)×9−5×28}=y{28×(−7)−9×4}=1{4×5−(−7)×(−7)}
⇒x(−63−140)=y(−196−36)=1(20−49)
⇒x−203=y−232=1−29
⇒x=(−203−29)=7andy=(−232−29)=8.
Hence, x=7andy=(−232−29)=8.
Example 11
Find the values of k for which the system of equations
kx−y=2,6x−2y=3
has (i) a unique solution, (ii) no solution. (iii) Is there a value of k for which the given system has infinitely many solutions?
The given system of equations is
kx−y−2=0,6x−2y−3=0,
This is of the form
a1x+b1y+c1=0anda2x+b2y+c2=0.
where a1=k,b1=−1,c1=−2anda2=6,b2=−2,c2=−3.
(i) For a unique solution, we must have a1a2≠b1b2.
∴k6≠−1−2⇒k6≠12⇒k≠3.
Hence, the given of equations will have a unique solution when k≠3.
(ii) For no solution, we must have a1a2=b1b2≠c1c2.
∴k6=−1−2≠−2−3
⇒k6=12≠23
⇒k6=12andk6≠23⇒k=3andk≠4.
Clearly, k=3 also satisfies the condition k≠4.
Hence, the given system of equations will have no solution when k=3.
(iii) For infinitely many solutions, we have a1a2=b1b2=c1c2,
i.e. k6=12=23, which is never possible, as 12≠23.
Hence, there is no real value of k for which the given system of equations has infinitely many solutions.
Example 12
A two digit number is obtained by either multiplying sum of the digits its by 8 and adding 1 or by multiplying the difference of the digits by 13 and adding 2. Find the number.
Let the digits at units place be x and the digit at tens place be y. Then,
Number =10y+x
According to the given conditions, we have
10y+x=8(x+y)+1⇒7x−2y+1=0
and, 10y+x=13(y−x)+2⇒14x−3y−2=0
x−2×−2−(−3)×1=−y7×−2−14×1=17×−3−14×−2
⇒x4+3=−y−14−14=1−21+28
⇒x7=y28=17
⇒x=77=1 and y=287=4
Hence, the number =10y+x=10×4+1=41.
Equations Reducible to a Pair of Linear Equations in Two Variables
Ab hum discuss karenge unn equations ke solution ke baare mei jo linear form mei nhi hai lekin linear form mei reduce kari ja sakti hai kuch substitutions se
For example, 2x+3y=13
5x−4y=−2
yha hum substitute kar sakte hai 1x ko p se aur 1y ko q se .
Example 13
Solve the following pair of equations by reducing them to a pair of linear equations :
5x−1+1y−2=2
6x−1−3y−2=1
Let us put 1x−1=pand1y−2=q. Then the given equations
5(1x−1)+(1y−2)=2 ...(1)
6(1x−1)−3(1y−2)=1 ...(2)
can be written as: 5p+q=2 ...(3)
6p–3q=1 ...(4)
Equations (3) and (4) form a pair of linear equations in the general form. Now, you can use any method to solve these equations. We get p=13 and q=13.
Now, substituting 1x−1 for p, we have
1x−1=13
i.e., x−1=3,i.e.,x=4
Similarly, substituting 1y−2 for q, we get
1y−2=13
i.e, 3=y−2,i.e.,y=5.
Hence, x=4,y=5 is the required solution of the given pair of equations.
Verification : Substitute x=4 and y=5 in (1) and (2) to check whether they are satisfied.
Example 14
Ved travels 600 km to his home partly by train and partly by car. He takes 8 hours if he travels 120 km by train and the rest by car. He takes 20 minutes longer if he travels 200 km by train and the rest by car. Find the speed of the train and the car.
Let the speed of the train be x km/hr and the speed of the car be y km/hr.
Case I : When he travels 120
km by train and the rest by car.
If Ved travels 120 km by train, then,
Distance travelled by car is (600−120) km =480 km.
Now, Time taken to cover 120 km by train =120x hrs [∴ Time = Distance Speed ]
Time taken to cover 480 km by car =480yhrs
It is given that the total time of the journey is 8 hours.
∴120x+480y=8
⇒8(15x+60y)=8
⇒15x+60y=1
⇒15x+60y−1=0 ...(i)
Case II : When he travels 200 km by train and the rest by car.
If Ved travels 200 km by train, then,
Distance travelled by car is (600−200) km =400 km.
Now, Time taken to cover 200 km by train =200x hrs
Time taken to cover 400 km by car =400y hrs
In this case the total time of the journey is 8 hours 20 minutes
∴200x+400y=8 hrs 20 minutes
⇒200x+400y=813 [∴ 8 hrs 20 minutes =82060hrs=813hrs]
⇒200x+400y=253
⇒25(8x+16y)=253
⇒8x+16y=13
⇒24x+48y=1
⇒24x+48y−1=0 ...(ii)
Putting 1x=u and 1y=v in equations (i) and (ii), we get
15u+60v−1=0 ...(iii),
24u+48v−1=0 ...(iv)
By using cross multiplication, we have
u60×−1−48×−1=−v15×−1−24×−1=115×48−24×60
⇒u−60+48=−v−15+24=1720−1440
⇒u−12=v−9=1−720
⇒u=−12−720=160 and v=−9−720=180
Now, u=1x⇒160=1x⇒x=60
and, v=1y=180⇒y=80
Hence, speed of train =60 km/hr and speed of car =80 km/hr.
Summary
1. Two linear equations in the same two variables are called a pair of linear equations in two variables. The most general form of a pair of linear equations is
a1x+b1y+c1=0
a2x+b2y+c2=0
where a1,a2,b1,b2,c1,c2 are real numbers, such that a21+b21≠0,a22+b22≠0.
2. Graphical Method : The graph of a pair of linear equations in two variables is represented by two lines.
(i) If the lines intersect at a point, then that point gives the unique solution of the two equations. In this case, the pair of equations is consistent.
(ii) If the lines coincide, then there are infinitely many solutions — each point on the line being a solution. In this case, the pair of equations is dependent (consistent).
(iii) If the lines are parallel, then the pair of equations has no solution. In this case, the pair of equations is inconsistent.
3. Algebraic Methods : (i) Substitution Method: By substituting a variable from one equation to other equation.
(ii) Elimination Method: By making coefficient of any variable equal and then eliminate that variable by adding or subtracting.
(iii) Cross-multiplication Method: By cross multiplying coefficient of other variable and dividing with 3rd variable.
4. If a pair of linear equations is given by a1x+b1y+c1=0 and a2x+b2y+c2=0, then:
(i) a1a2≠b1b1 : the pair of linear equations is consistent.
a1a2=b1b1≠c1c2: the pair of linear equations is inconsistent.
(iii) a1a2=b1b1=c1c2: the pair of linear equations is dependent and consistent.
5. There are several situations which can be mathematically represented by two equations that are not linear to start with. But we alter them so that they are reduced to a pair of linear equations.
6. 
Let's Revise
- An equation in the form ax+by+c=0, where a, b and c are real numbers, and a≠0 and b≠0, is called a linear equation in two variables x and y.
- Pair of linear equations in two variables:
⇒ General Form:
a1x + b1y + c1 = 0
a2x + b2y + c2 = 0,
yha a1,a2,b1,b2,c1,c2 real numbers hai aur variables x and y ke coefficients kabhi 0 nhi ho saktey.
⇒ Note: a21+b21≠0,a22+b22≠0.
- Representation of linear equations in two variables:
⇒ Algebraic Method
⇒ Graphical method
- Algebraic Method:
(1) Substitution Method: Iss method mein hum kisi ek linear equation se ek variable ki value dusri variable ki form mein nikaltey hai aur us varible ki value dusre equation mein put kar dete hai jisse dusre varibale ki value aati hai aur uska use karkey hume dono variables ki value mil jaati hai i.e. 1st equation se x ki value y ki form mein nikalkey 2nd equation mein x ki value ko put kar dete hai jisse y ki value real numbers ki form mein aati hai aur y ki value ko use karkey hume x ki value bhi mil jaati hai.
(2) Elimination Method: Iss method mein hum dono equations ko kisi aise factors se multiply kartey hai ki dono equation mein ek variable ka coefficient same ho jaye aur fir hum dono equation ko subtract kar dete hai jissey dusre variable ki value aa jaati hai aur fir us variable ki value ka use karkey hume cancelled variable ki value mil jaati hai.
(3) Cross Multiplication Method: For two equations;
a1x + b1y + c1 = 0
a2x + b2y + c2 = 0,
by this method we get x=b1c2−b2c1b2a1−b1a2 and y=c1a2−c2a1b2a1−b1a2 where b2a1−b1a2 ≠ 0.
- Graphical Representation:
(1) Agar wo line ek point pe meet karti hai to ek unique solution milega aur un linear equations ko consistent pair boltey hai.
(2) Agar dono lines parallel hai to iska mtlb hai ki un equations ka koi solution nhi hai aur un linear equation ke pair ko inconsistent pair boltey hai.
(3) Agar lines coincident hai to iska mtlb hai ki infinite solutions hai aur un linear equation ke pair ko dependent(consistent) pair of equations kahtey hai.
- Tips to remember:
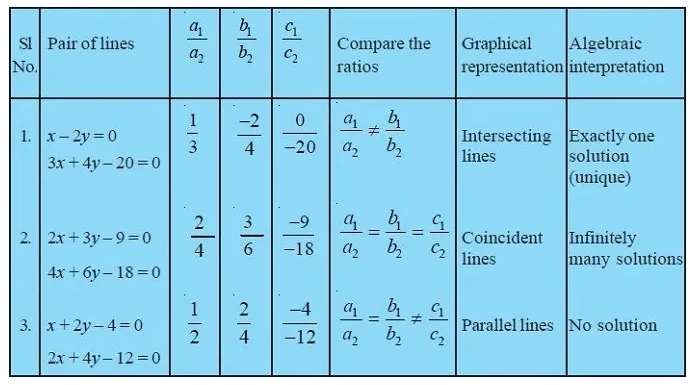
(1) If a1a2 ≠ b1b2 ⇒ intersecting lines ⇒ exactly one solution.
(2) If a1a2=b1b2=c1c2 ⇒ coincident lines ⇒ infinitely many solutions.
(3) a1a2=b1b2 ≠ c1c2 ⇒ parallel lines ⇒ no solution.