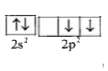
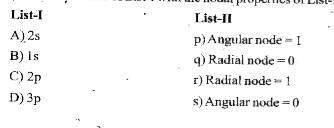LEVEL - III (Matching Column Type) from BRILLIANT PUBLICATION STRUCTURE OF ATOMS for Class 11
| Class 11 | CHEMISTRY |
| Chapter | STRUCTURE OF ATOMS |
| BRILLIANT PUBLICATION | LEVEL - III (Matching Column Type) |
| Medium | English |
| Academic Year | 2023-2024 |
Question 2
Energy required for excitation of electron in 1 mole H atom from ground state to 3rd excited state is 2.67 times (lesser than) dissociation energy per mole of H2(g). Calculate the amount of energy needed to excite each H atom of H2(g) confined in 1 L at 27∘C and 1 bar pressure. (R=0.083 bar litre K−1 mol−1,RB=1.1×10−7m−1).View SolutionQuestion 37
According to Bohr's theory, En= Total energy, Kn = Kinetic energy, Vn =Potential energy, rn□ = Radius of orbit.

Each of these questions contains two statements: Statement 1 and Statement2. Each of these questions has four alternative choices, only one of which is the correct answer.View SolutionQuestion 38
Statement 1 : The plots of probability density and radial probability function versus distance r from the nucleus for any particular orbital are not identical,
Statement 2 : Probability density is ψ2 whereas radial probability function represents probability of finding the electron in a shell of thickness dr.View SolutionQuestion 43
The hydrogen-like species Ļi^(2+) is in a spherically symmetric state S1 with one radial node. Upon absorbing light the ion undergoes transition to a state S2 The state S2 has one radial node and its energy is equal to the ground state energy of the hydrogen atom.
The state S1 is: 1s, 2s, 2p, 3sView SolutionQuestion 44
The hydrogen-like species Ļi2+ is in a spherically symmetric state S1 with one radial node. Upon absorbing light the ion undergoes transition to a state S2 The state S2 has one radial node and its energy is equal to the ground state energy of the hydrogen atom.
Energy of the state S1 in units of the hydrogen atom ground state energy is: View SolutionQuestion 45
The hydrogen-like species Ļi2+ is in a spherically symmetric state S1 with one radial node. Upon absorbing light the ion undergoes transition to a state S2 The state S2 has one radial node and its energy is equal to the ground state energy of the hydrogen atom.
The orbital angular momentum quantum number of the state S2 is:View SolutionQuestion 46
Werner Heisenberg considered the limits of how precisely we can measure the properties of an electron or other microscopic particle. He determined that there is a fundamental limit to how closely we can measure both position and momentum. The more accurately we measure the momentum of a particle, the less accurately we can determine its position. The converse is also true. This is summed up in what we now call the Heisenberg uncertainty principle. The equation is ΔxΔ(mv)≥h4π The uncertainty in the position or in the momentum of a macroscopic object like a baseball is too small to observe. However, the mass of microscopic object such as an electron is small enough for the uncertainty to be relatively large and significant.
If the uncertainties in position and momentum are equal, the uncertainty in the velocity is:View SolutionQuestion 47
Werner Heisenberg considered the limits of how precisely we can measure the properties of an electron or other microscopic particle. He determined that there is a fundamental limit to how closely we can measure both position and momentum. The more accurately we measure the momentum of a particle, the less accurately we can determine its position. The converse is also true. This is summed up in what we now call the Heisenberg uncertainty principle. The equation is ΔxΔ(mv)≥h4π The uncertainty in the position or in the momentum of a macroscopic object like a baseball is too small to observe. However, the mass of microscopic object such as an electron is small enough for the uncertainty to be relatively large and significant.
If the uncertainty in velocity and position is same, then the uncertainty in momentum will be:View SolutionQuestion 48
For one-electron species, the wave number of radiation emitted during the transition of electron from a higher energy state (n2) to a lower energy state (n1) is given by: ¯v=1λ=RH×Z(1n211n22) where RH=2πmsk2c4h3c is Rydberg constant for hydrogen atom. Now, considering nuclear motion, the accurate measurement would be obtained by replacing mass of electron (me) by the reduced mass (μ) in the above expression, defined as μ=mn×memn+me where mn = mass of nucleus. For Lyman series, nt=1 (fixed for all the lines) while n2=2,3,4.... For Balmer series: n1=2 (fixed for all the lines) while n2=3,4,5....
If proton in hydrogen nucleus is replaced by a positron having the same mass as that of an electron but same charge as that of proton, then considering the nuclear motion, the wavenumber of the lowest energy transition of He+ ion in Lyman series will be equal to View SolutionQuestion 49
For one-electron species, the wave number of radiation emitted during the transition of electron from a higher energy state (n2) to a lower energy state (n1) is given by: ¯v=1λ=RH×Z(1n211n22) where RH=2πmsk2c4h3c is Rydberg constant for hydrogen atom. Now, considering nuclear motion, the accurate measurement would be obtained by replacing mass of electron (me) by the reduced mass (μ) in the above expression, defined as μ=mn×memn+me where mn = mass of nucleus. For Lyman series, nt=1 (fixed for all the lines) while n2=2,3,4.... For Balmer series: n1=2 (fixed for all the lines) while n2=3,4,5....
The ratio of the wave numbers for the highest energy transition of electron in Lyman and Balmer series of hydrogen atom isView Solution
All Exercises from BRILLIANT PUBLICATION Class 11 CHEMISTRY STRUCTURE OF ATOMS
- LEVEL - I
- LEVEL - I (HOMEWORK)
- QUESTION
- LEVEL - II (ASSERTION - REASON)
- LEVEL-I
- LEVEL - II
- LEVEL-II
- LEVEL-II (ASSERTION - REASON TYPE)
- LEVEL - III (LINKED COMPREHENSION TYPE)
- LEVEL - III (MATCHING COLUMN TYPE)
- LEVEL - III (MULTIPLE CORRECT ANSWER TYPE)
- LEVEL - III (NUMERICAL TYPE)
- LEVEL - III (SINGLE CORRECT ANSWER TYPE)
- LEVEL - III (STATEMENTTYPE)
 ,
,  ,
, 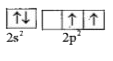 ,
,