द्विघात समीकरण कक्षा 11 गणित
भूमिका
बच्चों! इस अध्याय में हम द्विघात समीकरण के बारे में पढ़ेंगे, यह अध्याय आपके आगे आने वाली प्रतियोगी परीक्षा JEE को ध्यान मे रखकर बनाया गया है, इसमें हम बहुत ही basic से पढ़ते हुए आगे बढ़ेंगे। यह अध्याय प्रतियोगी परीक्षाओं के लिए बहुत महत्वपूर्ण है। प्रतिवर्ष JEE mains और अन्य परीक्षाओं में द्विघात समीकरण से 2-3 प्रश्न देखने को मिलेंगे।
आप प्रतिदिन Doubtnut की कक्षा देखें और अधिक से अधिक अभ्यास करें। आपकी इस अध्याय से संबंधित सभी समस्या दूर हो जाएगीं।
आइये पिछले अध्याय का पुनरावलोकन कर लेते है...
बच्चो कक्षा 10th में हमने द्विघात समीकरण पढ़ा हैं आइये जो हमने पढ़ा था उसे पुनः याद कर लेते हैं -
α और β हो, तो
α+β=−ba,αβ=ca
- गुणनखंड विधि
- पूर्ण वर्ग बनाकर हल करने की विधि
- द्विघातीय सूत्र (श्री धराचार्य सूत्र)
- गुणनखंड विधि
- पूर्ण वर्ग बनाकर हल करने की विधि
- द्विघाती सूत्र-
1. द्विघात समीकरण ax2+bx+c=0 के मूल −b±√b2−4ac2a द्वारा देय होते है, यदि b2−4ac≥0 हो|
2. यदि α व β द्विघात समीकरण ax2+bx+c=0 के दो मूल हैं तो
α=−b−√D2a और β=−b+√D2a
जहाँ D=b2−4ac
गुणनखण्डन द्वारा मिश्रित द्विघात समीकरण को हल करना -
STEP-1 सबसे पहले दिए गए समीकरण को द्विघात समीकरण के व्यापक रूप (ax2+bx+c=0) में बदलते है
STEP-2 मध्य पद को इस प्रकार विभक्त करे कि :
चर x के गुणांकों का गुणनफल = चर x2 का गुणांक × अचर पद
STEP-3 अब दोनों प्राप्त गुणनखंडो को अलग-अलग शून्य के बराबर रखेंगे
पूर्ण वर्ग विधि द्वारा समीकरण को हल करना -
STEP-1 सबसे पहले समीकरण में x2 का गुणांक 1 करेंगे
STEP-2समीकरण को a2+2ab+b2=(a+b)2
रूप मे लाने का प्रयास करते हैं
STEP-3 इसे आगे पूर्ण वर्ग बनाना है
(i) दो भिन्न वास्तविक मूल होते हैं यदि b2−4ac>0 हो।
(ii) दो बराबर मूल (अर्थात सम्पाती वास्तविक मूल) होते है, यदि b2−4ac=0 हो और
(iii) कोई वास्तविक मूल नहीं होते है, यदि b2−4ac<0 हो।
शेषफल प्रमेय (Remainder Theorem)
माना कि P(x) कोई एक या एक से अधिक घात का बहुपद हैं और a कोई वास्तविक संख्या है। यदि P(x) को (x-a) से विभाजित किया जाये तो शेषफल P(a) के बराबर होता है।गुणनखण्ड प्रमेय (Factor Theorem)
माना P(x) कोई एक या एक से अधिक घात का बहुपद हैं और a कोई वास्तविक संख्या इस प्रकार हैं कि P(a)=0,d(x−a),P(x) का एक गुणनखण्ड होता है।विलोमतः यदि (x - a) , P(x) का एक गुणनखण्ड हैं तो P(a)=0
उदाहरण 1
द्विघात समीकरण 9x2−15x+6=0 को पूर्ण वर्ग बनाने वाली विधि द्वारा हल कीजिए।
यहाँ दिया है,
9x2−15x+6=0
⇒x2−159x+69=0
⇒x2−53x+23=0
⇒x2−53x=−23
⇒x2−2(56x)=−23
⇒x2−2(56)x+(56)2
=(56)2−23
⇒(x−56)2=2536−23
⇒(x−56)2=25−2436
⇒(x−56)2=136
⇒x−56=±16
⇒x=56±16
⇒x=56+16=1
(धन चिह्न )
या x=56−16=23
(ऋण चिह्न )
⇒x=1 या 23
उदाहरण 2
k का वह मान ज्ञात कीजिए जिसके लिए द्विघात समीकरण (k+4)x2+(k+1)x+1=0 के मूल वास्तविक तथा बराबर हैं।
दी गई समीकरण की तुलना
Ax2+Bx+C=0
से करने पर,
A=k+4,B=k+1 और C=1
∴D=B2−4AC
⇒D=(k+1)2−4(k+4)
D=k2+2k+1−4k−16
D=k2−2k−15
D=(k−5)(k+3)
यदि दी गई समीकरण के मूल वास्तविक हैं,
तब D=0
⇒(k−5)(k+3)=0
⇒k=5,−3
1.द्विघात समीकरणों के आलेख
चर x में एक द्विघात समीकरण y=ax2+bx+c=0 है, जहाँ a,b,c वास्तविक संख्याएँ हैं और a≠0 है, तो द्विघात की आकृति परवलयाकार (परवलय के आकार की ) होती हैं। परवलय के ऊपर और नीचे की और खुले होना क्रमशः a>0 या a<0 पर निर्भर करता हैं।
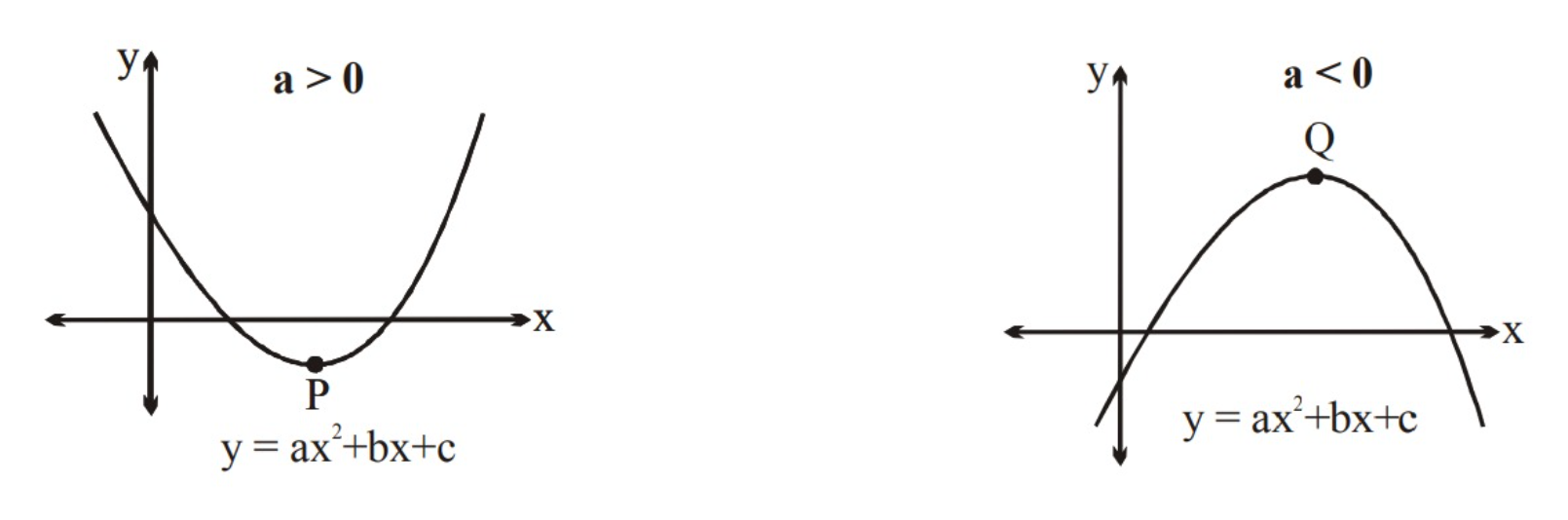
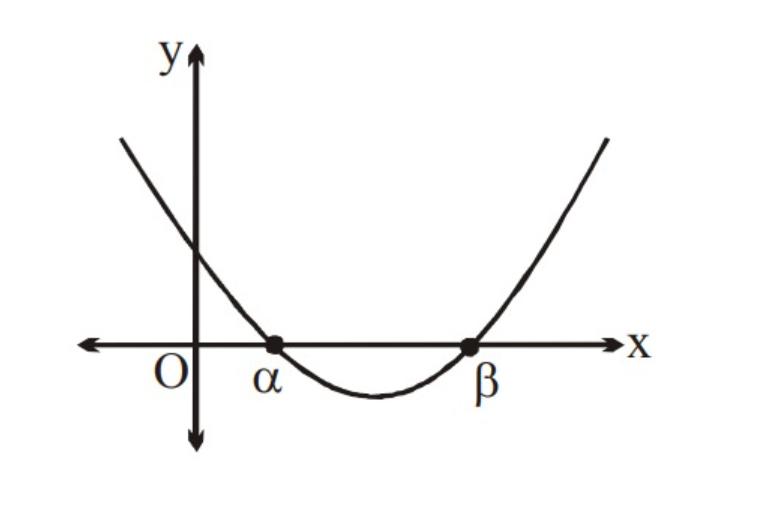
- यदि a>0 तथा D>0 है, तो द्विघात समीकरण के दो मूल होते हैं तथा आरेख x - अक्ष को दो भिन्न बिन्दुओं पर काटता हैं I
(i) α<x<β के लिये y ऋणात्मक है।
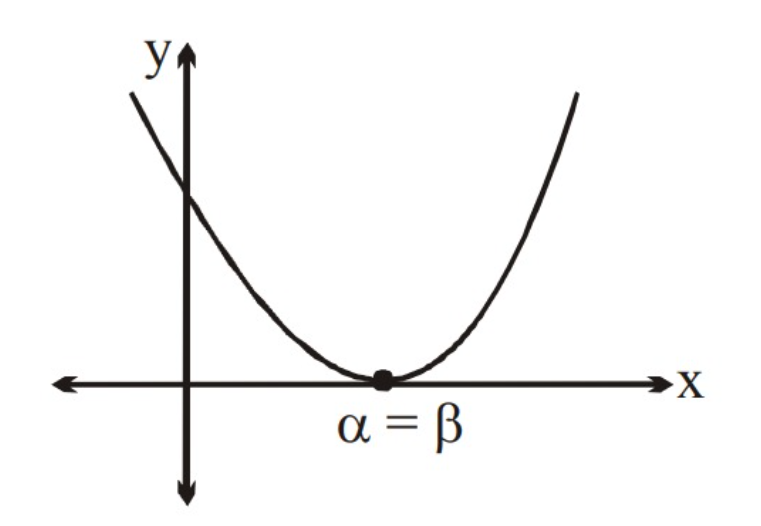
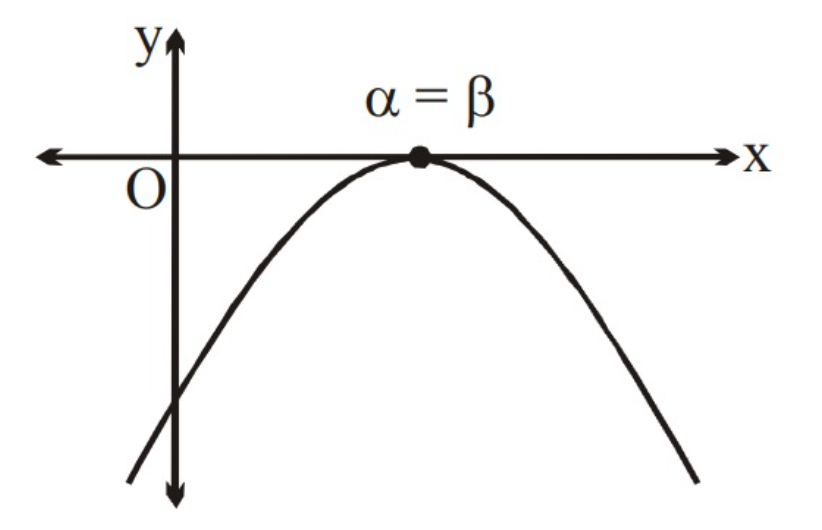
(ii) x<α या x>β के लिये y धनात्मक है। - यदि a>0 तथा D=0 है, तो आरेख x - अक्ष को स्पर्श करता हैं I
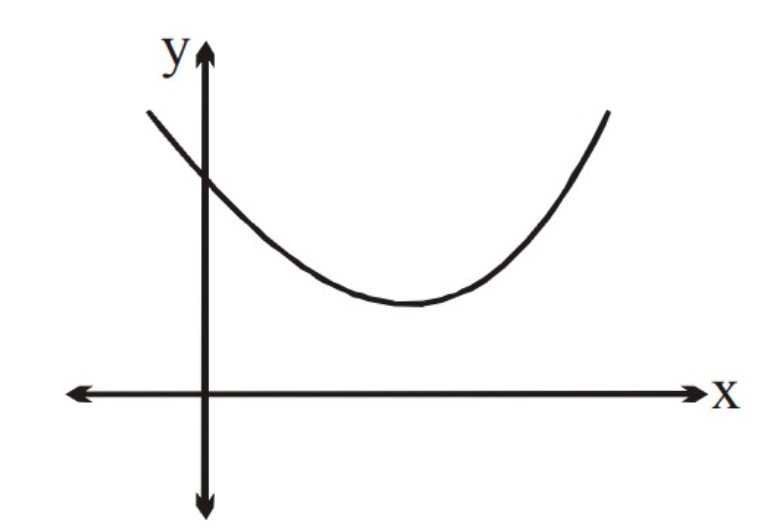
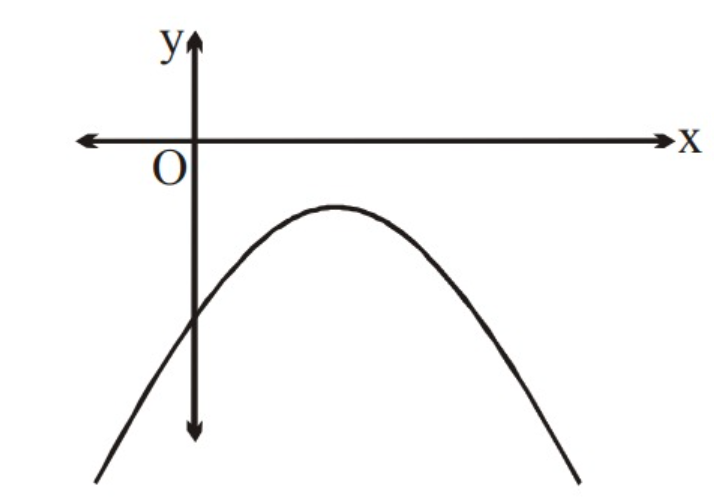
इस प्रकार की समीकरण सभी x∈R के लिए y=a(x−α)2 तथा y≥0 हैं - यदि a>0 तथा D<0 है, तो वक्र पूर्णतया x - अक्ष के ऊपर स्थित हैं I
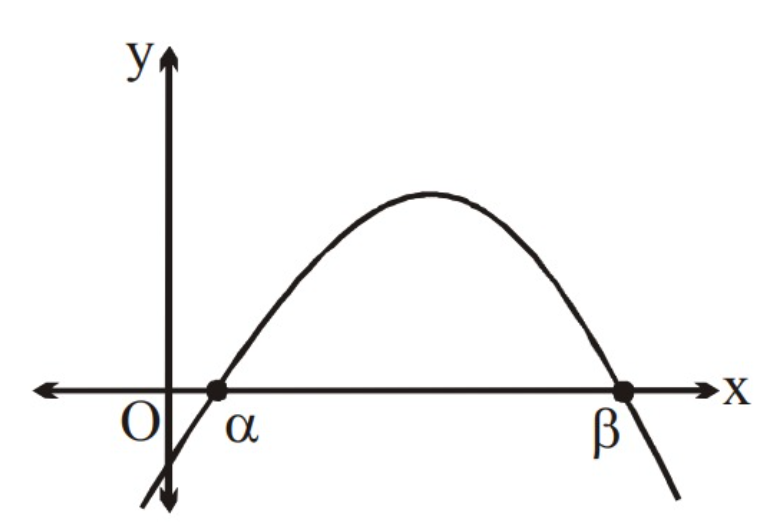
इस स्थिति में काल्पनिक मूल प्रकट होते हैं तथा सभी x∈R के लिए y>0 - यदि a<0 तथा D>0 है, तो द्विघात समीकरण के दो मूल होते हैं तथा आरेख नीचे की और हैं एवं x - अक्ष को दो भिन्न बिन्दुओं पर काटता हैं I
(i) α<x<β के लिये y धनात्मक है।
(ii) x<α या x>β के लिये y ऋणात्मक है। - यदि a<0 तथा D=0 है, तो आरेख x - अक्ष को नीचे स्पर्श करता हैं I
इस प्रकार की समीकरण सभी x∈R के लिए y≤0 हैं - यदि a<0 तथा D<0 है, तो वक्र पूर्णतया x - अक्ष के नीचे स्थित हैं I
इस स्थिति में सभी x∈R के लिए y<0
NOTE:
(1) सभी x∈R के लिये, द्विघात व्यंजक ax2+bx+c, जहाँ a,b,c∈R, धनात्मक है, यदि a>0 तथा D<0 (स्थिति-III)(2) सभी x∈R के लिये, द्विघात व्यंजक ax2+bx+c, जहाँ a,b,c∈R, ऋणात्मक है, यदि a<0 तथा D<0 (स्थिति-VI)
उदाहरण 3
यदि फलन y=16x2+8(a+5)x−7a−5 का आलेख X-अक्ष के ऊपर रहे तो a का मान ज्ञात कीजिये ?
चूंकि फलन y , x-अक्ष के ऊपर हैं अर्थात y धनात्मक होना चाहिए ।
: एक द्विघात समीकरण y=ax2+bx+c=0 में यदि a>0 तथा D<0 है, तो वक्र पूर्णतया x - अक्ष के ऊपर स्थित होता हैं I
चूँकि 16>0 अतः a>0, धनात्मक हैं
अब D<0
⇒ 64(a+5)2+64(7a+5)<0
⇒ a2+17a+30<0
⇒(a+15)(a+2)<0
a∈(−15,−2)
समीकरण के मूल और गुणांक के मध्य सम्बन्ध
α और β हो, तो
α+β=−ba
αβ=ca
α+β+γ=−ba
αβ+βγ+γα=ca
और αβγ=−da
α+β+γ+δ=−ba
αβ+αγ+αδ+βγ+βδ+γδ=ca
αβγ+βγδ+γδα+δαβ=−da
और αβγδ=ea
उदाहरण 4
यदि समीकरण 4β2+λβ−2=0 के मूल kk+1 और k+1k+2 के रूप में हैं तो, λ का मान क्या हैं ?
समीकरण
4β2+λβ−2=0 के मूल kk+1 तथा k+1k+2 हैं
तब, kk+1+k+1k+2=−λ4 . . . (i)
तथा kk+1×k+1K+2=−24
⇒ kk+2=−12
⇒2k=−k−2
⇒k=−23
k का मान समी (i) में रखने पर,
−23−23+1+−23+1−23+2=−λ4
⇒ −2313+1343=−λ4
⇒−2+14=−λ4
⇒λ=7
उदाहरण 5
एक त्रिघाती बहुपद ज्ञात करें जिसके शुन्यकों के योग, दो-दो शुन्यकों को लेकर गुणा करने पर गुणनफलों का योग, इसके तीनों शुन्यकों का गुणनफल क्रमश: 2,-7 और -14 है।
माना कि त्रिघाती बहुपद ax3+bx2+cx+d है।
तथा माना α,β,γ बहुपद ax3+bx2+cx+d के शून्यक हैं |
तब α+β+γ=−ba
⇒2=−ba
αβ+βγ+γα=ca
⇒−7=ca
αβγ=−da
⇒ −14=−da
⇒ax3+bx2+cx+d=0
=a(x3+bax2+cax+da)=0
=(x3+bax2+cax+da)=0
ba,ca,da के मान रखने पर, हम पाते हैं कि
(x3−2x2−7x+14)
इस तरह α,β,γ शून्यक वाला त्रिघाती बहुपद x3−2x2−7x+14 है।
इसे निम्न प्रकार से भी हल कर सकते हैं -
x3−(α+β+γ)x2+(αβ+βγ+γα)x−αβγ
⇒ x3−2x2+(−7x)−(−14)
⇒ x3−2x2−7x+14
वेवी-वक्र विधि
इसे अंतराल की विधि भी कहा जाता हैं
यह विधि f(x)g(x) के रूप की असमानताओं को हल करने के लिए उपयोग की जाती है, यह विधि इस तथ्य का उपयोग करती हैं कि f(x)g(x) केवल अपने मूल और लंबवत स्पर्शोन्मुख पर अपना चिह्न बदल सकता है, इसलिए हम f(x) और g(x) के मूलों का उपयोग विभिन्न अंतरालों पर फलन के ग्राफ को ज्ञात करने के लिए करते हैं।
इस प्रकार की असमिकाओं को हल करने हेतु निम्न प्रक्रिया अपनाते है।
- दिये गये व्यंजक का रेखीय गुणखण्ड करते है।
- सभी गुणनखण्डों में x के गुणांक को धनात्मक बनाते है।
- उन बिन्दुओं को अंकित करते है, जहाँ दिया गया व्यजंक संख्या रेखा पर शून्य हैं या अपरिभाषित है
- संख्या रेखा को दायीं से बायीं और धनात्मक या ऋणात्मक लेते है।
इसे निम्न उदहारण से समझ सकते हैं
3x−x2(x+4)2≥0
step-1. बहुपदो के गुणनखंड करने पर
step-2. सभी गुणनखंडो में चर के गुणांक को धनात्मक बनाने पर
step-3. ऋणात्मक चिह्न को हटाने के लिए दोनों पक्षों को -1 से गुणा करें
(याद रखें कि ऐसा करने से चिह्न बदल जायेंगे ):
step-4.प्रत्येक गुणनखंड को 0 के बराबर करने पर
वेवी- वक्र विधि का उपयोग करके, हम आसानी से उस अंतराल का पता लगा सकते हैं जिसमें दिए गए फलन का मान धनात्मक या ऋणात्मक होता है।
उपर्युक्त उदहारण के मूलो को संख्या रेखा पर निम्न प्रकार से दर्शाया जाता हैं,
संख्या रेखा पर दर्शाते समय निम्न बिंदुओं का ध्यान रखा जाता हैं
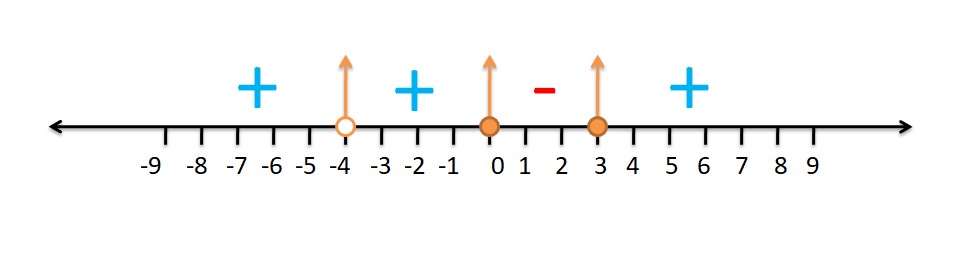
संख्या रेखा पर अंक अंकित करें, सबसे बड़ा मूल 3 से शुरू करें। धनात्मक भाग से एक वक्र शुरू करें व उस बिन्दु पर प्रतिच्छेद करें। वेवी वक्र विधि के अनुसार अब उस व्यंजक के घात पर ध्यान दें वह सम हैं या विषम, यहाँ (x−3) की घात (1) विषम हैं तब हमें प्राप्त अन्य निकटतम मूल (0) से वक्र की दिशा बदलनी होगी अर्थात ऋणात्मक भाग से धनात्मक भाग में, जबकि यदि घात सम होती तो वक्र ऋणात्मक भाग मे ही होता। अतः गुणक -4 के लिए वक्र की दिशा नहीं बदलेगी चूंकि इसके व्यंजक (x+4) की घात सम (2) है।
अब यदि असमिका ≥ या ≤ हो तब हमें x के उन मानो को लेना हैं जिसके लिए असमिका 0 के बराबर हो। जबकि वेवी वक्र विधि के अनुसार हमें ऐसे व्यंजकों के मूल को नहीं लेना हैं जो हर मे (-4) हो।
अतः हमारा उत्तर x∈[0,3] होगा।
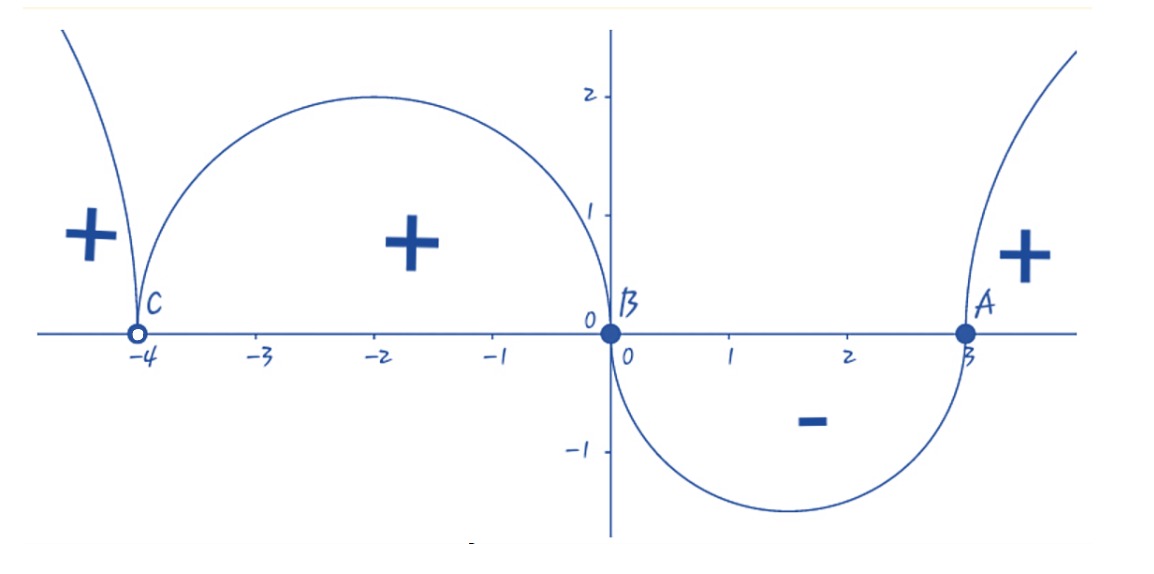
नीचे दिए गए चित्र से भी इसे दर्शा सकते हैं -
उदाहरण 6
x के मानों का वह समुच्चय प्राप्त करो जिसके लिए (x−1)5(x−2)3(x+3)10x2(x−4)<0
माना,
f(x)= (x−1)5(x−2)3(x+3)10x2(x−4)
उन बिन्दुओं को अंकित करते है, जहाँ दिया गया व्यजंक संख्या रेखा पर शून्य हैं या अपरिभाषित है
अब वेवी वक्र विधि से सबसे दायी ओर + से शुरुआत होती हैं।
इसके बाद जहाँ विषम घात होती हैं वहां चिह्न बदल जाता हैं और जहाँ सम घात होती हैं वहां चिह्न समान रहता हैं।
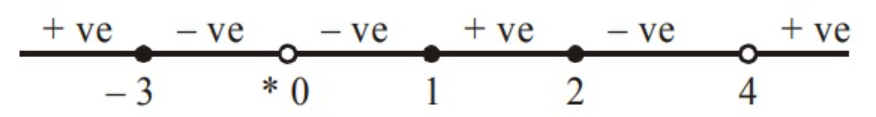
f(x)<0
⇒x∈[−3,0)∪(0,1]∪[2,4)
द्विघात फलन को दो रैखिक गुणनखंडो के रूप में व्यक्त करना
(Resolving a general quadratic expression in x and y into two linear factors)
f(x,y)=ax2+2hxy+by2+2gx+2fy+cउपरोक्त समीकरण को x में द्विघात समीकरण रूप में लिखने पर
ax2+2x(hy+g)+by2+2fy+c=0
x के लिये हल करने पर
द्विघाती सूत्र से
x
=−(hy+g)±√(hy+g)2−a(by2+2fy+c)a
ax+hy+g
=±√y2(h2−ab)+2y(hg−af)+(g2–ac)
अतः f(x, y) को दो रेखीय गुणनखण्डों के गुणनफल के रूप में लिखा जा सकता हैं यदि, वर्गमूल में दी गई राशि पूर्ण वर्ग हो ।
चूंकि वर्गमूल में दी गई राशि y में द्विघात समीकरण है। इसलिये यह पूर्ण वर्ग होगी यदि और केवल यदि D=0
(hg−af)2−(h2−ab)(g2−ac)=0
⇒abc+2fgh−af2−bg2−ch2=0
जो कि वांछित प्रतिबन्ध है।
इसे सारणिक रूप में लिखने पर
∣∣ ∣ ∣∣ahghbfgfc∣∣ ∣ ∣∣=0
उदाहरण 7
m का वह मान ज्ञात करो जिससे समीकरण 2x2+mxy+3y2−5y−2=0 के रेखीय गुणनखंड संभव हो जाये
2x2+mxy+3y2−5y−2=0
3y2+y(mx−5)y+2x2−2=0
a=3
b=(mx−5)
c=(2x2−2)
b2−4ac
=(mx−5)2−4×3×(2x2−2)
b2−4ac
=m2⋅x2+25−10mx−24x2+24
=x2(m2−24)−10mx+49
यह x में द्विघात समीकरण है।
यह पूर्ण वर्ग होगी यदि और केवल यदि D=0
b2=4ac
(10m)2=4×(m2−24)×49
25m2=49m2−49×24
m2=49
m=±7
2. द्विघात समीकरण ज्ञात करना
द्विघात समीकरण का निर्माण जिसके मूल α और β के सममित व्यंजक हैं
(Formation of quadratic equation whose roots are symmetric expression of α and β)
माना α तथा β द्विघात समीकरण ax2+bx+c=0 के मूल है, तो अन्य द्विघात समीकरण जिसके मूल 2α+3,2β+3 हैं उसे ज्ञात करते हैं
माना 2α+3=y
⇒α=y−32
दी गई समीकरण में α का मान रखने पर
चूंकि
α, द्विघात समीकरण ax2+bx+c=0 का एक मूल हैं अतः इसे समीकरण में रखने पर समीकरण का मान शून्य मिलेगा
a(y−3)24+b(y−3)2+c=0
a(y–3)2+2b(y−3)+4c=0
ay2+2y(b–3a)+9a–6b+4c=0
अतः
y में एक द्विघात प्राप्त होती है।
y को x से प्रतिस्थापित करने पर हमें वांछित समीकरण निम्न प्रकार प्राप्त होती है
ax2+2x(b−3a)+9a−6b+4c=0
अन्य उदाहरण
यदि α, β समीकरण ax2+bx+c=0 के मूल है, तो वह समीकरण जिसके मूल
- −α,−β
⇒ax2–bx+c=0 (x को −x से प्रतिस्थापन करने पर) - 1α,1β
⇒cx2+bx+a =0 (x को 1x से प्रतिस्थापन करने पर) - kα,kβ
⇒ax2+kbx+k2c=0 (x को xk से प्रतिस्थापन करने पर) - k+α,k+β
⇒a(x−k)2+b(x−k)+c=0 (x को (x−k) से प्रतिस्थापन करने पर) - αk,βk
⇒k2ax2+kbx+c=0 ( x को kx से प्रतिस्थापन करने पर)
उदाहरण 8
यदि समीकरण x2−5x+15=0 के मूल α तथा β हो वह समीकरण ज्ञात कीजिए जिसके मूल α2+β2 व αβ2 हो
चूँकि x2−5x+15=0 के मूल α तथा β हैं
अतः
∴ α+β=5 तथा αβ=15
माना समीकरण x2+px+q=0 के मूल α2+β2 व αβ2 हैं
∴ मूलो का योगफल,
α2+β2+αβ2=−p
⇒ (α+β)2−2αβ+αβ2=−p
⇒ 25−30+152=−p
⇒p=−52
तथा मूलो का गुणनफल,
(α2+β2)(αβ2)=q
⇒ [(α+β)2−2αβ](αβ2)=q
⇒ q=(25−30)152
q=−752
अतः p=−52,q=−752
उदाहरण 9
यदि α तथा β समीकरण x2+x+1=0 के मूल है, तब वह समीकरण क्या हैं जिसके मूल α19 और β7 हैं ?
दी गई द्विघात समीकरण, x2+x+1=0 के मूल निकालने पर
श्री-धराचार्य विधि से
x=−1±√1−42
=−1±i√32
x=−1+i√32,−1−i√32
या
x=ω तथा ω2
प्रश्न से मूल α,β हैं
अर्थात α=ω तथा β=ω2
⇒ α19=ω19=(ω3)6⋅ω=(1)6⋅ω=ω
⇒ β7=(ω2)7=ω14=(ω3)4⋅ω2 =(1)4⋅ω2=ω2
मूलो का योगफल
=α19+β7
=ω+ω2=−1
[चूंकि 1+ω+ω2=0]
तथा मूलो का गुणनफल
=α19⋅β7
=ω⋅ω2
=ω3=1
[∵ ω3=1]
अतः अभीष्ट द्विघात समीकरण, जिसके मूल α19 तथा β7 हैं निम्न हैं
x2−(α19+β7)x+(α19⋅β7)=0
⇒ x2−(−1)x+(1)=0
∴ x2+x+1=0
उभयनिष्ठ मूलो के लिए प्रतिबन्ध
जब उभयनिष्ठ मूलो की संख्या एक हो
(Condition for one common roots )
तथा a2x2+b2x+c2=0
का उभयनिष्ठ मूल α है।
अर्थात्
a1α2+b1α+c1=0
a2α2+b2α+c2=0
वज्र गुणन द्वारा
α2b1c2−b2c1=αa2c1−a1c2=1a1b2−a2b1
α=b1c2−b2c1a2c1−a1c2=a2c1−a1c2a1b2−a2b1
जो कि वांछित समीकरण है। यह एक प्रतिबन्ध भी हैं
अतः दो द्विघात समीकरणों के बीच एक मूल उभयनिष्ठ हो तो वह उपर्युक्त प्रतिबन्ध को संतुष्ट करेगा
जब उभयनिष्ठ मूलो की संख्या दो हो
(Condition for two common roots )
तथा a2x2+b2x+c2=0
के मध्य दो उभयनिष्ठ मूल है।
तब इनके संगत अनुपात आपस में बराबर होंगे अर्थात
a1a2=b1b2=c1c2
यह एक प्रतिबन्ध हैं
उदाहरण 10
द्विघात समीकरणों ax2+4x+20=0 तथा 16x2+bx+40=0 के दोनों मूल उभयनिष्ठ हैं । a तथा b का मान ज्ञात कीजिए ।
चूँकि द्विघात समीकरणों ax2+4x+20=0 तथा 16x2+bx+40=0 के दोनों मूल उभयनिष्ठ हैं , अतः
∴ a16=4b=2040
⇒a=2040×16=8
तथा
b=4020×4=8
∴ a=8,b=8
उदाहरण 11
दो समीकरणों x2+mx+1=0 और x2+x+m=0 के लिए m का मान ज्ञात कीजिये जिससे समीकरणों में कम -से - कम एक मूल उभयनिष्ठ हों ?
माना दिए हुए समीकरणों का उभयनिष्ठ मूल α हैं ।
तब, α2+mα+1=0
तथा α2+α+m=0
⇒ α2m2−1=α1−m=11−m
[व्रज -गुणन विधि से]
⇒ α1−m=11−m⇒α=1
तथा α2m2−1=11−m
⇒ α2−α2m=m2−1
[∵α=1]
1−m=m2−1
⇒ m2+m−2=0
⇒ (m+2)(m−1)=0
∴ m=1 तथा −2
3.उच्चतम एवं निम्नतम मान
बच्चो अब तक हमने द्विघात समीकरण ज्ञात करना सीखा हैं आगे हम द्विघात समीकरणों तथा परिमेय फलनों के उच्चतम व निम्नतम मान ज्ञात करेंगे।
y=ax2+bx+c भुज x=−b2a वाले बिन्दु पर a<0 या a>0 के अनुसार अधिकतम एवं न्यूनतम मान प्राप्त करता है।
y=a⋅x2+bx+c
y=a(x2+bxa+ca)
=a(x2+2⋅b2a⋅x+b24a2−b24a2+ca)
=a[(x+b2a)2+ca−b24a2]
=a(x+b2a)2+4ac−b24a
=a(x+b2a)2−D4a
अब यदि a<0 है, तब
y का मान −∞ की ओर बढ़ेगा चूंकि a<0 के लिए a(x+b2a)2 का मान ऋणात्मक होगा।
अतः इसका ymin निकालना संभव नहीं होगा परंतु यदि x+b2a=0 हो तब a(x+b2a)2=0 का मिलेगा।
अतः a<0 व x=−b2a पर y का अधिकतम मान निकाला जा सकता है।
अतः ymax=−D4a है।
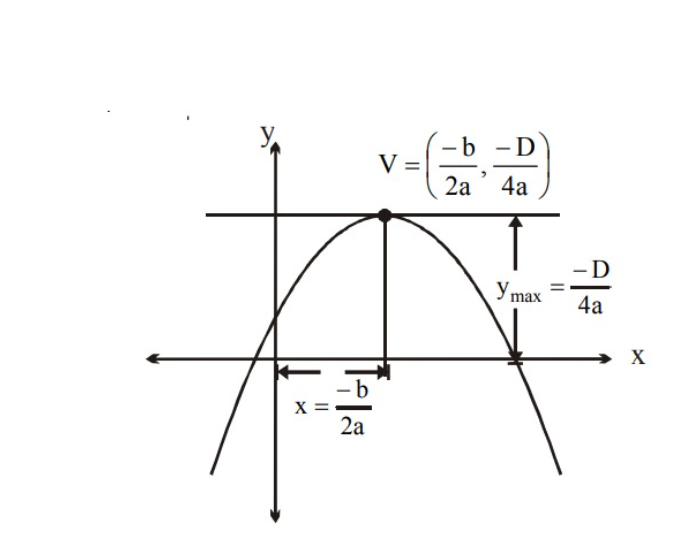
यदि a>0 है, तब
y का मान +∞ की ओर बढ़ेगा चूंकि a>0 के लिए a(x+b2a)2 का मान धनात्मक होगा।
अतः इसका ymax निकालना संभव नहीं होगा परंतु यदि x+b2a=0 हो तब a(x+b2a)2=0 का मिलेगा।
अतः a>0 व x=−b2a पर y का न्यूनतम मान निकाला जा सकता है।
अतः ymin=−D4a है।
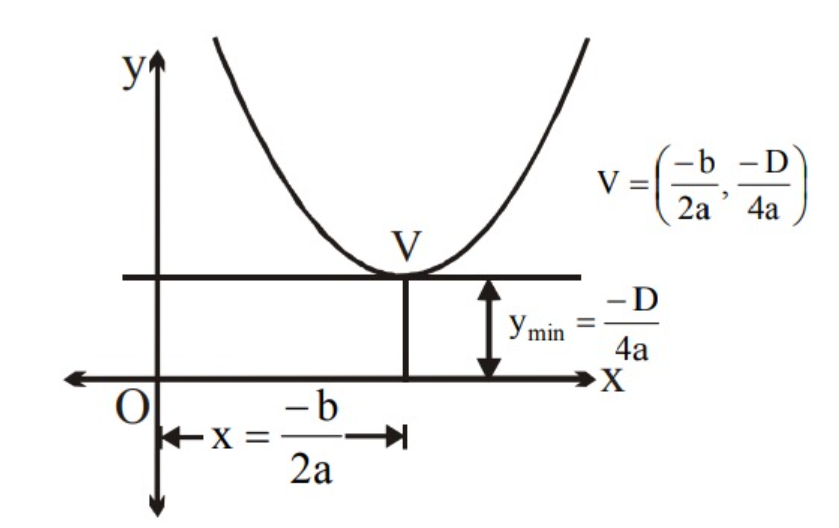
NOTE:
न्यूनतम तथा अधिकतम मान पूर्ण वर्ग बनाकर प्राप्त किये जा सकते हैं।
4. मूलो की स्थिति ज्ञात करना
माना एक द्विघात समीकरण f(x)=ax2+bx+c, a>0 हैं तथा इसके मूल संख्या रेखा पर स्थित है, जिनके मान विभिन्न है।
TYPE - 1(a): द्विघात समीकरण के दोनों मूल एक विशेष संख्या (d) से बड़े है।
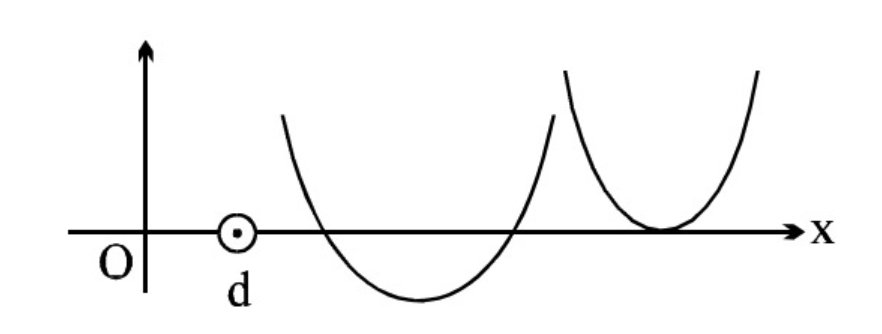
तब इसके लिये आवश्यक एवं पर्याप्त प्रतिबन्ध निम्न है
- a>0
- D≥0
- f(d)>0
- −b2a>d
TYPE - 1(b): द्विघात समीकरण के दोनों मूल एक विशेष संख्या (d) से छोटे (कम) है।
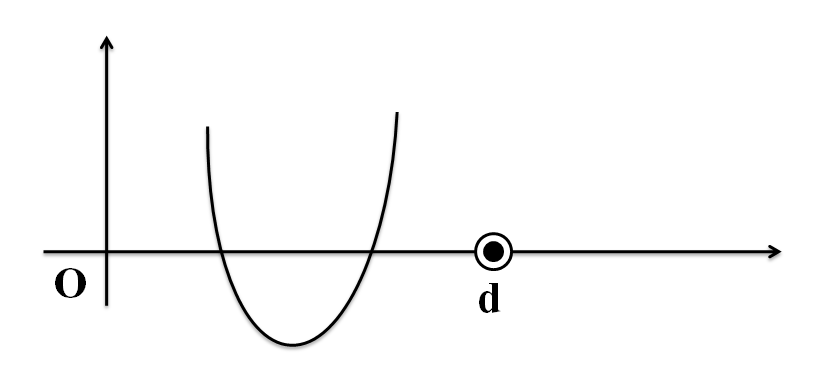
तब इसके लिये आवश्यक एवं पर्याप्त प्रतिबन्ध निम्न है
- a>0
- D≥0
- f(d)>0
- −b2a<d
TYPE - 2: दोनों मूल एक विशेष संख्या (d) के दोनों ओर स्थित है अर्थात एक मूल d से बड़ा हैं तथा अन्य मूल d से छोटा हैं या d दी गई समीकरण के मूलों के मध्य स्थित है।
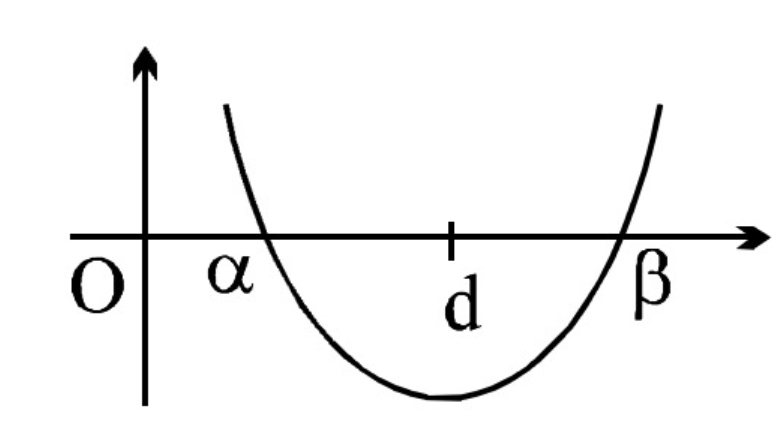
तब इसके लिये प्रतिबन्ध
- यदि a>0
तब f(d)<0 - यदि a<0
तब f(d)>0
यहाँ विविक्तकर उपयोगी नहीं है।
TYPE - 3: ठीक एक मूल अंतराल (d ,e ) में स्थित है।
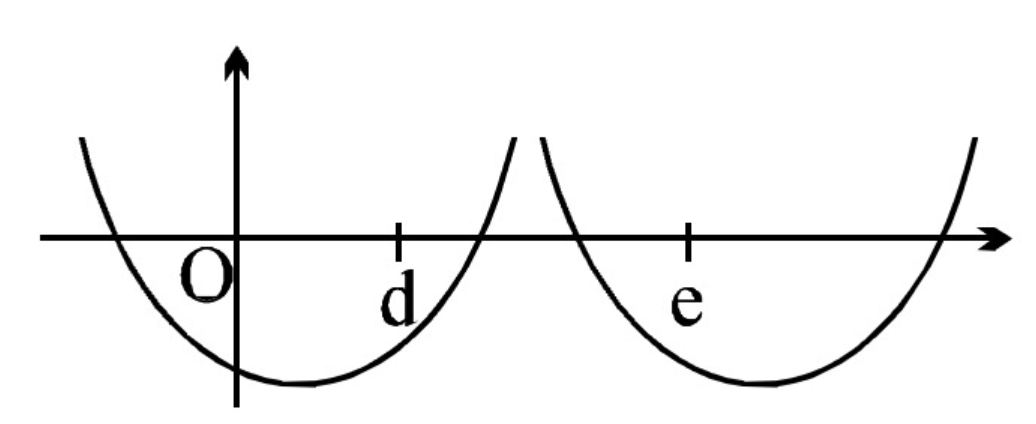
तब इसके लिये प्रतिबन्ध
- a≠0
- f(d).f(e)<0
- एक ओर अन्य स्थिति जबकि f(d).f(e)=0
(a) f(d)=0 के लिये अन्तिम बिन्दुओं की जाँच करते हैं अर्थात् एक मूल "d" हैं ।
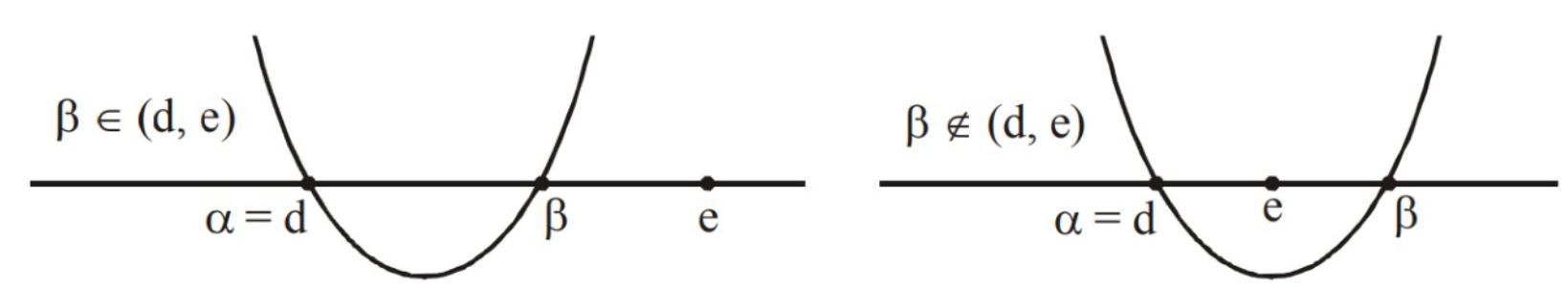
तब हम जांच करते हैं कि समीकरण का दूसरा मूल "d" तथा "e" के मध्य स्थित हैं या नहीं यदि दूसरा मूल इनके मध्य स्थित होता हैं तो हम उस अन्तः बिंदु को भी सम्मिलित करते है। (चित्र-1 )
और यदि दूसरा मूल इनके मध्य स्थित नहीं होता हैं तो हम उस अन्तः बिंदु को सम्मिलित नहीं करते है। (चित्र-2 )
(b) इसी प्रकार f(e)=0 के लिये हम दुसरे मूल की स्थिति जाँच करते है, कि यह "d" तथा "e" के मध्य स्थित हैं या नहीं ।
TYPE-4: जब दोनों मूल संख्या d तथा e (d<e) के मध्य है।
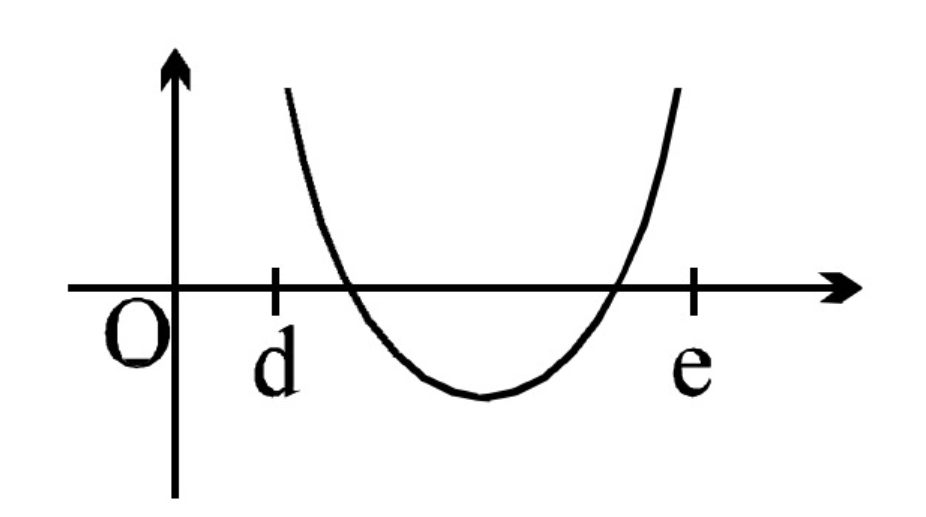
तब इसके लिये प्रतिबन्ध निम्न हैं
- a>0
- D≥0
- f(d)>0
- f(e)>0
- d<−b2a<e
TYPE-5: एक मूल e से बड़ा हैं तथा दूसरा मूल d से छोटा है।
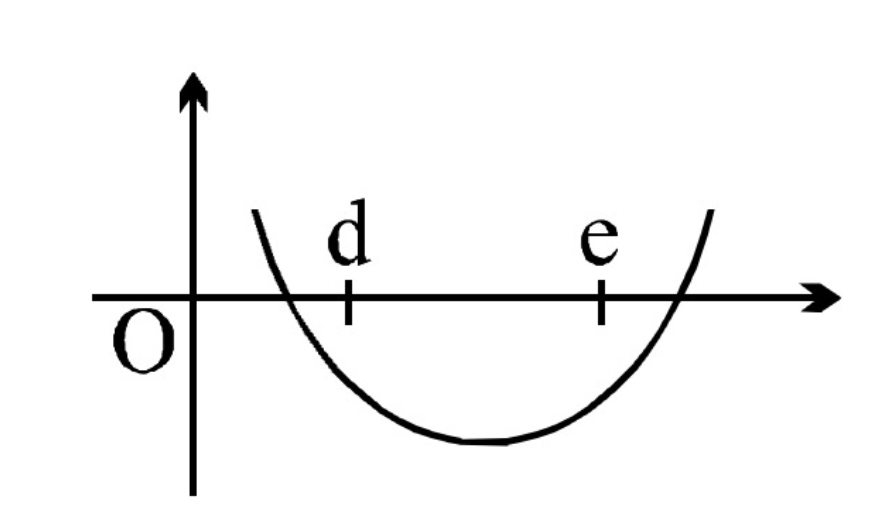
तब इसके प्रतिबन्ध निम्न है:
- f(d)<0 तथा f(e)<0 यदि (a>0)
द्विघात समीकरण के मूलों का चिह्न
समीकरण a⋅x2+bx+c=0 के लिए जिसमें a≠0, a,b,c∈R
- जब दोनों मूल धनात्मक है।
D≥0
−ba>0
ca>0 - दोनों मूल ऋणात्मक हो
D≥0
−ba<0
ca>0 - दोनों मूल विपरीत चिन्ह के हो -
यदि समीकरण में मूल α, β में से एक मूल धनात्मक और दूसरा मूल ऋणात्मक हो तो (अर्थात विपरीत चिह्न के हो तो )
ac<0 अथवा ca<0 - दोनों मूल विपरित चिन्ह के हो एवं परिमाण में एक समान हो
b=0
उदाहरण 12
यदि द्विघातीय समीकरण x2−2kx+k2+k−5=0 के दोनों मूल 5 से कम हैं तो k किस अंतराल में स्थित हैं ?
माना
f(x)=x2−2kx+k2+k−5
अब यदि द्विघात समीकरण के दोनों मूल एक विशेष संख्या (d) से छोटे (कम) है। तब इसके लिये आवश्यक एवं पर्याप्त प्रतिबन्ध निम्न है
- a>0
- D≥0
- f(d)>0
- −b2a<d
step (1)
a>0
1>0
step (2)
D≥0
=4k2−4(k2+k−5)≥0
=−4k+20≥0
⇒k≤5 . . . (i)
step (3)
मूलो का योगफल =−b2a<d
=−b2a<5
2k2<5
k<5 . . .(ii)
step (4)
⇒ f(5)>0
⇒ 25−10k+k2+k−5>0
⇒ k2−9k+20>0
⇒ k2−5k−4k+20>0
⇒ (k−5)(k−4)>0
∴ k<4 या k>5
समी (i), (ii) व (iii) से, k<4
उदाहरण 13
a का वह मान ज्ञात कीजिये , जिसके लिए समीकरण 2x2−2(2a+1)x+a(a+1)=0 का एक मूल a से छोटा व दूसरा मूल a से बड़ा होगा।
चूँकि a, समीकरण के दोनों मूलो के मध्य स्थित हैं ।
दोनों मूल एक विशेष संख्या (d) के दोनों ओर स्थित है। अर्थात एक मूल d से बड़ा हैं तथा अन्य मूल d से छोटा हैं या d दी गई समीकरण के मूलों के मध्य स्थित है। तब इसके लिये प्रतिबन्ध
- यदि a>0
तब f(d)<0 - यदि a<0
तब f(d)>0
माना
f(x)=2x2−2(2a+1)x+a(a+1)
चूँकि प्रश्न से a>0 अतः f(a)<0
⇒ 2a2−2a(2a+1)+a(a+1)<0
⇒ −a2−a<0⇒a2+a>0
⇒ a(1+a)>0
∴ a>0 या a<−1
a∈(−∞,−1)∪(0,∞)
उदाहरण 14
a का मान ज्ञात कीजिये जिसके लिए समीकरण x2+ax−4=0 का सबसे छोटा मूल (−1,2) के अंतराल में स्थित हैं
ठीक एक मूल अंतराल (d ,e ) में स्थित है। तब इसके लिये प्रतिबन्ध f(d).f(e)<0
यहां दिया हुआ हैं की छोटा मूल (-1,2) अंतराल में स्थित हैं अतः f(−1).f(2)<0
f(x)=x2+ax−4=0
f(−1)=1−a−4=−a−3
f(2)=4+2a−4=2a
प्रतिबन्ध से
f(−1).f(2)<0
(−a−3)(2a)<0
दो संख्याओ का गुणनफल शून्य से छोटा होता हैं यदि उनमे से एक संख्या धनात्मक तथा दूसरी संख्या ऋणात्मक हो
−a−3>0 तथा 2a<0
a<0 तथा a<−3
⇒a<−3
उदाहरण 15
द्विघात समीकरण x2−(m−3)x+m=0 (m∈R) में m का वह मान ज्ञात करो जिसके लिए इसके मूल
(i) वास्तविक एवं भिन्न-भिन्न हो
(ii) समान हो
(iii) अवास्तविक हो
(iv) विपरित चिन्ह के हो
(v) परिमाण में समान हो परन्तु चिन्ह विपरित हो।
(vi) धनात्मक हो
(vii) ऋणात्मक हो
(viii) कम से कम एक धनात्मक हो
माना f(x)=x2−(m−3)⋅x+m
(1) दोनो मूल वास्तविक एवं भिन्न-भिन्न हो
⇒D>0
⇒(m−3)2−4m>0
⇒m2−10m+9>0
⇒(m−1)(m−9)>0
⇒m∈(−∞,1)∪(9,∞)
(2) दोनो मूल एक समान हो
D=0
⇒m=9 या m=1
(3) दोनो मूल काल्पनिक हो
D<0
(m−1)(m−9)<0
⇒m∈(1,9)
(4) दोनो मूलो का चिन्ह एक दसरे से विपरीत हो
f(0)<0
m<0
m∈(−∞,0)
(5) दोनो मूलो का परिमाण समान हो लेकिन चिन्ह भिन्न हो
मूलो का योग शून्य होगा एवं D≥0
⇒m∈(−∞,1]∪[9,∞)
तथा m−3=0 , अर्थात् m=3
m का कोई भी मान नहीं होगा।
(6) दोनो मूल धनात्मक हो ,
D≥0
मूलों का योग एवं गुणनफल भी धनात्मक होगा
m−3>0 , तथा m>0
तथा m∈(−∞,1]∪[9,∞)
⇒m∈[9,∞)
(7) दोनो मूल ऋणात्मक होंगे
D≥0
मूलों का योग ऋणात्मक होगा एवं गुणनफल धनात्मक होगा
m−3<0, m>0, m∈(−∞,1]∪[9,∞)
⇒m∈(0,1]
(8) कम से कम एक मूल धनात्मक हो
(iv) एवं (vi) का संघ और m=0 (अर्थात् एक मूल शून्य भी हो सकता है)
m∈(−∞,0]∪[9,∞)
उदाहरण 16
द्विघात समीकरण x2−(m−3)x+m=0 (m∈R) में m का वह मान ज्ञात करो जिसके लिए इसके
(i) दोनो मूल अन्तराल (1, 2) में उपस्थित हो
(ii) कम में कम एक मूल अन्तराल (1, 2) में उपस्थित हो
(iii) एक मूल 2 से ज्यादा हो व दूसरा 1 से कम हो।
माना f(x)=x2−(m−3)⋅x+m
(1) दोनो मूल अन्तराल (1, 2) स्थित हो
f(1)>0
1−m+3+m>0
4>0
f(2)>0
4−2m+6+m>0
m<10
1<m−32<2
5<m<7......(1)
एवं D≥0
उदाहरण 15 से
m∈(−∞,1]∪[9,∞).....(2)
समीकरण 1 व 2 से
⇒ कोई हल नहीं
(2)
Case a:
केवल और केवल 1 मूल (1, 2) के मध्य उपस्थित हो
f(1).f(2)<0
m>10
Caseb
दोनो मूल (1, 2) के मध्य स्थित हो , (1) से m∈ϕ
अतः कम से कम एक मूल अन्तराल में उपस्थित होगा यदि
m∈(10,∞)
(3) एक मूल 2 से ज्यादा व दूसरा 1 से कम होने की परिस्थिति
f(1)<0.....(1)
f(2)<0
(1) से, f(1)<0 होना चाहिए , परन्तु f(1)=4
अतः उपरोक्त परिस्थिति हेतु m का कोई भी मान नहीं होगा।
5. लघुगणक असमानताएं
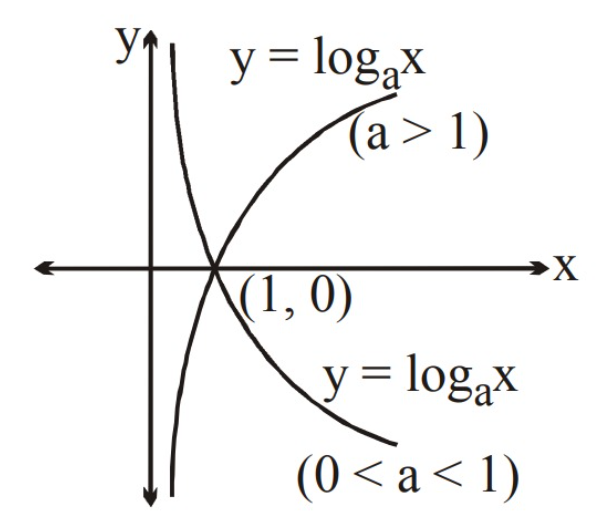
a>1 के लिये, logax>logay हैं तो ⇒x>y ,
इसका अभिप्राय यह हैं कि यदि आधार (a), इकाई से बड़ा है, अर्थात (a>1) तो जब असमिका से logarithm हटाया जाता हैं तो असमिका अपरिवर्तित रहती हैं
यदि आधार 1 से छोटा हैं अर्थात 0<a<1 के लिये, logax>logay हैं तो ⇒x<y ,
इसका अभिप्राय यह हैं कि यदि आधार (a), इकाई से छोटा है, अर्थात (a<1) तो जब असमिका से logarithm हटाया जाता हैं तो असमिका चिह्न विपरीत हो जाता हैं
अन्य प्रतिबंध
NOTE:
⇒ यदि आधार इकाई से छोटा है, तो logax का मान ह्यसमान हैं जैसे-जैसे x वर्धमान है।
⇒यदि आधार इकाई से बड़ा है, तो logaxवर्धमान हैं जैसे-जैसे x हासमान है।
उदाहरण 17
असमिका logsin(π3)(x2−3x+2)=2 का हल हैं
logsin(π3)(x2−3x+3)=2
दिया हैं =logaX=p, तथा यहां a=sin(π3)
चूँकि sin(π3)<1 अर्थात a<1
तब 0<X≤ap
(1) X≤ap
यहां a=sin(π3)=√32
⇒x2−3x+2≤34
⇒x2−3x+54≤0
⇒ 4x2−12x+5≤0
⇒ 4x2−10x−2x+5≤0
⇒(2x−5)(2x−1)≤0
⇒12≤x≤52 . . .(i)
तथा
(2)
X>0
x2−3x+2>0
⇒(x−1)(x−2)>0
⇒x<1 या x>2 . . . (ii)
समीकरण (i) व (ii) से,
x∈[12,1)∪(2,52]
उदाहरण 18
log2(x2−3x+18)<4 तब x का मान ज्ञात कीजिये
log2(x2−3x+18)<4
दिया हैं =logaX<p, तथा यहां a=2
चूँकि a>1
तब X<ap
X<ap
यहां a=2
⇒(x2−3x+18)<24
(x2−3x+2)<0
⇒ x2−2x−x+2<0
⇒ (x−2)(x−1)<0
⇒1<x<2
सारांश
(i) दो भिन्न वास्तविक मूल होते हैं यदि b2−4ac>0 हो।
(ii) दो बराबर मूल (अर्थात सम्पाती वास्तविक मूल) होते है, यदि b2−4ac=0 हो और
(iii) कोई वास्तविक मूल नहीं होते है, यदि b2−4ac<0 हो।
यदि a<0 तब f(x) का उच्चिष्ठ मान x=−b2a पर प्राप्त होगा।
एवं फलन f(x) का उच्चिष्ठ या निम्निष्ठ −D4a होगा
अन्यथा a.f(d)>0 होगा