शंकु परिच्छेद कक्षा 11 गणित
भूमिका
पिछले अध्याय में हमने रेखा के समीकरणों के विभिन्न रूपों का अध्ययन किया था। इस अध्याय में, हम कुछ अन्य वक्रों का अध्ययन करेंगे जैसे वृत्त (Circle), परवलय (Parabola), दीर्घवृत्त (Ellipse) और अतिपरवलय (Hyperbola)। इन वक्रों को शंकु परिच्छेद या सामान्यत: शांकव कहा जाता है क्योंकि इन्हें एक लंब वृत्तीय द्विशंकु और एक समतल के परिच्छेदन से प्राप्त किया जा सकता है।
आइये जानते है, शंकु परिच्छेद को और करीब से ....
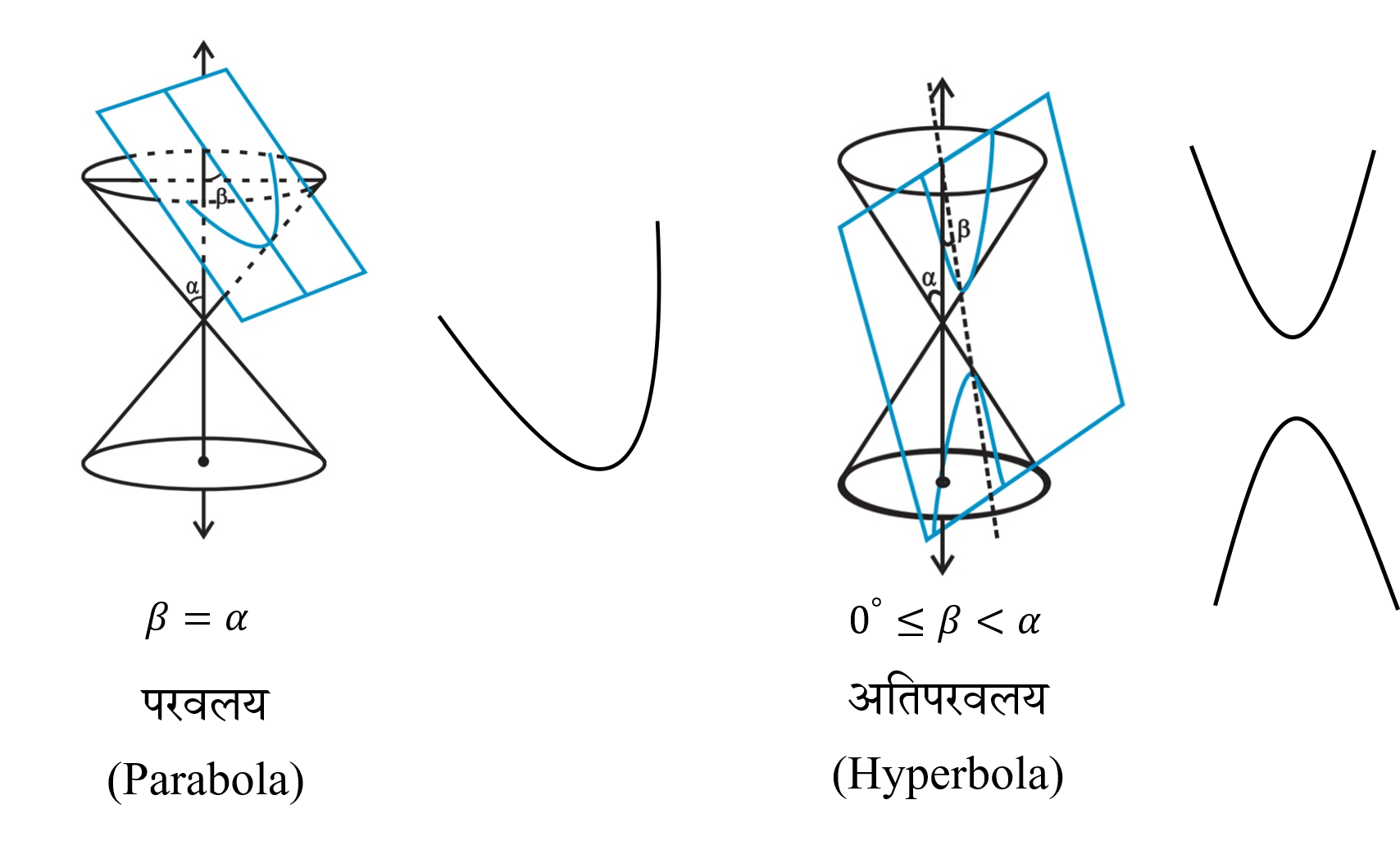
सर्वप्रथम देखते है कि द्विशंकु क्या है? इसे समझने के लिए हम एक ऊर्ध्वाधर रेखा l लेते है तथा उसकी किसी बिन्दु V से जाती हुई एक तिर्यक रेखा m खिचते है। इस स्थिति मे रेखा m, l से एक अचर कोण α बनाती है। तब यदि α कोण को स्थिर मानते हुए रेखा m को चारों ओर घुमाया जाए तो निम्न प्रकार कि आकृति मिलेगी।
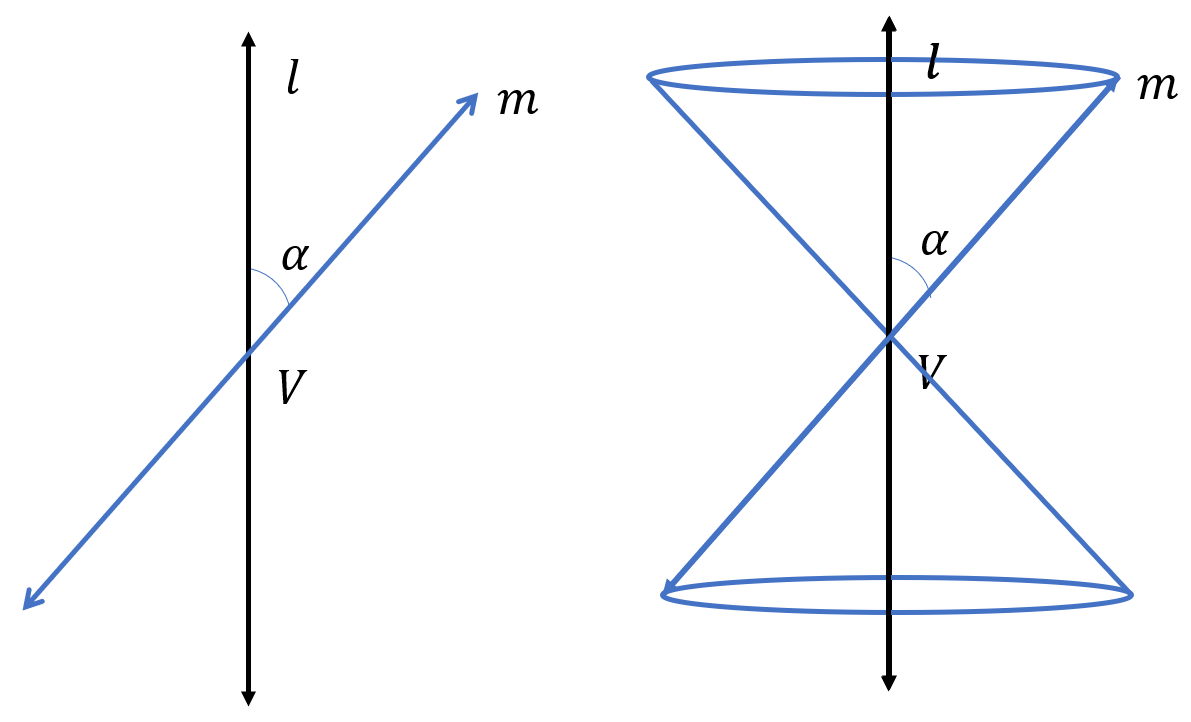
इसका दैनिक जीवन मे उदाहरण देखें तो दो आइसक्रीम के कोन को एक-दूसरे के उल्टे शीर्षों को स्पर्श करते हुए रखा जाए तो वह आकृति एक द्विशंकु होती है।
अब यदि एक तल द्विशंकु को काटे व ऊर्ध्वाधर के साथ β कोण बनाए तब, हमें β के भिन्न मानों के लिए द्विशंकु में भिन्न आकृतियाँ प्राप्त होगी। आइए इन्हे निम्न प्रकार से समझने का प्रयास करते है-
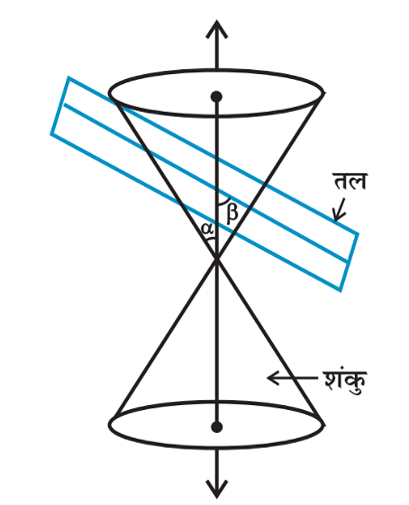
बच्चों जब तल, शंकु के नापे (शीर्ष के अतिरिक्त) को काटता है, तो हमें निम्नांकित स्थितियाँ प्राप्त होती है:
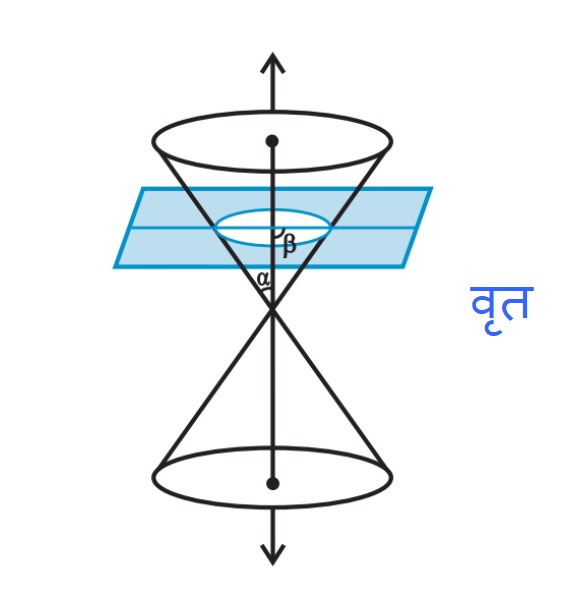
(a) जब β=90∘, तो परिच्छेद एक वृत्त होता है
(b) जब α<β<90∘, तो परिच्छेद एक दीर्घवृत्त होता है ।
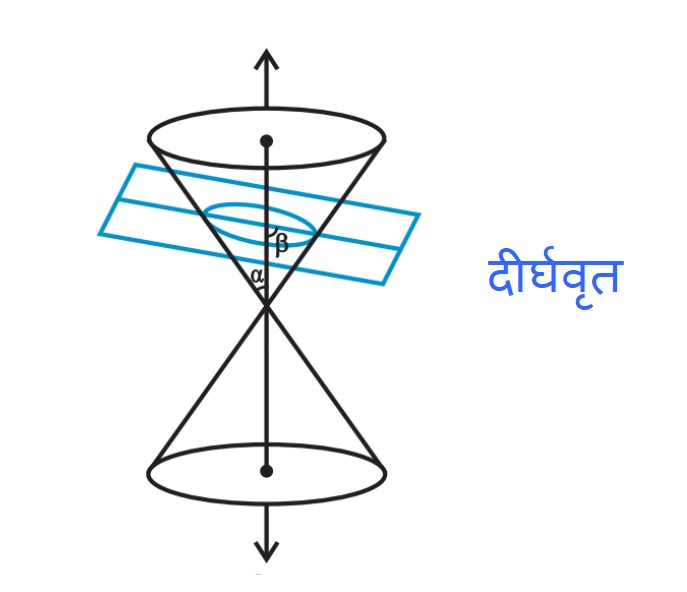
(c) जब β=α, तो परिच्छेद एक परवलय होता है ।
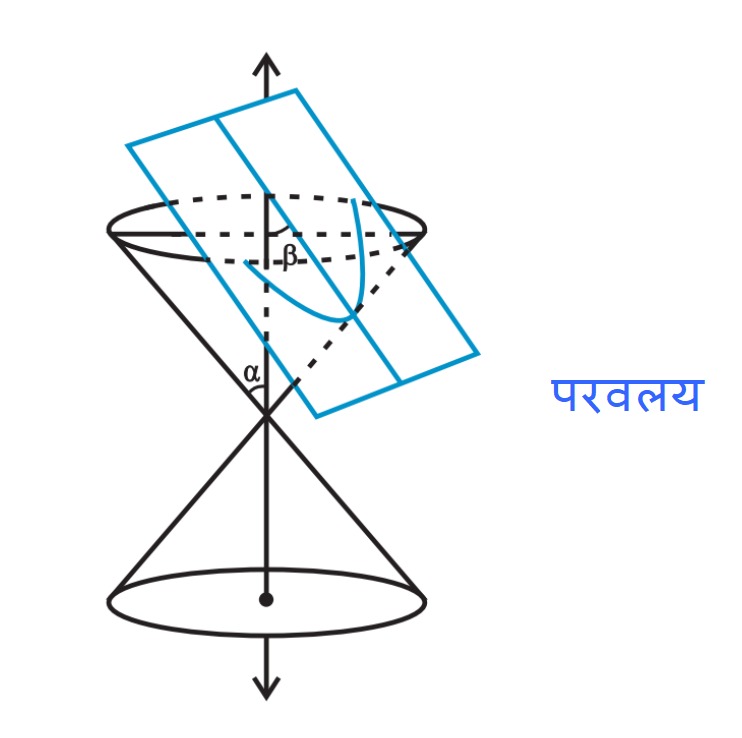
(उपरोक्त तीनों स्थितियों की प्रत्येक स्थिति में तल शंकु को नापे के पूर्णत: आर-पार काटता है।)
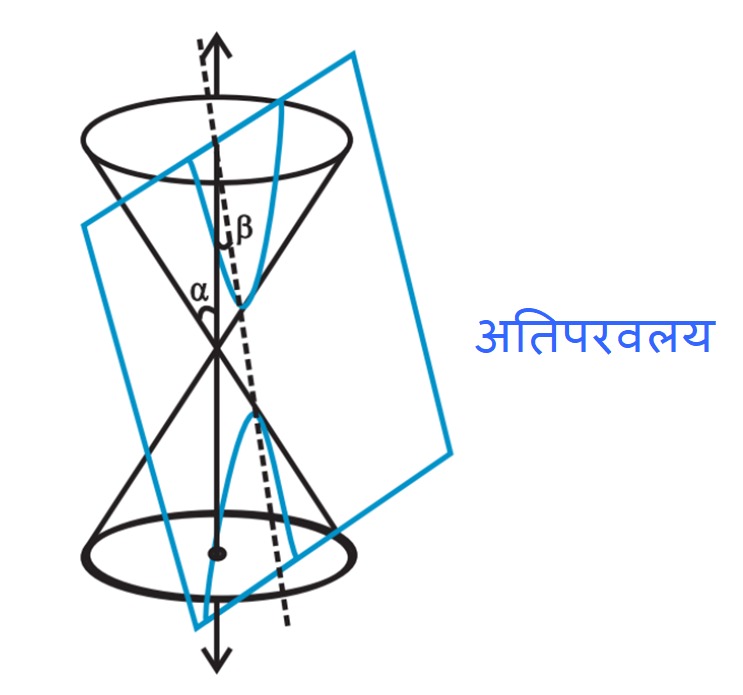
(d) जब 0≤β<α, तो तल शंकु के दोनों नेप्स (नापे) को काटता है तो परिच्छेद एक अतिपरवलय होता है।
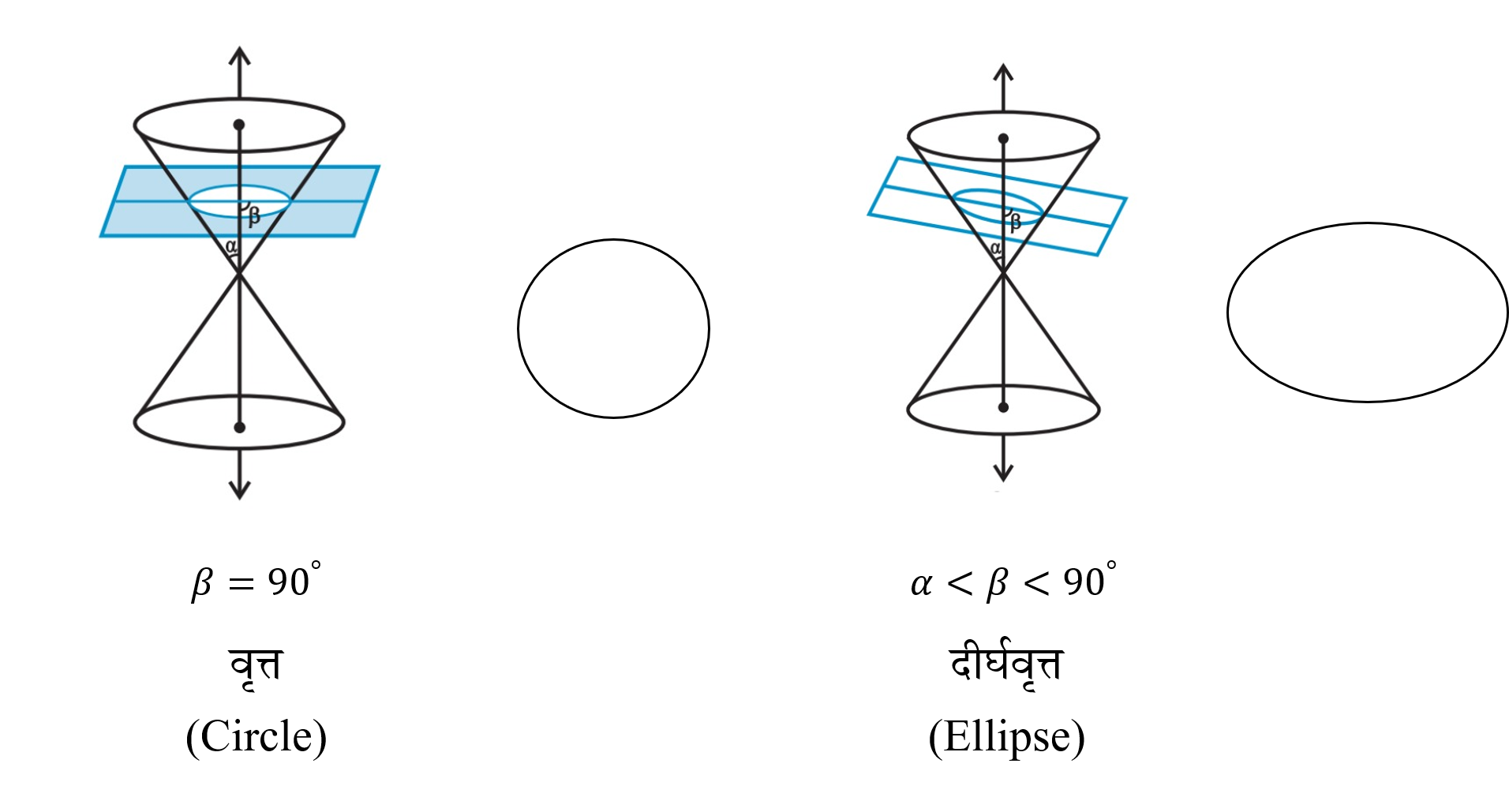
वृत्त
परिभाषा: वृत्त, तल के उन बिन्दुओ का समुच्चय होता है जो तल के एक स्थिर बिंदु से समान दूरी पर होते हैं।
स्थिर बिंदु को वृत्त का केंद्र (centre) कहते हैं तथा वृत्त पर किसी एक बिंदु की केंद्र से दूरी को वृत्त की त्रिज्या (radius) कहते हैं
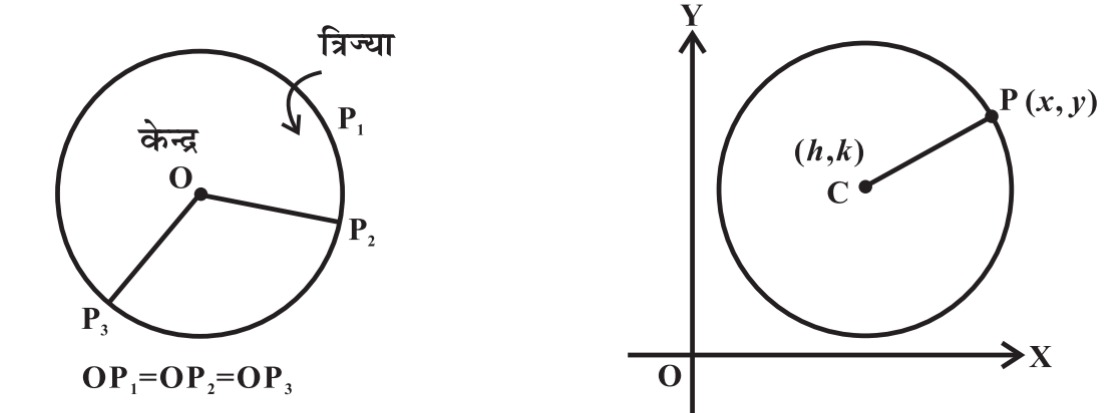
यदि वृत्त का केंद्र मूल बिंदु पर होता है तो वृत्त का समीकरण सरलतम होता है। फिर भी हम ज्ञात केंद्र तथा त्रिज्या के वृत्त का समीकरण निम्नलिखित प्रकार से व्युत्पन्न करेंगे -
वृत्त का केंद्र C(h,k) तथा त्रिज्या r ज्ञात है।
मान लीजिए वृत्त पर कोई बिंदु P(x,y) है तब परिभाषा से,
|CP|=r
दूरी सूत्र द्वारा, हम पाते हैं
√(x−h)2+(y−k)2=r
दोनों पक्षों मे वर्ग करने पर
(x−h)2+(y−k)2=r2
प्राप्त वृत्त का समीकरण है, अब यदि इसका विस्तार किया जाए तब
x2−2hx+h2+y2−2ky+k2=r2
x2+y2−2hx−2ky+h2+k2−r2=0
यहाँ h=−g, k=−f तथा h2+k2−r2=c से स्थानांतरित करने पर
x2+y2+2gx+2fy+c=0
यह वृत्त का व्यापक समीकरण है।
यहाँ वृत्त का केंद्र (h,k)⇒(−g,−f)
तथा चूंकि h2+k2−r2=c
अतः g2+f2−c=r2
त्रिज्या r=√g2+f2−c
उदाहरण 1
उस वृत्त का समीकरण ज्ञात कीजिए जिसका केंद्र (2,−1) है तथा जो बिंदु (3,6) से होकर जाता है।
वृत्त के केंद्र के निर्देशांक =(2,−1)
∴ वृत्त की त्रिज्या
= बिंदु (3,6) से केंद्र (2,−1) के बीच की दुरी
=√(2−3)2+(−1−6)2
=√1+49
=5√2
यदि (h,k) वृत्त का केंद्र तथा r वृत्त कि त्रिज्या है
तब वृत्त का समीकरण
(x−h)2+(y−k)2=r2
⇒ (x−2)2+(y+1)2=(5√2)2
⇒ (x−2)2+(y+1)2=(5√2)2
⇒ x2−4x+4+y2+2y+1=50
⇒ x2+y2−4x+2y−45=0
यही वृत्त का अभीष्ट समीकरण है।
उदाहरण 2
वृत्त x2+y2+4x+2y+1=0 की त्रिज्या तथा केन्द्र ज्ञात कीजिए।
वृत्त का समीकरण है :
x2+y2+4x+2y+1=0
(x2+4x)+(y2+2y+1)=0
(x2+2x.2+22−4)+(y2+2y+1)=0
(x+2)2+(y+1)2=4
समीकरण की तुलना,
(x−h)2+(y−k)2=r2 से करने पर,
(x−(−2))2+(y−(−1))2=22
अतः वृत्त का केन्द्र (−2,−1),
तथा इसकी त्रिज्या 2 इकाई है।
उदाहरण 3
वृत्त 3x2+3y2−6x+9y−8=0 का केन्द्र और त्रिज्या ज्ञात कीजिए।
दिया है,
वृत्त का समीकरण
3x2+3y2−6x+9y−8=0
समीकरण को 3 से भाग देने पर
⇒x2+y2−2x+3y−83=0
चूंकि वृत्त के व्यापक समीकरण
x2+y2+2gx+2fy+c=0 से
तुलना करने पर
2g=−2,2f=3,c=−83
⇒g=−1,f=32,c=−83
∴ वृत्त का केन्द्र =(−g,−f)
(1,−32)
और वृत्त की त्रिज्या
=√g2+f2−c
=√1+94−(−83)
=√1+94+83
=√12+27+3212
=√7112=√712√3 मात्रक
उदाहरण 4
वृत्त के समीकरण से तुलना करने पर उस वृत्त का समीकरण ज्ञात कीजिए जो x− अक्ष को स्पर्श करता है तथा जिसका केन्द्र (1,2) है।
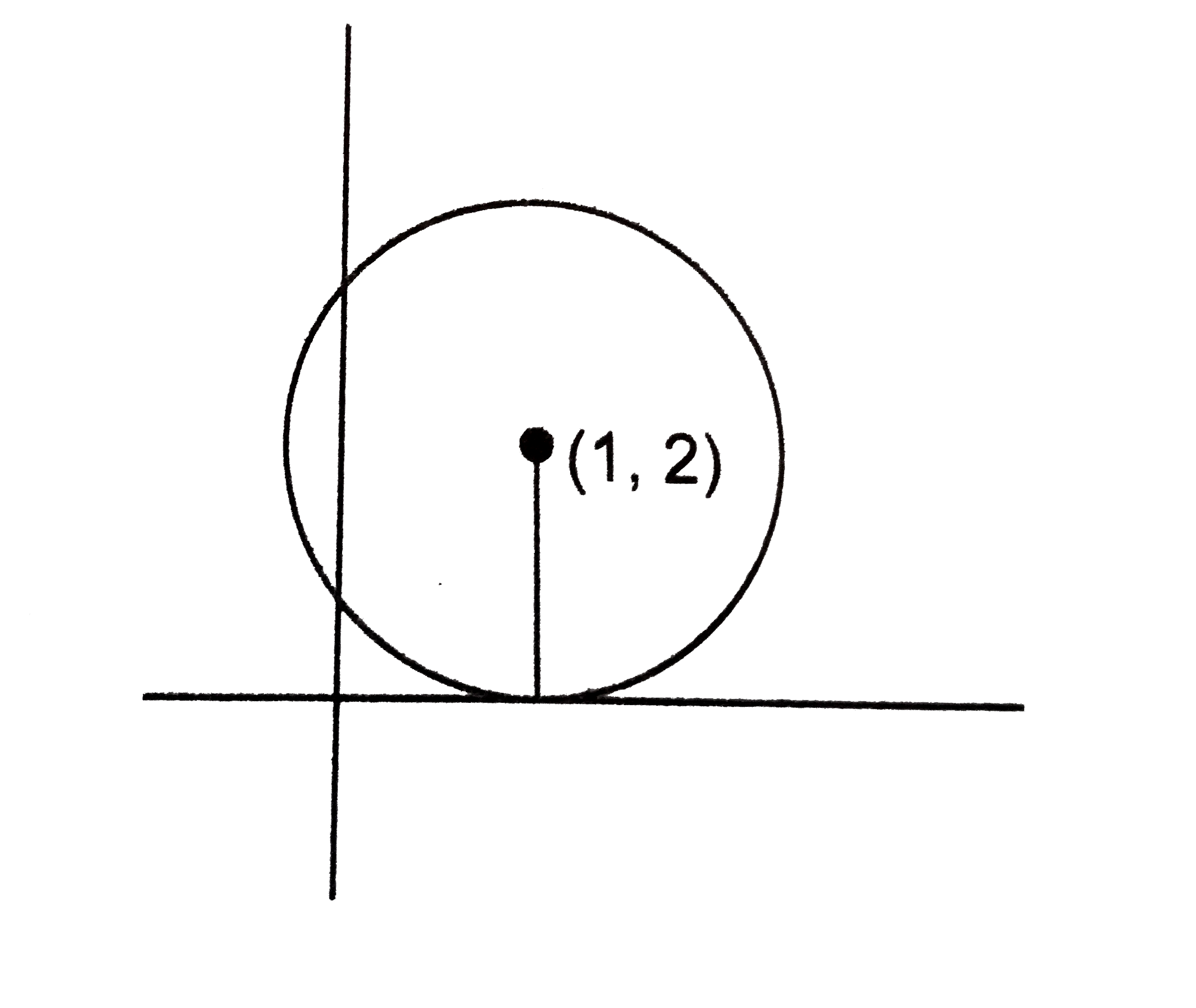
वृत्त का केन्द्र (h,k)=(1,2),
वृत्त X− अक्ष को स्पर्श करता है
∴ चित्रानुसार, वृत्त की त्रिज्या
a=2 मात्रक
अतः वृत्त का समीकरण
(x−h)2+(y−k)2=a2
⇒(x−1)2+(y−2)2=22
⇒x2+y2−2x−4y+5=4
⇒x2−2x+y2−4y+1=0
उदाहरण 5
सिद्ध कीजिए कि वृत्तों
x2+y2=1,
x2+y2−2x−6y=6 और
x2+y2−4x−12y−9=0
कि त्रिज्याएँ समान्तर श्रेणी में है।
वृत्त x2+y2=1 के लिये
त्रिज्या r1=√1=1 मात्रक
वृत्त x2+y2−2x−6y=6 के लिए
x2+y2−2x−6y−6=0
चूंकि वृत्त का व्यापक समीकरण
x2+2gx+y2+2fy+c=0
2g2=−2,2f2=−6,c2=−6
∴g2=−1,f2=−3,c2=−6
और त्रिज्या r2=√g22+f22−c2
=√1+9+6
=√16=4 मात्रक
और वृत्त x2+y2−4x−12y−9=0 के लिए
2g3=−4,2f3=−12,c3=−9
⇒g3=−2,f3=−6,c3=−9
∴r3=√g23+f23−c3
=√4+36+9=√49=7 मात्रक
अब r1+r3=1+7=8
2r2=2×4=8
अतः r2=r1+r32
∴r1,r2,r3 समान्तर श्रेणी में है।
उदाहरण 6
उस वृत्त का समीकरण ज्ञात कीजिए जो
बिंदुओं (0,−6),(1,1) और (7,−7) से होकर जाता है।
माना, वृत्त का समीकरण निम्न है
x2+y2+2gx+2fy+c=0 …(1)
यह बिंदु (0,−6) से होकर जाता है
0+36−12f+c=0
⇒−12f+c=−36 …(2)
वृत्त बिंदु (1,1) से होकर जाता है
1+1+2g+2f+c=0
⇒2g+2f+c=−2 ...(3)
वृत्त बिंदु (7,−7) से होकर जाता है
49+49+14g−14f+c=0
⇒14g−14f+c=−98 ...(4)
समीकरण (2) से (3) को और समीकरण (3) से (4) को घटाने पर
−2g−14f=−34 ...(5)
और −12g+16f=96 ...(6)
समीकरण (5) का 6 से गुणा करके उसमे से समीकरण (6) को घटाने पर
−12g−84f=−204 घटाने पर
−12g+16f=96−100f=−300
⇒f=3
समीकरण (2) से
−36+c=−36
−36+c=−36
⇒c=0
और समीकरण (5) से
−2g−42=−34
⇒g=−4
समीकरण (1) से वृत्त का समीकरण
x2+y2−8x+6y=0
परवलय
परिभाषा: एक परवलय तल के उन सभी बिंदुओं का समुच्चय है जो एक निश्चित सरल रेखा और तल के एक निश्चित बिंदु (जो रेखा पर स्थित नहीं है) से समान दूरी पर है।
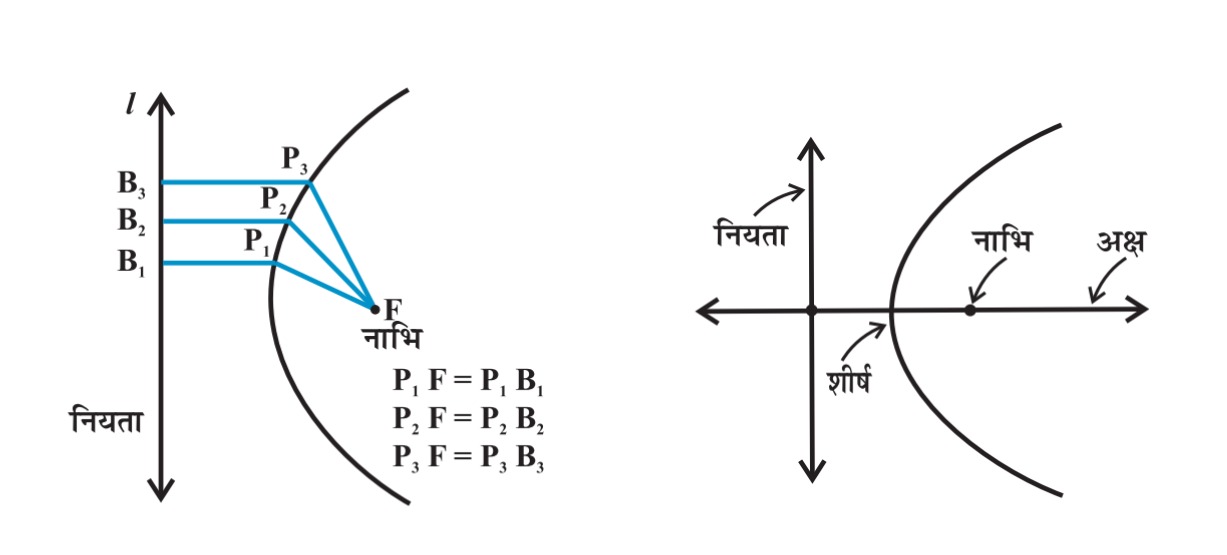
निश्चित सरल रेखा को परवलय की नियता (directrix) और निश्चित बिंदु F को परवलय की नाभि (focus) कहते हैं।
(अंग्रेजी भाषा में 'Para का अर्थ "से" व 'bola' का अर्थ फेंकना अर्थात् हवा में गेंद फेंकने से बना हुआ पथ।)
टिप्पणी : यदि निश्चित बिंदु निश्चित सरल रेखा पर स्थित हो तो तल के उन बिंदुओं का समुच्चय जो निश्चित बिंदु और निश्चित रेखा से समान दूरी पर है, निश्चित बिंदु से गुजरने वाली निश्चित रेखा पर लंबवत सरल रेखा होती है। हम इस सरल रेखा को परवलय की अपभ्रष्ट स्थिति कहते हैं।
परवलय की नाभि से जाने वाली तथा नियता पर लंब रेखा को परवलय का अक्ष कहा जाता है। परवलय का अक्ष जिस बिंदु पर परवलय को काटता है उसे परवलय का शीर्ष कहते है।
परवलय का प्रमाणिक समीकरण
परवलय का समीकरण सरलतम होता है यदि इसका शीर्ष मूल बिंदु पर हो और इसकी सममित अक्ष, x- अक्ष या y-अक्ष के अनुदिश होता है। परवलय के ऐसे चार संभव दिकविन्यास नीचे दर्शाए गए हैं।1. माना एक परवलय जिसकी नाभि F और नियता l है। नियता पर लंब FM बिंदु O पर समद्विभाजित होता हैं। इस प्रकार नाभि की नियता से दूरी 2a है।
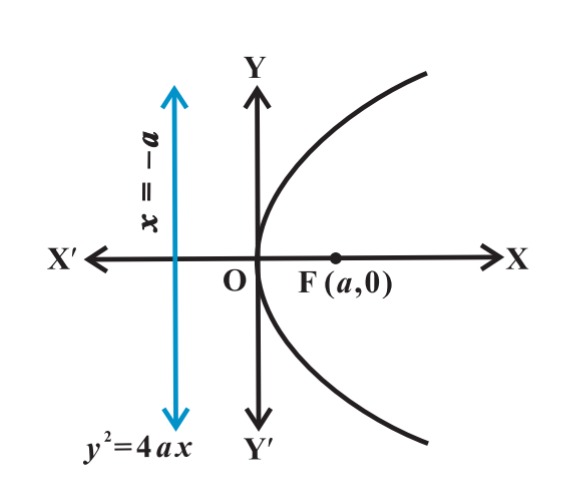
MO को X तक बढ़ाइए। परवलय की परिभाषा के अनुसार मध्य बिंदु O परवलय पर है और परवलय का शीर्ष कहलाता है। θ को मूल बिंदु मानकर OX को x−अक्ष और इसके लंबवत OY को y− अक्ष लीजिए तथा नाभि के निर्देशांक (a,0), a>0 है तथा नियता का समीकरण x+a=0 है।
चित्रानुसार परवलय पर कोई बिंदु P(x,y) इस प्रकार है कि
PF=PB
दूरी सूत्र से
PF=√(x−a)2+y2
PB=√(x+a)2+(y−y)2
क्योंकि PF=PB
√(x−a)2+y2=√(x+a)2
(x−a)2+y2=(x+a)2
y2=4ax
इस प्रकार परवलय पर कोई बिंदु समीकरण y2=4ax को संतुष्ट करता है।
परवलय के अन्य समीकरण
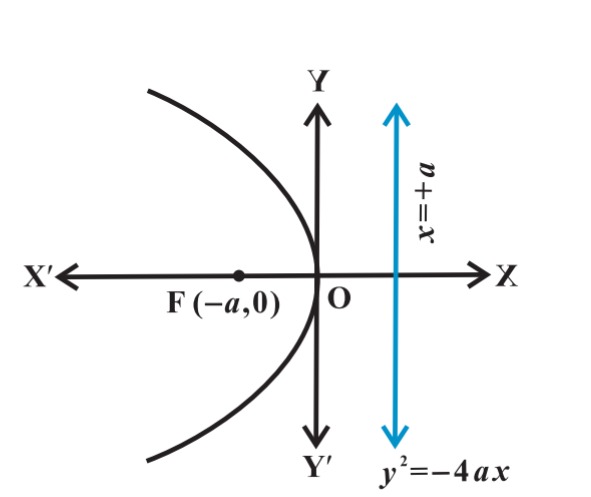
y2=−4ax
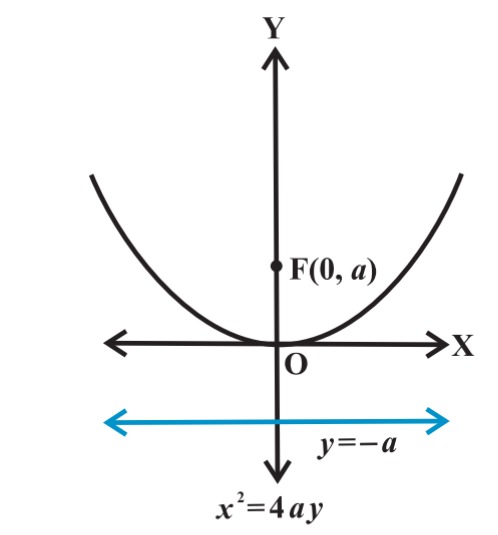
x2=4ay
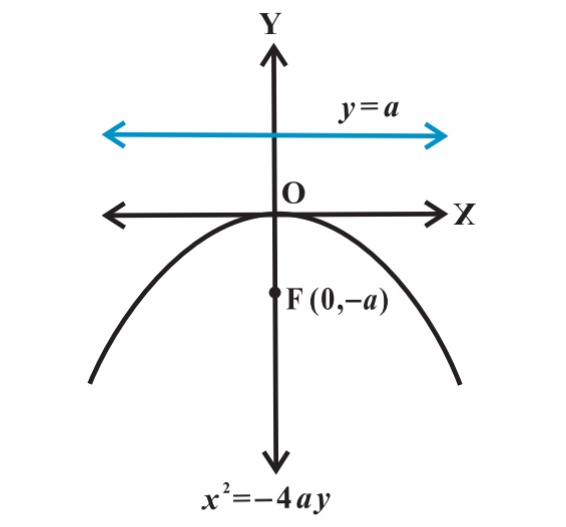
x2=−4ay
निष्कर्ष:
(a) x का गुणांक धनात्मक हो तो परवलय दाई ओर खुलता है।
(b) x का गुणांक ऋणात्मक हो तो परवलय बाई ओर खुलता है।
(a) y का गुणांक धनात्मक हो तो परवलय ऊपर की ओर खुलता है।
(b) y का गुणांक ऋणात्मक हो तो परवलय नीचे की ओर खुलता है।
नाभिलंब जीवा
परिभाषा: परवलय की नाभि से जाने वाली और परवलय की अक्ष के लंबवत रेखाखंड जिसके अंत बिंदु परवलय पर हों, को परवलय की नाभिलंब जीवा कहते हैं।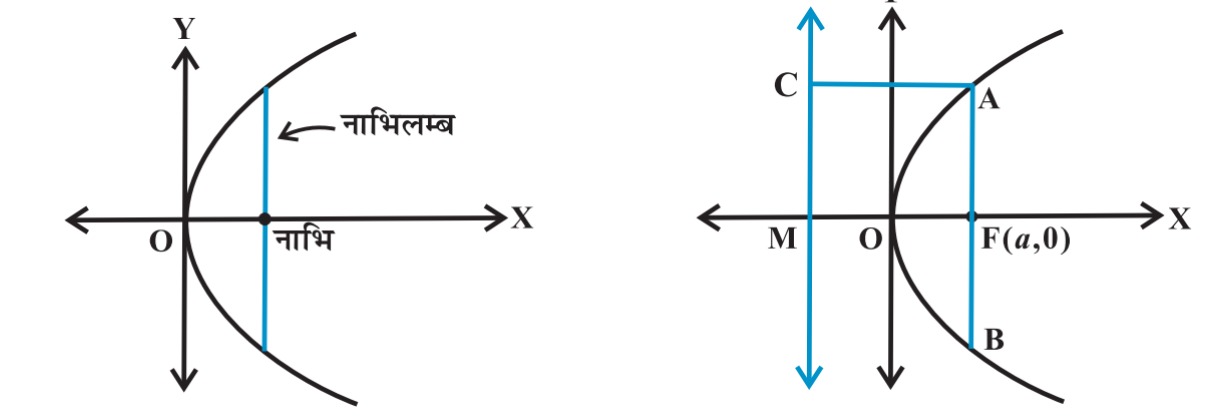
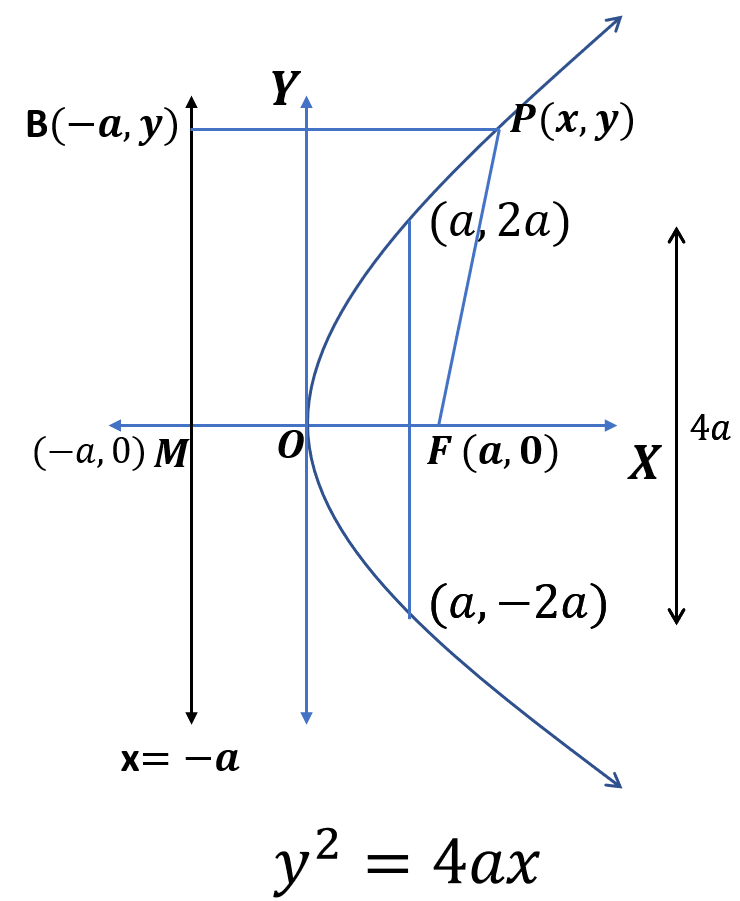
परवलय y2=4ax की नाभिलब जीवा की लंबाई ज्ञात करना
परवलय की परिभाषा के अनुसार, AF=AC
AC=FM=2a
AF=2a
और क्योंकि परवलय, x− अक्ष के परितः सममित है ।
अत: AF=FB
और इसलिए
AB= नाभिलंब जीवा की लंबाई =4a
चूंकि AF=FB=2a
अतः नाभिलंब जीवा के निर्देशांक A(a,2a) तथा B(a,−2a) होगा।
प्राचलिक निर्देशांक (Parametric Co-ordinates)
समीकरण y2=4ax में y=2at रखने पर x=at2 प्राप्त होगा, जहाँ t प्राचल है। यहाँ x=at2, y=2at समीकरण y2=4ax को t के सभी मानों के लिए संतुष्ट करते है। अतः परवलय y2=4ax पर किसी बिन्दु का निर्देशांक (at2,2at) होगा।
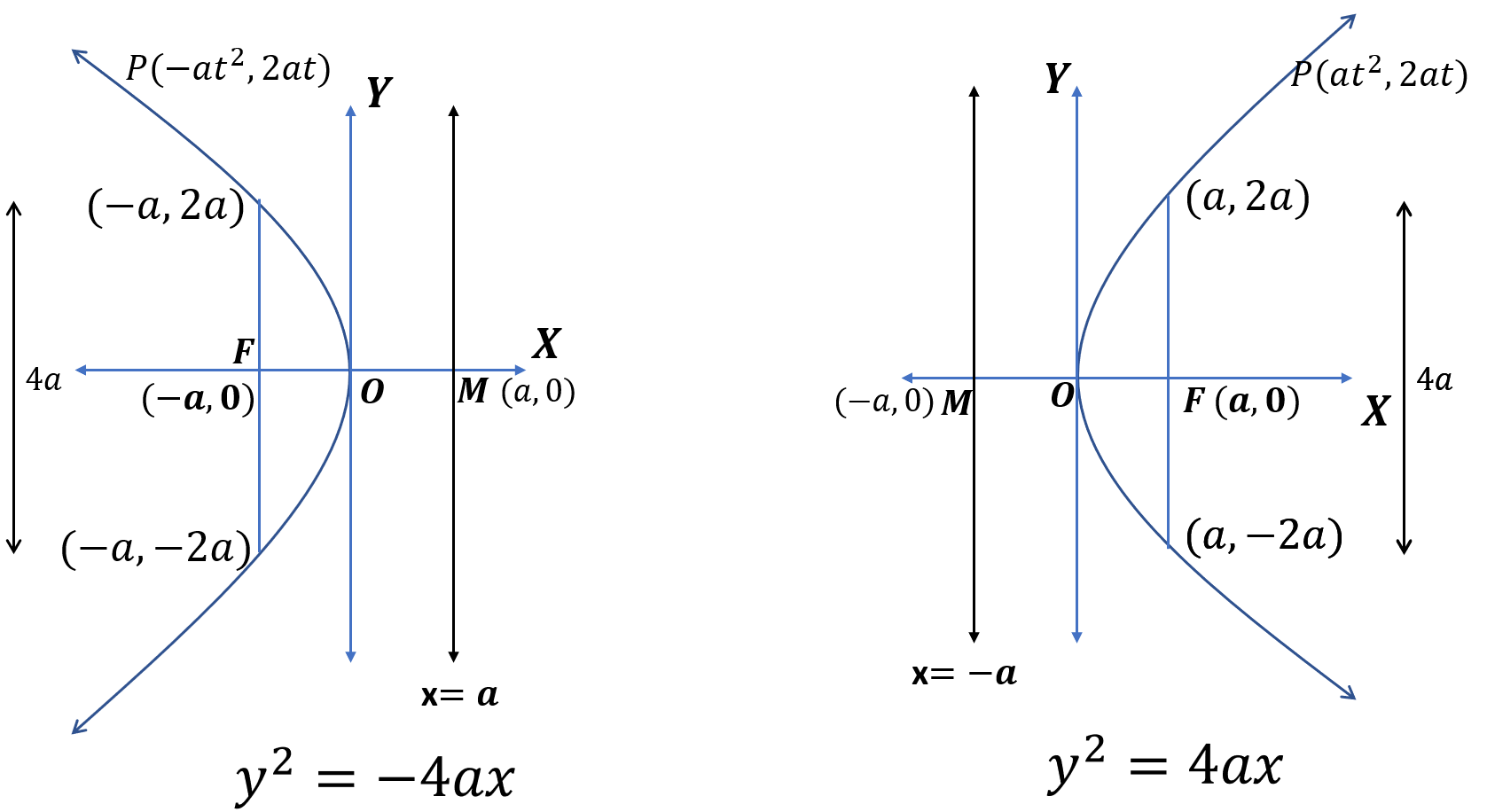
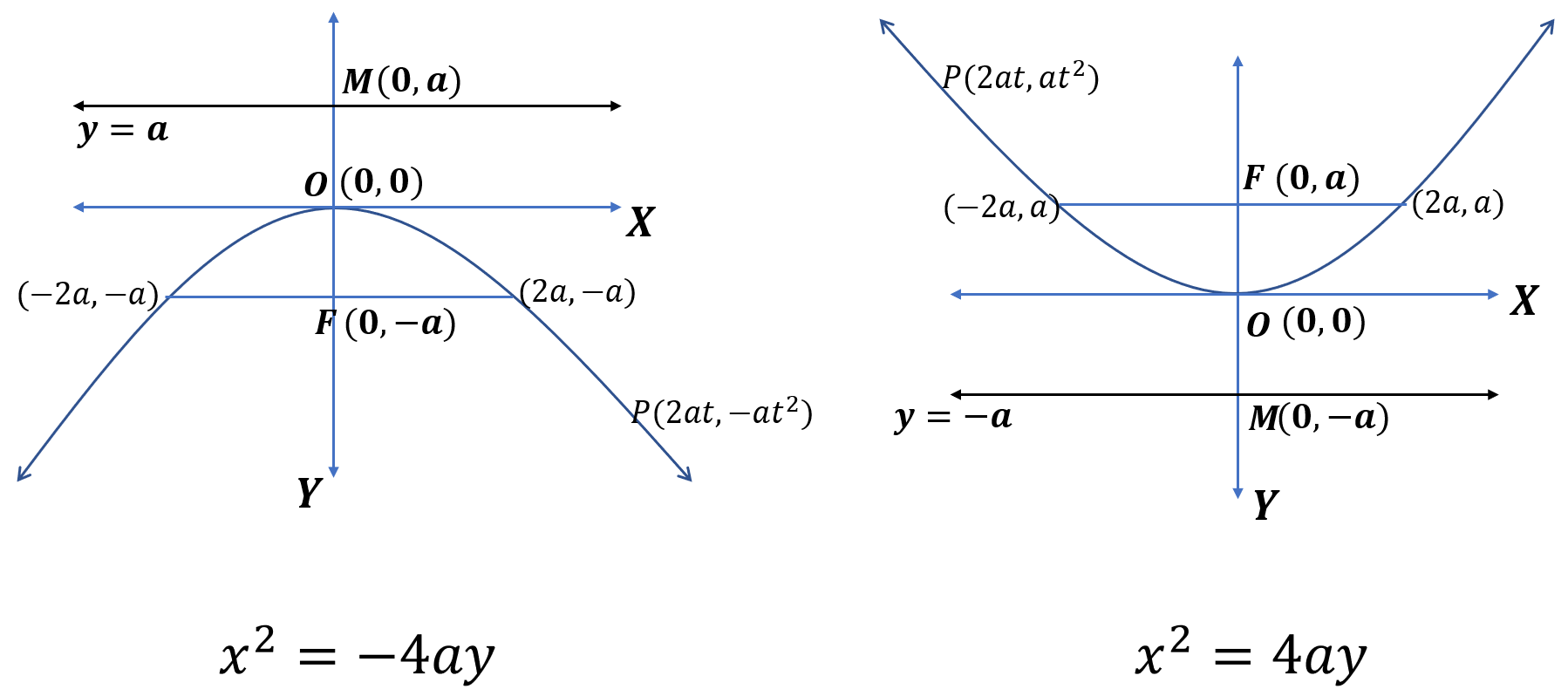
इसी प्रकार परवलयों के लिए कुछ महत्वपूर्ण मान निम्न तालिका में देख सकते है -
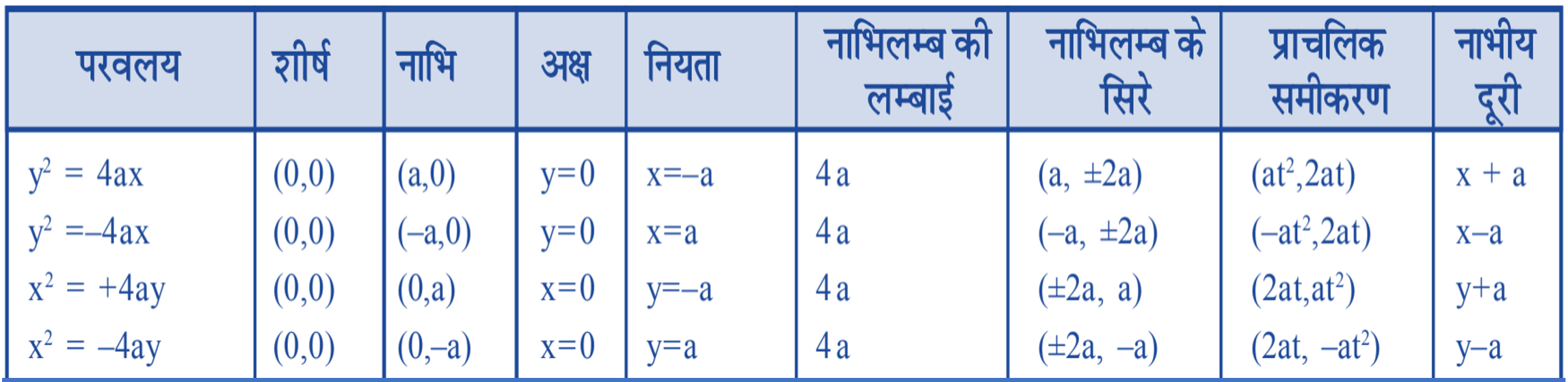
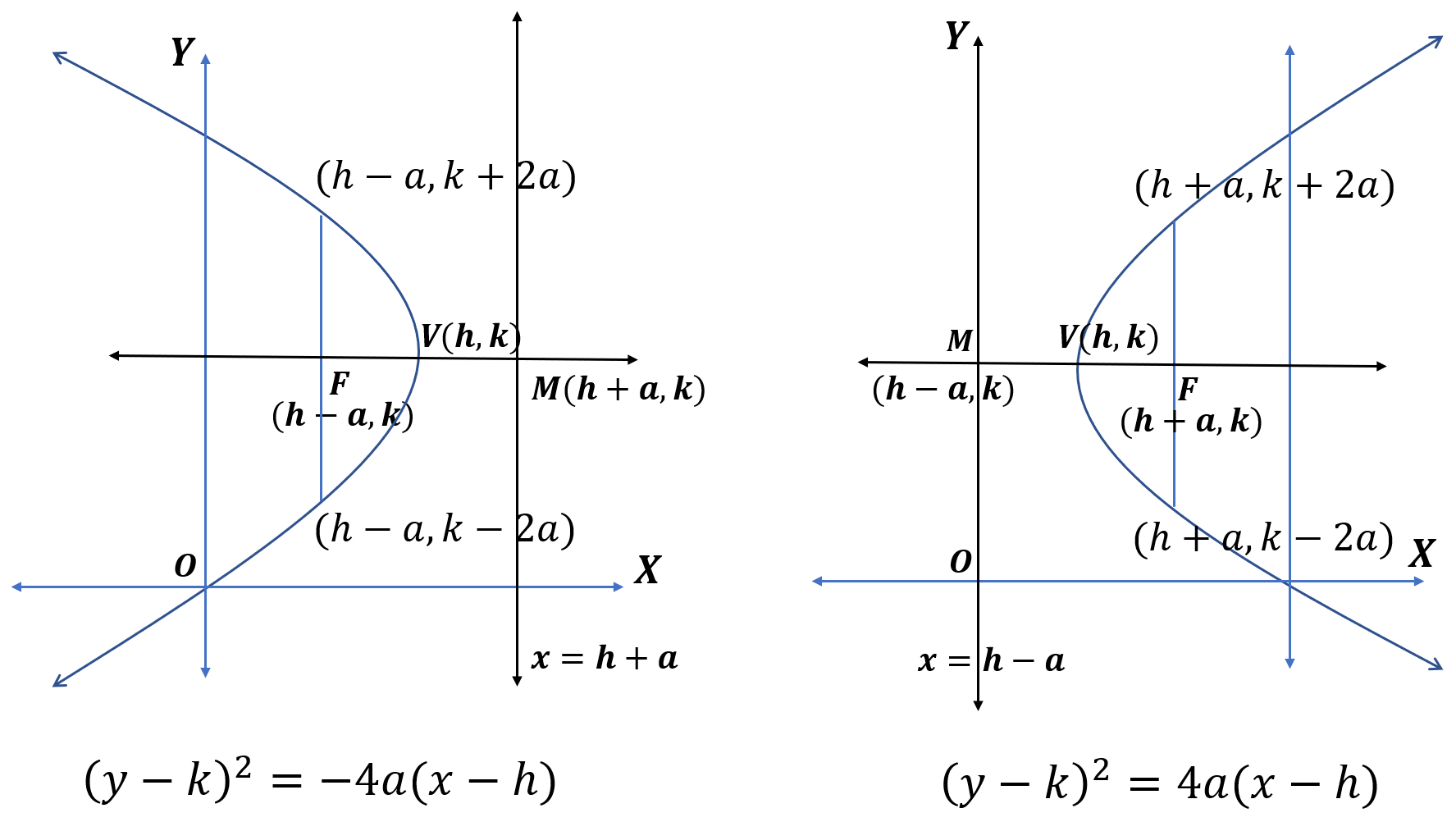
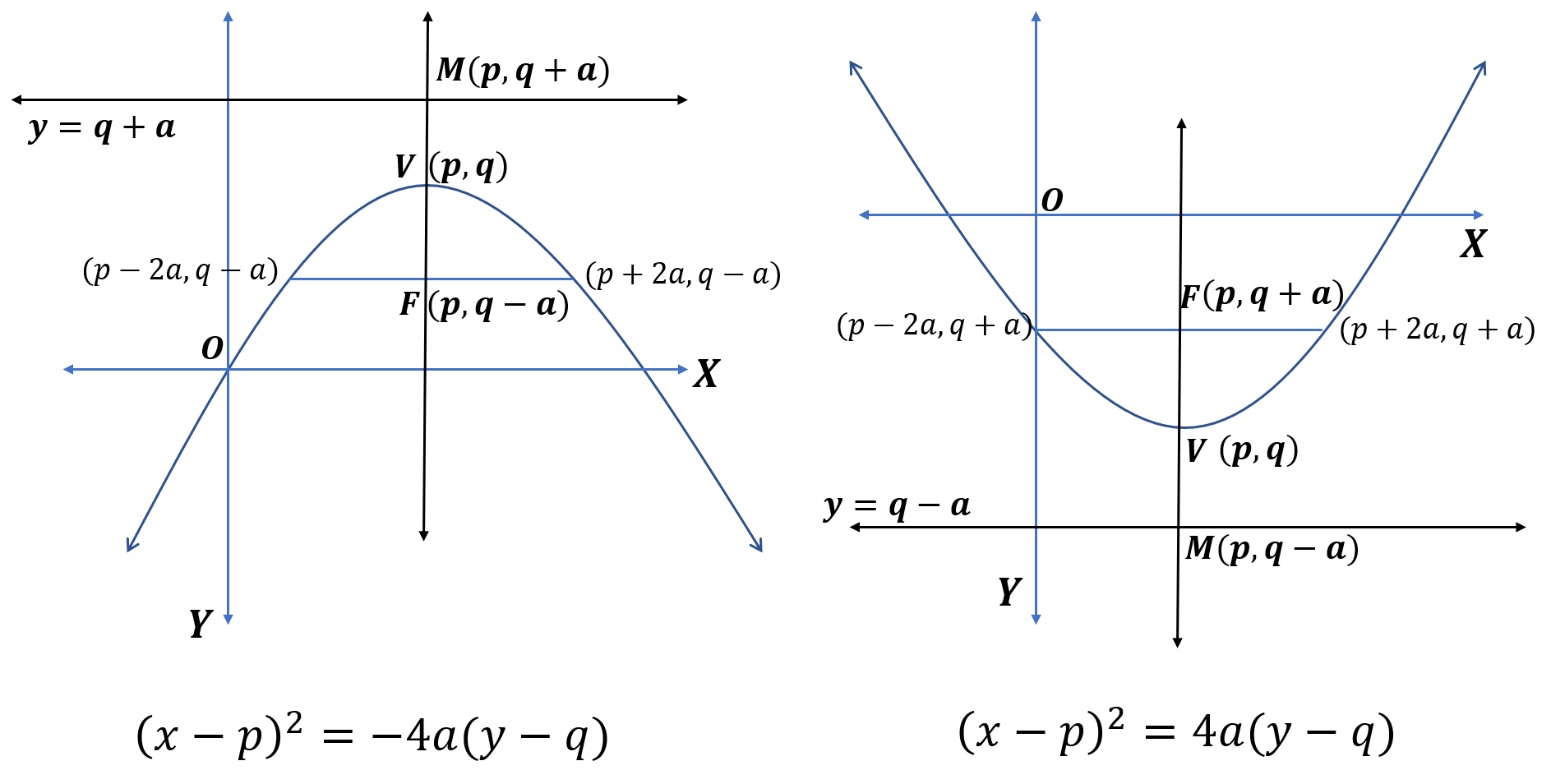
अब तक जिस प्रकार के परवलयों कि चर्चा हमने कि थी वहाँ परवलय का शीर्ष (0,0) था, अब यदि परवलय का शीर्ष (h,k) या (p,q) है तब
परवलय का समीकरण (y−k)2=4a(x−h) प्राप्त होगा, जब अक्ष x− अक्ष के समांतर हो।
परवलय का समीकरण (x−p)2=4a(y−q) प्राप्त होगा, जब अक्ष y− अक्ष के समांतर हो।

उदाहरण 7
परवलय y2=25x की नाभि के निर्देशांक तथा नियता का समीकरण ज्ञात कीजिए।
परवलय y2=25x तथा
परवलय y2=4ax की तुलना से
4a=25
a=254
नाभि के निर्देशांक (a,0)
=(254,0)
नियता का समीकरण
x+a=0
x+254=0
या
4x+25=0
अत: नाभि के निर्देशांक (254,0) तथा
नियता का समीकरण 4x+25=0.
उदाहरण 8
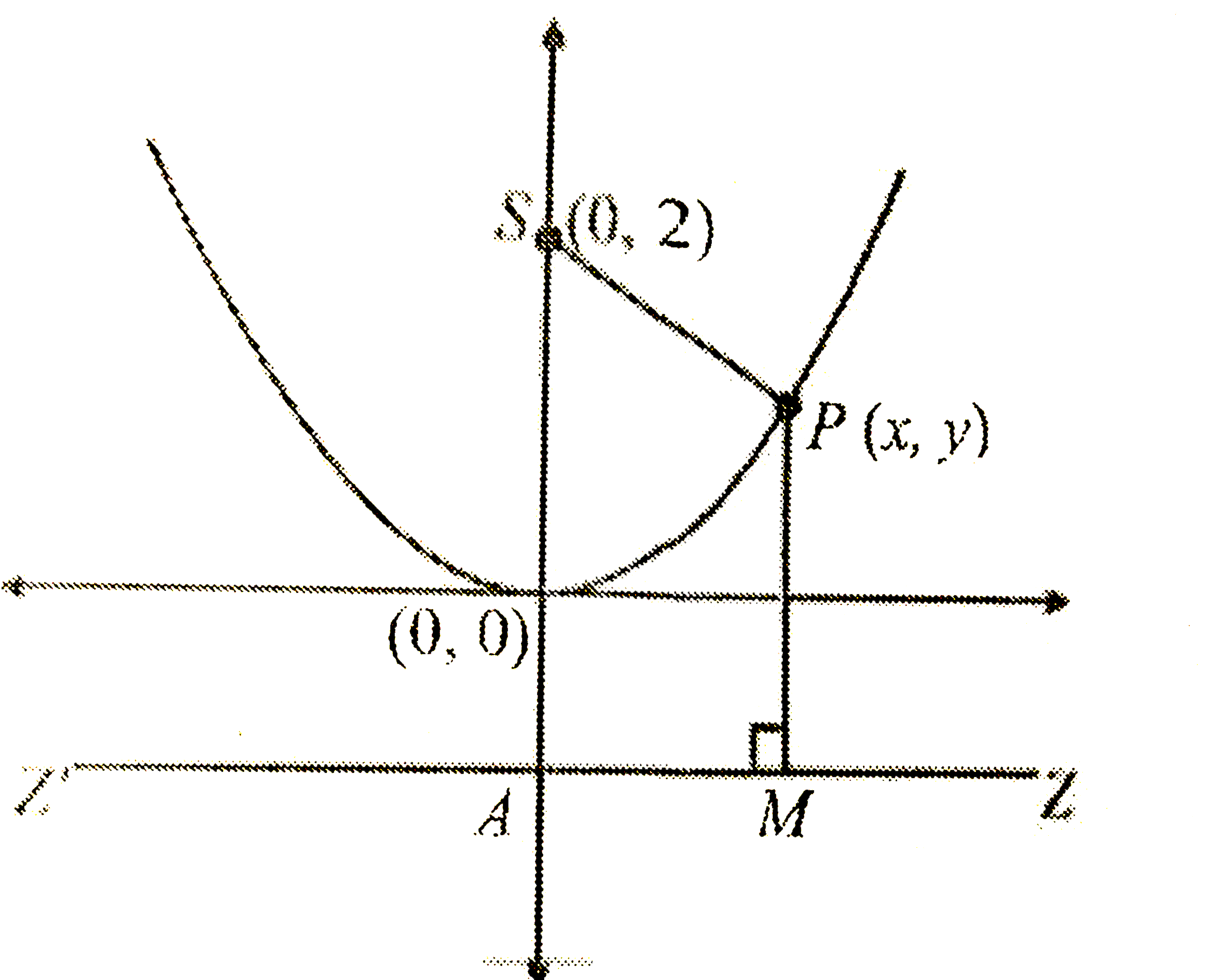
एक परवलय का समीकरण ज्ञात कीजिए जिसका शीर्ष (0,0) और नाभि (0,2) है।
A से x− अक्ष से समान्तर एक रेखा ZAZ' जो परवलय की नियता है
जिसका समीकरण y=−2 या y+2=0 है।
परवलय पर कोई बिन्दु P(x,y) लिया जिससे नियता ZAZ' पर लम्ब PM डाला तथा PS को मिलाया।
परवलय की परिभाषा से,
PS=PM
या (PS)2=(PM)2
(x−0)2+(y−2)2=(y+2)2
x2=(y+2)2−(y−2)2
x2=8y
उदाहरण 9
उस परवलय का समीकरण ज्ञात कीजिए, जिसकी नाभि (−8,−2) और y=2x−9 नियता का समीकरण है।
माना, परवलय की नाभि S(−8,−2) और P(x,y) परवलय पर कोई बिन्दु है।
अब परवलय की परिभाषा से SP=P बिन्दु की नियता से दुरी
⇒√(x+8)2+(y+2)2
=2x−y−9√22+(−1)2
दोनों पक्षों मे वर्ग करने पर
⇒5(x2+16x+64+y2+4y+4)
=4x2+y2+81−4xy−36x+18y
⇒x2+4y2+4xy+116x+2y+259
=0
उदाहरण 10
यदि परवलय y2=4ax की नाभीय जीवा के एक सिरे का निर्देशांक (at2,2at) है, तो दूसरे सिरे के निर्देशांक ज्ञात कीजिए।
माना परवलय की नाभीय जीवा PQ है जो नाभि S(a,0) से होकर जाती है।

इसके एक सिरे P के निर्देशांक (at2,2at) है।
माना दूसरे सिरे Q के निर्देशांक (at21,2at1) है
अब PQ रेखा का समीकरण
y−2at=2at1−2atat21−at2(x−at2)
y−2at=2a(t1−t)a(t1−t)(t1+t)(x−at2)
y−2at=2(t1+t)(x−at2)
S(a,0) इस रेखा पर स्थित है
∴0−2at=2t1+t(a−at2)
⇒−2at(t1+t)=2a(1−t2)
⇒−t(t1+t)=1−t2
⇒−tt1−t2=1−t2
⇒−tt1=1
→t1=−1t
∴Q बिन्दु के निर्देशांक
⇒(at21,2at1)
⇒(at2,−2at)
उदाहरण 11
सिद्ध कीजिए की प्राचल बिन्दु (2+t2,2t+1) एक परवलय निरूपित करता है। दिखाइए कि इसका शीर्ष (2,1) है।
दिए गये प्रचलिक समीकरण निम्नलिखित है,
x=2+t2 …(1)
y=2t+1 …(2)
⇒t=y−12
t का मान समीकरण (1) में रखने पर
x=2+(y−12)2
⇒x−2=(y−1)24
⇒(y−1)2=4(x−2)
⇒Y2=4X जो परवलय का समीकरण है,
शीर्ष के निर्देशांक के लिये
X=0,Y=0
⇒x−2=0,y−1=0
⇒x=2,y=1
अतः शीर्ष के निर्देशांक ⇒(2,1)
दीर्घवृत्त
परिभाषा: एक दीर्घवृत्त तल के उन बिंदुओं का समुच्चय है जिनका तल में दो स्थिर बिंदुओं से दूरी का योग अचर होता है।
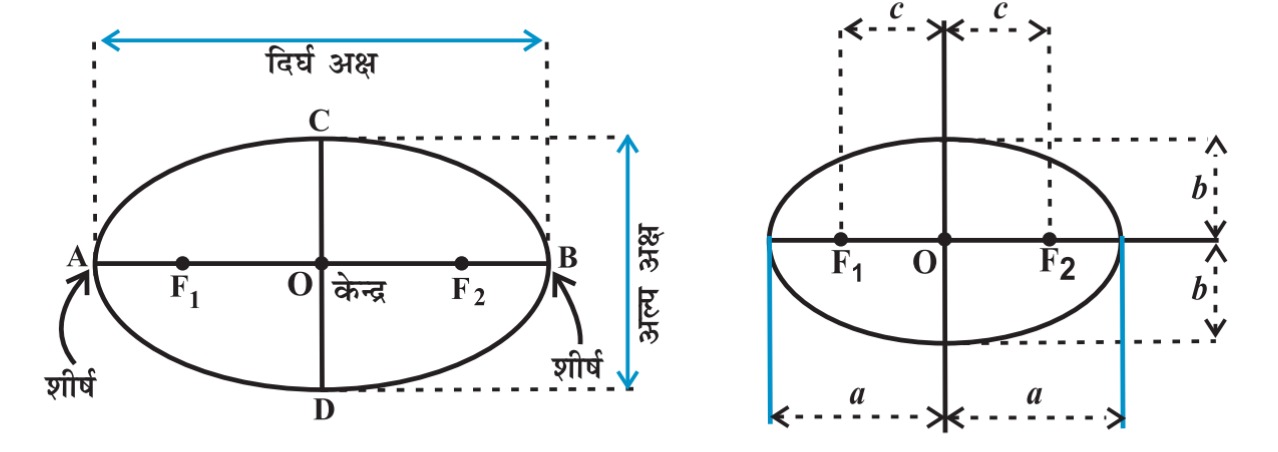
अर्ध-दीर्घ अक्ष, अर्ध-लघु अक्ष और दीर्घवृत्त के केंद्र से नाभि की दूरी के बीच में संबंध
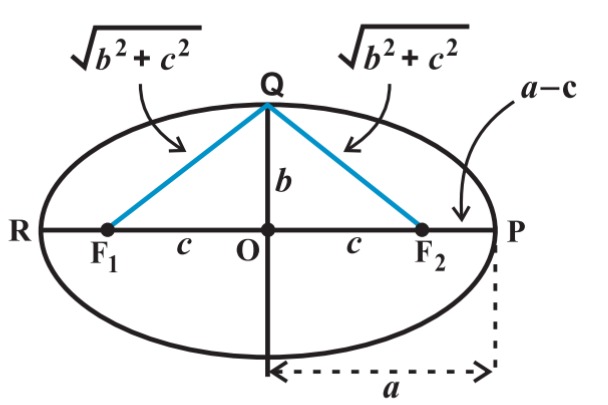
चित्रानुसार बिंदु P की नाभियों से दूरियों का योग
F1P+F2P=F1O+OP+F2P
=c+a+a−c=2a
अब लघु अक्ष पर एक अंत बिंदु Q की नाभियों से दूरियों का योग
F1Q+F2Q
=√b2+c2+√b2+c2
=2√b2+c2
P और Q दोनों दीर्घवृत्त पर स्थित हैं, अतः दीर्घवृत्त की परिभाषा से हम पाते हैं
2√b2+c2=2a
अर्थात् a=√b2+c2
a2=b2+c2
c=√a2−b2
एक दीर्घवृत्त की विशेष स्थितियाँ
उपरोक्त प्राप्त समीकरण c2=a2−b2 में यदि हम a का मान स्थिर रखें और c का मान 0 से a तक बढ़ायें, तो परिणामी दीर्घवृत्त के आकार निम्नाकित प्रकार से बदलेंगे।स्थिति (i) यदि c=0, हो तो दोनों नाभियाँ, दीर्घवृत्त के केंद्र में मिल जाती हैं और a2=b2 या a=b और इसलिए दीर्घवृत्त एक वृत्त बन जाता है।
इस प्रकार वृत्त, दीर्घवृत्त की विशेष स्थिति है।
स्थिति (ii) यदि c=a, हो तो b=0 और दीर्घवृत्त दोनों नाभियों को मिलाने वाले रेखाखंड F1F2 तक सिमट जाता है।
उत्केंद्रता (Eccentricity)
परिभाषा: दीर्घवृत्त की उत्केंद्रता, दीर्घवृत्त के केंद्र से नाभि और शीर्ष की दूरियों का अनुपात है। उत्केंद्रता को e के द्वारा निर्दिष्ट करते हैं,अर्थात् e=ca
क्योंकि नाभि की केंद्र से दूरी c है इसलिए उत्केंद्रता के पद में नाभि की केंद्र से दूरी ae है।
दीर्घवृत्त का मानक समीकरण
एक दीर्घवृत्त का समीकरण सरलतम होता है यदि दीर्घवृत्त का केंद्र मूल बिंदु पर हो और नाभियाँ x-अक्ष या y-अक्ष पर स्थित हों। ऐसे दो संभव दिकविन्यास निम्न हैं।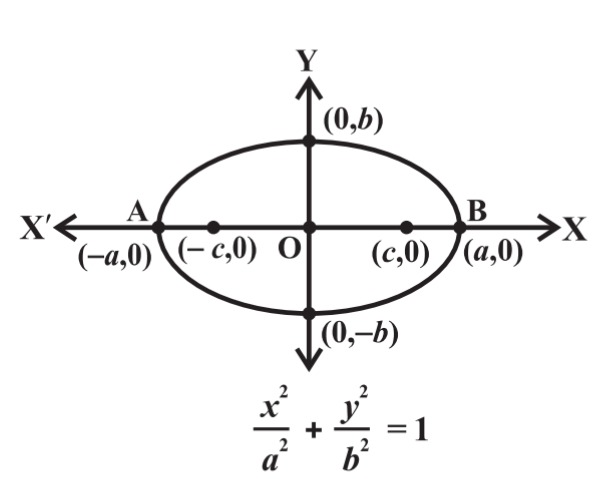
आकृति (a) में दर्शाए गए दीर्घवृत्त, जिसकी नाभियाँ x− अक्ष पर स्थित हैं, का समीकरण व्युत्पन्न करेंगे।
मान लीजिए F1और F2 नाभियाँ हैं और रेखाखंड F1F2 का मध्य बिंदु O है। मान लीजिए O मूल बिंदु हैं व O से F2 की ओर धनात्मक तथा O से F1 की ओर ऋणात्मक x− अक्ष है। माना O से x− अक्ष पर लंब रेखा y− अक्ष है। F1 के निर्देशाक (−c,0) तथा F2 के निर्देशाक (c,0) लेते हैं।
दीर्घवृत्त पर कोई बिंदु P(x,y) इस प्रकार है कि P से दोनों नाभियों की दूरियों का योग 2a है अर्थात्
PF1+PF2=2a
दूरी सूत्र से हम पाते हैं,
√(x+c)2+y2 + √(x−c)2+y2 =2a
√(x+c)2+y2=2a−√(x−c)2+y2
दोनों पक्षों का वर्ग करने पर, हम प्राप्त करते हैं
(x+c)2+y2=4a2−4a×√(x−c)2+y2+(x−c)2+y2
जिसे सरल करने पर मिलता है
√(x−c)2+y2=a−ca×x
पुनः वर्ग करने व सरल करने पर हमें प्राप्त होता है
x2a2+y2a2−c2 =1
x2a2+y2b2=1
(क्योंकि c2=a2−b2)
अतः दीर्घवृत्त पर कोई बिंदु
x2a2+y2b2=1
को संतुष्ट करता है।
एक दीर्घवृत्त, जिसका केंद्र दीर्घ अक्ष x-अक्ष के अनुदिश है, का समीकरण
x2a2+y2b2=1
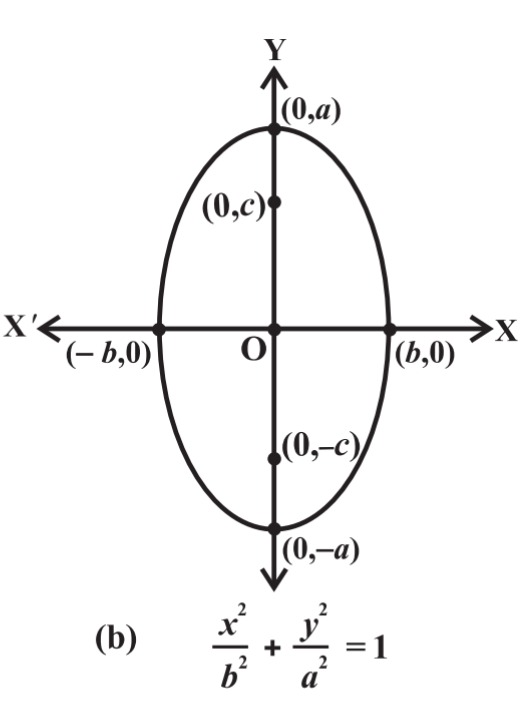
इसी प्रकार, आकृति (b) में, दर्शाए गए दीर्घवृत्त के समीकरण व्युत्पन्न कर सकते हैं।
x2b2+y2a2=1
अभी तक हमने जो दीर्घवृत्त का समीकरण देखा उसका केंद्र मूलबिंदु पर था, अब यदि दीर्घवृत्त का केंद्र (h,k) हो तब व्यापक समीकरणयदि दीर्घअक्ष x− अक्ष मे स्थित हो
(x−h)2a2+(y−k)2b2=1
यदि दीर्घअक्ष y− अक्ष मे स्थित हो
(x−h)2b2+(y−k)2a2=1
उदाहरण 12
वक्र 4x2+9y2=144 कि नाभि, उत्केन्द्रता, शीर्षों के निर्देशांक, नियताओं के समीकरण और नाभिलम्ब कि लम्बाई ज्ञात कीजिए।
दिया गया वक्र है,
4x2+9y2=144
4x2144+9y2144=1
x236+y216=1
x262+y242=1
यह दीर्घवृत्त निरूपित करता है।
यहाँ a2=62
अर्थात, a=6
तथा b2=42
अर्थात b=4
∵a>b
b2=a2(1−e2)
16=36(1−e2)
16=36−36e2
36e2=20
e2=2036=59
e=√53
नाभियाँ
(± ae,0)
(±6×√53,0)
(±2√5,0)
शीर्ष
(±a,0)
(±6,0)
नियताएँ
x=±ae
=±6√5/3=±18√5.
तथा
नाभिलम्ब कि लम्बाई
=2b2a=2×166=163
उदाहरण 13
उस दीर्घवृत्त का समीकरण ज्ञात कीजिए, जिसके शीर्ष (±2,0) और नाभियाँ (±1,0) है।
दिया है,
दीर्घवृत्त के शीर्ष (±2,0) व नाभि (±1,0) है।

अतः AA1=2a=4
a=2
SS1=2ae=2
ae=1
[∵a=2]
2e=1
या e=12
b2=a2(1−e2)
=4(1−14)=3
b=√3
दीर्घवृत्त की समीकरण
x2a2+y2b2=1
x24+y23=1
उदाहरण 14
उस दीर्घवृत्त का समीकरण ज्ञात कीजिए, जिसकी दीर्घ-अक्ष, x− अक्ष के अनुदिश है और (4,3) तथा (−1,4) दीर्घवृत्त पर स्थित है।
दिए गए बिन्दु है,
(4,3) और (−1,4) इन दोनों बिन्दुओं को क्रमश: दीर्घवृत्त के मानक रूप वाले समीकरण में रखने पर,
16a2+9b2=1...(i)
तथा 1a2+16b2=1....(ii)
समीकरण (ii) में 16 का गुणा करके समीकरण (i) को घटाने पर,
247b2=15 या
b2=24715
b2 का मान समीकरण (i) में रखने पर,
16a2+9×15247=1
16a2=1−135247=112247
a2=247×16112
a2=2477
अत: दीर्घवृत्त का समीकरण,
7x2247+15y2247=1 या
7x2+15y2=247
उदाहरण 15
उस दीर्घवृत्त का समीकरण ज्ञात कीजिए। जिसकी नाभियो के बीच दुरी 8 और नियताओ के बीच दुरी 18 है।
माना,
दीर्घवृत्त का समीकरण
x2a2+y2b2=1 तथा a>b है।
नाभियो के बीच दुरी =2ae=8
⇒ae=4 ….(1)
नियताओ के बीच दुरी =2ae=18
⇒ae=9 …(2)
समीकरण (1) और (2) कि गुणा करने पर
ae×ae=4×9
⇒a2=36
और b2=a2(1−e2)
=a2−(ae)2
=36−(4)2=20
अतः दीर्घवृत्त का समीकरण
x236+y220=1
उदाहरण 16
सिद्ध कीजिए कि व्रक x=4(cosθ+sinθ) और y=3(cosθ−sinθ) एक दीर्घवृत्त को निरूपित करता है।
माना,
x=4(cosθ+sinθ)
⇒x4=cosθ+sinθ…(1)
और y=3(cosθ−sinθ)
⇒y3=cosθ−sinθ…(2)
समीकरण (1) और (2) के वर्गो का योग करने पर
⇒x216+y29
=(cosθ+sinθ)2+(cosθ−sinθ)2
⇒x216+y29=2
⇒x232+y218=1
अतिपरवलय
परिभाषा: एक अतिपरवलय, तल के उन सभी बिंदुओं का समुच्चय है जिनकी तल में दो स्थिर बिंदुओं से दूरी का अंतर अचर होता है।
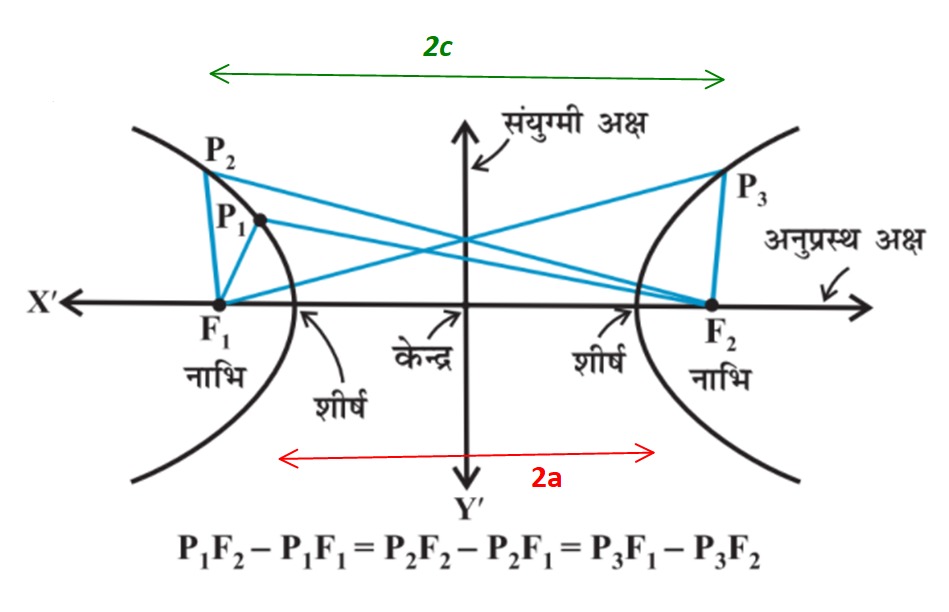
उत्केन्द्रता
दीर्घवृत्त की तरह ही अनुपात e=ca को अतिपरवलय की उत्केंद्रता कहते हैं। चूँकि c≥a , इसलिए उत्केंद्रता कभी भी एक से कम नहीं होती है। उत्केंद्रता के संबंध में, नाभियाँ केंद्र से ae की दूरी पर होती है।अतिपरवलय का मानक समीकरण
यदि अतिपरवलय का केंद्र मूल बिंदु पर और नाभियाँ x− अक्ष और y− अक्ष पर स्थित हों तो अतिपरवलय का समीकरण सरलतम होता है ऐसे दो संभव दिक् विन्यास आकृति में दर्शाए गए हैं।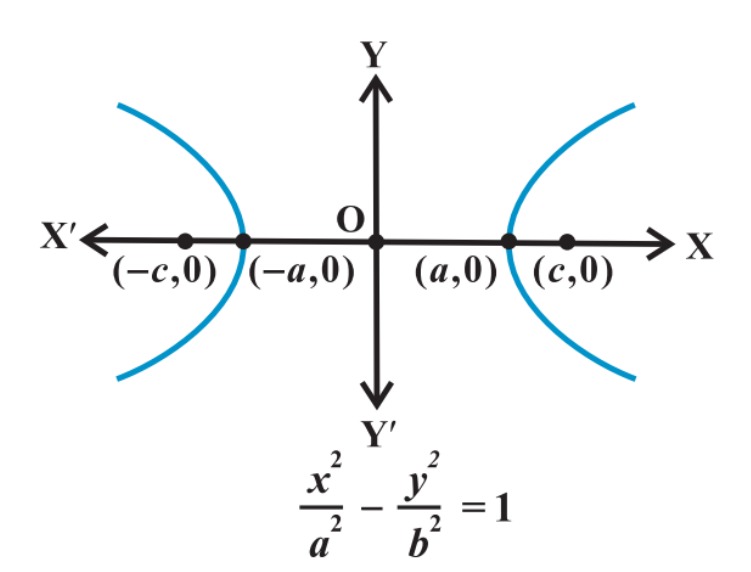
आकृति में दर्शाए गए अतिपरिवलय, जिसकी नाभियाँ x− अक्ष पर स्थित हैं का समीकरण
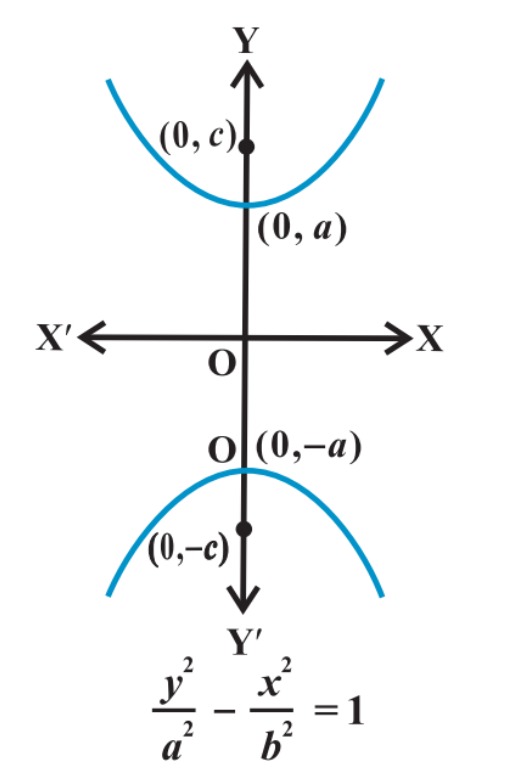
इस आकृति में दर्शाए गए अतिपरिवलय, जिसकी नाभियाँ y− अक्ष पर स्थित हैं का समीकरण
अतिपरवलयों के मानक समीकरण के निरीक्षण से निम्न निष्कर्ष प्राप्त होते हैं -
1. अतिपरवलय, दोनों निर्देशाक्षों के सापेक्ष सममित हैं क्योंकि यदि अतिपरवलय पर एक बिंदु (x,y) है तो बिंदु (−x,y), (x,−y) और (−x,−y) भी अतिपरवलय पर स्थित हैं।
2. अतिपरवलय की नाभियाँ सदैव अनुप्रस्थ अक्ष पर स्थित होती हैं। यह सदैव एक धनात्मक पद है जिसका हर अनुप्रस्थ अक्ष देता है। उदाहरणत: x29−y216=1 x− अक्ष के अनुदिश है और इसकी लंबाई 6 है जबकि y225−x216=1 y− अक्ष के अनुदिश है और इसकी लंबाई 10 है।
नाभिलंब जीवा
अतिपरवलय की नाभियों से जाने वाली और अनुप्रस्थ अक्ष पर लंबवत् रेखाखंड जिसके अंत बिंदु अतिपरवलय पर हों, को अतिपरवलय की नाभिलंब जीवा कहते हैं। दीर्घवृत्तों की भाँति, यह दर्शाना सरल है कि अतिपरवलय की नाभिलंब जीवा की लंबाई 2b2a है।अभी तक हमने जो अतिपरवलय का समीकरण देखा उसका केंद्र मूलबिंदु पर था, अब यदि अतिपरवलय का केंद्र (h,k) हो तब व्यापक समीकरण
यदि अनुप्रस्थ अक्ष, x− अक्ष मे स्थित हो
(x−h)2a2−(y−k)2b2=1
यदि अनुप्रस्थ अक्ष, y− अक्ष मे स्थित हो
(y−k)2a2−(x−h)2b2=1
उदाहरण 17
अतिपरवलय 4x2−16y2=9 की उत्केन्द्रता तथा नाभिलम्ब की लम्बाई ज्ञात कीजिए।
अतिपरवलय का समीकरण,
4x2−16y2=9
4x29−16y29=1
या x294−y2916=1
की तुलना x2a2−y2b2=1
से करने पर,
a2=94=±32
तथा b2=916=±34
अब उत्केन्द्रता,
b2=a2(e2−1)
916=94(e2−1)
e2−1=916×49
=14
e2=1+14=54
e=√52
नाभिलंब की लंबाई =2b2a
=2×91632=34
उदाहरण 18
उस अतिपरवलय का समीकरण ज्ञात कीजिए जिसकी नाभियाँ (±5,0) तथा अनुप्रस्थ अक्ष 8 है।
माना, अतिपरवलय का समीकरण
x2a2−y2b2=1 है।
दिया है,
नाभियाँ (±5,0)⇒(±ae,0)
⇒2ae=10
तथा अनुप्रस्थ अक्ष
⇒2a=8
⇒a=4
2×4e=10 या
e=102×4=54
b2=a2(e2−1)
=16(2516−1)=9
अत: अभीष्ट अतिपरवलय का समीकरण है :
x216−y29=1 या
9x2−16y2=144
उदाहरण 19
उस अतिपरवलय का समीकरण ज्ञात कीजिए, जिसकी नाभि (1,1) उत्केन्द्रता 2 और नियता का समीकरण x+y+1=0 है।
माना, नाभि S और अतिपरवलय के बिन्दु P से नियता पर लम्ब की लम्बाई PM है अब अतिपरवलय की परिभाषा से
शीर्ष A से नाभि S कि बीच कि दूरी =e× शीर्ष A से नियता P पर डाला गया लंब
√(x−1)2+(y−1)2
=2.x+y+1√12+12
⇒[(x−1)2+(y−1)2]
=42(x+y+1)2
⇒(x2−2x+1+y2−2y+1)
=2(x2+y2+2xy+2x+2y+1)
⇒x2+y2+6x+6y+4xy=0
सारांश
इस अध्याय में निम्नलिखित बिन्दुओ पर चर्चा किया गया है -
(x−h)2+(y−k)2=r2 है।
x2a2+y2b2=1
के नाभिलंब जीवा की लंबाई 2b2a
x2a2−y2b2=1 है।