परवलय कक्षा 11 गणित
भूमिका
बच्चों! इस अध्याय में हम वृत्त के बारे में पढ़ेंगे, यह अध्याय आपके आगे आने वाली प्रतियोगी परीक्षा JEE 2023 को ध्यान में रखकर बनाया गया है, इसमें हम बहुत ही basic से पढ़ते हुए आगे बढ़ेंगे।
पूर्व में हम बिंदुपथ के बारे में पढ़ चुके हैं, किसी बिंदु का बिंदुपथ किसी भी तरह का वक्र हो सकता है। इस वक्र का आकार दी हुई ज्यामितीय शर्तों पर निर्भर करेगा। इस अध्याय में हम उन्हीं बिंदुपथों के बारे में चर्चा करेंगे जो परवलय हैं।
यह अध्याय प्रतियोगी परीक्षाओं के लिए बहुत महत्वपूर्ण है। प्रतिवर्ष JEE Main और अन्य परीक्षाओं में इस अध्याय से 2−3 प्रश्न देखने को मिलेंगे।
आप प्रतिदिन Doubtnut की कक्षा देखें और अधिक से अधिक अभ्यास करें। आपकी इस अध्याय से संबंधित सभी समस्याएँ दूर हो जाएगीं।
आइए बच्चों परवलय को समझते हैं और करीब से...
शंकु-परिच्छेद (Conic section) :
एक शंकु परिच्छेद या शांकव , समतल में स्थित उस बिन्दु का बिंदुपथ है जो कि इस प्रकार गति करता है कि एक निश्चित बिन्दु से दूरी तथा एक स्थिर सरल रेखा से लम्बवत दूरी का अनुपात सदैव निश्चित रहता है।
शांकव का व्यापक समीकरण : नाभि-नियता गुणधर्म (General equation of a conic : focal directrix property) :
नाभि (p,q) तथा नियता lx+my+n=0 वाले शांकव का व्यापक समीकरण
(l2+m2)[(x−p)2+(y−q)2]=e2(lx+my+n)2=ax2+2hxy+by2+2gx+2fy+c=0 होता है।
शांकवों में अन्तर (Distinguishing between the conics) : शांकव परिच्छेद की प्रकृति, नाभि S की नियता के सापेक्ष स्थिति तथा उत्केन्द्रता e पर निर्भर करती है। स्थितियाँ इस प्रकार है।
स्थिति (i) जब नाभि नियता पर हो:
इस स्थिति में D=abc+2fgh−af2−bg2−ch2=0 तथा शांकव का व्यापक समीकरण एक रेखा-युग्म को प्रदर्शित करता है तथा यदि
e>1 रेखायें वास्तविक तथा भिन्न होंगी व S पर प्रदिच्छेदित होंगी।
e=1 रेखायें संपाती होगी।
e<1 रेखायें काल्पनिक होंगी।
स्थिति (ii) जब नाभि नियता पर न हो:
शांकव प्रदर्शित करेगा-

परवलय
परिभाषा: एक परवलय तल के उन सभी बिंदुओं का समुच्चय है जो एक निश्चित सरल रेखा और तल के एक निश्चित बिंदु (जो रेखा पर स्थित नहीं है) से समान दूरी पर है।
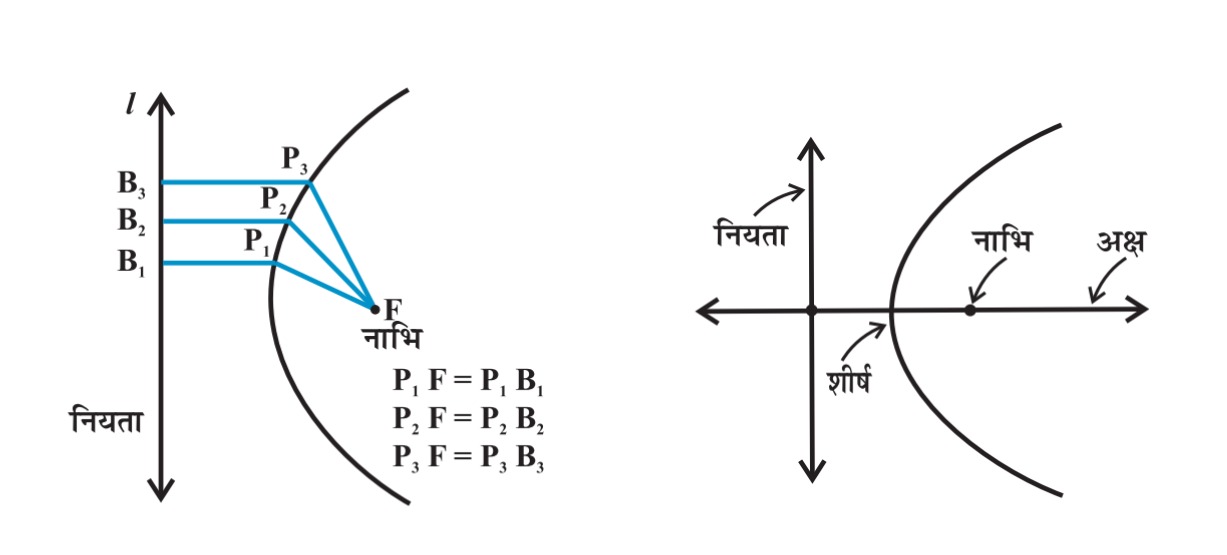
निश्चित सरल रेखा को परवलय की नियता (directrix) और निश्चित बिंदु F को परवलय की नाभि (focus) कहते हैं।
(अंग्रेजी भाषा में 'Para का अर्थ "से" व 'bola' का अर्थ फेंकना अर्थात् हवा में गेंद फेंकने से बना हुआ पथ।)
टिप्पणी : यदि निश्चित बिंदु निश्चित सरल रेखा पर स्थित हो तो तल के उन बिंदुओं का समुच्चय जो निश्चित बिंदु और निश्चित रेखा से समान दूरी पर है, निश्चित बिंदु से गुजरने वाली निश्चित रेखा पर लंबवत सरल रेखा होती है। हम इस सरल रेखा को परवलय की अपभ्रष्ट स्थिति कहते हैं।
परवलय की नाभि से जाने वाली तथा नियता पर लंब रेखा को परवलय का अक्ष कहा जाता है। परवलय का अक्ष जिस बिंदु पर परवलय को काटता है उसे परवलय का शीर्ष कहते है।
परवलय का मानक समीकरण
परवलय का समीकरण सरलतम होता है यदि इसका शीर्ष मूल बिंदु पर हो और इसकी सममित अक्ष, x- अक्ष या y-अक्ष के अनुदिश होता है। परवलय के ऐसे चार संभव दिकविन्यास नीचे दर्शाए गए हैं।
1. माना एक परवलय जिसकी नाभि F और नियता l है। नियता पर लंब FM बिंदु O पर समद्विभाजित होता हैं। इस प्रकार नाभि की नियता से दूरी 2a है।
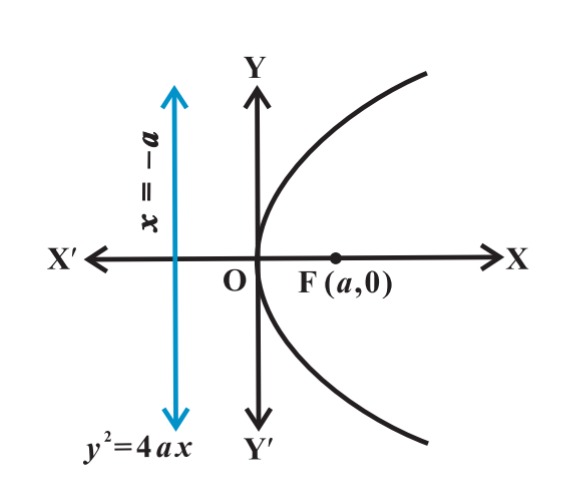
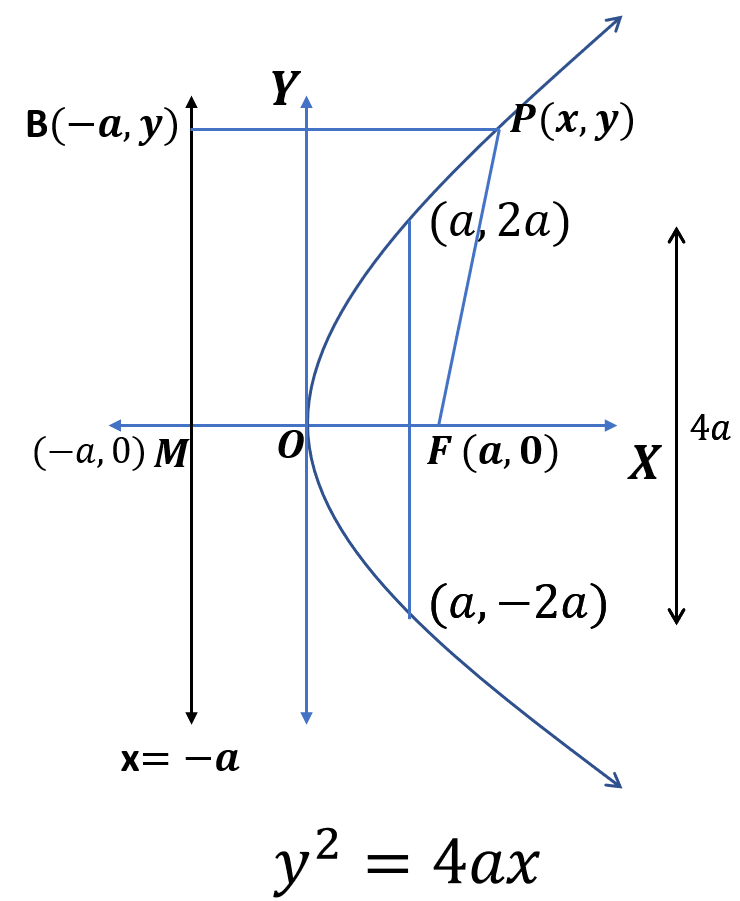
MO को X तक बढ़ाइए। परवलय की परिभाषा के अनुसार मध्य बिंदु O परवलय पर है और परवलय का शीर्ष कहलाता है। θ को मूल बिंदु मानकर OX को x−अक्ष और इसके लंबवत OY को y− अक्ष लीजिए तथा नाभि के निर्देशांक (a,0), a>0 है तथा नियता का समीकरण x+a=0 है।
चित्रानुसार परवलय पर कोई बिंदु P(x,y) इस प्रकार है कि
PF=PB
दूरी सूत्र से
PF=√(x−a)2+y2
PB=√(x+a)2+(y−y)2
क्योंकि PF=PB
√(x−a)2+y2=√(x+a)2
(x−a)2+y2=(x+a)2
y2=4ax
इस प्रकार परवलय पर कोई बिंदु समीकरण y2=4ax को संतुष्ट करता है।
नाभिलंब जीवा
परिभाषा: परवलय की नाभि से जाने वाली और परवलय की अक्ष के लंबवत रेखाखंड जिसके अंत बिंदु परवलय पर हों, को परवलय की नाभिलंब जीवा कहते हैं।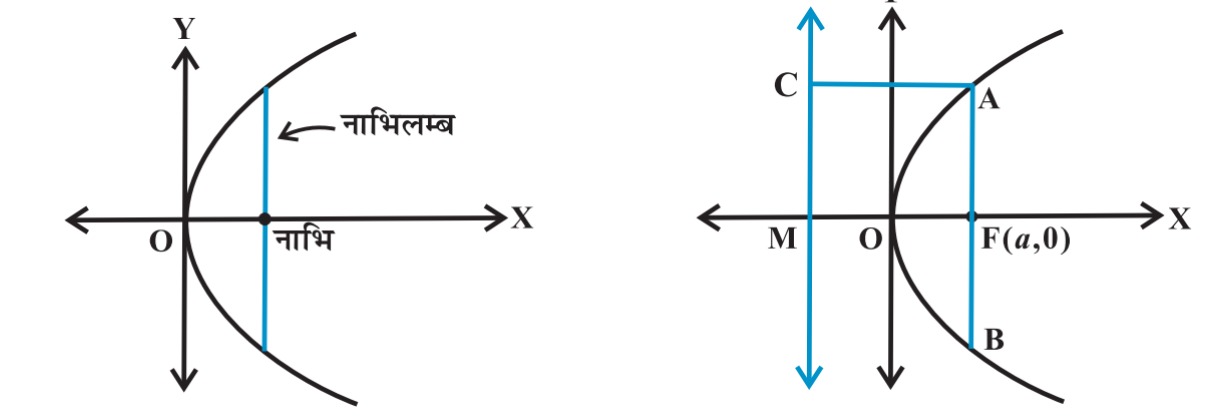
परवलय y2=4ax की नाभिलब जीवा की लंबाई ज्ञात करना
परवलय की परिभाषा के अनुसार, AF=AC
AC=FM=2a
AF=2a
और क्योंकि परवलय, x− अक्ष के परितः सममित है ।
अत: AF=FB
और इसलिए
AB= नाभिलंब जीवा की लंबाई =4a
चूंकि AF=FB=2a
अतः नाभिलंब जीवा के निर्देशांक A(a,2a) तथा B(a,−2a) होगा।
उदाहरण 1
परवलय y2=25x की नाभि के निर्देशांक तथा नियता का समीकरण ज्ञात कीजिए।
परवलय y2=25x तथा
परवलय y2=4ax की तुलना से
4a=25
a=254
नाभि के निर्देशांक (a,0)
=(254,0)
नियता का समीकरण
x+a=0
x+254=0
या
4x+25=0
अत: नाभि के निर्देशांक (254,0) तथा
नियता का समीकरण 4x+25=0.
परवलय के अन्य समीकरण
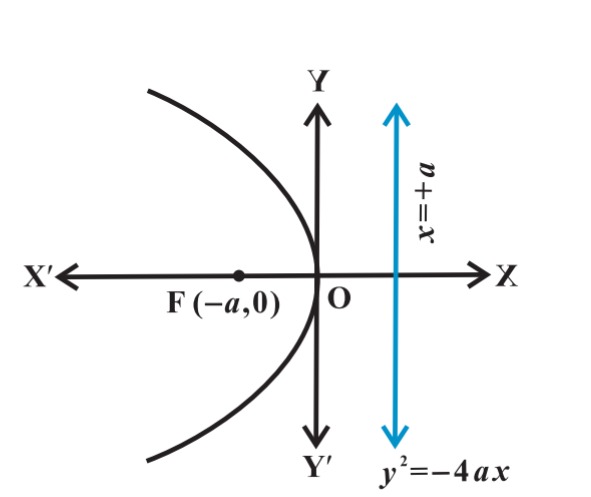
y2=−4ax
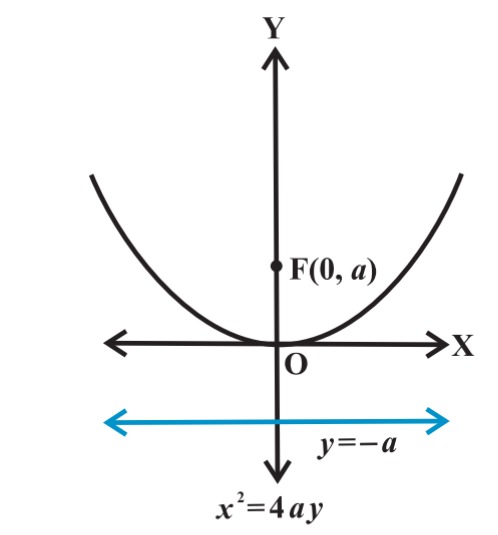
x2=4ay
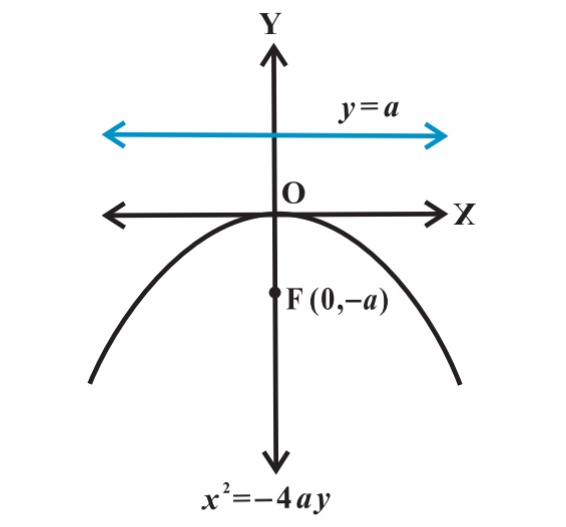
x2=−4ay
निष्कर्ष:
(a) x का गुणांक धनात्मक हो तो परवलय दाई ओर खुलता है।
(b) x का गुणांक ऋणात्मक हो तो परवलय बाई ओर खुलता है।
(a) y का गुणांक धनात्मक हो तो परवलय ऊपर की ओर खुलता है।
(b) y का गुणांक ऋणात्मक हो तो परवलय नीचे की ओर खुलता है।
उदाहरण 2
परवलय x2=−16y के अक्ष , शीर्ष , शीर्ष पर स्पर्शी , नाभि , नियता तथा नाभिलम्ब की लम्बाई ज्ञात कीजिए |
प्रश्नानुसार
परवलय का समीकरण x2=−16y.......(i)
परवलय (i) की तुलना x2=−4ay से करने पर
a=4
इसलिए
अर्थात y=−4,x=0
⇒(0,−4)
उदाहरण 3
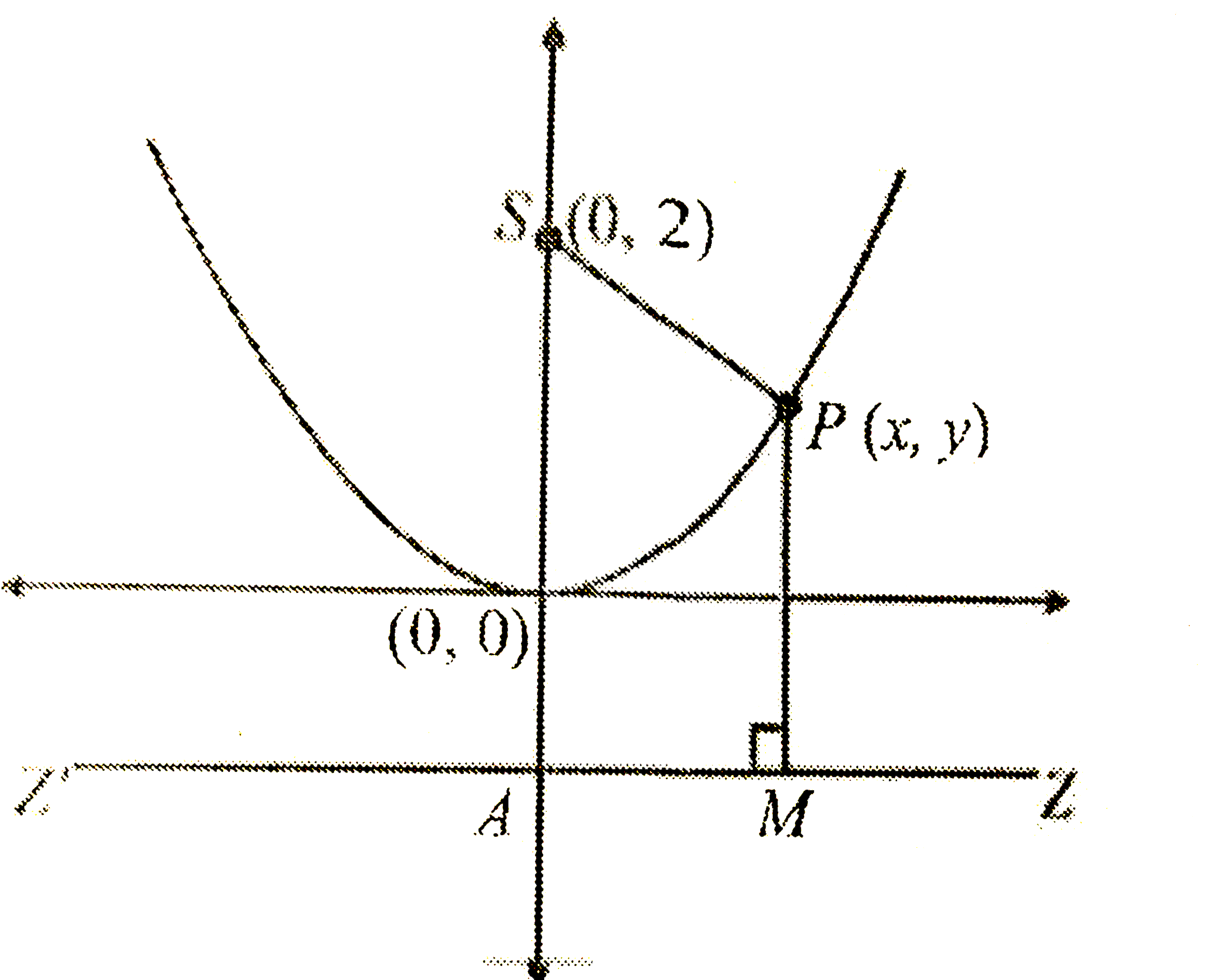
एक परवलय का समीकरण ज्ञात कीजिए जिसका शीर्ष (0,0) और नाभि (0,2) है।
A से x− अक्ष से समान्तर एक रेखा ZAZ' जो परवलय की नियता है
जिसका समीकरण y=−2 या y+2=0 है।
परवलय पर कोई बिन्दु P(x,y) लिया जिससे नियता ZAZ' पर लम्ब PM डाला तथा PS को मिलाया।
परवलय की परिभाषा से,
PS=PM
या (PS)2=(PM)2
(x−0)2+(y−2)2=(y+2)2
x2=(y+2)2−(y−2)2
x2=8y
परवलय का प्राचलिक समीकरण
प्राचलिक निर्देशांक (Parametric Co-ordinates)
समीकरण y2=4ax में y=2at रखने पर x=at2 प्राप्त होगा, जहाँ t प्राचल है। यहाँ x=at2, y=2at समीकरण y2=4ax को t के सभी मानों के लिए संतुष्ट करते है। अतः परवलय y2=4ax पर किसी बिन्दु का निर्देशांक (at2,2at) होगा।
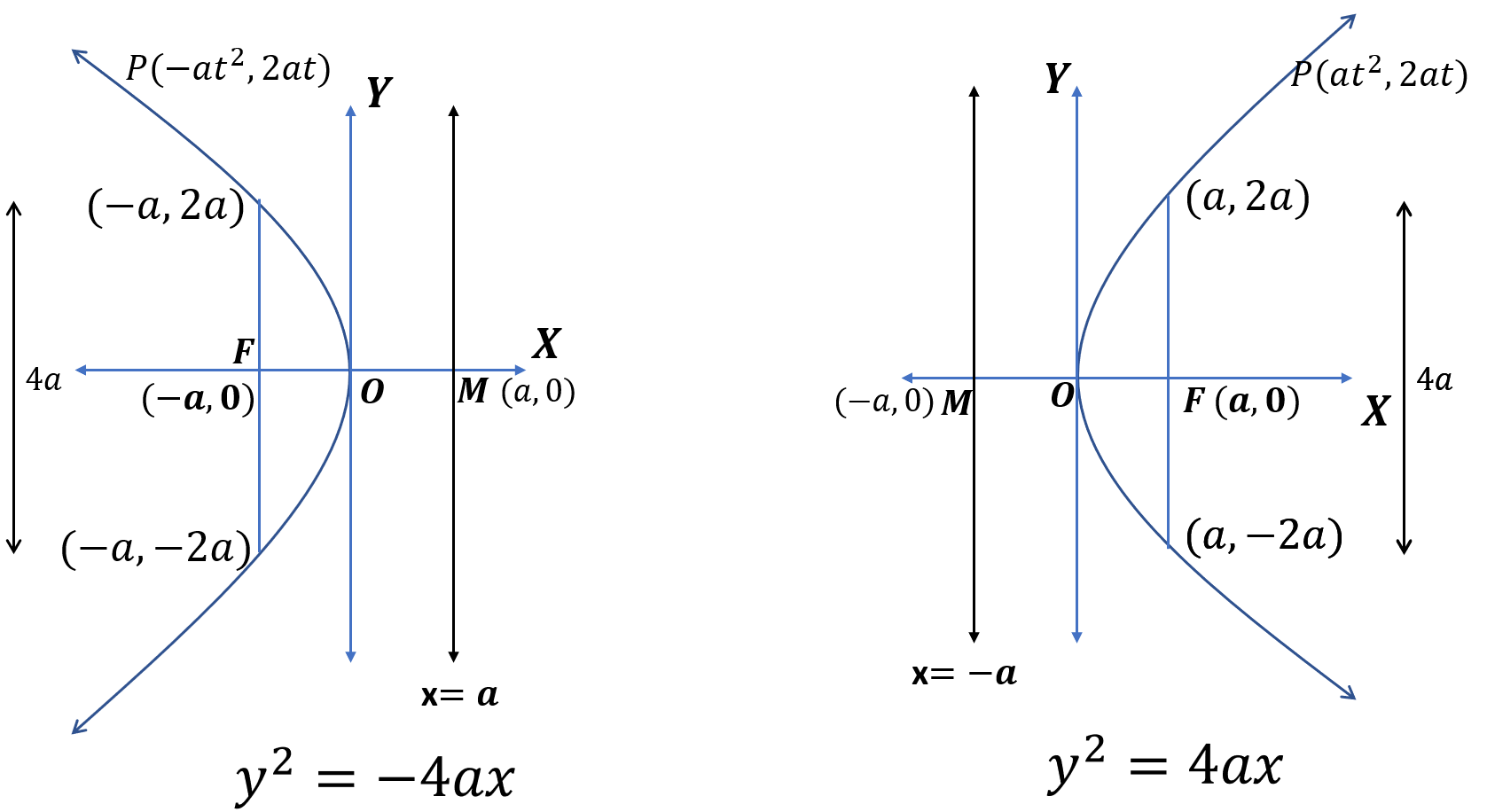
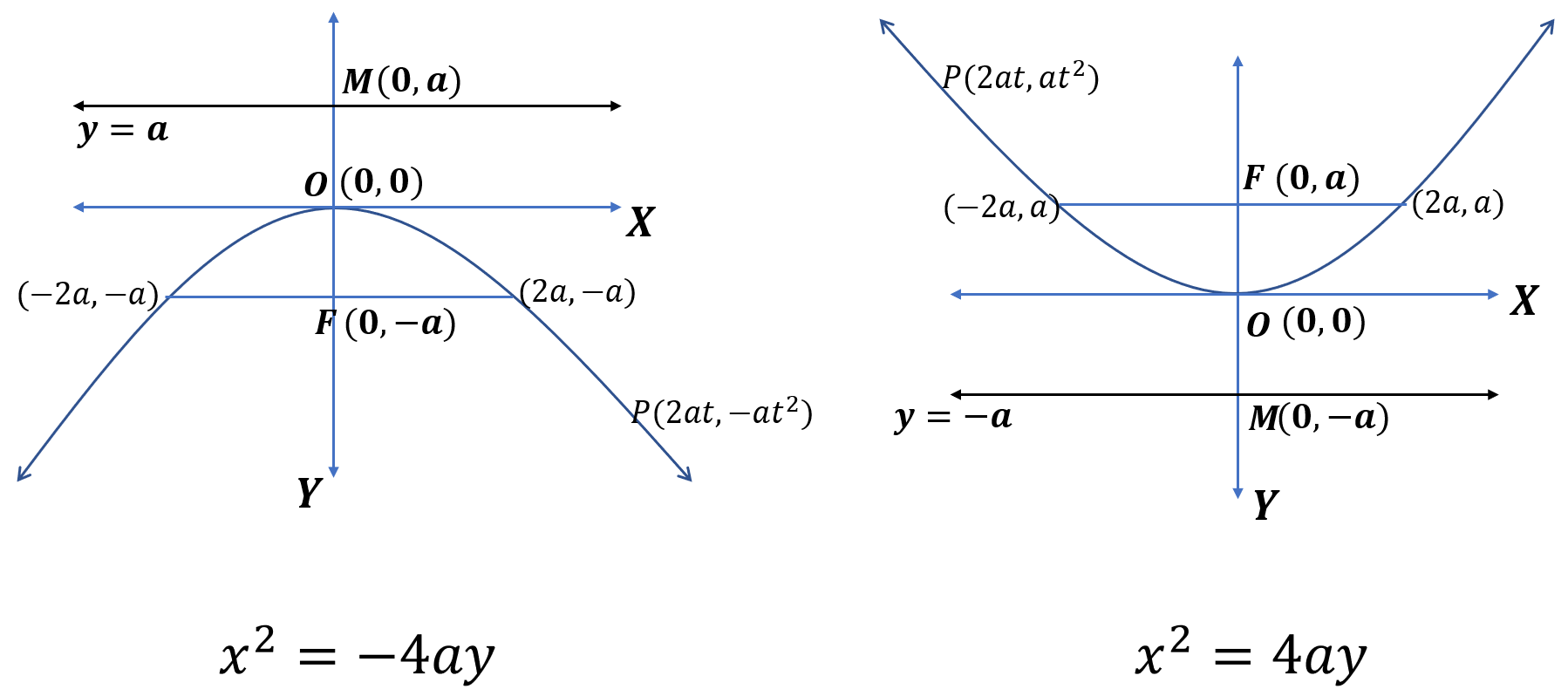
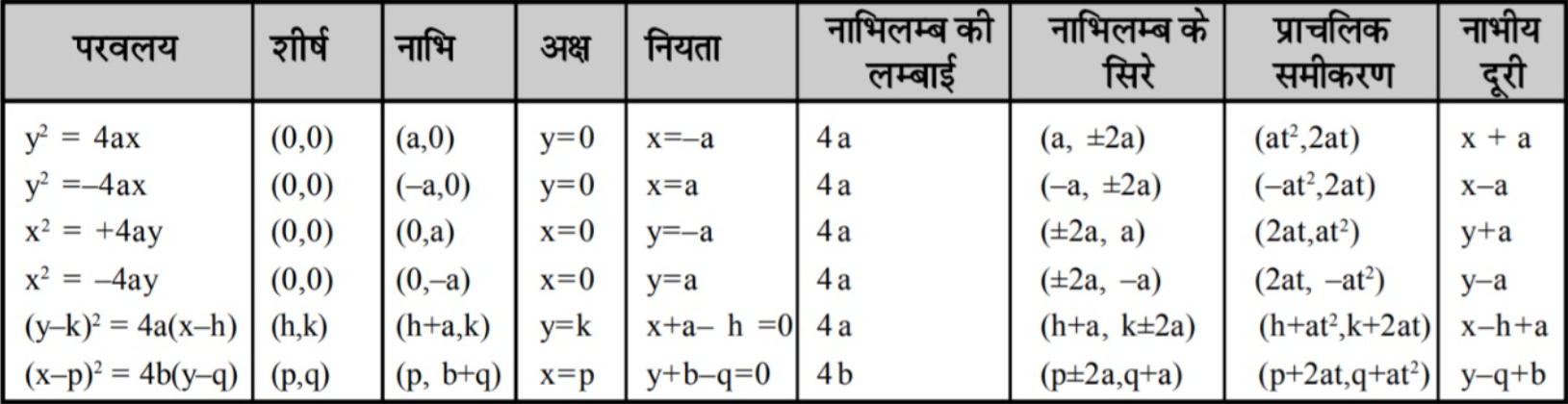
इसी प्रकार परवलयों के लिए कुछ महत्वपूर्ण मान निम्न तालिका में देख सकते है -
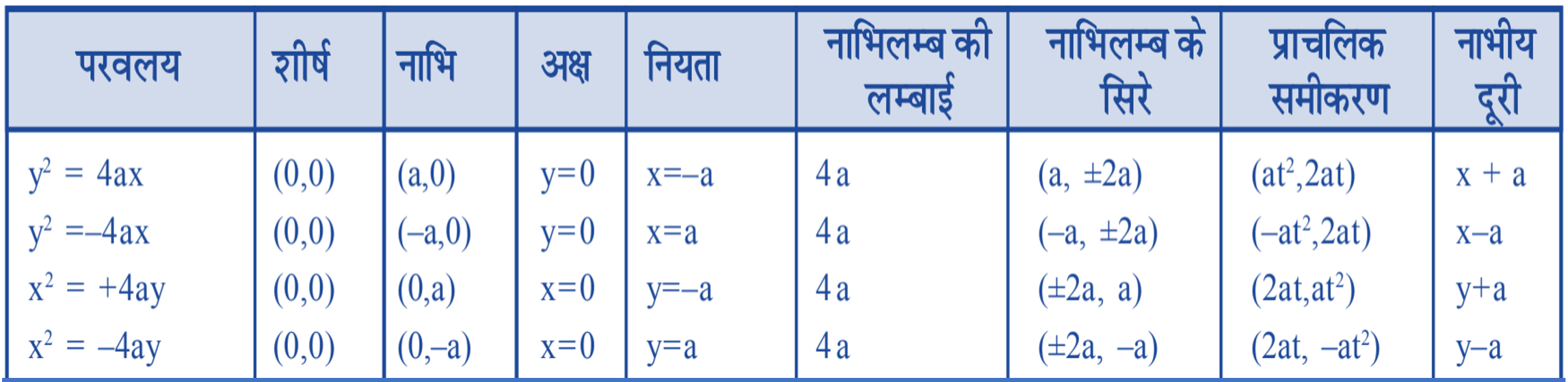
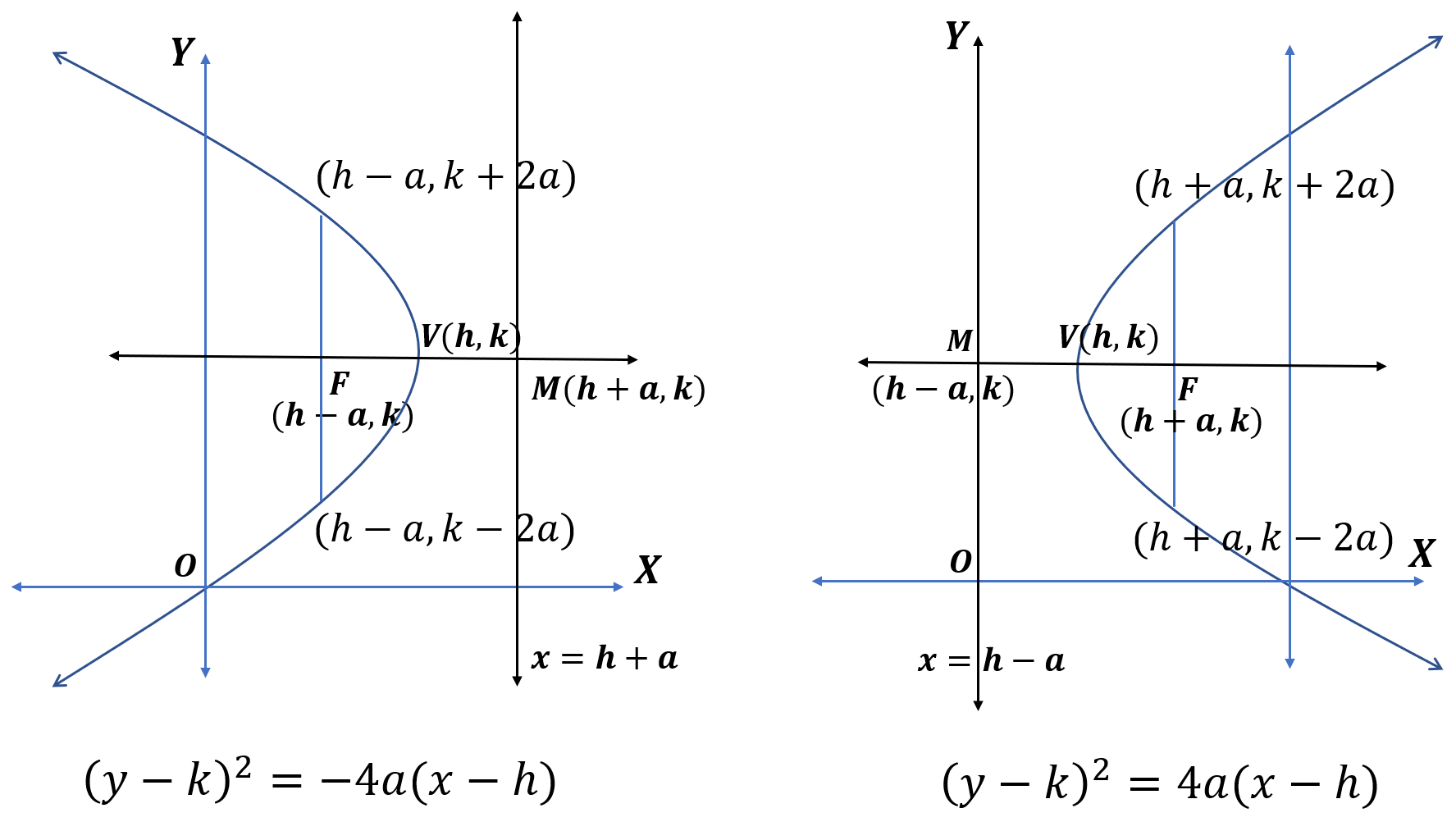
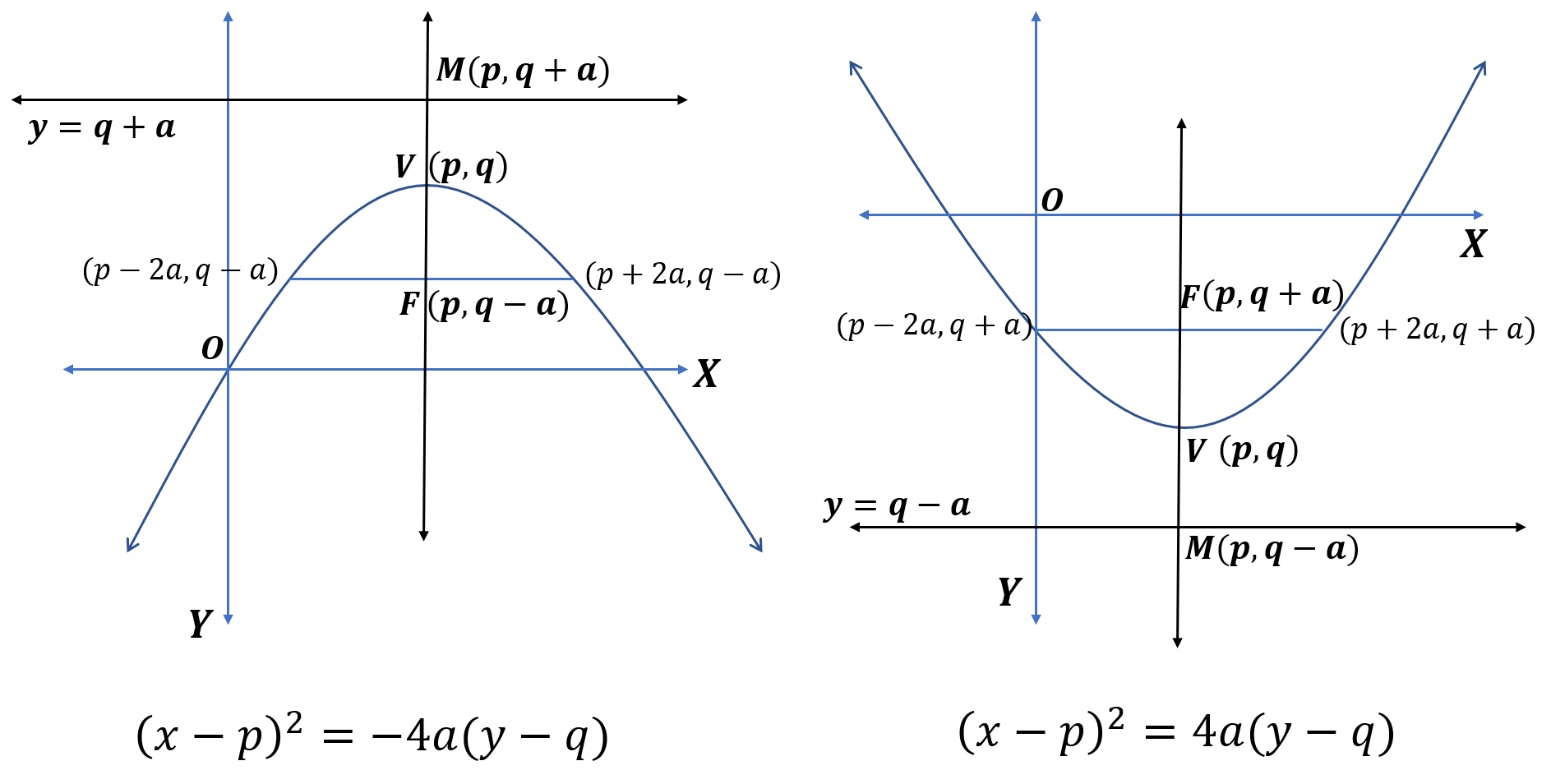
अब तक जिस प्रकार के परवलयों कि चर्चा हमने कि थी वहाँ परवलय का शीर्ष (0,0) था, अब यदि परवलय का शीर्ष (h,k) या (p,q) है तब
परवलय का समीकरण (y−k)2=4a(x−h) प्राप्त होगा, जब अक्ष x− अक्ष के समांतर हो।
परवलय का समीकरण (x−p)2=4a(y−q) प्राप्त होगा, जब अक्ष y− अक्ष के समांतर हो।

उदाहरण 4
उस परवलय का समीकरण ज्ञात कीजिए, जिसकी नाभि (−8,−2) और y=2x−9 नियता का समीकरण है।
माना, परवलय की नाभि S(−8,−2) और P(x,y) परवलय पर कोई बिन्दु है।
अब परवलय की परिभाषा से SP=P बिन्दु की नियता से दुरी
⇒√(x+8)2+(y+2)2=2x−y−9√22+(−1)2
दोनों पक्षों मे वर्ग करने पर
⇒5(x2+16x+64+y2+4y+4) =4x2+y2+81−4xy−36x+18y
⇒x2+4y2+4xy+116x+2y+259=0
उदाहरण 5
सिद्ध कीजिए की प्राचल बिन्दु (2+t2,2t+1) एक परवलय निरूपित करता है। दिखाइए कि इसका शीर्ष (2,1) है।
दिए गये प्रचलिक समीकरण निम्नलिखित है,
x=2+t2 …(1)
y=2t+1 …(2)
⇒t=y−12
t का मान समीकरण (1) में रखने पर
x=2+(y−12)2
⇒x−2=(y−1)24
⇒(y−1)2=4(x−2)
⇒Y2=4X जो परवलय का समीकरण है,
शीर्ष के निर्देशांक के लिये
X=0,Y=0
⇒x−2=0,y−1=0
⇒x=2,y=1
अतः शीर्ष के निर्देशांक ⇒(2,1)
उदाहरण 6
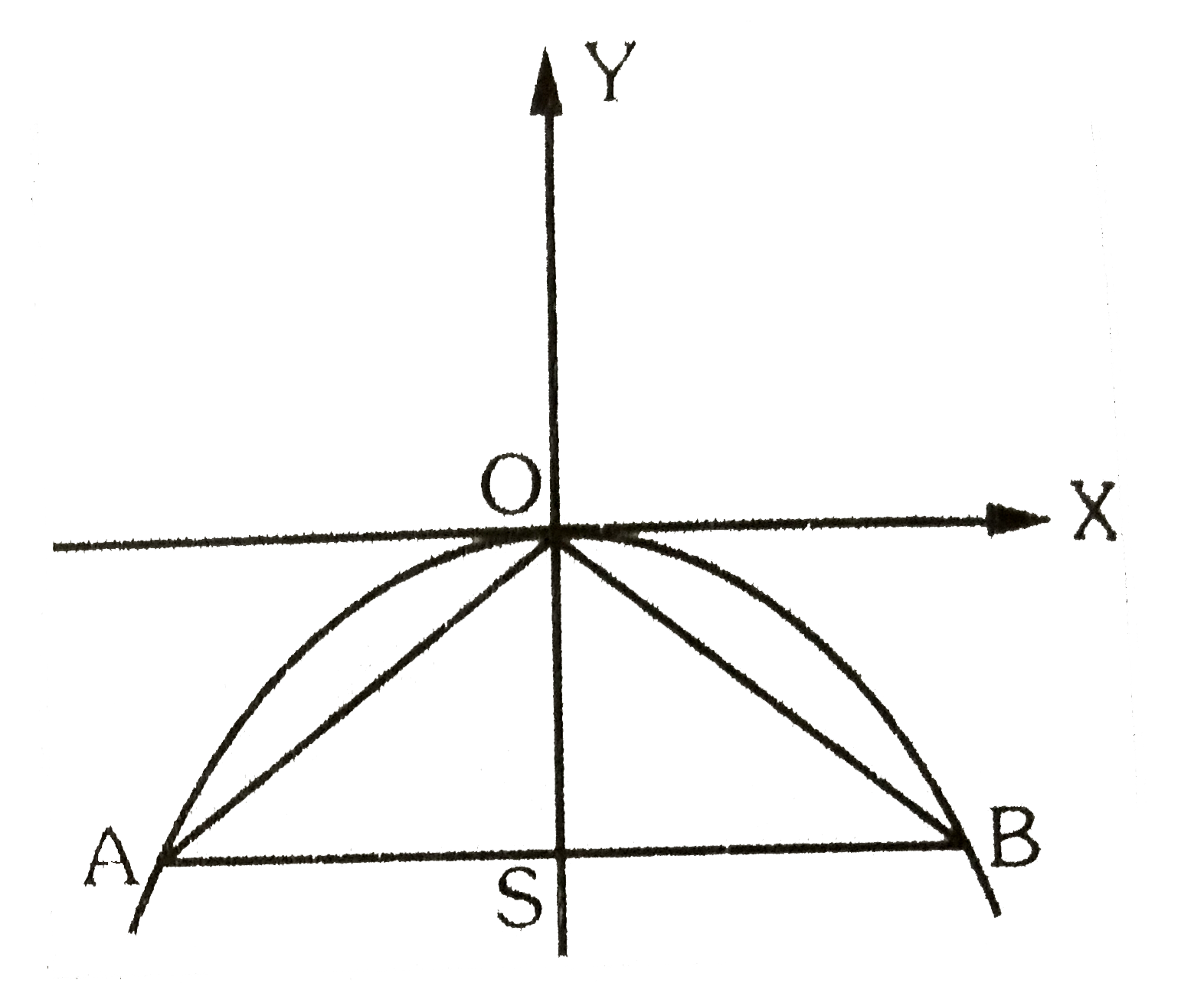
किसी परवलय x2=−36y के शीर्ष को इसके नाभिलम्ब जीवा के सिरों से मिलाने वाली रेखाओ से बने त्रिभुज का क्षेत्रफल ज्ञात कीजिए |
प्रश्नानुसार, दिया गया समीकरण
x2=−36y
x2=−4(9)y
⇒a=9>0
माना इस परवलय की नाभि S है जब ,
S≡(0,−a) या
S≡(0,9)
यहाँ AB नाभिलम्ब जीवा है इसलिए
y=−9
⇒x2=−36(−9)=324
⇒ x=±18
⇒ SB=18
अब त्रिभुज OAB का क्षेत्रफल
=2×ΔOSB का क्षेत्रफल
=2×(12×18×9)
=162 वर्ग इकाई
परवलय के सापेक्ष एक बिंदु की स्थिति
Position of a point relative to a parabola
उदाहरण 7
α का मान ज्ञात कीजिए जिसके लिए बिंदु (α−1,α) परवलय y2=4x के अंदर स्थित हो।
बिंदु (x1,y1) परवलय y2=4ax के अंदर होगा यदि व्यंजक y21−4a×x1 ऋणात्मक हो
अतः बिंदु (α−1,α) पर
(α)2−4(α−1)<0
α2−4α+4<0
α2−2α−2α+4<0
α(α−2)−2(α−2)<0
(α−2)(α−2)<0
(α−2)2<0
अतः α के वास्तविक मान के लिए यह संभव नहीं हैं अतः दिया गया बिन्दु परवलय के अंदर स्थित नहीं होगा
उदाहरण 8
परवलय y2+9−6y=5x के सापेक्ष बिंदु (1,4) की स्थिति है
माना S=y2+9−6y−5x
बिंदु (1,4) पर
S1=(4)2+9−6(4)−5(1)
=16+9−24−5
=25−29
=−4<0
अत: दिए गया बिंदु वक्र के अंदर है।
एक रेखा और एक परवलय का प्रतिच्छेदन
NOTE:
रेखा y=mx+c परवलय x2=4ay की स्पर्श रेखा होगी यदि c=−am2
उदाहरण 9
यदि रेखा y=3x+λ परवलय y2=4x को दो भिन्न बिन्दुओं पर प्रतिच्छेद करती है, तो λ के मानों का समुच्चय है
रेखा में से y का मान परवलय में रखने पर
(3x+λ)2=4x
9x2+(6λ−4)⋅x+λ2=0
रेखा परवलय के दो भिन्न बिन्दुओं पर काटती है।
D>0
4⋅(3λ−2)2−4.9λ2>0
9λ2−12λ+4−9λ2>0
λ<13
अतः λ∈(−∞,13)
परवलय की स्पर्श रेखा के विभिन्न रूप
(a) बिन्दु रूप (Point form) :
दिए गए परवलय के बिंदु (x1,y1) पर स्पर्श रेखा का समीकरण yy1=2a(x+x1) होता हैं
(b) प्रवणता रूप (Slope form) :
दिए गए परवलय की स्पर्श रेखा जिसकी प्रवणता 'm' है, का समीकरण y=mx+am ,(m≠0) होता है।
स्पर्श बिंदु (am2,2am) हैं
(c) प्राचल रूप (Parametric form) :
दिए गए परवलय के बिंदु P(t) पर स्पर्श रेखा का समीकरण ty=x+a⋅t2 होता हैं
नोट: बिंदु t1 व t2 पर स्पर्श रेखाओं का प्रतिच्छेद बिंदु |at1t2,a(t1+t2)| हैं
उदाहरण 10
परवलय y2=4x+5 की उस स्पर्श रेखा का समीकरण, जो रेखा y=2x+7 के समांतर है
परवलय y2=4x+5
अर्थात y2=4(x+54) किसी स्पर्श रेखा का समीकरण है
y=m(x+54)+1m [a=1]
यदि यह स्पर्श रेखा दी हुई रेखा y=2x+7 के समांतर है, तो m=2
अत: अभीष्ट स्पर्श रेखा का समीकरण है
y=2(x+54)+12
⇒y=2x+3
उदाहरण 11
रेखा y=2x+c, परवलय y2=16x पर स्पर्श होगी, यदि c बराबर है
परवलय y2=16x पर कोई स्पर्श रेखा है।
y=mx+4m
[y=mx+a/m]
यदि y=2x+c
परवलय की स्पर्श रेखा है, तो m=2
और c=4m
अत: c=42=2
उदाहरण 12
परवलयy2=9x पर स्पर्श रेखा की समीकरण ज्ञात कीजिए जो बिन्दु (4,10) से गुजरती है।
परवलय y2=9x की स्पर्श रेखा की समीकरण y=mx+94m हैं
चूंकि यह (4,10) से गुजरती है।
10=4m+94m
⇒16m2−40m+9=0
m=14,94
स्पर्श रेखाओं की समीकरण
y=x4+9 तथा y=94x+1 हैं
उदाहरण 13
यदि परवलय y2=8x पर स्पर्श रेखा, रेखा y=3x+5 के साथ 45∘ का कोण बनाती हो, तब इसकी समीकरण तथा स्पर्श बिन्दु ज्ञात कीजिए।
माना स्पर्श रेखा की प्रवणता m है।
tan45∘=∣∣∣3−m1+3m∣∣∣
⇒1+3m=±(3−m)
m=−2or12
जैसा कि हम जानते है कि परवलय y2=4ax की प्रवणता m की स्पर्श रेखा का समीकरण
y=mx+am तथा स्पर्शबिंदु (am2,2am) होता है।
m=−2 से, स्पर्श रेखा की समीकरण
y=−2x−1 तथा स्पर्श बिंदु (12,−2) है
m=12 से, स्पर्श रेखा की समीकरण
y=12⋅x+4 तथा स्पर्श बिंदु (8,8) हैं
परवलय के अभिलम्ब के विभिन्न रूप
(a) बिन्दु रूप (Point form):
दिए गए परवलय के बिन्दु (x1,y1) पर अभिलम्ब का समीकरण y−y1=−y12a(x−x1) होता हैं
(b) प्रवणता रूप (Slope form):
दिए गए परवलय के अभिलम्ब का समीकरण जिसकी प्रवणता m हैं, y=mx−2am−a⋅m3 होता है।
अभिलम्ब के पाद (am2,2am) है।
(c) प्राचल रूप (Parametric form) :
दिए गए परवलय के बिन्दु P(t) पर अभिलम्ब का समीकरण y+tx=2at+a⋅t3 होता है।
नोट:
बिन्दुओं t1 तथा t2 पर खींचे गए अभिलम्बों का प्रतिच्छेद बिंदु (a(t21+t22+t1t2+2),−at1t2(t1+t2)) होगा।
(i) यदि परवलय y2=4ax के बिंदु t1 पर खींचा गया अभिलम्ब परवलय को पुनः बिन्दु t2 पर मिलता है, तो t2=−(t1+2t1)
(IV) यदि परवलय y2=4ax के बिन्दुओं t1 व t2 पर खींचे गए अभिलम्ब पुनः परवलय पर स्थित बिन्दु, पर प्रतिच्छेदित करते है, तो
t1t2=2
t3=−(t1+t2)
तथा बिन्दुओं t1 तथा t2 को मिलाने वाली रेखा निश्चितबिंदु (−2a,0) से गुजरती है।
यदि परवलय पर खींचा गया अभिलम्ब P(h,k) से गुजरता है, तो
k=mh−2am−a⋅m3 अर्थात्
a⋅m3+m(2a−h)+k=0
यह m1+m2+m3=0
m1m2+m2m3+m3m1=2a−ha
m1m2m3=−ka देता हैं
जहाँm1,m2,m3 तीन संगामी अभिलम्बों की प्रवणतायें है :
उदाहरण 14
सिद्ध कीजिए कि परवलय y2=4ax के उस बिन्दु पर अभिलम्ब जीवा, जिसकी कोटि तथा भुज समान है, नाभि पर समकोण अन्तरित करती है।
माना P(at21,2at1)) पर अभिलम्ब वक्र को Q(at22,2at2) पर मिलता है।
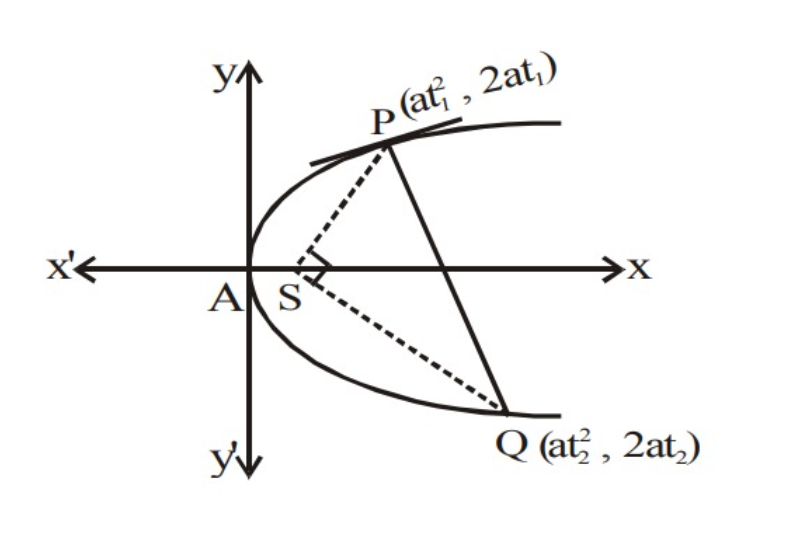
PQ अभिलम्ब जीवा है।
तथा
t2=−t1−2t1.....(i)
दिए गए प्रतिबन्ध से 2at1=at21
t1=2, समीकरण (i) से t2=−3
तब P(4a,4a) तथा Q(9a,−6a)
परन्तु नाभि S(a,0) हैं
SP की प्रवणता
=4a−04a−a=4a3a=43
SQ प्रवणता
=−6a−09a−a=−6a8a=−34
SP की प्रवणता SQ की प्रवणता
=43−34=−1
∠PSQ=π2
अर्थात् PO नाभि S पर समकोण अन्तरित करती है।
उदाहरण 15
यदि किसी बिन्दु से परवलय y2=4ax पर खींचे गए दो अभिलम्ब अक्ष के साथ α तथा β कोण इस प्रकार बनाते है कि tanα.tanβ=2. तो इस बिन्दु का बिन्दुपथ ज्ञात कीजिए।
माना बिन्दु (h,k) है।
परवलय y2=4ax पर किसी अभिलम्ब का समीकरण
y=mx−2am−a⋅m3 होता है।
चूंकि यहबिंदु (h,k) से होकर गुजरता है, अतः
k=mh−2am−a⋅m3
a⋅m3+m(2a−h)+k=0.....(i)
m1,m2,m3 समीकरण के मूल है, तो m1.m2.m3=−ka
परन्तु m1⋅m2=2,m3=−k2a
m3 समीकरण (i) का मूल हैं
a(−k2a)3−k2a(2a−h)+k=0
⇒k2=4ah
अतः बिन्दुपथ y2=4ax होगा
उदाहरण 16
परवलय y2=4ax के बिंदु (at21,2at1) पर अभिलम्ब खींचा गया है जो पुन: बिंदु (at22,2at2) पर मिलता है, तो सिद्ध कीजिये
t2=−t1−2t1
परवलय y2=4ax के बिंदु (at21,2at1) पर अभिलम्ब का समीकरण है।
(y−2at1)=−2at12a(x−at21)
∵ अभिलम्ब की प्रवणता
=−1(2ay)
=−2at12a
⇒y−2at1=−t1(x−at21)
∵ यह परवलय के बिंदु (at22,2at2) पर मिलता है।
∴2at2−2at1=t1(at22−at21)
−2t1=t2+t1
⇒t2=−t1−2t1
उदाहरण 17
बिन्दु (14,7) से वक्र y2−16x−8y=0 पर तीन अभिलम्ब खींचे जाते हैं। अभिलम्बों के पादों के निर्देशांक ज्ञात कीजिए।
दिया गया परवलय है
y2−16x−8y=0.....(i)
माना कि (14,7) से अभिलम्ब के पाद के निर्देशांक (α,β) है।
अब P(α,β) पर परवलय (i) की स्पर्श रेखा की समीकरण
yβ−8(x+α)−4(y+β)=0
या
(β−4)⋅y=8x+8a+4β.....(ii)
इसकी प्रवणता =8β−4
(α,β) पर परवलय (1) के अभिलम्ब की समीकरण
y−β=4−β8(x−α)
यह (14,7) से गुजरती हैं।
⇒7−β=4−β8(14−α)
⇒α=6ββ−4.......(iii)
तथा (α,β) परवलय (i) पर स्थित है, अर्थात्
β2−16α−8β=0....(iv)
(iii) से (iv) में α का मान रखने पर
β2−96ββ−4−8β=0
⇒β2(β−4)−96β−8β(β−4)=0
⇒β(β2−4β−96−8β+32)=0
⇒β(β2−12β−64)=0
⇒β(β−16)(β+4)=0
β=0,16,−4
(iii) से,
α=0 जब β=0
α=8 , जब β=16
α=3 जब β=−4
अतः अभिलम्ब के पाद (0,0),(8,16) तथा (3,−4) हैं
परवलय की स्पर्शी जीवा
बिन्दु P(x1,y1) से खींची गई स्पर्श रेखाओं की स्पर्श जीवा का समीकरण yy1=2a(x+x1) होता हैं
बिंदु (x1,y1) से खींची गई स्पर्श रेखाओं तथा स्पर्श जीवा से बने त्रिभुज का क्षेत्रफल (y21−4a⋅x1)322a अर्थात् (S1)322a तथा स्पर्श जीवा का अस्तित्व तभी होगा जबकि बिन्दु P अन्दर न हो ।
उदाहरण 18
यदि रेखा x−y−1=0 , परवलय y2=8x को P तथा Q पर प्रतिच्छेद करती है, तो P व Q पर स्पर्श रेखाओं का प्रतिच्छेद बिन्दु ज्ञात कीजिए।
माना (h,k) स्पर्श रेखओं का प्रतिच्छेद बिन्दु है, तब स्पर्श जीवा है
yk=4(x+h)
4x−yk+4h=0 .....(i)
परन्तु दी गई रेखा है
x−y−1=0.......(ii)
(i) तथा (ii) से तुलना करने पर
41=−k−1=4h−1
⇒h=−1,k=4
बिंदु =(−1,4)
उदाहरण 19
उस बिन्दु का बिन्दु पथ ज्ञात कीजिए जिसकी परवलय y2=4bx के सापेक्ष स्पर्श जीवा, परवलय y2=4ax की स्पर्श रेखा हो।
y2=4ax की स्पर्श रेखा की समीकरण y=mx+am.....(i)
माना यह परवलय y2=4bxके लिए बिन्दु P(h,k) के सापेक्ष स्पर्श जीवा है।
स्पर्श जीवा का समीकरण है.
yk=2b⋅(x+h)
y=2bk⋅x+2bhk.....(ii)
(i) तथा (ii) से
m=2bk
am=2bhk
⇒a=4b2hk2
P का बिन्दु पथ y2=4b2ax हैं
जीवा जिसका मध्य बिंदु दिया गया हो
परवलय y2=4ax की जीवा का समीकरण जिसका मध्य बिंदु (x1,y1) है,
y−y1=2a⋅(x−x1) होगा, जो कि T=S1 परिवर्तित हो जाती हैं जहाँ T=yy1−2a(x+x1) तथा S1=(y1)2−4ax1 है।
उदाहरण 20
परवलय y2=4ax की जीवा जो (p,q) से गुजरती है, के मध्य बिन्दु का बिन्दुपथ ज्ञात कीजिए।
माना P(h,k) , परवलय y2=4ax की जीवा का मध्य बिन्दु है,
तो जीवा की समीकरण yk−2a⋅(x+h)=k2−4ah है।
अत: यह (p,q) से गुजरती है
qk−2a⋅(p+h)=k2−4ah
अभीष्ट बिंदु पथ y2−2ax−qy+2ap=0 हैं
उदाहरण 21
y2=4ax की जीवा जो शीर्ष पर समकोण बनाती है, के मध्य बिन्दु का बिन्दुपथ ज्ञात कीजिए।
परवलय की जीवा जिसका मध्य बिन्दु (α,β) है, का समीकरण है
yβ−2a(x+α)=β2−4aα
⇒yβ−2ax=β2−2aα
yβ−2axβ2−2aα=1......(i)
अब रेखा युग्म OP तथा OQ का समीकरण, जो मूलबिन्दु O अर्थात् शीर्ष को, जीवा का परवलय y2=4ax के साथ प्रतिच्छेद बिन्दु P व Q को मिलाने पर बनी है, समीकऱण (1) के साथ समघात बनाने से प्राप्त होगी। अतः रेखा युग्म OP तथा OQ का समीकरण हैं
y2=4ax(yβ−2ax)β2−2aα
y2(β2−2aα)−4aβxy+8a2x2=0
यदि रेखायें OP तथा OQसमकोण पर है, तो
x2 का गुणांक +y2 का गुणांक =0 होगा।
अतः, β2−2aα+8a2=0
⇒β2=2a(α−4a) हैं
अतः (α,β) का बिन्दुपथ y2=2a(x−4a) हैं
सारांश
