रैखिक असमिकाएँ कक्षा 11 गणित
भूमिका
बच्चों, जैसे की आपने पिछली कक्षाओ मे समीकरणों का अध्ययन किया है, समीकरण ऐसे बीजीय व्यंजक होते है जिनके बीच मे बराबर का चिह्न लगता है अर्थात दोनों पक्षों (LHS व RHS) के मध्य = चिह्न का प्रयोग होता है। जिससे ज्ञात होता है की दोनों पक्ष के मान आपस मे बराबर है अथवा हम कह सकते है की इस प्रकार के कथन जहाँ दोनों पक्ष आपस मे बराबर हो ऐसे कथनों का गणितीय रूप समीकरण कहलाता है। अब यदि दोनों पक्ष के मान आपस मे बराबर न हो तो हम मध्य मे = चिह्न का प्रयोग नहीं कर सकते अर्थात हमे समीकरण प्राप्त नहीं होगा। इस प्रकार की स्थिति मे जहाँ हमें ऐसे कथन मिलते हैं जिनमें < (से कम), > (से अधिक), ≤ (से कम या बराबर), ≥ (से अधिक या बराबर) चिह्न प्रयुक्त होते हैं। इन्हें हम असमिकाएँ (Inequalities) कहते हैं।
इस अध्याय में, हम एक या दो चर राशियों की रैखिक असमिकाओं का अध्ययन करेंगे।
आइए बच्चों रैखिक असमिकाओ को समझते है और करीब से...
बच्चों! आइए असमिकाओ (Inequities) को समझने का प्रयास करते है, इसके लिए पहले एक समीकरण का उदाहरण कथन के रूप मे देखते है।
यदि हम कहे की सेबों की सँख्या, संतरों की सँख्या के बराबर है तो इसे हम कुछ इस प्रकार लिख सकते है।
- सेबों की सँख्या = संतरों की सँख्या
यह एक समीकरण है।
परन्तु यदि हम कहे सेबों की सँख्या, संतरों की सँख्या से अधिक है तो इसे हम कुछ इस प्रकार लिख सकते है।
- सेबों की सँख्या > संतरों की सँख्या
यह एक असमिका है।
- जैसे की हमने ऊपर असमिकाओ के लिए प्रयोग होने वाले चिन्हों को देखा था, जिनमें < (से कम), > (से अधिक), ≤ (से कम या बराबर), ≥ (से अधिक या बराबर) चिह्न प्रयुक्त होते हैं।
अतः हम असमिकाओ के लिए निम्नलिखित परिभाषा दे सकते है
एक असमिका, दो वास्तविक संख्याओं या दो बीजीय व्यंजकों में <, >, ≤ या ≥ के चिह्न के प्रयोग से बनती है।
आइए एक उदाहरण से इसे समझते है -
एक कक्षा के 6 छात्र - छात्राओ की ऊँचाइयाँ नीचे चित्र मे प्रदर्शित है -

आइए कुछ कथनों के बारे मे विचार करते है (यहाँ ऊँचाई को H से दर्शाते है)
160 cm ऊँचाई वाले बच्चों की सँख्या =1
H=160
चूँकि ऊपर चित्र मे आप देख सकते है 160 cm ऊँचाई वाले छात्र की सँख्या 1 है। यहाँ बराबर (=) चिह्न का प्रयोग हुआ है अतः यह एक समीकरण है।
160 cm से कम ऊँचाई वाले बच्चों की सँख्या =2
H<160
यहाँ आप देख सकते है H के दो मान प्राप्त हो सकते है चूँकि दो छात्र ऐसे है जिनकी ऊँचाई 154cm<160cm तथा 156cm<160cm है।
इसी प्रकार
160 cm से अधिक ऊँचाई वाले बच्चों की सँख्या =3 (165cm,168cm,168cm)
H>160
160 cm से कम या बराबर ऊँचाई वाले बच्चों की सँख्या =3 (154cm,156cm,160cm)
H≤160
160 cm से अधिक या बराबर ऊँचाई वाले बच्चों की सँख्या =4 (160cm,165cm,168cm,168cm)
H≥160
यहाँ आप देख सकते है की ऊपर जहाँ = चिह्न का प्रयोग हुआ है समीकरण तथा अन्य सभी असमिकाओ को दर्शाते है।
अब बच्चों यहाँ आप देख सकते है की H के विभिन्न मान हो सकते है अर्थात यह एक चर की भाँति व्यवहार करता है इस प्रकार के असमिकाओ को चरांक असमिका कहते है।
इसी प्रकार असमिकाओ के विभिन्न प्रकार के बारे मे आगे बात कर लेते है -
संख्यांक असमिका - वे असमिकाएँ जो केवल संख्याओ से संबंधित हो।
उदाहरण के लिए
5>3, 1<4
द्वि-असमिका - दो असमिकाओ को सम्मिलित रूप से लिखने पर हमे द्वि-असमिका प्राप्त होता है।
उदाहरण के लिए -
यदि 5, 3 से बड़ा है तथा 7 से छोटा है
3<5<7
यदि x, 5 से बड़ा या बराबर है तथा 7 से छोटा है
5≤x<7
रैखिक असमिकाएँ -
एक चर x के रैखिक असमिकाएँ
ax+b>0
ax+b<0
ax+b≥0
ax+b≤0
(a≠0)
दो चर x व y के रैखिक असमिकाएँ
ax+by>c
ax+by<c
ax+by≥c
ax+by≤c
(a≠0 तथा b≠0)
द्विघातीय असमिकाएँ -
एक चर x के द्विघातीय असमिकाएँ
ax2+bx+c>0
ax2+bx+c<0
ax2+bx+c≥0
ax2+bx+c≤0
(a≠0)
सुनिश्चित असमिकाएँ -
जिन असमिकाओ मे > या < चिन्हों का उपयोग होता है, सुनिश्चित असमिका कहलाता है।
एक चर राशि के रैखिक असमिकाओ का बीजगणितीय हल और उनका आलेखीय निरूपण
(Algebraic Solutions of Linear Inequalities in One Variable and their Graphical Representation)
आइए एक असमिका 2x<15 पर विचार करें
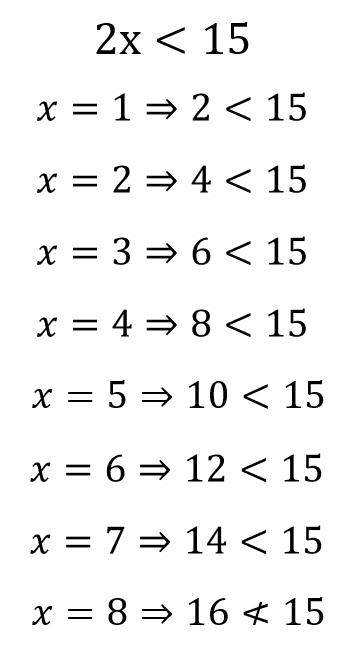
ऊपर आप देख सकते है की x के क्रमशः मानो 1,2,3....7 तक के लिए असमिका 2x<15 एक सत्य कथन है परन्तु x=8 के लिए असत्य हो जाता है चूँकि 16, 15 से बड़ी संख्या हैं , अर्थात 16>15
अतः हम कह सकते है की समुच्चय {1,2,3,4,5,6,7} असमिका 2x<15 का एक हल है।
इस प्रकार,
एक चर राशि के किसी असमिका का हल, चर राशि का वह मान है, जो इसे एक सत्य कथन बनाता हो।
असमिकाओं को हल करने के लिए हम निम्नलिखित नियमों का पालन करते हैं :
(1) एक असमिका के दोनों पक्षों में, असमिका के चिह्नों को प्रभावित किए बिना समान संख्याएँ जोड़ी (अथवा घटाई) जा सकती हैं।
असमिका 2>1 मे,
2+2>1+2
⇒4>3
(2) किसी असमिका के दोनों पक्षों को समान धनात्मक संख्याओं से गुणा (या भाग) किया जा सकता है। परंतु दोनों पक्षों को समान ऋणात्मक संख्याओं से गुणा (या भाग) करते समय असमिका के चिह्न परिवर्तित हो जाते हैं।
असमिका 2>1 मे,
2×2>1×2
⇒4>2
2×(−1)>1×(−1)
⇒−2<−1
असमीका के हल को संख्या रेखा पर दर्शाना
किसी असमीका के हल को संख्या रेखा पर दर्शाने के लिए निम्न नियमो का पालन करते हैं
किसी असमिका के हलो को अंतराल में निम्न प्रकार प्रदर्शित करते हैं:
खुला (विवृत्त) अन्तराल
(a,b)={x:,a<x<b}
प्रयुक्त प्रतीक
() या ][
बन्द (संवृत्त) अन्तराल
[a,b]={x:a≤x≤b}
प्रयुक्त प्रतीक
[ ]
वेवी-वक्र विधि
इसे अंतराल की विधि भी कहा जाता है
यह विधि f(x)g(x) के रूप की असमानताओं को हल करने के लिए उपयोग की जाती है, यह विधि इस तथ्य का उपयोग करती है कि f(x)g(x) केवल अपने मूल और लंबवत स्पर्शोन्मुख पर अपना चिह्न बदल सकता है, इसलिए हम f(x) और g(x) के मूलों का उपयोग विभिन्न अंतरालों पर फलन के ग्राफ को ज्ञात करने के लिए करते हैं।
इसे निम्न उदहारण से समझ सकते हैं
3x−x2(x+4)2≥0
step-1. बहुपदो के गुणनखंड करने पर
step-2. सभी गुणनखंडो में चर के गुणांक को धनात्मक बनाने पर
step-3. ऋणात्मक चिह्न को हटाने के लिए दोनों पक्षों को -1 से गुणा करें
(याद रखें कि ऐसा करने से चिह्न बदल जायेंगे ):
step-4.प्रत्येक गुणनखंड को 0 के बराबर करने पर
वेवी- वक्र विधि का उपयोग करके, हम आसानी से उस अंतराल का पता लगा सकते हैं जिसमें दिए गए फलन का मान धनात्मक या ऋणात्मक होता है।
उपर्युक्त उदहारण के मूलो को संख्या रेखा पर निम्न प्रकार से दर्शाया जाता हैं,
संख्या रेखा पर दर्शाते समय निम्न बिंदुओं का ध्यान रखा जाता हैं
संख्या रेखा पर अंक अंकित करें, सबसे बड़ा मूल 3 से शुरू करें। धनात्मक भाग से एक वक्र शुरू करें व उस बिन्दु पर प्रतिच्छेद करें। वेवी वक्र विधि के अनुसार अब उस व्यंजक के घात पर ध्यान दें वह सम है या विषम, यहाँ (x−3) की घात (1) विषम है तब हमें प्राप्त अन्य निकटतम मूल (0) से वक्र की दिशा बदलनी होगी अर्थात ऋणात्मक भाग से धनात्मक भाग में, जबकि यदि घात सम होती तो वक्र ऋणात्मक भाग मे ही होता। अतः गुणक -4 के लिए वक्र की दिशा नहीं बदलेगी चूंकि इसके व्यंजक (x+4) की घात सम (2) है।
अब यदि असमिका ≥ या ≤ हो तब हमें x के उन मानो को लेना है जिसके लिए असमिका 0 के बराबर हो। जबकि वेवी वक्र विधि के अनुसार हमें ऐसे व्यंजकों के मूल को नहीं लेना है जो हर मे (-4) हो।
अतः हमारा उत्तर x∈[0,3] होगा।
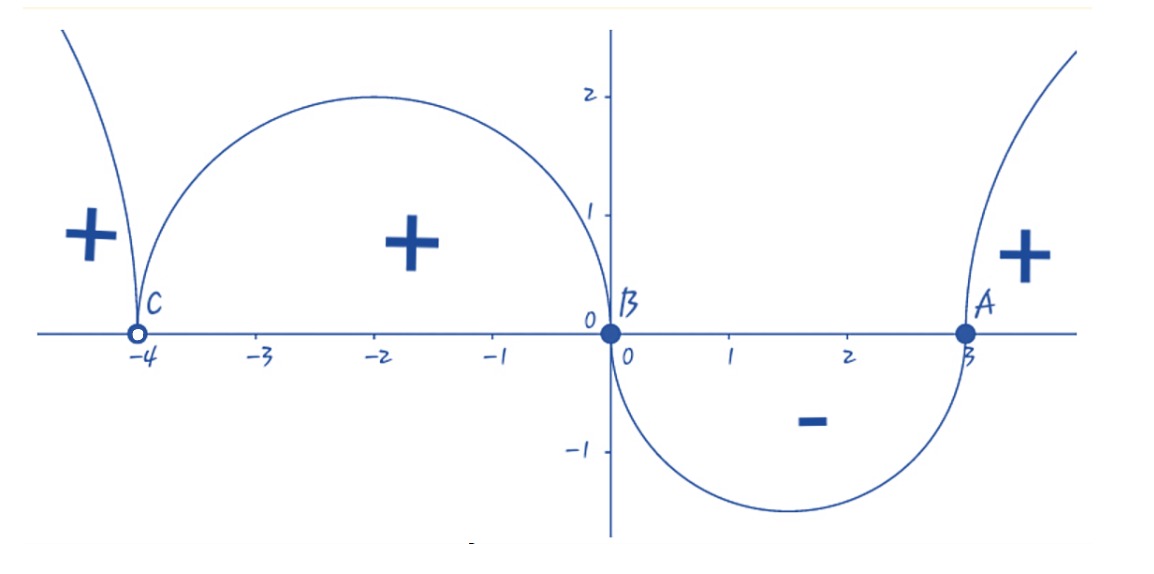
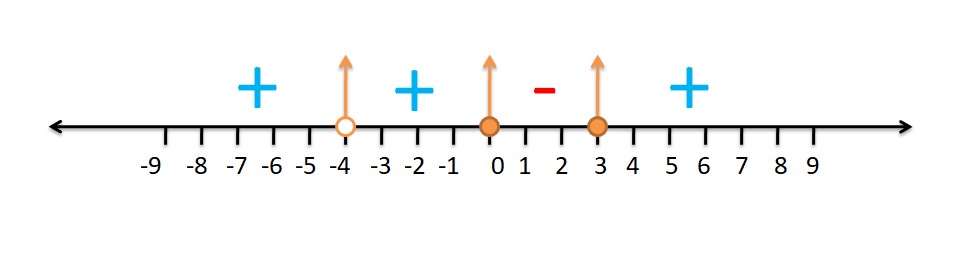
नीचे दिए गए चित्र से भी इसे दर्शा सकते है -
OMR (One Minute Revision)
उदाहरण 1
हल करें
∣∣∣x+14∣∣∣>74
दिया है,
∣∣∣x+14∣∣∣>74
⇒⎧⎨⎩x+14<−74x+14>74
⇒⎧⎨⎩x<−74−14x>74−14
⇒{x<−2x>32
∴ हल समुच्चय =(−∞,−2)∪(32,∞)
संख्या रेखा पर हल समुच्चय चित्र में मोटी लकीर से दर्शाया गया है, जिसमे रिक्त गोले से उन संख्याओ को दर्शाया गया है जो हल समुच्चय मे उपस्थित नहीं है।

उदाहरण 2
निम्नलिखित असमिकाओं को हल कीजिए -
(i) 3(x−2)5≥5(2−x)3
(ii) 1x−2<0
(iii) 2x−34+8≥2+4x3
(i) दिया है :
3(x−2)5≥5(2−x)3
⇒3x−65≥10−5x3
⇒3(3x−6)≥5(10−5x)
⇒9x−18≥50−25x
⇒9x+25x≥50+18
⇒34x≥68
⇒x≥6834=2
⇒x≥2
इसलिए दी गयी असमिका का हल समुच्चय [2,∞) है।
आलेखीय रूप में इसे निम्न प्रकार प्रदर्शित किया जा सकता है।

(ii) दिया है :
1x−2<0
⇒x−2<0
⇒x<2
⇒x∈(−∞,2)
अर्थात , दी गयी असमिका का हल समुच्चय (−∞,2) है ।
आलेखीय रूप में इसे निम्न प्रकार प्रदर्शित किया जा सकता है।
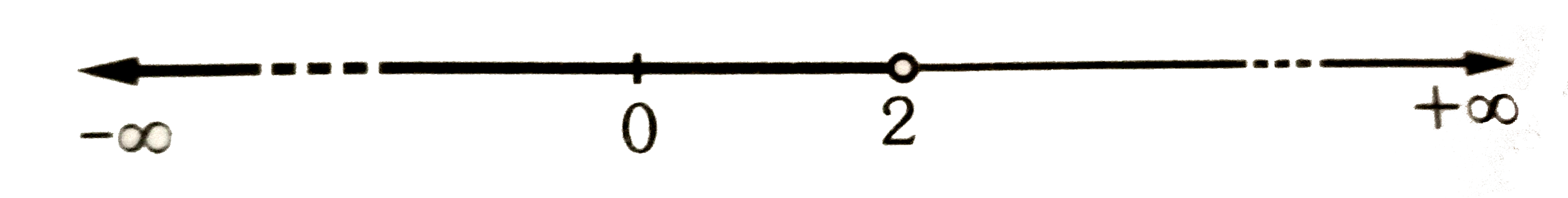
(iii) दिया है :
2x−34+8≥2+4x3
⇒2x−3+324≥6+4x3
⇒3(2x+29)≥4(6+4x)
⇒6x+87≥24+16x
⇒6x−16x≥24−87
⇒−10x≥−63
⇒x≤6310=6.3
अर्थात दी गयी असमिका का हल समुच्चय =(−∞,6.3]

दो चर राशियों के रैखिक असमिकाओ का आलेखीय हल
(Graphical Solution of Linear Inequalities in Two Variables)
जैसे की बच्चों आपने पहले 2 चरों वाले रैखिक समीकरण पढ़ा हुआ है, जिसे हम इस प्रकार दर्शाते है
ax+by+c=0
इसी प्रकार
दो चर वाले रैखिक असमिका मे >, ≥, <, या ≤ चिन्हों का प्रयोग होता है।
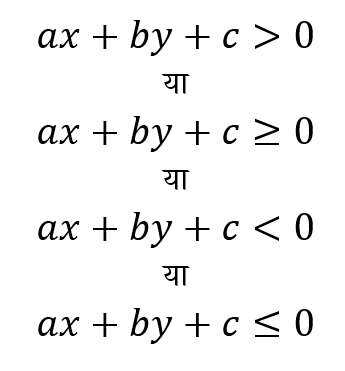
अब यदि कोई रैखिक समीकरण है तो उसका आलेख बनाना भी हमे आता है, उदाहरण के लिए
समीकरण x+y=6 को लेते है, यह एक रेखा को प्रदर्शित करता है तथा रेखा पर स्थित सभी बिन्दुओ को समीकरण संतुष्ट करता है अर्थात वे बिन्दु समीकरण के हल कहलाते है।
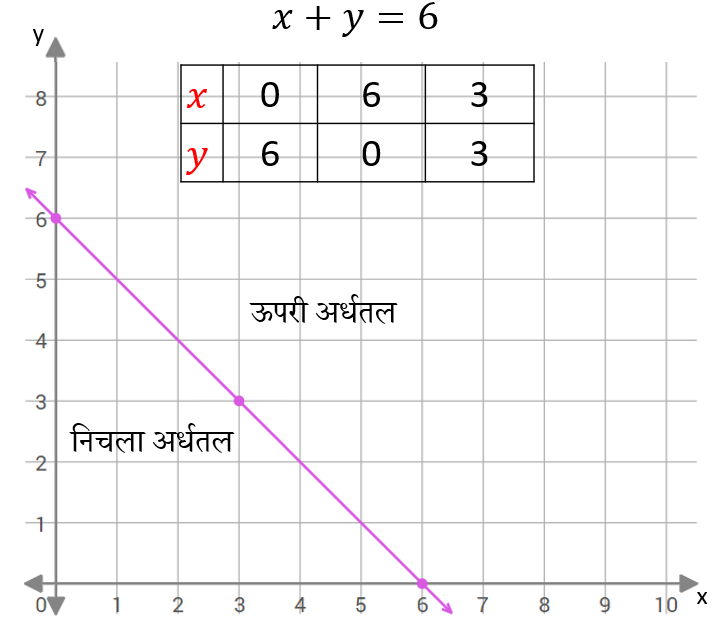
जैसा की हमने ऊपर देखा समीकरण से एक रेखा प्राप्त होती है जो तल को दो भागों मे बाँट रही है। यहाँ रेखा के ऊपर वाले भाग को ऊपरी अर्धतल तथा नीचे वाले भाग को निचला अर्धतल कहते है।
यदि असमिका मे चिह्न > तथा < का उपयोग हो तो निचले या ऊपरी अर्धतल के किसी बिन्दु के मान को असमिका मे रखकर देखते है तथा जिस अर्धतल का बिन्दु असमिका को संतुष्ट करता है वही अर्धतल उस असमिका का हल क्षेत्र होगा अर्थात वहाँ उपस्थित सभी बिन्दु असमिका को संतुष्ट करेंगे।
इसी प्रकार यदि असमिका मे चिह्न ≥ तथा ≤ का उपयोग हो तो उसका हल क्षेत्र निचले या ऊपरी अर्धतल के साथ - साथ रेखा के बिन्दु भी होंगे।
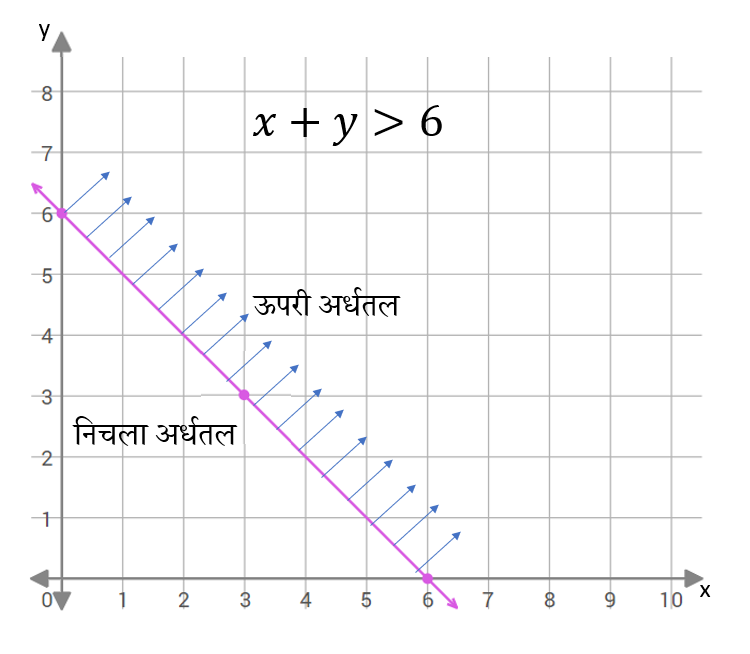
अब यदि असमिका x+y>6 ले तो
निचले अर्धतल का एक बिन्दु (0,0) रखकर देखते है
0>6 जो की असत्य है।
अर्थात ऊपरी अर्धतल असमिका का हल क्षेत्र है।
बिन्दु (3,4) ऊपरी अर्धतल मे है, असमिका मे रखने पर
3+4>6⇒7>6
जो की सत्य है।
[NOTE - यदि तल मे एक ऊर्ध्वाधर रेखा ले तो रेखा तल को दो भागों दायें अर्धतल तथा बाएं अर्धतल मे बँटेगा।]
OMR (One Minute Revision)
∗ यदि दो चरांकों की एक असमिका के चिह्न ≤ या ≥ हों तो रेखा पर स्थित बिन्दु, असमिका के हल में सम्मिलित होते हैं और असमिका का आलेख, समीकरण द्वारा निरूपित गहरी मोटी रेखा के बाई (नीचे) या दाई (ऊपर) होता है तथा उस क्षेत्र का कोई भी बिंदु असमिका को संतुष्ट करता है।
∗ यदि दो चरांकों की एक असमिका के चिह्न < या > हों तो रेखा पर स्थित बिंदु, असमिका के हल में सम्मिलित नहीं होते हैं और असमिका का आलेख, समीकरण द्वारा निरूपित दानेदार रेखा के बाईं (नीचे) या दाई (ऊपर) ओर होता है तथा उस क्षेत्र का कोई भी बिंदु असमिका को संतुष्ट करता है।
उदाहरण 3
निम्नलिखित असमिकाओं का आलेखीय हल ज्ञात कीजिए -
(i) x+y<2
(ii) x+y≥2
दी गयी दोनों असमिकाओं के संगत रैखिक समीकरण
x+y=2
⇒x2+y2=1
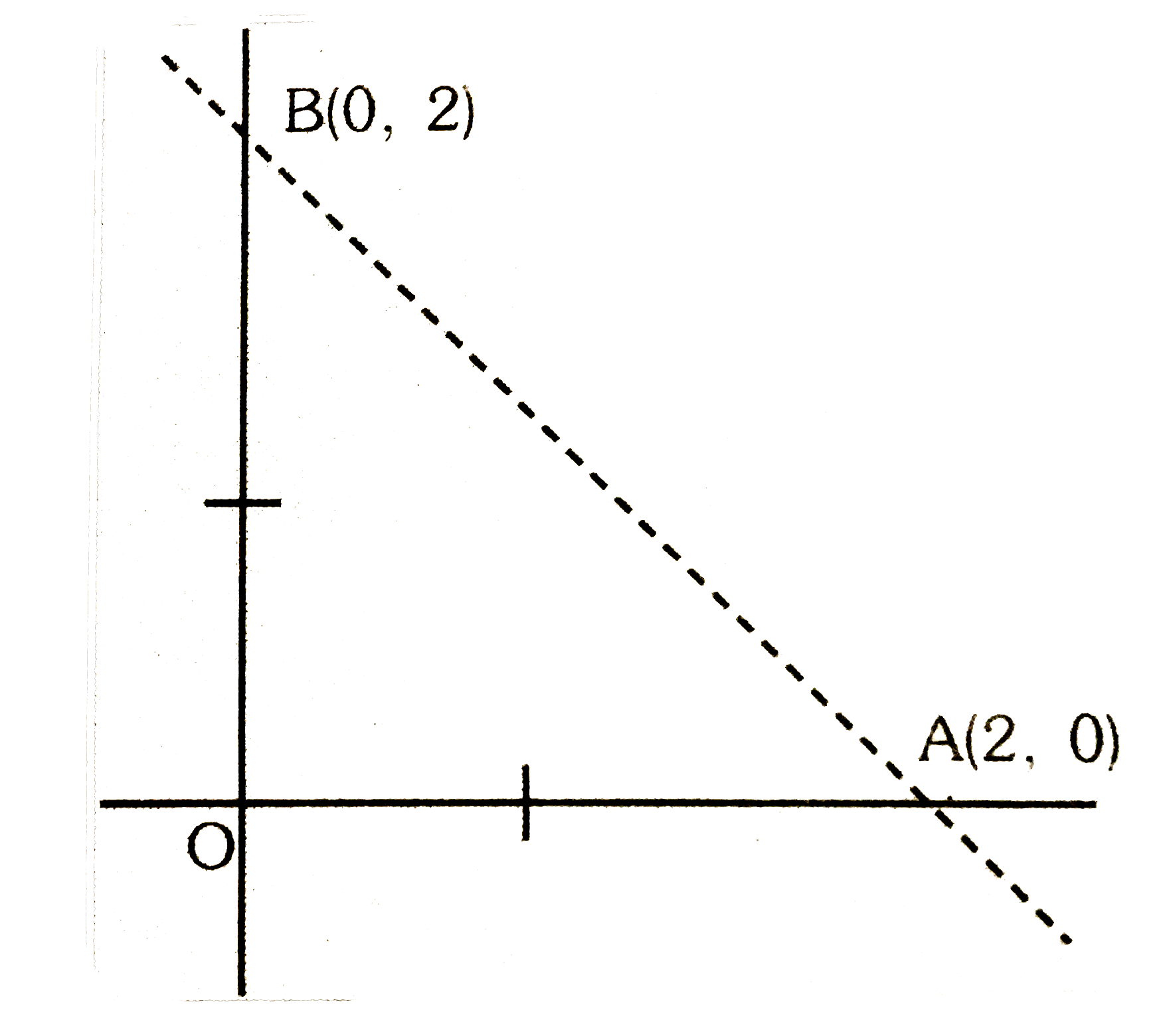
(i) क्योंकि (0,0),x+y<2 को संतुष्ट करता है । इसलिए इस असमिका का हल क्षेत्र वही होगा जिसमें मूल बिंदु स्थित है इस पार्श्व को छायांकित करने पर ।

(ii) स्पष्टतः (0,0),x+y≥2 को संतुष्ट नहीं करता । इसलिए इसका हल क्षेत्र निम्न छायांकित क्षेत्र होगा।
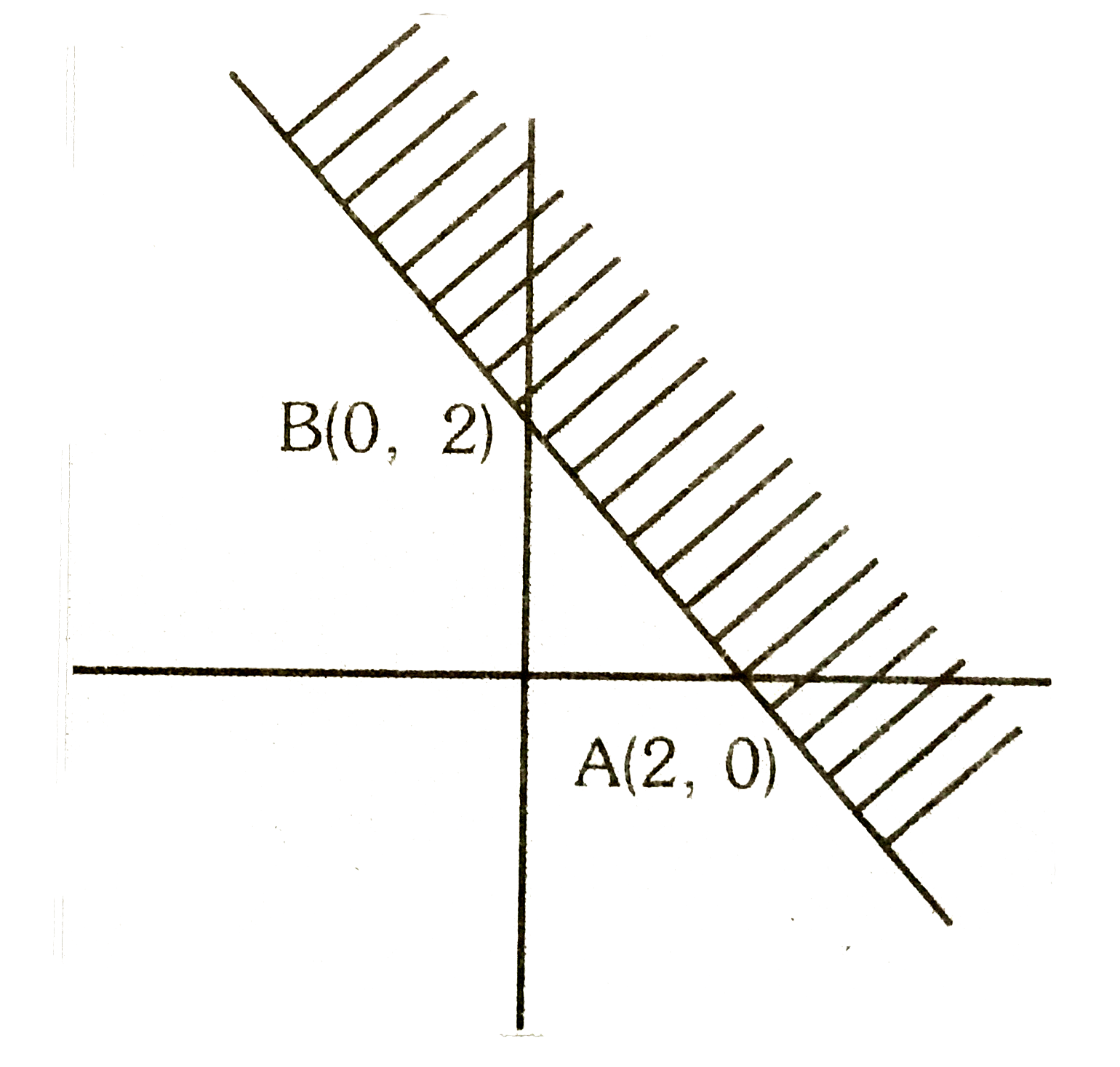
उदाहरण 4
निम्नलिखित असमिकाओं को आलेखीय विधि द्वारा हल कीजिए -
(i) 3y−5x<30
(ii) y+8>2x
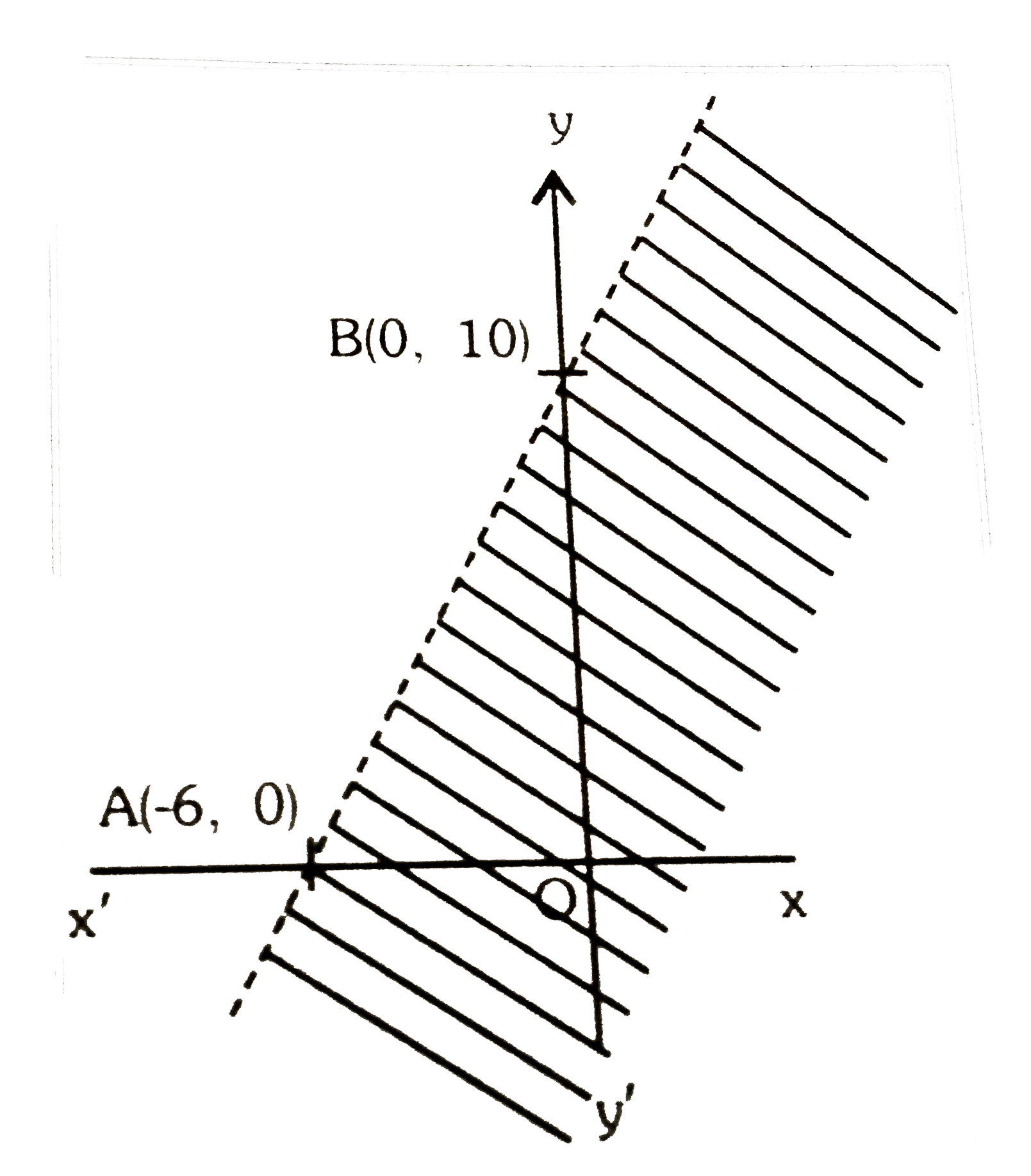
(i) दी गयी असमिका
3y−5x<30
संगत रैखिक समीकरण
3y−5x=30.......(1)
यदि y=0
⇒x=−6
इसलिए समीकरण (i) x- अक्ष को (-6,0) पर काटती है ।
पुनः
x=0
⇒y=10
⇒(i) y-अक्ष को (0,10) पर काटती है ।
स्पष्टतः O(0,0), रेखा 3y−5x=30 पर स्थित नहीं है।
असमिका (i) रेखा AB द्वारा बनाये गये उस खुले अर्द्ध -तल को निरूपित करती है जिसमें मूल बिंदु स्थित है क्योकि मूल बिंदु असमिका 3y−5x<30 को संतुष्ट करता हैं
इस प्रकार हल समुच्चय =
छायांकित क्षेत्र में रेखा (i) के बिंदुओं को छोड़कर सभी बिंदुओं का समुच्चय
(ii) दिया है:
y+8>2x
संगत रैखिक समीकरण
y+8=2x ...(ii)
यदि
y=0
⇒x=4
⇒ रेखा (ii) , x- अक्ष को (4,0) पर काटती है।
यदि x=0,y=-8
⇒ रेखा (ii) , y- अक्ष को (0,-8) पर काटती है।
माना A=(4,0),B=(0,-8)
स्पष्टतः O(0,0) दी गयी असमिका (ii) को संतुष्ट करता है ।
इस प्रकार दी गयी असमिका का हल समुच्चय =
छायांकित क्षेत्र में रेखा AB के बिंदुओं को लेकर सभी बिंदुओं का समुच्चय।

दो चर राशियों की असमिका निकाय का हल
(Solution of System of Linear Inequalities in Two Variables)
बच्चों आपने दो चरों वाले रैखिक समीकरणों के युग्मों का हल ज्ञात करना सीखा है।
दो रैखिक समीकरणों को हल करने पर जो उभयनिष्ठ बिन्दु प्राप्त होते है, रैखिक समीकरण युग्म के हल कहलाते है।
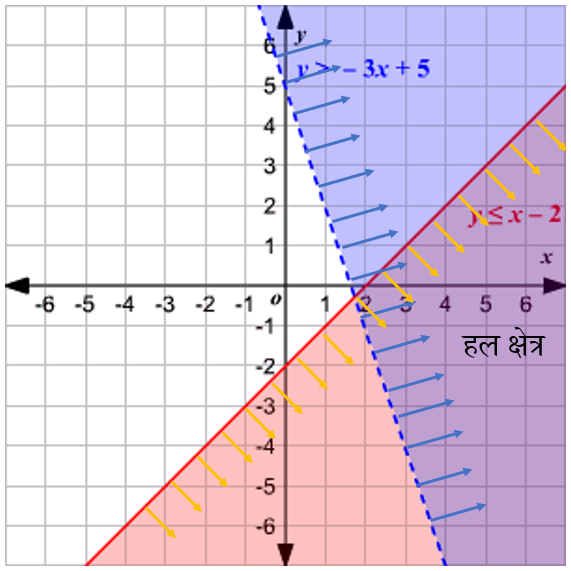
इसी प्रकार आप रैखिक असमिका युग्म को समझ सकते है, यहाँ हम रैखिक असमिकाओ के हल क्षेत्रों को देखेंगे तथा उनमे से दोनों रैखिक असमिकाओ के जो उभयनिष्ठ क्षेत्र आयेंगे वही असमिका युग्म के हल क्षेत्र होंगे।
उदाहरण के लिए आप नीचे आलेख देख सकते है
उदाहरण 5
निम्नलिखित असमिका निकाय का हल ज्ञात कीजिए -
4x+5>3x
−(x+3)+4≤−2x+5
दिया है :

इसलिए दोनों असमिकाओं का उभयनिष्ठ हल =(-5,4]
आलेखीय निरूपण:
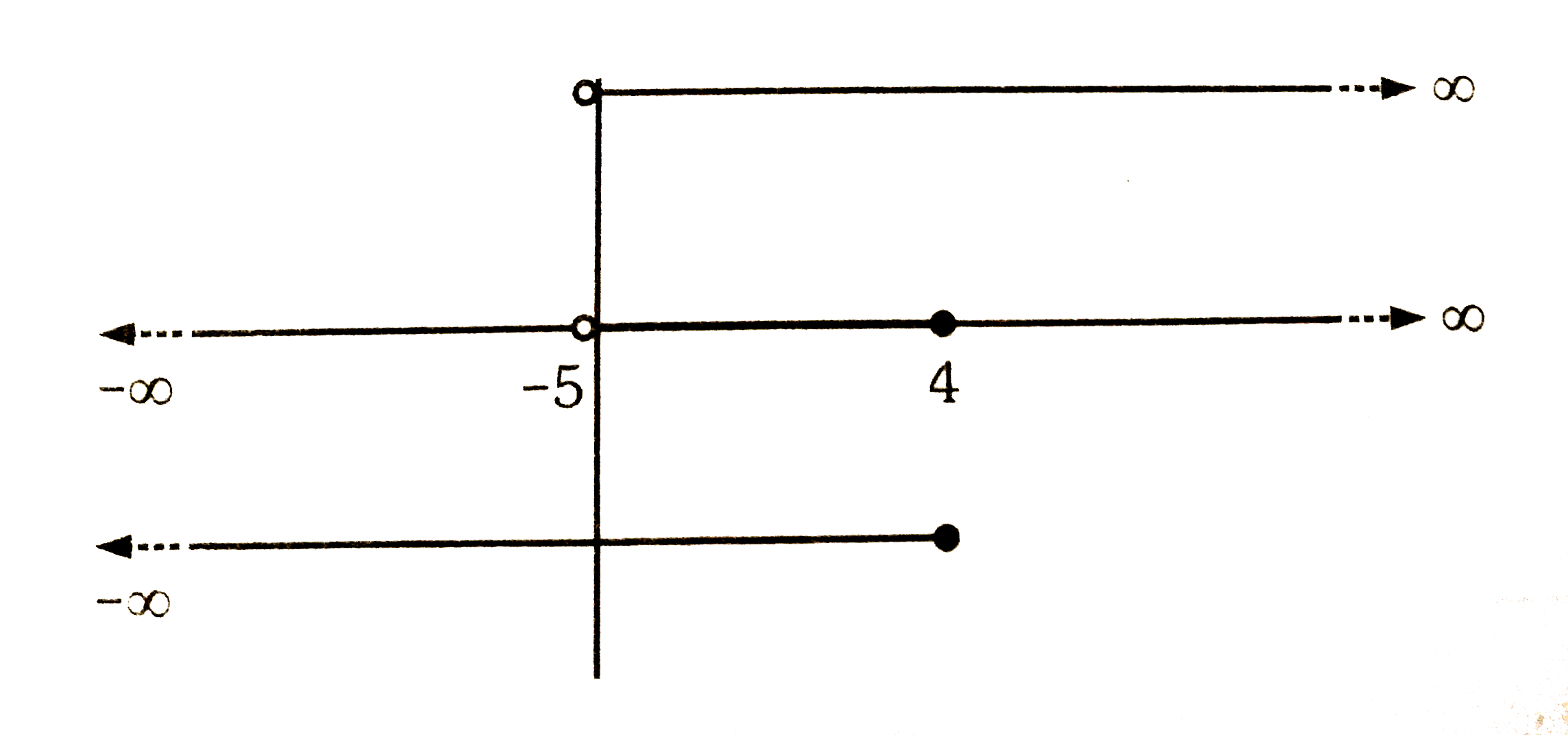
उदाहरण 6
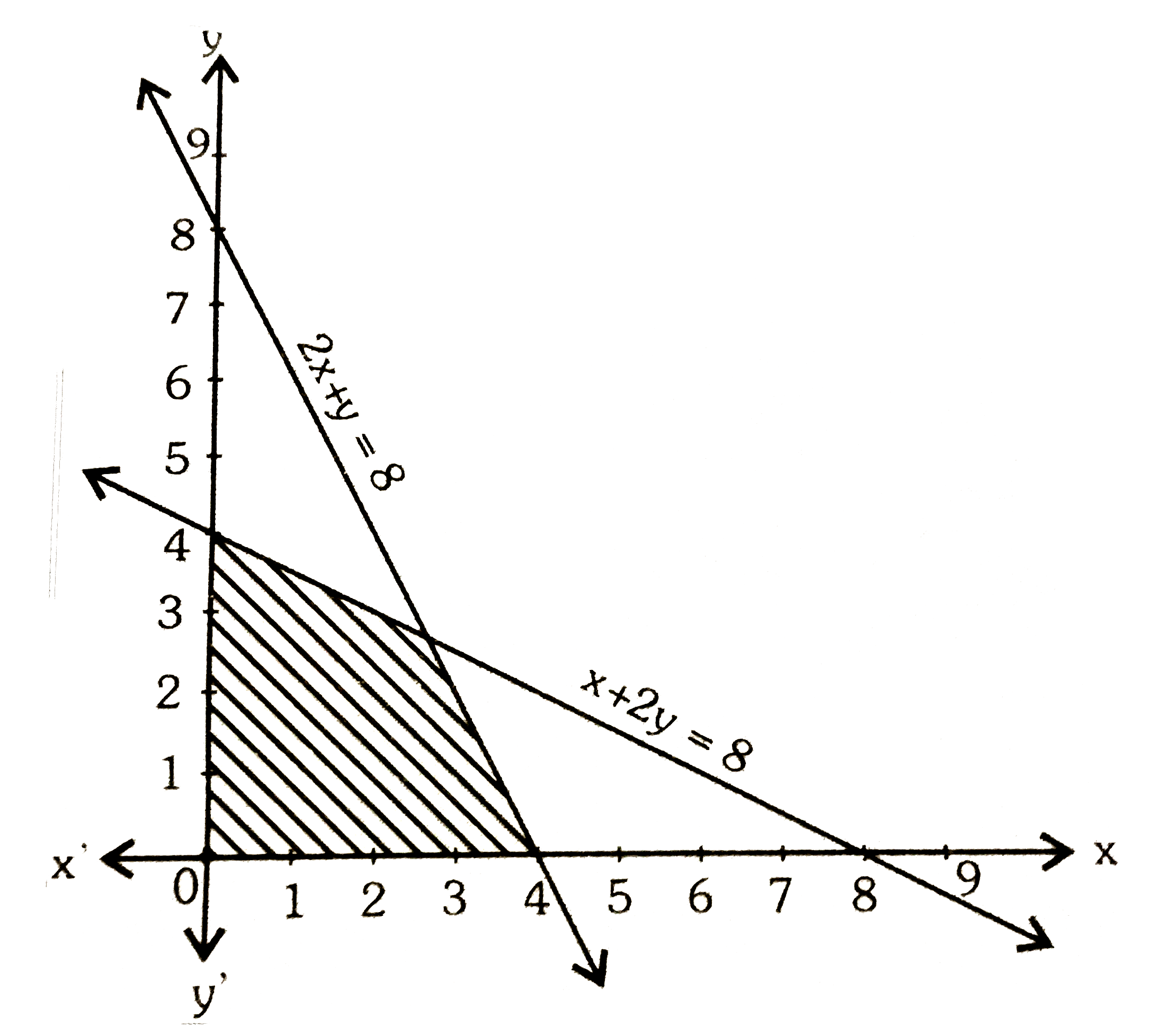
निम्नलिखित असमिका निकाय को आलेखीय विधि से हल कीजिए -
x+2y≤8 … (i)
2x+y≤8 … (ii)
x≥0 ... (iii)
y≥0 … (iv)
सर्वप्रथम
रेखाओं x+2y=8
तथा 2x+y=8 का आलेख खींचे ।
असमिका (i) व (ii) संगत रेखाओं के बिंदुओं सहित अपने से नीचे स्थित क्षेत्रों को निरूपित करती है ।
अब क्योंकि x≥0,y≥0 है ।
अतः प्रथम चतुर्थांश में स्थित सर्वनिष्ठ छायांकित क्षेत्र का प्रत्येक बिन्दु दिये गए असमिका निकाय के हल को निरूपित करता है|
सारांश
∗ एक असमिका, दो वास्तविक संख्याओं या दो बीजीय व्यंजकों में <, ≤, > या ≥ के चिह के प्रयोग से बनती है।
∗ एक असमिका के दोनों पक्षों में समान संख्या जोड़ी या घटायी जा सकती है। किसी असमिका के दोनों पक्षों को समान धनात्मक, संख्या से गुणा (या भाग) किया जा सकता है। परंतु दोनों पक्षों को समान ऋणात्मक संख्याओं से गुणा (या भाग) करने पर असमिका के चिह्न बदल जाते हैं।
∗ x के उन मानों (Values) को जो दिए गए असमिका को एक सत्य कथन बनाते हों, उन्हें असमिका का हल कहते हैं।
∗ x<a (या x>a) का संख्या रेखा पर आलेख खींचने के लिए संख्या रेखा पर संख्या a पर एक छोटा सा वृत्त बनाकर (जो रिक्त हो), a से बाई (या दाई) ओर की संख्या रेखा को गहरा काला कर देते हैं।
∗ x≤a (या x≥a) का संख्या रेखा पर आलेख खींचने के लिए संख्या रेखा पर संख्या a पर एक छोटा काला वृत्त बनाकर a से बाई (या दाई) ओर की संख्या रेखा को गहरा काला कर देते हैं।
∗ यदि दो चरांकों की एक असमिका के चिह्न ≤ या ≥ हों तो रेखा पर स्थित बिन्दु, असमिका के हल में सम्मिलित होते हैं और असमिका का आलेख, समीकरण द्वारा निरूपित गहरी मोटी रेखा के नीचे (बायीं और ) या ऊपर (दायी और ) होता है जो उस क्षेत्र का कोई भी बिंदु असमिका को संतुष्ट करता है।
∗ यदि दो चरांकों की एक असमिका के चिह्न < या > हों तो रेखा पर स्थित बिंदु, असमिका के हल में सम्मिलित नहीं होते हैं और असमिका का आलेख, समीकरण द्वारा निरूपित दानेदार रेखा के बाईं (नीचे) या दाई (ऊपर) होता है तथा उस क्षेत्र का कोई भी बिंदु असमिका को संतुष्ट करता है।
∗ असमिकाओं के निकाय का हल क्षेत्र, वह उभयनिष्ठ क्षेत्र है जो निकाय में सभी दी गई असमिकाओं को संतुष्ट करता है।
