गणितीय विवेचन कक्षा 11 गणित
भूमिका
इस अध्याय में हम गणितीय विवेचन से संबंधित कुछ मौलिक धारणाओं पर चर्चा करेंगे, गणितीय भाषा में विवेचन दो प्रकार के होते हैं।
आगमनात्मक (आगमिक) विवेचन
निगमनात्मक (निगमनिक) विवेचन
गणितीय आगमन (Mathematical Induction) के संदर्भ में हम आगमनात्मक विवेचन की चर्चा पहले कर चुके हैं। इस अध्याय में हम कुछ मूलभूत निगमनात्मक विवेचन पर चर्चा करेंगे। इस अध्याय में हम कथन, ज्ञात कथनो से नए कथन बनाना, परिमाणवाचक वाक्यांश, अंतर्भाव कथन, कथनो की वैधता आदि के बारे में पढ़ेंगे।
भूमिका
बच्चों! इस अध्याय में हम गणितीय विवेचन से संबंधित कुछ मौलिक धारणाओं के बारे में पढ़ेंगे, यह अध्याय आपके आगे आने वाली प्रतियोगी परीक्षा को ध्यान में रखकर बनाया गया है, इसमें हम बहुत ही basic से पढ़ते हुए आगे बढ़ेंगे।
गणितीय भाषा में विवेचन दो प्रकार के होते हैं।
आगमनात्मक (आगमिक) विवेचन
निगमनात्मक (निगमनिक) विवेचन
गणितीय आगमन (Mathematical Induction) के संदर्भ में हम आगमनात्मक विवेचन की चर्चा पहले कर चुके हैं। इस अध्याय में हम कुछ मूलभूत निगमनात्मक विवेचन पर चर्चा करेंगे। इस अध्याय में हम कथन, ज्ञात कथनो से नए कथन बनाना, परिमाणवाचक वाक्यांश, अंतर्भाव कथन, कथनो की वैधता आदि के बारे में पढ़ेंगे।
प्रतिवर्ष JEE Main और अन्य परीक्षाओं में इस अध्याय से 1−2 प्रश्न देखने को मिलेंगे।
आप प्रतिदिन Doubtnut की कक्षा देखें और अधिक से अधिक अभ्यास करें। आपकी इस अध्याय से संबंधित सभी समस्याएँ दूर हो जाएगीं।
आइए बच्चों कक्षा 10 का पुनरावलोकन करते है...
बच्चों आपने पिछली कक्षा में, किसी कथन को उसके विरोधात्मक वाक्य से सत्य सिद्ध करना सीखा हैं अर्थात विरोधाभास विधि का प्रयोग कर कथन को सत्य सिद्ध करना।
उदाहरण के लिए
√3 एक अपरिमेय संख्या है। यह कथन पिछली कक्षा में पढ़ा है और विरोधाभास विधि से सिद्ध भी किया है। अब आप ये दो वाक्य देखिए :
"सन् 2003 में भारत की राष्ट्रपति एक महिला थीं।"
"किसी हाथी का भार एक मनुष्य के भार से अधिक होता है।"
इन वाक्यों को पढ़ते ही हम तुरन्त निर्णय ले सकते हैं कि प्रथम वाक्य गलत (असत्य) तथा दूसरा वाक्य सही (सत्य) है, इस संबंध में कोई भ्रांति नहीं है। गणित में ऐसे वाक्यों को कथन कहते हैं।
इसके विपरीत निम्नलिखित वाक्य पर विचार कीजिए:
"महिलाएँ, पुरुषों से अधिक बुद्धिमान होती हैं।"
कुछ लोगों के विचार से यह वाक्य सत्य हो सकता है परन्तु कुछ अन्य इससे असहमत हो सकते हैं। इस वाक्य के बारे में हम यह नहीं कह सकते कि यह सत्य या असत्य है।
इस प्रकार का वाक्य गणित में कथन के रूप में स्वीकार्य नहीं है।
गणित के अध्ययन के दौरान हमें इस प्रकार के अनेक वाक्य मिलते हैं। कुछ उदाहरण इस प्रकार हैं:
इनमें से प्रथम दो वाक्य सत्य हैं और तीसरा वाक्य असत्य है। इन वाक्यों के बारे में कोई भी संदेह नहीं है, अतः ये कथन हैं।
चलिए तो हम इसे आगे पढ़ते हैं ....
आइए बच्चों कक्षा 10 का पुनरावलोकन करते है...
बच्चों आपने पिछली कक्षा में, किसी कथन को उसके विरोधात्मक वाक्य से सत्य सिद्ध करना सीखा हैं अर्थात विरोधाभास विधि का प्रयोग कर कथन को सत्य सिद्ध करना।
उदाहरण के लिए
√3 एक अपरिमेय संख्या है। यह कथन पिछली कक्षा में पढ़ा है और विरोधाभास विधि से सिद्ध भी किया है। अब आप ये दो वाक्य देखिए :
"सन् 2003 में भारत की राष्ट्रपति एक महिला थीं।"
"किसी हाथी का भार एक मनुष्य के भार से अधिक होता है।"
इन वाक्यों को पढ़ते ही हम तुरन्त निर्णय ले सकते हैं कि प्रथम वाक्य गलत (असत्य) तथा दूसरा वाक्य सही (सत्य) है, इस संबंध में कोई भ्रांति नहीं है। गणित में ऐसे वाक्यों को कथन कहते हैं।
इसके विपरीत निम्नलिखित वाक्य पर विचार कीजिए:
"महिलाएँ, पुरुषों से अधिक बुद्धिमान होती हैं।"
कुछ लोगों के विचार से यह वाक्य सत्य हो सकता है परन्तु कुछ अन्य इससे असहमत हो सकते हैं। इस वाक्य के बारे में हम यह नहीं कह सकते कि यह सत्य या असत्य है।
इस प्रकार का वाक्य गणित में कथन के रूप में स्वीकार्य नहीं है।
गणित के अध्ययन के दौरान हमें इस प्रकार के अनेक वाक्य मिलते हैं। कुछ उदाहरण इस प्रकार हैं:
इनमें से प्रथम दो वाक्य सत्य हैं और तीसरा वाक्य असत्य है। इन वाक्यों के बारे में कोई भी संदेह नहीं है, अतः ये कथन हैं।
चलिए तो हम इसे आगे पढ़ते हैं ....
कथन
एक वाक्य गणितानुसार कथन कहलाता है। "यदि वह या तो सत्य हो अथवा असत्य हो परंतु दोनों (सत्य और असत्य) न हो" अर्थात वाक्य सत्य है या असत्य इसमे कोई संदेह ना हो।
आइए ऐसे वाक्यों कि बात करते हैं जो अस्पष्ट हो अर्थात वाक्य के सत्य या असत्य होने में संदेह हो।
"x और y का योगफल 0 से अधिक है।"
यहाँ हम यह सुनिश्चित नहीं कर सकते कि वाक्य सत्य है अथवा असत्य है, जब तक हमें यह ज्ञात न हो कि x और y का मान क्या हैं?
उदाहरण के लिए, x=1, y=−3 के लिए यह असत्य है तथा x=1, y=0 के लिए यह सत्य है। अतः यह वाक्य एक कथन नहीं है।
अब वाक्य "प्रत्येक प्राकृत संख्याओं x और y का योगफल 0 से अधिक है" पर विचार करते है। यह एक कथन है, चूंकि प्राकृत संख्या n=1,2,3... है।
आगे कुछ अन्य प्रकार के वाक्यों पर चर्चा करते है -
1. आहा, कितना सुंदर !
यह कथन नहीं है चूंकि विस्मयादिबोधक (विस्मयबोधक) वाक्य है अर्थात सत्य या असत्य होने कि कोई संभावना नहीं है।
2. द्वार (दरवाजा) खोलिए।
यह एक आदेश है, अतः यह भी एक कथन नहीं है।
3. आप कहाँ जा रहे हैं?
यह कथन नहीं है चूंकि यह एक प्रश्न है, अतः सत्य या असत्य नहीं हो सकता है।
अतः गणितीय भाषा में इनमें से किसी भी प्रकार के वाक्य को कथन नहीं माना जा सकता।
कथनों का सत्यमान
किसी कथन के सत्यमान से तात्पर्य उस कथन के सत्य या असत्य होने का बोध कराने से है। इसके लिए विशेष अक्षरों का प्रयोग किया जाता है, यदि कथन सत्य है तो उसे T(true) तथा असत्य है तो F(false) से दर्शाया जाता है। यहाँ T व F, कथन का सत्यमान कहलाता है।
निम्न कथनों के सत्यमानो पर चर्चा करते है -
- प्रत्येक वर्ग एक आयत होता है।
T (चूंकि सत्य कथन है।) - एक वास्तविक संख्या या तो परिमय होता है या अपरिमेय।
T (चूंकि सत्य कथन है।) - एक वर्ग समीकरण के सदा वास्तविक मूल होते है।
F (चूंकि असत्य कथन है, काल्पनिक मूल भी हो सकते है।) - सभी पूर्णांक प्राकृत संख्या होते है।
F (चूंकि असत्य कथन है, ऋणात्मक पूर्णांक व शून्य प्राकृत संख्या नहीं होते।)
कथन
एक वाक्य गणितानुसार कथन कहलाता है। "यदि वह या तो सत्य हो अथवा असत्य हो परंतु दोनों (सत्य और असत्य) न हो" अर्थात वाक्य सत्य है या असत्य इसमे कोई संदेह ना हो।
आइए ऐसे वाक्यों कि बात करते हैं जो अस्पष्ट हो अर्थात वाक्य के सत्य या असत्य होने में संदेह हो।
"x और y का योगफल 0 से अधिक है।"
यहाँ हम यह सुनिश्चित नहीं कर सकते कि वाक्य सत्य है अथवा असत्य है, जब तक हमें यह ज्ञात न हो कि x और y का मान क्या हैं?
उदाहरण के लिए, x=1, y=−3 के लिए यह असत्य है तथा x=1, y=0 के लिए यह सत्य है। अतः यह वाक्य एक कथन नहीं है।
अब वाक्य "प्रत्येक प्राकृत संख्याओं x और y का योगफल 0 से अधिक है" पर विचार करते है। यह एक कथन है, चूंकि प्राकृत संख्या n=1,2,3... है।
आगे कुछ अन्य प्रकार के वाक्यों पर चर्चा करते है -
1. आहा, कितना सुंदर !
यह कथन नहीं है चूंकि विस्मयादिबोधक (विस्मयबोधक) वाक्य है अर्थात सत्य या असत्य होने कि कोई संभावना नहीं है।
2. द्वार (दरवाजा) खोलिए।
यह एक आदेश है, अतः यह भी एक कथन नहीं है।
3. आप कहाँ जा रहे हैं?
यह कथन नहीं है चूंकि यह एक प्रश्न है, अतः सत्य या असत्य नहीं हो सकता है।
अतः गणितीय भाषा में इनमें से किसी भी प्रकार के वाक्य को कथन नहीं माना जा सकता।
कथनों का सत्यमान
किसी कथन के सत्यमान से तात्पर्य उस कथन के सत्य या असत्य होने का बोध कराने से है। इसके लिए विशेष अक्षरों का प्रयोग किया जाता है, यदि कथन सत्य है तो उसे T(true) तथा असत्य है तो F(false) से दर्शाया जाता है। यहाँ T व F, कथन का सत्यमान कहलाता है।
निम्न कथनों के सत्यमानो पर चर्चा करते है -
- प्रत्येक वर्ग एक आयत होता है।
T (चूंकि सत्य कथन है।) - एक वास्तविक संख्या या तो परिमय होता है या अपरिमेय।
T (चूंकि सत्य कथन है।) - एक वर्ग समीकरण के सदा वास्तविक मूल होते है।
F (चूंकि असत्य कथन है, काल्पनिक मूल भी हो सकते है।) - सभी पूर्णांक प्राकृत संख्या होते है।
F (चूंकि असत्य कथन है, ऋणात्मक पूर्णांक व शून्य प्राकृत संख्या नहीं होते।)
उदाहरण 1
निम्नलिखित वाक्यों में से कौन-से वाक्य कथन है? अपने उत्तर का कारण दीजिए -
(i) मिस मोनिका एक अध्यापिका है।
(ii) आज का दिन अच्छा है।
(iii) √3 एक अपरिमेय संख्या है।
(iv) एक चतुर्भुज की चार भुजाएँ तथा चार शीर्ष होते है।
(v) सभी वर्ग त्रिभुज होते है।
(vi) आज मंगलवार है।
(vii) 4 एक सम संख्या है।
(viii) 4 एक अभाज्य संख्या है।
(ix) 6 तथा 7 का गुणनफल 42 होता है।
(x) −1 तथा 8 का गुणनफल 8 है।
(i) मिस मोनिका अध्यापिका हो भी सकती है या नहीं भी हो सकती है। यह मात्र एक दृष्टिकोण है। अत: यह कथन नहीं है।
(ii) कुछ लोगो के लिए आज का दिन अच्छा हो सकता है जबकि अन्य के लिए अच्छा नहीं होगा, अत: यह कथन नहीं है।
(iii) ∵√3 एक अपरिमेय संख्या होती है। अत: यह एक सत्य कथन है।
(iv) चतुर्भुज की परिभाषानुसार, चतुर्भुज में चार भुजाएँ तथा चार शीर्ष होते है। अत: यह एक सत्य कथन है।
(v) यह एक असत्य कथन है, क्योंकि वर्ग में चार भुजाएँ तथा त्रिभुज में तीन भुजाएँ होती है।
(vi) यह कथन नहीं है क्योंकि जिस दिन मंगलवार है। यह उसी दिन के लिए ठीक है अन्य दिनों के लिए नहीं। अतः इसकी सत्यता स्पष्ट नहीं है।
(vii) यह एक सत्य कथन है, क्योंकि सम संख्याएँ 2 से विभाज्य होती है।
(viii) यह एक असत्य कथन है, क्योकिं 4 अभाज्य संख्या नहीं होती है।
(ix) यह एक सत्य कथन है, क्योंकि 6×7=42
(x) यह एक असत्य कथन है, क्योंकि (−1)×(8)=−8
उदाहरण 1
निम्नलिखित वाक्यों में से कौन-से वाक्य कथन है? अपने उत्तर का कारण दीजिए -
(i) मिस मोनिका एक अध्यापिका है।
(ii) आज का दिन अच्छा है।
(iii) √3 एक अपरिमेय संख्या है।
(iv) एक चतुर्भुज की चार भुजाएँ तथा चार शीर्ष होते है।
(v) सभी वर्ग त्रिभुज होते है।
(vi) आज मंगलवार है।
(vii) 4 एक सम संख्या है।
(viii) 4 एक अभाज्य संख्या है।
(ix) 6 तथा 7 का गुणनफल 42 होता है।
(x) −1 तथा 8 का गुणनफल 8 है।
(i) मिस मोनिका अध्यापिका हो भी सकती है या नहीं भी हो सकती है। यह मात्र एक दृष्टिकोण है। अत: यह कथन नहीं है।
(ii) कुछ लोगो के लिए आज का दिन अच्छा हो सकता है जबकि अन्य के लिए अच्छा नहीं होगा, अत: यह कथन नहीं है।
(iii) ∵√3 एक अपरिमेय संख्या होती है। अत: यह एक सत्य कथन है।
(iv) चतुर्भुज की परिभाषानुसार, चतुर्भुज में चार भुजाएँ तथा चार शीर्ष होते है। अत: यह एक सत्य कथन है।
(v) यह एक असत्य कथन है, क्योंकि वर्ग में चार भुजाएँ तथा त्रिभुज में तीन भुजाएँ होती है।
(vi) यह कथन नहीं है क्योंकि जिस दिन मंगलवार है। यह उसी दिन के लिए ठीक है अन्य दिनों के लिए नहीं। अतः इसकी सत्यता स्पष्ट नहीं है।
(vii) यह एक सत्य कथन है, क्योंकि सम संख्याएँ 2 से विभाज्य होती है।
(viii) यह एक असत्य कथन है, क्योकिं 4 अभाज्य संख्या नहीं होती है।
(ix) यह एक सत्य कथन है, क्योंकि 6×7=42
(x) यह एक असत्य कथन है, क्योंकि (−1)×(8)=−8
ज्ञात कथनों से नए कथन बनाना
किसी कथन का निषेधन
किसी कथन को नकारना उस कथन का निषेधन कहलाता है।परिभाषा - प्रतीक p यदि एक कथन है, तो p का निषेधन वह कथन है जो p को नकारता है और इसे ~p से दर्शाते (निर्दिष्ट करते) हैं जिसे "p-नहीं" पढ़ा जाता है।
NOTE : किसी कथन p का सत्यमान यदि T है तो p के निषेधन ~p का सत्यमान F होगा। इसी प्रकार p का सत्यमान यदि F है तो p के निषेधन ~p का सत्यमान T होगा।
ज्ञात कथनों से नए कथन बनाना
किसी कथन का निषेधन
किसी कथन को नकारना उस कथन का निषेधन कहलाता है।परिभाषा - प्रतीक p यदि एक कथन है, तो p का निषेधन वह कथन है जो p को नकारता है और इसे ~p से दर्शाते (निर्दिष्ट करते) हैं जिसे "p-नहीं" पढ़ा जाता है।
NOTE : किसी कथन p का सत्यमान यदि T है तो p के निषेधन ~p का सत्यमान F होगा। इसी प्रकार p का सत्यमान यदि F है तो p के निषेधन ~p का सत्यमान T होगा।
उदाहरण 2
निम्नलिखित कथनो का निषेधन लिखिए -
(i) संख्या 2,7 से अधिक है।
(ii) √5 एक परिमेय संख्या नहीं है।
(iii) सभी त्रिभुज विषमबाहु नहीं होते है।
(iv) सभी भारतीय हिंदी बोलते है।
दिये कथनो के निषेधन इस प्रकार है -
(i) संख्या 2,7 से अधिक नहीं है।
(ii) √5 एक परिमेय संख्या है।
(iii) सभी त्रिभुज विषमबाहु होते है।
(iv) सभी भारतीय हिंदी नहीं बोलते है।
उदाहरण 2
निम्नलिखित कथनो का निषेधन लिखिए -
(i) संख्या 2,7 से अधिक है।
(ii) √5 एक परिमेय संख्या नहीं है।
(iii) सभी त्रिभुज विषमबाहु नहीं होते है।
(iv) सभी भारतीय हिंदी बोलते है।
दिये कथनो के निषेधन इस प्रकार है -
(i) संख्या 2,7 से अधिक नहीं है।
(ii) √5 एक परिमेय संख्या है।
(iii) सभी त्रिभुज विषमबाहु होते है।
(iv) सभी भारतीय हिंदी नहीं बोलते है।
मिश्र कथन (संयुक्त कथन)
'और (तथा)', 'या (अथवा)' आदि प्रकार के संयोजक शब्दों द्वारा एक या एक से अधिक कथन को जोड़कर अनेक गणितीय कथन प्राप्त किए जा सकते हैं।
परिभाषा - एक मिश्र कथन वह कथन है जो दो या दो से अधिक कथनों द्वारा बना हो, इसमें प्रत्येक कथन को घटक कथन कहते हैं।
मिश्र कथन (संयुक्त कथन)
'और (तथा)', 'या (अथवा)' आदि प्रकार के संयोजक शब्दों द्वारा एक या एक से अधिक कथन को जोड़कर अनेक गणितीय कथन प्राप्त किए जा सकते हैं।
परिभाषा - एक मिश्र कथन वह कथन है जो दो या दो से अधिक कथनों द्वारा बना हो, इसमें प्रत्येक कथन को घटक कथन कहते हैं।
उदाहरण 3
दो कथन निम्नवत है :
p:25,5 का गुणक है।
q:25,8 का गुणक है।
उपर्युक्त कथनो में 'तथा' और 'या' का प्रयोग करके मिश्र कथन की रचना कीजिए। दोनों स्थितियों में संयुक्त कथन कि जाँच कीजिए।
दिया है,
p:25,5 का गुणक है।
q:25,8 का गुणक है।
'तथा' से प्रयुक्त मिश्र कथन :
25, 5 तथा 8 का गुणज है।
यह असत्य कथन है।
'या' से प्रयुक्त मिश्र कथन :
25, 5 या 8 का गुणज है।
यह सत्य कथन है।
उदाहरण 3
दो कथन निम्नवत है :
p:25,5 का गुणक है।
q:25,8 का गुणक है।
उपर्युक्त कथनो में 'तथा' और 'या' का प्रयोग करके मिश्र कथन की रचना कीजिए। दोनों स्थितियों में संयुक्त कथन कि जाँच कीजिए।
दिया है,
p:25,5 का गुणक है।
q:25,8 का गुणक है।
'तथा' से प्रयुक्त मिश्र कथन :
25, 5 तथा 8 का गुणज है।
यह असत्य कथन है।
'या' से प्रयुक्त मिश्र कथन :
25, 5 या 8 का गुणज है।
यह सत्य कथन है।
उदाहरण 4
निम्नलिखित कथन के घटक कथन ज्ञात कीजिए और जाँचिए कि वे सत्य है या असत्य -
(i) √2 एक परिमेय संख्या है या एक अपरिमेय संख्या है।
(ii) 15 एक विषम संख्या तथा अभाज्य संख्या है।
(iii) 2,4 तथा 8 का एक गुणक 24 है।
(iv) एक वर्ग एक चतुर्भुज होता है और इसकी चारो भुजाएँ समान होती है।
(i) घटक कथन इस प्रकार है −
p:√2 एक परिमेय संख्या है।
q:√2 एक अपरिमेय संख्या है।
इसमें कथन p असत्य है तथा कथन q सत्य है।
इसमें संयोजक शब्द 'या' है।
(ii) घटक कथन इस प्रकार है −
p:15 एक विषम संख्या है।
q:15 एक अभाज्य संख्या है।
इसमें कथन p सत्य है तथा q असत्य है।
इसमें संयोजक शब्द 'तथा' है।
(iii) घटक कथन इस प्रकार है −
p:2 का एक गुणज 24 है।
q:4 का एक गुणज 24 है।
r:8 का एक गुणज 24 है।
अत: तीनो ही घटक कथन सत्य है।
इसमें संयोजक शब्द 'तथा' है।
(iv) घटक कथन इस प्रकार है −
p: एक वर्ग एक चतुर्भुज होता है।
q: एक वर्ग कि चारो भुजाएँ समान होती है।
अत: उपरोक्त दोनों ही कथन p तथा q सत्य है।
इसमें संयोजक शब्द 'और' है।
उदाहरण 4
निम्नलिखित कथन के घटक कथन ज्ञात कीजिए और जाँचिए कि वे सत्य है या असत्य -
(i) √2 एक परिमेय संख्या है या एक अपरिमेय संख्या है।
(ii) 15 एक विषम संख्या तथा अभाज्य संख्या है।
(iii) 2,4 तथा 8 का एक गुणक 24 है।
(iv) एक वर्ग एक चतुर्भुज होता है और इसकी चारो भुजाएँ समान होती है।
(i) घटक कथन इस प्रकार है −
p:√2 एक परिमेय संख्या है।
q:√2 एक अपरिमेय संख्या है।
इसमें कथन p असत्य है तथा कथन q सत्य है।
इसमें संयोजक शब्द 'या' है।
(ii) घटक कथन इस प्रकार है −
p:15 एक विषम संख्या है।
q:15 एक अभाज्य संख्या है।
इसमें कथन p सत्य है तथा q असत्य है।
इसमें संयोजक शब्द 'तथा' है।
(iii) घटक कथन इस प्रकार है −
p:2 का एक गुणज 24 है।
q:4 का एक गुणज 24 है।
r:8 का एक गुणज 24 है।
अत: तीनो ही घटक कथन सत्य है।
इसमें संयोजक शब्द 'तथा' है।
(iv) घटक कथन इस प्रकार है −
p: एक वर्ग एक चतुर्भुज होता है।
q: एक वर्ग कि चारो भुजाएँ समान होती है।
अत: उपरोक्त दोनों ही कथन p तथा q सत्य है।
इसमें संयोजक शब्द 'और' है।
संयोजक "और `(^^)`"
माना, P व Q दो घटक कथन है।
तब यहाँ हमें निम्न 4 स्थितियाँ प्राप्त होंगी -
दोनों ही कथन सत्य होंगे,
केवल पहला कथन सत्य होगा,
केवल दूसरा कथन सत्य होगा,
दोनों ही कथन असत्य होंगे।
PQP∧QTT TTF FFT FFF F
जहाँ T=true
F=false
शब्द 'या' से प्रयुक्त वाक्य (∨)
माना, P व Q दो घटक कथन है।
PQP∨QTT TTF TFT TFF F
जहाँ T=true
F=false
ऊपर दी गयी सारणी, सत्यता सारणी कहलाती है, यहाँ आप देख सकते है कि दो कथनों के लिए 4 स्थितियाँ है इसी प्रकार तीन कथनों के लिए 8 स्थितियाँ होती है। अब यदि सभी स्थितियों मे संयोजक अथवा अंतर्भाव (जिसके बारे मे आगे पढ़ेंगे) लगाने से प्राप्त कथन के लिए सभी का परिणाम T आए तो कथन पुनरुक्ति कहलाता है। इसी प्रकार यदि सभी के लिए F आए तो कथन विरोधिक्त कहलाता है।
संयोजक "और `(^^)`"
माना, P व Q दो घटक कथन है।
तब यहाँ हमें निम्न 4 स्थितियाँ प्राप्त होंगी -
दोनों ही कथन सत्य होंगे,
केवल पहला कथन सत्य होगा,
केवल दूसरा कथन सत्य होगा,
दोनों ही कथन असत्य होंगे।
PQP∧QTT TTF FFT FFF F
जहाँ T=true
F=false
शब्द 'या' से प्रयुक्त वाक्य (∨)
माना, P व Q दो घटक कथन है।
PQP∨QTT TTF TFT TFF F
जहाँ T=true
F=false
ऊपर दी गयी सारणी, सत्यता सारणी कहलाती है, यहाँ आप देख सकते है कि दो कथनों के लिए 4 स्थितियाँ है इसी प्रकार तीन कथनों के लिए 8 स्थितियाँ होती है। अब यदि सभी स्थितियों मे संयोजक अथवा अंतर्भाव (जिसके बारे मे आगे पढ़ेंगे) लगाने से प्राप्त कथन के लिए सभी का परिणाम T आए तो कथन पुनरुक्ति कहलाता है। इसी प्रकार यदि सभी के लिए F आए तो कथन विरोधिक्त कहलाता है।
उदाहरण 5
निम्नलिखित कथनो के संयोजन तथा वियोजन लिखे :
p: पेरिस फ्रांस में है।
q: लंदन इंग्लैंड में है।
संयोजन
p∧q: पेरिस फ्रांस में है और लंदन इंग्लैंड में है
वियोजन
p∨q: पेरिस फ्रांस में है या लंदन इंग्लैंड में है।
उदाहरण 5
निम्नलिखित कथनो के संयोजन तथा वियोजन लिखे :
p: पेरिस फ्रांस में है।
q: लंदन इंग्लैंड में है।
संयोजन
p∧q: पेरिस फ्रांस में है और लंदन इंग्लैंड में है
वियोजन
p∨q: पेरिस फ्रांस में है या लंदन इंग्लैंड में है।
उदाहरण 6
उदाहरण 6
उदाहरण 7
उदाहरण 7
उदाहरण 8
उदाहरण 8
उदाहरण 9
उदाहरण 9
उदाहरण 10
उदाहरण 10
उदाहरण 11
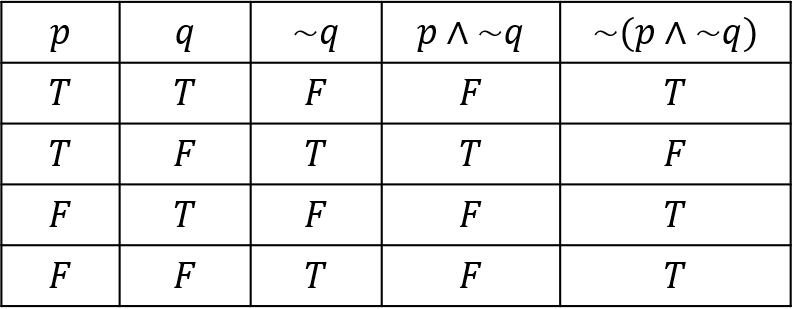
सिद्ध कीजिये कि निम्न कथन एक पुनरुक्ति है या विरोधिक्त
p∧(q∧~p)

p∧(q∧~p) के लिए सत्यमान सारणी से स्पष्ट है, यह एक विरोधिक्त है।
उदाहरण 11
सिद्ध कीजिये कि निम्न कथन एक पुनरुक्ति है या विरोधिक्त
p∧(q∧~p)

p∧(q∧~p) के लिए सत्यमान सारणी से स्पष्ट है, यह एक विरोधिक्त है।
OMR (One Minute Revision)
कुछ महत्वपूर्ण नियम −
- p∨p≡p
p∧p≡p - ~(~p)=p
- p∨q≡q∨p
p∧q≡q∧p - (p∨q)∨r≡p∨(q∨r)
(p∧q)∧r≡p∧(q∧r) - p∨(q∧r)≡(p∨q)∧(p∨r)
p∧(q∨r)≡(p∧q)∨(p∧r) - ~(p∧q)≡~p∨~q
~(p∨q)≡~p∧~q - p∨(p∧q)≡p
p∧(p∨q)≡p
OMR (One Minute Revision)
कुछ महत्वपूर्ण नियम −
- p∨p≡p
p∧p≡p - ~(~p)=p
- p∨q≡q∨p
p∧q≡q∧p - (p∨q)∨r≡p∨(q∨r)
(p∧q)∧r≡p∧(q∧r) - p∨(q∧r)≡(p∨q)∧(p∨r)
p∧(q∨r)≡(p∧q)∨(p∧r) - ~(p∧q)≡~p∨~q
~(p∨q)≡~p∧~q - p∨(p∧q)≡p
p∧(p∨q)≡p
परिमाणवाचक वाक्यांश
परिमाणवाचक वाक्यांश (सूक्ति) -
"एक ऐसे का अस्तित्व है" तथा "सभी के लिए या प्रत्येक के लिए" इन दोनों विशेष वाक्यांशों को परिमाणवाचक वाक्यांश कहते है।
उदहारण -
(i) एक ऐसी संख्या का अस्तित्व है, जो अपने वर्ग के बराबर है।
(ii) प्रत्येक वास्तविक संख्या x के लिए x,(x+1) से कम होता है।
(iii) भारत के हर एक राज्य/प्रदेश के लिए एक राजधानी का अस्तित्व है।
परिमाणवाचक वाक्यांश
परिमाणवाचक वाक्यांश (सूक्ति) -
"एक ऐसे का अस्तित्व है" तथा "सभी के लिए या प्रत्येक के लिए" इन दोनों विशेष वाक्यांशों को परिमाणवाचक वाक्यांश कहते है।
उदहारण -
(i) एक ऐसी संख्या का अस्तित्व है, जो अपने वर्ग के बराबर है।
(ii) प्रत्येक वास्तविक संख्या x के लिए x,(x+1) से कम होता है।
(iii) भारत के हर एक राज्य/प्रदेश के लिए एक राजधानी का अस्तित्व है।
उदाहरण 12
निम्नलिखित कथन में परिमाणवाचक वाक्यांश पहचानिये और कथन का निषेधन लिखिए -
भारत के हर राज्य/प्रदेश के लिए राजधानी का अस्तित्व है।
यह एक परिणामवाचक वाक्य है चूंकि
परिमाणवाचक वाक्यांश : हर/प्रत्येक के लिए
अतः निषेधन: भारत के हर राज्य/प्रदेश के लिए राजधानी का अस्तित्व नहीं है।
अथवा
भारत में एक ऐसे राज्य का अस्तित्व है जिसकी कोई राजधानी नहीं है।
उदाहरण 12
निम्नलिखित कथन में परिमाणवाचक वाक्यांश पहचानिये और कथन का निषेधन लिखिए -
भारत के हर राज्य/प्रदेश के लिए राजधानी का अस्तित्व है।
यह एक परिणामवाचक वाक्य है चूंकि
परिमाणवाचक वाक्यांश : हर/प्रत्येक के लिए
अतः निषेधन: भारत के हर राज्य/प्रदेश के लिए राजधानी का अस्तित्व नहीं है।
अथवा
भारत में एक ऐसे राज्य का अस्तित्व है जिसकी कोई राजधानी नहीं है।
उदाहरण 13
परिमाणवाचक वाक्यांश लिखकर निषेधन ज्ञात करें -
प्रत्येक वास्तविक संख्या x के लिए x, (x+1) से कम होता है।
परिमाणवाचक वाक्यांश : प्रत्येक वास्तविक संख्या के लिए
निषेधन : एक ऐसी वास्तविक संख्या x का अस्तित्व है, जिसके लिए x, (x+1) से अधिक है।
अथवा
एक ऐसी वास्तविक संख्या x का अस्तित्व है कि x, (x+1) से कम नहीं है।
उदाहरण 13
परिमाणवाचक वाक्यांश लिखकर निषेधन ज्ञात करें -
प्रत्येक वास्तविक संख्या x के लिए x, (x+1) से कम होता है।
परिमाणवाचक वाक्यांश : प्रत्येक वास्तविक संख्या के लिए
निषेधन : एक ऐसी वास्तविक संख्या x का अस्तित्व है, जिसके लिए x, (x+1) से अधिक है।
अथवा
एक ऐसी वास्तविक संख्या x का अस्तित्व है कि x, (x+1) से कम नहीं है।
अंतर्भाव कथन
अंतर्भाव "यदि-तो", "केवल यदि" और "यदि और केवल यदि" होता हैं।
सप्रतिबंध कथन
यदि P तथा Q दो कथन हैं तो उसका सप्रतिबंध कथन निम्न होता हैंयदि "P" तो "Q"
"P→Q"
यदि P तथा Q, दो कथन निम्न प्रकार है, तो "P→Q" निम्न सारणी से समझ सकते हैं -
PQP→QTT TTF FFT TFF T
जहाँ T=true
F=false
सप्रतिबंध कथन का नकारात्मक कथन
इसे निम्न प्रकार से व्यक्त करते हैं~(p→q)=p∧(~q)
जहाँ ~= निषेधन
∧= और / तथा
उदाहरण : राम मेहनत करेगा तो वह पास हो जायेगा।
उक्त कथन का नकारात्म्क कथन निम्न हैं −
राम मेहनत करेगा और वह पास नही होगा।
सप्रतिबंध कथन p→q का प्रतिधन
उदाहरण: यदि मौसम ठंडा रहेगा तो बर्फ पड़ेगी।
उक्त कथन का प्रतिधन -
यदि बर्फ नही पड़ेगी तो मौसम ठंडा नही होगा।
सप्रतिबंध कथन p→q का विलोम
उदाहरण: यदि मौसम ठंडा रहेगा तो बर्फ पड़ेगी।
उक्त कथन का विलोम कथन -
यदि बर्फ पड़ेगी तो मौसम ठंडा रहेगा।
द्विसप्रतिबंध कथन
द्विसप्रतिबंध कथन में "यदि और केवल यदि" का प्रयोग होता हैंयदि p तथा q दो कथन हैं तो उसका द्विसप्रतिबंध कथन निम्न होता हैं
p⇔q=(p→q)∧(q→p)
द्विसप्रतिबंध कथन का नकारात्मक कथन -
इसे निम्न प्रकार से व्यक्त करते हैं~(p⇔q)=~((p→q)∧(q→p))
~(p⇔q)=~(p→q)∨~(q→p)
~(p⇔q)=(p∧(~q))∨(q∧(~p))
जहाँ ∧= और
∨= या
→= यदि - तो
उदाहरण : △ABC एक समबाहु त्रिभुज होगा यदि और केवल यदि यह समान कोणीय हैं।
उक्त कथन का नकारात्मक कथन निम्न हैं −
△ABC एक समबाहु त्रिभुज होगा तथा यह समान कोणीय नहीं हैं या यह समान कोणीय हैं तथा △ABC समबाहु त्रिभुज नहीं होगा।
अंतर्भाव कथन
अंतर्भाव "यदि-तो", "केवल यदि" और "यदि और केवल यदि" होता हैं।
सप्रतिबंध कथन
यदि P तथा Q दो कथन हैं तो उसका सप्रतिबंध कथन निम्न होता हैंयदि "P" तो "Q"
"P→Q"
यदि P तथा Q, दो कथन निम्न प्रकार है, तो "P→Q" निम्न सारणी से समझ सकते हैं -
PQP→QTT TTF FFT TFF T
जहाँ T=true
F=false
सप्रतिबंध कथन का नकारात्मक कथन
इसे निम्न प्रकार से व्यक्त करते हैं~(p→q)=p∧(~q)
जहाँ ~= निषेधन
∧= और / तथा
उदाहरण : राम मेहनत करेगा तो वह पास हो जायेगा।
उक्त कथन का नकारात्म्क कथन निम्न हैं −
राम मेहनत करेगा और वह पास नही होगा।
सप्रतिबंध कथन p→q का प्रतिधन
उदाहरण: यदि मौसम ठंडा रहेगा तो बर्फ पड़ेगी।
उक्त कथन का प्रतिधन -
यदि बर्फ नही पड़ेगी तो मौसम ठंडा नही होगा।
सप्रतिबंध कथन p→q का विलोम
उदाहरण: यदि मौसम ठंडा रहेगा तो बर्फ पड़ेगी।
उक्त कथन का विलोम कथन -
यदि बर्फ पड़ेगी तो मौसम ठंडा रहेगा।
द्विसप्रतिबंध कथन
द्विसप्रतिबंध कथन में "यदि और केवल यदि" का प्रयोग होता हैंयदि p तथा q दो कथन हैं तो उसका द्विसप्रतिबंध कथन निम्न होता हैं
p⇔q=(p→q)∧(q→p)
द्विसप्रतिबंध कथन का नकारात्मक कथन -
इसे निम्न प्रकार से व्यक्त करते हैं~(p⇔q)=~((p→q)∧(q→p))
~(p⇔q)=~(p→q)∨~(q→p)
~(p⇔q)=(p∧(~q))∨(q∧(~p))
जहाँ ∧= और
∨= या
→= यदि - तो
उदाहरण : △ABC एक समबाहु त्रिभुज होगा यदि और केवल यदि यह समान कोणीय हैं।
उक्त कथन का नकारात्मक कथन निम्न हैं −
△ABC एक समबाहु त्रिभुज होगा तथा यह समान कोणीय नहीं हैं या यह समान कोणीय हैं तथा △ABC समबाहु त्रिभुज नहीं होगा।
OMR (One Minute Revision)
कुछ महत्वपूर्ण नियम −
- p→q≡~p∨q
p→q≡~q→~p - p∨q≡~p→q
p∧q≡~(p→~q) - ~(p→q)≡p∧~q
- (p→q)∧(p→r)≡p→(q∧r)
(p→r)∧(q→r)≡(p∨q)→r
(p→q)∨(p→r)≡p→(q∨r)
(p→r)∨(q→r)≡(p∧q)→r
OMR (One Minute Revision)
कुछ महत्वपूर्ण नियम −
- p→q≡~p∨q
p→q≡~q→~p - p∨q≡~p→q
p∧q≡~(p→~q) - ~(p→q)≡p∧~q
- (p→q)∧(p→r)≡p→(q∧r)
(p→r)∧(q→r)≡(p∨q)→r
(p→q)∨(p→r)≡p→(q∨r)
(p→r)∨(q→r)≡(p∧q)→r
उदाहरण 14
निम्नलिखित कथनों में से प्रत्येक को 'यदि-तो' रूप में लिखिए :
(i) आपको नौकरी मिलने का तात्पर्य है कि आपकी विश्वसनीयता अच्छी है।
(ii) केले का पेड़ फूलेगा यदि वह एक माह तक गरम बना रहे।
(i) यदि आपकी विश्वसनीयता अच्छी है तो आपको नौकरी मिलेगी।
(ii) यदि केले का पेड़ एक माह तक गरम बना रहे तो केले का पेड़ फूलेगा।
उदाहरण 14
निम्नलिखित कथनों में से प्रत्येक को 'यदि-तो' रूप में लिखिए :
(i) आपको नौकरी मिलने का तात्पर्य है कि आपकी विश्वसनीयता अच्छी है।
(ii) केले का पेड़ फूलेगा यदि वह एक माह तक गरम बना रहे।
(i) यदि आपकी विश्वसनीयता अच्छी है तो आपको नौकरी मिलेगी।
(ii) यदि केले का पेड़ एक माह तक गरम बना रहे तो केले का पेड़ फूलेगा।
उदाहरण 15
निम्नलिखित कथनो के प्रतिधनात्मक कथन लिखिए -
(i) यदि एक संख्या 9 से भाज्य है, तो वह 3 से भी भाज्य है।
(ii) एक संख्या x विषम है, तो x2 भी विषम है।
(iii) यदि एक त्रिभुज समबाहु है, तो समद्विबाहु भी है।
प्रतिधनात्मक कथन इस प्रकार से होंगे -
(i) यदि एक संख्या 3 से भाज्य नहीं है, तो वह 9 से भी भाज्य नहीं है।
अथवा
यदि एक संख्या 3 से अभाज्य है, तो वह 9 से भी अभाज्य है।
(ii) यदि एक संख्या x2 विषम नहीं है, तो x भी विषम नहीं है।
अथवा
यदि एक संख्या x2 सम है, तो x भी सम है।
(iii) यदि एक त्रिभुज समद्विबाहु नहीं है, तो वह समबाहु भी नहीं है।
उदाहरण 15
निम्नलिखित कथनो के प्रतिधनात्मक कथन लिखिए -
(i) यदि एक संख्या 9 से भाज्य है, तो वह 3 से भी भाज्य है।
(ii) एक संख्या x विषम है, तो x2 भी विषम है।
(iii) यदि एक त्रिभुज समबाहु है, तो समद्विबाहु भी है।
प्रतिधनात्मक कथन इस प्रकार से होंगे -
(i) यदि एक संख्या 3 से भाज्य नहीं है, तो वह 9 से भी भाज्य नहीं है।
अथवा
यदि एक संख्या 3 से अभाज्य है, तो वह 9 से भी अभाज्य है।
(ii) यदि एक संख्या x2 विषम नहीं है, तो x भी विषम नहीं है।
अथवा
यदि एक संख्या x2 सम है, तो x भी सम है।
(iii) यदि एक त्रिभुज समद्विबाहु नहीं है, तो वह समबाहु भी नहीं है।
उदाहरण 16
निम्नलिखित कथन का प्रतिधनात्मक, विलोम और प्रतिलोम कथन लिखिए −
यदि x एक विषम संख्या है तो यह अभाज्य है।
प्रतिधनात्मक - यदि x अभाज्य संख्या नहीं है, तो यह विषम संख्या नहीं है।
विलोम - यदि x एक अभाज्य संख्या है तो यह विषम है।
प्रतिलोम - यदि x एक विषम संख्या नहीं है, तो यह अभाज्य नहीं है।
उदाहरण 16
निम्नलिखित कथन का प्रतिधनात्मक, विलोम और प्रतिलोम कथन लिखिए −
यदि x एक विषम संख्या है तो यह अभाज्य है।
प्रतिधनात्मक - यदि x अभाज्य संख्या नहीं है, तो यह विषम संख्या नहीं है।
विलोम - यदि x एक अभाज्य संख्या है तो यह विषम है।
प्रतिलोम - यदि x एक विषम संख्या नहीं है, तो यह अभाज्य नहीं है।
उदाहरण 17
निम्नलिखित कथनो में से प्रत्येक को p यदि और केवल यदि q के रूप में पुनः लिखिए :
(i) यदि आप दूरदर्शन देखते है, तो आपका मन मुक्त होता है तथा यदि आपका मन मुक्त है, तो आप दूरदर्शन देखते है।
(ii) आपके द्वारा A− ग्रेड प्राप्त करने के लिए यह अनिवार्य और पर्याप्त है की आप गृहकार्य नियमित रूप से करते है।
(iii) यदि एक चतुर्भुज समान कोणिक है, तो वह एक आयत होता है तथा यदि एक चतुर्भुज आयत है, तो वह समान कोणिक होता है।
(i) आप टेलीविजन देखते हैं यदि और केवल यदि आपका मन मुक्त है।
(ii) आप A− ग्रेड पाते हैं यदि और केवल यदि आप समस्त गृहकार्य नियमित रूप से करते हैं।
(iii) एक चतुर्भुज सामान कोणिक है यदि और केवल यदि वह एक आयत है।
उदाहरण 17
निम्नलिखित कथनो में से प्रत्येक को p यदि और केवल यदि q के रूप में पुनः लिखिए :
(i) यदि आप दूरदर्शन देखते है, तो आपका मन मुक्त होता है तथा यदि आपका मन मुक्त है, तो आप दूरदर्शन देखते है।
(ii) आपके द्वारा A− ग्रेड प्राप्त करने के लिए यह अनिवार्य और पर्याप्त है की आप गृहकार्य नियमित रूप से करते है।
(iii) यदि एक चतुर्भुज समान कोणिक है, तो वह एक आयत होता है तथा यदि एक चतुर्भुज आयत है, तो वह समान कोणिक होता है।
(i) आप टेलीविजन देखते हैं यदि और केवल यदि आपका मन मुक्त है।
(ii) आप A− ग्रेड पाते हैं यदि और केवल यदि आप समस्त गृहकार्य नियमित रूप से करते हैं।
(iii) एक चतुर्भुज सामान कोणिक है यदि और केवल यदि वह एक आयत है।
उदाहरण 18
सिद्ध कीजिये कि निम्न कथन एक पुनरुक्ति है या विरोधिक्त
(p⇔q∧r)⇒(~r⇒~p)
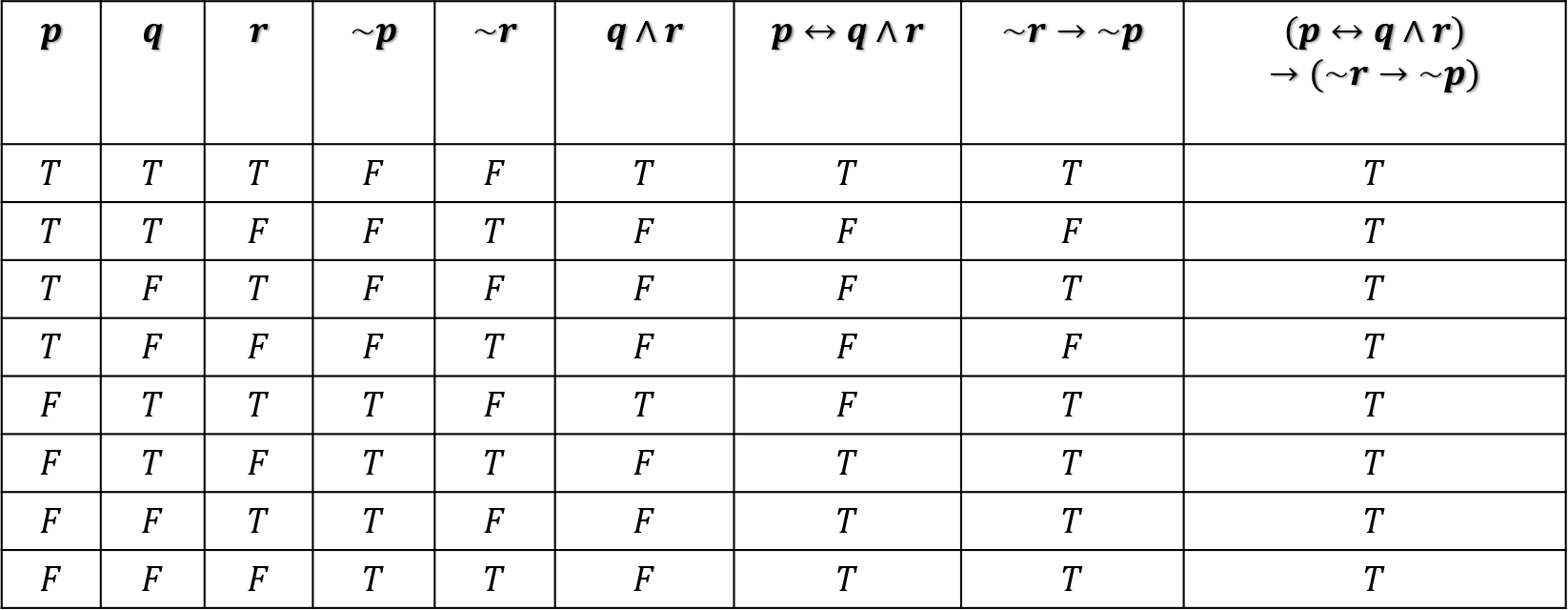
(p⇔q∧r)⇒(~r⇒~p) के लिए सत्यमान सारणी से स्पष्ट है, यह एक पुनरुक्ति है।
उदाहरण 18
सिद्ध कीजिये कि निम्न कथन एक पुनरुक्ति है या विरोधिक्त
(p⇔q∧r)⇒(~r⇒~p)

(p⇔q∧r)⇒(~r⇒~p) के लिए सत्यमान सारणी से स्पष्ट है, यह एक पुनरुक्ति है।
उदाहरण 19
निम्न कथन के लिए बताइए, यह एक पुनरुक्ति है या विरोधिक्त
(p⇔q)∨(r⇒p)
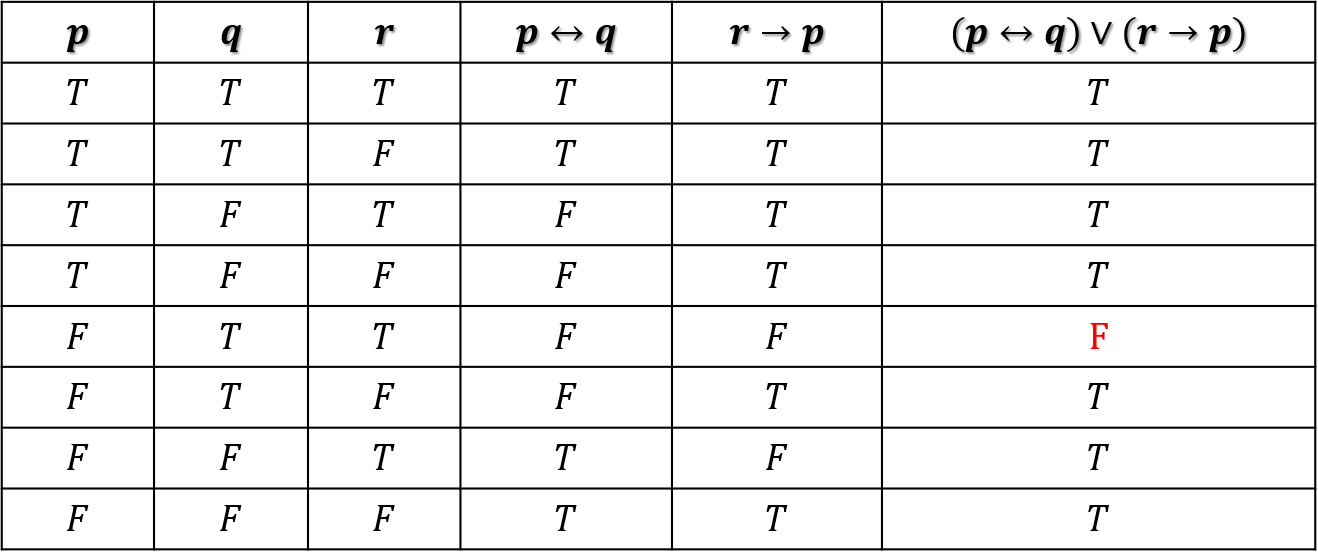
(p⇔q)∨(r⇒p) के लिए सत्यमान सारणी से स्पष्ट है, यह एक पुनरुक्ति या विरोधिक्त नहीं है।
उदाहरण 19
निम्न कथन के लिए बताइए, यह एक पुनरुक्ति है या विरोधिक्त
(p⇔q)∨(r⇒p)

(p⇔q)∨(r⇒p) के लिए सत्यमान सारणी से स्पष्ट है, यह एक पुनरुक्ति या विरोधिक्त नहीं है।
कथनों की वैधता
किसी भी कथन की जांच करने के लिए, कि वह सत्य हैं या नहीं हम निम्न नियमो का पालन करते हैं −
नियम (1)
संयोजक "और" से प्रयुक्त कथन
यदि p तथा q गणितीय कथन हैं, तो यह सिद्ध करने के लिए कि कथन "p और q" सत्य है, हम निम्नलिखित चरणों का अनुसरण करते हैं
चरण 1: दर्शाइए कि कथन p सत्य है।
चरण 2: दर्शाइए कि कथन q सत्य है।
नियम (2)
संयोजक "या" से प्रयुक्त कथन
यदि p तथा q गणितीय कथन हैं, तो कथन "p या q " को सत्य सिद्ध करने के लिए हम निम्नलिखित स्थितियों में से किसी एक को सत्य प्रमाणित करते हैं।
स्थिति 1. यह मानते हुए कि p असत्य है, q को अनिवार्यतः सत्य प्रमाणित कीजिए।
स्थिति 2. यह मानते हुए कि q असत्य है, p को अनिवार्यत: सत्य प्रमाणित कीजिए।
नियम (3)
वाक्यांश "यदि-तो" से प्रयुक्त कथन
कथन "यदि p तो q" को सत्य सिद्ध करने के लिए हम निम्नलिखित स्थितियों में किसी एक को सत्य प्रमाणित करते हैं।
स्थिति 1. यह मानते हुए कि p सत्य है, q को अनिवार्यतः सत्य प्रमाणित कीजिए (प्रत्यक्ष विधि)।
स्थिति 2. यह मानते हुए कि q असत्य है, p को भी अनिवार्यतः असत्य प्रमाणित कीजिये (प्रतिधनात्मक विधि)।
नियम (4)
वाक्यांश (प्रतिबंध) “यदि और केवल यदि" से प्रयुक्त कथन
कथन "p, यदि और केवल यदि q" को सत्य सिद्ध करने के लिए हमें यह प्रमाणित करने की आवश्यकता है कि,
स्थिति 1. p सत्य है तो q सत्य है।
स्थिति 2. यदि q सत्य है तो p सत्य है।
किसी भी कथन की जांच करने के लिए की वह सत्य हैं या नहीं हम निम्न विधियों का प्रयोग करते हैं -
- प्रत्यक्ष विधि
- प्रतिधनात्मक विधि
- प्रत्युदाहरण के प्रयोग की विधि
- विरोधोक्ति विधि
इन सब विधियों के एक-एक उदाहरण क्रमशः निम्नलिखित हैं −
कथनों की वैधता
किसी भी कथन की जांच करने के लिए, कि वह सत्य हैं या नहीं हम निम्न नियमो का पालन करते हैं −
नियम (1)
संयोजक "और" से प्रयुक्त कथन
यदि p तथा q गणितीय कथन हैं, तो यह सिद्ध करने के लिए कि कथन "p और q" सत्य है, हम निम्नलिखित चरणों का अनुसरण करते हैं
चरण 1: दर्शाइए कि कथन p सत्य है।
चरण 2: दर्शाइए कि कथन q सत्य है।
नियम (2)
संयोजक "या" से प्रयुक्त कथन
यदि p तथा q गणितीय कथन हैं, तो कथन "p या q " को सत्य सिद्ध करने के लिए हम निम्नलिखित स्थितियों में से किसी एक को सत्य प्रमाणित करते हैं।
स्थिति 1. यह मानते हुए कि p असत्य है, q को अनिवार्यतः सत्य प्रमाणित कीजिए।
स्थिति 2. यह मानते हुए कि q असत्य है, p को अनिवार्यत: सत्य प्रमाणित कीजिए।
नियम (3)
वाक्यांश "यदि-तो" से प्रयुक्त कथन
कथन "यदि p तो q" को सत्य सिद्ध करने के लिए हम निम्नलिखित स्थितियों में किसी एक को सत्य प्रमाणित करते हैं।
स्थिति 1. यह मानते हुए कि p सत्य है, q को अनिवार्यतः सत्य प्रमाणित कीजिए (प्रत्यक्ष विधि)।
स्थिति 2. यह मानते हुए कि q असत्य है, p को भी अनिवार्यतः असत्य प्रमाणित कीजिये (प्रतिधनात्मक विधि)।
नियम (4)
वाक्यांश (प्रतिबंध) “यदि और केवल यदि" से प्रयुक्त कथन
कथन "p, यदि और केवल यदि q" को सत्य सिद्ध करने के लिए हमें यह प्रमाणित करने की आवश्यकता है कि,
स्थिति 1. p सत्य है तो q सत्य है।
स्थिति 2. यदि q सत्य है तो p सत्य है।
किसी भी कथन की जांच करने के लिए की वह सत्य हैं या नहीं हम निम्न विधियों का प्रयोग करते हैं -
- प्रत्यक्ष विधि
- प्रतिधनात्मक विधि
- प्रत्युदाहरण के प्रयोग की विधि
- विरोधोक्ति विधि
इन सब विधियों के एक-एक उदाहरण क्रमशः निम्नलिखित हैं −
उदाहरण 20
प्रत्यक्ष विधि से जाँचिए कि नीचे दिया गया कथन सत्य है अथवा नहीं।
यदि x,y ∈ Z इस प्रकार है कि x तथा y विषम है, तो xy भी विषम है।
मान लीजिए,
p:x,y∈z इस प्रकार है कि x तथा y विषम है।
q:xy विषम है।
कथन कि वैधता को प्रमाणित करने के लिए यह मान लीजिए कि यदि कथन p सत्य हो, तो q भी सत्य होगा।
∴x=2m+1 तथा
y=2n+1
जहाँ x तथा y विषम पूर्णाक है।
अब x×y
=(2m+1)(2n+1)
=4mn+2n+2m+1
=2(2mn+n+m)+1
=2(k)+1
(माना k=2mn+n+m)
इससे स्पष्ट है कि कथन q भी विषम है।
अतः दिया गया कथन सत्य है।
उदाहरण 20
प्रत्यक्ष विधि से जाँचिए कि नीचे दिया गया कथन सत्य है अथवा नहीं।
यदि x,y ∈ Z इस प्रकार है कि x तथा y विषम है, तो xy भी विषम है।
मान लीजिए,
p:x,y∈z इस प्रकार है कि x तथा y विषम है।
q:xy विषम है।
कथन कि वैधता को प्रमाणित करने के लिए यह मान लीजिए कि यदि कथन p सत्य हो, तो q भी सत्य होगा।
∴x=2m+1 तथा
y=2n+1
जहाँ x तथा y विषम पूर्णाक है।
अब x×y
=(2m+1)(2n+1)
=4mn+2n+2m+1
=2(2mn+n+m)+1
=2(k)+1
(माना k=2mn+n+m)
इससे स्पष्ट है कि कथन q भी विषम है।
अतः दिया गया कथन सत्य है।
उदाहरण 21
प्रतिधानात्मक विधि से सिद्ध कीजिये कि कथन यदि x एक ऐसी वास्तविक संख्या है कि
x3+4x=0 तो x=0
माना,
r: x एक ऐसी वास्तविक संख्या है कि x3+4x=0
q: x=0
अतः p:r⇒q
प्रतिधानात्मक वाक्य :
~q⇒~r
यदि x=0 नहीं है तो x एक वास्तविक संख्या नहीं है कि x3+4x=0
माना, x≠0 (x=0 असत्य है)
अब
x3+4x=0
x(x2+4)=0
x=0 जो कि असत्य है
तथा x2+4=0⇒ x2=−4
x=2i
अतः x काल्पनिक होगा अर्थात वास्तविक नहीं होगा।
अतः कथन सिद्ध हुआ।
उदाहरण 21
प्रतिधानात्मक विधि से सिद्ध कीजिये कि कथन यदि x एक ऐसी वास्तविक संख्या है कि
x3+4x=0 तो x=0
माना,
r: x एक ऐसी वास्तविक संख्या है कि x3+4x=0
q: x=0
अतः p:r⇒q
प्रतिधानात्मक वाक्य :
~q⇒~r
यदि x=0 नहीं है तो x एक वास्तविक संख्या नहीं है कि x3+4x=0
माना, x≠0 (x=0 असत्य है)
अब
x3+4x=0
x(x2+4)=0
x=0 जो कि असत्य है
तथा x2+4=0⇒ x2=−4
x=2i
अतः x काल्पनिक होगा अर्थात वास्तविक नहीं होगा।
अतः कथन सिद्ध हुआ।
उदाहरण 22
एक प्रत्युदाहरण द्वारा सिद्ध कीजिए कि निम्नलिखित कथन असत्य है, "यदि n एक विषम पूर्णांक है, तो n एक अभाज्य संख्या है।"
प्रदत्त कथन "यदि p तो q" के रूप का है। हमें इसे असत्य सिद्ध करना है जिसके लिए हमें यह दर्शाना है कि "यदि p तो ~q" है। इसके लिए हमें किसी एक ऐसे विषम पूर्णांक को खोजना है, जो अभाज्य नहीं हो। आइए इसे समझते है −
चूंकि विषम पूर्णांक n: 1,3,5,7,9,11,13...
तथा अभाज्य संख्या :2,3,5,7,11,13...
यहाँ संख्या 1 तथा 9 इस प्रकार का एक विषम पूर्णांक है जो कि अभाज्य संख्या नहीं है। अतः यदि n एक विषम पूर्णांक है, तो n एक अभाज्य संख्या नहीं है। अतः हम निष्कर्ष निकालते हैं कि प्रदत्त कथन असत्य है।
उदाहरण 22
एक प्रत्युदाहरण द्वारा सिद्ध कीजिए कि निम्नलिखित कथन असत्य है, "यदि n एक विषम पूर्णांक है, तो n एक अभाज्य संख्या है।"
प्रदत्त कथन "यदि p तो q" के रूप का है। हमें इसे असत्य सिद्ध करना है जिसके लिए हमें यह दर्शाना है कि "यदि p तो ~q" है। इसके लिए हमें किसी एक ऐसे विषम पूर्णांक को खोजना है, जो अभाज्य नहीं हो। आइए इसे समझते है −
चूंकि विषम पूर्णांक n: 1,3,5,7,9,11,13...
तथा अभाज्य संख्या :2,3,5,7,11,13...
यहाँ संख्या 1 तथा 9 इस प्रकार का एक विषम पूर्णांक है जो कि अभाज्य संख्या नहीं है। अतः यदि n एक विषम पूर्णांक है, तो n एक अभाज्य संख्या नहीं है। अतः हम निष्कर्ष निकालते हैं कि प्रदत्त कथन असत्य है।
उदाहरण 23
विरोधिक्त विधि से निम्न कथन की वैधता की जाँच कीजिये यदि n एक ऐसी वास्तविक संख्या है कि n>3 तो n2>9
यदि n एक वास्तविक संख्या है कि
n>3 तो n2>9
माना, n बड़ी नहीं है 3 से
तब या तो n=3 अथवा n<3
n=3 तो n2=9
यदि n<3 अर्थात n=3−k (माना k धनात्मक संख्या है।), तो
n2=(3−k)2
=32−6k+k2
=9−6k+k2
=9−k(6−k)
यह स्पष्ट है कि जब n,3 से छोटा है तब तक n2,9 से अधिक नहीं हो सकता है अतः जब n>3 तभी n2>9 दिया गया कथन सत्य है।
उदाहरण 23
विरोधिक्त विधि से निम्न कथन की वैधता की जाँच कीजिये यदि n एक ऐसी वास्तविक संख्या है कि n>3 तो n2>9
यदि n एक वास्तविक संख्या है कि
n>3 तो n2>9
माना, n बड़ी नहीं है 3 से
तब या तो n=3 अथवा n<3
n=3 तो n2=9
यदि n<3 अर्थात n=3−k (माना k धनात्मक संख्या है।), तो
n2=(3−k)2
=32−6k+k2
=9−6k+k2
=9−k(6−k)
यह स्पष्ट है कि जब n,3 से छोटा है तब तक n2,9 से अधिक नहीं हो सकता है अतः जब n>3 तभी n2>9 दिया गया कथन सत्य है।
सारांश
इस अध्याय में हमने निम्नलिखित बिंदुओं की व्याख्या की है:
कथन "यदि P तो Q" को निम्नलिखित तरीकों से लिखा ज़ा सकता है,
p अंतर्भाव (सप्रतिबंध) q (प्रतीक p⇒q से निरूपित)
p पर्याप्त प्रतिबंध है q के लिए
q अनिवार्य प्रतिबंध है p के लिए
p केवल यदि q
कथन "P यदि तो केवल यदि Q" को निम्नलिखित तरीकों से लिखा ज़ा सकता है,
p अंतर्भाव (द्विसप्रतिबंध) q (प्रतीक p⇔q से निरूपित)
- (1) प्रत्यक्ष विधि
(2) प्रतिधनात्मक विधि
(3) विरोधोक्ति विधि
(4) प्रत्युदाहरण के प्रयोग की विधि
सारांश
इस अध्याय में हमने निम्नलिखित बिंदुओं की व्याख्या की है:
कथन "यदि P तो Q" को निम्नलिखित तरीकों से लिखा ज़ा सकता है,
p अंतर्भाव (सप्रतिबंध) q (प्रतीक p⇒q से निरूपित)
p पर्याप्त प्रतिबंध है q के लिए
q अनिवार्य प्रतिबंध है p के लिए
p केवल यदि q
कथन "P यदि तो केवल यदि Q" को निम्नलिखित तरीकों से लिखा ज़ा सकता है,
p अंतर्भाव (द्विसप्रतिबंध) q (प्रतीक p⇔q से निरूपित)
- (1) प्रत्यक्ष विधि
(2) प्रतिधनात्मक विधि
(3) विरोधोक्ति विधि
(4) प्रत्युदाहरण के प्रयोग की विधि