क्रमचय और संचय कक्षा 11 गणित
भूमिका
बच्चों आइए एक नया अध्याय क्रमचय और संचय का परिचय देखते है, यह गणित का वह भाग है जिसमें हम गिनने योग्य विभिन्न प्रकार की संरचनाओं का अध्ययन करते है।
दैनिक जीवन में हमें ऐसी समस्याएँ मिलती हैं जिससे यह जानना पड़ता है कि किसी कार्य को करने के कितने तरीके हैं। इसके लिए उस कार्य को करने के कुल संभावित तरीकों को जानना पड़ता है।
सामान्यतः क्रमचय (Permutation) का तात्पर्य वस्तुओं या मूल्यों के क्रमपरिवर्तन (क्रमबद्ध रूप से पुनर्व्यवस्थित करना) से है, इसे हम कुछ इस प्रकार भी कह सकते है की कुछ मानों के एक समुच्चय को विशेष क्रम में व्यवस्थित करना ही क्रमचय है।
तथा गणित में किसी समुच्चय से कुछ वस्तुओं का चयन करने के तरीकों का अध्ययन एवं उनकी संख्या संचय (Combination) कहलाती है। संचय में चयन की गयी वस्तुओं के क्रम का महत्व नहीं होता जबकि क्रमचय मे क्रम का महत्व होता है।
इस अध्याय मे हम क्रमगुणित संकेतन, क्रमचय, संचय तथा उनके कुछ गुणधर्मों का अध्ययन करेंगे।
भूमिका
बच्चों ! इस अध्याय में हम क्रमचय तथा संचय के बारे में पढ़ेंगे, यह अध्याय आपके आगे आने वाली प्रतियोगी परीक्षा JEE 2023 को ध्यान में रखकर बनाया गया है, इसमें हम बहुत ही basic से पढ़ते हुए आगे बढ़ेंगे।
दैनिक जीवन में हमें ऐसी समस्याएँ मिलती हैं जिससे यह जानना पड़ता है कि किसी कार्य को करने के कितने तरीके हैं। इसके लिए उस कार्य को करने के कुल संभावित तरीकों को जानना पड़ता है।
सामान्यतः क्रमचय (Permutation) का तात्पर्य वस्तुओं या मूल्यों के क्रमपरिवर्तन (क्रमबद्ध रूप से पुनर्व्यवस्थित करना) से है, इसे हम कुछ इस प्रकार भी कह सकते है की कुछ मानों के एक समुच्चय को विशेष क्रम में व्यवस्थित करना ही क्रमचय है।
तथा गणित में किसी समुच्चय से कुछ वस्तुओं का चयन करने के तरीकों का अध्ययन एवं उनकी संख्या संचय (Combination) कहलाती है। संचय में चयन की गयी वस्तुओं के क्रम का महत्व नहीं होता जबकि क्रमचय मे क्रम का महत्व होता है।
इस अध्याय मे हम क्रमगुणित संकेतन, क्रमचय, संचय तथा उनके कुछ गुणधर्मों का अध्ययन करेंगे।
यह अध्याय प्रतियोगी परीक्षाओं के लिए बहुत महत्वपूर्ण है। प्रतिवर्ष JEE mains और अन्य परीक्षाओं में क्रमचय-संचय से 2-3 प्रश्न देखने को मिलेंगे।
आप प्रतिदिन Doubtnut की कक्षा देखें और अधिक से अधिक अभ्यास करें। आपकी इस अध्याय से संबंधित सभी समस्या दूर हो जाएगीं।
आइए बच्चों क्रमचय और संचय को समझते है और करीब से...
जैसा कि हमने ऊपर क्रमचय व संचय का परिचय देखा था, अब क्रमचय व संचय को समझने के लिए सबसे पहले वस्तु या संख्याओ को आपस मे व्यवस्थित करने के आधारभूत सिद्धांत को समझने का प्रयास करते है। आइए इसे उदाहरण से समझते हैं-
माना हमारे पास एक खाली कुर्सी (Vacant chair) है तथा तीन लड़के रमेश, महेश और सुरेश हैं। अब इस कुर्सी को भरने के कुल कितने तरीके हैं।
एक खाली कुर्सी रमेश या महेश या सुरेश द्वारा भरा जा सकता है, अर्थात् 3 तरीके से भरा जा सकता है। दूसरे शब्दों में इस कार्य को करने के कुल 3 तरीके हैं । एक रिक्त स्थान को 3 भिन्न वस्तुओं से भरने के 3 भिन्न तरीके हैं।
अब हम एक दूसरे प्रश्न पर विचार करते हैं। माना कि दो लड़के A और B हैं और इन्हें एक कतार में बैठाना है। तो इसका एक संभव तरीका यह है कि A को पहले स्थान तथा B को दूसरे स्थान पर बैठाया जाए। तथा दूसरा संभव तरीका यह है कि B को पहले स्थान पर तथा A को दूसरे स्थान पर बैठाया जाए।
इनके अलावा और कोई तरीका संभव नहीं है अर्थात् AB या BA कुल 2 तरीके से इन्हें बैठाया जा सकता है।
अतः हम कह सकते हैं कि इस स्थिति में विन्यासो की संख्या (Number of arrangements) 2 है । यहाँ हम देखते हैं कि AB तथा BA में क्रम (order) का विचार भी होता है क्योंकि AB तथा BA दो भिन्न (different) विन्यास (arrangement) हैं।
एक और उदाहरण देखिए
मान लें की आपके पास 3 पेंट (P), 2 शर्ट (S), व 2 टाई (T) है तब आप इसे कितने प्रकार से पहन सकते है जबकि आपको एक शर्ट, एक पेंट व एक टाई पहनना है। आइए देखते है इन्हे किन - किन प्रकार से पहना जा सकता है।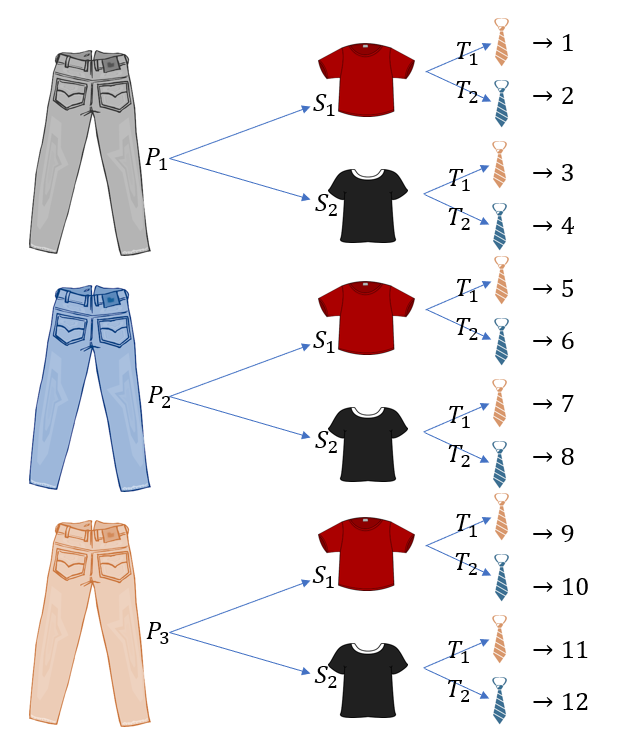
ऊपर चित्र मे देखे यदि किसी एक पेंट (P1) को लिया जाए तो उसके साथ एक शर्ट (S1) का पहले चयन करें अब इस जोड़े के साथ टाई (T1,T2) का चयन 2 प्रकार (P1S1T1 तथा P1S2T2) से किया जा सकता है। अतः यहाँ से 2 प्रकार से पेंट, शर्ट व टाई का चयन किया जा सकता है। इसी प्रकार उसी पेंट (P1) को लेकर दूसरे शर्ट (S2) को ले तब पुनः 2 नए प्रकार से पेंट, शर्ट व टाई का चयन किया जाएगा।
इसी प्रकार से हमे चयन करते हुए कुल 12 तरीके प्राप्त होंगे जैसा की ऊपर चित्र मे दर्शाया गया है।
अब यह तब तक संभव है जब तक की वस्तुएँ या संखयाएँ सीमित या कम संख्या मे हो।
अब क्या हो यदि 100 पेंट, 70 शर्ट, 50 टाई को साथ मे चयन करने के तरीके पूछे जाए? तो क्या हम इन्हे ऊपर दिए तरीके से हल कर पाएंगे? आप समझ सकते है की इतनी बढ़ी गणना करना कठिन होगा।
इसके लिए हमे समुच्चयों के आपस मे जोड़े बनाने के तरीके को समझना होगा इसे उसी उदाहरण से समझते है
पेंट P:{P1,P2,P3}=3
शर्ट S:{S1,S2}=2
टाई T:{T1,T2}=2
यहाँ से पेंट व शर्ट के जोड़े बनाने के तरीके P×S={(P1,S1),(P1,S2),(P2,S1),(P2,S2),(P3,S1),(P3,S2)}=6
अर्थात P×S=3×2=6
इसी प्रकार पेंट, शर्ट व टाई के जोड़े बनाने के तरीके P×S×T
={(P1,S1,T1),(P1,S1,T2),(P1,S2,T1),(P1,S2,T2),(P2,S1,T1),(P2,S1,T2),(P2,S2,T1),(P2,S2,T2),(P3,S1,T1),(P3,S1,T2),(P3,S2,T1),(P3,S2,T2)}=12
अर्थात P×S×T=3×2×2=12
इसे कुछ इस प्रकार हल कर सकते है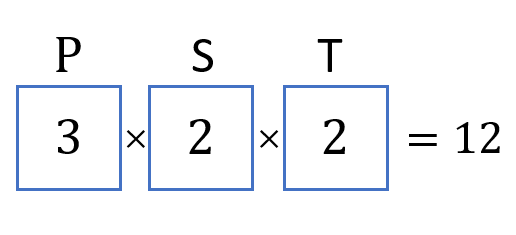
ऊपर आपने देखा वस्तु के अनुसार उन्हे एक-एक स्थान दे दिया गया तथा उसके पश्चात उनके संगत समुच्चयों मे स्थित वस्तुओं की सँख्या ले लिया गया। अब जैसे की हमने ऊपर समझा था, वस्तुओं के समुच्चयो (समुच्चय का मान) को आपस मे गुणा करने पर हमे कुल व्यवस्थाएं प्राप्त हो जाएगी।
अब जैसे की हमने कहा था यदि 100 पेंट, 70 शर्ट, 50 टाई लिए जाए तो इसका निम्न होगा 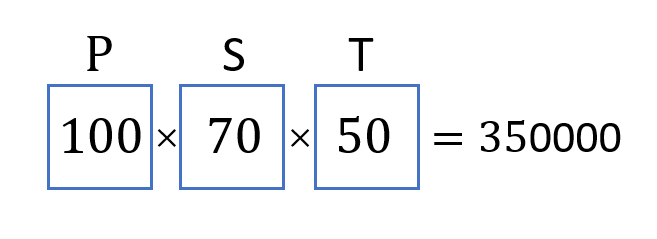
यहाँ आप देख सकते है की पेंट, शर्ट व टाई को विभिन्न प्रकार से पहनने के 350000 तरीके हो सकते है।
इस प्रकार हम कह सकते है की यदि एक घटना m भिन्न तरीकों से घटित हो सकती है, तदोपरांत एक अन्य घटना n भिन्न तरीकों से घटित हो सकती है, तो दिए हुए क्रम में दोनों घटनाओं के भिन्न तरीकों से घटित होने की कुल भिन्न संख्या m×n है।
यदि घटनाएं स्वतंत्र हो तब गणना का आधारभूत सिद्धांत से इस प्रकार आप आसानी से हल प्राप्त कर सकते है परन्तु यदि कोई शर्त या प्रतिबंध दिया गया हो तो उसका भी पालन करना अनिवार्य है। जिसे हम आगे पढ़ेंगे।
आइए बच्चों क्रमचय और संचय को समझते है और करीब से...
जैसा कि हमने ऊपर क्रमचय व संचय का परिचय देखा था, अब क्रमचय व संचय को समझने के लिए सबसे पहले वस्तु या संख्याओ को आपस मे व्यवस्थित करने के आधारभूत सिद्धांत को समझने का प्रयास करते है। आइए इसे उदाहरण से समझते हैं-
माना हमारे पास एक खाली कुर्सी (Vacant chair) है तथा तीन लड़के रमेश, महेश और सुरेश हैं। अब इस कुर्सी को भरने के कुल कितने तरीके हैं।
एक खाली कुर्सी रमेश या महेश या सुरेश द्वारा भरा जा सकता है, अर्थात् 3 तरीके से भरा जा सकता है। दूसरे शब्दों में इस कार्य को करने के कुल 3 तरीके हैं । एक रिक्त स्थान को 3 भिन्न वस्तुओं से भरने के 3 भिन्न तरीके हैं।
अब हम एक दूसरे प्रश्न पर विचार करते हैं। माना कि दो लड़के A और B हैं और इन्हें एक कतार में बैठाना है। तो इसका एक संभव तरीका यह है कि A को पहले स्थान तथा B को दूसरे स्थान पर बैठाया जाए। तथा दूसरा संभव तरीका यह है कि B को पहले स्थान पर तथा A को दूसरे स्थान पर बैठाया जाए।
इनके अलावा और कोई तरीका संभव नहीं है अर्थात् AB या BA कुल 2 तरीके से इन्हें बैठाया जा सकता है।
अतः हम कह सकते हैं कि इस स्थिति में विन्यासो की संख्या (Number of arrangements) 2 है । यहाँ हम देखते हैं कि AB तथा BA में क्रम (order) का विचार भी होता है क्योंकि AB तथा BA दो भिन्न (different) विन्यास (arrangement) हैं।
एक और उदाहरण देखिए
मान लें की आपके पास 3 पेंट (P), 2 शर्ट (S), व 2 टाई (T) है तब आप इसे कितने प्रकार से पहन सकते है जबकि आपको एक शर्ट, एक पेंट व एक टाई पहनना है। आइए देखते है इन्हे किन - किन प्रकार से पहना जा सकता है।
ऊपर चित्र मे देखे यदि किसी एक पेंट (P1) को लिया जाए तो उसके साथ एक शर्ट (S1) का पहले चयन करें अब इस जोड़े के साथ टाई (T1,T2) का चयन 2 प्रकार (P1S1T1 तथा P1S2T2) से किया जा सकता है। अतः यहाँ से 2 प्रकार से पेंट, शर्ट व टाई का चयन किया जा सकता है। इसी प्रकार उसी पेंट (P1) को लेकर दूसरे शर्ट (S2) को ले तब पुनः 2 नए प्रकार से पेंट, शर्ट व टाई का चयन किया जाएगा।
इसी प्रकार से हमे चयन करते हुए कुल 12 तरीके प्राप्त होंगे जैसा की ऊपर चित्र मे दर्शाया गया है।
अब यह तब तक संभव है जब तक की वस्तुएँ या संखयाएँ सीमित या कम संख्या मे हो।
अब क्या हो यदि 100 पेंट, 70 शर्ट, 50 टाई को साथ मे चयन करने के तरीके पूछे जाए? तो क्या हम इन्हे ऊपर दिए तरीके से हल कर पाएंगे? आप समझ सकते है की इतनी बढ़ी गणना करना कठिन होगा।
इसके लिए हमे समुच्चयों के आपस मे जोड़े बनाने के तरीके को समझना होगा इसे उसी उदाहरण से समझते है
पेंट P:{P1,P2,P3}=3
शर्ट S:{S1,S2}=2
टाई T:{T1,T2}=2
यहाँ से पेंट व शर्ट के जोड़े बनाने के तरीके P×S={(P1,S1),(P1,S2),(P2,S1),(P2,S2),(P3,S1),(P3,S2)}=6
अर्थात P×S=3×2=6
इसी प्रकार पेंट, शर्ट व टाई के जोड़े बनाने के तरीके P×S×T
={(P1,S1,T1),(P1,S1,T2),(P1,S2,T1),(P1,S2,T2),(P2,S1,T1),(P2,S1,T2),(P2,S2,T1),(P2,S2,T2),(P3,S1,T1),(P3,S1,T2),(P3,S2,T1),(P3,S2,T2)}=12
अर्थात P×S×T=3×2×2=12
इसे कुछ इस प्रकार हल कर सकते है
ऊपर आपने देखा वस्तु के अनुसार उन्हे एक-एक स्थान दे दिया गया तथा उसके पश्चात उनके संगत समुच्चयों मे स्थित वस्तुओं की सँख्या ले लिया गया। अब जैसे की हमने ऊपर समझा था, वस्तुओं के समुच्चयो (समुच्चय का मान) को आपस मे गुणा करने पर हमे कुल व्यवस्थाएं प्राप्त हो जाएगी।
अब जैसे की हमने कहा था यदि 100 पेंट, 70 शर्ट, 50 टाई लिए जाए तो इसका निम्न होगा 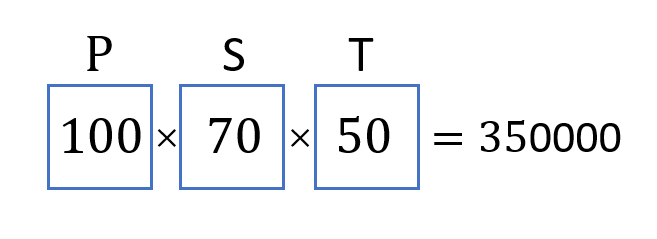
यहाँ आप देख सकते है की पेंट, शर्ट व टाई को विभिन्न प्रकार से पहनने के 350000 तरीके हो सकते है।
इस प्रकार हम कह सकते है की यदि एक घटना m भिन्न तरीकों से घटित हो सकती है, तदोपरांत एक अन्य घटना n भिन्न तरीकों से घटित हो सकती है, तो दिए हुए क्रम में दोनों घटनाओं के भिन्न तरीकों से घटित होने की कुल भिन्न संख्या m×n है।
यदि घटनाएं स्वतंत्र हो तब गणना का आधारभूत सिद्धांत से इस प्रकार आप आसानी से हल प्राप्त कर सकते है परन्तु यदि कोई शर्त या प्रतिबंध दिया गया हो तो उसका भी पालन करना अनिवार्य है। जिसे हम आगे पढ़ेंगे।
उदाहरण 1
अंग्रेजी वर्णमाला के प्रथम दस अक्षरों से कितने चार अक्षर के कोड बनाये जा सकते है। यदि किसी अक्षर की पुनरावृत्ति नहीं हो रही है।

अब गणना के आधारभूत सिद्धान्तों से ,
अभीष्ट संख्या = 10×9×8×7=5040
उदाहरण 1
अंग्रेजी वर्णमाला के प्रथम दस अक्षरों से कितने चार अक्षर के कोड बनाये जा सकते है। यदि किसी अक्षर की पुनरावृत्ति नहीं हो रही है।

अब गणना के आधारभूत सिद्धान्तों से ,
अभीष्ट संख्या = 10×9×8×7=5040
उदाहरण 2
100 व 1000 के मध्य ऐसी कितनी संख्याएँ है जिनके सभी अंक भिन्न होते हैं ?
हम जानते हैं की 100 से 1000 के मध्य की संख्या में हमेशा 3 अंक होते हैं । अतः सभी संभावित 3 अंकों वाली संख्या जिसमें तीन अंक भिन्न हैं, को प्राप्त करेंगे तथा 0 को सैकड़े के स्थान पर नहीं रख सकते , अतः सैकड़े का स्थान 9 अंकों अर्थात,
1, 2, 3, ...... 9 से भरा जायेगा । इस प्रकार सैकड़े के स्थान चयन की कुल 9 विधियाँ है । अब 9 अंक शेष है जिनमें 0 भी शामिल है । इसलिए दहाई अंक का स्थान इस 9 अंकों से भरा जायेगा तथा शेष इकाई स्थान को 8 अंकों से भरा जायेगा। इस प्रकार कुल संख्याएँ =
9×9×8=648
उदाहरण 2
100 व 1000 के मध्य ऐसी कितनी संख्याएँ है जिनके सभी अंक भिन्न होते हैं ?
हम जानते हैं की 100 से 1000 के मध्य की संख्या में हमेशा 3 अंक होते हैं । अतः सभी संभावित 3 अंकों वाली संख्या जिसमें तीन अंक भिन्न हैं, को प्राप्त करेंगे तथा 0 को सैकड़े के स्थान पर नहीं रख सकते , अतः सैकड़े का स्थान 9 अंकों अर्थात,
1, 2, 3, ...... 9 से भरा जायेगा । इस प्रकार सैकड़े के स्थान चयन की कुल 9 विधियाँ है । अब 9 अंक शेष है जिनमें 0 भी शामिल है । इसलिए दहाई अंक का स्थान इस 9 अंकों से भरा जायेगा तथा शेष इकाई स्थान को 8 अंकों से भरा जायेगा। इस प्रकार कुल संख्याएँ =
9×9×8=648
क्रमगुणित संकेतन
(Factorial notation)
क्रमगुणित या Factorial का संकेत ! या ⌊ होता है,
यदि n प्राकृत सँख्याओ को प्रदर्शित करता है तो n! या ⌊n, n प्राकृत सँख्या के गुणनफल को दर्शाता है।
जिसे हम क्रमगुणित n या n! Factorial (फेक्टोरियल) कहते है।
अतः ⌊n=n!=n×(n−1)×(n−2)×.........×3×2×1
यहाँ से हम समझ सकते है की किसी दी गई प्राकृत सँख्या का क्रमगुणन (Factorial) उस सँख्या व उससे छोटी सभी प्राकृत संख्याओ का गुणा होता है।
अतः n के स्थान पर कोई प्राकृत सँख्या रखने पर
5!=5×4×3×2×1
यहाँ आप देख सकते है की 5! (Factorial) से तात्पर्य 5 व उससे छोटी सभी प्राकृत सँख्याओ का गुणनफल है।
11!=11×10×9×8×7×.......×2×1
क्रमगुणित संकेतन
(Factorial notation)
क्रमगुणित या Factorial का संकेत ! या ⌊ होता है,
यदि n प्राकृत सँख्याओ को प्रदर्शित करता है तो n! या ⌊n, n प्राकृत सँख्या के गुणनफल को दर्शाता है।
जिसे हम क्रमगुणित n या n! Factorial (फेक्टोरियल) कहते है।
अतः ⌊n=n!=n×(n−1)×(n−2)×.........×3×2×1
यहाँ से हम समझ सकते है की किसी दी गई प्राकृत सँख्या का क्रमगुणन (Factorial) उस सँख्या व उससे छोटी सभी प्राकृत संख्याओ का गुणा होता है।
अतः n के स्थान पर कोई प्राकृत सँख्या रखने पर
5!=5×4×3×2×1
यहाँ आप देख सकते है की 5! (Factorial) से तात्पर्य 5 व उससे छोटी सभी प्राकृत सँख्याओ का गुणनफल है।
11!=11×10×9×8×7×.......×2×1
OMR (One Minute Revision)
m!±n!≠(m±n)!
m!×n!≠(m×n)!
OMR (One Minute Revision)
m!±n!≠(m±n)!
m!×n!≠(m×n)!
उदाहरण 3
उदाहरण 3
यदि x∈N , तो निम्नलिखित समीकरण को हल कीजिए
19!+110!=x11!
19!+110!=x11!
⇒19!+110⋅9!=x11!
⇒19![1+110]=x11!
⇒19![1+110]=x11×10×9!
⇒1110=x11×10
⇒x=121
उदाहरण 4
यदि x∈N , तो निम्नलिखित समीकरण को हल कीजिए
19!+110!=x11!
19!+110!=x11!
⇒19!+110⋅9!=x11!
⇒19![1+110]=x11!
⇒19![1+110]=x11×10×9!
⇒1110=x11×10
⇒x=121
उदाहरण 4
मान ज्ञात कीजिए
n!r!(n−r)!, जहाँ n = 5, r = 2
n!=n×(n−1)×......×1
=n!r!(n−r)!
=5!2!(5−2)!
=5!2!⋅3!
=5×4×3!2!⋅3!
=5×2
=10
उदाहरण 5
मान ज्ञात कीजिए
n!r!(n−r)!, जहाँ n = 5, r = 2
n!=n×(n−1)×......×1
n!r!(n−r)!
=5!2!(5−2)!
=5!2!⋅3!
=5×4×3!2!⋅3!
=5×2
=10
क्रमचय
(Permutation)
क्रमचय - क्रमचय एक निश्चित क्रम मे बना विन्यास होता है, जिसे दी गई वस्तुओं या संख्याओ में से एक समय मे कुछ या सभी वस्तुओं को लेकर बनाया जाता है। अर्थात कुछ मानों (values) के एक समुच्चय (set) को विशेष क्रम में व्यवस्थित करना क्रमचय है।
इसे इस प्रकार समझ सकते है
यदि हमे कुछ अक्षर दिए गए हो तो अक्षरों के विभिन्न विन्यासों अर्थात किसी शब्द मे उपस्थित अक्षरों को जितने विभिन्न प्रकार से दर्शाया जा सकता है, उनकी संभव स्थितियों की गणना करते हैं। इसमे प्रत्येक विन्यास दूसरे से भिन्न होते हैं, यहाँ शब्दों में अक्षरों के लिखने का क्रम महत्वपूर्ण है।
जैसे- ROSE, REOS,.....
इनमें से प्रत्येक विन्यास विभिन्न अक्षरों में से एक समय में सभी को साथ लेकर बनाया गया हैं ।
अब यदि सभी अक्षरों को न लेकर कुछ अक्षरों को ले तो उतने अक्षरों के लिए क्रमचय कहलाएगा।
जैसे- NUMBER शब्द के 3 अक्षरों से बना क्रमचय =
NUM, NMU,MUN,NUB,.....
इनमें से प्रत्येक विन्यास 3 विभिन्न अक्षरों को एक समय में साथ लेकर बनाया गया हैं ।
क्रमचय
(Permutation)
क्रमचय - क्रमचय एक निश्चित क्रम मे बना विन्यास होता है, जिसे दी गई वस्तुओं या संख्याओ में से एक समय मे कुछ या सभी वस्तुओं को लेकर बनाया जाता है। अर्थात कुछ मानों (values) के एक समुच्चय (set) को विशेष क्रम में व्यवस्थित करना क्रमचय है।
इसे इस प्रकार समझ सकते है
यदि हमे कुछ अक्षर दिए गए हो तो अक्षरों के विभिन्न विन्यासों अर्थात किसी शब्द मे उपस्थित अक्षरों को जितने विभिन्न प्रकार से दर्शाया जा सकता है, उनकी संभव स्थितियों की गणना करते हैं। इसमे प्रत्येक विन्यास दूसरे से भिन्न होते हैं, यहाँ शब्दों में अक्षरों के लिखने का क्रम महत्वपूर्ण है।
जैसे- ROSE, REOS,.....
इनमें से प्रत्येक विन्यास विभिन्न अक्षरों में से एक समय में सभी को साथ लेकर बनाया गया हैं ।
अब यदि सभी अक्षरों को न लेकर कुछ अक्षरों को ले तो उतने अक्षरों के लिए क्रमचय कहलाएगा।
जैसे- NUMBER शब्द के 3 अक्षरों से बना क्रमचय =
NUM, NMU,MUN,NUB,.....
इनमें से प्रत्येक विन्यास 3 विभिन्न अक्षरों को एक समय में साथ लेकर बनाया गया हैं ।
क्रमचय, जब सभी वस्तुएं भिन्न-भिन्न हैं
जब सभी वस्तुएं भिन्न-भिन्न हैं तो हम इन्हे दो प्रकार से व्यक्त कर सकते हैं
(i) क्रमचय में वस्तुओं की पुनरावृत्ति की अनुमति नहीं हो
(ii) क्रमचय में वस्तुओं की पुनरावृत्ति की अनुमति हो
क्रमचय, जब सभी वस्तुएं भिन्न-भिन्न हैं
जब सभी वस्तुएं भिन्न-भिन्न हैं तो हम इन्हे दो प्रकार से व्यक्त कर सकते हैं
(i) क्रमचय में वस्तुओं की पुनरावृत्ति की अनुमति नहीं हो
(ii) क्रमचय में वस्तुओं की पुनरावृत्ति की अनुमति हो
प्रमेय 1
n विभिन्न वस्तुओं में से एक समय में r वस्तुओं को लेकर बनाए गए क्रमचयों की संख्या को प्रतीक nPr से निरूपित करते हैं, जहाँ
nPr=n.(n−1).(n−2)...(n−r+1)
जहाँ 0≤r≤n तथा किसी भी क्रमचय में वस्तुओं की पुनरावृत्ति की अनुमति नहीं है
अब जैसे की हम n मे से r वस्तुओं को चुन रहे है तो r रिक्त बॉक्स को लेंगे तथा उसमे n वस्तुओं को भिन्न - भिन्न प्रकार से चुनकर व्यवस्थित करेंगे, तथा साथ ही यहाँ शर्तों पर ध्यान देना भी आवश्यक है।
आप इसे निम्न प्रकार से समझ सकते है 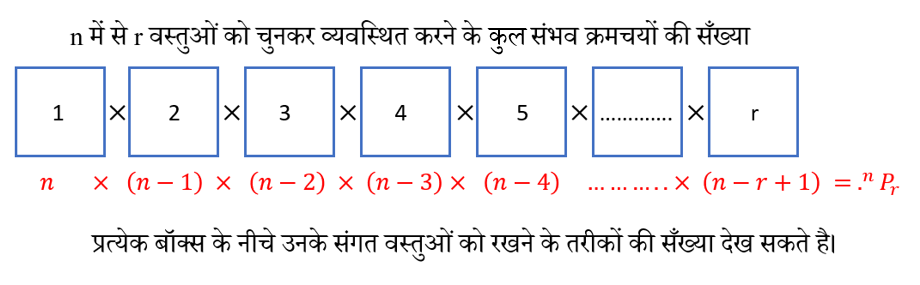
आगे nPr का सूत्र निरूपित करने का प्रयास करते है,
nPr=n.(n−1).(n−2)...(n−r+1)(n−r)(n−r−1)...3⋅2⋅1(n−r)(n−r−1)...3⋅2⋅1
nPr=n!(n−r)!,
0≤r≤n
प्रमेय 1
n विभिन्न वस्तुओं में से एक समय में r वस्तुओं को लेकर बनाए गए क्रमचयों की संख्या को प्रतीक nPr से निरूपित करते हैं, जहाँ
nPr=n.(n−1).(n−2)...(n−r+1)
जहाँ 0≤r≤n तथा किसी भी क्रमचय में वस्तुओं की पुनरावृत्ति की अनुमति नहीं है
अब जैसे की हम n मे से r वस्तुओं को चुन रहे है तो r रिक्त बॉक्स को लेंगे तथा उसमे n वस्तुओं को भिन्न - भिन्न प्रकार से चुनकर व्यवस्थित करेंगे, तथा साथ ही यहाँ शर्तों पर ध्यान देना भी आवश्यक है।
आप इसे निम्न प्रकार से समझ सकते है 
आगे nPr का सूत्र निरूपित करने का प्रयास करते है,
nPr=n.(n−1).(n−2)...(n−r+1)(n−r)(n−r−1)...3⋅2⋅1(n−r)(n−r−1)...3⋅2⋅1
nPr=n!(n−r)!,
0≤r≤n
प्रमेय 2
n विभिन्न वस्तुओं में से एक समय में r वस्तुओं को लेकर बने क्रमचय की संख्या, जबकि वस्तुओं के पुनरावृत्ति की अनुमति हो, nr होती है।
अब जैसे की हम n मे से r वस्तुओं को चुन रहे है तो r रिक्त बॉक्स को लेंगे तथा उसमे n वस्तुओं को भिन्न - भिन्न प्रकार से चुनकर व्यवस्थित करेंगे, तथा यहां पुनरावृत्ति कर सकते हैं
आप इसे निम्न प्रकार से समझ सकते है 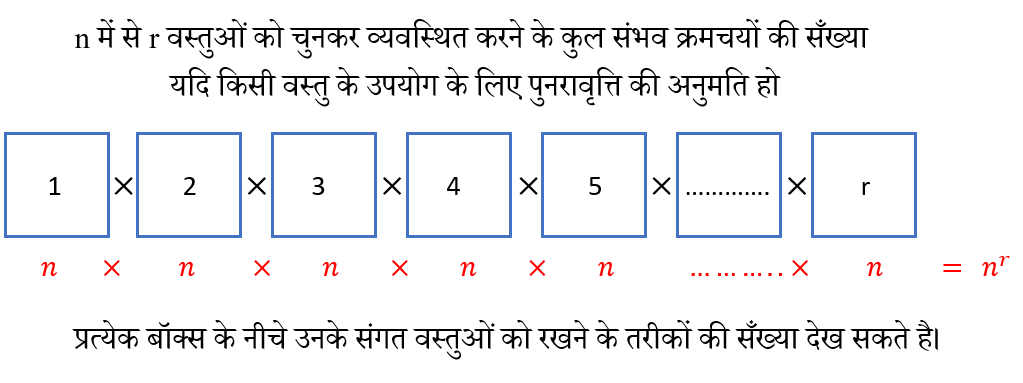
प्रमेय 2
n विभिन्न वस्तुओं में से एक समय में r वस्तुओं को लेकर बने क्रमचय की संख्या, जबकि वस्तुओं के पुनरावृत्ति की अनुमति हो, nr होती है।
अब जैसे की हम n मे से r वस्तुओं को चुन रहे है तो r रिक्त बॉक्स को लेंगे तथा उसमे n वस्तुओं को भिन्न - भिन्न प्रकार से चुनकर व्यवस्थित करेंगे, तथा यहां पुनरावृत्ति कर सकते हैं
आप इसे निम्न प्रकार से समझ सकते है 
उदाहरण 5
शब्द 'LOGARITHM' के अक्षरों से कितने शब्द बनाये जा सकते हैं ?
(i) कितने शब्द L से प्रारम्भ होंगे ?
(ii) कितने शब्द L से प्रारम्भ होकर M पर समाप्त होंगे ?
(iii) कितने शब्द Lसे प्रारम्भ नहीं होंगे ?
(iv) कितने शब्दों में स्वर एक साथ होंगे ?
(v) कितने शब्दों में स्वर एक साथ नहीं होंगे ?
चूंकि शब्द 'LOGARITHM' में 9 अक्षर हैं।
∴9 अक्षरों से बनने वाले शब्दों की संख्या
=9P9
=9!
(i) L से प्रारम्भ होने वाले शब्दों के लिए, हमारे पास 8 अक्षर शेष हैं, जिनसे बनने वाले कुल विन्यासों की संख्या
=8P8=8!
(ii) ऐसे शब्दों की संख्या जो L से प्रारम्भ होंगे तथा M पर समाप्त हों इसके लिए शेष अक्षर = 7
जिनके कुल विन्यासों की संख्या =7P7
(iii) L से प्रारम्भ न होने वाले शब्दों के लिए पहला स्थान L को छोड़कर शेष 8 में से किसी भी एक अक्षर से भरा जा सकता है तथा शेष स्थान 8P8=8! प्रकार से भरा जा सकता है ।
∴ ऐसे शब्दों की कुल संख्या जो L से प्रारम्भ नहीं होते है =8.8!
(iv) दिए गए शब्द में O,A,I तीन स्वर हैं । इनकों एक साथ रखना हैं इसलिए इनको एक साथ रख कर इन्हे एक अक्षर मान लेते हैं अतः कुल अक्षरों की संख्या 7 होगी ।
∴ इनसे बने कुल शब्दों की संख्या=7P7=7!
O,A,I को साथ रखने की कुल विधियाँ =3P3=3!
∴ कुल वांछित शब्दों की संख्या =3!×7!
(v) ऐसे शब्दों की संख्या, जिनमें स्वर एक साथ न हो =9!−3!.7!
=66×7!
उदाहरण 6
शब्द 'LOGARITHM' के अक्षरों से कितने शब्द बनाये जा सकते हैं ?
(i) कितने शब्द L से प्रारम्भ होंगे ?
(ii) कितने शब्द L से प्रारम्भ होकर M पर समाप्त होंगे ?
(iii) कितने शब्द Lसे प्रारम्भ नहीं होंगे ?
(iv) कितने शब्दों में स्वर एक साथ होंगे ?
(v) कितने शब्दों में स्वर एक साथ नहीं होंगे ?
चूंकि शब्द 'LOGARITHM' में 9 अक्षर हैं।
∴9 अक्षरों से बनने वाले शब्दों की संख्या
=9P9
=9!
(i) L से प्रारम्भ होने वाले शब्दों के लिए, हमारे पास 8 अक्षर शेष हैं, जिनसे बनने वाले कुल विन्यासों की संख्या
=8P8=8!
(ii) ऐसे शब्दों की संख्या जो L से प्रारम्भ होंगे तथा M पर समाप्त हों इसके लिए शेष अक्षर = 7
जिनके कुल विन्यासों की संख्या =7P7
(iii) L से प्रारम्भ न होने वाले शब्दों के लिए पहला स्थान L को छोड़कर शेष 8 में से किसी भी एक अक्षर से भरा जा सकता है तथा शेष स्थान 8P8=8! प्रकार से भरा जा सकता है ।
∴ ऐसे शब्दों की कुल संख्या जो L से प्रारम्भ नहीं होते है =8.8!
(iv) दिए गए शब्द में O,A,I तीन स्वर हैं । इनकों एक साथ रखना हैं इसलिए इनको एक साथ रख कर इन्हे एक अक्षर मान लेते हैं अतः कुल अक्षरों की संख्या 7 होगी ।
∴ इनसे बने कुल शब्दों की संख्या=7P7=7!
O,A,I को साथ रखने की कुल विधियाँ =3P3=3!
∴ कुल वांछित शब्दों की संख्या =3!×7!
(v) ऐसे शब्दों की संख्या, जिनमें स्वर एक साथ न हो =9!−3!.7!
=66×7!
उदाहरण 6
0,1,2,3,4,5, 6 से 4 अंको की 4000 से बड़ी कितनी संख्याएँ बनाई जा सकती है यदि अंको की पुनरावृत्ति की जा सकती है।
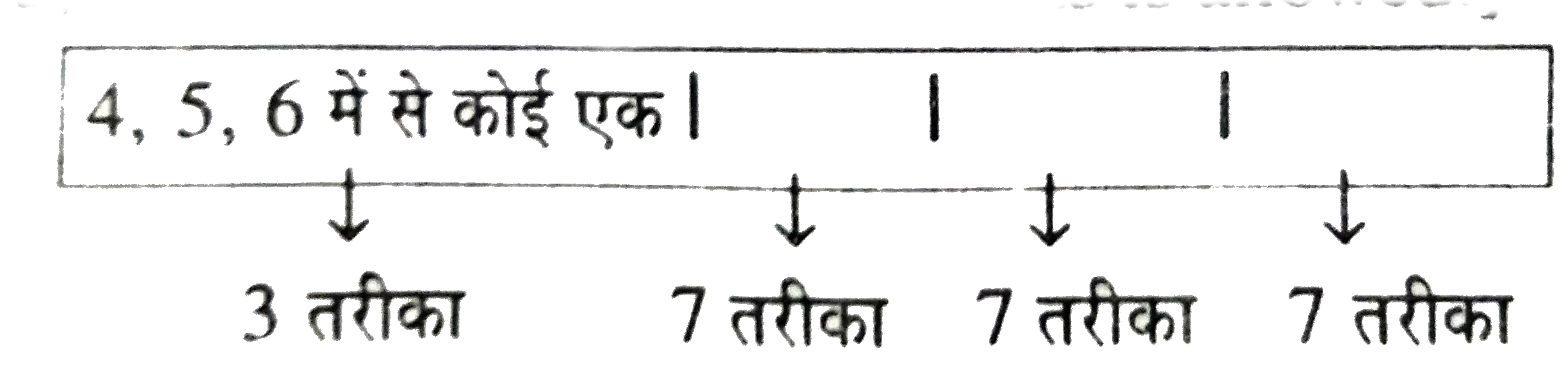
चूँकि 4000 से बड़ी संख्या बनानी है, अतः हजार वाले स्थान पर 4, 5, 6 में से कोई एक संख्या रखी जा सकती है।
∴ हजार वाले स्थान को भरने का तरीका = 3
चूँकि अंको की पुनरावृत्ति की जा सकती है,
इसलिए सैकड़ा दहाई और इकाई में से प्रत्येक स्थान को 7 दिये हए अंको में से किसी एक से, 7 तरीके से भरा जा सकता है।
अतः 4 अंको की 4000 और उससे बड़ी संख्याओं की संख्या =3×7×7×7=1029
∴ 4 अंको की 4000 से बड़ी संख्याओं की संख्या
=1029−1(4000 को घटा देंगे)=1028 (चूँकि 4000 से बड़ी सँख्या चाहिए)
उदाहरण 7
0,1,2,3,4,5, 6 से 4 अंको की 4000 से बड़ी कितनी संख्याएँ बनाई जा सकती है यदि अंको की पुनरावृत्ति की जा सकती है।

चूँकि 4000 से बड़ी संख्या बनानी है, अतः हजार वाले स्थान पर 4, 5, 6 में से कोई एक संख्या रखी जा सकती है।
∴ हजार वाले स्थान को भरने का तरीका = 3
चूँकि अंको की पुनरावृत्ति की जा सकती है,
इसलिए सैकड़ा दहाई और इकाई में से प्रत्येक स्थान को 7 दिये हए अंको में से किसी एक से, 7 तरीके से भरा जा सकता है।
अतः 4 अंको की 4000 और उससे बड़ी संख्याओं की संख्या =3×7×7×7=1029
∴ 4 अंको की 4000 से बड़ी संख्याओं की संख्या
=1029−1(4000 को घटा देंगे)=1028 (चूँकि 4000 से बड़ी सँख्या चाहिए)
उदाहरण 7
यदि 2P(5,3)=P(n,4) तो n का मान ज्ञात कीजिए ।
प्रश्नानुसार
2P(5,3)=P(n,4)
⇒P(n,4)=2P(5,3)
⇒n!(n−4)!=2.5!(5−3)!=2.5!2!
⇒n(n−1)(n−2)(n−3)(n−4)!(n−4)!=5!
⇒n(n−1)(n−2)(n−3)=5!
⇒n(n−1)(n−2)(n−3)=5.4.3.2.1
⇒n(n−1)(n−2)(n−3)
=5(5−1)(5−2)(5−3)
⇒n=5
उदाहरण 8
यदि 2P(5,3)=P(n,4) तो n का मान ज्ञात कीजिए ।
प्रश्नानुसार
2P(5,3)=P(n,4)
⇒P(n,4)=2P(5,3)
⇒n!(n−4)!=2.5!(5−3)!=2.5!2!
⇒n(n−1)(n−2)(n−3)(n−4)!(n−4)!=5!
⇒n(n−1)(n−2)(n−3)=5!
⇒n(n−1)(n−2)(n−3)=5.4.3.2.1
⇒n(n−1)(n−2)(n−3)
=5(5−1)(5−2)(5−3)
⇒n=5
उदाहरण 8
1,2,3,4,5,6 अंकों का प्रयोग करते हुए तीन अंकों को कितनी विषम संख्याएँ बनायी जा सकती हैं ??
(i) अंकों की पुनरावृत्ति सम्भव नहीं है ।
(ii) अंकों की पुनरावृत्ति सम्भव है ।
हम जानते हैं की किसी भी विषम संख्या के लिए इकाई के स्थान पर 1, 3 या 5 के अंक के चाहिए ।
इस प्रकार इकाई के स्थान को भरने के कुल प्रकार = 3
(i) अब क्योकि अंकों की पुनरावृत्ति सम्भव नहीं है , इसलिए दहाई का स्थान शेष पाँच अंकों से प्रकार से भरा जा सकता है ।
अब 4 अंक शेष हैं इसलिए सैकड़े का स्थान 4 प्रकार से भरा जा सकता है ।
इसलिए वांछित संख्याओं की कुल संख्या =3×5×4=60
(ii) यदि कुल अंकों की पुनरावृत्ति सम्भव है तब सैकड़े व दहाई के स्थान 6-6 प्रकारों से भरा जा सकता है ।
इसलिए वांछित संख्याओं की कुल संख्या =3×6×6=108
उदाहरण 9
1,2,3,4,5,6 अंकों का प्रयोग करते हुए तीन अंकों को कितनी विषम संख्याएँ बनायी जा सकती हैं ??
(i) अंकों की पुनरावृत्ति सम्भव नहीं है ।
(ii) अंकों की पुनरावृत्ति सम्भव है ।
हम जानते हैं की किसी भी विषम संख्या के लिए इकाई के स्थान पर 1, 3 या 5 के अंक के चाहिए ।
इस प्रकार इकाई के स्थान को भरने के कुल प्रकार = 3
(i) अब क्योकि अंकों की पुनरावृत्ति सम्भव नहीं है , इसलिए दहाई का स्थान शेष पाँच अंकों से प्रकार से भरा जा सकता है ।
अब 4 अंक शेष हैं इसलिए सैकड़े का स्थान 4 प्रकार से भरा जा सकता है ।
इसलिए वांछित संख्याओं की कुल संख्या =3×5×4=60
(ii) यदि कुल अंकों की पुनरावृत्ति सम्भव है तब सैकड़े व दहाई के स्थान 6-6 प्रकारों से भरा जा सकता है ।
इसलिए वांछित संख्याओं की कुल संख्या =3×6×6=108
क्रमचय, जब सभी वस्तुएं भिन्न-भिन्न नहीं हैं
जब सभी वस्तुओं में से कुछ वस्तुएं समान प्रकार की होती हैं तो हम इन्हे निम्न प्रकार ज्ञात कर सकते हैं
क्रमचय, जब सभी वस्तुएं भिन्न-भिन्न नहीं हैं
जब सभी वस्तुओं में से कुछ वस्तुएं समान प्रकार की होती हैं तो हम इन्हे निम्न प्रकार ज्ञात कर सकते हैं
प्रमेय 3
n वस्तुओं के क्रमचयों की सँख्या, यदि p वस्तुएँ समान प्रकार की है तथा शेष भिन्न प्रकार की है, निम्न होती हैं
n!p!
चुकि इस प्रकार के क्रमचयो की संख्या ज्ञात करने के लिए हम समान प्रकार की वस्तुओं का कुल क्रमचयो की संख्या में भाग देते हैं इसे निम्न उदाहरण से समझा जा सकता हैं
यदि हमारे पास 1 नीली तथा 2 लाल गेंदे है तब
यहाँ आप देख सकते है की इन चारों गेंदों को आपस मे भिन्न भिन्न प्रकार से जमा सकते है परन्तु दो लाल गेंदे आपस मे यदि जमाई जाए तो क्या कोई अंतर दिखाई देगा क्योंकि देखने मे दोनों एक समान होंगी।
अतः वे विन्यास जो लाल गेंदे आपस मे जमाने से प्राप्त हुए वो दो बार आएंगे , इसलिए समान होने के कारण उन्हे भाग दे देंगे।
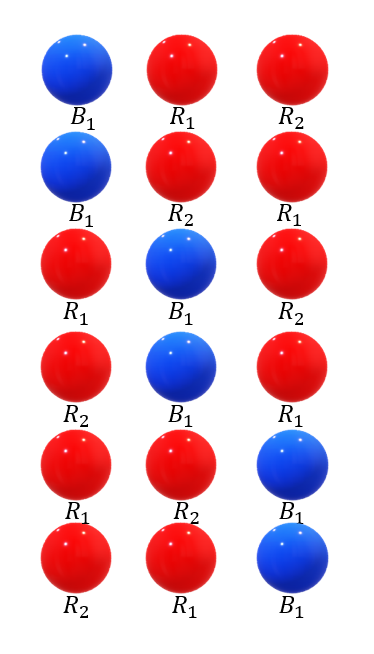
3 वस्तुओं को आपस मे 3! प्रकार से दर्शाया जा सकता है, अतः 6 विन्यास प्राप्त हुए परन्तु आप ऊपर चित्र मे स्थित 6 विन्यासों मे देख सकते है की जब वे आपस में स्थान बदलते है तो वे एक समान दिखाई देते है तथा आपस मे 2! प्रकार से स्थान बदल सकते है। अतः 2! से भाग देकर उचित क्रमचयों की सँख्या निकाल सकते है अतः
3!2!=3
इसी प्रकार
n वस्तुओं के क्रमचयों की सँख्या, यदि p1 एक प्रकार की, p2 वस्तुएँ दूसरे प्रकार की, इसी प्रकार........ pr वस्तुएँ r प्रकार की है तो क्रमचयो की संख्या=
n!p1!⋅p2!⋅p3!......pr!
प्रमेय 3
n वस्तुओं के क्रमचयों की सँख्या, यदि p वस्तुएँ समान प्रकार की है तथा शेष भिन्न प्रकार की है, निम्न होती हैं
n!p!
चुकि इस प्रकार के क्रमचयो की संख्या ज्ञात करने के लिए हम समान प्रकार की वस्तुओं का कुल क्रमचयो की संख्या में भाग देते हैं इसे निम्न उदाहरण से समझा जा सकता हैं
यदि हमारे पास 1 नीली तथा 2 लाल गेंदे है तब
यहाँ आप देख सकते है की इन चारों गेंदों को आपस मे भिन्न भिन्न प्रकार से जमा सकते है परन्तु दो लाल गेंदे आपस मे यदि जमाई जाए तो क्या कोई अंतर दिखाई देगा क्योंकि देखने मे दोनों एक समान होंगी।
अतः वे विन्यास जो लाल गेंदे आपस मे जमाने से प्राप्त हुए वो दो बार आएंगे , इसलिए समान होने के कारण उन्हे भाग दे देंगे।

3 वस्तुओं को आपस मे 3! प्रकार से दर्शाया जा सकता है, अतः 6 विन्यास प्राप्त हुए परन्तु आप ऊपर चित्र मे स्थित 6 विन्यासों मे देख सकते है की जब वे आपस में स्थान बदलते है तो वे एक समान दिखाई देते है तथा आपस मे 2! प्रकार से स्थान बदल सकते है। अतः 2! से भाग देकर उचित क्रमचयों की सँख्या निकाल सकते है अतः
3!2!=3
इसी प्रकार
n वस्तुओं के क्रमचयों की सँख्या, यदि p1 एक प्रकार की, p2 वस्तुएँ दूसरे प्रकार की, इसी प्रकार........ pr वस्तुएँ r प्रकार की है तो क्रमचयो की संख्या=
n!p1!⋅p2!⋅p3!......pr!
उदाहरण 9
यदि शब्द BAZAR के अक्षरों को शब्दकोष क्रम में विन्यासित किया जाए, तो 50वां शब्द ज्ञात कीजिये ?
चूँकि शब्दकोश में Alphabet के क्रम से शब्दों को लिखा जाता हैं अतः
A से प्रारम्भ होने वाले शब्दों की संख्या =4!=24
B से प्रारम्भ होने वाले शब्दों की संख्या =4!2!=12
R से प्रारम्भ होने वाले शब्दो की संख्या =4!2!=12
अतः 49वां शब्द ZAABR तथा 50वां शब्द ZAARB होगा ।
उदाहरण 10
4 लाल , 3 पिली तथा 2 हरी डिस्को को एक पंक्ति में कितने प्रकार से व्यवस्थित
किया जा सकता है , यदि एक ही रंग की डिस्क में कोई अंतर नहीं है ?
डिस्को की कुल संख्या =4+3+2=9
इन 9 डिस्को में से 4 डिस्के लाल है, 3 डिस्के पिली है तथा 2 डिस्के हरी है
अतः डिस्को को व्यवस्थित करने की अभीष्ट संख्या
=9!4!⋅3!⋅2!=1260
संचय
(Combination)
संचय - किसी दिए गए वस्तुओं के समूह मे से बिना क्रम के कुछ या सभी वस्तुओं को चुनना संचय कहलाता है।
इसे समझने के लिए क्रमचय के साथ इसकी तुलना करते है।
अक्षरों ABC के दो अक्षरों को लेकर यदि कुल संभव क्रमचयों की सँख्या देखे तो
3P2=3!(3−2)!=61!=6

अब अक्षरों ABC के दो अक्षरों को लेकर यदि कुल संभव संचयों की सँख्या देखे तो हमे क्रमों पर ध्यान नहीं देना है अर्थात AB व BA का समान अर्थ होगा अर्थात यह दोनों एक ही क्रम के कहलाएंगे। इसी प्रकार अन्य क्रमों मे भी पालन करेंगे।
अर्थात निम्न संचय होंगे
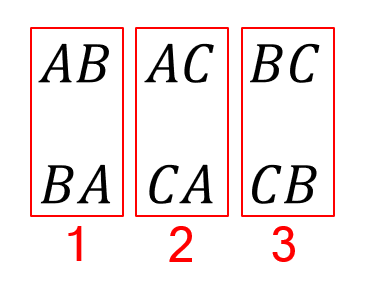
आइए इससे संबंधित महत्वपूर्ण सूत्र देखते हैं
सूत्र-1
nPr=nCr⋅r!
चूंकि nPr=(n!)(n−r)!
अतः
nCr=(n!)(n−r)!⋅r!
जैसे की आपने ऊपर उदाहरण देखा था
3 मे से 2 अक्षरों को चुनने पर क्रमचयो की संख्या 6 तथा संचयों की सँख्या 3 प्राप्त हुई थी। आइए इसका जांच कर लेते है
3C2
=3!(3−2)!⋅2!
=61!⋅2!
=61⋅2
=3
संचय से संबंधित कुछ महत्वपूर्ण परिणाम देखते है
(i) nC0=(n!)(n−0)!⋅0!=1
यहाँ 0!=1
(ii) nCn=(n!)(n−n)!⋅(n!)=1
(iii) nCn−r
=(n!)(n−(n−r))!⋅(n−r)!
=(n!)(n−r)!⋅r!
=nCr
(iv) यदि
nCa=nCb
a=b या
a+b=n
सूत्र-2
nCr+nCr−1=n+1Cr
हल
nCr+nCr−1
=n!r!(n−r)!+n!(r−1)!(n−r+1)!
=n!r⋅(r−1)!(n−r)!+n!(r−1)!(n−r+1)(n−r)!
=n!(r−1)!(n−r)![1r+1n−r+1]
=n!(r−1)!(n−r)!⋅[n−r+1+rr(n−r+1)]
=(n+1)⋅n!r⋅(r−1)!(n+1−r)⋅(n−r)!
=(n+1)!r!(n+1−r)!
=n+1Cr
संचय
(Combination)
संचय - किसी दिए गए वस्तुओं के समूह मे से बिना क्रम के कुछ या सभी वस्तुओं को चुनना संचय कहलाता है।
इसे समझने के लिए क्रमचय के साथ इसकी तुलना करते है।
अक्षरों ABC के दो अक्षरों को लेकर यदि कुल संभव क्रमचयों की सँख्या देखे तो
3P2=3!(3−2)!=61!=6

अब अक्षरों ABC के दो अक्षरों को लेकर यदि कुल संभव संचयों की सँख्या देखे तो हमे क्रमों पर ध्यान नहीं देना है अर्थात AB व BA का समान अर्थ होगा अर्थात यह दोनों एक ही क्रम के कहलाएंगे। इसी प्रकार अन्य क्रमों मे भी पालन करेंगे।
अर्थात निम्न संचय होंगे

आइए इससे संबंधित महत्वपूर्ण सूत्र देखते हैं
सूत्र-1
nPr=nCr⋅r!
चूंकि nPr=(n!)(n−r)!
अतः
nCr=(n!)(n−r)!⋅r!
जैसे की आपने ऊपर उदाहरण देखा था
3 मे से 2 अक्षरों को चुनने पर क्रमचयो की संख्या 6 तथा संचयों की सँख्या 3 प्राप्त हुई थी। आइए इसका जांच कर लेते है
3C2
=3!(3−2)!⋅2!
=61!⋅2!
=61⋅2
=3
संचय से संबंधित कुछ महत्वपूर्ण परिणाम देखते है
(i) nC0=(n!)(n−0)!⋅0!=1
यहाँ 0!=1
(ii) nCn=(n!)(n−n)!⋅(n!)=1
(iii) nCn−r
=(n!)(n−(n−r))!⋅(n−r)!
=(n!)(n−r)!⋅r!
=nCr
(iv) यदि
nCa=nCb
a=b या
a+b=n
सूत्र-2
nCr+nCr−1=n+1Cr
हल
nCr+nCr−1
=n!r!(n−r)!+n!(r−1)!(n−r+1)!
=n!r⋅(r−1)!(n−r)!+n!(r−1)!(n−r+1)(n−r)!
=n!(r−1)!(n−r)![1r+1n−r+1]
=n!(r−1)!(n−r)!⋅[n−r+1+rr(n−r+1)]
=(n+1)⋅n!r⋅(r−1)!(n+1−r)⋅(n−r)!
=(n+1)!r!(n+1−r)!
=n+1Cr
उदाहरण 10
दिया है ,
C(n,r):C(n,r+1)=1:2 और
C(n,r+1):C(n,r+2)=2:3
तब n किसके तुल्य है ?
दिया है,
C(n,r):C(n,r+1)=1.2
⇒nCr:nCr+1=1:2
⇒n!r!(n−r)!n!(r+1)!(n−r−1)!=12
⇒r+1n−r=12
⇒2r+2=n−r
⇒n=3r+2 ....(i)
तथा उसी प्रकार
C(n,r+1):C(n,r+2)=2:3 में,
⇒r+2n−r−1=23
⇒5r+8=2n
⇒r=(2n−8)5 ....(ii)
अब r का मान सभी (i) में रखने पर,
n=3(2n−85)+2
⇒n=14
उदाहरण 11
यदि C(28,2r)=C(28,2r−4) है, तो r किसके बराबर है ?
दिया है,
C(28,2r)=C(28,2r−4)
⇒28C2r=28C2r−4
[nCx=nCy⇒x+y=n]
⇒2r+(2r−4)=28
⇒4r=32
⇒r=8
उदाहरण 11
कितने प्रकार से 9 खिलौनों को 4 बच्चो में बाँटा जा सकता है, जिससे की सबसे छोटे बच्चे को 3 खिलौने तथा बाकि बच्चो को 2 खिलौने मिले ?
सबसे छोटे बच्चे को खिलौने मिलने के प्रकार =9C3
दूसरे बच्चे को खिलौने मिलने के प्रकार =6C2
तीसरे बच्चे को खिलौने मिलने के प्रकार 4C2
चौथे बच्चे को खिलौने मिलने के प्रकार =2C2
∴ कुल चयन की संख्या
=9C3×6C2×4C2×2C2
=9!6!3!×6!4!2!×4!2!2!×2!2!0!
=7560
उदाहरण 12
किसी कॉलेज की एक कक्षा में 50 विद्यार्थी है । वे कितने प्रकार से 3 प्रतिनिधि कॉलेज यूनियन के लिए चुन सकते है ?
50 विद्यार्थियों में से 3 विद्यार्थियों को चुनने का अभीष्ट तरीका
=50C3=50!3!47!
[nCr=n!r!(n−r)!]
=50⋅49⋅483!=19600
उदाहरण 12
52 ताशों की एक गडडी से 4 पत्तों को चुनने के तरीकों की संख्या ज्ञात करो इन तरीकों में से कितनों में
(i) चारों पत्ते एक की प्रकार (suit) के हैं ?
(ii) चारों पत्ते विभिन्न प्रकारों के हैं ?
(iii) चारो पत्तो में तस्वीरें हैं
(iv) दो पत्ते लाल तथा दो पत्ते काले हैं ?
(v) चारों पत्ते एक ही रंग के हैं ?
52 ताशों में से 4 पत्तों को चुनने के प्रकार =52C4
=52!48!4!
=270725
(i) 52 ताशों की गड्डी में 4 प्रकार के पत्ते ( ईंट, चिड़ी हुकुम, पान ) होते हैं ।
गड्डी में प्रत्येक प्रकार के पत्तों की संख्या =13
चारों पत्ते एक ही प्रकार के होंगे यदि वह ईंट, चिड़ी हुकुम अथवा पान के हैं ।
ईंट के पत्तों 13 में से 4 को चुनने के प्रकार =13C4
चिड़ी के 13 पत्तों में से 4 को चुनने के प्रकार =13C4
हुकुम के 13 पत्तों में से 4 को चुनने के प्रकार =13C4
पान के 13 पत्तों में से 4 को चुनने के प्रकार =13C4
अतः योग सिद्धान्त से कुल प्रकार
=13C4+13C4+13C4+13C4
=4×13C4
=4×13×12×11×10×9!(4×3×2×1)(9!)
=2×13×11×10
=2860
(ii) गड्डी में प्रत्येक प्रकार के पत्तों की संख्या =13
चारों पत्ते चार भिन्न प्रकार के होंगे यदि प्रत्येक प्रकार का चुना जाए।
ईंट के 13 पत्तों में से 1 को चुनने के प्रकार =13C1=13
चिड़ी के 13 पत्तों में से 1 को चुनने के प्रकार =13C1=13
हुकुम के 13 पत्तों में से 1 को चुनने के प्रकार =13C1=13
पान के 13 पत्तों में से 1 को चुनने के प्रकार =13C1=13
अतः गुणन सिद्धांत से कुल प्रकार =13×13×13×13=134=28561
(iii) गड्डी में कुल 12 तस्वीरें होती है जिनमें से 4 पत्ते 12C4 प्रकार से चुने जा सकते हैं ।
अतः कुल प्रकार
=12C4
= 12×11×10×9×8!(4×3×2×1)(8!)
=11×5×9=495
(iv) गड्डी में 26 लाल तथा 26 काले पत्ते होते हैं ।
26 लाल पत्तों में से 2 चुनने के प्रकार =26C2
26 काले पत्तों में से 2 चुनने के प्रकार =26C2
अतः गुणन सिद्धान्त से
2 लाल तथा 2 काले पत्ते चुनने के प्रकार =26C2×26C2
=26×252×1×26×252×1
=13×25×13×25
=105625
(v) चारों पत्ते एक ही रंग के होंगे यदि वह लाल अथवा काले रंग के हैं
26 लाल पत्तों में से 4 चुनने के प्रकार =26C4
26 काले पत्तों में से 4 चुनने के प्रकार =26C4
योग सिद्धान्त से कुल प्रकार =26C4+26C4
2×26C4
=2×26×25×24×23×22!(4×3×2×1)(22!)
=29900
उदाहरण 13
52 ताशों की एक गडडी से 4 पत्तों को चुनने के तरीकों की संख्या ज्ञात करो इन तरीकों में से कितनों में
(i) चारों पत्ते एक की प्रकार (suit) के हैं ?
(ii) चारों पत्ते विभिन्न प्रकारों के हैं ?
(iii) चारो पत्तो में तस्वीरें हैं
(iv) दो पत्ते लाल तथा दो पत्ते काले हैं ?
(v) चारों पत्ते एक ही रंग के हैं ?
52 ताशों में से 4 पत्तों को चुनने के प्रकार =52C4
=52!48!4!
=270725
(i) 52 ताशों की गड्डी में 4 प्रकार के पत्ते ( ईंट, चिड़ी हुकुम, पान ) होते हैं ।
गड्डी में प्रत्येक प्रकार के पत्तों की संख्या =13
चारों पत्ते एक ही प्रकार के होंगे यदि वह ईंट, चिड़ी हुकुम अथवा पान के हैं ।
ईंट के पत्तों 13 में से 4 को चुनने के प्रकार =13C4
चिड़ी के 13 पत्तों में से 4 को चुनने के प्रकार =13C4
हुकुम के 13 पत्तों में से 4 को चुनने के प्रकार =13C4
पान के 13 पत्तों में से 4 को चुनने के प्रकार =13C4
अतः योग सिद्धान्त से कुल प्रकार
=13C4+13C4+13C4+13C4
=4×13C4
=4×13×12×11×10×9!(4×3×2×1)(9!)
=2×13×11×10
=2860
(ii) गड्डी में प्रत्येक प्रकार के पत्तों की संख्या =13
चारों पत्ते चार भिन्न प्रकार के होंगे यदि प्रत्येक प्रकार का चुना जाए।
ईंट के 13 पत्तों में से 1 को चुनने के प्रकार =13C1=13
चिड़ी के 13 पत्तों में से 1 को चुनने के प्रकार =13C1=13
हुकुम के 13 पत्तों में से 1 को चुनने के प्रकार =13C1=13
पान के 13 पत्तों में से 1 को चुनने के प्रकार =13C1=13
अतः गुणन सिद्धांत से कुल प्रकार =13×13×13×13=134=28561
(iii) गड्डी में कुल 12 तस्वीरें होती है जिनमें से 4 पत्ते 12C4 प्रकार से चुने जा सकते हैं ।
अतः कुल प्रकार
=12C4
= 12×11×10×9×8!(4×3×2×1)(8!)
=11×5×9=495
(iv) गड्डी में 26 लाल तथा 26 काले पत्ते होते हैं ।
26 लाल पत्तों में से 2 चुनने के प्रकार =26C2
26 काले पत्तों में से 2 चुनने के प्रकार =26C2
अतः गुणन सिद्धान्त से
2 लाल तथा 2 काले पत्ते चुनने के प्रकार =26C2×26C2
=26×252×1×26×252×1
=13×25×13×25
=105625
(v) चारों पत्ते एक ही रंग के होंगे यदि वह लाल अथवा काले रंग के हैं
26 लाल पत्तों में से 4 चुनने के प्रकार =26C4
26 काले पत्तों में से 4 चुनने के प्रकार =26C4
योग सिद्धान्त से कुल प्रकार =26C4+26C4
2×26C4
=2×26×25×24×23×22!(4×3×2×1)(22!)
=29900
उदाहरण 13
4 पुरुषो तथा 6 महिलाओं से एक 5 सदस्यों की समिति बनाई जाती है, तब उन तरीको की संख्या बताइए जिसमे समिति में पुरुष बहुमत में हो ?
4 पुरुष तथा 6 महिलाओं को लेकर एक 5 सदस्यों की समिति का गठन निम्न प्रकार से किया जा सकता है
Men (4)Women (6)0514233241
जब पुरुष बहुमत में है, तब समिति गठित करने के तरीको की संख्या
=4C3 6C2+4C4 6C1
=66
उदाहरण 14
9 उपलबध पाठ्यक्रमों में से, एक विद्यार्थी 5 पाठ्यक्रमों का चयन कितने प्रकार से कर सकता है? यदि प्रत्येक विद्यार्थी के लिए 2 विशिष्ठ पाठ्यक्रम अनिवार्य है?
कुल उपलब्ध पाठ्यक्रमों की संख्या = 9
पाठ्यक्रमों की संख्या जिसका चुनाव करना है = 5
दो विशिष्ठ पाठ्यक्रम अनिवार्य है अतः विद्यार्थी को दो विशिष्ठ पाठ्यक्रम तथा शेष सात पाठ्यक्रमों में से तीन का चुनाव करना है ।
2 विशिष्ठ पाठयक्रमो में से 2 का चुनाव करने का तरीका =2C2
शेष 7 पाठ्यक्रमों में से 3 का चुनाव करने का तरीका =7C3
अतः अभीष्ट संख्या =2C2×7C3
=1×7×6×5×4!(7−3)!×3!=35
वृत्तीय क्रमचय
(Circular permutation)
एक पंक्ति में वस्तुओं का क्रमचय रेखीय क्रमचय कहलाता है। यदि हम वस्तुओं को एक बन्द वक्र के अनुदिश व्यवस्थित करते हैं, तो यह वृत्तीय क्रमचय कहलाता है।
इसलिये वृत्तीय क्रमचय में, हम एक वस्तु को स्थिर मानकर शेष वस्तुओं को रेखीय विन्यासों की स्थिति के अनुसार व्यवस्थित करते है।
CASE-(1)
n भिन्न-भिन्न वस्तुओं के वृत्तीय क्रमचयों की संख्या (n−1)! हैं
इसे एक उदाहरण से समझने का प्रयास करते हैं -
माना 5 वस्तुओं A,B,C,D,E को एक बन्द वक्र के चारों ओर व्यवस्थित करना वृत्तीय क्रमचय कहलाता है।

माना सभी वृत्तीय क्रमचयों की संख्या x है। उपरोक्त वृत्तीय क्रमचय, 5 रेखीय क्रमचय के तुल्य है, जो ABCDEF, EABCD, DEABC, CDEAB, BCDEA द्वारा दिये जाते है।
यहाँ एक वृत्तीय क्रमचय, 5x रेखीय क्रमचयों के तुल्य है, जो निम्न द्वारा दिये जाते है
5x=5!
x=5!5
x=5(5−1)!5
x=(5−1)!
इसी प्रकार n वस्तुओ के लिए nx=n!
x=n!n=(n−1)!
CASE-2
यदि दक्षिणावर्त एवं वामावर्त को समान माना जाये तो वृत्तीय क्रमचयों की संख्या (n−1)!2 द्वारा दी जाती है। यदि हम फूलों या मोतियों को एक माला में व्यवस्थित करते है, तो दक्षिणावर्त एव बामावर्त दिशा में कोई भेद नहीं है।
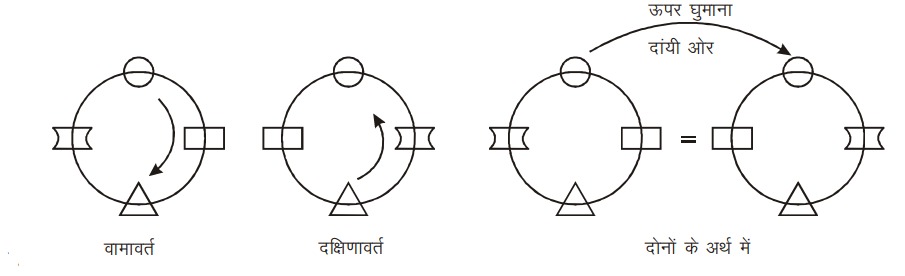
महत्वपूर्ण बिन्दु
n!p1!⋅p2!⋅p3!......pr!
- a=b या a+b=n
उदाहरण 14
6 बालक ओर 5 बालिकाएँ एक गोल मेज के चारों ओर कितने प्रकार से बैठ सकते है , यदि दो बालिकाएँ एक साथ न बैठें ?
6 बालकों को गोल मेज के चारों ओर बैठाने के क्रम = 5!=120
इन बालकों के बीच 6 स्थान होंगें जिनमें से 5 स्थानों पर बालिकाओं को बैठाने के क्रम =6P5=6!1!=720
∴अभीष्ट क्रम
=120×720
=86400
उदाहरण 15
6 व्यक्ति एक गोल मेज के चारों ओर कितने प्रकार से बैठ सकते है , यदि किन्ही दो क्रमों में सबके पड़ोसी समान न हों ?
दक्षिणावर्त्त और वामावर्त्त दिशा में पड़ोसी समान नहीं है ।
अतः यदि पड़ोसी समान नहीं है , तो 6 व्यक्तियों को गोल मेज के चारो ओर बैठाने के क्रम
=12×(6−1)!
=1202
=60
महत्वपूर्ण बिन्दु
n!p1!⋅p2!⋅p3!......pr!
- a=b या a+b=n
