स्थूल द्रव्य के गुण कक्षा 11 भौतिकी
भूमिका
इस अध्याय में हम ठोसों के प्रत्यास्थ व्यवहार, प्रतिबल तथा विकृति के बारे में अध्ययन करेंगे। साथ ही हुक का नियम, यंग के प्रत्यास्थता गुणांक का भी अध्ययन करेंगे। अध्याय के अंत में द्रव्यों के प्रत्यास्थ व्यवहार के अनुप्रयोग के बारे में जानेंगे।
भूमिका
इस अध्याय में हम ठोसों के प्रत्यास्थ व्यवहार, प्रतिबल तथा विकृति के बारे में अध्ययन करेंगे। साथ ही हुक का नियम, यंग के प्रत्यास्थता गुणांक का भी अध्ययन करेंगे। अध्याय के अंत में द्रव्यों के प्रत्यास्थ व्यवहार के अनुप्रयोग के बारे में जानेंगे।
ठोसों में प्रत्यास्थता
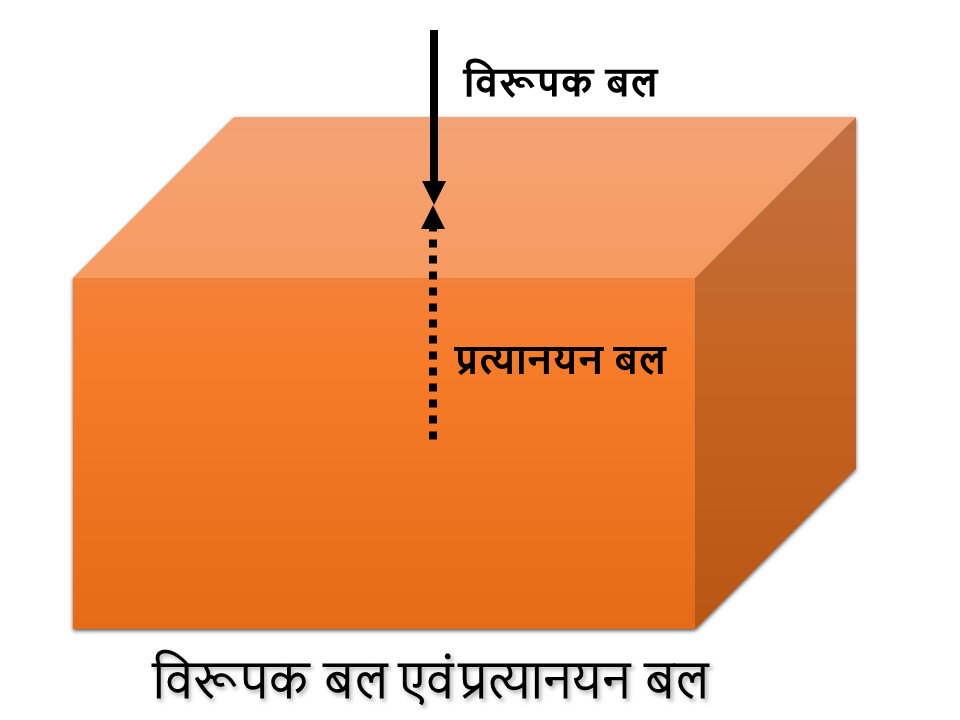
जब हम किसी वस्तु पर बाह्य बल लगाते है तो उसमे कुछ न कुछ विरूपण उत्पन्न हो जाता है। इस स्थिति में लगने वाले बल को विरूपण बल कहते है।
परिभाषा- किसी वस्तु का वह गुण जिसके कारण वस्तु विरूपक बल लगाने से उत्पन्न परिवर्तन का विरोध करती है और जब विरूपक बल को हटा लिया जाता है तो वस्तु अपनी मूल अवस्था में लौट आती है, वस्तु के इसी गुण को ही प्रत्यास्थता कहते है।
जिन वस्तुओ में प्रत्यास्थता का गुण पाया जाता है उन्हें प्रत्यास्थ वस्तु कहते है।
प्रत्यास्थता का कारण :
किसी ठोस में उसके अणुओं या परमाणुओं के बीच लगने वाले बल को अन्तराण्विक बल कहते हैं। इसी बल के वजह से ठोस के अणु आपस में जुड़े रहते है।
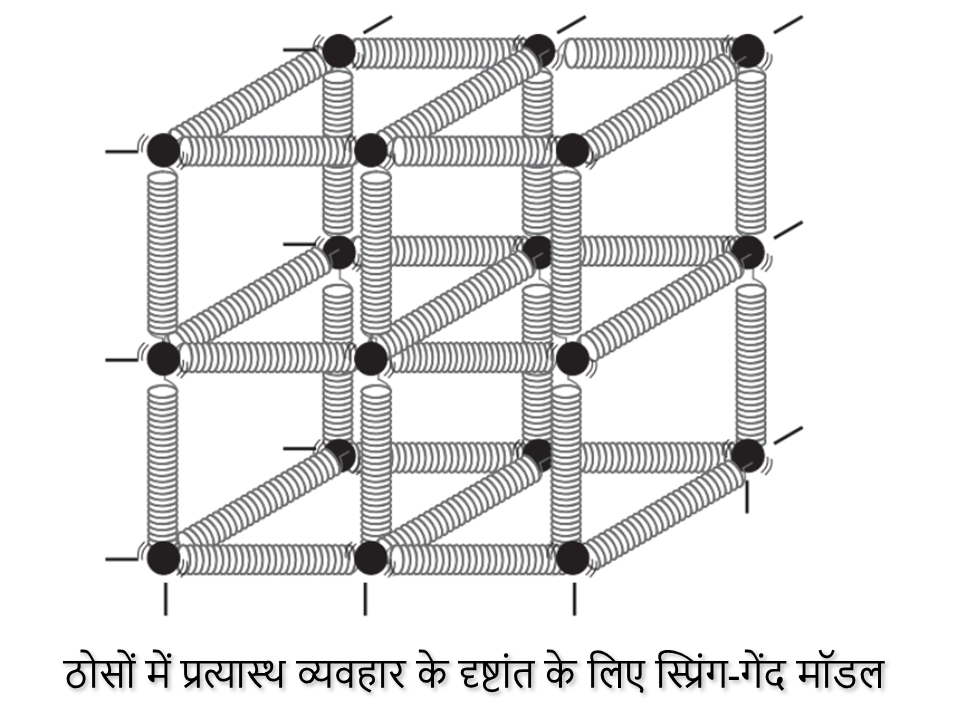
जब किसी ठोस पर विरुपक बल लगाया जाता है तो ठोस के अणुओं के मध्य की दूरी परिवर्तित हो जाती है और चूंकि हमने बताया की ठोस के अणु आपस में ऐसे व्यवहार करते है जैसे वे स्प्रिंग से जुड़े हो इसलिए विरुपक बल लगने से जब इनके अणुओं के मध्य की दूरी परिवर्तित हो जाती है तो इनके मध्य प्रत्यानयन बल कार्य करता है।
और जब वस्तु पर आरोपित विरूपक बल हटा लिया जाता है तो इस प्रत्यानयन बल के कारण वस्तु के कण अपनी पूर्व स्थिति ग्रहण कर लेते है जिससे वस्तु का आकार व आकृति भी इसकी पूर्व स्थिति में आ जाता है, वस्तु का यह गुण प्रत्यास्थत गुण कहलाता है जो विरुपक बल हटा लेने पर उन्हें इनकी पूर्व स्थिति में जाने का प्रयास करता है।
पूर्णतः प्रत्यास्थ वस्तु :
वह वस्तु जिसमे बाह्य बल लगाने में उसके आकृति परिवर्तन हो जाती है और बाह्य (बाहरी) बल हटाने के पश्चात् पूर्णतः अपनी प्रारम्भिक अवस्था में आ जाती है, पूर्णत: प्रत्यास्थ वस्तु कहलाती है।
उदाहरण - क्वार्टज (Quartz)- लगभग पूर्णतया प्रत्यास्थ वस्तु है।

प्लास्टिक वस्तु :
- वे वस्तुएँ जिनमें विरूपक बल का विरोध करने का गुण नहीं होता है, प्लास्टिक वस्तुएँ कहलाती है।
- वे वस्तुएँ जो बाहरी बल हटा लेने के पश्चात् भी विकृत अवस्था में रहती है। प्लास्टिक वस्तुएँ कहलाती है।

प्रत्यानयन बल :
जब किसी वस्तु पर बाह्य विरुपक बल लगाया जाता है तो अन्तर आणविक बल के कारण पदार्थ के अन्दर एक आन्तरिक प्रतिरोध उत्पन्न हो जाता है जिसे आन्तरिक प्रतिक्रिया बल या आन्तरिक प्रत्यानयन बल कहते है।
संतुलन की स्थिति में आन्तरिक प्रतिक्रिया बल का संख्यात्मक मान बाह्य विरुपक बल के बराबर होता है।
ठोसों में प्रत्यास्थता
जब हम किसी वस्तु पर बाह्य बल लगाते है तो उसमे कुछ न कुछ विरूपण उत्पन्न हो जाता है। इस स्थिति में लगने वाले बल को विरूपण बल कहते है।
परिभाषा- किसी वस्तु का वह गुण जिसके कारण वस्तु विरूपक बल लगाने से उत्पन्न परिवर्तन का विरोध करती है और जब विरूपक बल को हटा लिया जाता है तो वस्तु अपनी मूल अवस्था में लौट आती है, वस्तु के इसी गुण को ही प्रत्यास्थता कहते है।
जिन वस्तुओ में प्रत्यास्थता का गुण पाया जाता है उन्हें प्रत्यास्थ वस्तु कहते है।
प्रत्यास्थता का कारण :
किसी ठोस में उसके अणुओं या परमाणुओं के बीच लगने वाले बल को अन्तराण्विक बल कहते हैं। इसी बल के वजह से ठोस के अणु आपस में जुड़े रहते है।

जब किसी ठोस पर विरुपक बल लगाया जाता है तो ठोस के अणुओं के मध्य की दूरी परिवर्तित हो जाती है और चूंकि हमने बताया की ठोस के अणु आपस में ऐसे व्यवहार करते है जैसे वे स्प्रिंग से जुड़े हो इसलिए विरुपक बल लगने से जब इनके अणुओं के मध्य की दूरी परिवर्तित हो जाती है तो इनके मध्य प्रत्यानयन बल कार्य करता है।
और जब वस्तु पर आरोपित विरूपक बल हटा लिया जाता है तो इस प्रत्यानयन बल के कारण वस्तु के कण अपनी पूर्व स्थिति ग्रहण कर लेते है जिससे वस्तु का आकार व आकृति भी इसकी पूर्व स्थिति में आ जाता है, वस्तु का यह गुण प्रत्यास्थत गुण कहलाता है जो विरुपक बल हटा लेने पर उन्हें इनकी पूर्व स्थिति में जाने का प्रयास करता है।
पूर्णतः प्रत्यास्थ वस्तु :
वह वस्तु जिसमे बाह्य बल लगाने में उसके आकृति परिवर्तन हो जाती है और बाह्य (बाहरी) बल हटाने के पश्चात् पूर्णतः अपनी प्रारम्भिक अवस्था में आ जाती है, पूर्णत: प्रत्यास्थ वस्तु कहलाती है।
उदाहरण - क्वार्टज (Quartz)- लगभग पूर्णतया प्रत्यास्थ वस्तु है।

प्लास्टिक वस्तु :
- वे वस्तुएँ जिनमें विरूपक बल का विरोध करने का गुण नहीं होता है, प्लास्टिक वस्तुएँ कहलाती है।
- वे वस्तुएँ जो बाहरी बल हटा लेने के पश्चात् भी विकृत अवस्था में रहती है। प्लास्टिक वस्तुएँ कहलाती है।

प्रत्यानयन बल :
जब किसी वस्तु पर बाह्य विरुपक बल लगाया जाता है तो अन्तर आणविक बल के कारण पदार्थ के अन्दर एक आन्तरिक प्रतिरोध उत्पन्न हो जाता है जिसे आन्तरिक प्रतिक्रिया बल या आन्तरिक प्रत्यानयन बल कहते है।
संतुलन की स्थिति में आन्तरिक प्रतिक्रिया बल का संख्यात्मक मान बाह्य विरुपक बल के बराबर होता है।
प्रतिबल
जब किसी वस्तु पर विरूपक बल लगाया जाता है तो इस बल के कारण वस्तु के आकार या आकृति अथवा दोनों में परिवर्तन हो जाता है। और जैसा की हमने प्रत्यास्थता के कारण में पढ़ा की वस्तु में अणु इस प्रकार व्यवस्थित रहते है जैसे वे स्प्रिंगों से जुड़े हो।
अतः जब विरूपक बल द्वारा किसी वस्तु के आकार व आकृति में परिवर्तन किया जाता है तो इसके अणु वस्तु को पुनः इसकी मूल अवस्था में लाने का प्रयास करते है जिससे इसके अणुओ के मध्य एक आंतरिक प्रतिक्रिया उत्पन्न हो जाती है और यह आन्तरिक प्रतिक्रिया वस्तु में हुए परिवर्तन का विरोध करती है और वस्तु को इसकी पूर्व अवस्था में लाने प्रयास करती है।
परिभाषा:- वस्तु के एकांक अनुप्रस्थ काट के क्षेत्रफल पर कार्यरत आंतरिक प्रतिक्रिया बल को प्रतिबल कहते है।
किसी वस्तु पर एकांक क्षेत्रफल पर आरोपित बल का मान है जो उस वस्तु पर आरोपित हो रहा है।
प्रतिबल को σ द्वारा प्रदर्शित किया जाता है जिसका निम्न सूत्र होता है-
σ=FA
यहॉँ σ = प्रतिबल
F = बल
A = अनुप्रस्थ क्षेत्रफल
प्रतिबल का SI मात्रक Nm−2 (न्यूटन/मीटर2) या पास्कल होता है तथा इसकी विमा [ML−1T−2] होती है।
प्रतिबल के प्रकार :
किसी वस्तु पर लगने वाले बल के आधार पर प्रतिबल को दो भागो में बांटा गया है :-
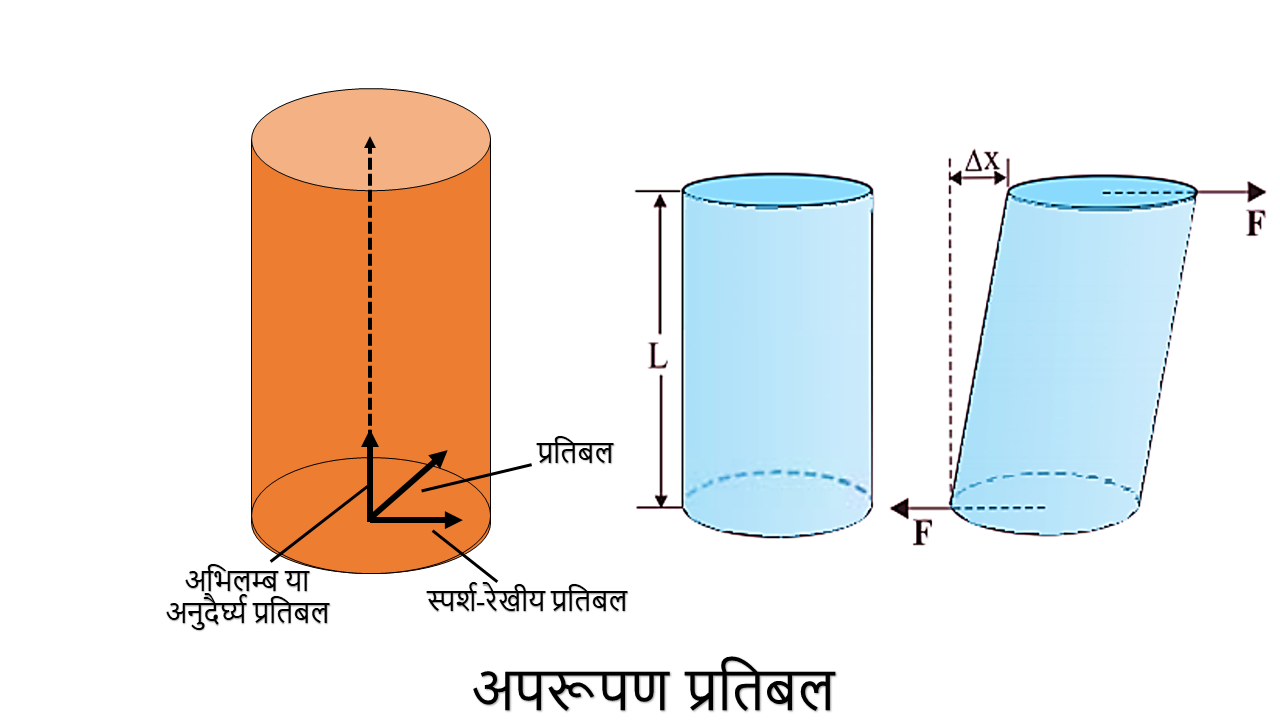
- अभिलंब प्रतिबल या अनुदैर्ध्य प्रतिबल
- स्पर्शीय प्रतिबल या अपरूपण प्रतिबल
अभिलंब प्रतिबल :
जब किसी वस्तु पर लगने वाला प्रतिबल या उसका अवयव वस्तु के अनुप्रस्थ काट के लम्बवत् कार्य करता है, तो इस प्रकार के प्रतिबल को अभिलंब प्रतिबल या अनुदैर्ध्य प्रतिबल कहते हैं।
अभिलंब प्रतिबल दो प्रकार के होते हैं:-
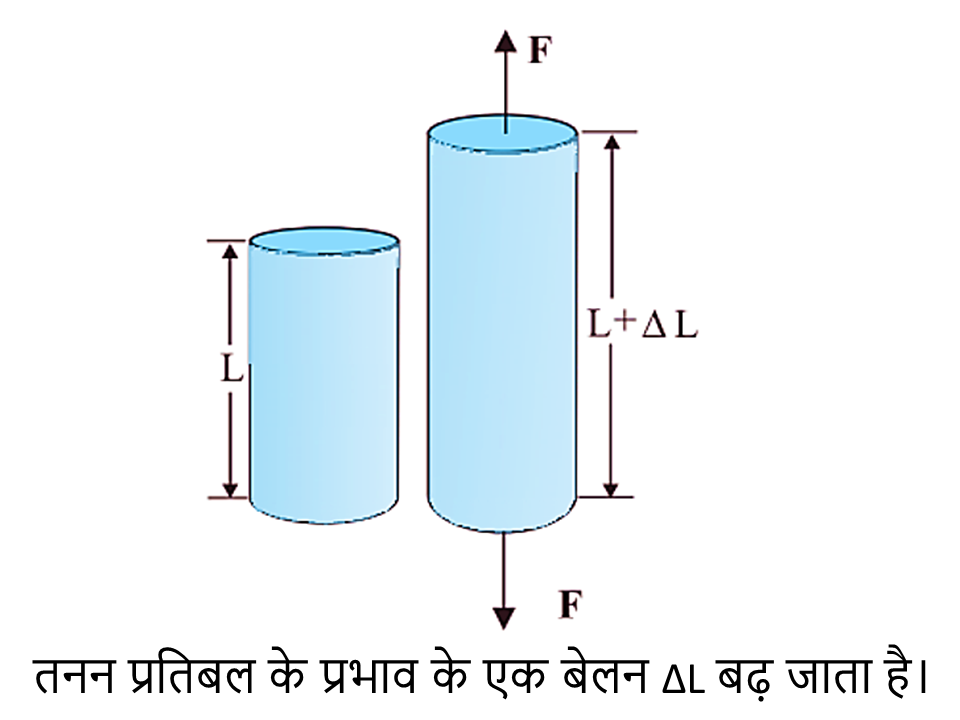
- तनन प्रतिबल :- वस्तु की लम्बाई में वृद्धि होने पर उत्पन्न अनुदैर्ध्य प्रतिबल को तनन प्रतिबल कहते हैं।
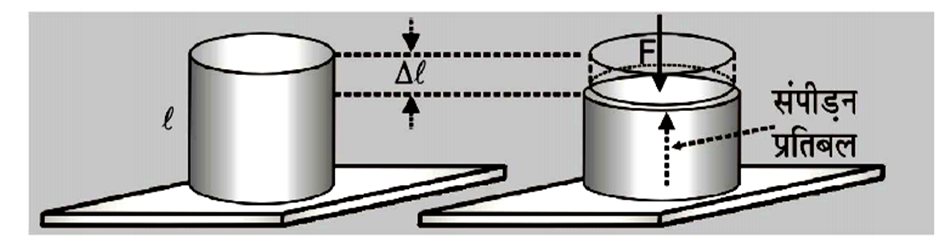
- सम्पीड़न प्रतिबल :-वस्तु की लम्बाई में कमी होने पर उत्पन्न अनुदैर्ध्य प्रतिबल को सम्पीडन प्रतिबल कहते हैं।
अपरूपण प्रतिबल :
जब किसी वस्तु पर लगने वाला प्रतिबल या उसका अवयव वस्तु के अनुप्रस्थ काट के स्पर्श रेखीय या समान्तर कार्य करता है, तो इसे स्पर्शीय या अपरूपण प्रतिबल कहते है।
प्रतिबल
जब किसी वस्तु पर विरूपक बल लगाया जाता है तो इस बल के कारण वस्तु के आकार या आकृति अथवा दोनों में परिवर्तन हो जाता है। और जैसा की हमने प्रत्यास्थता के कारण में पढ़ा की वस्तु में अणु इस प्रकार व्यवस्थित रहते है जैसे वे स्प्रिंगों से जुड़े हो।
अतः जब विरूपक बल द्वारा किसी वस्तु के आकार व आकृति में परिवर्तन किया जाता है तो इसके अणु वस्तु को पुनः इसकी मूल अवस्था में लाने का प्रयास करते है जिससे इसके अणुओ के मध्य एक आंतरिक प्रतिक्रिया उत्पन्न हो जाती है और यह आन्तरिक प्रतिक्रिया वस्तु में हुए परिवर्तन का विरोध करती है और वस्तु को इसकी पूर्व अवस्था में लाने प्रयास करती है।
परिभाषा:- वस्तु के एकांक अनुप्रस्थ काट के क्षेत्रफल पर कार्यरत आंतरिक प्रतिक्रिया बल को प्रतिबल कहते है।
किसी वस्तु पर एकांक क्षेत्रफल पर आरोपित बल का मान है जो उस वस्तु पर आरोपित हो रहा है।
प्रतिबल को σ द्वारा प्रदर्शित किया जाता है जिसका निम्न सूत्र होता है-
σ=FA
यहॉँ σ = प्रतिबल
F = बल
A = अनुप्रस्थ क्षेत्रफल
प्रतिबल का SI मात्रक Nm−2 (न्यूटन/मीटर2) या पास्कल होता है तथा इसकी विमा [ML−1T−2] होती है।

प्रतिबल के प्रकार :
किसी वस्तु पर लगने वाले बल के आधार पर प्रतिबल को दो भागो में बांटा गया है :-
- अभिलंब प्रतिबल या अनुदैर्ध्य प्रतिबल
- स्पर्शीय प्रतिबल या अपरूपण प्रतिबल
अभिलंब प्रतिबल :
जब किसी वस्तु पर लगने वाला प्रतिबल या उसका अवयव वस्तु के अनुप्रस्थ काट के लम्बवत् कार्य करता है, तो इस प्रकार के प्रतिबल को अभिलंब प्रतिबल या अनुदैर्ध्य प्रतिबल कहते हैं।
अभिलंब प्रतिबल दो प्रकार के होते हैं:-
- तनन प्रतिबल :- वस्तु की लम्बाई में वृद्धि होने पर उत्पन्न अनुदैर्ध्य प्रतिबल को तनन प्रतिबल कहते हैं।

- सम्पीड़न प्रतिबल :-वस्तु की लम्बाई में कमी होने पर उत्पन्न अनुदैर्ध्य प्रतिबल को सम्पीडन प्रतिबल कहते हैं।

अपरूपण प्रतिबल :
जब किसी वस्तु पर लगने वाला प्रतिबल या उसका अवयव वस्तु के अनुप्रस्थ काट के स्पर्श रेखीय या समान्तर कार्य करता है, तो इसे स्पर्शीय या अपरूपण प्रतिबल कहते है।

विकृति
जब किसी वस्तु पर बाह्य विरूपक बल आरोपित किया जाता है, तो उसके आकार या आकृति या दोनों में परिवर्तन होता है, अर्थात् वस्तु की लम्बाई, आयतन या आकार में परिवर्तन होता है। वस्तु के आकार में परिवर्तन तथा प्रारंभिक आकार के अनुपात को विकृति कहते हैं।
दूसरे शब्दों में, विरूपक बल के कारण किसी वस्तु की एकांक विमा में होने वाले परिवर्तन को विकृति कहते हैं।
गणितीय रूप में,
विकृति दो समान राशियों का अनुपात है, अतः इसका कोई मात्रक नहीं होता है। यह एक विमाहीन राशि है। इसका विमीय सूत्र [M0L0T0] होता है।
विकृति के प्रकार :
विकृति तीन प्रकार की होती हैं:-
- अनुदैर्ध्य विकृति
- आयतन विकृति
- अपरूपण विकृति
अनुदैर्ध्य विकृति :
विरूपक बल के कारण किसी वस्तु के लम्बाई में परिवर्तन तथा प्रारंभिक लम्बाई के अनुपात को अनुदैर्ध्य विकृति कहते हैं।
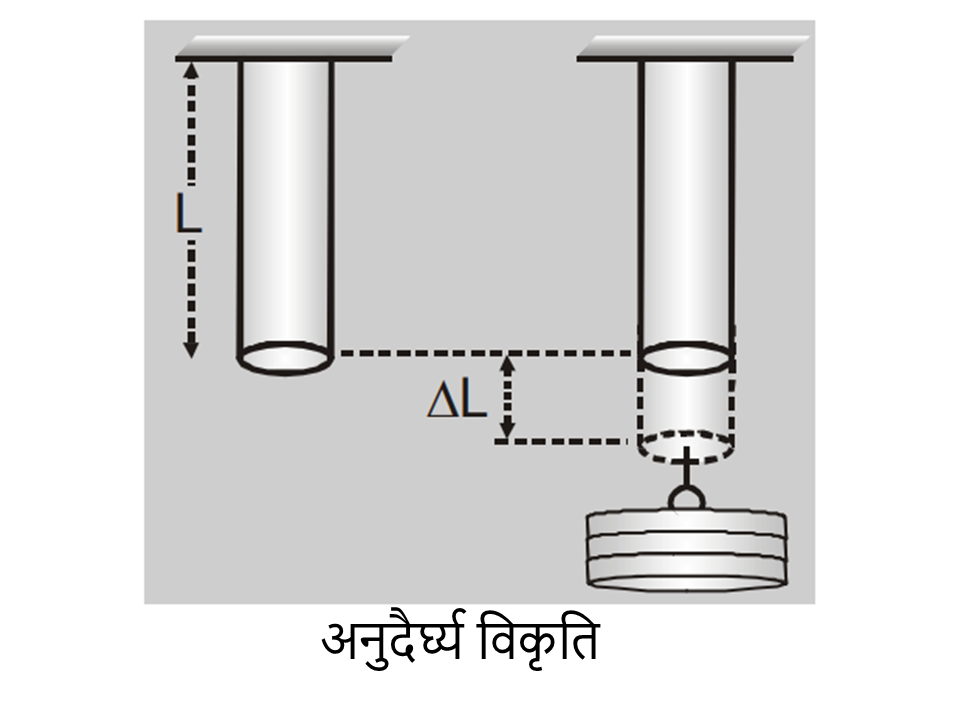
अनुदैर्ध्य विकृति =ΔLL
आयतन विकृति :
किसी बाह्य विरूपक बल द्वारा किसी वस्तु के आयतन में किये गये परिवर्तन तथा उसके प्रारंभिक आयतन के अनुपात को वस्तु की आयतन विकृति कहते हैं।
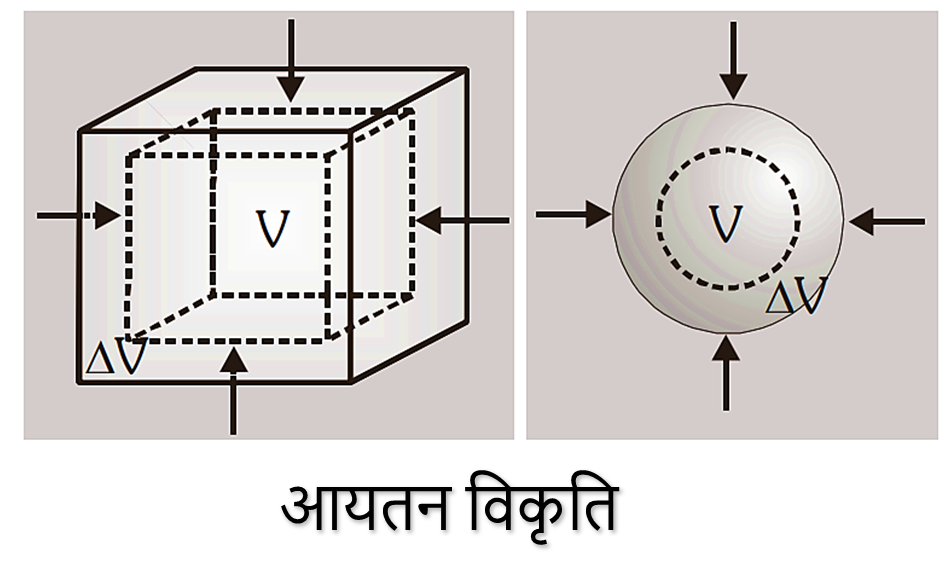
आयतन विकृति =ΔVV
अपरूपण विकृति :
जब किसी वस्तु पर उसकी सतह के समान्तर विरूपक बल इस प्रकार लगाया जाता है कि उसका आयतन स्थिर रहे, किन्तु उसकी आकृति में परिवर्तन हो जाये तो इस प्रकार की वस्तु में उत्पन्न विकृति को अपरूपण विकृति कहते हैं। इसका मान उसके समान्तर सतहों के कोणीय विस्थापन के तुल्य होता है।
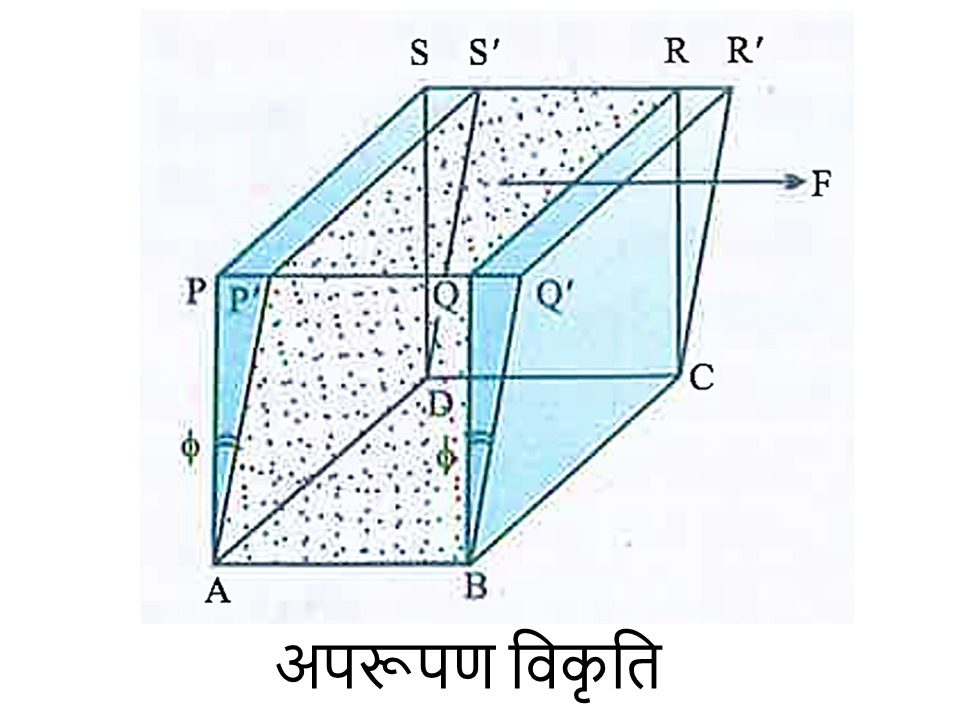
चित्र के अनुसार माना कि ABCDPQRS एक घन है, जिसके निचले पृष्ठ को स्थिर रखकर ऊपरी पृष्ठ PQRS स्पर्शीय विरूपक बल F आरोपित किया जाता है, जिससे घन की नई आकृति ABCDP'Q'R'S' हो जाती है।
पृष्ठ ABCD के सापेक्ष पृष्ठ PQRS का कोणीय विस्थापन,
कोण ϕ को अपरूपण कोण या शुद्ध अपरूपण कहते हैं, इसका मान अपरूपण विकृति के तुल्य होती है।
अपरूपण विकृति =ϕ
अब यदि ϕ का मान बहुत कम हो, तो
अपरूपण विकृति =PP'PA
अपरूपण विकृति = (दोनों सतहों का आपेक्षिक विस्थापन)/(दोनों सतहों के बीच की दूरी)
अर्थात् जब किसी वस्तु पर स्पर्श-रेखीय दिशा में बल इस प्रकार लगाया जाता है कि उसकी आकृति में परिवर्तन हो, परन्तु आयतन में नहीं तो बल लगाने वाले पृष्ठ का उसके सम्मुख पृष्ठ के सापेक्ष विस्थापन तथा दोनों पृष्ठों के बीच की दूरी के अनुपात को उस वस्तु की अपरूपण विकृति कहते हैं। यह विकृति केवल ठोस पदार्थों में होती है।
विकृति
जब किसी वस्तु पर बाह्य विरूपक बल आरोपित किया जाता है, तो उसके आकार या आकृति या दोनों में परिवर्तन होता है, अर्थात् वस्तु की लम्बाई, आयतन या आकार में परिवर्तन होता है। वस्तु के आकार में परिवर्तन तथा प्रारंभिक आकार के अनुपात को विकृति कहते हैं।
दूसरे शब्दों में, विरूपक बल के कारण किसी वस्तु की एकांक विमा में होने वाले परिवर्तन को विकृति कहते हैं।
गणितीय रूप में,
विकृति दो समान राशियों का अनुपात है, अतः इसका कोई मात्रक नहीं होता है। यह एक विमाहीन राशि है। इसका विमीय सूत्र [M0L0T0] होता है।
विकृति के प्रकार :
विकृति तीन प्रकार की होती हैं:-
- अनुदैर्ध्य विकृति
- आयतन विकृति
- अपरूपण विकृति
अनुदैर्ध्य विकृति :
विरूपक बल के कारण किसी वस्तु के लम्बाई में परिवर्तन तथा प्रारंभिक लम्बाई के अनुपात को अनुदैर्ध्य विकृति कहते हैं।

अनुदैर्ध्य विकृति =ΔLL
आयतन विकृति :
किसी बाह्य विरूपक बल द्वारा किसी वस्तु के आयतन में किये गये परिवर्तन तथा उसके प्रारंभिक आयतन के अनुपात को वस्तु की आयतन विकृति कहते हैं।

आयतन विकृति =ΔVV
अपरूपण विकृति :
जब किसी वस्तु पर उसकी सतह के समान्तर विरूपक बल इस प्रकार लगाया जाता है कि उसका आयतन स्थिर रहे, किन्तु उसकी आकृति में परिवर्तन हो जाये तो इस प्रकार की वस्तु में उत्पन्न विकृति को अपरूपण विकृति कहते हैं। इसका मान उसके समान्तर सतहों के कोणीय विस्थापन के तुल्य होता है।

चित्र के अनुसार माना कि ABCDPQRS एक घन है, जिसके निचले पृष्ठ को स्थिर रखकर ऊपरी पृष्ठ PQRS स्पर्शीय विरूपक बल F आरोपित किया जाता है, जिससे घन की नई आकृति ABCDP'Q'R'S' हो जाती है।
पृष्ठ ABCD के सापेक्ष पृष्ठ PQRS का कोणीय विस्थापन,
कोण ϕ को अपरूपण कोण या शुद्ध अपरूपण कहते हैं, इसका मान अपरूपण विकृति के तुल्य होती है।
अपरूपण विकृति =ϕ
अब यदि ϕ का मान बहुत कम हो, तो
अपरूपण विकृति =PP'PA
अपरूपण विकृति = (दोनों सतहों का आपेक्षिक विस्थापन)/(दोनों सतहों के बीच की दूरी)
अर्थात् जब किसी वस्तु पर स्पर्श-रेखीय दिशा में बल इस प्रकार लगाया जाता है कि उसकी आकृति में परिवर्तन हो, परन्तु आयतन में नहीं तो बल लगाने वाले पृष्ठ का उसके सम्मुख पृष्ठ के सापेक्ष विस्थापन तथा दोनों पृष्ठों के बीच की दूरी के अनुपात को उस वस्तु की अपरूपण विकृति कहते हैं। यह विकृति केवल ठोस पदार्थों में होती है।
हुक का नियम
सन् 1678 में सर्वप्रथम ब्रिटिश वैज्ञानिक रॉबर्ट हुक ने अनेक प्रयोगों से प्राप्त परिणामों के आधार पर किसी वस्तु पर लगाये गये विरूपक बल तथा उसके कारण वस्तु में हुए परिवर्तन के बीच संबंध स्थापित किया। इस आधार पर उन्होंने एक नियम का प्रतिपादन किया, जिसे हुक का नियम कहते हैं।
हुक के नियमानुसार, "प्रत्यास्थता सीमा के अन्तर्गत वस्तु पर आरोपित तनाव उसमें उत्पन्न विस्तार के अनुक्रमानुपाती होता है।"
बाद में ब्रिटेन के वैज्ञानिक थॉमस यंग ने इसे विस्तृत रूप देकर यह कहा कि "प्रत्यास्थता की सीमा के अन्तर्गत किसी वस्तु पर लगने वाला प्रतिबल उसमें उत्पन्न विकृति के समानुपाती होता है।"
इस नियम को हुक का नियम कहते हैं । अर्थात् इस नियम के अनुसार,
प्रतिबल =E× विकृति
जहाँ E एक समानुपातिक स्थिरांक है, जिसे वस्तु का प्रत्यास्थता गुणांक कहते हैं।
महत्वपूर्ण बिंदु :
- जब पदार्थ तनन प्रतिबल के अन्तर्गत होता है तो प्रत्यानयन बल का कारण अन्तराणविक आकर्षण होता है, जबकि सम्पीड़न प्रतिबल के अन्तर्गत, प्रत्यानयन बल अंतराणविक प्रतिकर्षण होता है।
- यदि विरुपक बल सतह से θ कोण पर हो, जहाँ θ≠0 एवं θ=90° हो तो स्पर्श रेखीय एवं अभिलम्ब प्रतिबल दोनो उत्पन्न होता है।
- बल की दिशा में रेखीय विकृति अनुदैर्ध्य विकृति कहलाती है, जबकि बल की दिशा के लम्बवत्, पार्श्व विकृति कहलाती है।
हुक का नियम
सन् 1678 में सर्वप्रथम ब्रिटिश वैज्ञानिक रॉबर्ट हुक ने अनेक प्रयोगों से प्राप्त परिणामों के आधार पर किसी वस्तु पर लगाये गये विरूपक बल तथा उसके कारण वस्तु में हुए परिवर्तन के बीच संबंध स्थापित किया। इस आधार पर उन्होंने एक नियम का प्रतिपादन किया, जिसे हुक का नियम कहते हैं।
हुक के नियमानुसार, "प्रत्यास्थता सीमा के अन्तर्गत वस्तु पर आरोपित तनाव उसमें उत्पन्न विस्तार के अनुक्रमानुपाती होता है।"
बाद में ब्रिटेन के वैज्ञानिक थॉमस यंग ने इसे विस्तृत रूप देकर यह कहा कि "प्रत्यास्थता की सीमा के अन्तर्गत किसी वस्तु पर लगने वाला प्रतिबल उसमें उत्पन्न विकृति के समानुपाती होता है।"
इस नियम को हुक का नियम कहते हैं । अर्थात् इस नियम के अनुसार,
प्रतिबल =E× विकृति
जहाँ E एक समानुपातिक स्थिरांक है, जिसे वस्तु का प्रत्यास्थता गुणांक कहते हैं।
महत्वपूर्ण बिंदु :
- जब पदार्थ तनन प्रतिबल के अन्तर्गत होता है तो प्रत्यानयन बल का कारण अन्तराणविक आकर्षण होता है, जबकि सम्पीड़न प्रतिबल के अन्तर्गत, प्रत्यानयन बल अंतराणविक प्रतिकर्षण होता है।
- यदि विरुपक बल सतह से θ कोण पर हो, जहाँ θ≠0 एवं θ=90° हो तो स्पर्श रेखीय एवं अभिलम्ब प्रतिबल दोनो उत्पन्न होता है।
- बल की दिशा में रेखीय विकृति अनुदैर्ध्य विकृति कहलाती है, जबकि बल की दिशा के लम्बवत्, पार्श्व विकृति कहलाती है।
प्रतिबल-विकृति ग्राफ
हुक के नियम के अनुसार किसी वस्तु में उत्पन्न प्रतिबल विकृति के समानुपाती होता है, परन्तु यह नियम केवल प्रत्यास्थता की सीमा में लघु विकृतियों के लिये सत्य होता है।
यदि किसी एकसमान परिच्छेद वाले तार को एक दृढ़ आधार से कसकर उसके मुक्त सिरे पर भार लटकाया जाये तथा उसमें क्रमशः वृद्धि की जाये, तो तार की लम्बाई में क्रमशः वृद्धि होती जाती है।
अतः यदि तार में उत्पन्न प्रतिबल तथा विकृति के मध्य ग्राफ खींचा जाये तो प्राप्त वक्र चित्र के जैसा होता है।
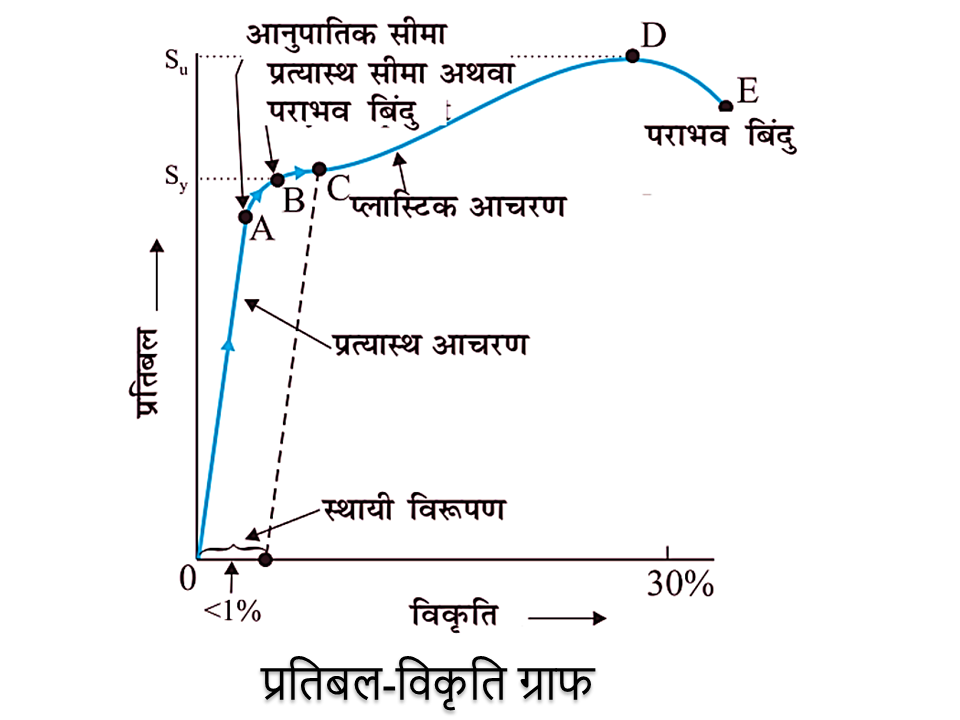
ग्राफ का वर्णन :
- ग्राफ का प्रथम भाग OA एक सीधी रेखा है, जिससे यह स्पष्ट होता है कि बिन्दु A तक तार की लम्बाई में वृद्धि उस पर लटकाये गये द्रव्यमान के अनुक्रमानुपाती होती है। अर्थात् इस भाग में हुक का नियम लागू होता है।
- बिन्दु A पर प्रतिबल के मान को आनुपातिक सीमा कहते हैं। बिन्दु A से आगे का भाग वक्रीय होता है, जिससे यह स्पष्ट होता है कि अब तार पर भार बढ़ाने से तार की लम्बाई में वृद्धि भार के अनुक्रमानुपाती न होकर, उससे अधिक होती है तथा बिन्दु B तक प्रत्यास्थता का गुण बना रहता है।
- अतः बिन्दु B तक यदि तार से भार हटा लिया जाये तो तार अपनी पूर्वावस्था में आ जाता है। बिन्दु B के संगत प्रतिबल के मान को प्रत्यास्थता की सीमा कहते हैं।
- बिन्दु B से आगे तार पर लटके द्रव्यमान में वृद्धि करने पर उसकी लम्बाई में तेजी से वृद्धि होती है तथा बिन्दु B को पराभव बिन्दु कहते हैं, संगत प्रतिबल के मान को पराभव सामर्थ्य कहते हैं।
- इसके पश्चात् प्रतिबल और बढ़ाने पर प्रत्यास्थ व्यवहार समाप्त होकर प्लास्टिक आचरण आरंभ हो जाता है तथा बिन्दु C इस प्रकार प्राप्त होता है कि बल हटा लेने पर तार की लम्बाई में स्थायी वृद्धि हो जाती है अर्थात् भार हटा लेने पर वक्र CBAO पथ का अनुसरण न कर CO' का अनुसरण करता है। अर्थात् शून्य भार में स्थायी विकृति OO' उत्पन्न हो जाता है।
- अब यदि भार में और वृद्धि की जाये तो लम्बाई में वृद्धि और अधिक तेजी से होती है तथा अधिकतम प्रतिबल वाले बिन्दु D तक पहुँच जाता है।
- इस बिन्दु पर तार पतला होना आरंभ हो जाता है। इस बिन्दु को पराभव बिन्दु कहते हैं तथा भार में कमी करने पर भी तार पतला होता रहता है अर्थात् तार का पदार्थ एक श्यान तरल की भाँति व्यवहार करता है तथा बिन्दु E तक पहुँच कर टूट जाता है। इस बिन्दु को त्रोटन बिन्दु कहते हैं तथा इसके संगत भार को त्रोटन भार कहते हैं।
- उस अधिकतम प्रतिबल को जिसे कोई तार टूटने से पहले तक सहन कर सकता है, भंजन प्रतिबल कहते हैं तथा ग्राफ के बिन्दु B से E तक के क्षेत्र को प्लास्टिक क्षेत्र कहते हैं।
रबर की प्रतिबल-विकृति ग्राफ :
इंजीनियरिंग संरचना का डिजाइन करते समय यह ध्यान रखते हैं कि अधिकतम प्रतिबल, त्रोटन प्रतिबल के एक निश्चित अंश से अधिक न हो। इस अंश को कार्यकारी प्रतिबल कहते हैं। त्रोटन प्रतिबल और कार्यकारी प्रतिबल के अनुपात को सुरक्षा गुणक कहा जाता है।
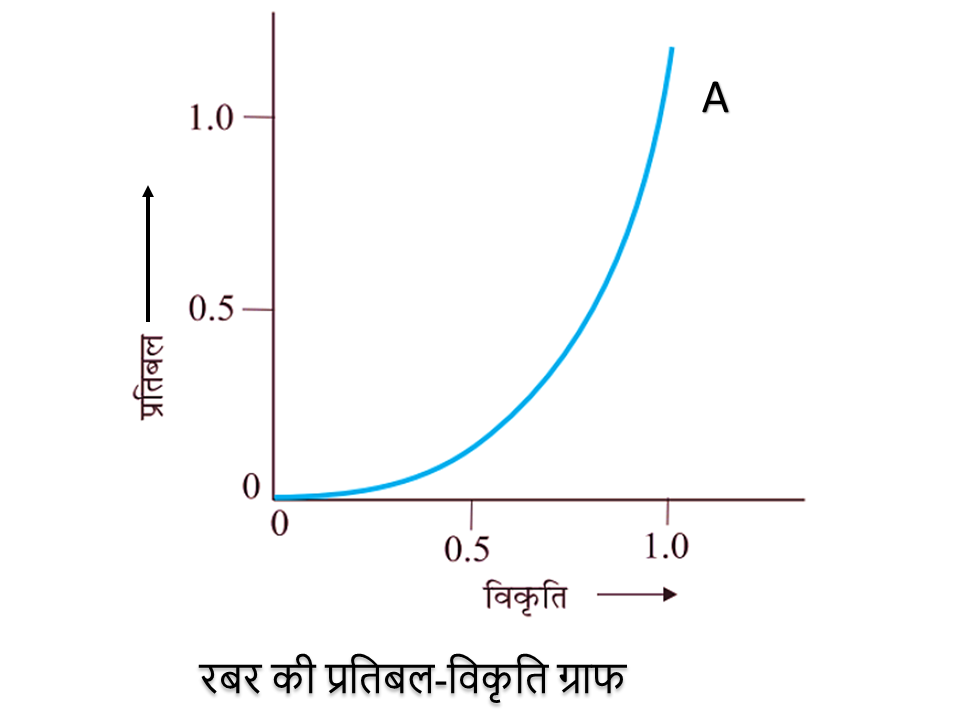
- रबर में एक विशेष गुण होता है। इसकी लम्बाई में बार-बार वृद्धि करने पर भी बल हटाने पर वह अपनी प्रारंभिक स्थिति में आ जाता है।
- रबर की प्लास्टिक सीमा नहीं होती अर्थात् निश्चित सीमा तक खींचने पर वह टूट जाता है।रबर के लिये प्रतिबल विकृति वक्र चित्र में प्रदर्शित किया गया है।
- जिससे यह स्पष्ट है कि रबर की प्रत्यास्थता सीमा बहुत अधिक होती है। परन्तु वह हुक नियम का पालन नहीं करती, क्योंकि OA सरल रेखा न होकर वक्राकार है।
- रबर के समान ऐसे पदार्थ जो अधिक सीमा तक खींचे जा सकते हैं इलेस्टोमर कहलाते हैं।
प्रतिबल-विकृति ग्राफ
हुक के नियम के अनुसार किसी वस्तु में उत्पन्न प्रतिबल विकृति के समानुपाती होता है, परन्तु यह नियम केवल प्रत्यास्थता की सीमा में लघु विकृतियों के लिये सत्य होता है।
यदि किसी एकसमान परिच्छेद वाले तार को एक दृढ़ आधार से कसकर उसके मुक्त सिरे पर भार लटकाया जाये तथा उसमें क्रमशः वृद्धि की जाये, तो तार की लम्बाई में क्रमशः वृद्धि होती जाती है।
अतः यदि तार में उत्पन्न प्रतिबल तथा विकृति के मध्य ग्राफ खींचा जाये तो प्राप्त वक्र चित्र के जैसा होता है।

ग्राफ का वर्णन :
- ग्राफ का प्रथम भाग OA एक सीधी रेखा है, जिससे यह स्पष्ट होता है कि बिन्दु A तक तार की लम्बाई में वृद्धि उस पर लटकाये गये द्रव्यमान के अनुक्रमानुपाती होती है। अर्थात् इस भाग में हुक का नियम लागू होता है।
- बिन्दु A पर प्रतिबल के मान को आनुपातिक सीमा कहते हैं। बिन्दु A से आगे का भाग वक्रीय होता है, जिससे यह स्पष्ट होता है कि अब तार पर भार बढ़ाने से तार की लम्बाई में वृद्धि भार के अनुक्रमानुपाती न होकर, उससे अधिक होती है तथा बिन्दु B तक प्रत्यास्थता का गुण बना रहता है।
- अतः बिन्दु B तक यदि तार से भार हटा लिया जाये तो तार अपनी पूर्वावस्था में आ जाता है। बिन्दु B के संगत प्रतिबल के मान को प्रत्यास्थता की सीमा कहते हैं।
- बिन्दु B से आगे तार पर लटके द्रव्यमान में वृद्धि करने पर उसकी लम्बाई में तेजी से वृद्धि होती है तथा बिन्दु B को पराभव बिन्दु कहते हैं, संगत प्रतिबल के मान को पराभव सामर्थ्य कहते हैं।
- इसके पश्चात् प्रतिबल और बढ़ाने पर प्रत्यास्थ व्यवहार समाप्त होकर प्लास्टिक आचरण आरंभ हो जाता है तथा बिन्दु C इस प्रकार प्राप्त होता है कि बल हटा लेने पर तार की लम्बाई में स्थायी वृद्धि हो जाती है अर्थात् भार हटा लेने पर वक्र CBAO पथ का अनुसरण न कर CO' का अनुसरण करता है। अर्थात् शून्य भार में स्थायी विकृति OO' उत्पन्न हो जाता है।
- अब यदि भार में और वृद्धि की जाये तो लम्बाई में वृद्धि और अधिक तेजी से होती है तथा अधिकतम प्रतिबल वाले बिन्दु D तक पहुँच जाता है।
- इस बिन्दु पर तार पतला होना आरंभ हो जाता है। इस बिन्दु को पराभव बिन्दु कहते हैं तथा भार में कमी करने पर भी तार पतला होता रहता है अर्थात् तार का पदार्थ एक श्यान तरल की भाँति व्यवहार करता है तथा बिन्दु E तक पहुँच कर टूट जाता है। इस बिन्दु को त्रोटन बिन्दु कहते हैं तथा इसके संगत भार को त्रोटन भार कहते हैं।
- उस अधिकतम प्रतिबल को जिसे कोई तार टूटने से पहले तक सहन कर सकता है, भंजन प्रतिबल कहते हैं तथा ग्राफ के बिन्दु B से E तक के क्षेत्र को प्लास्टिक क्षेत्र कहते हैं।
रबर की प्रतिबल-विकृति ग्राफ :
इंजीनियरिंग संरचना का डिजाइन करते समय यह ध्यान रखते हैं कि अधिकतम प्रतिबल, त्रोटन प्रतिबल के एक निश्चित अंश से अधिक न हो। इस अंश को कार्यकारी प्रतिबल कहते हैं। त्रोटन प्रतिबल और कार्यकारी प्रतिबल के अनुपात को सुरक्षा गुणक कहा जाता है।

- रबर में एक विशेष गुण होता है। इसकी लम्बाई में बार-बार वृद्धि करने पर भी बल हटाने पर वह अपनी प्रारंभिक स्थिति में आ जाता है।
- रबर की प्लास्टिक सीमा नहीं होती अर्थात् निश्चित सीमा तक खींचने पर वह टूट जाता है।रबर के लिये प्रतिबल विकृति वक्र चित्र में प्रदर्शित किया गया है।
- जिससे यह स्पष्ट है कि रबर की प्रत्यास्थता सीमा बहुत अधिक होती है। परन्तु वह हुक नियम का पालन नहीं करती, क्योंकि OA सरल रेखा न होकर वक्राकार है।
- रबर के समान ऐसे पदार्थ जो अधिक सीमा तक खींचे जा सकते हैं इलेस्टोमर कहलाते हैं।
उदाहरण 1
समान पदार्थ के दो तारों की त्रिज्याओं का अनुपात 2 : 1 है।
प्रतिबल =
⇒
उदाहरण 1
समान पदार्थ के दो तारों की त्रिज्याओं का अनुपात 2 : 1 है।
प्रतिबल =
⇒
उदाहरण 2
A अनुप्रस्थ काट क्षेत्रफल वाली एक छड़ के सिरों पर समान तथा विपरीत तनन बल F लगाया जाता है। छड़ से होकर गुजर रहे एक तल पर विचार कीजिये जो छड़ की लम्बाई के लम्बवत् तल के साथ θ कोण बनाता है।
(a) F, A तथा θ के पदों में इस तल पर तनन प्रतिबल क्या है ?
(b) F, A तथा θ के पदों में इस तल पर अपरूपण प्रतिबल क्या है ?
तनन प्रतिबल =
यहाँ AN = क्षेत्रफल =(Acosθ)
तथा अभिलम्ब बल FN=Fcosθ
अतः तनन प्रतिबल =Fcosθ(Acosθ)
⇒Fcos2θA
(b) अपरूपण प्रतिबल = (स्पर्श रेखीय बल/क्षेत्रफल)
यहाँ AN= क्षेत्रफल तथा स्पर्श रेखीय बल =Fsinθ
अतः अपरूपण प्रतिबल =Fcosθ(Acosθ)
=FsinθcosθA=Fsin2θ2A
उदाहरण 2
A अनुप्रस्थ काट क्षेत्रफल वाली एक छड़ के सिरों पर समान तथा विपरीत तनन बल F लगाया जाता है। छड़ से होकर गुजर रहे एक तल पर विचार कीजिये जो छड़ की लम्बाई के लम्बवत् तल के साथ θ कोण बनाता है।
(a) F, A तथा θ के पदों में इस तल पर तनन प्रतिबल क्या है ?
(b) F, A तथा θ के पदों में इस तल पर अपरूपण प्रतिबल क्या है ?
तनन प्रतिबल =
यहाँ AN = क्षेत्रफल =(Acosθ)
तथा अभिलम्ब बल FN=Fcosθ
अतः तनन प्रतिबल =Fcosθ(Acosθ)
⇒Fcos2θA
(b) अपरूपण प्रतिबल = (स्पर्श रेखीय बल/क्षेत्रफल)
यहाँ AN= क्षेत्रफल तथा स्पर्श रेखीय बल =Fsinθ
अतः अपरूपण प्रतिबल =Fcosθ(Acosθ)
=FsinθcosθA=Fsin2θ2A
उदाहरण 3
1m लम्बी एवं 2 mm त्रिज्या की एक तार के ऊपरी सिरे को कसा गया है। निचले सिरे को 45° के कोण से घुमाया जाता है तो अपरूपण कोण होगा?
ϕ=rtθ=2×10−31×45∘=0.09∘
उदाहरण 3
1m लम्बी एवं 2 mm त्रिज्या की एक तार के ऊपरी सिरे को कसा गया है। निचले सिरे को 45° के कोण से घुमाया जाता है तो अपरूपण कोण होगा?
ϕ=rtθ=2×10−31×45∘=0.09∘
उदाहरण 4
दो पदार्थों A व B के प्रतिबल और विकृति के मध्य ग्राफ चित्र में दिखाया गया है। निम्न बिन्दु समझाइए।
(a) किस पदार्थ के लिये या प्रत्यास्थता गुणांक का मान अधिक है।
(b) इन दोनों पदार्थों में से कौनसा पदार्थ अधिक तन्य (dictile) है।
(c ) इन दोनों पदार्थो में से कौनसा पदार्थ अधिक भंगुर है
(d) इन पदार्थों में कौनसा अधिक मजबूत है। अपने उत्तरों के कारण भी लिखिए।
पदार्थ A का यंग प्रत्यास्थता गुणांक अधिक है। क्योंकि A का ढाल B से अधिक है।
पदार्थ अधिक तन्य होगा यदि इसके भंजन बिन्दु तथा प्रत्यास्थ सीमा के मध्य प्लास्टिक परास अधिक होती है। अत: पदार्थ A पदार्थ B की तुलना में अधिक तन्य हैं।
पदार्थ भंगुर होगा यदि प्रत्यास्थ सीमा एवं भंजन प्रतिबल के मध्य प्लास्टिक परास अल्प हो। अत: पदार्थ B अधिक भंगुर होगा।
किसी तार के भंजन के लिए जितने अधिक प्रतिबल की आवश्यकता होगी उतना ही वह तार अधिक मजबूत होगा। अत: तार A , तार B की तुलना में अधिक मजबूत है।
उदाहरण 4
दो पदार्थों A व B के प्रतिबल और विकृति के मध्य ग्राफ चित्र में दिखाया गया है। निम्न बिन्दु समझाइए।
(a) किस पदार्थ के लिये या प्रत्यास्थता गुणांक का मान अधिक है।
(b) इन दोनों पदार्थों में से कौनसा पदार्थ अधिक तन्य (dictile) है।
(c ) इन दोनों पदार्थो में से कौनसा पदार्थ अधिक भंगुर है
(d) इन पदार्थों में कौनसा अधिक मजबूत है। अपने उत्तरों के कारण भी लिखिए।
पदार्थ A का यंग प्रत्यास्थता गुणांक अधिक है। क्योंकि A का ढाल B से अधिक है।
पदार्थ अधिक तन्य होगा यदि इसके भंजन बिन्दु तथा प्रत्यास्थ सीमा के मध्य प्लास्टिक परास अधिक होती है। अत: पदार्थ A पदार्थ B की तुलना में अधिक तन्य हैं।
पदार्थ भंगुर होगा यदि प्रत्यास्थ सीमा एवं भंजन प्रतिबल के मध्य प्लास्टिक परास अल्प हो। अत: पदार्थ B अधिक भंगुर होगा।
किसी तार के भंजन के लिए जितने अधिक प्रतिबल की आवश्यकता होगी उतना ही वह तार अधिक मजबूत होगा। अत: तार A , तार B की तुलना में अधिक मजबूत है।
उदाहरण 5
10kg की एक वस्तु को 30 cm लम्बे तार से जोड़ा गया है इसका भंजन प्रतिबल 4.8×107N/m2 है। तार के अनुप्रस्थ काट का क्षेत्रफल 10−6m2 है। भंजन के लिए आवश्यक कोणीय वेग ज्ञात कीजिए।
mω2lA = भंजन प्रतिबल
⇒ω=√(BS)Aml
=√4.8×107×10−610×.03=4rad/s
उदाहरण 5
10kg की एक वस्तु को 30 cm लम्बे तार से जोड़ा गया है इसका भंजन प्रतिबल 4.8×107N/m2 है। तार के अनुप्रस्थ काट का क्षेत्रफल 10−6m2 है। भंजन के लिए आवश्यक कोणीय वेग ज्ञात कीजिए।
mω2lA = भंजन प्रतिबल
⇒ω=√(BS)Aml
=√4.8×107×10−610×.03=4rad/s
उदाहरण 6
एल्युमिनियम का भंजन प्रतिबल 7.5×108dyne/cm2 है उर्ध्वाधर तार की अधिकतम लम्बाई जो अपने भार से उर्ध्वाधर बिना टूटे लटकाया जा सके। (एल्युमिनियम का घनत्व =2.7g/cm3 तथा g=980cm/s2 )
मानाकि l तार की अधिकतम लम्बाई है जो उर्ध्वाधर बिना टूटे लटका सकते है।
द्रव्यमान (m) = अनुप्रस्थकाट क्षेत्रफल (A) × लम्बाई (l) × धनत्व (ρ)
तार का भार =mg=Alρg यह अधिकतम बल है जिस पर तार स्थिर है।
∴ भंजन प्रतिबल =lAρgA=lρg
या 7.5×108=l×2.7×980
या l=7.5×1082.7×980
⇒2.834×105cm=2.83km
उदाहरण 6
एल्युमिनियम का भंजन प्रतिबल 7.5×108dyne/cm2 है उर्ध्वाधर तार की अधिकतम लम्बाई जो अपने भार से उर्ध्वाधर बिना टूटे लटकाया जा सके। (एल्युमिनियम का घनत्व =2.7g/cm3 तथा g=980cm/s2 )
मानाकि l तार की अधिकतम लम्बाई है जो उर्ध्वाधर बिना टूटे लटका सकते है।
द्रव्यमान (m) = अनुप्रस्थकाट क्षेत्रफल (A) × लम्बाई (l) × धनत्व (ρ)
तार का भार =mg=Alρg यह अधिकतम बल है जिस पर तार स्थिर है।
∴ भंजन प्रतिबल =lAρgA=lρg
या 7.5×108=l×2.7×980
या l=7.5×1082.7×980
⇒2.834×105cm=2.83km
प्रत्यास्थता गुणांक
हुक के नियमानुसार, प्रत्यास्थता सीमा के अंतर्गत किसी वस्तु पर लगने वाला प्रतिबल उसमें उत्पन्न विकृति के अनुक्रमानुपाती होता है। अर्थात्
प्रतिबल =E× विकृति
या
जहाँ E एक नियतांक है, जिसे वस्तु की प्रत्यास्थता गुणांक या प्रत्यास्थता स्थिरांक कहते है। यह वस्तु की प्रकृति पर निर्भर करता है। अर्थात् अलग-अलग वस्तुओं का प्रत्यास्थता गुणांक अलग-अलग होता है।
अतः प्रत्यास्थता गुणांक = प्रतिबल/विकृति
अर्थात् प्रत्यास्थता सीमा के अंतर्गत किसी वस्तु पर लगने वाला प्रतिबल तथा उसमे उत्पन्न विकृति के अनुपात को वस्तु का प्रत्यास्थता गुणांक कहते है। इसे E से व्यक्त करते है।
प्रत्यास्थता गुणांक का मात्रक :
प्रत्यास्थता गुणांक प्रतिबल तथा विकृति का अनुपात होता है तथा विकृति का कोई मात्रक नहीं होता है।
अतः प्रत्यास्थता गुणांक का मात्रक वही होता है, हो प्रतिबल का होता है। अर्थात् S.I. पद्धति में इसका मात्रक न्यूटन/ मीटर2 एवं C.G.S. पद्धति में डाईन/सेमी2 होता है।
प्रत्यास्थता गुणांक का विमीय सूत्र :-
[E]=[ML−1T−2M0L0T0]
[E]=ML−1T−2
प्रत्यास्थता गुणांक के प्रकार :
प्रत्यास्थता गुणांक प्रतिबल और विकृति का अनुपात होता है। वस्तुओं में विकृति तीन प्रकार की होती है, इसी आधार पर प्रत्यास्थता गुणांक भी निम्न तीन प्रकार के होते हैं :-
- यंग प्रत्यास्थता गुणांक या यंग मापांक :- यदि किसी वस्तु पर बाह्य विरूपक बल लगाने से उसमें अनुदैर्ध्य विकृति उत्पन्न होती है, तो प्रत्यास्थता गुणांक यंग मापांक कहलाता है।
- आयतन प्रत्यास्थता गुणांक :- यदि किसी वस्तु पर बाह्य विरूपक बल लगाने से उसमें आयतन विकृति उत्पन्न होती है, तो आयतन प्रत्यास्थता गुणांक कहलाता है।
- दृढ़ता गुणांक :- यदि किसी वस्तु पर बाह्य विरूपक बल लगाने से उसमें यदि अपरूपण विकृति उत्पन्न होती है, तो दृढ़ता गुणांक कहलाता है।
प्रत्यास्थता गुणांक
हुक के नियमानुसार, प्रत्यास्थता सीमा के अंतर्गत किसी वस्तु पर लगने वाला प्रतिबल उसमें उत्पन्न विकृति के अनुक्रमानुपाती होता है। अर्थात्
प्रतिबल =E× विकृति
या
जहाँ E एक नियतांक है, जिसे वस्तु की प्रत्यास्थता गुणांक या प्रत्यास्थता स्थिरांक कहते है। यह वस्तु की प्रकृति पर निर्भर करता है। अर्थात् अलग-अलग वस्तुओं का प्रत्यास्थता गुणांक अलग-अलग होता है।
अतः प्रत्यास्थता गुणांक = प्रतिबल/विकृति
अर्थात् प्रत्यास्थता सीमा के अंतर्गत किसी वस्तु पर लगने वाला प्रतिबल तथा उसमे उत्पन्न विकृति के अनुपात को वस्तु का प्रत्यास्थता गुणांक कहते है। इसे E से व्यक्त करते है।
प्रत्यास्थता गुणांक का मात्रक :
प्रत्यास्थता गुणांक प्रतिबल तथा विकृति का अनुपात होता है तथा विकृति का कोई मात्रक नहीं होता है।
अतः प्रत्यास्थता गुणांक का मात्रक वही होता है, हो प्रतिबल का होता है। अर्थात् S.I. पद्धति में इसका मात्रक न्यूटन/ मीटर2 एवं C.G.S. पद्धति में डाईन/सेमी2 होता है।
प्रत्यास्थता गुणांक का विमीय सूत्र :-
[E]=[ML−1T−2M0L0T0]
[E]=ML−1T−2
प्रत्यास्थता गुणांक के प्रकार :
प्रत्यास्थता गुणांक प्रतिबल और विकृति का अनुपात होता है। वस्तुओं में विकृति तीन प्रकार की होती है, इसी आधार पर प्रत्यास्थता गुणांक भी निम्न तीन प्रकार के होते हैं :-
- यंग प्रत्यास्थता गुणांक या यंग मापांक :- यदि किसी वस्तु पर बाह्य विरूपक बल लगाने से उसमें अनुदैर्ध्य विकृति उत्पन्न होती है, तो प्रत्यास्थता गुणांक यंग मापांक कहलाता है।
- आयतन प्रत्यास्थता गुणांक :- यदि किसी वस्तु पर बाह्य विरूपक बल लगाने से उसमें आयतन विकृति उत्पन्न होती है, तो आयतन प्रत्यास्थता गुणांक कहलाता है।
- दृढ़ता गुणांक :- यदि किसी वस्तु पर बाह्य विरूपक बल लगाने से उसमें यदि अपरूपण विकृति उत्पन्न होती है, तो दृढ़ता गुणांक कहलाता है।
यंग प्रत्यास्थता गुणांक
प्रत्यास्थता सीमा के अन्तर्गत किसी वस्तु में अनुदैर्ध्य प्रतिबल तथा उत्पन्न अनुदैर्ध्य विकृति के अनुपात को उस वस्तु की यंग प्रत्यास्थता गुणांक या यंग मापांक कहते हैं। इसे Y से व्यक्त करते हैं।
अर्थात्
अब यदि किसी तार की प्रारंभिक लम्बाई L तथा अनुप्रस्थ काट का क्षेत्रफल A है। उसके एक सिरे को दृंढ आधार से कसकर दूसरे सिरे पर लम्बाई की दिशा में F बल आरोपित करने से लम्बाई में वृद्धि l होती है।
एवं अनुदैर्ध्य विकृति =lL
अतः समीकरण (2) में इन मानों को रखने पर,
यही तार के पदार्थ के यंग प्रत्यास्थता गुणांक का सूत्र है, जिससे यह स्पष्ट है की यदि A=1 मात्रक तथा l=L हो, तो समीकरण (3) से,
अर्थात् "किसी पदार्थ का यंग प्रत्यास्थता गुणांक का आंकिक मान उस बल के बराबर होता है, जो उस पदार्थ के एकांक अनुप्रस्थ काट वाले तार की लम्बाई को दुगुना कर दे, जबकि यह परिवर्तन प्रत्यास्थता की सीमा में हों।"
मात्रक : पद्धति में यंग प्रत्यास्थता गुणांक का मात्रक न्यूटन/मीटर2 (Nm2) तथा C.G.S. पद्धति में डाइन/सेमी2 होता है।
विमीय सूत्र :
Y=MLT−2LL2L
Y=[ML−1T−2]
यंग प्रत्यास्थता गुणांक
प्रत्यास्थता सीमा के अन्तर्गत किसी वस्तु में अनुदैर्ध्य प्रतिबल तथा उत्पन्न अनुदैर्ध्य विकृति के अनुपात को उस वस्तु की यंग प्रत्यास्थता गुणांक या यंग मापांक कहते हैं। इसे Y से व्यक्त करते हैं।
अर्थात्
अब यदि किसी तार की प्रारंभिक लम्बाई L तथा अनुप्रस्थ काट का क्षेत्रफल A है। उसके एक सिरे को दृंढ आधार से कसकर दूसरे सिरे पर लम्बाई की दिशा में F बल आरोपित करने से लम्बाई में वृद्धि l होती है।
एवं अनुदैर्ध्य विकृति =lL
अतः समीकरण (2) में इन मानों को रखने पर,
यही तार के पदार्थ के यंग प्रत्यास्थता गुणांक का सूत्र है, जिससे यह स्पष्ट है की यदि A=1 मात्रक तथा l=L हो, तो समीकरण (3) से,
अर्थात् "किसी पदार्थ का यंग प्रत्यास्थता गुणांक का आंकिक मान उस बल के बराबर होता है, जो उस पदार्थ के एकांक अनुप्रस्थ काट वाले तार की लम्बाई को दुगुना कर दे, जबकि यह परिवर्तन प्रत्यास्थता की सीमा में हों।"
मात्रक : पद्धति में यंग प्रत्यास्थता गुणांक का मात्रक न्यूटन/मीटर2 (Nm2) तथा C.G.S. पद्धति में डाइन/सेमी2 होता है।
विमीय सूत्र :
Y=MLT−2LL2L
Y=[ML−1T−2]
किसी तार के द्रव्य के यंग गुणांक का मापन
तनाव के अंतर्गत किसी तार के द्रव्य के यंग गुणांक का मापन करने के लिए एक प्रारूपिक प्रायोगिक व्यवस्था नीचे चित्र में दिखाई गई है।
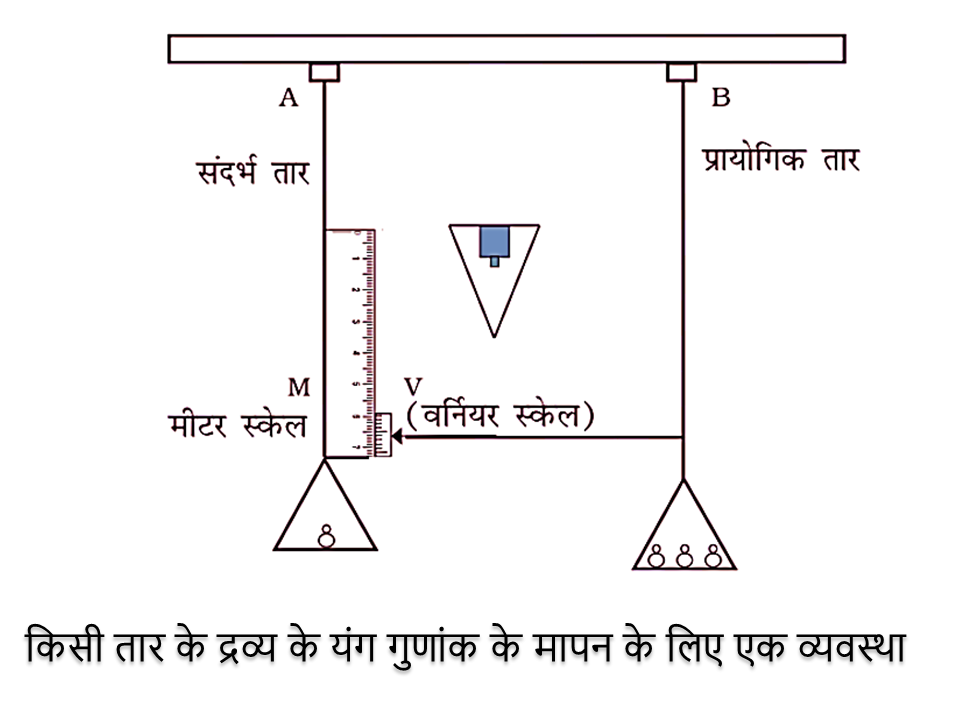
प्रायोगिक व्यवस्था :
- इस प्रयोग में दो लंबे सीधे तार, जिनकी लंबाई तथा त्रिज्या बराबर हों, किसी स्थिर दृढ़ आधार से अगल-बगल लटके होते हैं। तार A संदर्भ तार कहलाता है।
- इसमें मिलीमीटर की एक मुख्य स्केल M तथा एक भार रखने के लिए एक पलड़ा लगा होता है। तार B प्रायोगिक तार कहलाता है इसमें समान अनुप्रस्थ परिच्छेद का होता है और इसमें भी एक पलड़ा लगा होता है जिसमें ज्ञात भारों को रखा जा सकता है।
- प्रायोगिक तार B की तली पर एक संकेतक में एक वर्नियर स्केल V जोड़ दिया जाता है तथा मुख्य स्केल M संदर्भ तार A से जोड़ा जाता है। पलड़े में रखे भार नीचे की ओर एक बल लगाते हैं और प्रायोगिक तार को तनक प्रतिबल के अंतर्गत विस्तारित कर देते हैं।
- तार में विस्तार (लंबाई में वृद्धि) को वर्नियर व्यवस्था से नाप लिया जाता है।
प्रायोगिक व्याख्या :
- कमरे के ताप में अंतर के कारण होने वाली लंबाई में किसी परिवर्तन की प्रतिपूर्ति करने के लिए संदर्भ तार का इस्तेमाल किया जाता है क्योंकि प्रायोगिक तार की लंबाई में ताप के कारण किसी परिवर्तन के साथ-साथ संदर्भ तार की लम्बाई में भी उतना ही परिवर्तन होगा।
- आरंभ में संदर्भ तथा प्रायोगिक, दोनों तारों पर एक छोटा-सा भार रख देते हैं ताकि तार सीधे रहें और फिर वर्नियर का पाठ्यांक नोट कर लेते हैं।
- अब प्रायोगिक तार को तनक प्रतिबल के अंतर्गत लाने के लिए उस पर धीरे-धीरे और भार चढ़ाते जाते हैं तथा वर्नियर का पाठ्यांक नोट करते जाते हैं।
- दो वर्नियर पाठ्यांकों में अंतर तार में उत्पन्न विस्तार बताता है।
मान लें कि प्रायोगिक तार की प्रारंभिक त्रिज्या तथा लंबाई क्रमशः r तथा L है तो तार के अनुप्रस्थ परिच्छेद का क्षेत्रफल πr2 होगा।
मान लें कि द्रव्यमान M से तार में उत्पन्न विस्तार ΔL है। इस प्रकार, प्रत्यारोपित बल Mg के बराबर हुआ, जहाँ g गुरुत्वीय त्वरण है।
हम जानते है प्रायोगिक तार के द्रव्य का यंग गुणांक-
Y=Mgπr2×LΔL
Y=Mg×Lπr2×ΔL
किसी तार के द्रव्य के यंग गुणांक का मापन
तनाव के अंतर्गत किसी तार के द्रव्य के यंग गुणांक का मापन करने के लिए एक प्रारूपिक प्रायोगिक व्यवस्था नीचे चित्र में दिखाई गई है।

प्रायोगिक व्यवस्था :
- इस प्रयोग में दो लंबे सीधे तार, जिनकी लंबाई तथा त्रिज्या बराबर हों, किसी स्थिर दृढ़ आधार से अगल-बगल लटके होते हैं। तार A संदर्भ तार कहलाता है।
- इसमें मिलीमीटर की एक मुख्य स्केल M तथा एक भार रखने के लिए एक पलड़ा लगा होता है। तार B प्रायोगिक तार कहलाता है इसमें समान अनुप्रस्थ परिच्छेद का होता है और इसमें भी एक पलड़ा लगा होता है जिसमें ज्ञात भारों को रखा जा सकता है।
- प्रायोगिक तार B की तली पर एक संकेतक में एक वर्नियर स्केल V जोड़ दिया जाता है तथा मुख्य स्केल M संदर्भ तार A से जोड़ा जाता है। पलड़े में रखे भार नीचे की ओर एक बल लगाते हैं और प्रायोगिक तार को तनक प्रतिबल के अंतर्गत विस्तारित कर देते हैं।
- तार में विस्तार (लंबाई में वृद्धि) को वर्नियर व्यवस्था से नाप लिया जाता है।
प्रायोगिक व्याख्या :
- कमरे के ताप में अंतर के कारण होने वाली लंबाई में किसी परिवर्तन की प्रतिपूर्ति करने के लिए संदर्भ तार का इस्तेमाल किया जाता है क्योंकि प्रायोगिक तार की लंबाई में ताप के कारण किसी परिवर्तन के साथ-साथ संदर्भ तार की लम्बाई में भी उतना ही परिवर्तन होगा।
- आरंभ में संदर्भ तथा प्रायोगिक, दोनों तारों पर एक छोटा-सा भार रख देते हैं ताकि तार सीधे रहें और फिर वर्नियर का पाठ्यांक नोट कर लेते हैं।
- अब प्रायोगिक तार को तनक प्रतिबल के अंतर्गत लाने के लिए उस पर धीरे-धीरे और भार चढ़ाते जाते हैं तथा वर्नियर का पाठ्यांक नोट करते जाते हैं।
- दो वर्नियर पाठ्यांकों में अंतर तार में उत्पन्न विस्तार बताता है।
मान लें कि प्रायोगिक तार की प्रारंभिक त्रिज्या तथा लंबाई क्रमशः r तथा L है तो तार के अनुप्रस्थ परिच्छेद का क्षेत्रफल πr2 होगा।
मान लें कि द्रव्यमान M से तार में उत्पन्न विस्तार ΔL है। इस प्रकार, प्रत्यारोपित बल Mg के बराबर हुआ, जहाँ g गुरुत्वीय त्वरण है।
हम जानते है प्रायोगिक तार के द्रव्य का यंग गुणांक-
Y=Mgπr2×LΔL
Y=Mg×Lπr2×ΔL
अपरूपण गुणांक
प्रत्यास्थता की सीमा के अन्दर किसी वस्तु के स्पर्शीय प्रतिबल तथा अपरूपक विकृति के अनुपात को उस वस्तु के पदार्थ का अपरूपण गुणांक या दृढ़ता प्रत्यास्थता गुणांक कहते है। इसे G से प्रदर्शित किया जाता है।
माना एक A क्षेत्रफल की वस्तु है जिस पर F मान का स्पर्श रेखीय बल आरोपित किया जा रहा है जिसके कारण इस वस्तु में θ अपरूपक विकृति उत्पन्न हो जाती है।
अपरूपक विकृति =θ
परिभाषा से,
अपरूपण गुणांक = स्पर्शीय प्रतिबल / अपरूपक विकृति
G=FA×θ
अपरूपक प्रतिबल σs को ऐसे भी व्यक्त किया जा सकता है-
अपरूपण गुणांक का SI मात्रक Nm−2 या Pa होता है। इसका विमा [ML−1T−2] होती है।
अपरूपण गुणांक
प्रत्यास्थता की सीमा के अन्दर किसी वस्तु के स्पर्शीय प्रतिबल तथा अपरूपक विकृति के अनुपात को उस वस्तु के पदार्थ का अपरूपण गुणांक या दृढ़ता प्रत्यास्थता गुणांक कहते है। इसे G से प्रदर्शित किया जाता है।
माना एक A क्षेत्रफल की वस्तु है जिस पर F मान का स्पर्श रेखीय बल आरोपित किया जा रहा है जिसके कारण इस वस्तु में θ अपरूपक विकृति उत्पन्न हो जाती है।
अपरूपक विकृति =θ
परिभाषा से,
अपरूपण गुणांक = स्पर्शीय प्रतिबल / अपरूपक विकृति
G=FA×θ
अपरूपक प्रतिबल σs को ऐसे भी व्यक्त किया जा सकता है-
अपरूपण गुणांक का SI मात्रक Nm−2 या Pa होता है। इसका विमा [ML−1T−2] होती है।
आयतन गुणांक
प्रत्यास्थता सीमा के भीतर, किसी वस्तु के अभिलम्ब प्रतिबल और आयतन विकृति के अनुपात को उस वस्तु के पदार्थ का आयतन प्रत्यास्थता गुणांक कहते है, इसे B या K द्वारा प्रदर्शित किया जाता है।
माना किसी वस्तु का आयतन V है तथा इसका अनुप्रस्थ क्षेत्रफल A है, इस वस्तु पर F मान का अभिलम्ब बल आरोपित किया जाता है इस बल के कारण वस्तु के आयतन में ΔV परिवर्तन आ जाता है। अतः
आयतन विकृति =ΔVV
आयतन प्रत्यास्थता गुणांक की परिभाषा से अभिलम्ब प्रतिबल तथा आयतन विकृति के अनुपात को आयतन प्रत्यास्थता गुणांक कहा जाता है। अतः
आयतन प्रत्यास्थता गुणांक (B) = अभिलम्ब प्रतिबल / आयतन विकृति
B=F.VA.ΔV
आयतन प्रत्यास्थता गुणांक का मात्रक Nm−2 होता है। इसका विमीय सूत्र [ML−1T−2] होती है।
आयतन गुणांक
प्रत्यास्थता सीमा के भीतर, किसी वस्तु के अभिलम्ब प्रतिबल और आयतन विकृति के अनुपात को उस वस्तु के पदार्थ का आयतन प्रत्यास्थता गुणांक कहते है, इसे B या K द्वारा प्रदर्शित किया जाता है।
माना किसी वस्तु का आयतन V है तथा इसका अनुप्रस्थ क्षेत्रफल A है, इस वस्तु पर F मान का अभिलम्ब बल आरोपित किया जाता है इस बल के कारण वस्तु के आयतन में ΔV परिवर्तन आ जाता है। अतः
आयतन विकृति =ΔVV
आयतन प्रत्यास्थता गुणांक की परिभाषा से अभिलम्ब प्रतिबल तथा आयतन विकृति के अनुपात को आयतन प्रत्यास्थता गुणांक कहा जाता है। अतः
आयतन प्रत्यास्थता गुणांक (B) = अभिलम्ब प्रतिबल / आयतन विकृति
B=F.VA.ΔV
आयतन प्रत्यास्थता गुणांक का मात्रक Nm−2 होता है। इसका विमीय सूत्र [ML−1T−2] होती है।
प्रतिबल, विकृति तथा विभिन्न प्रत्यास्थ गुणांक सारणी
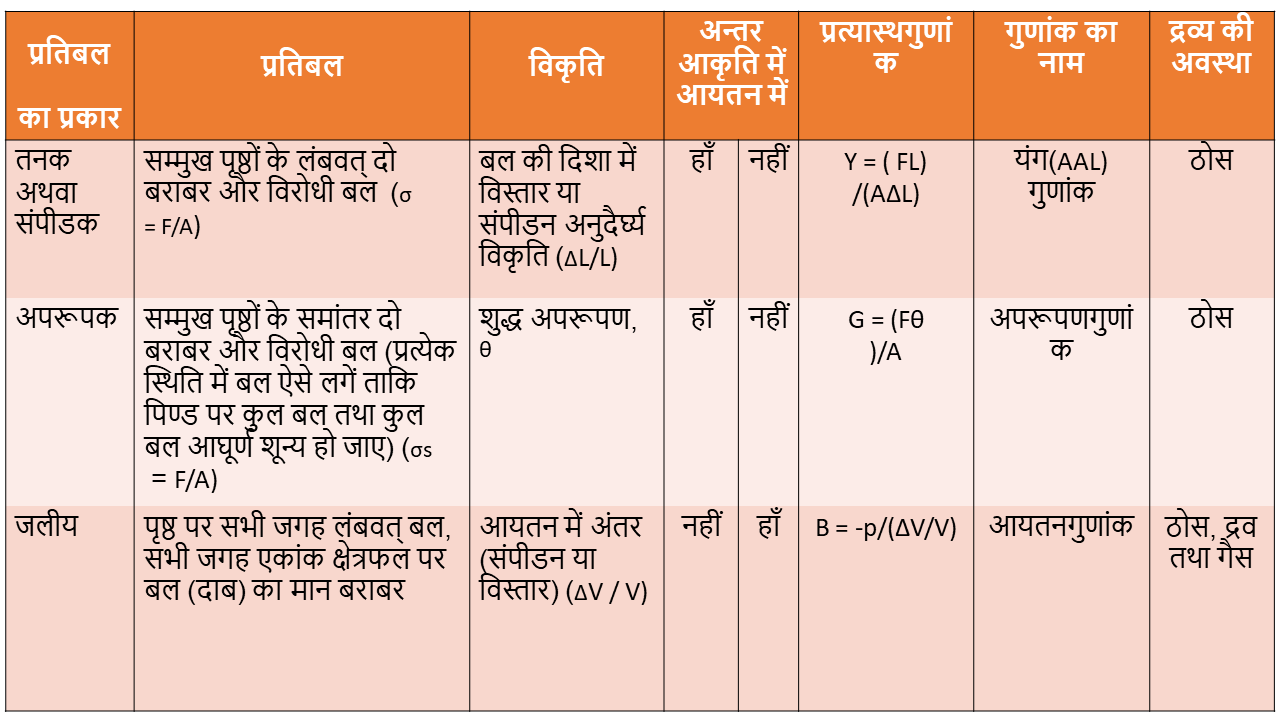
प्रतिबल, विकृति तथा विभिन्न प्रत्यास्थ गुणांक सारणी

पॉइसन अनुपात
प्रत्यास्थता सीमा के अंतर्गत किसी वस्तु में उत्पन्न अनुप्रस्थ विकृति तथा अनुदैर्ध्य विकृति के अनुपात को उस वस्तु की पॉइसन निष्पत्ति कहते हैं। इसे σ से व्यक्त करते है। अतः
जब किसी वस्तु पर तनाव बल लगाकर उसकी लम्बाई में वृद्धि की जाती है तो उसके अनुप्रस्थ परिच्छेद में कमी हो जाती है। अर्थात् लम्बाई में वृद्धि के कारण अनुदैर्ध्य विकृति उत्पन्न होती है तथा अनुप्रस्थ परिच्छेद में कमी के कारण अनुप्रस्थ या अभिलम्ब विकृति उत्पन्न होती है।
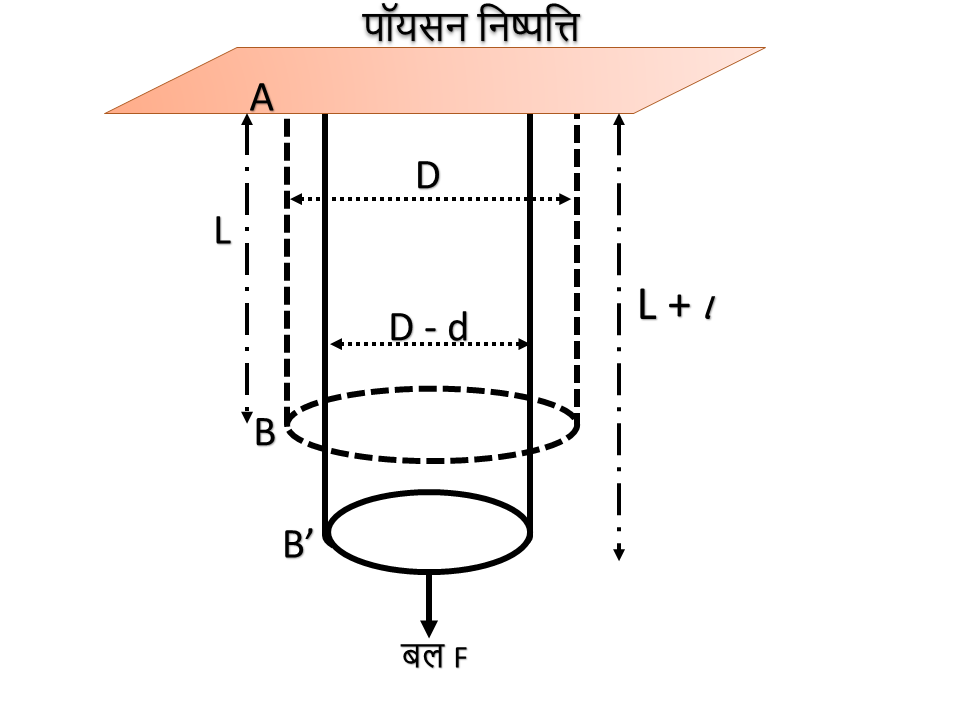
एवं अनुदैर्ध्य विकृति =lL
समीकरण (4) में इन मानों को रखने पर,
σ=−dLDl ......(5)
यही किसी वस्तु के पॉइसन निष्पत्ति का सूत्र है जहाँ ऋण चिन्ह यह प्रदर्शित करता है कि लम्बाई तथा व्यास में एक-दूसरे के विपरीत परिवर्तन होता है।
मात्रक एवं विमीय सूत्र :
पॉइसन निष्पत्ति दो विकृतियों का अनुपात है। अतः इसका कोई मात्रक नहीं होता। इसी प्रकार यह एक विमाहीन राशि है। अतः इसका विमीय सूत्र [M0L0T0] होगा।
पॉइसन अनुपात
प्रत्यास्थता सीमा के अंतर्गत किसी वस्तु में उत्पन्न अनुप्रस्थ विकृति तथा अनुदैर्ध्य विकृति के अनुपात को उस वस्तु की पॉइसन निष्पत्ति कहते हैं। इसे σ से व्यक्त करते है। अतः
जब किसी वस्तु पर तनाव बल लगाकर उसकी लम्बाई में वृद्धि की जाती है तो उसके अनुप्रस्थ परिच्छेद में कमी हो जाती है। अर्थात् लम्बाई में वृद्धि के कारण अनुदैर्ध्य विकृति उत्पन्न होती है तथा अनुप्रस्थ परिच्छेद में कमी के कारण अनुप्रस्थ या अभिलम्ब विकृति उत्पन्न होती है।

एवं अनुदैर्ध्य विकृति =lL
समीकरण (4) में इन मानों को रखने पर,
σ=−dLDl ......(5)
यही किसी वस्तु के पॉइसन निष्पत्ति का सूत्र है जहाँ ऋण चिन्ह यह प्रदर्शित करता है कि लम्बाई तथा व्यास में एक-दूसरे के विपरीत परिवर्तन होता है।
मात्रक एवं विमीय सूत्र :
पॉइसन निष्पत्ति दो विकृतियों का अनुपात है। अतः इसका कोई मात्रक नहीं होता। इसी प्रकार यह एक विमाहीन राशि है। अतः इसका विमीय सूत्र [M0L0T0] होगा।
स्वयं के भार के कारण तार की लम्बाई में वृद्धि
माना कि M द्रव्यमान तथा L लम्बाई की रस्सी को उर्ध्वाधर लटकाया गया है। चूंकि रस्सी के भिन्न-भिन्न बिन्दुओं पर तनाव भी भिन्न-भिन्न होगा। इसलिये भिन्न-भिन्न बिन्दुओं पर प्रतिबल के साथ विकृति भी भिन्न-भिन्न होगी।
- निलम्बन बिन्दु पर अधिकतम प्रतिबल होगा।
- निम्नतम बिन्दु पर न्यूनतम प्रतिबल होगा।
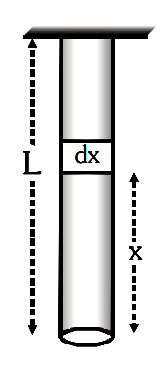
माना कि निचले सिरे से x दूरी पर एक dx भाग है तो तनाव
T=(ML)×xg
- इसलिये प्रतिबल= TA=(ML)xgA
- विकृति = dydx
Y = (प्रतिबल)/(विकृति) = MLxgAdydx
(ML)xgAdx=Ydy
रस्सी की पूर्ण लम्बाई के लिये(ML)xgAdx=Ydy
MgLA∫L0xdx=Y∫△l0dy
याMgLAL22=Y△l
याΔl=MgL2AY
स्वयं के भार के कारण तार की लम्बाई में वृद्धि
माना कि M द्रव्यमान तथा L लम्बाई की रस्सी को उर्ध्वाधर लटकाया गया है। चूंकि रस्सी के भिन्न-भिन्न बिन्दुओं पर तनाव भी भिन्न-भिन्न होगा। इसलिये भिन्न-भिन्न बिन्दुओं पर प्रतिबल के साथ विकृति भी भिन्न-भिन्न होगी।
- निलम्बन बिन्दु पर अधिकतम प्रतिबल होगा।
- निम्नतम बिन्दु पर न्यूनतम प्रतिबल होगा।

माना कि निचले सिरे से x दूरी पर एक dx भाग है तो तनाव
T=(ML)×xg
- इसलिये प्रतिबल= TA=(ML)xgA
- विकृति = dydx
Y = (प्रतिबल)/(विकृति) = MLxgAdydx
(ML)xgAdx=Ydy
रस्सी की पूर्ण लम्बाई के लिये(ML)xgAdx=Ydy
MgLA∫L0xdx=Y∫△l0dy
याMgLAL22=Y△l
याΔl=MgL2AY
खींचे हुए तार की स्थितिज ऊर्जा
जब एक तार को खींचते हैं तो अन्तराणविक बलों के विरूद्ध कार्य किया जाता है जो प्रत्यास्थ स्थितिज ऊर्जा के रूप संग्रहित हो जाता है।
Lo लम्बाई के तार को x दूरी खींचने पर प्रत्यास्थ प्रत्यानयन बल :
- F= प्रतिबल × क्षेत्रफल = Y[xLo]A
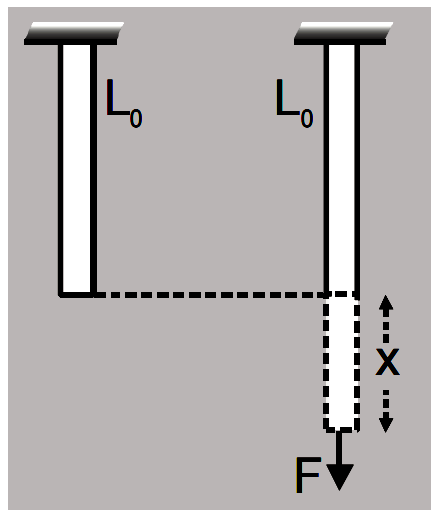
अब तार को dx दूरी खींचने पर प्रत्यास्थ प्रत्यानयन बलों के विरूद्ध किया गया कार्य
dW=Fdx=YALoxdx
तार को x=0 से x=△l तक खींचने में किया गया कुल कार्यW=∫△l0YALoxdx=YALo[x22]△l0
तथा W=YA(△l)22Lo=12×Y×(△lL0)2AL0
यही किया गया कार्य खींचे हुए तार की स्थितिज ऊर्जा होगी अर्थातU=12×Y×(△lL0)2AL0
खींचे हुए तार की स्थितिज ऊर्जा
जब एक तार को खींचते हैं तो अन्तराणविक बलों के विरूद्ध कार्य किया जाता है जो प्रत्यास्थ स्थितिज ऊर्जा के रूप संग्रहित हो जाता है।
Lo लम्बाई के तार को x दूरी खींचने पर प्रत्यास्थ प्रत्यानयन बल :
- F= प्रतिबल × क्षेत्रफल = Y[xLo]A

अब तार को dx दूरी खींचने पर प्रत्यास्थ प्रत्यानयन बलों के विरूद्ध किया गया कार्य
dW=Fdx=YALoxdx
तार को x=0 से x=△l तक खींचने में किया गया कुल कार्यW=∫△l0YALoxdx=YALo[x22]△l0
तथा W=YA(△l)22Lo=12×Y×(△lL0)2AL0
यही किया गया कार्य खींचे हुए तार की स्थितिज ऊर्जा होगी अर्थातU=12×Y×(△lL0)2AL0
प्रत्यास्थता को प्रभावित करने वाले कारक
प्रत्यास्थता पर ताप का प्रभाव :
जब ताप बढ़ाया जाता है तो अन्तराण्विक बल के कमजोर होने के कारण प्रत्यास्थता का गुण सामान्यत: कम होता जाता है, अत: प्रत्यास्थता गुणांक घटता है। प्लास्टिकता ताप के साथ बढ़ती है। विशेष प्रकार के स्टील के लिये प्रत्यास्थता गुणांक ताप के साथ परिवर्तित नहीं होता है। यह 'INVAR STEEL' कहलाता है।
प्रत्यास्थता पर अशुद्धि का प्रभाव :
अशुद्धि मिलाने पर Y थोड़ा सा बढ़ जाता है। अशुद्धि मिलाने से तार के अन्दर प्रभावी रूप से अन्तर आण्विक आकर्षण बल बढ़ जाता है। इसलिए बाह्य बल का आसानी से विरोध किया जा सकता है।
अन्तरपरमाणुक बल नियतांक :
Y = यंग प्रत्यास्थता गुणांक ; r0 = अन्तरपरमाणुक दूरी सामान्य परिस्थितियों में।
महत्वपूर्ण बिंदु :
- ठोसों के लिए K का मान अधिकतम एवं गैसों के लिये न्यूनतम होता है।
- आयतन प्रत्यास्थता गुणांक सर्वप्रथम मैक्सवेल ने दिया।
- आदर्श दृढ़ वस्तु के लिये तीनों प्रत्यास्थता गुणांक का मान अनन्त होगा। दृढ़ता गुणांक (G) ठोस पदार्थ का गुण है क्योंकि तरल की कोई निश्चित आकृति नहीं होती है।
- तार को खींचने में किया गया यह कार्य तार में प्रत्यास्थ स्थितिज ऊर्जा के रूप में संचित होता है
- प्रत्यास्थ स्थितिज ऊर्जा घनत्व U=WV= 1/2 (प्रतिबल x विकृति)
- स्थितिज ऊर्जा घनत्व = प्रतिबल विकृत वक्र के अन्दर का क्षेत्रफल
- यंग प्रत्यास्थता गुणांक = प्रतिबल विकृति वक्र का ढाल
प्रत्यास्थता को प्रभावित करने वाले कारक
प्रत्यास्थता पर ताप का प्रभाव :
जब ताप बढ़ाया जाता है तो अन्तराण्विक बल के कमजोर होने के कारण प्रत्यास्थता का गुण सामान्यत: कम होता जाता है, अत: प्रत्यास्थता गुणांक घटता है। प्लास्टिकता ताप के साथ बढ़ती है। विशेष प्रकार के स्टील के लिये प्रत्यास्थता गुणांक ताप के साथ परिवर्तित नहीं होता है। यह 'INVAR STEEL' कहलाता है।
प्रत्यास्थता पर अशुद्धि का प्रभाव :
अशुद्धि मिलाने पर Y थोड़ा सा बढ़ जाता है। अशुद्धि मिलाने से तार के अन्दर प्रभावी रूप से अन्तर आण्विक आकर्षण बल बढ़ जाता है। इसलिए बाह्य बल का आसानी से विरोध किया जा सकता है।
अन्तरपरमाणुक बल नियतांक :
Y = यंग प्रत्यास्थता गुणांक ; r0 = अन्तरपरमाणुक दूरी सामान्य परिस्थितियों में।
महत्वपूर्ण बिंदु :
- ठोसों के लिए K का मान अधिकतम एवं गैसों के लिये न्यूनतम होता है।
- आयतन प्रत्यास्थता गुणांक सर्वप्रथम मैक्सवेल ने दिया।
- आदर्श दृढ़ वस्तु के लिये तीनों प्रत्यास्थता गुणांक का मान अनन्त होगा। दृढ़ता गुणांक (G) ठोस पदार्थ का गुण है क्योंकि तरल की कोई निश्चित आकृति नहीं होती है।
- तार को खींचने में किया गया यह कार्य तार में प्रत्यास्थ स्थितिज ऊर्जा के रूप में संचित होता है
- प्रत्यास्थ स्थितिज ऊर्जा घनत्व U=WV= 1/2 (प्रतिबल x विकृति)
- स्थितिज ऊर्जा घनत्व = प्रतिबल विकृत वक्र के अन्दर का क्षेत्रफल
- यंग प्रत्यास्थता गुणांक = प्रतिबल विकृति वक्र का ढाल
उदाहरण 7
दो तार समान धातु के बने हैं। पहले तार की लम्बाई दूसरे तार की आधी है और इसका व्यास दूसरे तार का दुगना है। यदि दोनों तारों को समान भार से भारित किया गया है तो उनकी लम्बाई में वृद्धि का अनुपात की गणना कीजिये।
Y=FAΔll
⇒Δl=FlAY=Flπr2Y
Δl1Δl2=4Fl1πd21Y×πd22Y4Fl2
l1l2×d22d21=12×1(2)2=18
उदाहरण 7
दो तार समान धातु के बने हैं। पहले तार की लम्बाई दूसरे तार की आधी है और इसका व्यास दूसरे तार का दुगना है। यदि दोनों तारों को समान भार से भारित किया गया है तो उनकी लम्बाई में वृद्धि का अनुपात की गणना कीजिये।
Y=FAΔll
⇒Δl=FlAY=Flπr2Y
Δl1Δl2=4Fl1πd21Y×πd22Y4Fl2
l1l2×d22d21=12×1(2)2=18
उदाहरण 8
0.25 cm व्यास के दो तारों, जिनमें एक स्टील का और दूसरा पीतल का है, को भार बांधकर चित्र में दर्शाए अनुसार लटकाया गया है। बिना भार लटकाए स्टील तथा ताँबे के तारों की लम्बाईयाँ क्रमश: 1.5m व 1.0 m है
2.0×1011Pa
व 0.91×1011Pa है
( 1Pa−1N/m2 )
स्टील के तार की लम्बाई मे वृद्धि
ΔlS=MglSπr2YS
=(4+6)×9.8×1.53.14×(0.125×10−2)2×2×1011
=1.49×10−4m
पीतल के तार की लम्बाई में वृद्धि
Δlb=MglSπr2YS
=(4+6)×9.8×1.53.14×(0.125×10−2)2×0.91×1011
=1.31×10−4m
उदाहरण 8
0.25 cm व्यास के दो तारों, जिनमें एक स्टील का और दूसरा पीतल का है, को भार बांधकर चित्र में दर्शाए अनुसार लटकाया गया है। बिना भार लटकाए स्टील तथा ताँबे के तारों की लम्बाईयाँ क्रमश: 1.5m व 1.0 m है
2.0×1011Pa
व 0.91×1011Pa है
( 1Pa−1N/m2 )
स्टील के तार की लम्बाई मे वृद्धि
ΔlS=MglSπr2YS
=(4+6)×9.8×1.53.14×(0.125×10−2)2×2×1011
=1.49×10−4m
पीतल के तार की लम्बाई में वृद्धि
Δlb=MglSπr2YS
=(4+6)×9.8×1.53.14×(0.125×10−2)2×0.91×1011
=1.31×10−4m
उदाहरण 9
एक नगण्य द्रव्यमान की 1 m लम्बी तथा 10−6m अनुप्रस्थ काट के क्षेत्रफल की ताँबे के तार के एक सिरे को एक चिकनी क्षैतिज मेज से दृढ़ता पूर्वक जोड़ा जाता है। दूसरे सिरे से 1kg द्रव्यमान की गेंद जुड़ी है। तार तथा गेंद दोनों 20 rad/s के कोणीय वेग से घूम रहे हैं। यदि तार की लम्बाई में वृद्धि 103 मी. हो तो ताँबे का यंग का प्रत्यास्थता गुणांक ज्ञात कीजिए?
∴ अभिकेन्द्रीय बल F=mω2r
∴ तार में प्रतिबल =FA=mω2rA,
तार में विकृति =Δll
यंग प्रत्यास्थता गुणांक Y=
=1×(20)2×(1)210−6×10−3=4×1011N/m2
उदाहरण 9
एक नगण्य द्रव्यमान की 1 m लम्बी तथा 10−6m अनुप्रस्थ काट के क्षेत्रफल की ताँबे के तार के एक सिरे को एक चिकनी क्षैतिज मेज से दृढ़ता पूर्वक जोड़ा जाता है। दूसरे सिरे से 1kg द्रव्यमान की गेंद जुड़ी है। तार तथा गेंद दोनों 20 rad/s के कोणीय वेग से घूम रहे हैं। यदि तार की लम्बाई में वृद्धि 103 मी. हो तो ताँबे का यंग का प्रत्यास्थता गुणांक ज्ञात कीजिए?
∴ अभिकेन्द्रीय बल F=mω2r
∴ तार में प्रतिबल =FA=mω2rA,
तार में विकृति =Δll
यंग प्रत्यास्थता गुणांक Y=
=1×(20)2×(1)210−6×10−3=4×1011N/m2
उदाहरण 10
3.0 m लम्बे तार की लम्बाई में कितनी वृद्धि होगी। यदि इसके एक सिरे पर 10 kg भार को लटकाया जाये एवं दूसरे सिरा स्थिर हो। , तार का व्यास 0.4 mm है। (ताँब Y=1011N/m2,g=9.8m/s2 )
Δl=F×lπr2×Y
=98×3×722×(0.2×10−3)2×1011
=98×2188×103=2.339cm
उदाहरण 10
3.0 m लम्बे तार की लम्बाई में कितनी वृद्धि होगी। यदि इसके एक सिरे पर 10 kg भार को लटकाया जाये एवं दूसरे सिरा स्थिर हो। , तार का व्यास 0.4 mm है। (ताँब Y=1011N/m2,g=9.8m/s2 )
Δl=F×lπr2×Y
=98×3×722×(0.2×10−3)2×1011
=98×2188×103=2.339cm
उदाहरण 11
10−6m2 अनुप्रस्थकाट क्षेत्रफल के एक स्टील के तार की लम्बाई को 0.5% बढ़ाने में आवश्यक बल ज्ञात करो? (दिया है स्टील के लिए Y=2×1011N/m2 )
lL×100=0.5%⇒lL=5×10−3
अतः F=YAlL
=2×1011×10−6×5×10−3=103N
उदाहरण 11
10−6m2 अनुप्रस्थकाट क्षेत्रफल के एक स्टील के तार की लम्बाई को 0.5% बढ़ाने में आवश्यक बल ज्ञात करो? (दिया है स्टील के लिए Y=2×1011N/m2 )
lL×100=0.5%⇒lL=5×10−3
अतः F=YAlL
=2×1011×10−6×5×10−3=103N
उदाहरण 12
1m लम्बे तार में विस्तार को ग्राफ में प्रदर्शित किया गया है जिसका एक सिरा छत के शीर्ष से लटका है तथा दूसरे सिरे पर W भार लटकाया गया है। यदि तार का अनुप्रस्थ काट क्षेत्रफल 1mm2 है ,तार के यंग मापांक की गणना करें:
Y=F/AΔl/l=WlAΔl
⇒WΔl=YAl=slope
⇒Y=lA(slope)
=110−6(40−20(2−1)×10−3)=2×1010N/m2
उदाहरण 12
1m लम्बे तार में विस्तार को ग्राफ में प्रदर्शित किया गया है जिसका एक सिरा छत के शीर्ष से लटका है तथा दूसरे सिरे पर W भार लटकाया गया है। यदि तार का अनुप्रस्थ काट क्षेत्रफल 1mm2 है ,तार के यंग मापांक की गणना करें:
Y=F/AΔl/l=WlAΔl
⇒WΔl=YAl=slope
⇒Y=lA(slope)
=110−6(40−20(2−1)×10−3)=2×1010N/m2
उदाहरण 13
एक रबर की रस्सी की लम्बाई 8m अपने स्वयं के वजन के कारण इसकी लंबाई में वृद्धि होगी ? (दिया है : रबर का यंग प्रत्यास्थता गुणांक =5×106N/m2 और घनत्व=1.5×103Kg/m3 तथा g=10m/s2 )
Δl=ρgl22Y
=1.5×103×10×8×82×5×106
=9.6×10−2m
=9.6×10−2×103mm=96mm
उदाहरण 13
एक रबर की रस्सी की लम्बाई 8m अपने स्वयं के वजन के कारण इसकी लंबाई में वृद्धि होगी ? (दिया है : रबर का यंग प्रत्यास्थता गुणांक =5×106N/m2 और घनत्व=1.5×103Kg/m3 तथा g=10m/s2 )
Δl=ρgl22Y
=1.5×103×10×8×82×5×106
=9.6×10−2m
=9.6×10−2×103mm=96mm
उदाहरण 14
यदि एक गोले को 1 km गहराई पर स्थित समुद्र तल पर ले जाया जाए तो उसके आयतन में 0.01% की कमी हो जाती है। गोले के पदार्थ का आयतन प्रत्यास्थता गुणांक ज्ञात कीजिए। (g=980cm/s2)
|ΔV|V=0.01100,
h=1km=105cm,
ρ=1g/cm3,
ΔP=hρg=105×1×980dyne/cm2
K=ΔP|ΔV|/V
=ΔP×V|ΔV|
=10×5×980×1000.01dyne/cm−2
=9.8×1011dyne/cm2
उदाहरण 14
यदि एक गोले को 1 km गहराई पर स्थित समुद्र तल पर ले जाया जाए तो उसके आयतन में 0.01% की कमी हो जाती है। गोले के पदार्थ का आयतन प्रत्यास्थता गुणांक ज्ञात कीजिए। (g=980cm/s2)
|ΔV|V=0.01100,
h=1km=105cm,
ρ=1g/cm3,
ΔP=hρg=105×1×980dyne/cm2
K=ΔP|ΔV|/V
=ΔP×V|ΔV|
=10×5×980×1000.01dyne/cm−2
=9.8×1011dyne/cm2
उदाहरण 15
रबर की डोरी का अनुप्रस्थ काट क्षेत्रफल 1mm2 तथा बिना खींची लम्बाई 10 cm है 12 cm तक खीचने के पश्चात मुक्त कर के 5 ग्राम द्रव्यमान प्रक्षेपित किया जाता है। रबर के लिये यंग प्रत्यास्थता गुणांक 5×108N/m2 है। डोरी का वेग ज्ञात कीजिये।
डोरी में तनाव
=YALΔl
=5×108×1×10−6×2×10−210×10−2=100N
जब द्रव्यमान को छोड़ा जाता है तो संचित प्रत्यास्थ ऊर्जा = द्रव्यमान की गतिज ऊर्जा
⇒12F×Δl=12mv2
v=√F×Δlm
=√100×2×10−25×10−3=20m/s
उदाहरण 15
रबर की डोरी का अनुप्रस्थ काट क्षेत्रफल 1mm2 तथा बिना खींची लम्बाई 10 cm है 12 cm तक खीचने के पश्चात मुक्त कर के 5 ग्राम द्रव्यमान प्रक्षेपित किया जाता है। रबर के लिये यंग प्रत्यास्थता गुणांक 5×108N/m2 है। डोरी का वेग ज्ञात कीजिये।
डोरी में तनाव
=YALΔl
=5×108×1×10−6×2×10−210×10−2=100N
जब द्रव्यमान को छोड़ा जाता है तो संचित प्रत्यास्थ ऊर्जा = द्रव्यमान की गतिज ऊर्जा
⇒12F×Δl=12mv2
v=√F×Δlm
=√100×2×10−25×10−3=20m/s
उदाहरण 16
इस्पात के लिए यंग प्रत्यास्थता गुणांक 2×1011N/m2 है।अन्तरापरमाणुक दुरी 3.2∘A हो तो अन्तरापरमाणुक बल का मान होगा।
k=Y×r0
=2×1011×3.2×10−10=64N/m
उदाहरण 16
इस्पात के लिए यंग प्रत्यास्थता गुणांक 2×1011N/m2 है।अन्तरापरमाणुक दुरी 3.2∘A हो तो अन्तरापरमाणुक बल का मान होगा।
k=Y×r0
=2×1011×3.2×10−10=64N/m