ध्वनि तरंगे कक्षा 11 भौतिकी
भूमिका
पिछले अध्याय में हमने अनुप्रस्थ तरंगे, प्रगामी तरंगों में विस्थापन, तरंगों के अध्यारोपण का सिद्धांत, तथा तरंगों का परावर्तन के बारे में अध्ययन किया है। इस अध्याय में हम ध्वनि तरंगोंं के विषय में अध्ययन करेंगे और हम अनुदैर्ध्य तरंगे, आर्गन पाइप, ध्वनि तरंगों में विस्पंद के बारे में अध्ययन करेंगे।
अध्याय के अंत में ध्वनि तरंगों के डॉप्लर प्रभाव के बारे में जानेंगे।
भूमिका
पिछले अध्याय में हमने अनुप्रस्थ तरंगे, प्रगामी तरंगों में विस्थापन, तरंगों के अध्यारोपण का सिद्धांत, तथा तरंगों का परावर्तन के बारे में अध्ययन किया है। इस अध्याय में हम ध्वनि तरंगोंं के विषय में अध्ययन करेंगे और हम अनुदैर्ध्य तरंगे, आर्गन पाइप, ध्वनि तरंगों में विस्पंद के बारे में अध्ययन करेंगे।
अध्याय के अंत में ध्वनि तरंगों के डॉप्लर प्रभाव के बारे में जानेंगे।
अनुदैर्ध्य तरंगोंं की चाल
जब किसी माध्यम में अनुदैर्ध्य तरंग गमन करती है तो माध्यम के कण तरंग संचरण की दिशा में ही आगे-पीछे कम्पन्न करते हैं। फलस्वरूप माध्यम के दाब और घनत्व में परिवर्तन हो जाता है। दाब परिवर्तन का सम्बन्ध माध्यम की प्रत्यास्थता से होता है। किसी माध्यम में अनुदैर्ध्य तरंगोंं की चाल निम्न सूत्र से दी जाती है -
v=√Eρ
जहाँ E माध्यम की प्रत्यास्थता तथा d घनत्व है।ठोसों में अनुदैर्ध्य तरंगोंं की चाल :
ठोसों के लिये प्रत्यास्थता गुणांक E के स्थान पर यंग प्रत्यास्थता गुणांक Y लिखते हैं। अत: किसी ठोस में अनुदैर्ध्य तरंगोंं की चाल
v=√Yρ
द्रवों में अनुदैर्ध्य तरंगोंं की चाल :
द्रवों में अनुदैर्ध्य तरंगोंं की चाल निम्न सूत्र द्वारा दी जाती है-
v=√Kρ
जहाँ K द्रव का आयतन प्रत्यास्थता गुणांक तथा ρ घनत्व है।गैसों में ध्वनि की चाल के लिए न्यूटन का सूत्र :
गैसीय माध्यम में ध्वनि की चाल निम्न सूत्र द्वारा दी जाती है -
v=√Pρ
जहाँ P गैसीय माध्यम का प्रत्यास्थता गुणांक तथा ρ घनत्व है।N.T.P. पर वायु में ध्वनि की चाल की गणना :
P=hdg=0.76×13.6×103×9.8 न्यूटन/मीटर2 तथा ρ=1.293 किग्रा/मीटर3 समीकरण में मान रखने पर,
v=√0.76×13.6×103×9.81.293
v=280 मीटर/सेकण्ड
किन्तु N.T.P. पर वायु में ध्वनि की चाल का प्रायोगिक मान 332 मीटर/सेकण्ड प्राप्त होता है।v=280 मीटर/सेकण्ड
अनुदैर्ध्य तरंगोंं की चाल
जब किसी माध्यम में अनुदैर्ध्य तरंग गमन करती है तो माध्यम के कण तरंग संचरण की दिशा में ही आगे-पीछे कम्पन्न करते हैं। फलस्वरूप माध्यम के दाब और घनत्व में परिवर्तन हो जाता है। दाब परिवर्तन का सम्बन्ध माध्यम की प्रत्यास्थता से होता है। किसी माध्यम में अनुदैर्ध्य तरंगोंं की चाल निम्न सूत्र से दी जाती है -
v=√Eρ
जहाँ E माध्यम की प्रत्यास्थता तथा d घनत्व है।ठोसों में अनुदैर्ध्य तरंगोंं की चाल :
ठोसों के लिये प्रत्यास्थता गुणांक E के स्थान पर यंग प्रत्यास्थता गुणांक Y लिखते हैं। अत: किसी ठोस में अनुदैर्ध्य तरंगोंं की चाल
v=√Yρ
द्रवों में अनुदैर्ध्य तरंगोंं की चाल :
द्रवों में अनुदैर्ध्य तरंगोंं की चाल निम्न सूत्र द्वारा दी जाती है-
v=√Kρ
जहाँ K द्रव का आयतन प्रत्यास्थता गुणांक तथा ρ घनत्व है।गैसों में ध्वनि की चाल के लिए न्यूटन का सूत्र :
गैसीय माध्यम में ध्वनि की चाल निम्न सूत्र द्वारा दी जाती है -
v=√Pρ
जहाँ P गैसीय माध्यम का प्रत्यास्थता गुणांक तथा ρ घनत्व है।N.T.P. पर वायु में ध्वनि की चाल की गणना :
P=hdg=0.76×13.6×103×9.8 न्यूटन/मीटर2 तथा ρ=1.293 किग्रा/मीटर3 समीकरण में मान रखने पर,
v=√0.76×13.6×103×9.81.293
v=280 मीटर/सेकण्ड
किन्तु N.T.P. पर वायु में ध्वनि की चाल का प्रायोगिक मान 332 मीटर/सेकण्ड प्राप्त होता है।v=280 मीटर/सेकण्ड
लाप्लास संशोधन
ध्वनि के वेग के सैद्धान्तिक तथा प्रायोगिक मानो के मध्य अन्तर को हटाने के लिए लाप्लास ने न्यूटन के सूत्र को संशोधित किया। उन्होने माना कि ध्वनि का वायु में संचरण रुद्वोष्म प्रक्रम होता है अत: रुद्धोष्म प्रक्रम का प्रत्यास्थता गुणांक = γP अत:
v=√γPρ=√1.41×279=331.3ms
(चूँकि γ=1.41) जो कि वायु में ध्वनि के प्रायोगिक मान (332ms) के लगभग समान है। जिससे यह सिद्ध होता है कि गैसों में रुद्धोष्म रूप से संचरित होती है।NTP पर वायु में ध्वनि का वेग 332ms होता है इससे यह निष्कर्ष निकलता है कि :-
- यदि किसी दूरी पर स्थित सायरन से हम अपनी घड़ी को मिलाए तो यह वास्तविक समय से पीछे हो जाएगी।
- यदि हम किसी स्पर्धा में प्रारम्भ बिन्दु से ध्वनि सुनकर समय का आंकलन करे तो यह वास्तविक से कम होगा।
- बादलों में बिजली चमकने पर प्रकाश और ध्वनि का साथ साथ उत्पन्न होते है परन्तु c>v तो प्रकाश, आवाज (ध्वनि) से पहले आयेगा।
लाप्लास संशोधन
ध्वनि के वेग के सैद्धान्तिक तथा प्रायोगिक मानो के मध्य अन्तर को हटाने के लिए लाप्लास ने न्यूटन के सूत्र को संशोधित किया। उन्होने माना कि ध्वनि का वायु में संचरण रुद्वोष्म प्रक्रम होता है अत: रुद्धोष्म प्रक्रम का प्रत्यास्थता गुणांक = γP अत:
v=√γPρ=√1.41×279=331.3ms
(चूँकि γ=1.41) जो कि वायु में ध्वनि के प्रायोगिक मान (332ms) के लगभग समान है। जिससे यह सिद्ध होता है कि गैसों में रुद्धोष्म रूप से संचरित होती है।NTP पर वायु में ध्वनि का वेग 332ms होता है इससे यह निष्कर्ष निकलता है कि :-
- यदि किसी दूरी पर स्थित सायरन से हम अपनी घड़ी को मिलाए तो यह वास्तविक समय से पीछे हो जाएगी।
- यदि हम किसी स्पर्धा में प्रारम्भ बिन्दु से ध्वनि सुनकर समय का आंकलन करे तो यह वास्तविक से कम होगा।
- बादलों में बिजली चमकने पर प्रकाश और ध्वनि का साथ साथ उत्पन्न होते है परन्तु c>v तो प्रकाश, आवाज (ध्वनि) से पहले आयेगा।
विभिन्न तथ्यों का प्रभाव
(1) ताप का प्रभाव :
किसी गैसीय माध्यम में ध्वनि की चाल का सूत्र है -
v=√γPρ
आदर्श गैस समीकरण से
PV=RT⇒P=RTV
मान रखने पर,
v=√γRTρ×V
याv=√γRTM
जहाँ M=d×V = गैस का अणुभारकिसी गैस के लिए γ,R और M नियत राशि हैं।
v∝√T ......(1)
अत: किसी गैस में ध्वनि की चाल परम ताप के वर्गमूल के अनुक्रमानुपाती होती है। सम्बन्ध (1) से
vtv0=√TtT0=√273+t273+0
या द्विपद प्रमेय से लगभगvt=v0(1+t273)12=v0(1+1546t)
याvt=v0+v0546t
v0=332 मीटर/सेकण्ड रखने पर,vt=v0+332546t
याvt=v0+0.61t मीटर/सेकण्ड
अतः गैस के ताप में 1°C की वृद्धि होने पर ध्वनि की चाल 0.61 मीटर/सेकण्ड बढ़ जाती है।(2) आर्द्रता का प्रभाव :
आर्द्रता को बढ़ाने पर घनत्व कम होता है तो सूत्र v=√γPρ से निष्कर्ष निकाल सकते है कि आर्द्रता बढ़ाने पर ध्वनि का वेग बढ़ता है।
इसलिए समान ताप पर आर्द्र वायु में ध्वनि की चाल शुष्क वायु की अपेक्षा थोड़ी बढ़ जाती है। इसी कारण वर्षा ऋतु में कल-कारखानों के सायरन तथा रेल की सीटियाँ ग्रीष्म ऋतु की अपेक्षा अधिक सुनाई पड़ती है।
(3) वायु की गति का प्रभाव :
यदि वायु चल रही है तो ध्वनि की चाल भी बदल जाती है। यदि ध्वनि की वास्तविक चाल v है तथा वायु की चाल u है तब
- वायु की दिशा में ध्वनि की चाल (v+u) होगी तथा
- वायु के चलने की विपरीत दिशा में यह (v−u) होगी।
विभिन्न तथ्यों का प्रभाव
(1) ताप का प्रभाव :
किसी गैसीय माध्यम में ध्वनि की चाल का सूत्र है -
v=√γPρ
आदर्श गैस समीकरण से
PV=RT⇒P=RTV
मान रखने पर,
v=√γRTρ×V
याv=√γRTM
जहाँ M=d×V = गैस का अणुभारकिसी गैस के लिए γ,R और M नियत राशि हैं।
v∝√T ......(1)
अत: किसी गैस में ध्वनि की चाल परम ताप के वर्गमूल के अनुक्रमानुपाती होती है। सम्बन्ध (1) से
vtv0=√TtT0=√273+t273+0
या द्विपद प्रमेय से लगभगvt=v0(1+t273)12=v0(1+1546t)
याvt=v0+v0546t
v0=332 मीटर/सेकण्ड रखने पर,vt=v0+332546t
याvt=v0+0.61t मीटर/सेकण्ड
अतः गैस के ताप में 1°C की वृद्धि होने पर ध्वनि की चाल 0.61 मीटर/सेकण्ड बढ़ जाती है।(2) आर्द्रता का प्रभाव :
आर्द्रता को बढ़ाने पर घनत्व कम होता है तो सूत्र v=√γPρ से निष्कर्ष निकाल सकते है कि आर्द्रता बढ़ाने पर ध्वनि का वेग बढ़ता है।
इसलिए समान ताप पर आर्द्र वायु में ध्वनि की चाल शुष्क वायु की अपेक्षा थोड़ी बढ़ जाती है। इसी कारण वर्षा ऋतु में कल-कारखानों के सायरन तथा रेल की सीटियाँ ग्रीष्म ऋतु की अपेक्षा अधिक सुनाई पड़ती है।
(3) वायु की गति का प्रभाव :
यदि वायु चल रही है तो ध्वनि की चाल भी बदल जाती है। यदि ध्वनि की वास्तविक चाल v है तथा वायु की चाल u है तब
- वायु की दिशा में ध्वनि की चाल (v+u) होगी तथा
- वायु के चलने की विपरीत दिशा में यह (v−u) होगी।
उदाहरण 1
स्वरित्र जिसकी आवृत्ति n = 300 Hz है, 5 विस्पन्द/सेकण्ड उत्पन्न करता है। यदि ज्ञात स्वरित्र द्विभुज की भुजा पर अशुद्धि लगा दी जाये तो विस्पन्दों की संख्या घट जाती है तो अज्ञात स्वरित्र की आवृत्ति ज्ञात कीजिए।

उदाहरण 1
स्वरित्र जिसकी आवृत्ति n = 300 Hz है, 5 विस्पन्द/सेकण्ड उत्पन्न करता है। यदि ज्ञात स्वरित्र द्विभुज की भुजा पर अशुद्धि लगा दी जाये तो विस्पन्दों की संख्या घट जाती है तो अज्ञात स्वरित्र की आवृत्ति ज्ञात कीजिए।

उदाहरण 2
एक स्वरित्र द्विभुज जिसकी आवृत्ति n = 158Hz है 3 विस्पन्द/सेकण्ड उत्पन्न करता है यदि हम अज्ञात स्वरित्र को घिस दें तो विस्पन्दों की संख्या 7 हो जाती है तो अज्ञात स्वरित्र की आवृत्ति ज्ञात कीजिए?
घिसने से पहले विस्पंद 158±3 अत: 155 या 161
घिसने के बाद विस्पंद b = 7

उदाहरण 2
एक स्वरित्र द्विभुज जिसकी आवृत्ति n = 158Hz है 3 विस्पन्द/सेकण्ड उत्पन्न करता है यदि हम अज्ञात स्वरित्र को घिस दें तो विस्पन्दों की संख्या 7 हो जाती है तो अज्ञात स्वरित्र की आवृत्ति ज्ञात कीजिए?
घिसने से पहले विस्पंद 158±3 अत: 155 या 161
घिसने के बाद विस्पंद b = 7

उदाहरण 3
41 स्वरित्र द्विभुज श्रेणीक्रम में इस प्रकार व्यवस्थित है कि प्रत्येक स्वरित्र अपने पड़ोसी स्वरित्र से 3 विस्पन्द उत्पन्न करता है यदि अन्तिम स्वरित्र की आवृत्ति प्रथम स्वरित्र की आवृत्ति की तीन गुनी हो तो प्रथम, 11 वें, 16 वें, 21 वें तथा अन्तिम स्वरित्र की आवृत्तियाँ ज्ञात कीजिए?
n1=n (माना)
n2=n+b
n3=n+2b
n4=n+3b
............
............
n41=n+40b
अतः n41=3n (प्रश्नानुसार)
अतः n41=n+40×3
3n=n+120
n=60Hz
प्रथम स्वरित्र की आवृत्ति
n1=n=60Hz
11 वें स्वरित्र की आवृत्ति
n11=n+10b=90Hz,
16 वें स्वरित्र की आवृत्ति
n16=n+15b=105Hz,
21 वें स्वरित्र की आवृत्ति
n21=n+20b=120Hz,
41 वें स्वरित्र की आवृत्ति
n41=n+40b=180Hz
उदाहरण 3
41 स्वरित्र द्विभुज श्रेणीक्रम में इस प्रकार व्यवस्थित है कि प्रत्येक स्वरित्र अपने पड़ोसी स्वरित्र से 3 विस्पन्द उत्पन्न करता है यदि अन्तिम स्वरित्र की आवृत्ति प्रथम स्वरित्र की आवृत्ति की तीन गुनी हो तो प्रथम, 11 वें, 16 वें, 21 वें तथा अन्तिम स्वरित्र की आवृत्तियाँ ज्ञात कीजिए?
n1=n (माना)
n2=n+b
n3=n+2b
n4=n+3b
............
............
n41=n+40b
अतः n41=3n (प्रश्नानुसार)
अतः n41=n+40×3
3n=n+120
n=60Hz
प्रथम स्वरित्र की आवृत्ति
n1=n=60Hz
11 वें स्वरित्र की आवृत्ति
n11=n+10b=90Hz,
16 वें स्वरित्र की आवृत्ति
n16=n+15b=105Hz,
21 वें स्वरित्र की आवृत्ति
n21=n+20b=120Hz,
41 वें स्वरित्र की आवृत्ति
n41=n+40b=180Hz
उदाहरण 4
एक ही दिशा में गतिशील समान आवृत्ति n तथा आयाम A वाली तीन सरल आवर्ती तरंगें वायु में इस प्रकार से अध्यारोपित होती है कि अध्यारोपण में दिये गये बिन्दु P पर पहली, दूसरी तथा तीसरी तरंग के कला कोण क्रमश: ϕ,ϕ+π2 व (ϕ+π) प्राप्त होते हैं। अब जैसे ही तरंगें गति करती है तो अध्यारोपण के परिणामस्वरूप -
(1) आयाम 3A वाली आवर्ती, असरल आवर्त तरंग प्राप्त होती है।
(2) आयाम 3A वाली अप्रगामी सरल आवर्त तरंग प्राप्त होती है।
(3) आयाम A वाली सरल आवर्त प्रगामी तरंग प्राप्त होती है।
(4) अध्यारोपित परिणामी तरंग का वेग, प्रत्येक तरंग के वेग के समान प्राप्त होती है।
उत्तर (3, 4)
चूंकि एक ही दिशा में गतिशील पहली तरंग एवं तीसरी तरंग के कला कोण क्रमश: ϕ व (ϕ+π) है, वे कंपन माध्यम के प्रत्येक बिन्दु पर विपरीत कला में अध्यारोपित होती है तथा एक-दूसरे को निरस्त कर देती हैं (विस्थापन, वेग एवं त्वरण में), परिणाम स्वरूप ये तरंगे एक-दूसरे को नष्ट कर देती है।
अत: केवल दूसरी तरंग ही शेष बचती है जो कि A आयाम वाली सरल आवर्ती तरंग के रूप में प्राप्त होती है। परिणामी तरंग का वेग, प्रत्येक तरंग के वेग के समान प्राप्त होता है।
उदाहरण 4
एक ही दिशा में गतिशील समान आवृत्ति n तथा आयाम A वाली तीन सरल आवर्ती तरंगें वायु में इस प्रकार से अध्यारोपित होती है कि अध्यारोपण में दिये गये बिन्दु P पर पहली, दूसरी तथा तीसरी तरंग के कला कोण क्रमश: ϕ,ϕ+π2 व (ϕ+π) प्राप्त होते हैं। अब जैसे ही तरंगें गति करती है तो अध्यारोपण के परिणामस्वरूप -
(1) आयाम 3A वाली आवर्ती, असरल आवर्त तरंग प्राप्त होती है।
(2) आयाम 3A वाली अप्रगामी सरल आवर्त तरंग प्राप्त होती है।
(3) आयाम A वाली सरल आवर्त प्रगामी तरंग प्राप्त होती है।
(4) अध्यारोपित परिणामी तरंग का वेग, प्रत्येक तरंग के वेग के समान प्राप्त होती है।
उत्तर (3, 4)
चूंकि एक ही दिशा में गतिशील पहली तरंग एवं तीसरी तरंग के कला कोण क्रमश: ϕ व (ϕ+π) है, वे कंपन माध्यम के प्रत्येक बिन्दु पर विपरीत कला में अध्यारोपित होती है तथा एक-दूसरे को निरस्त कर देती हैं (विस्थापन, वेग एवं त्वरण में), परिणाम स्वरूप ये तरंगे एक-दूसरे को नष्ट कर देती है।
अत: केवल दूसरी तरंग ही शेष बचती है जो कि A आयाम वाली सरल आवर्ती तरंग के रूप में प्राप्त होती है। परिणामी तरंग का वेग, प्रत्येक तरंग के वेग के समान प्राप्त होता है।
उदाहरण 5
दो कंपायमान स्वरित्र प्रगामी तरंगें उत्पन्न करते हैं जिन्हें y1=4sin(500πt) तथा y2=2sin(506πt) द्वारा प्रदर्शित किया जाता है। इन स्वरित्रों को एक व्यक्ति के कान के समीप लाया जाता है। यह व्यक्ति α विस्पन्द प्रति सेकण्ड सुनेगा जिनमें उच्चिष्ठ तथा निम्निष्ठ तीव्रताओं के अनुपात का मान β है। β−α का मान ज्ञात कीजिये।
y1=4sin(500πt)
y2=2sin(506πt)
विस्पंदों की संख्या 253−250=3 beat/sec
⇒α=3beats/sec
चूंकि I1∝(16)
व I2∝4
⇒ImaxImin=(√I1+√I2)2(√I1−√I2)2
⇒(4+24−2)2
=(62)2=9⇒β=9
अत: β−α=9−3=6
उदाहरण 5
दो कंपायमान स्वरित्र प्रगामी तरंगें उत्पन्न करते हैं जिन्हें y1=4sin(500πt) तथा y2=2sin(506πt) द्वारा प्रदर्शित किया जाता है। इन स्वरित्रों को एक व्यक्ति के कान के समीप लाया जाता है। यह व्यक्ति α विस्पन्द प्रति सेकण्ड सुनेगा जिनमें उच्चिष्ठ तथा निम्निष्ठ तीव्रताओं के अनुपात का मान β है। β−α का मान ज्ञात कीजिये।
y1=4sin(500πt)
y2=2sin(506πt)
विस्पंदों की संख्या 253−250=3 beat/sec
⇒α=3beats/sec
चूंकि I1∝(16)
व I2∝4
⇒ImaxImin=(√I1+√I2)2(√I1−√I2)2
⇒(4+24−2)2
=(62)2=9⇒β=9
अत: β−α=9−3=6
उदाहरण 6
दो ध्वनि विस्तारक यंत्र नीचे चित्र में दर्शाए अनुसार एक दूसरे से 3m की दूरी पर स्थित हैं तथा एक ही कला में हैं। यह मानते हुए कि स्पीकरों से निकलने वाली ध्वनियों के आयाम श्रोता की स्थिति पर, जो कि किसी एक स्पीकर के सामने 4.0 m दूर पर है, सन्निकटत: समान है। यह ज्ञात कीजिए कि किन आवृत्तियों के लिए श्रोता न्यूनतम संकेत सुनेगा। वायु में ध्वनि की चाल 330 m/s है।
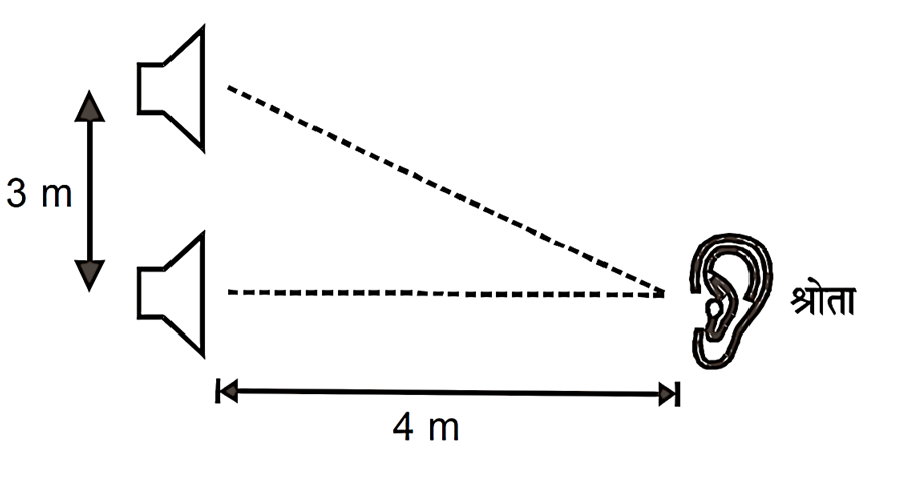
दूसरे स्पीकर से श्रोता की दूरी
=√(3)2+(4)2
=√25=5m
पथान्तर =(5−4.0)m=1m
पूर्ण विनाशी व्यतिकरण के लिये
1m=(2m+1)λ/2
⇒λ=22m+1 मीटर
इसके अनुसार आवृत्तियाँ
n=[330×(2m+1)]/2s−1,
जहाँ m=0,1,2,3,4,.........
=165(2m+1)s−1
जहाँ m=0,1,2,3,4,........
अत: वे आवृत्तियाँ जिनके लिए श्रोता को न्यूनतम तीव्रता सुनाई देगी
165Hz,495Hz,825Hz,..............
उदाहरण 6
दो ध्वनि विस्तारक यंत्र नीचे चित्र में दर्शाए अनुसार एक दूसरे से 3m की दूरी पर स्थित हैं तथा एक ही कला में हैं। यह मानते हुए कि स्पीकरों से निकलने वाली ध्वनियों के आयाम श्रोता की स्थिति पर, जो कि किसी एक स्पीकर के सामने 4.0 m दूर पर है, सन्निकटत: समान है। यह ज्ञात कीजिए कि किन आवृत्तियों के लिए श्रोता न्यूनतम संकेत सुनेगा। वायु में ध्वनि की चाल 330 m/s है।

दूसरे स्पीकर से श्रोता की दूरी
=√(3)2+(4)2
=√25=5m
पथान्तर =(5−4.0)m=1m
पूर्ण विनाशी व्यतिकरण के लिये
1m=(2m+1)λ/2
⇒λ=22m+1 मीटर
इसके अनुसार आवृत्तियाँ
n=[330×(2m+1)]/2s−1,
जहाँ m=0,1,2,3,4,.........
=165(2m+1)s−1
जहाँ m=0,1,2,3,4,........
अत: वे आवृत्तियाँ जिनके लिए श्रोता को न्यूनतम तीव्रता सुनाई देगी
165Hz,495Hz,825Hz,..............
उदाहरण 7
दो समतल आवर्ती ध्वनि तरंगे निम्न समीकरणों द्वारा व्यक्त की जाती है -
y1(x,t)=Asin(0.5πx−100πt)
y2(x,t)=Asin(0.48πx−96πt)
(सभी राशियाँ MKS प्रणाली में है।)
(a) प्रेक्षक 1 सेकण्ड में कितनी बार अधिकतम तीव्रता सुनेगा?
(b) ध्वनि की चाल कितनी है?
(c) x = 0 एवं t = 0.25 सेकण्ड पर y1+y2 का आयाम क्या है?
(a) विस्पन्द अवृत्ति =f1−f2
=12π[100π−96π]=2
अत: प्रेक्षक एक सेकण्ड में दो बार अधिकतम तीव्रता सुनेगा।
(b) ध्वनि तरंग की चाल =ω1k1
=100π0.5π=200ms−1
(c ) x = 0 तथा t = 0.25s पर
y1=0 तथा y2=0
∴y1+y2=0
उदाहरण 7
दो समतल आवर्ती ध्वनि तरंगे निम्न समीकरणों द्वारा व्यक्त की जाती है -
y1(x,t)=Asin(0.5πx−100πt)
y2(x,t)=Asin(0.48πx−96πt)
(सभी राशियाँ MKS प्रणाली में है।)
(a) प्रेक्षक 1 सेकण्ड में कितनी बार अधिकतम तीव्रता सुनेगा?
(b) ध्वनि की चाल कितनी है?
(c) x = 0 एवं t = 0.25 सेकण्ड पर y1+y2 का आयाम क्या है?
(a) विस्पन्द अवृत्ति =f1−f2
=12π[100π−96π]=2
अत: प्रेक्षक एक सेकण्ड में दो बार अधिकतम तीव्रता सुनेगा।
(b) ध्वनि तरंग की चाल =ω1k1
=100π0.5π=200ms−1
(c ) x = 0 तथा t = 0.25s पर
y1=0 तथा y2=0
∴y1+y2=0
उदाहरण 8
200, 203 व 207 हर्ट्ज आवृत्ति के तीन स्वरित्र द्विभुजों को एक साथ ध्वनित किया जाता है। विस्पंद आवृत्ति ज्ञात कीजिए।
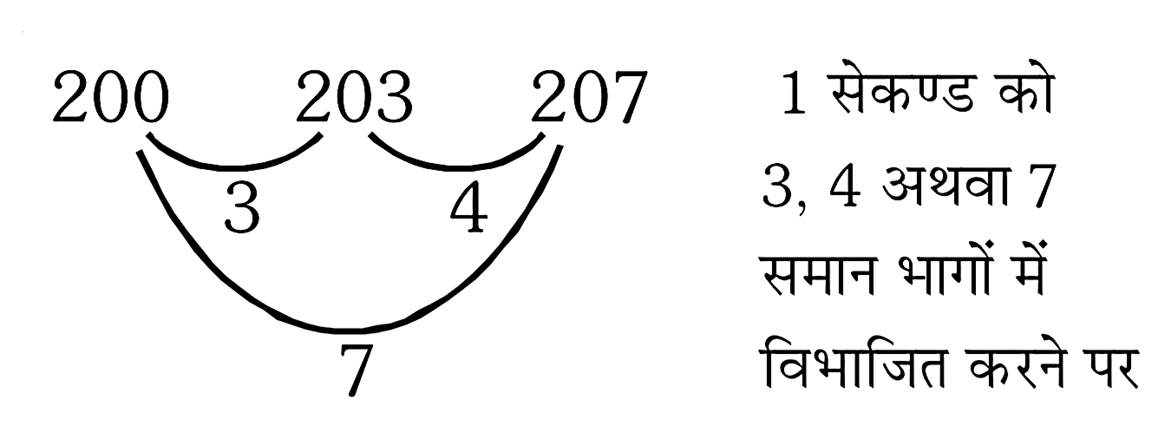
13 23 (33)
14 24 34 (44)
17 27 37 47 57 67 (77)
उभयनिष्ठ समय अन्तराल को हटाने पर एक सेकण्ड में कुल उच्चिष्ठ 3+3+6=12
उदाहरण 8
200, 203 व 207 हर्ट्ज आवृत्ति के तीन स्वरित्र द्विभुजों को एक साथ ध्वनित किया जाता है। विस्पंद आवृत्ति ज्ञात कीजिए।

13 23 (33)
14 24 34 (44)
17 27 37 47 57 67 (77)
उभयनिष्ठ समय अन्तराल को हटाने पर एक सेकण्ड में कुल उच्चिष्ठ 3+3+6=12
ऑर्गन पाइप में कम्पन
जब समान आवृत्ति तथा समान आयाम की दो अनुदैर्ध्य तरंगें माध्यम में विपरीत दिशा में संचरित होती हुई अध्यारोपित होती है तो अप्रगामी तरंग का निर्माण करती है। ये तरंगें समरूप व्यास की बेलनाकार नली के वायु स्तम्भ में उत्पन्न होती है। ये ध्वनि उत्पन्न करने वाली नलियाँ ऑर्गन पाईप कहलाती है।
बन्द ऑर्गन पाईप में वायु स्तम्भ के कम्पन :
नली का एक सिरा बन्द तथा दूसरा सिरा खुला होने पर इसे बन्द ऑर्गन पाईप कहते हैं। खुले सिरे पर फूंक मारने पर एक तरंग बन्द सिरे की ओर गति करती है जहाँ से यह खुले सिरे की ओर परावर्तित होती है। जैसे ही तरंग खुले सिरे पर पहुँचती है यह पुन: परावर्तित होती है। इस प्रकार दो अनुदैर्ध्य तरंगें विपरीत दिशा में अध्यारोपित होती है तथा अप्रगामी तरंग का निर्माण करती है।
बन्द सिरे पर चूंकि कण कम्पन करने के लिये स्वतन्त्र नहीं होते हैं निस्पन्द बनाते हैं जबकि खुले सिरे पर कण अधिकतम कम्पन करने के लिये स्वतन्त्र होने से प्रस्पन्द का निर्माण करते हैं।
चूंकि खुले सिरे पर फूंक मारने पर स्तम्भ खुले सिरे पर प्रस्पन्द तथा बन्द सिरे पर निस्पन्द का निर्माण करते हुये कम्पन करता है यदि पाईप की लम्बाई l, तरंगदैर्ध्य λ तथा आर्गन पाईप में ध्वनि का वेग v हो तो
स्थिति (i) :
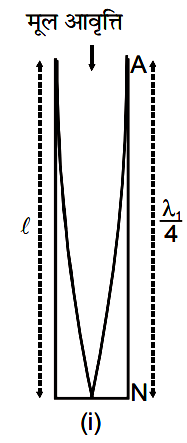
माना m=1 के संगत वायु-स्तम्भ में स्थापित तरंगों की तरंगदैर्घ्य λ1 है। तब, समीकरण
λ=4l2m−1.....(1) से,
l=λ14⇒λ1=4l
कम्पन की यह विधा चित्र में दिखायी गई है। इसमें खुले सिरे पर एक प्रस्पन्द (A) तथा बन्द सिरे पर एक निस्पन्द (N) होगा।
इस विधा में उत्पन्न कम्पन की आवृत्ति
n1=vλ1=v4l.....(2)
जहाँ v वायु में ध्वनि की चाल है। यह कम्पन की निम्नतम आवृत्ति है तथा इसे बन्द पाइप में वायु-स्तम्भ की 'मूल आवृत्ति' कहते हैं। पाइप में उत्पन्न ध्वनि स्वर को मूल स्वरक अथवा प्रथम संनादि कहते हैं। यह तब उत्पन्न होता है जब इस पाइप के खुले सिरे पर धीरे से फूँक मारते हैं।
स्थिति (ii) :
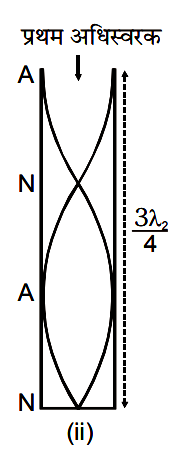
माना m=2 के संगत वायु-स्तम्भ में स्थापित स्थायी तरंगोंं की तरंगदैर्घ्य λ2 है। तब समीकरण (1) से
l=3λ24⇒λ2=4l3
कम्पन की यह विधा चित्र (ii) में दिखायी गई है। इस विधा में पाइप के खुले व बन्द सिरों के बीच एक अतिरिक्त प्रस्पन्द (A) तथा एक अतिरिक्त निस्पन्द (N) होगा इस विधा में कम्पन की आवृत्ति
n2=vλ2=v4l3=3v4l=3n1{समीकरण (2) से}
अर्थात् इस दशा में पाइप में उत्पन्न स्वरक की आवृत्ति, मूल स्वरक की आवृत्ति की तीन गुनी है। यह बन्द पाइप का 'प्रथम अधिस्वरक' है। इसे 'तृतीय संनादी' भी कहते हैं। यह तब इससे भी ऊँचे अधिस्वरक उत्पन्न किये जा सकते हैं जब वायु-स्तम्भ के खुले सिरे पर बलपूर्वक फूँक मारें।
स्थिति (iii) :
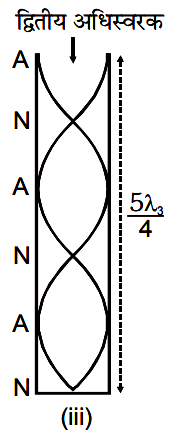
माना m=3 के संगत, वायु-स्तम्भ में स्थापित स्थायी तरंगोंं की तरंगदैर्घ्य λ3 है। तब समीकरण (1) से
l=5λ34⇒λ3=4l5
कम्पन की यह विधा चित्र (iii) में दिखाई गई है इस विधा में पाइप के खुले तथा बन्द सिरों के बीच दो अतिरिक्त प्रस्पन्द (A) तथा दो अतिरिक्त निस्पन्द (N) होंगे। इस विधा में उत्पन्न कम्पन की आवृत्ति
n3=vλ3=v4l5=5v4l=5n1
अर्थात् इस दशा में पाइप में उत्पन्न स्वरक की आवृत्ति मूल स्वरक की आवृत्ति की पाँच गुनी है। यह बन्द पाइप का द्वितीय अधिस्वरक अथवा पंचम संनादी है।
इससे यह विदित है कि कम्पन की mth विधा की आवृत्ति
nm=vλm=v4l2m−1=(2m−1)v4l
इस गणना से स्पष्ट है कि बन्द पाइप के मूल स्वरक तथा अधिस्वरकों की आवृत्तियों में निम्न प्रकार सम्बन्ध है:
n1:n2:n3=1:3:5.....
अर्थात् बन्द पाइप से केवल विषम संनादी ही उत्पन्न हो सकते है।
खुले ऑर्गन पाईप में वायु स्तम्भ के कम्पन :
जब नली के दोनों सिरे खुले हो तो यह खुला ऑर्गन पाईप कहलाता है। खुले सिरे पर फूंक मारने पर तरंग दूसरे सिरे की ओर गति करती है जहाँ से खुले सिरे की ओर परावर्तित होती है। विपरीत दिशा में गति करती हुई तरंगें अध्यारोपित होकर अप्रगामी तरंग का निर्माण करती है। अब पाईप दोनों सिरों से खुला है जिससे खुले सिरो पर प्रस्पंद का निर्माण होता है। अतः खुले सिरे पर फूंक मारने पर प्रत्येक सिरो पर प्रस्पन्द का निर्माण होता है तथा मध्य में निस्पन्द बनता है।
यदि पाईप की लम्बाई l, तरंगदैर्ध्य λ तथा ऑर्गन पाईप में ध्वनि का वेग v हो तो
λ=2lm.....(a)
स्थिति (i) :
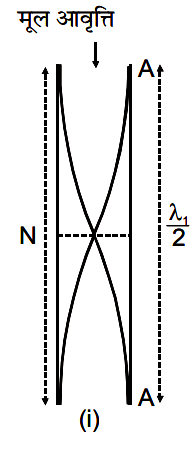
माना m=1 के संगत वायु-स्तम्भ में स्थापित स्थायी तरंगोंं की तरंगदैर्घ्य λ1 है। तब समीकरण (1) से
l=λ12⇒λ1=2l
कम्पन की यह विधा चित्र (i) में दिखाई गई है। इसमें दोनों खुले सिरों पर प्रस्पंद (A) तथा पाइप के बीच में एक निस्पन्द (N) होगा। इस विधा में कम्पन की आवृत्ति
n1=vλ1=v2l....(b)
जहाँ v वायु में ध्वनि की चाल है।
यह कम्पन की निम्नतम आवृत्ति है तथा इसे खुले पाइप में वायु-स्तम्भ की 'मूल' आवृत्ति कहते हैं। पाइप में उत्पन्न ध्वनि स्वर को मूल स्वरक (अथवा प्रथम संनादी) कहते हैं। यह तब उत्पन्न होता है जब हम पाइप के एक सिरे पर 'धीरे से' फूँक मारते हैं।
स्थिति (ii) :
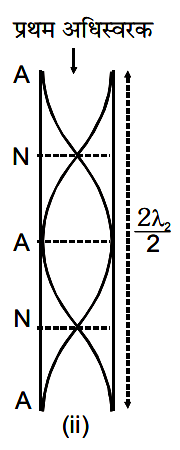
माना m=2 के संगत, वायु-स्तम्भ में स्थापित स्थायी तरंगोंं की तरंगदैर्घ्य λ2 है।
तब समीकरण (a) से,
l=2λ22⇒λ2=2l2
कम्पन की यह विधा चित्र (ii) में दिखायी गई है। इस विधा में पाइप के सिरों के बीच एक अतिरिक्त प्रस्पन्द (A) तथा एक अतिरिक्त निस्पन्द (N) होगा। इस विधा में कम्पन की आवृत्ति
n2=vλ2=2v2l=2n1 {समीकरण (b) से}
अर्थात् इस स्वरक की आवृत्ति मूल स्वरक की आवृत्ति की दोगुनी है। यह खुले पाइप का प्रथम अधिस्वरक अथवा द्वितीय संनादी है।
स्थिति (iii) :
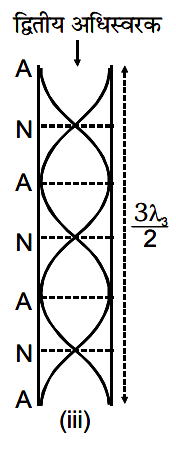
माना m=3 के संगत, वायु-स्तम्भ में स्थापित स्थायी तरंगोंं की तरंगदैर्घ्य λ3 है।
तब समीकरण (a) से
l=3λ32⇒λ3=2l3
कम्पन की यह विधा चित्र (iii) में दिखायी गई है। इसमें दोनों सिरों के बीच तीन निस्पन्द हैं। इस विधा में कम्पन की आवृत्ति
n3=vλ3=3v2l=3n1{समीकरण (b) से}
अर्थात् इस दशा में उत्पन्न स्वरक की आवृत्ति मूल स्वरक की आवृत्ति की तीन गुनी है। यह पाइप का 'द्वितीय अधिस्वरक' (अथवा तृतीय संनादी) है।
इससे यह विदित है कि कम्पन की mth विधा की आवृत्ति
nm=vλm=v2lm=mv2l
इस गणना से यह स्पष्ट है कि खुले पाइप के मूल स्वरक तथा अधिस्वरकों की आवृत्तियों में निम्नलिखित सम्बन्ध है:
n1:n2:n3.....=1:2:3....
अर्थात् खुले पाइप से सम तथा विषम दोनों प्रकार के संनादी उत्पन्न हो सकते हैं।
यही कारण है कि खुले ऑर्गन पाइप से उत्पन्न ध्वनि, बन्द पाइप से उत्पन्न ध्वनि की अपेक्षा अधिक मधुर होती है। वायु का ताप अथवा वायु में आर्द्रता बढ़ जाने पर वायु में ध्वनि की चाल भी बढ़ जाती है। अतः प्रत्येक दशा में ऑर्गन पाइप से उत्पन्न स्वर की आवृत्ति बढ़ जाती है।
समान लम्बाई के खुले तथा बन्द ऑर्गन पाइपों में मूल आवृत्तियों की तुलना :
बन्द पाइप से उत्पन्न स्वरक की मूल आवृत्ति (n1)=v4l तथा खुले पाइप से उत्पन्न स्वरक की मूल आवृत्ति (n1)=v2l
अतः
(n1)open(n1)close=v2lv4l=21
अर्थात् खुले पाइप से उत्पन्न स्वरक की मूल आवृत्ति उसी लम्बाई के बन्द पाइप से उत्पन्न स्वरक की मूल आवृत्ति की दोगुनी होती है।
ऑर्गन पाइप में कम्पन
जब समान आवृत्ति तथा समान आयाम की दो अनुदैर्ध्य तरंगें माध्यम में विपरीत दिशा में संचरित होती हुई अध्यारोपित होती है तो अप्रगामी तरंग का निर्माण करती है। ये तरंगें समरूप व्यास की बेलनाकार नली के वायु स्तम्भ में उत्पन्न होती है। ये ध्वनि उत्पन्न करने वाली नलियाँ ऑर्गन पाईप कहलाती है।
बन्द ऑर्गन पाईप में वायु स्तम्भ के कम्पन :
नली का एक सिरा बन्द तथा दूसरा सिरा खुला होने पर इसे बन्द ऑर्गन पाईप कहते हैं। खुले सिरे पर फूंक मारने पर एक तरंग बन्द सिरे की ओर गति करती है जहाँ से यह खुले सिरे की ओर परावर्तित होती है। जैसे ही तरंग खुले सिरे पर पहुँचती है यह पुन: परावर्तित होती है। इस प्रकार दो अनुदैर्ध्य तरंगें विपरीत दिशा में अध्यारोपित होती है तथा अप्रगामी तरंग का निर्माण करती है।
बन्द सिरे पर चूंकि कण कम्पन करने के लिये स्वतन्त्र नहीं होते हैं निस्पन्द बनाते हैं जबकि खुले सिरे पर कण अधिकतम कम्पन करने के लिये स्वतन्त्र होने से प्रस्पन्द का निर्माण करते हैं।
चूंकि खुले सिरे पर फूंक मारने पर स्तम्भ खुले सिरे पर प्रस्पन्द तथा बन्द सिरे पर निस्पन्द का निर्माण करते हुये कम्पन करता है यदि पाईप की लम्बाई l, तरंगदैर्ध्य λ तथा आर्गन पाईप में ध्वनि का वेग v हो तो
स्थिति (i) :

माना m=1 के संगत वायु-स्तम्भ में स्थापित तरंगों की तरंगदैर्घ्य λ1 है। तब, समीकरण
λ=4l2m−1.....(1) से,
l=λ14⇒λ1=4l
कम्पन की यह विधा चित्र में दिखायी गई है। इसमें खुले सिरे पर एक प्रस्पन्द (A) तथा बन्द सिरे पर एक निस्पन्द (N) होगा।
इस विधा में उत्पन्न कम्पन की आवृत्ति
n1=vλ1=v4l.....(2)
जहाँ v वायु में ध्वनि की चाल है। यह कम्पन की निम्नतम आवृत्ति है तथा इसे बन्द पाइप में वायु-स्तम्भ की 'मूल आवृत्ति' कहते हैं। पाइप में उत्पन्न ध्वनि स्वर को मूल स्वरक अथवा प्रथम संनादि कहते हैं। यह तब उत्पन्न होता है जब इस पाइप के खुले सिरे पर धीरे से फूँक मारते हैं।
स्थिति (ii) :

माना m=2 के संगत वायु-स्तम्भ में स्थापित स्थायी तरंगोंं की तरंगदैर्घ्य λ2 है। तब समीकरण (1) से
l=3λ24⇒λ2=4l3
कम्पन की यह विधा चित्र (ii) में दिखायी गई है। इस विधा में पाइप के खुले व बन्द सिरों के बीच एक अतिरिक्त प्रस्पन्द (A) तथा एक अतिरिक्त निस्पन्द (N) होगा इस विधा में कम्पन की आवृत्ति
n2=vλ2=v4l3=3v4l=3n1{समीकरण (2) से}
अर्थात् इस दशा में पाइप में उत्पन्न स्वरक की आवृत्ति, मूल स्वरक की आवृत्ति की तीन गुनी है। यह बन्द पाइप का 'प्रथम अधिस्वरक' है। इसे 'तृतीय संनादी' भी कहते हैं। यह तब इससे भी ऊँचे अधिस्वरक उत्पन्न किये जा सकते हैं जब वायु-स्तम्भ के खुले सिरे पर बलपूर्वक फूँक मारें।
स्थिति (iii) :

माना m=3 के संगत, वायु-स्तम्भ में स्थापित स्थायी तरंगोंं की तरंगदैर्घ्य λ3 है। तब समीकरण (1) से
l=5λ34⇒λ3=4l5
कम्पन की यह विधा चित्र (iii) में दिखाई गई है इस विधा में पाइप के खुले तथा बन्द सिरों के बीच दो अतिरिक्त प्रस्पन्द (A) तथा दो अतिरिक्त निस्पन्द (N) होंगे। इस विधा में उत्पन्न कम्पन की आवृत्ति
n3=vλ3=v4l5=5v4l=5n1
अर्थात् इस दशा में पाइप में उत्पन्न स्वरक की आवृत्ति मूल स्वरक की आवृत्ति की पाँच गुनी है। यह बन्द पाइप का द्वितीय अधिस्वरक अथवा पंचम संनादी है।
इससे यह विदित है कि कम्पन की mth विधा की आवृत्ति
nm=vλm=v4l2m−1=(2m−1)v4l
इस गणना से स्पष्ट है कि बन्द पाइप के मूल स्वरक तथा अधिस्वरकों की आवृत्तियों में निम्न प्रकार सम्बन्ध है:
n1:n2:n3=1:3:5.....
अर्थात् बन्द पाइप से केवल विषम संनादी ही उत्पन्न हो सकते है।
खुले ऑर्गन पाईप में वायु स्तम्भ के कम्पन :
जब नली के दोनों सिरे खुले हो तो यह खुला ऑर्गन पाईप कहलाता है। खुले सिरे पर फूंक मारने पर तरंग दूसरे सिरे की ओर गति करती है जहाँ से खुले सिरे की ओर परावर्तित होती है। विपरीत दिशा में गति करती हुई तरंगें अध्यारोपित होकर अप्रगामी तरंग का निर्माण करती है। अब पाईप दोनों सिरों से खुला है जिससे खुले सिरो पर प्रस्पंद का निर्माण होता है। अतः खुले सिरे पर फूंक मारने पर प्रत्येक सिरो पर प्रस्पन्द का निर्माण होता है तथा मध्य में निस्पन्द बनता है।
यदि पाईप की लम्बाई l, तरंगदैर्ध्य λ तथा ऑर्गन पाईप में ध्वनि का वेग v हो तो
λ=2lm.....(a)
स्थिति (i) :

माना m=1 के संगत वायु-स्तम्भ में स्थापित स्थायी तरंगोंं की तरंगदैर्घ्य λ1 है। तब समीकरण (1) से
l=λ12⇒λ1=2l
कम्पन की यह विधा चित्र (i) में दिखाई गई है। इसमें दोनों खुले सिरों पर प्रस्पंद (A) तथा पाइप के बीच में एक निस्पन्द (N) होगा। इस विधा में कम्पन की आवृत्ति
n1=vλ1=v2l....(b)
जहाँ v वायु में ध्वनि की चाल है।
यह कम्पन की निम्नतम आवृत्ति है तथा इसे खुले पाइप में वायु-स्तम्भ की 'मूल' आवृत्ति कहते हैं। पाइप में उत्पन्न ध्वनि स्वर को मूल स्वरक (अथवा प्रथम संनादी) कहते हैं। यह तब उत्पन्न होता है जब हम पाइप के एक सिरे पर 'धीरे से' फूँक मारते हैं।
स्थिति (ii) :

माना m=2 के संगत, वायु-स्तम्भ में स्थापित स्थायी तरंगोंं की तरंगदैर्घ्य λ2 है।
तब समीकरण (a) से,
l=2λ22⇒λ2=2l2
कम्पन की यह विधा चित्र (ii) में दिखायी गई है। इस विधा में पाइप के सिरों के बीच एक अतिरिक्त प्रस्पन्द (A) तथा एक अतिरिक्त निस्पन्द (N) होगा। इस विधा में कम्पन की आवृत्ति
n2=vλ2=2v2l=2n1 {समीकरण (b) से}
अर्थात् इस स्वरक की आवृत्ति मूल स्वरक की आवृत्ति की दोगुनी है। यह खुले पाइप का प्रथम अधिस्वरक अथवा द्वितीय संनादी है।
स्थिति (iii) :

माना m=3 के संगत, वायु-स्तम्भ में स्थापित स्थायी तरंगोंं की तरंगदैर्घ्य λ3 है।
तब समीकरण (a) से
l=3λ32⇒λ3=2l3
कम्पन की यह विधा चित्र (iii) में दिखायी गई है। इसमें दोनों सिरों के बीच तीन निस्पन्द हैं। इस विधा में कम्पन की आवृत्ति
n3=vλ3=3v2l=3n1{समीकरण (b) से}
अर्थात् इस दशा में उत्पन्न स्वरक की आवृत्ति मूल स्वरक की आवृत्ति की तीन गुनी है। यह पाइप का 'द्वितीय अधिस्वरक' (अथवा तृतीय संनादी) है।
इससे यह विदित है कि कम्पन की mth विधा की आवृत्ति
nm=vλm=v2lm=mv2l
इस गणना से यह स्पष्ट है कि खुले पाइप के मूल स्वरक तथा अधिस्वरकों की आवृत्तियों में निम्नलिखित सम्बन्ध है:
n1:n2:n3.....=1:2:3....
अर्थात् खुले पाइप से सम तथा विषम दोनों प्रकार के संनादी उत्पन्न हो सकते हैं।
यही कारण है कि खुले ऑर्गन पाइप से उत्पन्न ध्वनि, बन्द पाइप से उत्पन्न ध्वनि की अपेक्षा अधिक मधुर होती है। वायु का ताप अथवा वायु में आर्द्रता बढ़ जाने पर वायु में ध्वनि की चाल भी बढ़ जाती है। अतः प्रत्येक दशा में ऑर्गन पाइप से उत्पन्न स्वर की आवृत्ति बढ़ जाती है।
समान लम्बाई के खुले तथा बन्द ऑर्गन पाइपों में मूल आवृत्तियों की तुलना :
बन्द पाइप से उत्पन्न स्वरक की मूल आवृत्ति (n1)=v4l तथा खुले पाइप से उत्पन्न स्वरक की मूल आवृत्ति (n1)=v2l
अतः
(n1)open(n1)close=v2lv4l=21
अर्थात् खुले पाइप से उत्पन्न स्वरक की मूल आवृत्ति उसी लम्बाई के बन्द पाइप से उत्पन्न स्वरक की मूल आवृत्ति की दोगुनी होती है।
अनुनाद नली
यह एक बन्द ऑर्गन पाइप होता है जिसके वायु-स्तम्भ की लम्बाई घटाई अथवा बढ़ाई जा सकती है। जब इसके मुँह पर एक कम्पन करता हुआ स्वरित्र लाते हैं, तो इसके वायु-स्तम्भ में स्वरित्र की आवृत्ति के प्रणोदित कम्पन (forced vibrations) होने लगते हैं।
यदि हम वायु-स्तम्भ की लम्बाई इस प्रकार समायोजित कर लें कि इसकी कोई एक स्वाभाविक आवृत्ति स्वरित्र की आवृत्ति के बराबर हो जायें तो वायु-स्तम्भ के प्रणोदित कम्पनों का आयाम बहुत बढ़ जाता है। इस घटना को 'अनुनाद' कहते हैं। इस दशा में नली के वायु-स्तम्भ को 'अनुनाद-स्तम्भ' (resonance column) कहते हैं तथा नली से तीव्र ध्वनि निकलने लगती है।
संरचना :
अनुनाद नली पीतल अथवा काँच की लगभग 1 मीटर लम्बी तथा 5 सेमी व्यास की एक नली T होती है स्टैण्ड पर लगी रहती है।
इसका निचला सिरा रबर की एक नली के द्वारा एक जल से भरे बर्तन B से जुडा होता है। रबर की नली पर एक पिंचकॉक P लगा रहता है। बर्तन B को ऊपर-नीचे खिसका करके पिंचकाक P के द्वारा नली T में जल के तल को ऊपर-नीचे कर सकते है। तल की स्थिति पढ़ने के लिए T के साथ एक काँच की पतली नली C जुड़ी रहती है जिसके सहारे एक पैमाना S लगा रहता है।
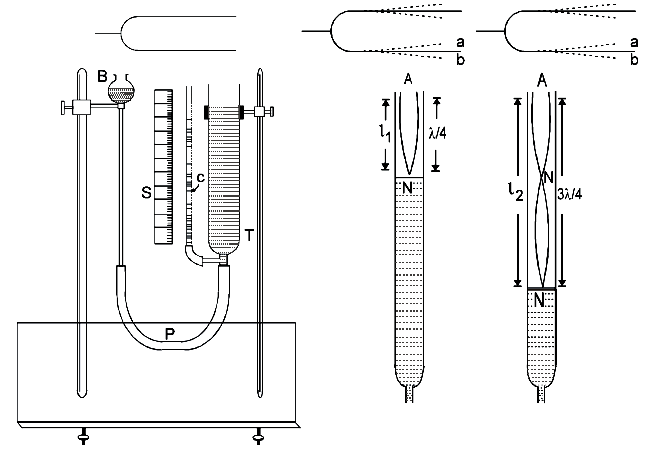
अनुनाद नली से वायु में ध्वनि की चाल ज्ञात करना :
इसके लिये जल के बर्तन B को ऊपर उठाकर नली T में जल के तल को नली के मुँह तक ले जाते है। फिर पिंचकॉक P को कसकर, B को नीचे कर देते है। इससे जल का तल नली T में ऊपर ही ठहरा रहता है। अब एक स्वरित्र को बजाकर नली T के मुँह पर लाते है और धीरे-धीरे पिंचकॉक खोलकर जल के तल को नली T में नीचे गिराते हैं । इससे वायु-स्तम्भ की लम्बाई बढ़ने लगती है। T में एक विशेष लम्बाई पर नली से तीव्र ध्वनि सुनाई देती है। यह अनुनाद की पहली अवस्था है।
इस स्थिति में नली के भीतर निम्नलिखित प्रक्रिया होती है -
- प्रथम अनुनाद के लिए l1=λ4
- द्वितीय अनुनाद के लिए l2=3λ4⇒l2−l1=λ2⇒λ=2(l2−l1)
- vt=nλ=2n(l2−l1).....(a)
यदि ध्वनि की चाल ज्ञात हो, तो समीकरण (a) से स्वरित्र की आवृत्ति n की गणना कर सकते है।
अंत्य संशोधन :
अनुनाद नली में प्रस्पंद ठीक खुले सिरे पर न बनकर थोड़ा बाहर x दूरी पर बनता है।
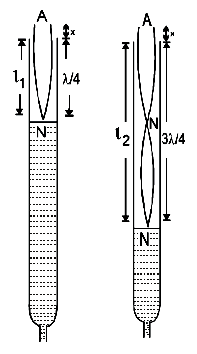
अत: अनुनाद की पहली व दूसरी अवस्थाओं में वायु-स्तंभ की लम्बाइयाँ क्रमश: (l1+x) तथा (l2+x) होती है। तब
- प्रथम अनुनाद के लिए l1+x=λ4 .....(1)
- द्वितीय अनुनाद के लिए l2+x=3λ4 .......(2)
l2−l1=λ2⇒λ=2(l2−l1)
λ का मान समी. (1) में रखने पर
l1+x=2(l2−l1)4
l1+x=l2−l12
x=l2−3l12
स्पष्टतः वायु स्तम्भ के अनुनाद की दूसरी लम्बाई l2, पहली लम्बाई l1 की ठीक तीन गुनी नहीं, बल्कि तीन गुने से कुछ अधिक होती है।
अनुनाद नली
यह एक बन्द ऑर्गन पाइप होता है जिसके वायु-स्तम्भ की लम्बाई घटाई अथवा बढ़ाई जा सकती है। जब इसके मुँह पर एक कम्पन करता हुआ स्वरित्र लाते हैं, तो इसके वायु-स्तम्भ में स्वरित्र की आवृत्ति के प्रणोदित कम्पन (forced vibrations) होने लगते हैं।
यदि हम वायु-स्तम्भ की लम्बाई इस प्रकार समायोजित कर लें कि इसकी कोई एक स्वाभाविक आवृत्ति स्वरित्र की आवृत्ति के बराबर हो जायें तो वायु-स्तम्भ के प्रणोदित कम्पनों का आयाम बहुत बढ़ जाता है। इस घटना को 'अनुनाद' कहते हैं। इस दशा में नली के वायु-स्तम्भ को 'अनुनाद-स्तम्भ' (resonance column) कहते हैं तथा नली से तीव्र ध्वनि निकलने लगती है।
संरचना :
अनुनाद नली पीतल अथवा काँच की लगभग 1 मीटर लम्बी तथा 5 सेमी व्यास की एक नली T होती है स्टैण्ड पर लगी रहती है।
इसका निचला सिरा रबर की एक नली के द्वारा एक जल से भरे बर्तन B से जुडा होता है। रबर की नली पर एक पिंचकॉक P लगा रहता है। बर्तन B को ऊपर-नीचे खिसका करके पिंचकाक P के द्वारा नली T में जल के तल को ऊपर-नीचे कर सकते है। तल की स्थिति पढ़ने के लिए T के साथ एक काँच की पतली नली C जुड़ी रहती है जिसके सहारे एक पैमाना S लगा रहता है।

अनुनाद नली से वायु में ध्वनि की चाल ज्ञात करना :
इसके लिये जल के बर्तन B को ऊपर उठाकर नली T में जल के तल को नली के मुँह तक ले जाते है। फिर पिंचकॉक P को कसकर, B को नीचे कर देते है। इससे जल का तल नली T में ऊपर ही ठहरा रहता है। अब एक स्वरित्र को बजाकर नली T के मुँह पर लाते है और धीरे-धीरे पिंचकॉक खोलकर जल के तल को नली T में नीचे गिराते हैं । इससे वायु-स्तम्भ की लम्बाई बढ़ने लगती है। T में एक विशेष लम्बाई पर नली से तीव्र ध्वनि सुनाई देती है। यह अनुनाद की पहली अवस्था है।
इस स्थिति में नली के भीतर निम्नलिखित प्रक्रिया होती है -
- प्रथम अनुनाद के लिए l1=λ4
- द्वितीय अनुनाद के लिए l2=3λ4⇒l2−l1=λ2⇒λ=2(l2−l1)
- vt=nλ=2n(l2−l1).....(a)
यदि ध्वनि की चाल ज्ञात हो, तो समीकरण (a) से स्वरित्र की आवृत्ति n की गणना कर सकते है।
अंत्य संशोधन :
अनुनाद नली में प्रस्पंद ठीक खुले सिरे पर न बनकर थोड़ा बाहर x दूरी पर बनता है।

अत: अनुनाद की पहली व दूसरी अवस्थाओं में वायु-स्तंभ की लम्बाइयाँ क्रमश: (l1+x) तथा (l2+x) होती है। तब
- प्रथम अनुनाद के लिए l1+x=λ4 .....(1)
- द्वितीय अनुनाद के लिए l2+x=3λ4 .......(2)
l2−l1=λ2⇒λ=2(l2−l1)
λ का मान समी. (1) में रखने पर
l1+x=2(l2−l1)4
l1+x=l2−l12
x=l2−3l12
स्पष्टतः वायु स्तम्भ के अनुनाद की दूसरी लम्बाई l2, पहली लम्बाई l1 की ठीक तीन गुनी नहीं, बल्कि तीन गुने से कुछ अधिक होती है।
विस्पन्द
जब कभी दो 'लगभग' समान आवृत्ति वाली ध्वनि की तरंगें एक साथ उत्पन्न की जाती हैं, तो उनके अध्यारोपण से जो परिणामी ध्वनि उत्पन्न होती है उसकी तीव्रता बारी-बारी से बढ़ती और घटती है। ध्वनि की तीव्रता में होने वाले इस चढ़ाव व उतराव की घटना को 'विस्पन्द' कहते हैं।
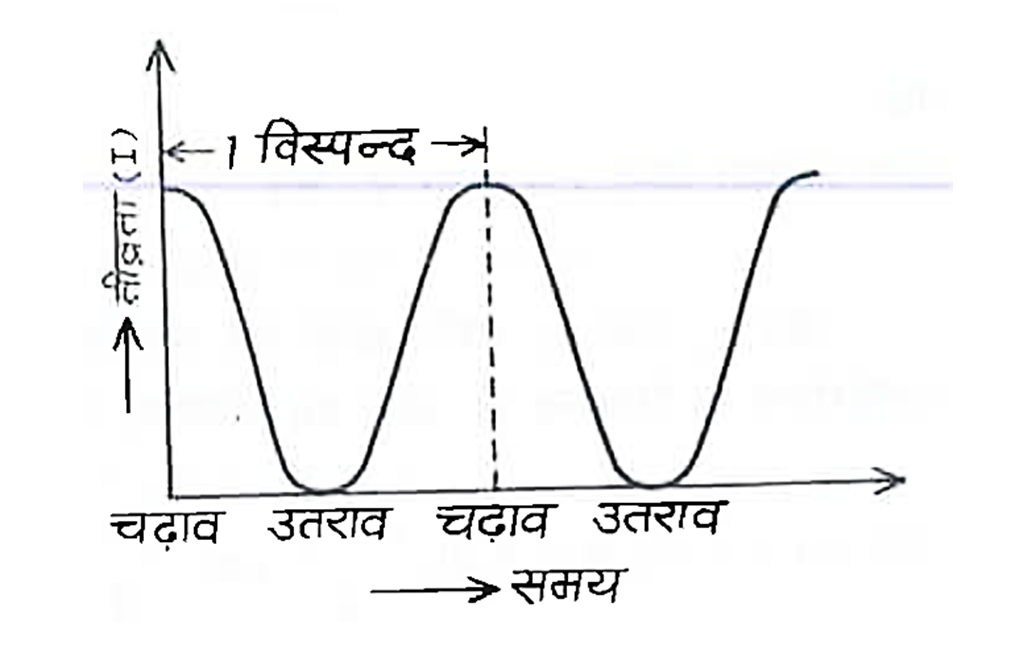
व्याख्या :
विस्पन्द की घटना ध्वनि के व्यतिकरण का एक विशेष उदाहरण है। जब दो ध्वनि-स्रोत साथ-साथ बजाये जाते हैं, तो माध्यम में दो तरंगें चलने लगती हैं। यदि ये तरंगें किसी बिन्दु पर एक ही कला में मिलती हैं, तो वहाँ ध्वनि की तीव्रता अधिकतम होती है परन्तु यदि ये विपरीत कलाओं में मिलती हैं, तो ध्वनि की तीव्रता न्यूनतम होती है। यदि दोनों तरंगोंं की आवृत्तियाँ बिल्कुल बराबर हैं, तो किसी भी बिन्दु पर तरंगोंं का कलान्तर स्थिर रहता है।
अतः वहाँ ध्वनि की तीव्रता भी स्थिर रहती है। परन्तु यदि आवृत्तियों में कुछ अन्तर है, तो किसी बिन्दु विशेष पर उनका कलान्तर बदलता रहता है। अतः उस बिन्दु पर तरंगें एकान्तर क्रम से एक ही कला में तथा विपरीत कलाओं में मिलती रहती हैं। अतः श्रोता को उसी बिन्दु पर ध्वनि की तीव्रता बढ़ती घटती सुनाई देती है।
ग्राफ द्वारा विवेचना :
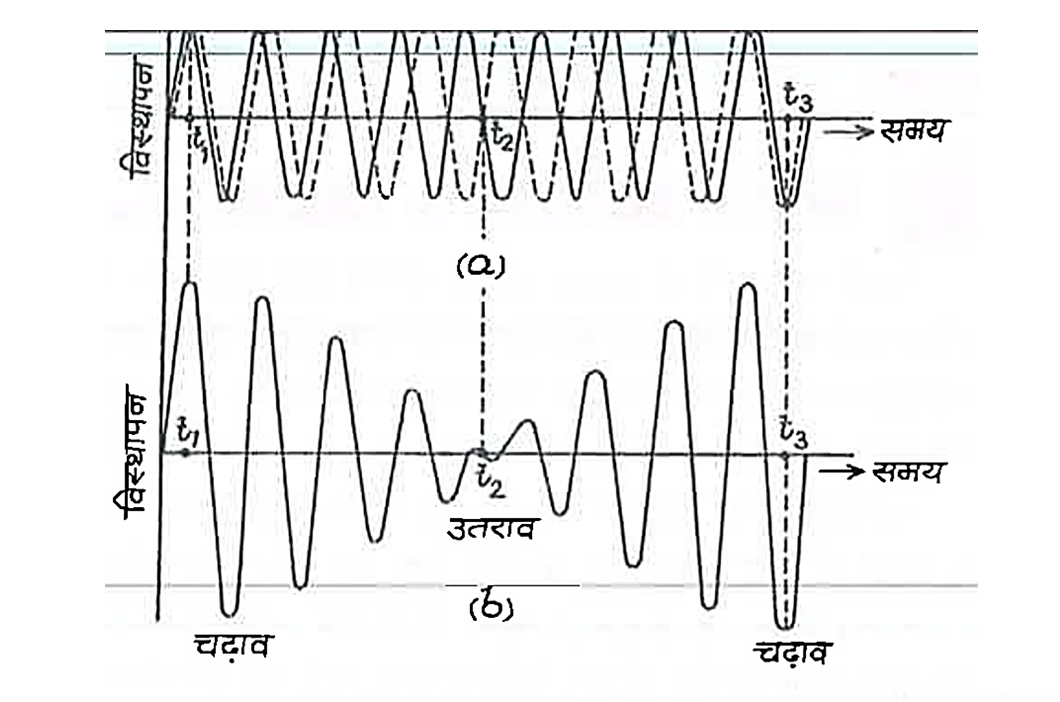
चित्र (a) में दो तरंगोंं के द्वारा किसी बिन्दु पर उत्पन्न किये गये कम्पनों के विस्थापन वक्र खींचे गये हैं। अविछिन्न वक्र वाले कम्पन की आवृत्ति विछिन्न वक्र वाले कम्पन की आवृत्ति से अधिक है। t1 समय पर दोनों तरंगें एक ही कला में हैं, अतः इस समय बिन्दु का परिणामी आयाम अधिकतम है। परन्तु चूँकि आवृत्तियों में थोड़ा-सा अन्तर है, अतः समय के साथ-साथ एक वक्र दूसरी के सापेक्ष हटती जाती है तथा परिणामी आयाम घटता जाता है। t2 समय पर वक्र एक-दूसरे के विपरीत हो जाती हैं, अतः परिणामी आयाम शून्य हो जाता है। t3 समय पर जबकि दोनों तरंगें पुनः एक ही कला में आ जाती हैं, परिणामी आयाम पुनः अधिकतम हो जाता है।
चित्र (b) में परिणामी वक्र खींची गई है जो कि परिणामी आयाम के उतार-चढ़ाव को प्रदर्शित करती है। चूंकि ध्वनि की तीव्रता आयाम के वर्ग के अनुक्रमानुपाती होती है, अतः तीव्रता का उतार-चढ़ाव भी इसी प्रकार की वक्र द्वारा प्रदर्शित होगा।
विस्पन्द आवृत्ति :
माना दो ध्वनि-स्रोत जिनकी कोणीय आवृत्तियाँ ω1 व ω2 हैं तथा प्रत्येक का आयाम a है, एक ही दिशा में तरंगें भेज रहे हैं। कोणीय आवृत्ति ω1, ω2 से कुछ ही अधिक है।
माना कि इन तरंगोंं के कारण माध्यम के किसी कण का किसी क्षण अलग-अलग विस्थापन y1 व y2 है। तब सरल आवर्त गति की समीकरण के अनुसार,
y1=asin(ω1t−kx)
तथा y2=asin(ω2t−kx)
माना प्रक्षेपण बिन्दु x=0 पर है। तब
y1=asinω1t=asin2πn1t
तथा y2=asinω2t=asin2πn2t
जहाँ n1 तथा n2 ध्वनि-स्त्रोतों की आवृत्तियाँ हैं।
अध्यारोपण के सिद्धान्त से, कण का परिणामी विस्थापन
y=y1+y2
y=asin2πn1t+asin2πn2t
सूत्र sinA+sinB=2sin(A+B2)cos(A−B2) से,
y=2asin{π(n1+n2)t}cos{π(n1−n2)t}
y=2acos{π(n1−n2)t}sin{π(n1+n2)t}
यदि 2acos{π(n1−n2)t}=A रख दें, तो
y=Asinπ(n1+n2)t
इस समीकरण से स्पष्ट है कि दोनों तरंगोंं के प्रभाव के कारण कण सरल आवर्त गति में कम्पन करता है तथा उसके कम्पन का आयाम A हैं।
विस्पंदों के व्यावहारिक उपयोग :
- आवृत्ति ज्ञात करना : यदि हमें किसी स्वरित्र की आवृत्ति n1 ज्ञात हो, तो हम किसी दूसरे स्वरित्र की आवृत्ति जो लगभग n1 के बराबर है, विस्पन्दों की सहायता से ज्ञात कर सकते हैं।
- बाजों को समस्वरण करना : बाजे वाले अपने बाजों को समस्वरण करने के लिए विस्पन्दों का उपयोग करते हैं। वे दो बाजों को एक के बाद एक करके बजाते हैं तथा एक की आवृत्ति को इस प्रकार समायोजित करते हैं कि इसकी ध्वनि उसके कानों को दूसरे बाजे की ध्वनि के समान प्रतीत होने लगे। इस प्रकार वे दोनों बाजों की आवृत्तियों को लगभग बराबर कर लेते हैं। फिर वे उन्हें एक-साथ बजाकर विस्पन्द सुनते हैं।
- खानों में खतरनाक गैसों का पता लगाने में : इसके लिए समान प्रकार के दो छोटे पाइप लेकर एक पाइप में शुद्ध वायु तथा दूसरे पाइप में खान की वायु प्रवाहित करते हैं। यदि खान की वायु शुद्ध है, तो दोनों पाइप समस्वरित (tuned) होते हैं, अतः विस्पन्द सुनाई नहीं देते। परन्तु यदि खान की वायु में खतरनाक गैसें (जैसे मेथेन) मिली हैं, तो वायु का घनत्व कम हो जाता है तथा ध्वनि वेग बढ़ जाता है। ध्वनि वेग बढ़ने से उस पाइप द्वारा उत्पन्न स्वर की आवृत्ति बदल जाती है, अतः विस्पन्द सुनाई देने लगते हैं।
विस्पन्द
जब कभी दो 'लगभग' समान आवृत्ति वाली ध्वनि की तरंगें एक साथ उत्पन्न की जाती हैं, तो उनके अध्यारोपण से जो परिणामी ध्वनि उत्पन्न होती है उसकी तीव्रता बारी-बारी से बढ़ती और घटती है। ध्वनि की तीव्रता में होने वाले इस चढ़ाव व उतराव की घटना को 'विस्पन्द' कहते हैं।

व्याख्या :
विस्पन्द की घटना ध्वनि के व्यतिकरण का एक विशेष उदाहरण है। जब दो ध्वनि-स्रोत साथ-साथ बजाये जाते हैं, तो माध्यम में दो तरंगें चलने लगती हैं। यदि ये तरंगें किसी बिन्दु पर एक ही कला में मिलती हैं, तो वहाँ ध्वनि की तीव्रता अधिकतम होती है परन्तु यदि ये विपरीत कलाओं में मिलती हैं, तो ध्वनि की तीव्रता न्यूनतम होती है। यदि दोनों तरंगोंं की आवृत्तियाँ बिल्कुल बराबर हैं, तो किसी भी बिन्दु पर तरंगोंं का कलान्तर स्थिर रहता है।
अतः वहाँ ध्वनि की तीव्रता भी स्थिर रहती है। परन्तु यदि आवृत्तियों में कुछ अन्तर है, तो किसी बिन्दु विशेष पर उनका कलान्तर बदलता रहता है। अतः उस बिन्दु पर तरंगें एकान्तर क्रम से एक ही कला में तथा विपरीत कलाओं में मिलती रहती हैं। अतः श्रोता को उसी बिन्दु पर ध्वनि की तीव्रता बढ़ती घटती सुनाई देती है।
ग्राफ द्वारा विवेचना :

चित्र (a) में दो तरंगोंं के द्वारा किसी बिन्दु पर उत्पन्न किये गये कम्पनों के विस्थापन वक्र खींचे गये हैं। अविछिन्न वक्र वाले कम्पन की आवृत्ति विछिन्न वक्र वाले कम्पन की आवृत्ति से अधिक है। t1 समय पर दोनों तरंगें एक ही कला में हैं, अतः इस समय बिन्दु का परिणामी आयाम अधिकतम है। परन्तु चूँकि आवृत्तियों में थोड़ा-सा अन्तर है, अतः समय के साथ-साथ एक वक्र दूसरी के सापेक्ष हटती जाती है तथा परिणामी आयाम घटता जाता है। t2 समय पर वक्र एक-दूसरे के विपरीत हो जाती हैं, अतः परिणामी आयाम शून्य हो जाता है। t3 समय पर जबकि दोनों तरंगें पुनः एक ही कला में आ जाती हैं, परिणामी आयाम पुनः अधिकतम हो जाता है।
चित्र (b) में परिणामी वक्र खींची गई है जो कि परिणामी आयाम के उतार-चढ़ाव को प्रदर्शित करती है। चूंकि ध्वनि की तीव्रता आयाम के वर्ग के अनुक्रमानुपाती होती है, अतः तीव्रता का उतार-चढ़ाव भी इसी प्रकार की वक्र द्वारा प्रदर्शित होगा।
विस्पन्द आवृत्ति :
माना दो ध्वनि-स्रोत जिनकी कोणीय आवृत्तियाँ ω1 व ω2 हैं तथा प्रत्येक का आयाम a है, एक ही दिशा में तरंगें भेज रहे हैं। कोणीय आवृत्ति ω1, ω2 से कुछ ही अधिक है।
माना कि इन तरंगोंं के कारण माध्यम के किसी कण का किसी क्षण अलग-अलग विस्थापन y1 व y2 है। तब सरल आवर्त गति की समीकरण के अनुसार,
y1=asin(ω1t−kx)
तथा y2=asin(ω2t−kx)
माना प्रक्षेपण बिन्दु x=0 पर है। तब
y1=asinω1t=asin2πn1t
तथा y2=asinω2t=asin2πn2t
जहाँ n1 तथा n2 ध्वनि-स्त्रोतों की आवृत्तियाँ हैं।
अध्यारोपण के सिद्धान्त से, कण का परिणामी विस्थापन
y=y1+y2
y=asin2πn1t+asin2πn2t
सूत्र sinA+sinB=2sin(A+B2)cos(A−B2) से,
y=2asin{π(n1+n2)t}cos{π(n1−n2)t}
y=2acos{π(n1−n2)t}sin{π(n1+n2)t}
यदि 2acos{π(n1−n2)t}=A रख दें, तो
y=Asinπ(n1+n2)t
इस समीकरण से स्पष्ट है कि दोनों तरंगोंं के प्रभाव के कारण कण सरल आवर्त गति में कम्पन करता है तथा उसके कम्पन का आयाम A हैं।
विस्पंदों के व्यावहारिक उपयोग :
- आवृत्ति ज्ञात करना : यदि हमें किसी स्वरित्र की आवृत्ति n1 ज्ञात हो, तो हम किसी दूसरे स्वरित्र की आवृत्ति जो लगभग n1 के बराबर है, विस्पन्दों की सहायता से ज्ञात कर सकते हैं।
- बाजों को समस्वरण करना : बाजे वाले अपने बाजों को समस्वरण करने के लिए विस्पन्दों का उपयोग करते हैं। वे दो बाजों को एक के बाद एक करके बजाते हैं तथा एक की आवृत्ति को इस प्रकार समायोजित करते हैं कि इसकी ध्वनि उसके कानों को दूसरे बाजे की ध्वनि के समान प्रतीत होने लगे। इस प्रकार वे दोनों बाजों की आवृत्तियों को लगभग बराबर कर लेते हैं। फिर वे उन्हें एक-साथ बजाकर विस्पन्द सुनते हैं।
- खानों में खतरनाक गैसों का पता लगाने में : इसके लिए समान प्रकार के दो छोटे पाइप लेकर एक पाइप में शुद्ध वायु तथा दूसरे पाइप में खान की वायु प्रवाहित करते हैं। यदि खान की वायु शुद्ध है, तो दोनों पाइप समस्वरित (tuned) होते हैं, अतः विस्पन्द सुनाई नहीं देते। परन्तु यदि खान की वायु में खतरनाक गैसें (जैसे मेथेन) मिली हैं, तो वायु का घनत्व कम हो जाता है तथा ध्वनि वेग बढ़ जाता है। ध्वनि वेग बढ़ने से उस पाइप द्वारा उत्पन्न स्वर की आवृत्ति बदल जाती है, अतः विस्पन्द सुनाई देने लगते हैं।
उदाहरण 9
A और B दो स्वरित्र द्विभुज साथ-साथ स्वरित्र होने पर प्रति सेकण्ड 8 विस्पंद उत्पन्न करते हैं। एक सिरे से बन्द पाईप में एक गैस का 37.5 सेमी स्तम्भ अपनी मूल विधा में स्वरित्र A से अनुनादित होता है जबकि स्वरित्र B इसी गैस 38.5 सेमी स्तम्भ से अनुनादित होता है। दोनों स्वरित्र द्विभुजों की आवृत्तियाँ परिकलित कीजिए।
स्वरित्र A के लिए λ14=37.5
अतः n1=Vλ1=V4×37.5
स्वरित्र B के लिए λ24=38.5
∴n2=Vλ2=V4×38.5
∴n1−n2=8
⇒V4×37.5−V4×38.5=8
∴V=(8×4×37.5×38.5)
n1=8×4×37.5×38.54×37.5
n1=308Hz
एवं n2=308−8=300Hz
उदाहरण 9
A और B दो स्वरित्र द्विभुज साथ-साथ स्वरित्र होने पर प्रति सेकण्ड 8 विस्पंद उत्पन्न करते हैं। एक सिरे से बन्द पाईप में एक गैस का 37.5 सेमी स्तम्भ अपनी मूल विधा में स्वरित्र A से अनुनादित होता है जबकि स्वरित्र B इसी गैस 38.5 सेमी स्तम्भ से अनुनादित होता है। दोनों स्वरित्र द्विभुजों की आवृत्तियाँ परिकलित कीजिए।
स्वरित्र A के लिए λ14=37.5
अतः n1=Vλ1=V4×37.5
स्वरित्र B के लिए λ24=38.5
∴n2=Vλ2=V4×38.5
∴n1−n2=8
⇒V4×37.5−V4×38.5=8
∴V=(8×4×37.5×38.5)
n1=8×4×37.5×38.54×37.5
n1=308Hz
एवं n2=308−8=300Hz
उदाहरण 10
वायु स्तम्भों तथा रस्सी में अप्रगामी तरंगोंं के बारे में स्तम्भ-I में बताया गया है तथा स्वर की आवृत्ति को स्तम्भ-II में दिया गया है।
[v = माध्यम में ध्वनि का वेग]
| क्र.सं. | स्तम्भ-I | स्तम्भ-II |
|---|---|---|
| 1. | (A) दोनों सिरों से खुली हुई नली के लिये द्वितीय सन्नादि | (P) V4l |
| 2. | (B) एक सिरे पर बन्द नली के लिये मूल आवृत्ति | (Q) V2l |
| 3. | (C) एक सिरे पर बन्द नली के लिये प्रथम अधिस्वरक | (R) 3V4l |
| 4. | (D) दोनों सिरों से बंधी हुई रस्सी के लिये मूल आवृत्ति | (S) Vl |
उत्तर ⇒
(A)→(S); (B)→(P);
(C)→(R); (D)→(Q)
(A) के लिए: खुले ऑर्गन पाइप के लिए द्वितीय सन्नादि =2(V2l)
(B) के लिए: बंद ऑर्गन पाइप के लिए मूल आवृत्ति =V4l
(C) के लिए: बंद ऑर्गन पाइप के लिये प्रथम अधिस्वरक =3V4l
(D) के लिए: दोनों सिरों से बंधी हुई रस्सी के लिए मूल आवृत्ति =V2l
उदाहरण 10
वायु स्तम्भों तथा रस्सी में अप्रगामी तरंगोंं के बारे में स्तम्भ-I में बताया गया है तथा स्वर की आवृत्ति को स्तम्भ-II में दिया गया है।
[v = माध्यम में ध्वनि का वेग]
| क्र.सं. | स्तम्भ-I | स्तम्भ-II |
|---|---|---|
| 1. | (A) दोनों सिरों से खुली हुई नली के लिये द्वितीय सन्नादि | (P) V4l |
| 2. | (B) एक सिरे पर बन्द नली के लिये मूल आवृत्ति | (Q) V2l |
| 3. | (C) एक सिरे पर बन्द नली के लिये प्रथम अधिस्वरक | (R) 3V4l |
| 4. | (D) दोनों सिरों से बंधी हुई रस्सी के लिये मूल आवृत्ति | (S) Vl |
उत्तर ⇒
(A)→(S); (B)→(P);
(C)→(R); (D)→(Q)
(A) के लिए: खुले ऑर्गन पाइप के लिए द्वितीय सन्नादि =2(V2l)
(B) के लिए: बंद ऑर्गन पाइप के लिए मूल आवृत्ति =V4l
(C) के लिए: बंद ऑर्गन पाइप के लिये प्रथम अधिस्वरक =3V4l
(D) के लिए: दोनों सिरों से बंधी हुई रस्सी के लिए मूल आवृत्ति =V2l
उदाहरण 11
यदि मूल आवृत्ति 1400 हर्ट्ज वाले OOP (खुले आर्गन पाइप) को 30% पानी में डुबो दिया जाये तो उत्पन्न आवृत्ति ज्ञात कीजिए।
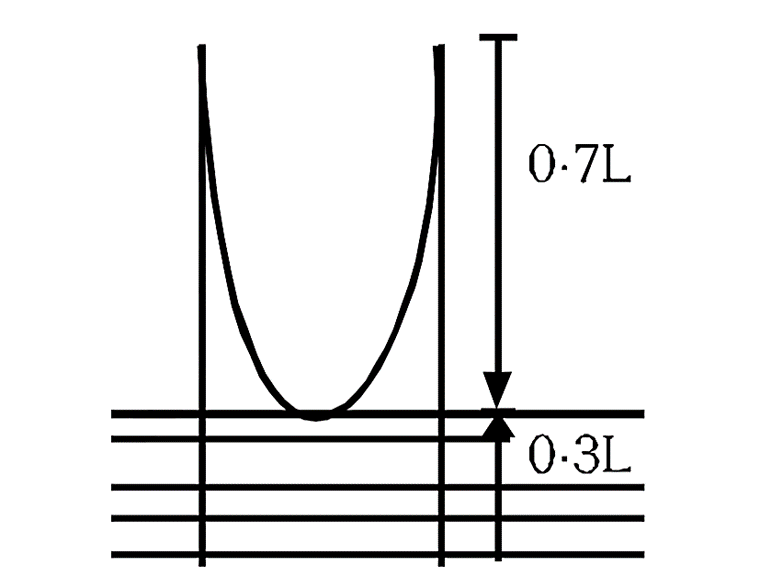
v2L=1400Hz
⇒vL=2800Hz
n'=v4L'
=v4[0.7L]=v2.8L
=28002.8=1000Hz
उदाहरण 11
यदि मूल आवृत्ति 1400 हर्ट्ज वाले OOP (खुले आर्गन पाइप) को 30% पानी में डुबो दिया जाये तो उत्पन्न आवृत्ति ज्ञात कीजिए।

v2L=1400Hz
⇒vL=2800Hz
n'=v4L'
=v4[0.7L]=v2.8L
=28002.8=1000Hz
उदाहरण 12
एक पीजो इलेक्ट्रिक क्वार्टज़ प्लेट की मोटाई 0.005 m है यह गुंजयमान परिस्थितियों में कंपन कर रही है।
यदि क्वार्ट्ज के लिए Y=8×1010N/m2 और ρ=2.65×103kg/m3 हो तो इसकी मूल आवृत्ति की गणना करो।
हम जानते है कि ठोसों में अनुदैर्ध्य तरंगे
v=√vρ,
अत: v=√8×10102.65×103
=5.5×103m/s
प्लेट की मूल अवस्था के लिए (λ/2)=L
अत: λ=2×5×10−3
=10−2m
परन्तु v=fλ, अर्थात् f=(v/λ)
अत: f=[5.5×103/10−2]
=5.5×105Hz
=550kHz
उदाहरण 12
एक पीजो इलेक्ट्रिक क्वार्टज़ प्लेट की मोटाई 0.005 m है यह गुंजयमान परिस्थितियों में कंपन कर रही है।
यदि क्वार्ट्ज के लिए Y=8×1010N/m2 और ρ=2.65×103kg/m3 हो तो इसकी मूल आवृत्ति की गणना करो।
हम जानते है कि ठोसों में अनुदैर्ध्य तरंगे
v=√vρ,
अत: v=√8×10102.65×103
=5.5×103m/s
प्लेट की मूल अवस्था के लिए (λ/2)=L
अत: λ=2×5×10−3
=10−2m
परन्तु v=fλ, अर्थात् f=(v/λ)
अत: f=[5.5×103/10−2]
=5.5×105Hz
=550kHz
उदाहरण 13
एक "COP" को दो समान भागों में काट दिया जाये तों, अब इन दोनों भागों की आवृत्तियाँ ज्ञात करिए, जबकि प्रारम्भ में इसका मान "n" था।
n=V4l
n'1=V2(l2)
=Vl=4(v4l)
=4n,
n2=V4(l2)
=V2l
=2(V4l)=2n
उदाहरण 13
एक "COP" को दो समान भागों में काट दिया जाये तों, अब इन दोनों भागों की आवृत्तियाँ ज्ञात करिए, जबकि प्रारम्भ में इसका मान "n" था।
n=V4l
n'1=V2(l2)
=Vl=4(v4l)
=4n,
n2=V4(l2)
=V2l
=2(V4l)=2n
उदाहरण 14
एक बंद ऑर्गन पाइप (COP) का 9th अधिस्वर (O.T.) 1900Hz. है तो समान लंबाई के OOP के लिए मूल आवृत्ति क्या होगी?
19n=1900,
n=100
OOP=2n=200Hz
समान लम्बाई की OOP के लिये मूल आवृत्ति COP की आवृत्ति की दुगनी होती है।
उदाहरण 14
एक बंद ऑर्गन पाइप (COP) का 9th अधिस्वर (O.T.) 1900Hz. है तो समान लंबाई के OOP के लिए मूल आवृत्ति क्या होगी?
19n=1900,
n=100
OOP=2n=200Hz
समान लम्बाई की OOP के लिये मूल आवृत्ति COP की आवृत्ति की दुगनी होती है।
उदाहरण 15
दो COP जिनकी लम्बाईयां 20 cm व 20.5 cm होने पर 5 beat/sec का उत्पादन होता है। COP की आवृत्तियां ज्ञात करिए।
nn+5=2020.5
n=200 For 20.5cm
n+5=205 For 20cm
उदाहरण 15
दो COP जिनकी लम्बाईयां 20 cm व 20.5 cm होने पर 5 beat/sec का उत्पादन होता है। COP की आवृत्तियां ज्ञात करिए।
nn+5=2020.5
n=200 For 20.5cm
n+5=205 For 20cm
उदाहरण 16
एक बंद आर्गन नलिका का पहला अधिस्वरक, खुली आर्गन नलिका का तीसरा अधिस्वरक एक दिये गये स्वरित्र के साथ समस्वरित हैं, तो इनकी लम्बाईयों का अनुपात ज्ञात करिए।
बन्द आर्गन नलिका का पहला अधिस्वरक =3V4lc0
खुली आर्गन नलिका का तीसरा अधिस्वरक =4V2l0
प्रश्नानुसार दोनों बराबर है ∴3V4lc=4V2l0
⇒lcl0=38
उदाहरण 16
एक बंद आर्गन नलिका का पहला अधिस्वरक, खुली आर्गन नलिका का तीसरा अधिस्वरक एक दिये गये स्वरित्र के साथ समस्वरित हैं, तो इनकी लम्बाईयों का अनुपात ज्ञात करिए।
बन्द आर्गन नलिका का पहला अधिस्वरक =3V4lc0
खुली आर्गन नलिका का तीसरा अधिस्वरक =4V2l0
प्रश्नानुसार दोनों बराबर है ∴3V4lc=4V2l0
⇒lcl0=38
उदाहरण 17
एक ध्वनि स्रोत 200 किलो हर्ट्ज़ आवृत्ति की पराश्रव्य तरंगें उत्पन्न कर रहा है। यह ध्वनि पानी की सतह पर आपतित है। तरंगदैर्ध्य का मान ज्ञात करिए
(a) परावर्तित ध्वनि में
(b) पारगमित ध्वनि में
वायु में ध्वनि का वेग = 340 m/s, पानी में ध्वनि का वेग = 1480 m/s
तरंग दैर्ध्य λ =
(a) परावर्तित ध्वनि वायु में गमन करेगी अत:
λ=340200×103
=1.7×10−3m
(b) पारगामित ध्वनि पानी में गमन करेगी अत:
λ=1480200×103
=7.4×10−3m
उदाहरण 17
एक ध्वनि स्रोत 200 किलो हर्ट्ज़ आवृत्ति की पराश्रव्य तरंगें उत्पन्न कर रहा है। यह ध्वनि पानी की सतह पर आपतित है। तरंगदैर्ध्य का मान ज्ञात करिए
(a) परावर्तित ध्वनि में
(b) पारगमित ध्वनि में
वायु में ध्वनि का वेग = 340 m/s, पानी में ध्वनि का वेग = 1480 m/s
तरंग दैर्ध्य λ =
(a) परावर्तित ध्वनि वायु में गमन करेगी अत:
λ=340200×103
=1.7×10−3m
(b) पारगामित ध्वनि पानी में गमन करेगी अत:
λ=1480200×103
=7.4×10−3m
ध्वनि का डॉप्लर प्रभाव
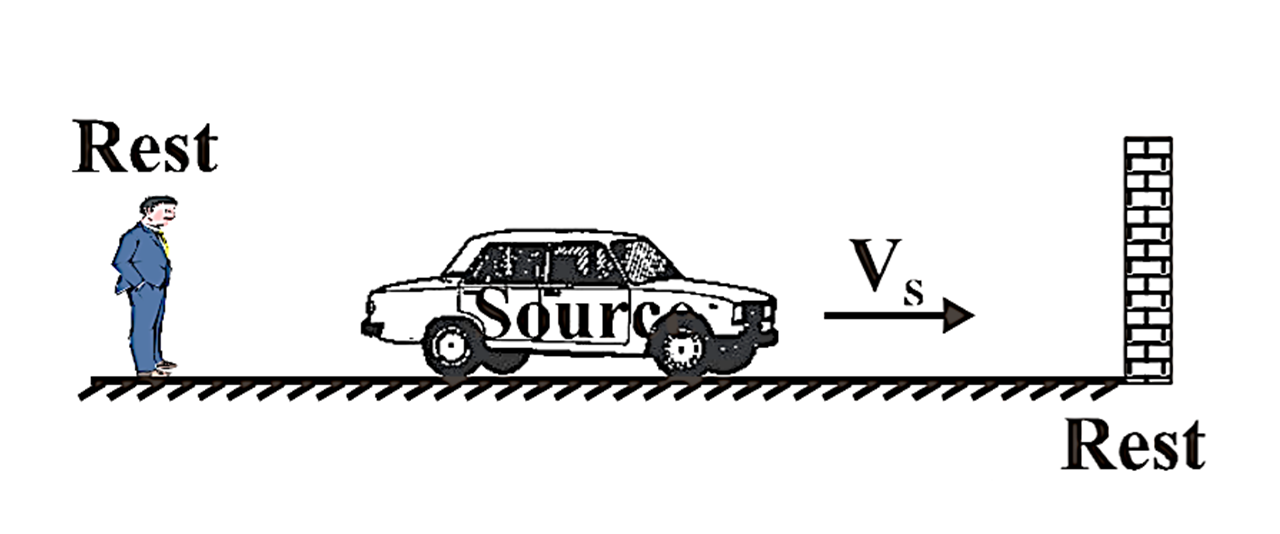
- किसी ध्वनि स्त्रोत एवं प्रेक्षक के बीच आपेक्षिक गति के कारण, ध्वनि स्त्रोत की आवृत्ति में होने वाले आभासी परिवर्तन की परिघटना को डॉप्लर प्रभाव कहते हैं।
- स्त्रोत, प्रेक्षक एवं माध्यम का वेग, स्त्रोत एवं प्रेक्षक को मिलाने वाली रेखा के अनुदिश होता है।
- स्त्रोत एवं प्रेक्षक का वेग, ध्वनि के वेग से कम होता है।
संकेताशर (Notations) :
- n→ ध्वनि स्त्रोत की वास्तविक आवृत्ति
- λ→ ध्वनि स्त्रोत से उत्पन्न ध्वनि तरंग का वास्तविक तरंगदैर्ध्य
- v→ ध्वनि का वेग
- v0→ प्रेक्षक या श्रोता का वेग
- n'→ प्रेक्षक द्वारा प्रेक्षित या आभासी आवृत्ति
- λ'→ प्रेक्षित या आभासी तरंगदैर्ध्य
- vs→ ध्वनि स्त्रोत का वेग
- vw→ हवा का वेग
Case I :-
(i) स्त्रोत गतिशील, प्रेक्षक स्थिर, माध्यम स्थिर :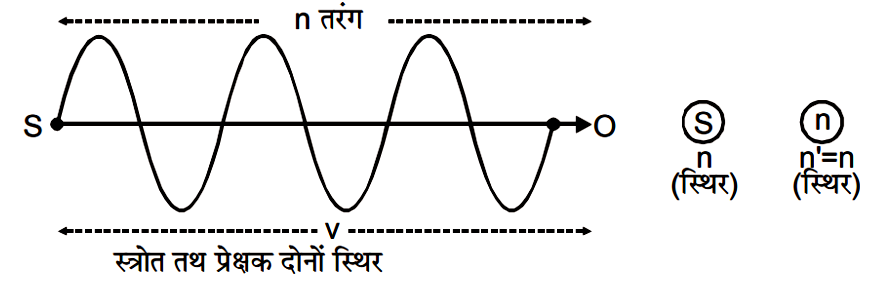
माना कि स्त्रोत S एवं प्रेक्षक O के बीच दूरी v है। v ध्वनि का वेग है। यदि स्त्रोत की आवृत्ति n हो तो स्त्रोत द्वारा एक सेकण्ड में n तरंगे उत्सर्जित होंगी। यही n तरंगें v दूरी में फैलेंगी। अत: तरंगदैर्ध्य (या तरंग लम्बाई)
λ=vn
(ii) जब स्त्रोत, स्थिर प्रेक्षक की ओर गति करता है :माना स्त्रोत S, स्थिर प्रेक्षक की ओर vs वेग से गति करना प्रारम्भ करता है। एक सैकण्ड बाद n तरंगें (v−vs) दूरी में फैलेंगी। अत: अब प्रेक्षक को ध्वनि की आवृत्ति n' तथा तरंगदैर्ध्य λ' प्रतीत होगी।
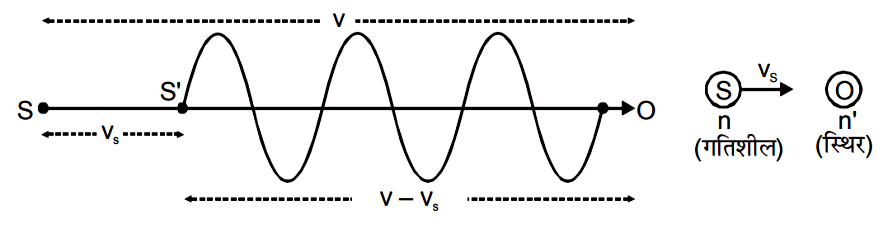
अत: आभासी तरंगदैर्ध्य
λ'=v−vsn
तथा आभासी आवृत्ति,n'=vλ'=vv+vsn=n(vv+vs)
अत: जब ध्वनि स्त्रोत, प्रेक्षक की ओर गति करता है तो आभासी आवृत्ति n', वास्तविक आवृत्ति n से अधिक होती है।(iii) जब स्त्रोत, स्थिर प्रेक्षक से दूर की ओर गति करता है :
इस स्थिति में n तरंगे v+vs दूरी में फैलेगी।
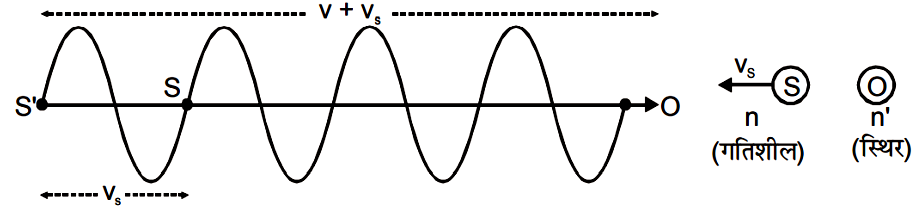
अतः आभासी तरंगदैर्ध्य
λ'=v+vsn=v+vsnλ
तथा आभासी आवृत्ति,n'=vλ'=vv+vsn=n(vv+vs)
अत: n',n से कम होगी (n>n')Case II :-
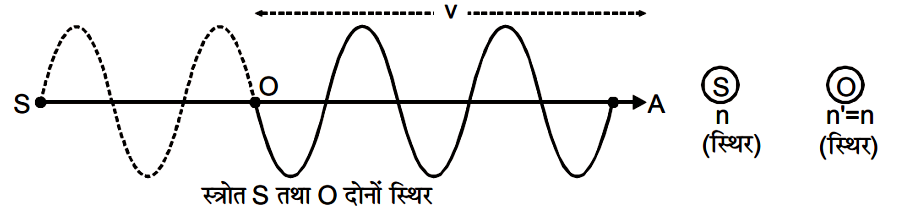
(i) प्रेक्षक गतिशील, स्त्रोत स्थिर, माध्यम स्थिर :माना कि स्त्रोत (S) एवं प्रेक्षक (O) उनकी स्थितियों पर स्थिर है। तब स्त्रोत S द्वारा प्रसारित n तरंगे, एक सैकण्ड में प्रेक्षक O को पार करती है तथा स्थान OA(=v) में फैलती है।
(ii) जब प्रेक्षक, स्थिर स्त्रोत की ओर गतिशील है :
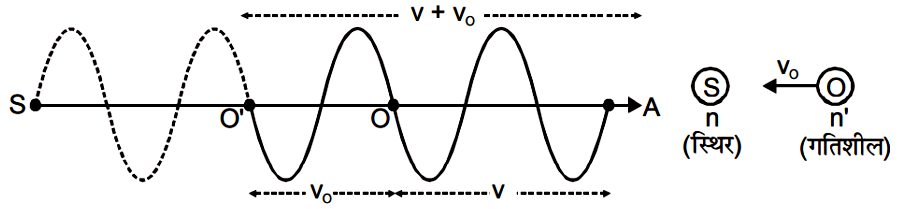
जब प्रेक्षक O स्थिर स्त्रोत S की ओर v वेग से गति करता है तो यह v दूरी एक सैकण्ड में तय करता है। अत: प्रेक्षक AO दूरी में स्थित n तरंगें ही प्राप्त नहीं करता बल्कि OO'(=v0) दूरी में स्थित अतिरिक्त Δn तरंगें भी प्राप्त करता है। अत: एक सैकण्ड में प्रेक्षक द्वारा प्राप्त कुल तरंगे अर्थात
- आभासी आवृत्ति (n') = वास्तविक तरंगे (n) + अतिरिक्त तरंगे (Δn)
n'=vλ+v0λ=v+v0vn=n(v+v0v)
(iii) जब प्रेक्षक, स्थिर स्त्रोत से दूर की ओर गतिशील है :इस स्थिति में n तरंगें v−v0 दूरी में फैलेगी।
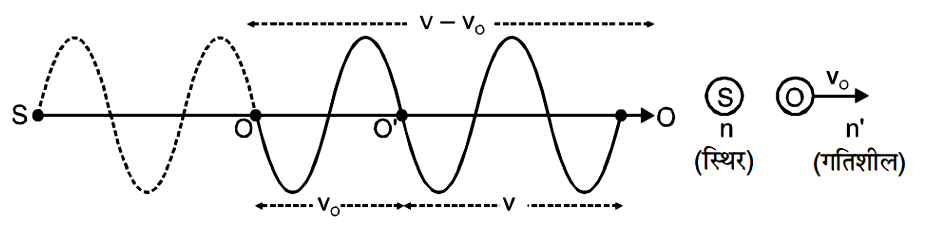
जब प्रेक्षक, स्त्रोत से v0 वेग से दूर गतिशील होता है तो वह वास्तविक तरंगोंं से Δn तरंगें कम प्राप्त करता है। अत: प्रेक्षक को प्राप्त कुल तरंगें अर्थात्
- आभासी आवृत्ति (n') = वास्तविक तरंगोंं की संख्या (n) - तरंगोंं की संख्या में कमी (Δn)
n'=vλ−v0λ=v−v0λ=v−v0vn=(v−v0v)n
Case III :-
माध्यम की गति का प्रभाव :डॉप्लर प्रभाव का व्यापक सूत्र n'=n[v±v0v−+vs] .....(1)
यदि माध्यम (वायु) भी vm वेग स्त्रोत तथा प्रेक्षक की दिशा में गतिशील है तो ध्वनि का वेग, प्रेक्षक के सापेक्ष v±vm (यदि ध्वनि के विपरीत हो तो ऋण चिन्ह) होगा अतः
n'=n(v±vm−+v0v±vm−+vs)
नोट :- जब S तथा O दोनों स्थिर हो (अर्थात् vs=v0=0) तो वायु की गति के कारण आवृत्ति पर कोई प्रभाव नहीं होगा।डॉप्लर प्रभाव के अनुप्रयोग :
गतिमान पिण्डों की आवृत्तियों में, डॉप्लर प्रभाव के कारण आने वाले अंतर का उपयोग, सेना, औषधि विज्ञान, खगोलिकी जैसे विविध क्षेत्रों में पिण्डों का वेग मापने के लिए किया जाता है। इसका उपयोग पुलिस यह जाँचने के लिए भी करती है कि कोई गाड़ी गतिसीमा से अधिक गति से तो नहीं चलाई जा रही।
ज्ञात आवृत्ति की ध्वनि या विद्युत चुंबकीय तरंगोंं को गतिमान पिण्ड की ओर भेजा जाता है। मॉनीटरिंग स्टेशन पर, पिण्ड द्वारा परावर्तित तरंगें प्राप्त करके इनकी आवृत्ति ज्ञात की जाती है। इन दो आवृत्तियों का अंतर डॉप्लर विस्थापन कहलाता है।
हवाई अड्डों पर वायुयानों के मार्गदर्शन के लिए, सेना में शत्रु यानों के संसूचन के लिए इस विधि का उपयोग किया जाता है। खगोल भौतिकीविद तारों का वेग मापने के लिए इसका उपयोग करते हैं।
डॉक्टर लोग हृदय स्पंदनों और शरीर के विभिन्न अंगों में रक्त प्रवाह का अध्ययन करने के लिए इसका उपयोग करते हैं। यहाँ वे पराध्वनि तरंगोंं का उपयोग करते हैं और सामान्य व्यवहार में इसे सोनोग्राफी कहा जाता है। पराध्वनि तरंगें व्यक्ति के शरीर में प्रवेश करती हैं और इनमें से कुछ परावर्तित हो जाती हैं तथा रक्त की गति और हृदय के वाल्वों के स्पंदन के विषय में जानकारी प्रदान करती है, इसमें भ्रूण के हृदय का स्पंदन भी शामिल है। हृदय से परावर्तित तरंगोंं से जो चित्र बनता है उसे इकोकार्डियोग्राम कहा जाता है।
ध्वनि का डॉप्लर प्रभाव
- किसी ध्वनि स्त्रोत एवं प्रेक्षक के बीच आपेक्षिक गति के कारण, ध्वनि स्त्रोत की आवृत्ति में होने वाले आभासी परिवर्तन की परिघटना को डॉप्लर प्रभाव कहते हैं।
- स्त्रोत, प्रेक्षक एवं माध्यम का वेग, स्त्रोत एवं प्रेक्षक को मिलाने वाली रेखा के अनुदिश होता है।
- स्त्रोत एवं प्रेक्षक का वेग, ध्वनि के वेग से कम होता है।
संकेताशर (Notations) :
- n→ ध्वनि स्त्रोत की वास्तविक आवृत्ति
- λ→ ध्वनि स्त्रोत से उत्पन्न ध्वनि तरंग का वास्तविक तरंगदैर्ध्य
- v→ ध्वनि का वेग
- v0→ प्रेक्षक या श्रोता का वेग
- n'→ प्रेक्षक द्वारा प्रेक्षित या आभासी आवृत्ति
- λ'→ प्रेक्षित या आभासी तरंगदैर्ध्य
- vs→ ध्वनि स्त्रोत का वेग
- vw→ हवा का वेग
Case I :-
(i) स्त्रोत गतिशील, प्रेक्षक स्थिर, माध्यम स्थिर :
माना कि स्त्रोत S एवं प्रेक्षक O के बीच दूरी v है। v ध्वनि का वेग है। यदि स्त्रोत की आवृत्ति n हो तो स्त्रोत द्वारा एक सेकण्ड में n तरंगे उत्सर्जित होंगी। यही n तरंगें v दूरी में फैलेंगी। अत: तरंगदैर्ध्य (या तरंग लम्बाई)
λ=vn
(ii) जब स्त्रोत, स्थिर प्रेक्षक की ओर गति करता है :माना स्त्रोत S, स्थिर प्रेक्षक की ओर vs वेग से गति करना प्रारम्भ करता है। एक सैकण्ड बाद n तरंगें (v−vs) दूरी में फैलेंगी। अत: अब प्रेक्षक को ध्वनि की आवृत्ति n' तथा तरंगदैर्ध्य λ' प्रतीत होगी।

अत: आभासी तरंगदैर्ध्य
λ'=v−vsn
तथा आभासी आवृत्ति,n'=vλ'=vv+vsn=n(vv+vs)
अत: जब ध्वनि स्त्रोत, प्रेक्षक की ओर गति करता है तो आभासी आवृत्ति n', वास्तविक आवृत्ति n से अधिक होती है।(iii) जब स्त्रोत, स्थिर प्रेक्षक से दूर की ओर गति करता है :
इस स्थिति में n तरंगे v+vs दूरी में फैलेगी।

अतः आभासी तरंगदैर्ध्य
λ'=v+vsn=v+vsnλ
तथा आभासी आवृत्ति,n'=vλ'=vv+vsn=n(vv+vs)
अत: n',n से कम होगी (n>n')Case II :-
(i) प्रेक्षक गतिशील, स्त्रोत स्थिर, माध्यम स्थिर :माना कि स्त्रोत (S) एवं प्रेक्षक (O) उनकी स्थितियों पर स्थिर है। तब स्त्रोत S द्वारा प्रसारित n तरंगे, एक सैकण्ड में प्रेक्षक O को पार करती है तथा स्थान OA(=v) में फैलती है।

(ii) जब प्रेक्षक, स्थिर स्त्रोत की ओर गतिशील है :

जब प्रेक्षक O स्थिर स्त्रोत S की ओर v वेग से गति करता है तो यह v दूरी एक सैकण्ड में तय करता है। अत: प्रेक्षक AO दूरी में स्थित n तरंगें ही प्राप्त नहीं करता बल्कि OO'(=v0) दूरी में स्थित अतिरिक्त Δn तरंगें भी प्राप्त करता है। अत: एक सैकण्ड में प्रेक्षक द्वारा प्राप्त कुल तरंगे अर्थात
- आभासी आवृत्ति (n') = वास्तविक तरंगे (n) + अतिरिक्त तरंगे (Δn)
n'=vλ+v0λ=v+v0vn=n(v+v0v)
(iii) जब प्रेक्षक, स्थिर स्त्रोत से दूर की ओर गतिशील है :इस स्थिति में n तरंगें v−v0 दूरी में फैलेगी।

जब प्रेक्षक, स्त्रोत से v0 वेग से दूर गतिशील होता है तो वह वास्तविक तरंगोंं से Δn तरंगें कम प्राप्त करता है। अत: प्रेक्षक को प्राप्त कुल तरंगें अर्थात्
- आभासी आवृत्ति (n') = वास्तविक तरंगोंं की संख्या (n) - तरंगोंं की संख्या में कमी (Δn)
n'=vλ−v0λ=v−v0λ=v−v0vn=(v−v0v)n
Case III :-
माध्यम की गति का प्रभाव :डॉप्लर प्रभाव का व्यापक सूत्र n'=n[v±v0v−+vs] .....(1)
यदि माध्यम (वायु) भी vm वेग स्त्रोत तथा प्रेक्षक की दिशा में गतिशील है तो ध्वनि का वेग, प्रेक्षक के सापेक्ष v±vm (यदि ध्वनि के विपरीत हो तो ऋण चिन्ह) होगा अतः
n'=n(v±vm−+v0v±vm−+vs)
नोट :- जब S तथा O दोनों स्थिर हो (अर्थात् vs=v0=0) तो वायु की गति के कारण आवृत्ति पर कोई प्रभाव नहीं होगा।डॉप्लर प्रभाव के अनुप्रयोग :
गतिमान पिण्डों की आवृत्तियों में, डॉप्लर प्रभाव के कारण आने वाले अंतर का उपयोग, सेना, औषधि विज्ञान, खगोलिकी जैसे विविध क्षेत्रों में पिण्डों का वेग मापने के लिए किया जाता है। इसका उपयोग पुलिस यह जाँचने के लिए भी करती है कि कोई गाड़ी गतिसीमा से अधिक गति से तो नहीं चलाई जा रही।
ज्ञात आवृत्ति की ध्वनि या विद्युत चुंबकीय तरंगोंं को गतिमान पिण्ड की ओर भेजा जाता है। मॉनीटरिंग स्टेशन पर, पिण्ड द्वारा परावर्तित तरंगें प्राप्त करके इनकी आवृत्ति ज्ञात की जाती है। इन दो आवृत्तियों का अंतर डॉप्लर विस्थापन कहलाता है।
हवाई अड्डों पर वायुयानों के मार्गदर्शन के लिए, सेना में शत्रु यानों के संसूचन के लिए इस विधि का उपयोग किया जाता है। खगोल भौतिकीविद तारों का वेग मापने के लिए इसका उपयोग करते हैं।
डॉक्टर लोग हृदय स्पंदनों और शरीर के विभिन्न अंगों में रक्त प्रवाह का अध्ययन करने के लिए इसका उपयोग करते हैं। यहाँ वे पराध्वनि तरंगोंं का उपयोग करते हैं और सामान्य व्यवहार में इसे सोनोग्राफी कहा जाता है। पराध्वनि तरंगें व्यक्ति के शरीर में प्रवेश करती हैं और इनमें से कुछ परावर्तित हो जाती हैं तथा रक्त की गति और हृदय के वाल्वों के स्पंदन के विषय में जानकारी प्रदान करती है, इसमें भ्रूण के हृदय का स्पंदन भी शामिल है। हृदय से परावर्तित तरंगोंं से जो चित्र बनता है उसे इकोकार्डियोग्राम कहा जाता है।
ध्वनि के परावर्तन में डॉप्लर प्रभाव (प्रतिध्वनि)
जब ध्वनि परावर्तक से परावर्तित होती है तो प्रेक्षक दो स्वर प्राप्त करता है, एक सीधा स्त्रोत से तथा दूसरा परावर्तक से। यदि दोनों आवृत्तियाँ भिन्न-भिन्न है तब इन तरंगोंं के अध्यारोपण से विस्पन्द बनते हैं तथा विस्पन्द आवृत्ति से हम स्त्रोत की चाल ज्ञात कर सकते हैं।
Case I :-
जब स्त्रोत एक स्थिर दीवार की ओर गति करता है।- n'D= सीधी आभासी आवृत्ति
n'= आभासी आवृत्ति
n'R= परावर्तित आभासी आवृत्ति
n'=(VV−VS)n
n'R=n'
b=Δn
=n'R−n'D=0
n'=(VV−VS)n
b=Δn
=(VV−VS−VV+VS)n
=2VSVnV2−V2S≅(2VSV)n
नोट :- स्थिर दीवार आपतित ध्वनि के लिए श्रोता का तथा परावर्तित ध्वनि के लिए स्त्रोत का कार्य करती है।
Case II :-
जब स्त्रोत व श्रोता दोनों स्थिर दीवार की ओर गति करते है।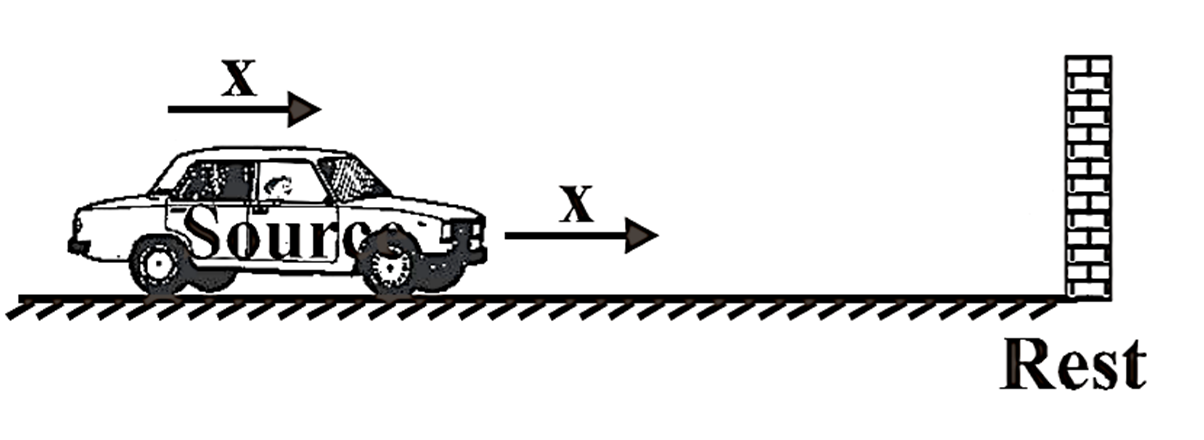
n'=(VV−x)n
n'R=(V+xV)n'
=[V+xV][VV−x]n
n'R=(V+xV−x)n
b=n'R−n'D
=(V+xV−x)n−n
b=2xV−xn
स्थितियाँ जब ध्वनि तरंगोंं के लिए डॉप्लर प्रभाव प्रेक्षित नहीं होता है :
- जब ध्वनि का स्त्रोत तथा प्रेक्षक दोनों स्थिर हो तब डॉप्लर प्रभाव प्रेक्षित नहीं होता है।
- जब स्त्रोत तथा प्रेक्षक दोनों समान दिशा में समान वेग से गतिशील हो।
- जब स्त्रोत तथा प्रेक्षक दोनों परस्पर लम्बवत् दिशाओं में गतिशील हो।
- जब केवल माध्यम गति कर रहा हो।
- जब स्त्रोत तथा प्रेक्षक के मध्य की दूरी नियत हो।
ध्वनि के परावर्तन में डॉप्लर प्रभाव (प्रतिध्वनि)
जब ध्वनि परावर्तक से परावर्तित होती है तो प्रेक्षक दो स्वर प्राप्त करता है, एक सीधा स्त्रोत से तथा दूसरा परावर्तक से। यदि दोनों आवृत्तियाँ भिन्न-भिन्न है तब इन तरंगोंं के अध्यारोपण से विस्पन्द बनते हैं तथा विस्पन्द आवृत्ति से हम स्त्रोत की चाल ज्ञात कर सकते हैं।
Case I :-
जब स्त्रोत एक स्थिर दीवार की ओर गति करता है।- n'D= सीधी आभासी आवृत्ति
n'= आभासी आवृत्ति
n'R= परावर्तित आभासी आवृत्ति

n'=(VV−VS)n
n'R=n'
b=Δn
=n'R−n'D=0

n'=(VV−VS)n
b=Δn
=(VV−VS−VV+VS)n
=2VSVnV2−V2S≅(2VSV)n
नोट :- स्थिर दीवार आपतित ध्वनि के लिए श्रोता का तथा परावर्तित ध्वनि के लिए स्त्रोत का कार्य करती है।
Case II :-
जब स्त्रोत व श्रोता दोनों स्थिर दीवार की ओर गति करते है।
n'=(VV−x)n
n'R=(V+xV)n'
=[V+xV][VV−x]n
n'R=(V+xV−x)n
b=n'R−n'D
=(V+xV−x)n−n
b=2xV−xn
स्थितियाँ जब ध्वनि तरंगोंं के लिए डॉप्लर प्रभाव प्रेक्षित नहीं होता है :
- जब ध्वनि का स्त्रोत तथा प्रेक्षक दोनों स्थिर हो तब डॉप्लर प्रभाव प्रेक्षित नहीं होता है।
- जब स्त्रोत तथा प्रेक्षक दोनों समान दिशा में समान वेग से गतिशील हो।
- जब स्त्रोत तथा प्रेक्षक दोनों परस्पर लम्बवत् दिशाओं में गतिशील हो।
- जब केवल माध्यम गति कर रहा हो।
- जब स्त्रोत तथा प्रेक्षक के मध्य की दूरी नियत हो।
प्रकाश में डॉप्लर प्रभाव
- प्रकाश-स्त्रोत तथा प्रेक्षक की सापेक्ष गति के कारण, प्रकाश की आवृत्ति (अथवा तरंगदैर्ध्य) में प्रेक्षित आभासी परिवर्तन को 'प्रकाश में डॉप्लर प्रभाव' कहते है।
अर्थात् जब प्रेक्षक अथवा स्त्रोत किसी चाल से (चाहे स्त्रोत, प्रेक्षक की ओर या प्रेक्षक स्त्रोत की ओर) गति करे, आवृत्ति में परिवर्तन समान ही प्रेक्षित होता है।
निकट आने की स्थिति में
n'=n(1+vc1−vc)12
तथा
दूर जाने की स्थिति में
n'=n(1−vc1+vc)12
तथा
यदि v<<C तब निकट आने की स्थिति में
n'≈n(1+vc),
दूर जाने की स्थिति में
n'≈n(1−vc)
अतः कम चाल पर प्रकाश तथा ध्वनि में डॉप्लर प्रभाव समान सूत्रों से ज्ञात करते हैं।
डॉप्लर विस्थापन :
जब दूर स्थित तारों से उत्सर्जित विकिरणों का रेडियो दूरदर्शी द्वारा विश्लेषण किया जाता है तथा इसकी तुलना दृश्य स्पेक्ट्रम पर माध्य तरंगदैर्ध्य पर केन्द्रित उनकी प्राकृतिक विकिरण तरंगदैर्ध्य से की जाती है तो यह प्रेक्षित होता है कि उत्सर्जित विकिरण में लाल या बैंगनी सिरे की ओर विस्थापन होता है।लाल विस्थापन :
Δλ=λ'−λ
=(vc)λ
⇒Δλ=vcλ
बैंगनी विस्थापन (या नीला विस्थापन) :
Δλ=λ'−λ
=−(vc)λ
⇒Δλ=−vcλ
निकट आने की स्थिति में आवृत्ति बढ़ती है जबकि तरंगदैर्ध्य घटती है अर्थात् विस्थापन Δλ, स्पेक्ट्रम के नीले सिरे की ओर होता है जबकि दूर जाने की स्थिति में आवृत्ति घटती है तथा तरंगदैर्ध्य बढ़ती है अर्थात विस्थापन लाल सिरे की ओर होता है।
प्रकाश के डॉप्लर प्रभाव का अनुप्रयोग :
प्रकाश के डॉप्लर प्रभाव से तारों तथा गैलेक्सियों की गति का अनुमान लगाया जाता है। तारों से आने वाले प्रकाश के स्पेक्ट्रम में हाइड्रोजन, हीलियम, सोडियम, इत्यादि तत्वों की स्पेक्ट्रमी रेखाएँ पायी जाती है।
यदि कोई तारा पृथ्वी पर स्थित प्रेक्षक से दूर जा रहा हो अथवा प्रेक्षक की ओर आ रहा हो, तो इसके प्रकाश की स्पेक्ट्रमी रेखाएँ स्पेक्ट्रम के दीर्घ तरंगदैर्ध्य (लाल) अथवा लघु तरंगदैर्ध्य (बैंगनी) भाग की ओर विस्थापित हो जायेंगी। इस घटना से तारे का वेग ज्ञात किया जा सकता है।
प्रकाश में डॉप्लर प्रभाव
- प्रकाश-स्त्रोत तथा प्रेक्षक की सापेक्ष गति के कारण, प्रकाश की आवृत्ति (अथवा तरंगदैर्ध्य) में प्रेक्षित आभासी परिवर्तन को 'प्रकाश में डॉप्लर प्रभाव' कहते है।
अर्थात् जब प्रेक्षक अथवा स्त्रोत किसी चाल से (चाहे स्त्रोत, प्रेक्षक की ओर या प्रेक्षक स्त्रोत की ओर) गति करे, आवृत्ति में परिवर्तन समान ही प्रेक्षित होता है।
निकट आने की स्थिति में
n'=n(1+vc1−vc)12
तथा
दूर जाने की स्थिति में
n'=n(1−vc1+vc)12
तथा
यदि v<<C तब निकट आने की स्थिति में
n'≈n(1+vc),
दूर जाने की स्थिति में
n'≈n(1−vc)
अतः कम चाल पर प्रकाश तथा ध्वनि में डॉप्लर प्रभाव समान सूत्रों से ज्ञात करते हैं।
डॉप्लर विस्थापन :
जब दूर स्थित तारों से उत्सर्जित विकिरणों का रेडियो दूरदर्शी द्वारा विश्लेषण किया जाता है तथा इसकी तुलना दृश्य स्पेक्ट्रम पर माध्य तरंगदैर्ध्य पर केन्द्रित उनकी प्राकृतिक विकिरण तरंगदैर्ध्य से की जाती है तो यह प्रेक्षित होता है कि उत्सर्जित विकिरण में लाल या बैंगनी सिरे की ओर विस्थापन होता है।लाल विस्थापन :
Δλ=λ'−λ
=(vc)λ
⇒Δλ=vcλ
बैंगनी विस्थापन (या नीला विस्थापन) :
Δλ=λ'−λ
=−(vc)λ
⇒Δλ=−vcλ
निकट आने की स्थिति में आवृत्ति बढ़ती है जबकि तरंगदैर्ध्य घटती है अर्थात् विस्थापन Δλ, स्पेक्ट्रम के नीले सिरे की ओर होता है जबकि दूर जाने की स्थिति में आवृत्ति घटती है तथा तरंगदैर्ध्य बढ़ती है अर्थात विस्थापन लाल सिरे की ओर होता है।
प्रकाश के डॉप्लर प्रभाव का अनुप्रयोग :
प्रकाश के डॉप्लर प्रभाव से तारों तथा गैलेक्सियों की गति का अनुमान लगाया जाता है। तारों से आने वाले प्रकाश के स्पेक्ट्रम में हाइड्रोजन, हीलियम, सोडियम, इत्यादि तत्वों की स्पेक्ट्रमी रेखाएँ पायी जाती है।
यदि कोई तारा पृथ्वी पर स्थित प्रेक्षक से दूर जा रहा हो अथवा प्रेक्षक की ओर आ रहा हो, तो इसके प्रकाश की स्पेक्ट्रमी रेखाएँ स्पेक्ट्रम के दीर्घ तरंगदैर्ध्य (लाल) अथवा लघु तरंगदैर्ध्य (बैंगनी) भाग की ओर विस्थापित हो जायेंगी। इस घटना से तारे का वेग ज्ञात किया जा सकता है।
उदाहरण 18
दो स्वरित्रों A तथा B की मूल आवृत्ति 85 Hz है O के विपरीत ओर स्थित हैं। ये स्थिर प्रेक्षक O के सापेक्ष 10 m/s वेग से गति करते हैं। स्वरित्र A प्रेक्षक से दूर जबकि स्वरित्र B प्रेक्षक की ओर गति करता है। स्वरित्र A की गति की दिशा में हवा 10 m/s चाल से बह रही है। प्रेक्षक द्वारा प्रेक्षित विस्पन्द आवृत्ति (हर्ट्ज़ में) ज्ञात कीजिए।
[वायु में ध्वनि की चाल 340 m/s लें]
fobserver for source 'A'=f0[vsound−vmediumvsound−vmedium+vsource]
=3334f0
fobserver for source 'B' =f0[vsound+vmediumvsound+vmedium−vsource]
=3534f0
∴ विस्पंद आवृत्ति =f1−f2
=(35−3334)f0=5
उदाहरण 18
दो स्वरित्रों A तथा B की मूल आवृत्ति 85 Hz है O के विपरीत ओर स्थित हैं। ये स्थिर प्रेक्षक O के सापेक्ष 10 m/s वेग से गति करते हैं। स्वरित्र A प्रेक्षक से दूर जबकि स्वरित्र B प्रेक्षक की ओर गति करता है। स्वरित्र A की गति की दिशा में हवा 10 m/s चाल से बह रही है। प्रेक्षक द्वारा प्रेक्षित विस्पन्द आवृत्ति (हर्ट्ज़ में) ज्ञात कीजिए।
[वायु में ध्वनि की चाल 340 m/s लें]
fobserver for source 'A'=f0[vsound−vmediumvsound−vmedium+vsource]
=3334f0
fobserver for source 'B' =f0[vsound+vmediumvsound+vmedium−vsource]
=3534f0
∴ विस्पंद आवृत्ति =f1−f2
=(35−3334)f0=5
उदाहरण 19

बिन्दु A पर खड़े व्यक्ति को ट्रेन के हॉर्न की आवृत्ति क्या सुनाई देगी जब ट्रेन का इंजन B पर हॉर्न बजाता है।
n'=(vv−vscosθ)n
AB दिशा में वेग =vscosθ
=[120×518]×cosθ
=120×518×35
=20m/sec
⇒n'=(340340−20)×640
=680Hz.
उदाहरण 19

बिन्दु A पर खड़े व्यक्ति को ट्रेन के हॉर्न की आवृत्ति क्या सुनाई देगी जब ट्रेन का इंजन B पर हॉर्न बजाता है।
n'=(vv−vscosθ)n
AB दिशा में वेग =vscosθ
=[120×518]×cosθ
=120×518×35
=20m/sec
⇒n'=(340340−20)×640
=680Hz.
उदाहरण 20
स्टेशन यार्ड में खड़ी कोई रेलगाड़ी शांत वायु में 400 हर्ट्ज आवृत्ति की सीटी बजा रही है। तभी 10 ms−1 चाल से यार्ड से स्टेशन की ओर वायु बहने लगती है। स्टेशन के प्लेटफार्म पर खड़े किसी प्रेक्षक के लिए ध्वनि की आवृत्ति, तरंगदैर्ध्य तथा चाल क्या है? क्या यह स्थिति उस स्थिति के समरूप है जिसमें वायु शांत हो तथा प्रेक्षक 10 ms−1 चाल से यार्ड की ओर दौड़ रहा हो? शांत वायु में ध्वनि की चाल 340 ms−1 ले सकते है।
यहाँ स्रोत और प्रेक्षक दोनों विरामावस्था में है। जब स्रोत से प्रेक्षक की ओर हवा चलना आरम्भ होती है तब ध्वनि का प्रभावी वेग,
vsound=v+vm
=340+10=350ms−1
चूंकि स्रोत और प्रेक्षक के बीच कोई सापेक्ष गति नहीं है। अत: आवृत्ति समान रहती है। अर्थात 400Hz.
इसलिये तरंदैर्ध्य λ=vsoundn=350400=0.875m
दोनों परिस्थितियाँ एकदम सर्वसम नहीं है क्योंकि दूसरी स्थिति में माध्यम विरामावस्था में है जबकि प्रेक्षक गतिशील है।
उदाहरण 20
स्टेशन यार्ड में खड़ी कोई रेलगाड़ी शांत वायु में 400 हर्ट्ज आवृत्ति की सीटी बजा रही है। तभी 10 ms−1 चाल से यार्ड से स्टेशन की ओर वायु बहने लगती है। स्टेशन के प्लेटफार्म पर खड़े किसी प्रेक्षक के लिए ध्वनि की आवृत्ति, तरंगदैर्ध्य तथा चाल क्या है? क्या यह स्थिति उस स्थिति के समरूप है जिसमें वायु शांत हो तथा प्रेक्षक 10 ms−1 चाल से यार्ड की ओर दौड़ रहा हो? शांत वायु में ध्वनि की चाल 340 ms−1 ले सकते है।
यहाँ स्रोत और प्रेक्षक दोनों विरामावस्था में है। जब स्रोत से प्रेक्षक की ओर हवा चलना आरम्भ होती है तब ध्वनि का प्रभावी वेग,
vsound=v+vm
=340+10=350ms−1
चूंकि स्रोत और प्रेक्षक के बीच कोई सापेक्ष गति नहीं है। अत: आवृत्ति समान रहती है। अर्थात 400Hz.
इसलिये तरंदैर्ध्य λ=vsoundn=350400=0.875m
दोनों परिस्थितियाँ एकदम सर्वसम नहीं है क्योंकि दूसरी स्थिति में माध्यम विरामावस्था में है जबकि प्रेक्षक गतिशील है।
उदाहरण 21
किसी पनडुब्बी से आबद्ध कोई 'सोनार' निकाय 40.0 किलो हर्ट्ज़ आवृत्ति पर प्रचालन करता है। कोई शत्रु-पनडुब्बी 360 किमी/घण्टा चाल से इस सोनार की ओर गति करती है। पनडुब्बी से परावर्तित ध्वनि की आवृत्ति क्या है? जल में ध्वनि की चाल 1450 मी/से लीजिए।
जैसा कि शत्रु की पनडुब्बी द्वारा ध्वनि सुनी जा जाती है।
क्योंकि यहाँ प्रेक्षक (शत्रु का जहाज) स्रोत (SONAR) की ओर गति कर रहा है।
∴ आभासी आवृत्ति n'=(v+v0v−vs)n
=(1450+1001450)×40×103
=15501450×40×103Hz
ध्वनि के परावर्तन पश्चात दुश्मन का जहाज n' आवृत्ति वाले स्रोत की तरह कार्य करता है। यह स्रोत 100ms−1 की चाल से प्रेक्षक (SONAR) की ओर गति करता है।
∴ शत्रु के जहाज से परावर्तित ध्वनि की आभासी आवृत्ति
n''=(v−v0v−vs)n'
=(1450−01450−100)×(15501450×40×103)
=45.93kHz
उदाहरण 21
किसी पनडुब्बी से आबद्ध कोई 'सोनार' निकाय 40.0 किलो हर्ट्ज़ आवृत्ति पर प्रचालन करता है। कोई शत्रु-पनडुब्बी 360 किमी/घण्टा चाल से इस सोनार की ओर गति करती है। पनडुब्बी से परावर्तित ध्वनि की आवृत्ति क्या है? जल में ध्वनि की चाल 1450 मी/से लीजिए।
जैसा कि शत्रु की पनडुब्बी द्वारा ध्वनि सुनी जा जाती है।
क्योंकि यहाँ प्रेक्षक (शत्रु का जहाज) स्रोत (SONAR) की ओर गति कर रहा है।
∴ आभासी आवृत्ति n'=(v+v0v−vs)n
=(1450+1001450)×40×103
=15501450×40×103Hz
ध्वनि के परावर्तन पश्चात दुश्मन का जहाज n' आवृत्ति वाले स्रोत की तरह कार्य करता है। यह स्रोत 100ms−1 की चाल से प्रेक्षक (SONAR) की ओर गति करता है।
∴ शत्रु के जहाज से परावर्तित ध्वनि की आभासी आवृत्ति
n''=(v−v0v−vs)n'
=(1450−01450−100)×(15501450×40×103)
=45.93kHz
उदाहरण 22
दो रेलगाडियाँ विपरीत दिशाओं में 126 km/hr की चाल से चल रही है। जब ये एक दूसरे को पार करती है, उनमें से एक सीटी बजाती है। यदि सीटी के स्वर की आवृत्ति 2.22 किलोहर्ट्ज़ है तो दूसरी रेलगाड़ी में स्थित श्रोता द्वारा सुनी गयी आवृत्ति ज्ञात कीजिए।
(a) रेलगाड़ियों के एक दूसरे को पार करने से पहले
(b) रेलगाड़ियों के एक दूसरे को पार करने के बाद (vsound=335m/s)
यहाँ v1=126×518=35m/s
(a) →v1 v1←
प्रेक्षित आवृत्ति n'=(v+v1v−v1)×n
=(335+35335−35)×2220
=2738Hz
(b) v1← →v1
प्रेक्षित आवृत्ति n'=(v−v1v+v1)×n
=(335−35335+35)×2220
=1800Hz
उदाहरण 22
दो रेलगाडियाँ विपरीत दिशाओं में 126 km/hr की चाल से चल रही है। जब ये एक दूसरे को पार करती है, उनमें से एक सीटी बजाती है। यदि सीटी के स्वर की आवृत्ति 2.22 किलोहर्ट्ज़ है तो दूसरी रेलगाड़ी में स्थित श्रोता द्वारा सुनी गयी आवृत्ति ज्ञात कीजिए।
(a) रेलगाड़ियों के एक दूसरे को पार करने से पहले
(b) रेलगाड़ियों के एक दूसरे को पार करने के बाद (vsound=335m/s)
यहाँ v1=126×518=35m/s
(a) →v1 v1←
प्रेक्षित आवृत्ति n'=(v+v1v−v1)×n
=(335+35335−35)×2220
=2738Hz
(b) v1← →v1
प्रेक्षित आवृत्ति n'=(v−v1v+v1)×n
=(335−35335+35)×2220
=1800Hz
उदाहरण 23
एक तारा जो 5000 Å तरंग दैर्ध्य के विकिरण उत्सर्जित कर रहा है, 1.5×103m/s वेग से पृथ्वी के समीप आ रहा है। पृथ्वी द्वारा ग्रहण किये गये विकिरण की तरंगदैर्ध्य में परिवर्तन की गणना कीजिये।
Δλ=vcλ
=1.5×1033×108×5000
=0.025Å
उदाहरण 23
एक तारा जो 5000 Å तरंग दैर्ध्य के विकिरण उत्सर्जित कर रहा है, 1.5×103m/s वेग से पृथ्वी के समीप आ रहा है। पृथ्वी द्वारा ग्रहण किये गये विकिरण की तरंगदैर्ध्य में परिवर्तन की गणना कीजिये।
Δλ=vcλ
=1.5×1033×108×5000
=0.025Å
उदाहरण 24
एक व्यक्ति स्कूटर पर 36 km/hr की चाल के साथ फैक्टरी से दूर जाते हुए, फैक्टरी का सायरन सुनता है। यदि सायरन की वास्तविक आवृत्ति 700 हर्ट्ज़ है और स्कूटर की दिशा में 36 किमी/घंटा की गति से हवा चल रही है, तो व्यक्ति द्वारा सुनी गई प्रेक्षित आवृत्ति ज्ञात कीजिये। (दिया है: ध्वनि की गति = 340m/s)
इस स्थिति में n'=(v+w−v0v+w)n
जहाँ w=v0=36km/hr=10m/s
n'=(340+10−10340+10)×700
=340350×700
=680Hz
उदाहरण 24
एक व्यक्ति स्कूटर पर 36 km/hr की चाल के साथ फैक्टरी से दूर जाते हुए, फैक्टरी का सायरन सुनता है। यदि सायरन की वास्तविक आवृत्ति 700 हर्ट्ज़ है और स्कूटर की दिशा में 36 किमी/घंटा की गति से हवा चल रही है, तो व्यक्ति द्वारा सुनी गई प्रेक्षित आवृत्ति ज्ञात कीजिये। (दिया है: ध्वनि की गति = 340m/s)
इस स्थिति में n'=(v+w−v0v+w)n
जहाँ w=v0=36km/hr=10m/s
n'=(340+10−10340+10)×700
=340350×700
=680Hz