Level 1 from ARIHANT PHYSICS Chapter 13 SIMPLE HARMONIC MOTION for Class 11
| Class 11 | PHYSICS |
| Chapter | SIMPLE HARMONIC MOTION |
| ARIHANT PHYSICS | Level 1 |
| Medium | English |
| Academic Year | 2023-2024 |
Question 1
(i) The acceleration (a) of a particle moving along a straight line is related to time (t) as per the differential equation d2adt2=−ba. b is a positive constant. Is the particle performing SHM? If yes, what is the time period?
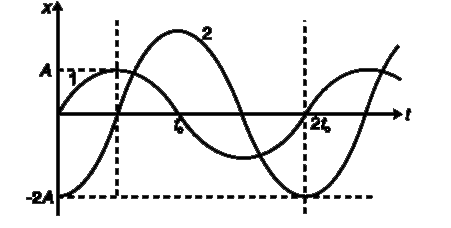
(ii) A particle is executing SHM on a straight line. A and B are two points at which its velocity is zero. It passes through a certain point P (AP>PB) with a speed of 3m/s at times recorded as t = 0, 0.5 s, 2.0 s, 2.5 s, 4.0 s, 4.5 s......Determine the maximum speed of the particle and also the ratio AP/PB. View SolutionQuestion 3
A particle moves along X axis such that its acceleration is given by a=−β(x−2),where β is a positive constant and x is the position co-ordinate.
(a) Is the motion simple harmonic?
(b) Calculate the time period of oscillations.
(c) How far is the origin of co-ordinate system from the equilibrium position? View SolutionQuestion 4
A particle is performing simple harmonic motion along the x axis about the origin. The amplitude of oscillation is a. A large number of photographs of the particle are shot at regular intervals of time with a high speed camera. It was found that photographs having the particle at x1+Δx were maximum in number and photographs having the particle at x2+Δx were least in number. What are values of x1 and x2? View SolutionQuestion 5
Position vector of a particle as a function of time is given by
→R=(asinωtˆi+(acosωt)ˆj+(bsinω0t)ˆk
The particle appears to be performing simple harmonic motion along z direction, to an observer moving in xy plane.
(a) Describe the path of the observer.
(b) Write the distance travelled by the observer himself in the time interval he sees the particle completing one oscillation. View SolutionQuestion 6
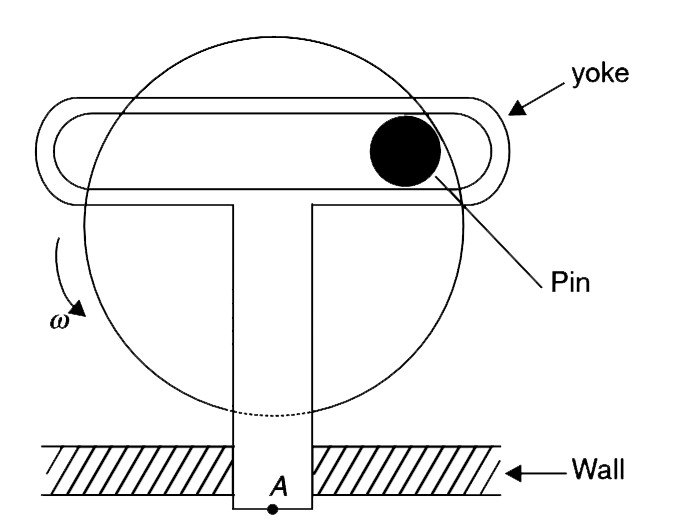
A wheel is revolving at an angular speed of ω. A pin welded at the circumference of the wheel forces a T shaped body to move up and down. The pin slides freely inside the slot of the yoke as the wheel rotates. The T shaped body is constrained to move vertically by a set of walls
(a) Find the time period of oscillatory motion of point A at the base of the T shaped body
(b) Is the motion of A simple harmonic?
View SolutionQuestion 7
(i) A particle is performing simple harmonic motion with time period T. At an instant its speed is 60% of its maximum value and is increasing. After an interval Δt its speed becomes 80% of its maximum value and is decreasing. Find the smallest value of Δt in terms of T.
(ii) A particle is doing SHM of amplitude 0.5 m and period π seconds. When in a position of instantaneous rest, it is given an impulse which imparts a velocity of 1m/s towards the equilibrium position. Find the new amplitude of oscillation and find how much less time will it take to arrive at the next position of instantaneous rest as compared to the case if the impulse had not been applied. View SolutionQuestion 8
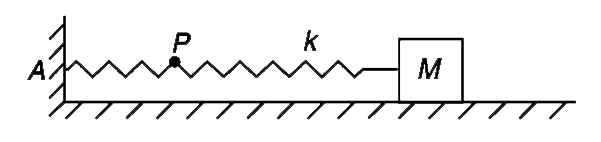
A block of mass M is tied to a spring of force constant k and placed on a smooth horizontal surface. The natural length of the spring is L. P is a point on the spring at a distance L4 from its fixed end. The block is set in oscillations with amplitude A. Find the maximum speed of point P on the spring.
View SolutionQuestion 9
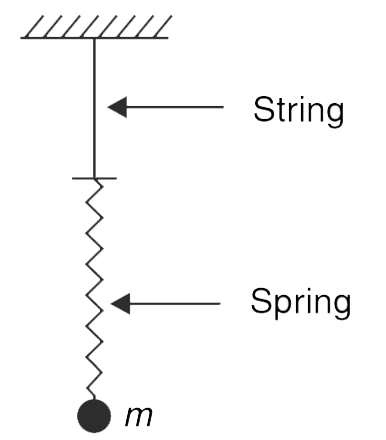
A particle of mass m is suspended with the help of a spring and an inextensible string as shown in the figure. Force constant of the spring is k. The particle is pulled down from its equilibrium position by a distance x and released.
(a) Find maximum value of x for which the motion of the particle will remain simple harmonic.
(b) Find maximum tension in the string if
x=mg2k
View SolutionQuestion 10
A block of mass M is placed on top of a hole in a horizontal table. A spring of force constant k is connected to the block through the hole. The other end of the massless spring has a particle of mass m connected to it. With what maximum amplitude can the particle oscillate up and down such that the block does not lose contact with the table?
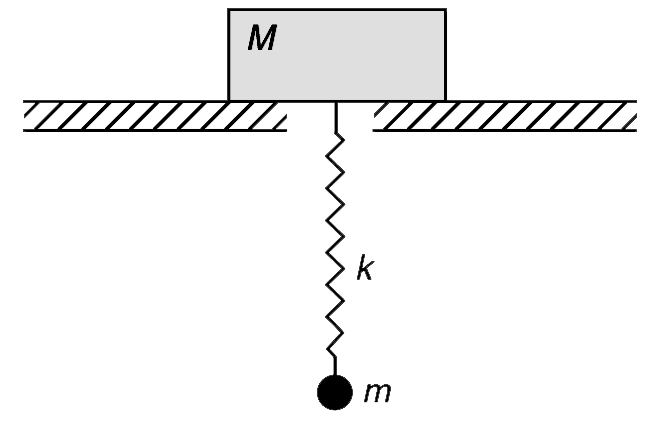View SolutionQuestion 11
A block of mass m is moving along positive x direction on a smooth horizontal surface with velocity u. It enters a rough horizontal region at x = 0. The coefficient of friction in this rough region varies according to μ=ax, where a is a positive constant and x is displacement of the block in the rough region. Find the time for which the block will slide in this rough regionView SolutionQuestion 12
(i) In the shown arrangement, both springs are relaxed. The coefficient of friction between m2 and m1 is μ. There is no friction between m1 and the horizontal surface. The blocks are displaced slightly and released. They move together without slipping on each other.
(a) If the small displacement of blocks is x then find the magnitude of acceleration of m2. What is time period of oscillations ?
(b) Find the ratio m1m2 so that the frictional force on m2 acts in the direction of its displacement from the mean position.
(ii) Two small blocks of same mass m are connected to two identical springs as shown in fig. Both springs have stiffness K and they are in their natural length when the blocks are at point O. Both the blocks are pushed so that one of the springs get compressed by a distance a and the other by a/2. Both the blocks are released from this position simultaneously. Find the time period of oscillations of the blocks if - (neglect the dimensions of the blocks)
(a) Collisions between them are elastic.
(b) Collisions between them are perfectly inelastic.
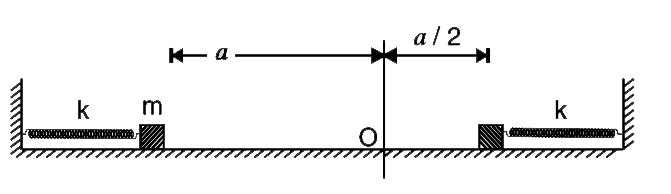View SolutionQuestion 13
Two blocks of mass 10 kg and 2 kg are connected by an ideal spring of spring constant K=800N/m and the system is placed on a horizontal surface as shown.
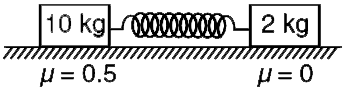
The coefficient of friction between 10 kg block and surface is 0.5 but friction is absent between 2 kg and the surface. Initially blocks are at rest and spring is relaxed. The 2 kg block is displaced to elongate the spring by 1 cm and is then released. (a) Will 10 kg block move subsequently? (b) Draw a graph representing variation of magnitude of frictional force on 10 kg block with time. Time t is measured from that instant when 2 kg block is released to move. View SolutionQuestion 14
A particle of mass m is tied at the end of a light string of length L, whose other end is fixed at point C (fig), and is revolving in a horizontal circle of radius r to form a conical pendulum. A parallel horizontal beam of light forms shadow of the particle on a vertical wall.
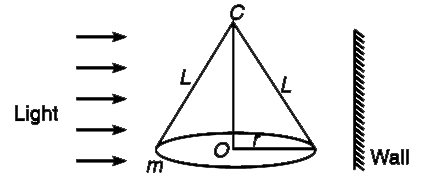
If the tension in the string is F find -
(a) The maximum acceleration of the shadow moving on the wall.
(b) The time period of the shadow moving on the wall. View SolutionQuestion 15
A small ball of mass m is attached to the middle of a tightly stretched perfectly flexible wire AB of length 2 l (figure ). The ball is given a small lateral displacement in horizontal direction and released. The initial tension (T) in the wire is high and change in it due to small lateral displacement of the ball can be neglected. Prove that the ball will perform simple harmonic motion, and calculate the period. If there is a device which can change the tension in the wire at will , how will the time period change if tension in the wire is increased
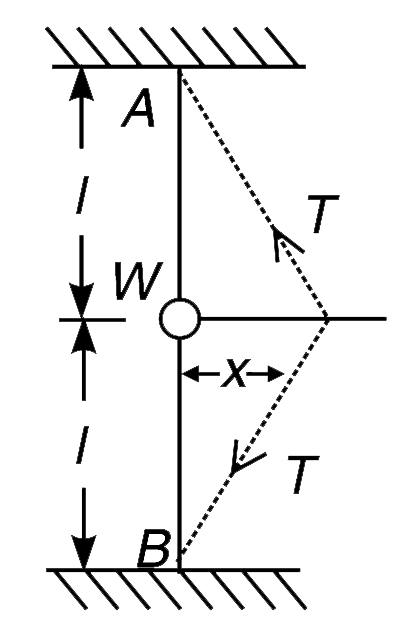View SolutionQuestion 16
A simple pendulum oscillating with a small amplitude has a time period of T=1.0s . A horizontal thin rod is now placed beneath the point of suspension at a distance equal to half the length of the pendulum. The string collides with the rod once in each oscillation and there is no loss of energy in such collisions. Find the new time period T of the pendulumView SolutionQuestion 17
(i) A small steel ball (B) is at rest on the edge of a table of height h. Another identical steel ball (A) is tied to a light string of length L =1.0 m and is released from the position shown so that it swings like a pendulum. At the lowest position of its path it hits the ball B which is at rest. Ball B flies off the table and hits the ground in time t. After collision the ball A keeps moving for a time t before coming to rest for the first time. Find the value of h if t = t. Collision between the balls is head on and coefficient of restitution is e = 0.995.
(ii) A pendulum has a particle of mass m attached to a massless rod of length L. The rod is released from a position where it makes an angle θ0(>π2) with the vertical. The time period of oscillation is observed to be T0. Another similar pendulum has a rod of length 2L. Time period of this pendulum when released from position θ0 is T. Which is larger T or T0 ?
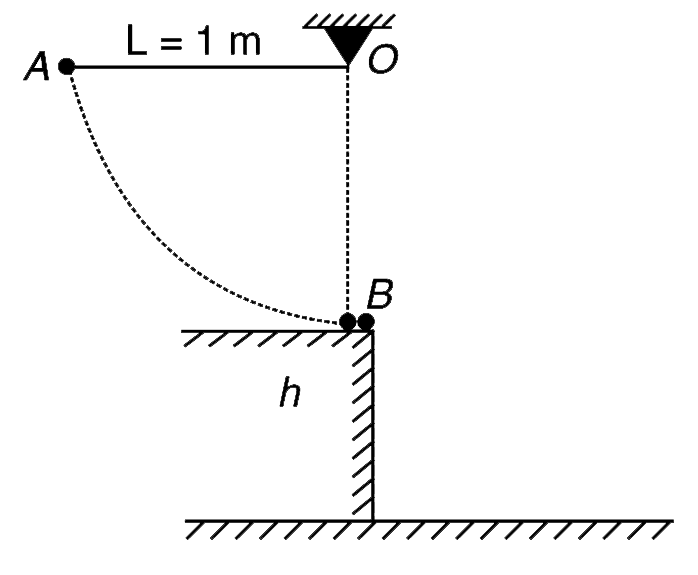View SolutionQuestion 18
A disc of mass M = 2m and radius R is pivoted at its centre. The disc is free to rotate in the vertical plane about its horizontal axis through its centre O. A particle of mass m is stuck on the periphery of the disc. Find the frequency of small oscillations of the system about its equilibrium position.
View SolutionQuestion 19
A rigid body is to be suspended like a physical pendulum so as to have a time period of T=0.2π second for small amplitude oscillations. The minimum distance of the point of suspension from the centre of mass of the body is l1=0.4m to get this time period. Find the maximum distance (l2) of a point of suspension from the centre of mass of the body so as to get the same time period. [g=10m/s2]View SolutionQuestion 20
A square plate of mass M and side length L is hinged at one of its vertex (A) and is free to rotate about it. Find the time period of small oscillations if
(a) the plate performs oscillations in the vertical plane of the figure. (Axis is perpendicular to figure.)
(b) the plate performs oscillations about a horizontal axis passing through A lying in the plane of the figure.
View Solution
