A particle of mass m is tied at the end of a light string of length L, whose other end is fixed at point C (fig), and is revolving in a horizontal circle of radius r to form a conical pendulum. A parallel horizontal beam of light forms shadow of the particle on a vertical wall.

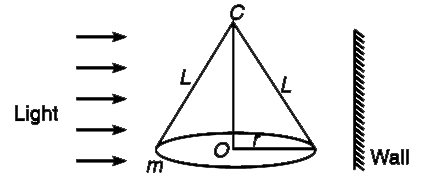
If the tension in the string is F find -
(a) The maximum acceleration of the shadow moving on the wall.
(b) The time period of the shadow moving on the wall.

Video Solution

Text Solution

Verified by Experts

The correct Answer is: $(a) \frac{1}{m} \sqrt{F^{2} - {(m g)}^{2}}, (b) 2 π {(\frac{m^{2} r^{2}}{F^{2} - {(m g)}^{2}})}^{1 / 4}$

Updated on:21/07/2023

Answer

Step by step video, text & image solution for A particle of mass m is tied at the end of a light string of length L, whose other end is fixed at point C (fig), and is revolving in a horizontal circle of radius r to form a conical pendulum. A parallel horizontal beam of light forms shadow of the particle on a vertical wall. If the tension in the string is F find - (a) The maximum acceleration of the shadow moving on the wall. (b) The time period of the shadow moving on the wall. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.

Updated on:21/07/2023

Class 11 PHYSICS SIMPLE HARMONIC MOTION

Topper's Solved these Questions

Knowledge Check

A particle of mass 200 g is attached to an ideal string of length 1.30 m whose upper end is fixed to ceiling. The particle is made to revolve in a horizontal circle of radius 50 cm. The tension in the string is (g = 10 m/ $s^{2}$ )
A $\frac{13}{6} N$
B $\frac{11}{6} N$
C $\frac{26}{5} N$
DZero
A particle of maas m is attched to a light string of length l, the other end of which is fixed. Initially the string is kept horizontal and the particle is given an upwrd velocity v. The particle is just able to complete a circle
AThe string becomes slack when the partice reaches its highest point
BThe velocity of the particle becomes zero at the highest point.
CThe kinetic energy of the ball in initial position was $\frac{1}{2} m v^{2} = m \frac{g}{}$
DThe particle again passes through the initial position.
A paricle of mass $m$ is tied to a light string of length $L$ and moving in a horizontal circle of radius $r$ with speed $v$ as shown. The forces acting on the particle are

A $m g and T$
B $m g, T, \frac{m v^{2}}{r}$ directed in wards
C $m g, T, \frac{m v^{2}}{r}$ directed outewards
D $\frac{m v^{2}}{r}$ only

ARIHANT-SIMPLE HARMONIC MOTION-Level 3

Home
Ask Doubt
Profile

The correct Answer is:(a)1m√F2−(mg)2,(b)2π(m2r2F2−(mg)2)1/4

Topper's Solved these Questions

Similar Questions

Knowledge Check

A particle of mass 200 g is attached to an ideal string of length 1.30 m whose upper end is fixed to ceiling. The particle is made to revolve in a horizontal circle of radius 50 cm. The tension in the string is (g = 10 m/s2)

A particle of maas m is attched to a light string of length l, the other end of which is fixed. Initially the string is kept horizontal and the particle is given an upwrd velocity v. The particle is just able to complete a circle

A paricle of mass m is tied to a light string of length L and moving in a horizontal circle of radius r with speed v as shown. The forces acting on the particle are

ARIHANT-SIMPLE HARMONIC MOTION-Level 3

The correct Answer is: $(a) \frac{1}{m} \sqrt{F^{2} - {(m g)}^{2}}, (b) 2 π {(\frac{m^{2} r^{2}}{F^{2} - {(m g)}^{2}})}^{1 / 4}$

A particle of mass 200 g is attached to an ideal string of length 1.30 m whose upper end is fixed to ceiling. The particle is made to revolve in a horizontal circle of radius 50 cm. The tension in the string is (g = 10 m/ $s^{2}$ )

A paricle of mass $m$ is tied to a light string of length $L$ and moving in a horizontal circle of radius $r$ with speed $v$ as shown. The forces acting on the particle are