All Questions from ARIHANT PHYSICS Chapter 15 TEMPERATURE AND THERMAL EXPANSION for Class 11
| Class 11 | PHYSICS |
| Chapter | TEMPERATURE AND THERMAL EXPANSION |
| ARIHANT PHYSICS | All Questions |
| Medium | English |
| Academic Year | 2023-2024 |
Question 2
Height of mercury in a barometer is h0=76.0 cm at a temperature of θ1=20∘C. If the actual atmospheric pressure does not change, but the temperature of the air, and hence the temperature of the mercury and the tube rises to θ2=35∘C, what will be the height of mercury column in the barometer now? Coefficient of volume expansion of mercury and coefficient of linear expansion of glass are
γHg=1.8×10−4.∘C−1,αg=0.09×10−4.∘C−1View SolutionQuestion 4
Two rods of different metals having the same area of cross section A are placed between the two massive walls as shown is Fig. The first rod has a length l1, coefficient of linear expansion α1 and Young's modulus Y1. The correcsponding quantities for second rod are l2,α2 and Y2. The temperature of both the rods is now raised by t∘C.
i. Find the force with which the rods act on each other (at higher temperature) in terms of given quantities.
ii. Also find the length of the rods at higher temperature.
View SolutionQuestion 5
Two rods of equal cross-sections, one of copper and the other of steel are joined to from a composite rod of length 2.0m at 20∘C the length of the copper rod is 0.5m. When the temperature is raised to 120∘C, the length of composite rod increases to 2.002m. If the composite rod is fixed between two rigid walls and thus not allowed to expand, it is found that the length of the component rod also do not change with increase in temperature. Calculate the Young's modulus of steel. Given Young's modulus of copper =1.3×1011N/m2 the coefficient of linear expansion of copper αC=1.6×10−5/.∘cView SolutionQuestion 6
Assume that the coefficient of linear expansion of the material of a rod remains constant, equal to α∘C−1 for a fairly large range of temperature. Length of the rod is L0 at temperature θ0. (a) Find the length of the rod at a high temperature θ. (b) Approximate the answer obtained in (a) to show that the length of the rod for small changes in temperature is given by L=L0[1+α(δ−δ0)] View SolutionQuestion 7
In a compensated pendulum a triangular frame ABC is made using two different metals. AB of length l1 is made using a metal having coefficient of linear expansion α1. BC and AC of length l2 each have coefficient of linear expansion α2. A heavy bob is attached at C. Pendulum can oscillate about the pivot D. Find l2l1 so that distance of bob from the pivot point D does not change with change in temperature.
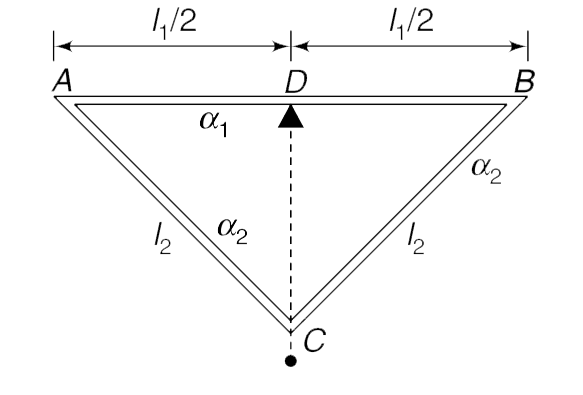View Solution