Two rods of different metals having the same area of cross section A are placed between the two massive walls as shown is Fig. The first rod has a length l1, coefficient of linear expansion α1 and Young's modulus Y1. The correcsponding quantities for second rod are l2,α2 and Y2. The temperature of both the rods is now raised by t∘C.
i. Find the force with which the rods act on each other (at higher temperature) in terms of given quantities.
ii. Also find the length of the rods at higher temperature.

The correct Answer is:(a) F=AT(l1α1+l2α2)(l1Y1+l2Y2)
(b) (l1+l1α1T−FAl1Y1),(l2+l2α2T−FAl2Y2)
Step by step video, text & image solution for Two rods of different metals having the same area of cross section A are placed between the two massive walls as shown is Fig. The first rod has a length l_1, coefficient of linear expansion alpha_1 and Young's modulus Y_1. The correcsponding quantities for second rod are l_2,alpha_2 and Y_2. The temperature of both the rods is now raised by t^@C. i. Find the force with which the rods act on each other (at higher temperature) in terms of given quantities. ii. Also find the length of the rods at higher temperature. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Two rods of length L1 and L2 are made of materials of coefficients of linear expansions α1 an α2 respectively such that L1α1=L2α2. The temperature of the rods is increased by ΔT and correspondingly the change in their respective lengths be ΔL1 and ΔL2
View SolutionTwo metal rods of the same length and area of cross-section are fixed end to end between rigid supports. The materials of the rods have Young module Y1 and Y2 , and coefficient of linear expansion α1 and α2 . The junction between the rod does not shift and the rods are cooled
View Solution
Knowledge Check
A rod has length L0 at a reference temperature T0, coefficient of linear expansion α, Young's modulus Y, area of cross section A. Rod lie unconstrained on a smooth surface temperature of rod is increased bby ΔT. Mark the correct statement
AFinal length of rod is given by L=L0(1+αΔT) for all the range of values of α.BIf average coefficient of linear expansion is constant as L varies the general expression for the final length is L=L0eαΔTCRod is unstrained as it expandsDCoefficient of expansion is defined as α=1LdLdtA metal rod having coefficient of linear expansion (α) and Young's modulus (Y) is heated to raise the temperature by Δθ. The stress exerted by the rod
AYαΔθBYΔθαCYαΔθDαΔθYA metal rof having coefficient of linear expansion α and Young's modulus Y is heated to raise its temperature by Δθ. The stress exerted by the rod is
AYαΔθBYΔθαCYαΔθDαΔθY
Two rods AB and BC of equal cross-sectional area are joined together and clamped between two fixed supports as shown in the figure. For the rod AB and road BC lengths are l1 and l2 coefficient of linear expansion are α1 and α2, young's modulus are Y1 and Y2, densities are ρ1 and ρ2 respectively. Now the temperature of the compound rod is increased by θ. Assume of that there is no significant change in the lengths of rod due to heating. then the time taken by transverse wave pulse to travel from end A to other end C of the compound rod is directly proportional to
_E01_086_Q01.png)
View SolutionThere are two rods of length l1 l2 and coefficient of linear expansions are α1 and α2 respectively.
Find equivalent coefficient of thermal expansion for their combination in series.
View SolutionThe coefficient of linear expansion of a rod is α and its length is L. The increase in temperature required to increase its legnth by 1% is
View SolutionTwo rods of different materials are placed between massive walls as shown in figure. The cross section of the rods is A, their moduil of elastricity are E1 and E2 respectively. If rods are heated by t degrees, then (coefficients of liner expansion of material of rods are α1 and α2 respectively)
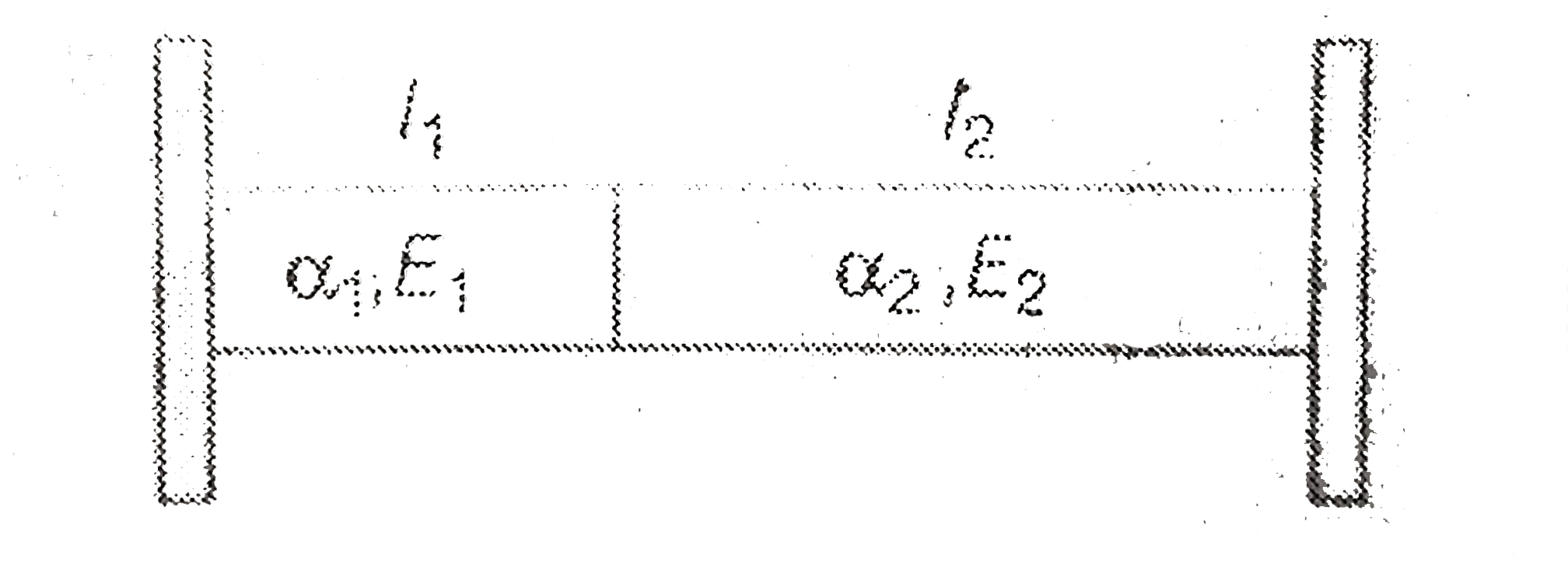
View SolutionA steel rod of length L0 . has a cross sectional area A. The force required to stretch this rod by the same amount as the expansion produced by heating it through ΔT is (coefficient of linear expansion of steel is α and young's modulus for steel is Y ).
View Solution
