Comprehension from CENGAGE PHYSICS (ENGLISH) Chapter 13 LINEAR AND ANGULAR SIMPLE HARMONIC MOTION for Class 11
| Class 11 | PHYSICS |
| Chapter | LINEAR AND ANGULAR SIMPLE HARMONIC MOTION |
| CENGAGE PHYSICS (ENGLISH) | Comprehension |
| Medium | English |
| Academic Year | 2023-2024 |
Question 1
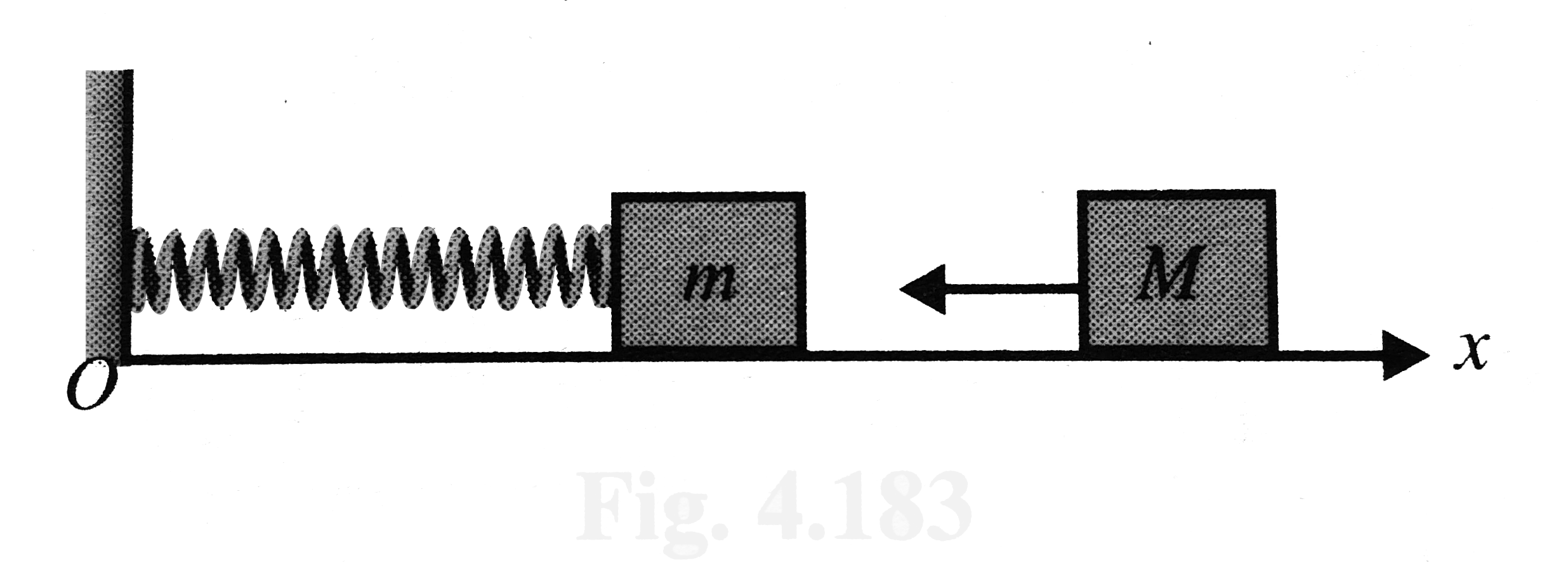
One end of an ideal spring is fixed to a wall at origin O and axis of spring is parallel to x-axis. A block of mass m=1kg is attached to free end of the spring and it is performing SHM. Equation of position of the block in co-ordinate system shown in figure is x=10+3sin(10t). Here, t is in second and x in cm. Another block of mass M=3kg, moving towards the origin with velocity 30cm/s collides with the block performing SHM at t=0 and gets stuck to it. Calculate

(a) new amplitude of oscillations,
(b) neweqution for position of the combined body,
( c) loss of energy during collision. Neglect friction.View SolutionQuestion 2
One end of an ideal spring in fixed in a wall at origin O and axis of spring is paralllel to the x-axis . A block of mass m=1kg is attached to the free end of the spring and it is performing SHm. Equation of position of the block in coordinate system Shown in Fig. is x=10+3sin(10t), where t is in second and x in cm. Another block of mass M=3kg moving towards the origin with velocity 30cms collides with the block performing SHM at t=0 and gets stuck to it.
Q. Angular frequency of oscillation after collision is
 View Solution
View SolutionQuestion 3
One end of an ideal spring in fixed in a wall at origin O and axis of spring is paralllel to the x-axis . A block of mass m=1kg is attached to the free end of the spring and it is performing SHm. Equation of position of the block in coordinate system Shown in Fig. is x=10+3sin(10t), where t is in second and x in cm. Another block of mass M=3kg moving towards the origin with velocity 30cms collides with the block performing SHM at t=0 and gets stuck to it.
Q. Angular frequency of oscillation after collision is
 View Solution
View SolutionQuestion 4
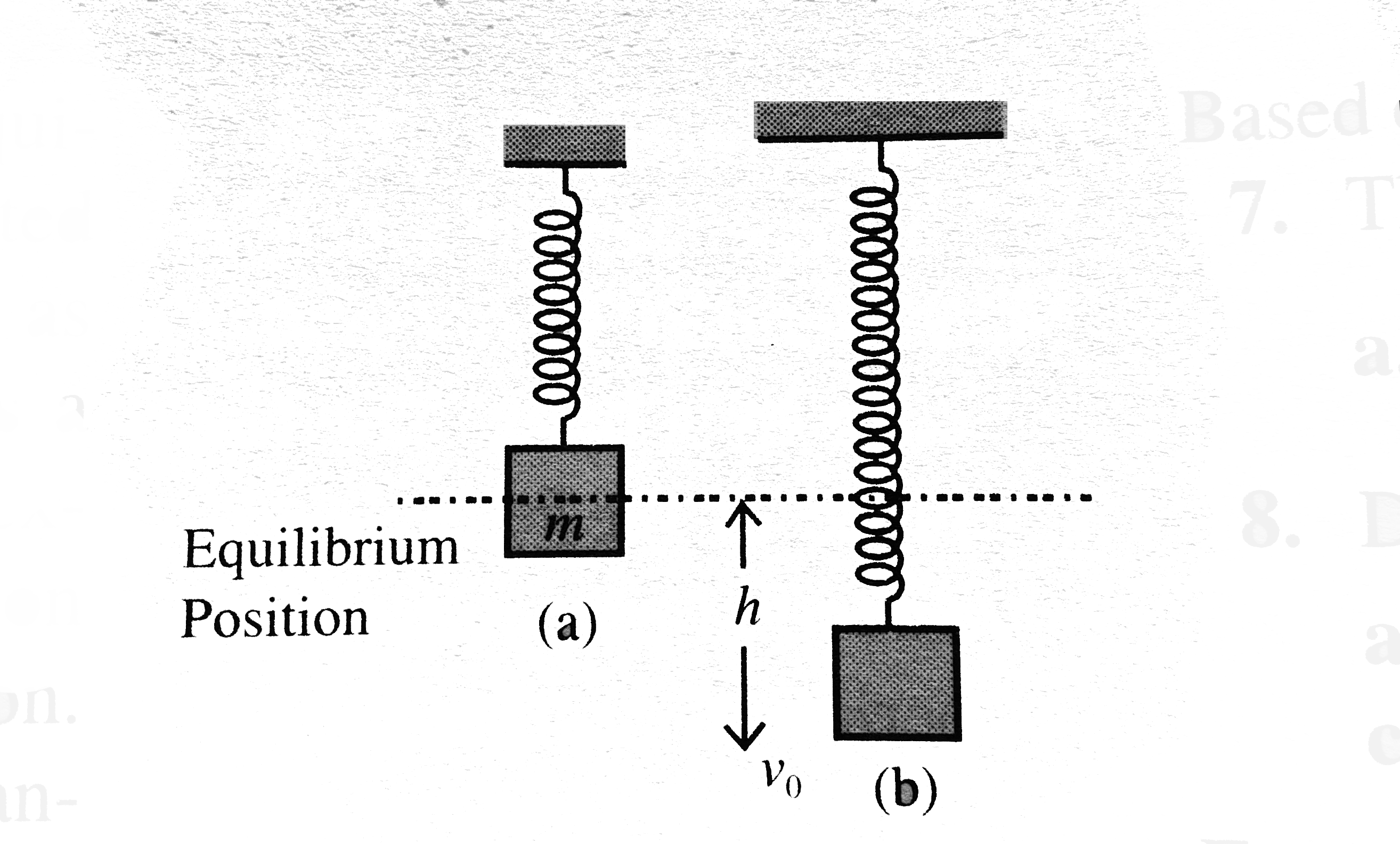
A block of mass m is connected to a spring constant k and is at rest in equilibrium as shown. Now, the block is Displacement by h below its equilibrium position and imparted a speed v0 towards down as shown in the Fig. As a result of the jerk, the block executes simple harmonic motion about its equilibrium position. Based on this information, answer the following question.
Q. The amplitude of oscillation is View SolutionQuestion 5
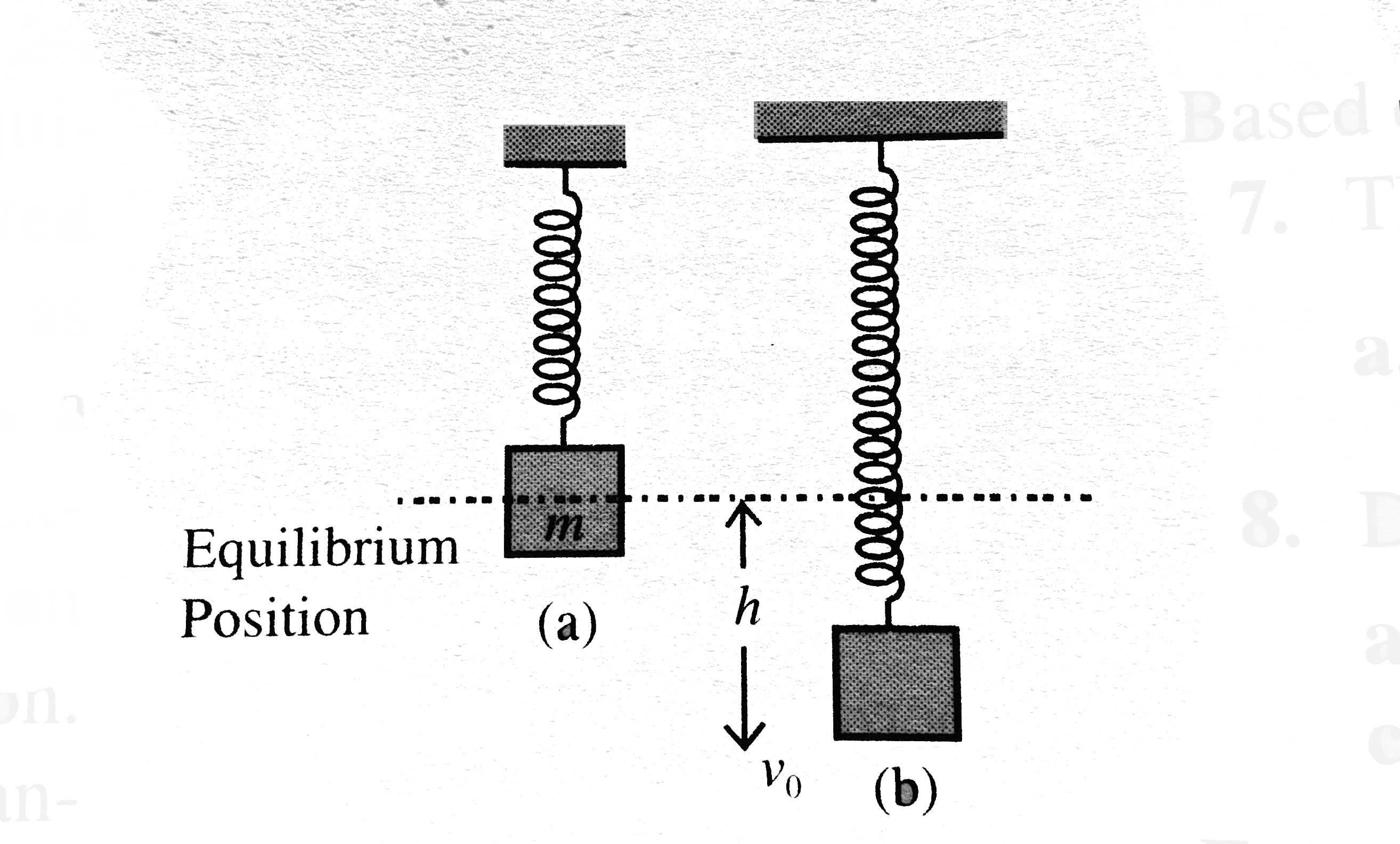
A block of mass m is connected to a spring constant k and is at rest in equilibrium as shown. Now, the block is Displacement by h below its equilibrium position and imparted a speed v0 towards down as shown in the Fig. As a result of the jerk, the block executes simple harmonic motion about its equilibrium position. Based on this information, answer the following question.
Q. The equation for the simple harmonic motion is View SolutionQuestion 6
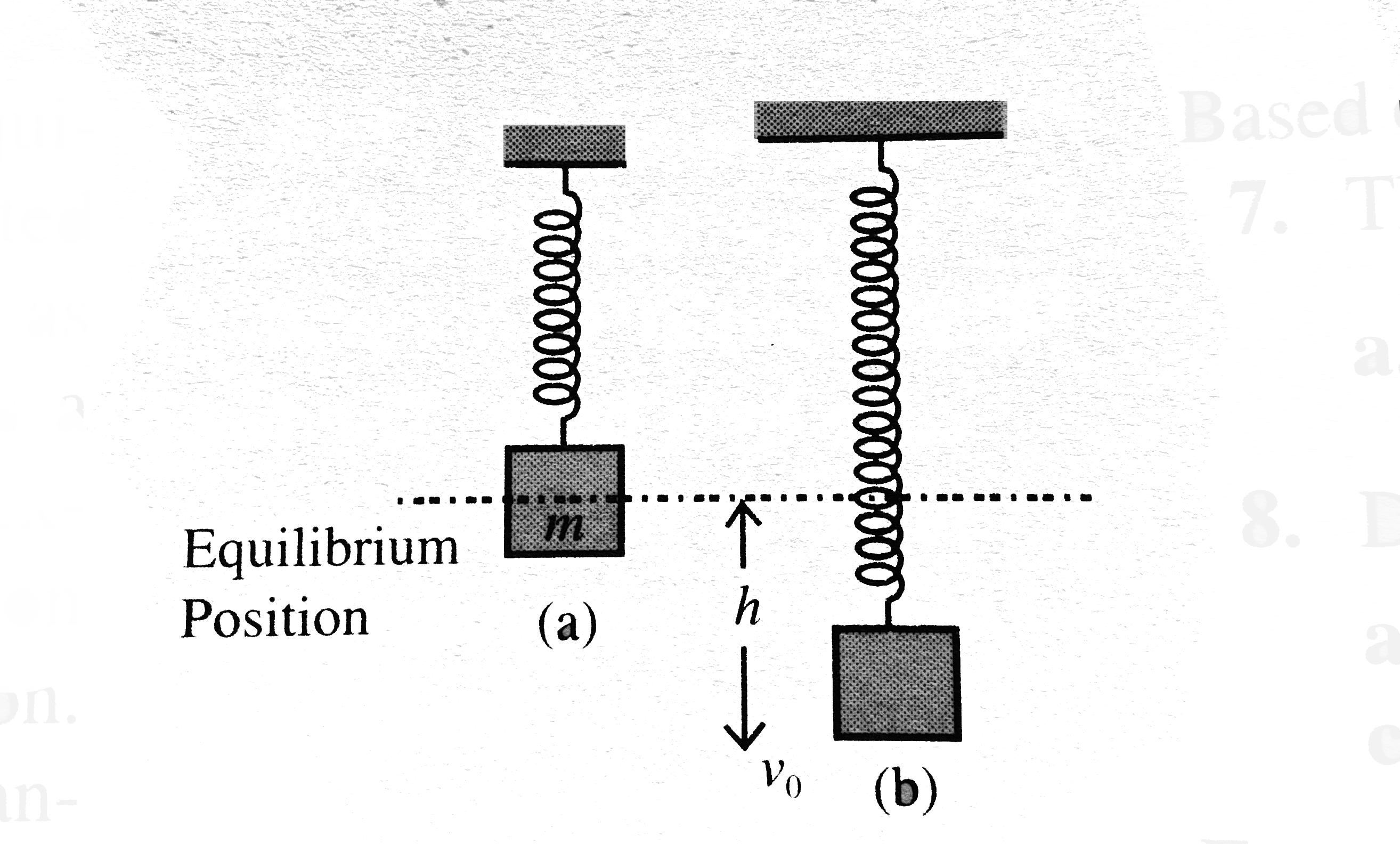
A block of mass m is connected to a spring constant k and is at rest in equilibrium as shown. Now, the block is Displacement by h below its equilibrium position and imparted a speed v0 towards down as shown in the Fig. As a result of the jerk, the block executes simple harmonic motion about its equilibrium position. Based on this information, answer the following question.
Q. Find the time taken by the block to cross the mean position for the first time.View SolutionQuestion 7

A block of mass m is connected to a spring of spring constant k as shown in Fig. The block is found at its equilibrium position t=1s and it has a velocity of +0.25ms at t=2s. The time period of oscillation is 6 s. Based on the given information answer the following question: Q. the amplitude of oscillation is View SolutionQuestion 8

A block of mass m is connected to a spring of spring constant k as shown in Fig. The block is found at its equilibrium position t=1s and it has a velocity of +0.25ms at t=2s. The time period of oscillation is 6 s. Based on the given information answer the following question:
Q. Determine the velocity of particle at t=5s.View SolutionQuestion 9
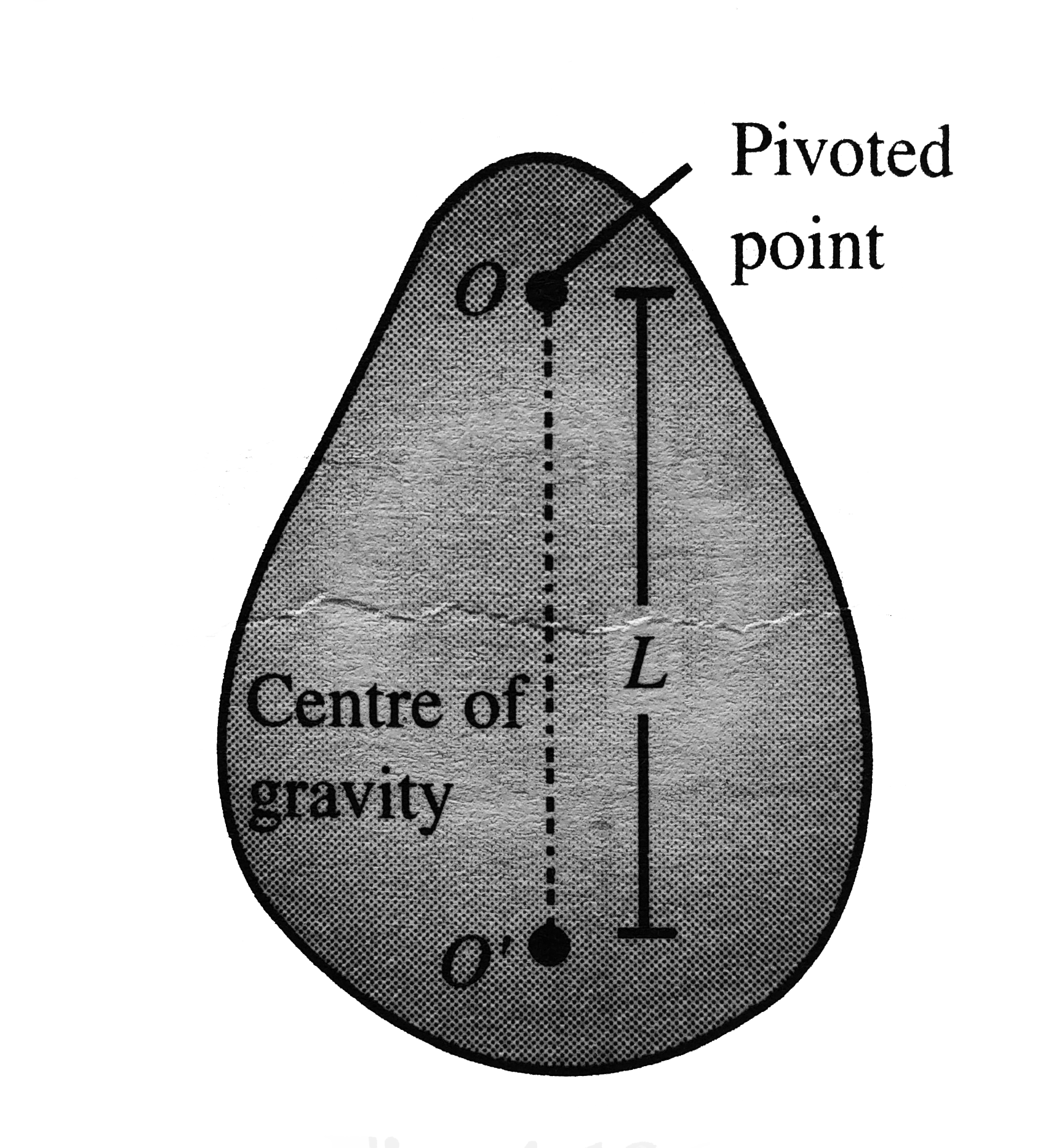
In physical pendulum, the time period for small oscillation is given by T=2π√IMgd where I is the moment of inertial of the body about an axis passing through a pivoted point O and perpendicular to the plane of oscillation and d is the separation point between centre of gravity and the pivoted point. In the physical pendulum a speacial point exists where if we concentrate the entire mass of body, the resulting simple pendulum (w.r.t. pivot point O) will have the same time period as that of physical pendulum This point is termed centre of oscillation.
T=2π√IMgd=2π√Lg Moreover, this point possesses two other important remarkable properties:
Property I: Time period of physical pendulum about the centre of oscillation (if it would be pivoted) is same as in the original case.
Property II: If an impulse is applied at the centre of oscillatioin in the plane of oscillation, the effect of this impulse at pivoted point is zero. Because of this property, this point is also known as the centre of percussion. From the given information answer the following question:
Q. A uniform rod of mass M and length L is pivoted about point O as shown in Figgt It is slightly rotated from its mean position so that it performs angular simple harmonic motion. For this physical pendulum, determine the time period oscillation.View SolutionQuestion 10
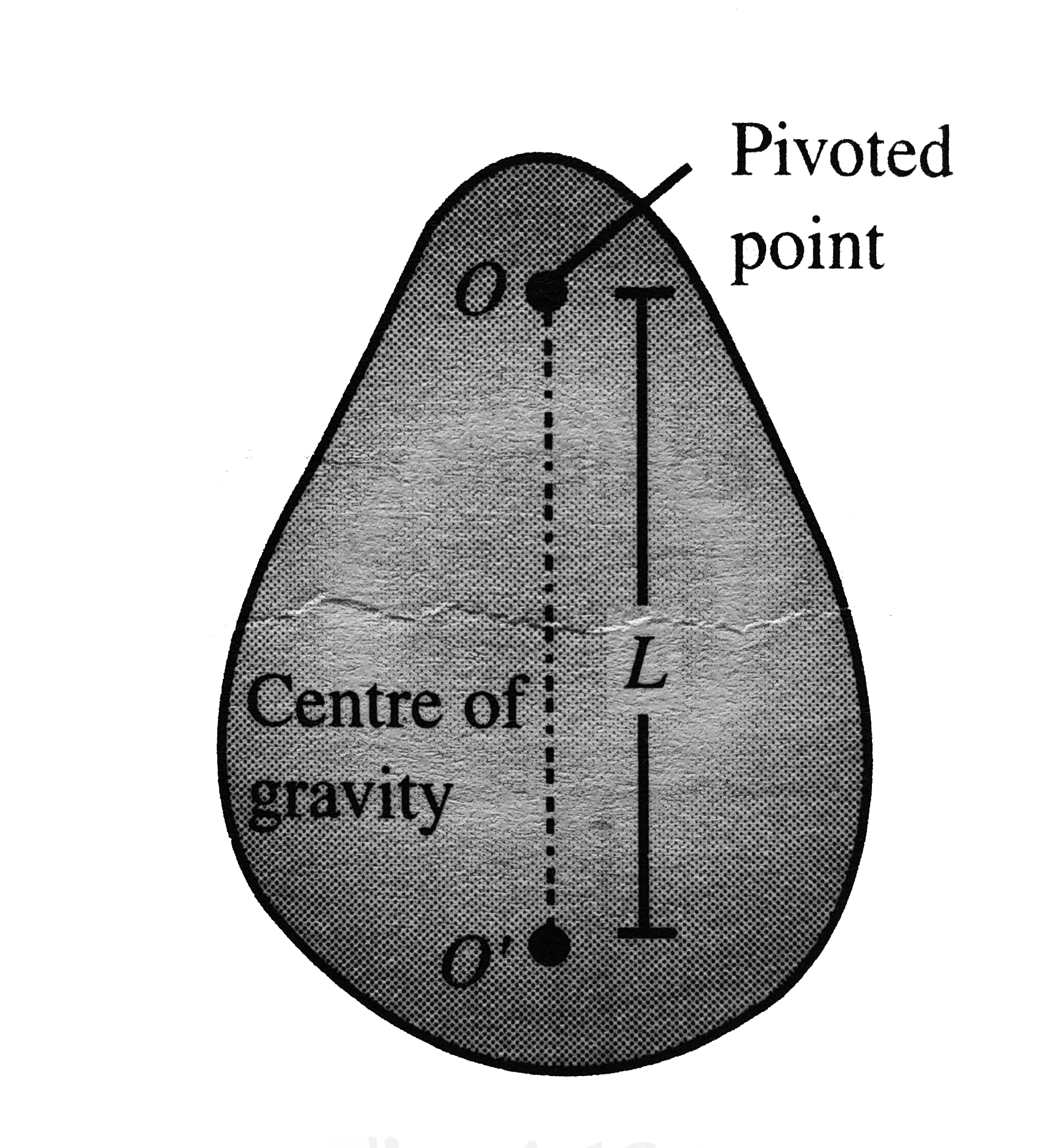
In physical pendulum, the time period for small oscillation is given by T=2π√IMgd where I is the moment of inertial of the body about an axis passing through a pivoted point O and perpendicular to the plane of oscillation and d is the separation point between centre of gravity and the pivoted point. In the physical pendulum a speacial point exists where if we concentrate the entire mass of body, the resulting simple pendulum (w.r.t. pivot point O) will have the same time period as that of physical pendulum This point is termed centre of oscillation.
T=2π√IMgd=2π√Lg Moreover, this point possesses two other important remarkable properties:
Property I: Time period of physical pendulum about the centre of oscillation (if it would be pivoted) is same as in the original case.
Property II: If an impulse is applied at the centre of oscillatioin in the plane of oscillation, the effect of this impulse at pivoted point is zero. Because of this property, this point is also known as the centre of percussion. From the given information answer the following question:
Q. For the above question, locate the centre of oscillation.
 View Solution
View SolutionQuestion 11
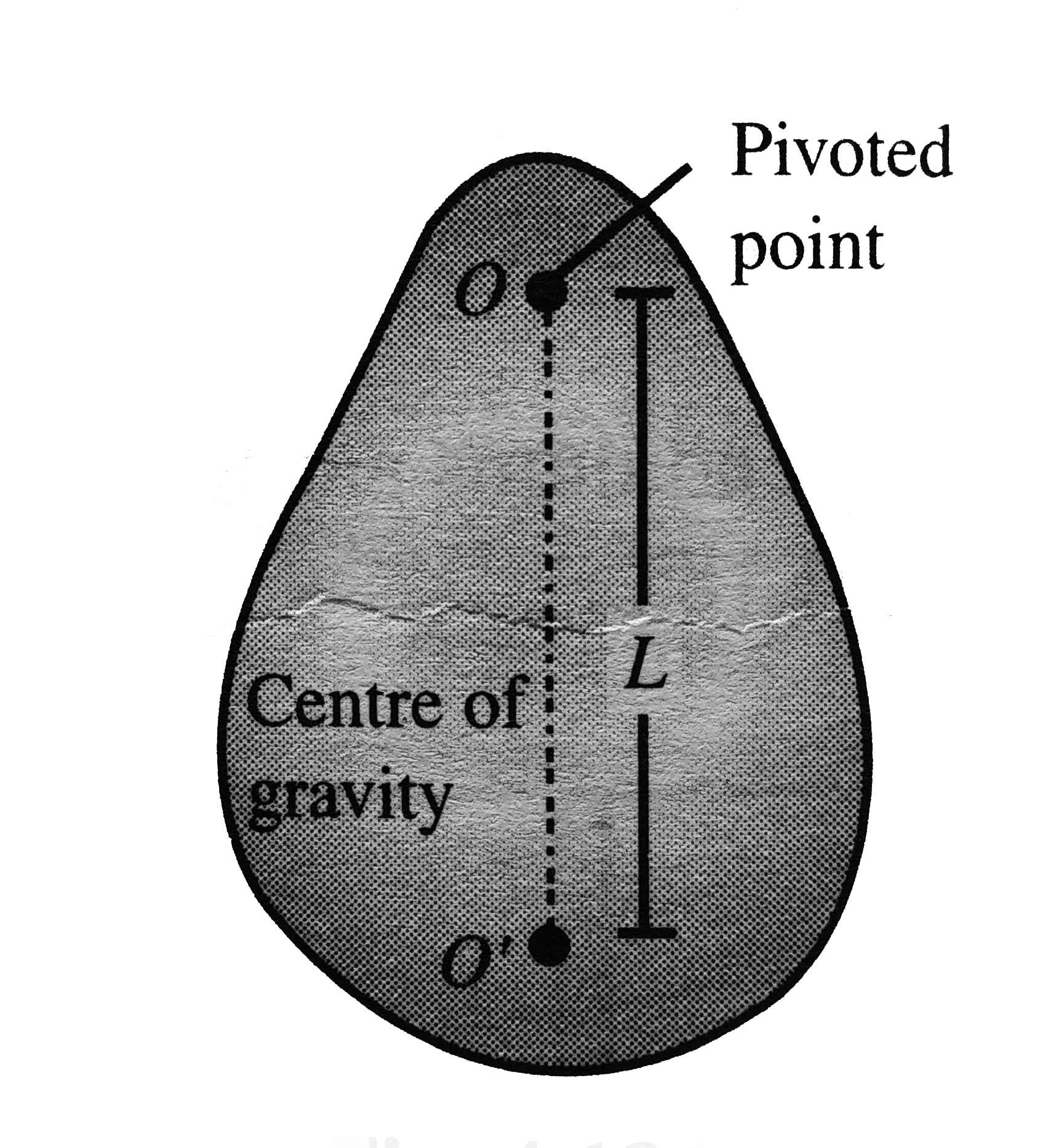
In physical pendulum, the time period for small oscillation is given by T=2π√IMgd where I is the moment of inertial of the body about an axis passing through a pivoted point O and perpendicular to the plane of oscillation and d is the separation point between centre of gravity and the pivoted point. In the physical pendulum a speacial point exists where if we concentrate the entire mass of body, the resulting simple pendulum (w.r.t. pivot point O) will have the same time period as that of physical pendulum This point is termed centre of oscillation.
T=2π√IMgd=2π√Lg Moreover, this point possesses two other important remarkable properties:
Property I: Time period of physical pendulum about the centre of oscillation (if it would be pivoted) is same as in the original case.
Property II: If an impulse is applied at the centre of oscillatioin in the plane of oscillation, the effect of this impulse at pivoted point is zero. Because of this property, this point is also known as the centre of percussion. From the given information answer the following question:
Q. If an impulse J is applied at the centre of oscillation in the plane of oscillation, then angular velocity of the rod will be .
 View Solution
View SolutionQuestion 12
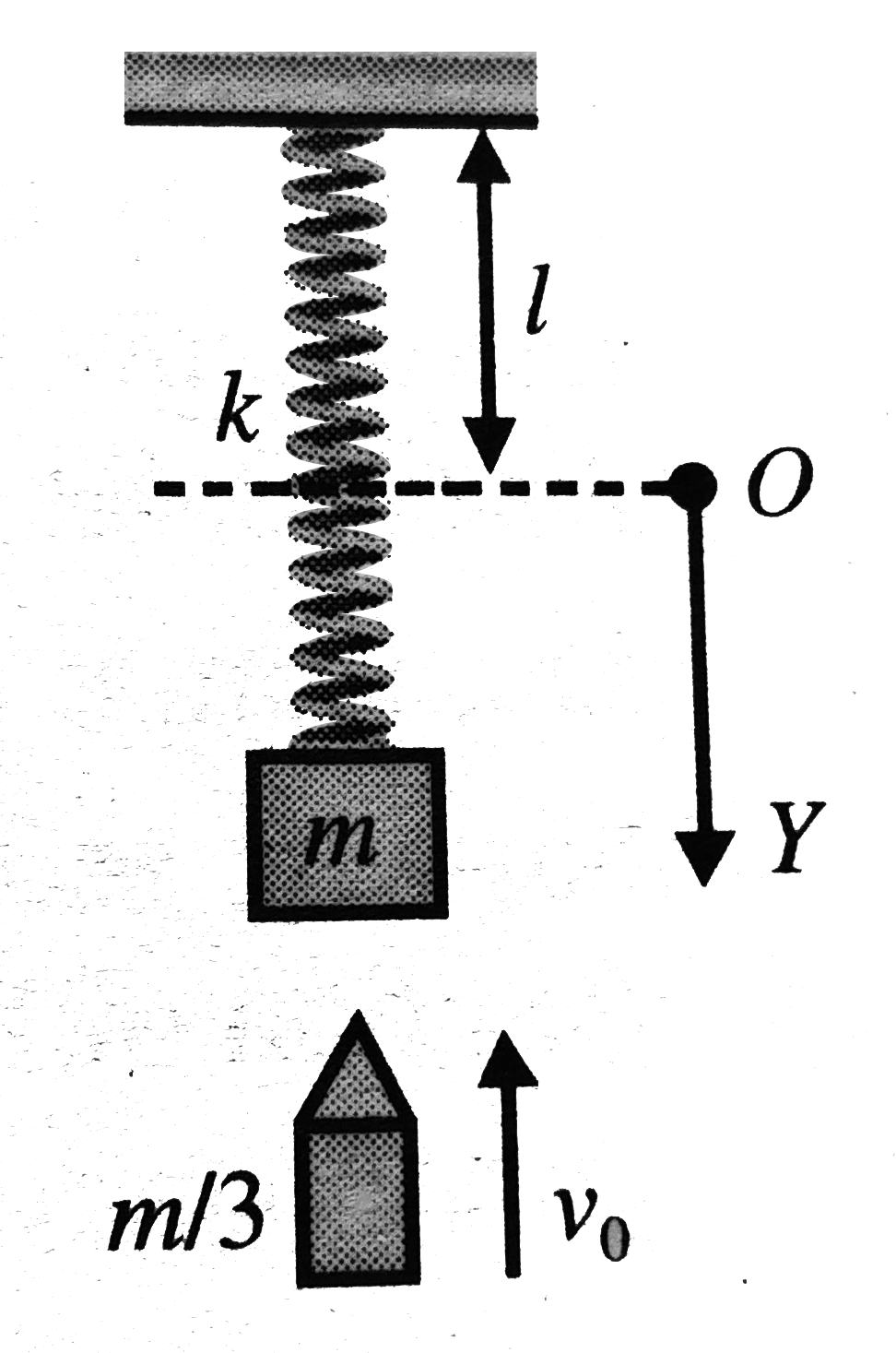
A block of mass m is suspended from one end of a light spring as shown. The origin O is considered at distance equal to natural length of the spring from the ceiling and vertical downwards direction as positive y-axis. When the system is in equilibrium a bullet of mass m3 moving in vertical up wards direction with velocity v0 strikes the block and embeds into it. As a result, the block (with bullet embedded into it) moves up and start oscillating. Based on the given information, answer the following question:
Q. The amplitude of oscillation would be View SolutionQuestion 13
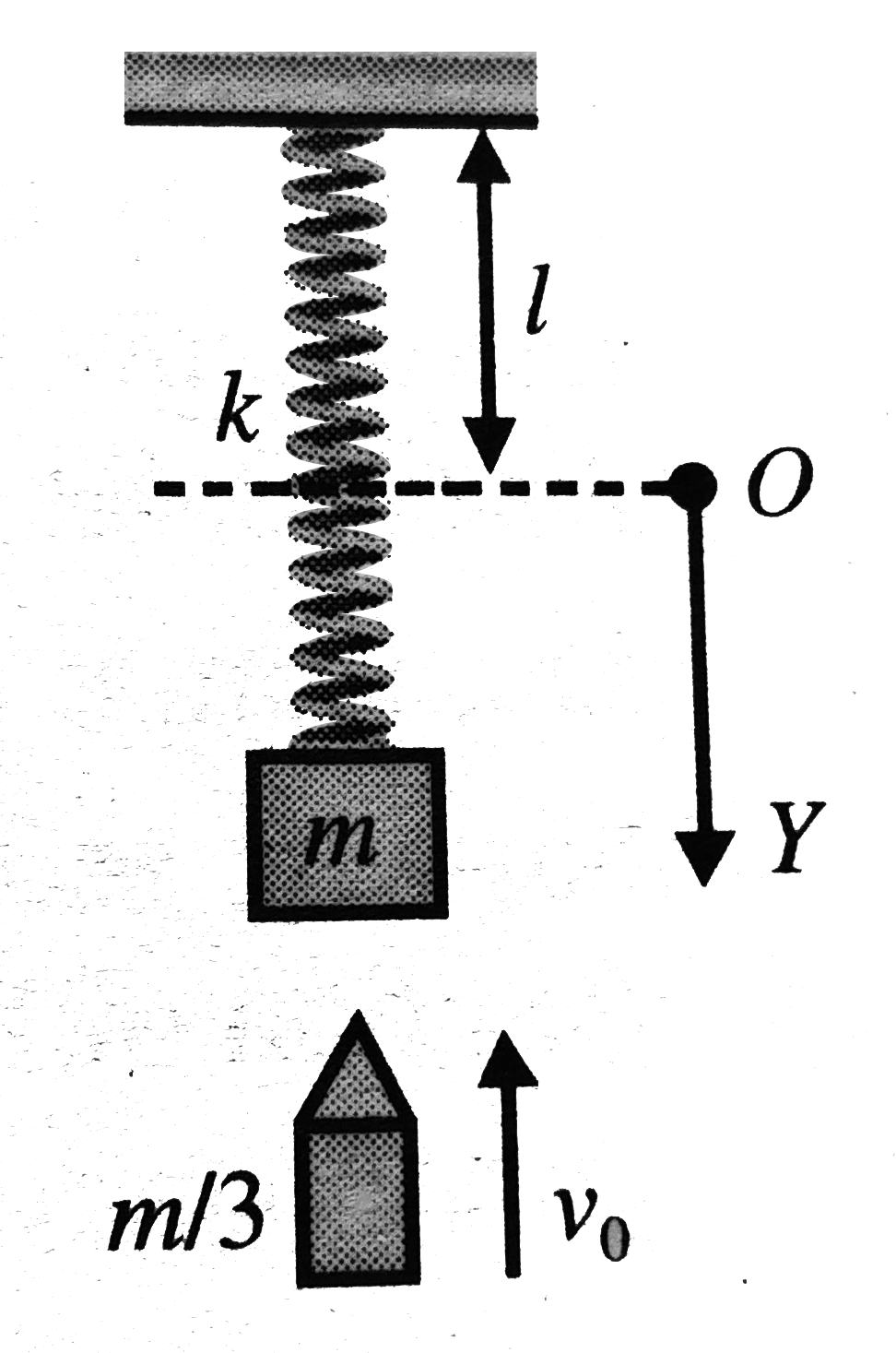
A block of mass m is suspended from one end of a light spring as shown. The origin O is considered at distance equal to natural length of the spring from the ceiling and vertical downwards direction as positive y-axis. When the system is in equilibrium a bullet of mass m3 moving in vertical up wards direction with velocity v0 strikes the block and embeds into it. As a result, the block (with bullet embedded into it) moves up and start oscillating. Based on the given information, answer the following question:
Q. The amplitude of oscillation would be View SolutionQuestion 14
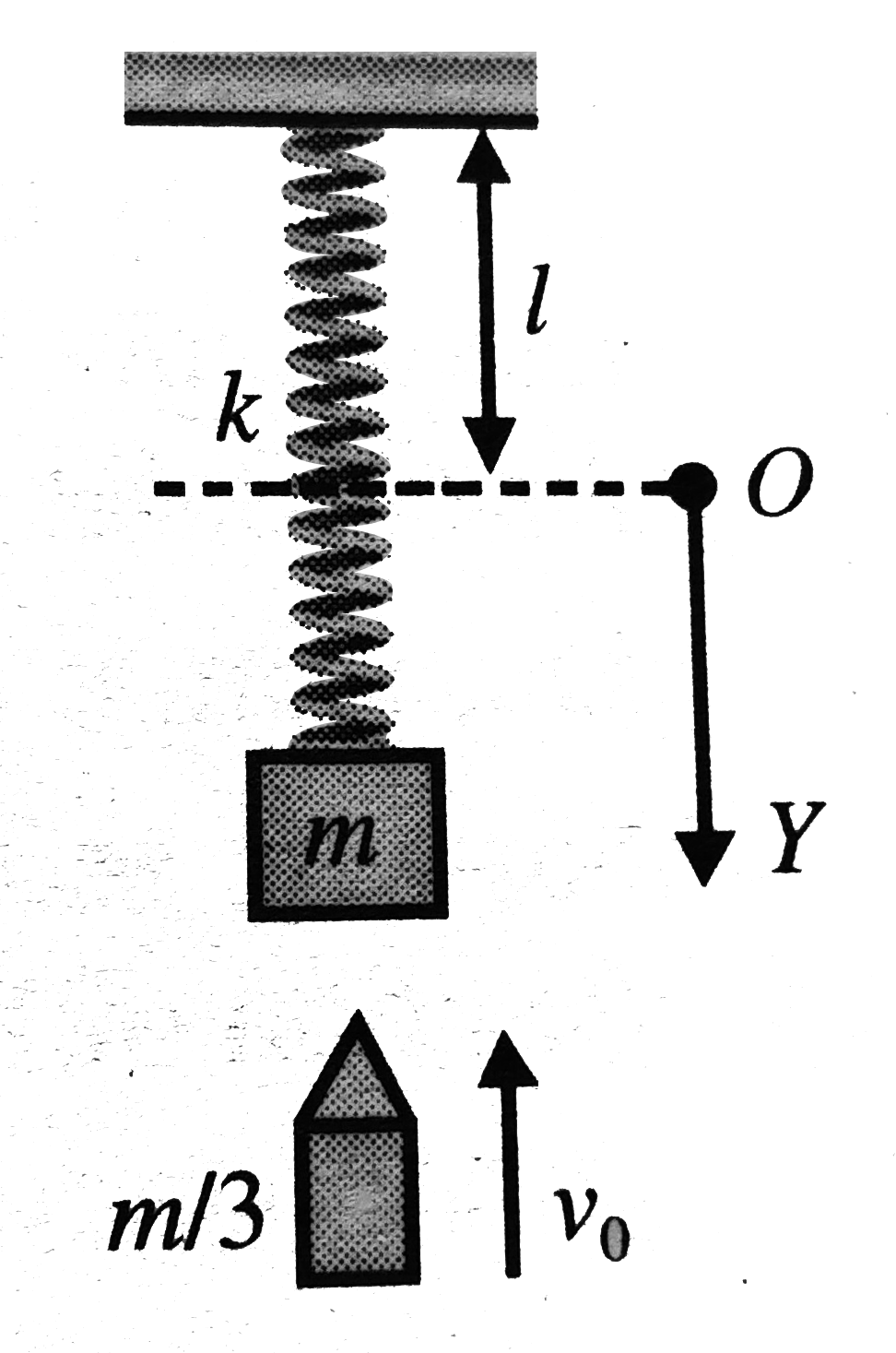
A block of mass m is suspended from one end of a light spring as shown. The origin O is considered at distance equal to natural length of the spring from the ceiling and vertical downwards direction as positive y-axis. When the system is in equilibrium a bullet of mass m3 moving in vertical up wards direction with velocity v0 strikes the block and embeds into it. As a result, the block (with bullet embedded into it) moves up and start oscillating. Based on the given information, answer the following question:
Q. The time taken by the block bullet system to move from y=mgk (initial equilibrium position) to y=0 (natural length of spring) is (A represents the amplitude of motion)View SolutionQuestion 15
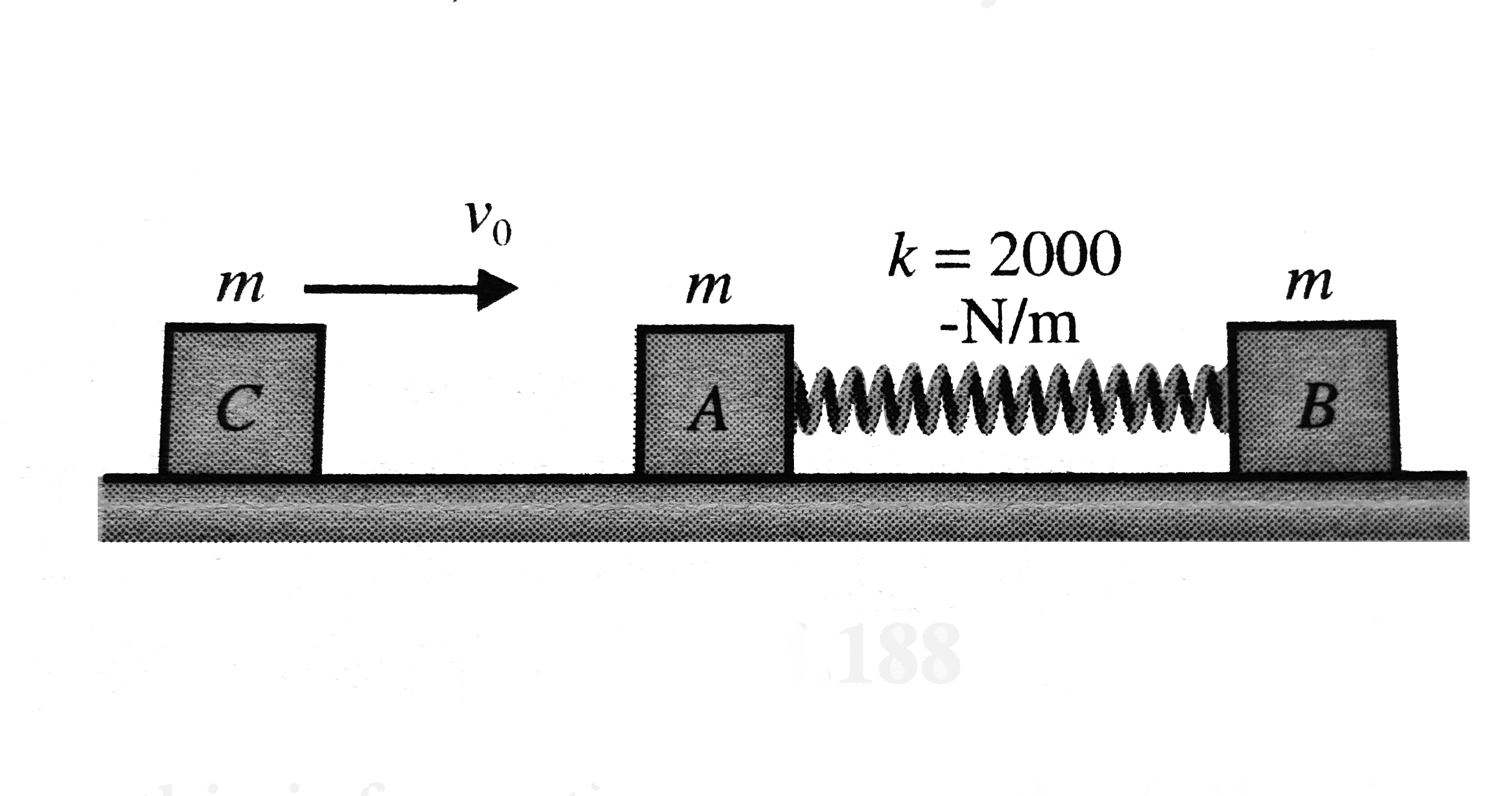
Two identical blocks A and B, each of mass m=3kg, are connected with the help of an ideal spring and placed on a smooth horizontal surface as shown in Fig. Another identical blocks C moving velocity v0=0.6ms collides with A and sticks to it, as a result, the motion of system takes place in some way
Based on this information answer the following questions:
Q. After the collision of C and A, the combined body and block B would
Option1
oscillate about centre of mass of system and centre of mass is at rest.
Option2
oscillate about centre of mass of system and centre of mass is moving.
Option3
oscillate but about different location other than the centre of mass.
Option4
not oscillate.View SolutionQuestion 16
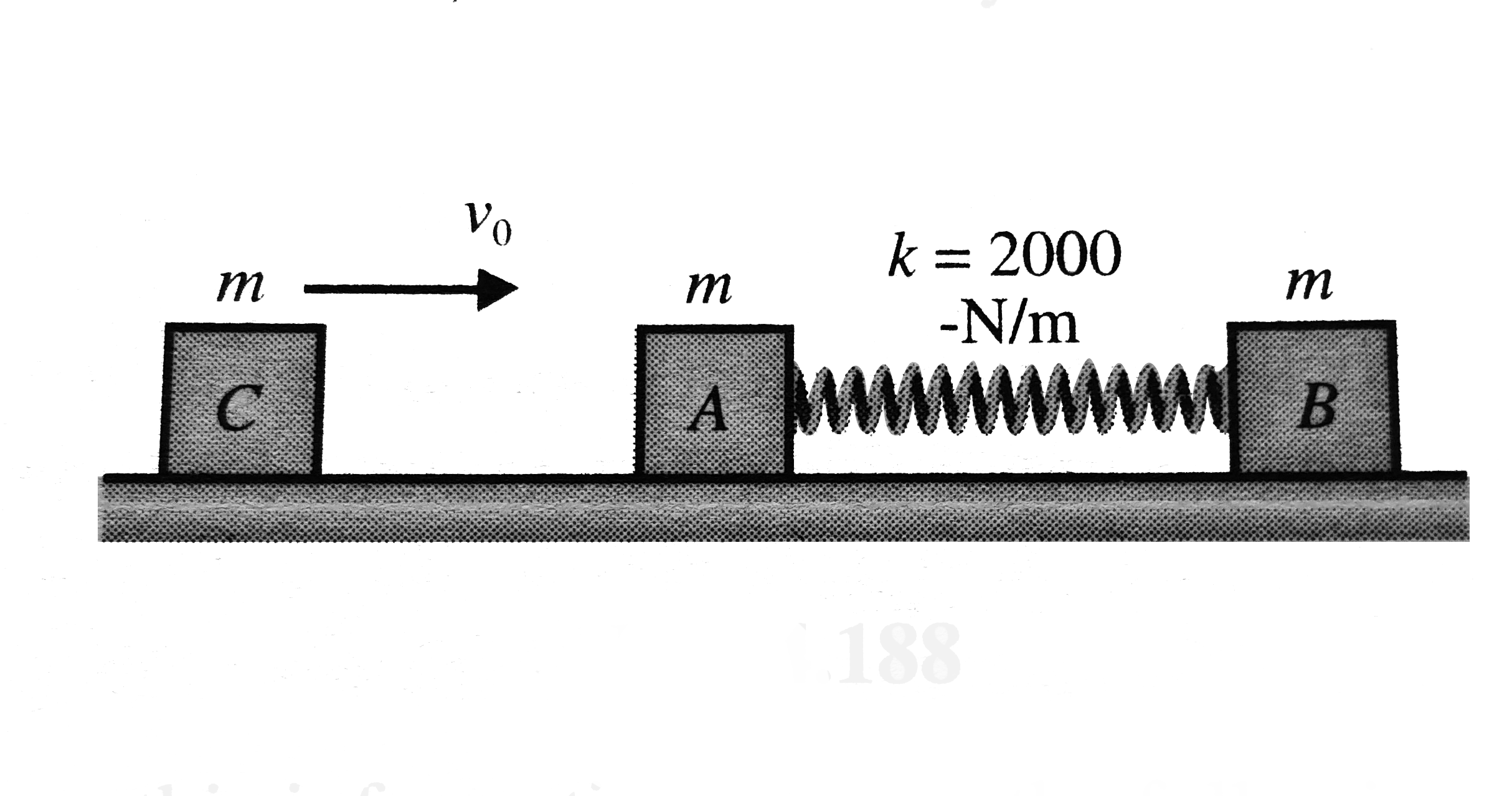
Two identical blocks A and B, each of mass m=3kg, are connected with the help of an ideal spring and placed on a smooth horizontal surface as shown in Fig. Another identical blocks C moving velocity v0=0.6ms collides with A and sticks to it, as a result, the motion of system takes place in some way
Based on this information answer the following questions:
Q. Oscillation energy of the system i.e., part of the energy which is oscillation (changing) between potention and kinetic forms is View SolutionQuestion 17
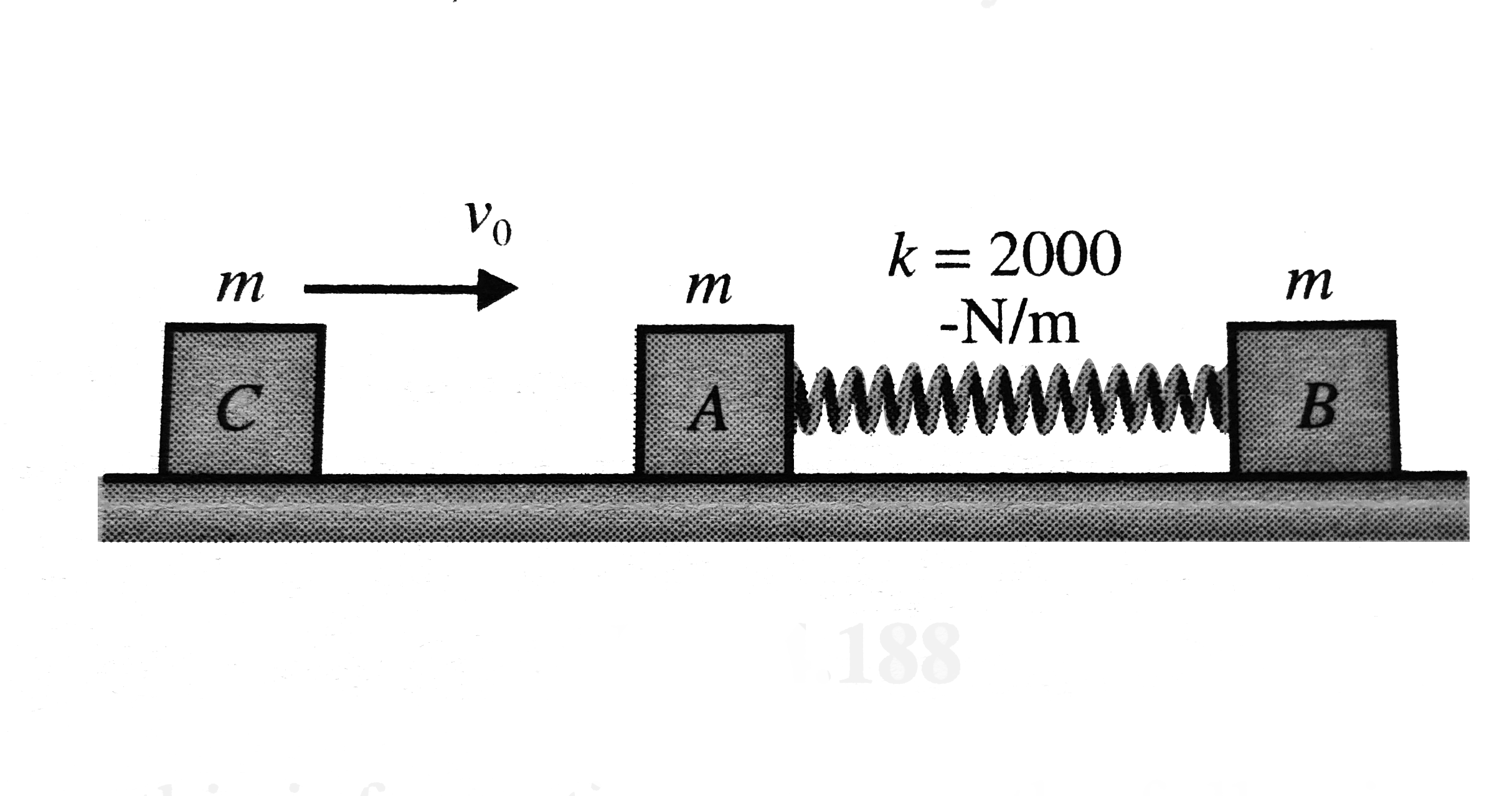
Two identical blocks A and B, each of mass m=3kg, are connected with the help of an ideal spring and placed on a smooth horizontal surface as shown in Fig. Another identical blocks C moving velocity v0=0.6ms collides with A and sticks to it, as a result, the motion of system takes place in some way
Based on this information answer the following questions:
Q. The maximum compression of the spring is View SolutionQuestion 18

A small block of mass m is fixed at upper end of a massive vertical spring of spring constant k=2mgL and natural length 10L The lower end of spring is free and is at a height L from fixed horizontal floor as shown. The spring is initially unstressed and the spring block system is released from rest in the shown position.
Q. At the instant the speed of block is maximum the magitude of force exeted by the spring on the block is View SolutionQuestion 19

A small block of mass m is fixed at upper end of a massive vertical spring of spring constant k=2mgL and natural length 10L The lower end of spring is free and is at a height L from fixed horizontal floor as shown. The spring is initially unstressed and the spring block system is released from rest in the shown position.
Q. As the block is coming down, the maximum speed attained by the block is View SolutionQuestion 20

A small block of mass m is fixed at upper end of a massive vertical spring of spring constant k=2mgL and natural length 10L The lower end of spring is free and is at a height L from fixed horizontal floor as shown. The spring is initially unstressed and the spring block system is released from rest in the shown position.
Q. Till the blocks reaches its lowest position for the first time, the time duration for which the spring remains compressed is View SolutionQuestion 21
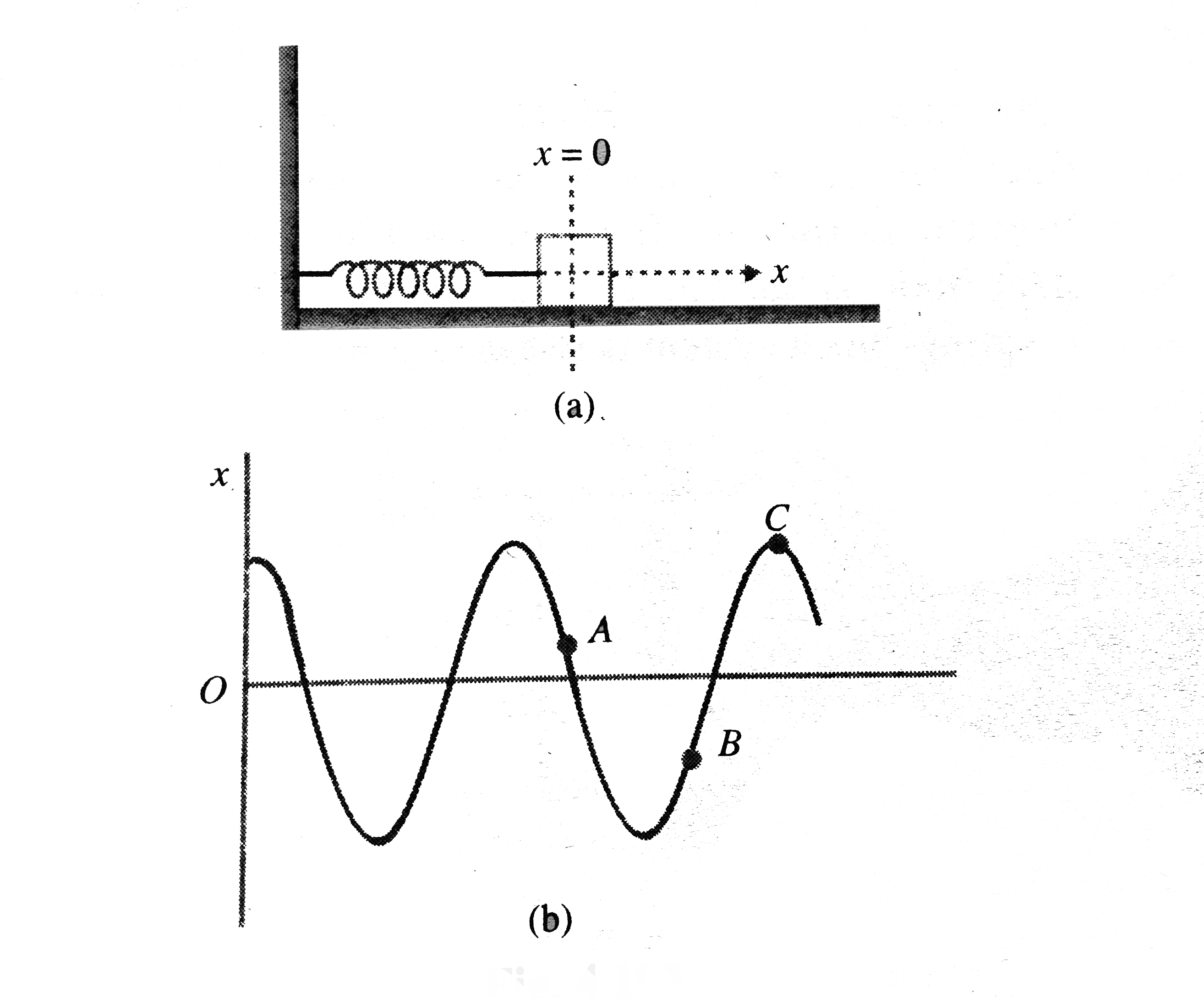
A 100 g block is connected to a horizontal massless spring of force constant 25.6Nm As shown in Fig. the block is free to oscillate on a horizontal frictionless surface. The block is displaced 3 cm from the equilibrium position and , at t=0, it is released from rest at x=0 It executes simple harmonic motion with the postive x-direction indecated in Fig. The position time (x−t) graph of motion of the block is as shown in Fig.
Velocity of the block as a function of time can be expressed as View SolutionQuestion 22

A spring having a spring constant k is fixed to a vertical wall as shown in Fig. A block of mass m moves with velocity v torards the spring from a parallel wall opposite to this wall. The mass hits the free end of the spring compressing it and is decelerated by the spring force and comes to rest and then turns the spring is decelerated by the spring force and comes to rest and then turns back till the spring acquires its natural length and contact with the spring is broken. In this process, it regains its angular speed in the opposite direction and makes a perfect elastice collision on the opposite left wall and starts moving with same speed as before towards right. The above processes are repeated and there is periodic oscillation.
Q. What is the maximum compression produced in the spring?View SolutionQuestion 23

A spring having a spring constant k is fixed to a vertical wall as shown in Fig. A block of mass m moves with velocity v torards the spring from a parallel wall opposite to this wall. The mass hits the free end of the spring compressing it and is decelerated by the spring force and comes to rest and then turns the spring is decelerated by the spring force and comes to rest and then turns back till the spring acquires its natural length and contact with the spring is broken. In this process, it regains its angular speed in the opposite direction and makes a perfect elastice collision on the opposite left wall and starts moving with same speed as before towards right. The above processes are repeated and there is periodic oscillation.
Q. What is the time period of oscillation ?View SolutionQuestion 24
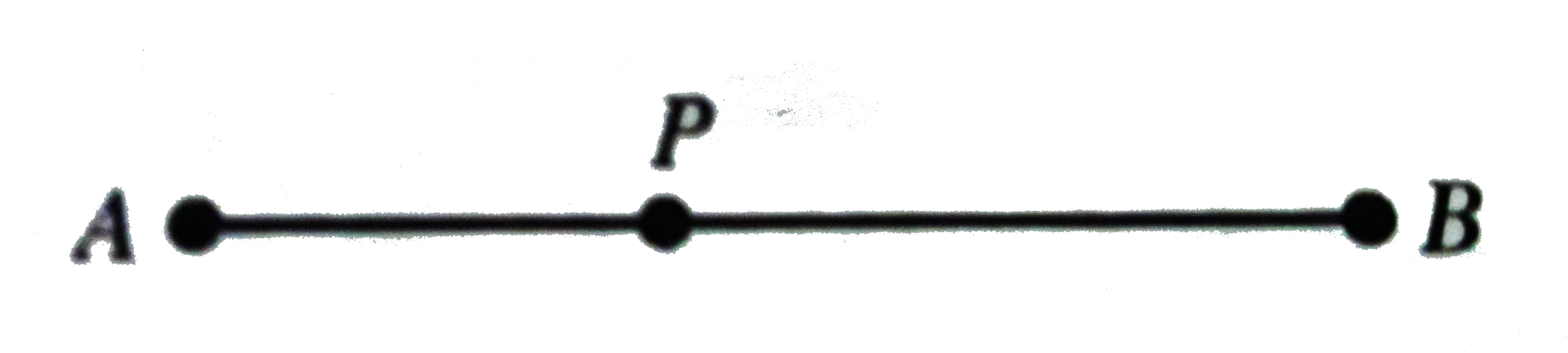
A and B are two fixed points at ta distance 3l apart. A particle of mass m placed at a point P experiences the force 2(mgl)→PA and the force (mgl)→PB sumultaneously. Initially at t=0, the particle is projected from A towards B with speed 3√gl.
Q. Tha particle moves simple harmonically with period T and amplitude A.View SolutionQuestion 25
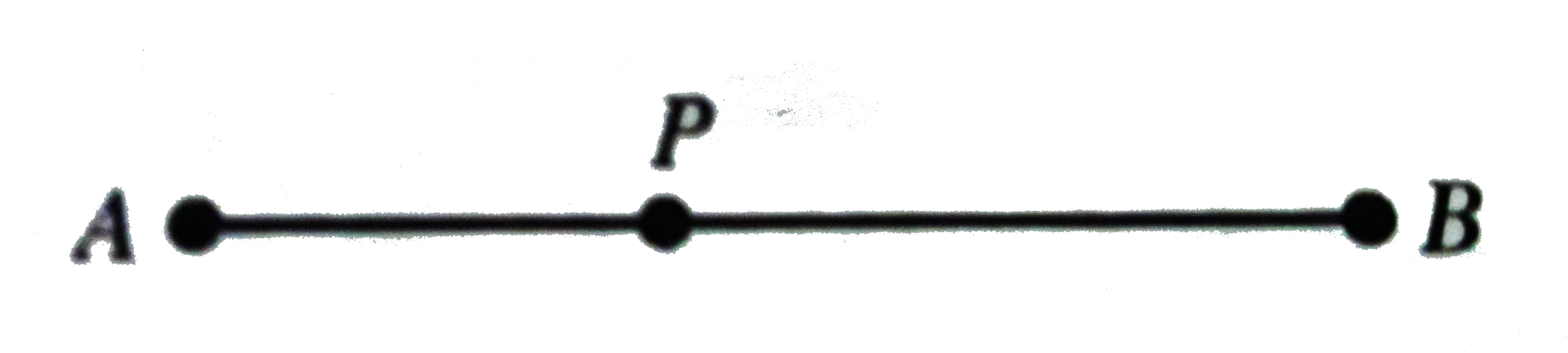
A and B are two fixed points at ta distance 3l apart. A particle of mass m placed at a point P experiences the force 2(mgl)→PA and the force (mgl)→PB simultaneously. Initially at t=0, the particle is projected from A towards B with speed 3√gl.
Q. The particle moves simple harmonically with period T and amplitude A.View SolutionQuestion 26
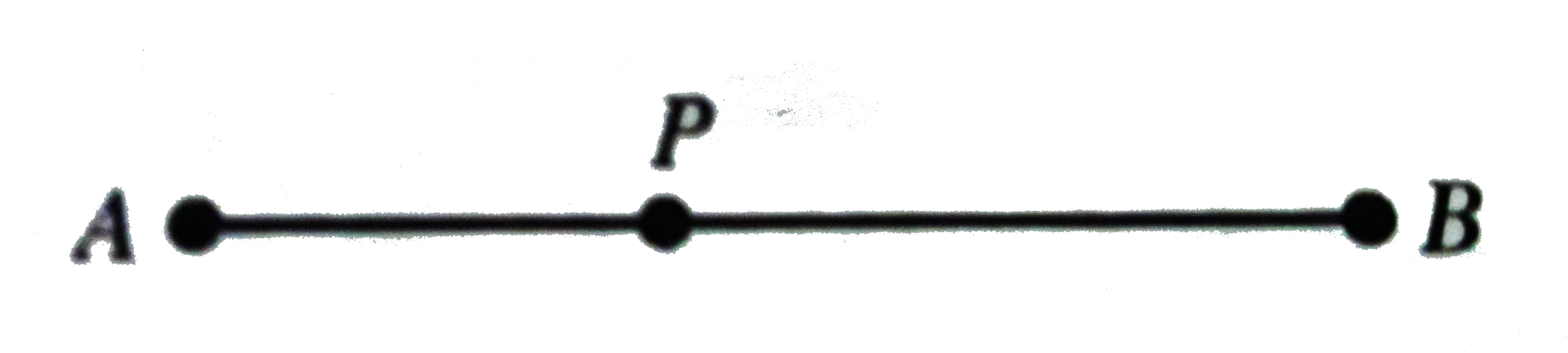
A and B are two fixed points at ta distance 3l apart. A particle of mass m placed at a point P experiences the force 2(mgl)→PA and the force (mgl)→PB simultaneously. Initially at t=0, the particle is projected from A towards B with speed 3√gl.
Q. The particle moves simple harmonically with period T and amplitude A.View SolutionQuestion 27
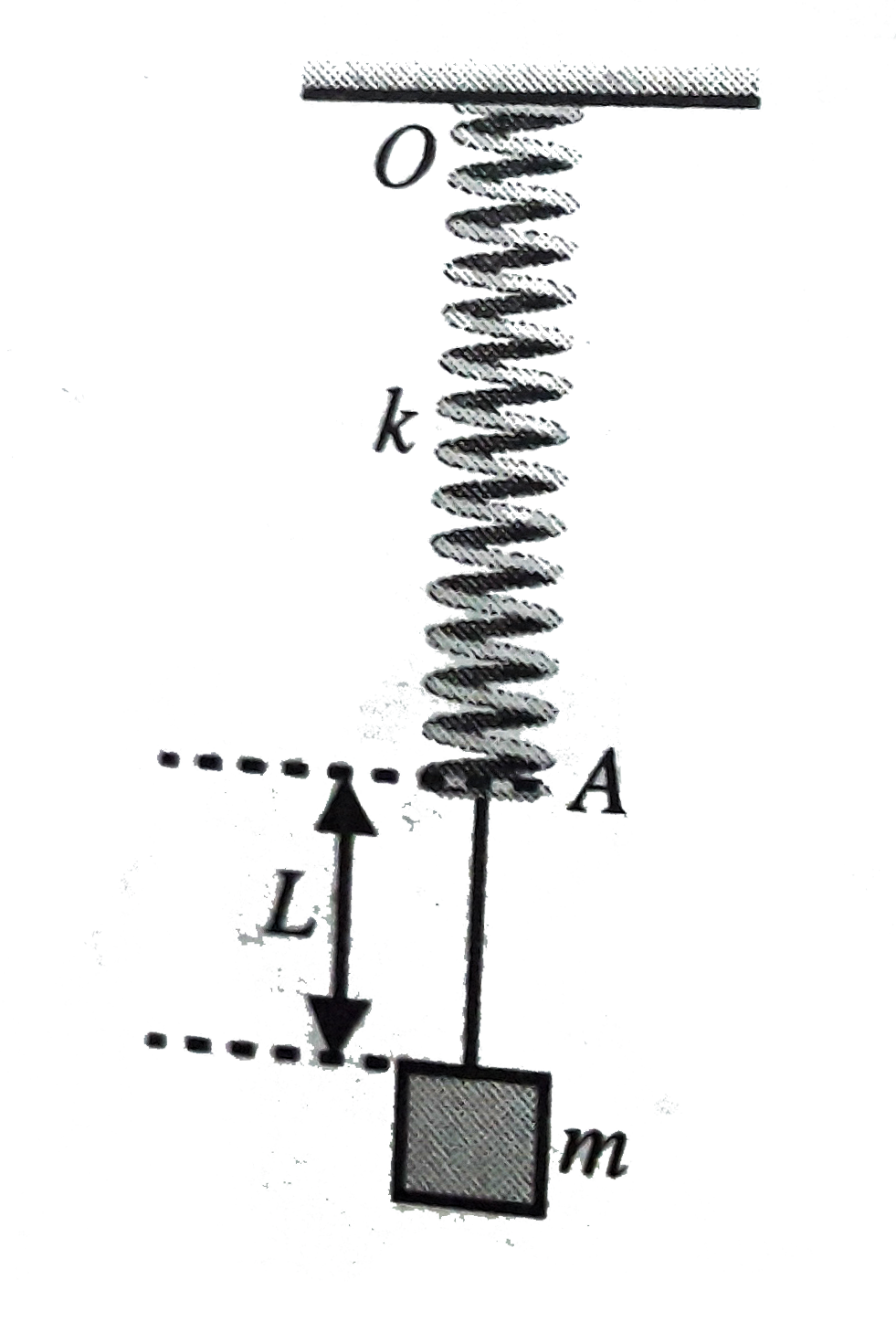
A body of mass m is attached by an inelastic string to a suspended spring of spring constant k. Both the string and the spring have negligible mass and the string is inextensible and of length L. Initially, the mass m is at rest.
Q. If the mass m is now raised up to point A (the top end of the string see fig. and allowed to fall from rest, the maximum extension of the spring in the subsequent motion will beView Solution