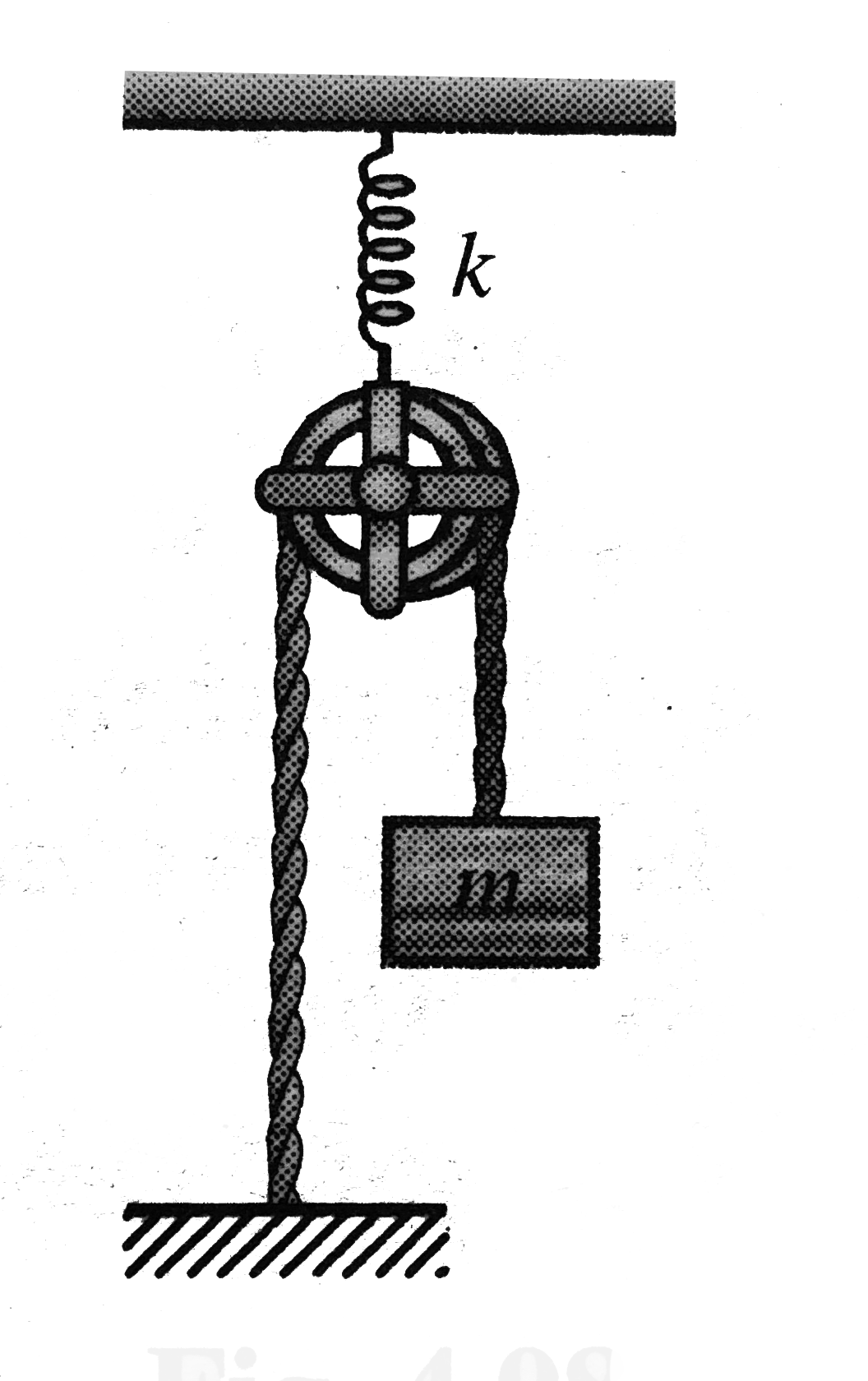Illustration from CENGAGE PHYSICS (ENGLISH) Chapter 11:LINEAR AND ANGULAR SIMPLE HARMONIC MOTION for Class 11
| Class 11 | PHYSICS |
| Chapter | LINEAR AND ANGULAR SIMPLE HARMONIC MOTION |
| CENGAGE PHYSICS (ENGLISH) | Illustration |
| Medium | English |
| Academic Year | 2023-2024 |
Question 11
Shows the displacement time graph of a partical excuting SHM with a time period T. Four points 1,n2,3 and 4 are market on the graph where the displacement is half that of the amplitude.
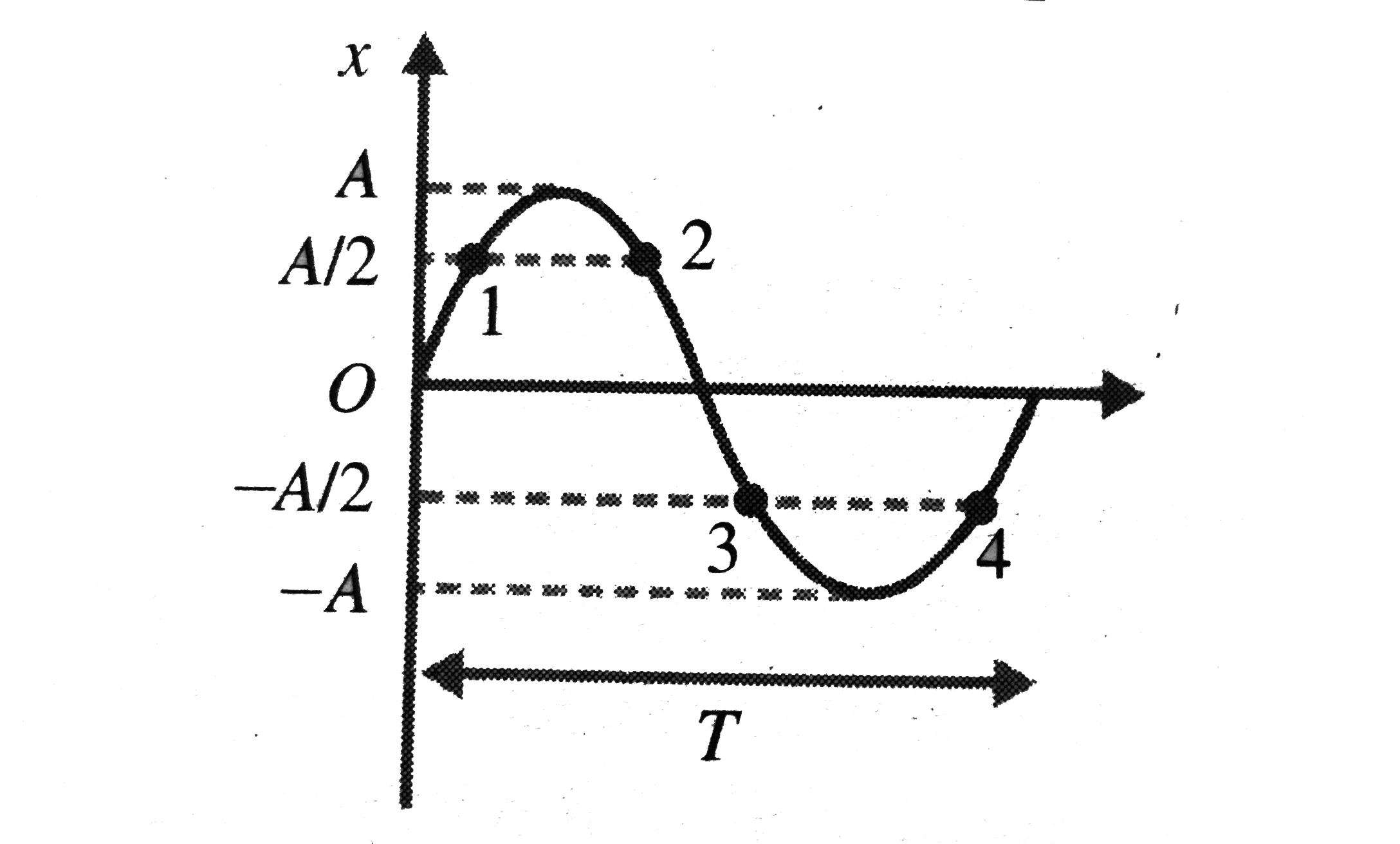
a. Identify the point of same displacement but with opposite direction of motion . Find the time difference between them.
b. Identify the point where the particals move in the same difference. Find the time difference between them. View SolutionQuestion 13
A partical excutes SHM with amplitudeA and angular frequency ω. At an instant the particle is at a distance A/5 from the mean position and is moving away from it. Find the time after which it will come back to this position again and also find the time after which it will pass through the mean position.View SolutionQuestion 19
If a partical moves in a potential energy held U=U0−ax+bx2, where are a and b partical constents obtian an expression for the force acting on if as a function of position. At what point does the force vanish? Is this a point of stable equilibriun ?
Calculate the force constant and friquency of the partical.View SolutionQuestion 21
A partical of mass 0.2kg undergoes SHM according to the equation x(t)=3sin(πt+π/4).
i. What is the total energy of the partical if potential energy of zero at mean position ?
ii. What are the kinetic and potential energies of partical at time t=1s?
iii. At what time instants is the particals energies purely kinetic?View SolutionQuestion 22
A partical of mass 0.2kg executes simple harmonic motion along a path of length 0.2m at the rate of 600oscillations per minute. Assum at t=0. The partical start SHM in positive direction. Find the kinetic potential energies in joules when the displacement is x=A/2 where, A stands for the amplitude.View SolutionQuestion 31
A person normally weighing 60kg stands on a platform which oscillates up and down harmonically at a frequency 2.0sec−1 and an amplitude 5.0cm . If a machine on the platform gives the person's weight against time deduce the maximum and minimum reading it will shown, Takeg=10m/sec2.View SolutionQuestion 34
Two light spring of force constants k1andk2 and a block of mass m are in the line AB on a smooth horizontal table such that one end of each spring is fixed on right supports and the other end is free as shown in figure

The distance CD between the free ends of the spring is 60cm. If the block (k1=1.8N/m,k2=3.2N/mandm=200g). Is the motion simple harmonic?View SolutionQuestion 37
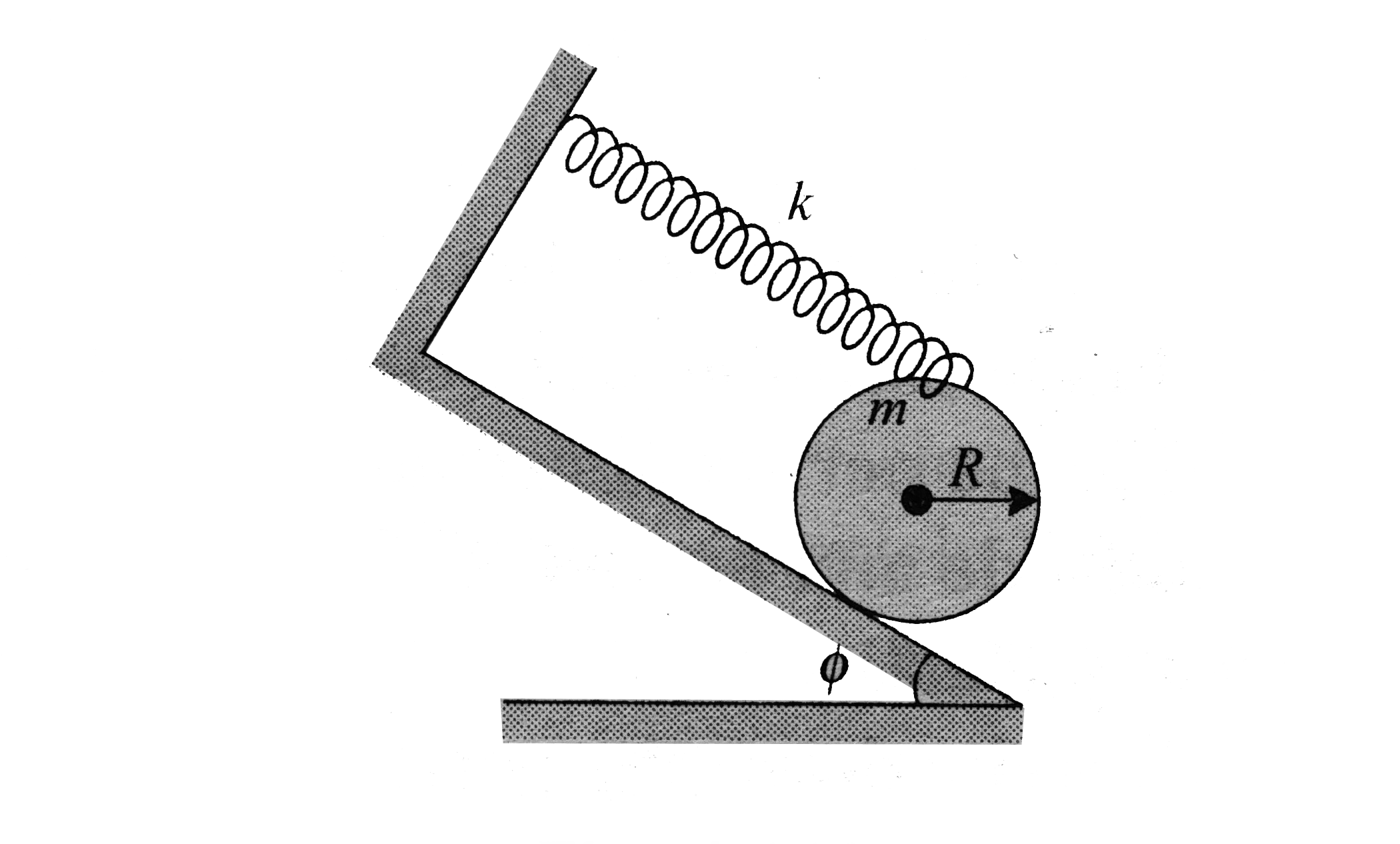
A solid cylinder of mass m is attached to a horizontal spring with force constant k. The cylinder can roll without slipping along the horizontal plane. (See the accompanying figure.) Show that the center of mass of the cylinder executes simple harmonic motion with a period T=2π√3m2k, if displaced from mean position.
 View Solution
View SolutionQuestion 39
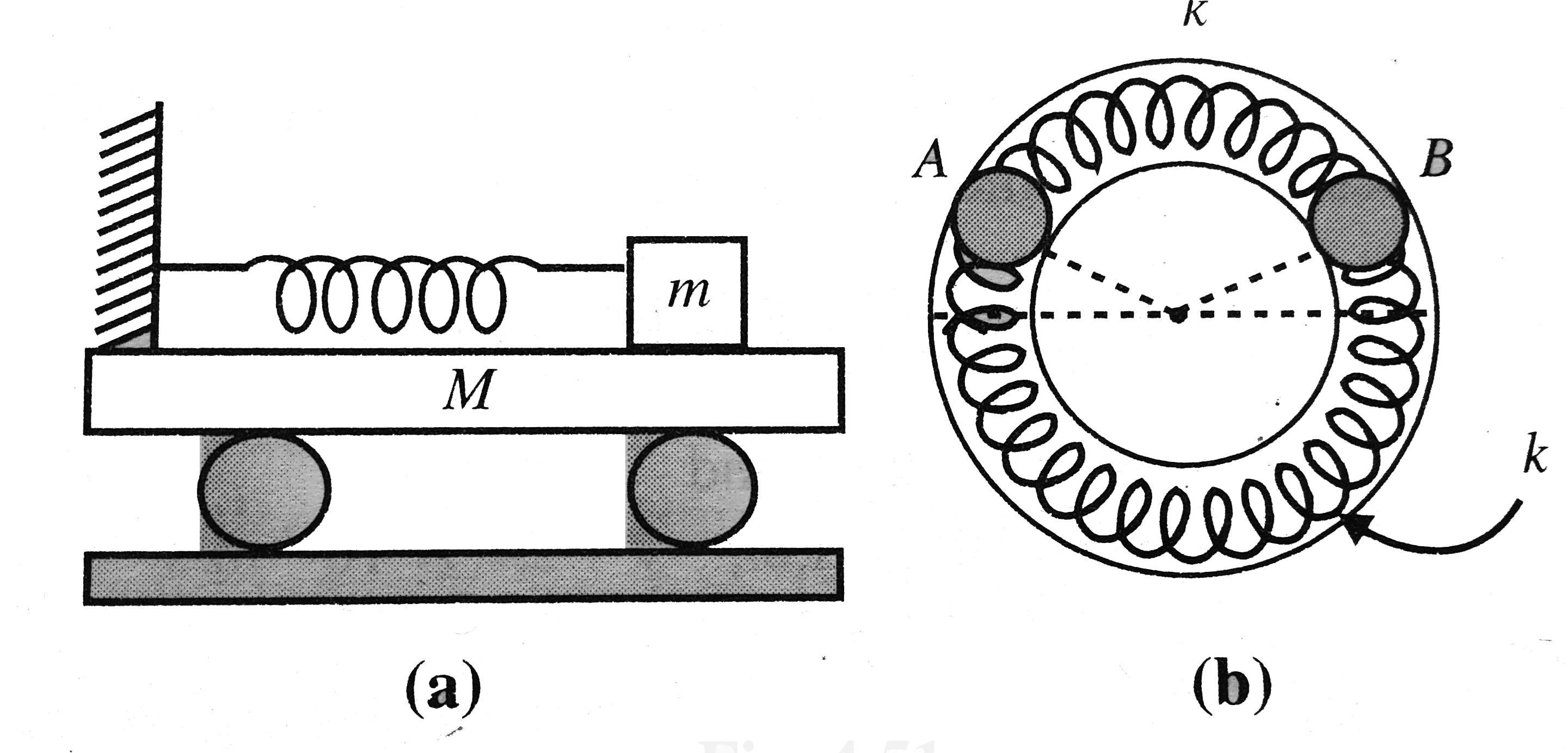
Two identical balls AandB eavh of mass 0.1kg are attached to two identical mass less is springs. The spring-mass system is consetrained to move inside a right smooth pipe bent in the form of a circle as shown in figure . The pipe is fixed in a horigental plane. The center of the balls can move in a circle of radius 0.06m. Each spring has a natural length of 0.06πm and force constant 0.1N/m. Initially, both the balls are displaced bu an angle θ=π/6 dadius withrespect to diameter PQ of the circle and released from rest.
a. Calculate the frequency of oscillation of the ball B.
b. What is the total energy of the system ?
c. Find the speed of the bal A when A and B are at the two ends of the diameter PQ.
 View Solution
View SolutionQuestion 40
The system shown in the figure can move on a smooth surface. They are initially compressed by 6cm and then released, then choose the correct options.

(a) The system performs, SHM with time period π10s
(b) The block of mass 3kg perform SHM with amplitude 4cm
( c) The block of mass 6kg will have maximum momentum of 2.40kg−m/s
(d) The time periods of two blocks are in the ratio of 1:√2 View SolutionQuestion 41
A simple pendulum of length 40 cm oscillates with an angular amplitude of 0.04 rad. Find a. the time period b. the linear amplitude of the bob, c. The speed of the bob when the string makes 0.02 rad with the vertical and d. the angular acceleration when the bob is in momentarily rest. Take g=10ms−2.View SolutionQuestion 42
A ball is suspended by a thread of length l at the point O on an incline wall as shown. The inclination of the wall with the vertical is (a)the thread is displacement througha small angle away from the vertical and (b) the ball is released. Find the period of obcillation of pendulum. Consider both cases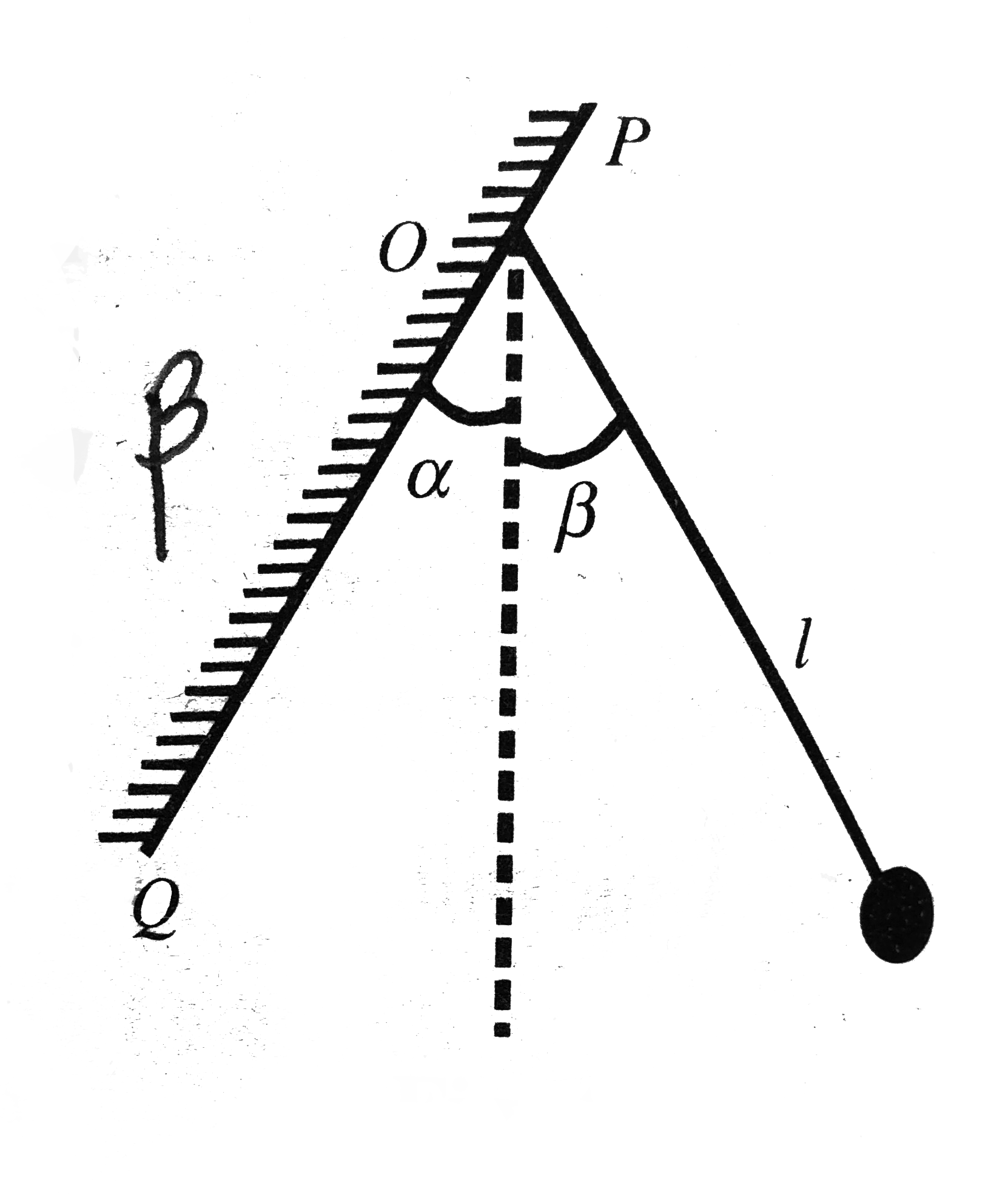
a. α>β
b. α<β
Assuming that any impact between the wall and the ball is elastic.View SolutionQuestion 47
A uniform disc of radius 5.0 cm and mass 200g is fixed at its centre to a metal wire, the other end of which is fixed with a clamp. The hanging disc is rotated about the wire through an angle and is released. If the disc makes torsional oscillations with time period 0.20s, find the torsional constant of the wire.View SolutionQuestion 48
Assume that a tunnel is dug across the earth (radius=R) passing through its centre. Find the time a particle takes to cover the length of the tunnel if (a) it is projected into the tunnel with a speed of √(gR) (b) it is relased from a height R above the tunnel (c ) it is thrown vertically upward along the length of tunnel with a speed of √gR.View SolutionQuestion 53
A uniform horizontal plank is resting symmetrically in a horizontal position on two cylindrical droms , which are apinning in in opposite direction about their horizontal axes with equal angular velocity . The distance between the axes with equal angular velocity. The distance between the axes is 2L and the coefficient of friction between the plank and cylender is μ . If the plank is displaced slightly from the equilibrium position along its length and released, show that it performs simple horizontal motion. Caculate also the time period of motion.View SolutionQuestion 54
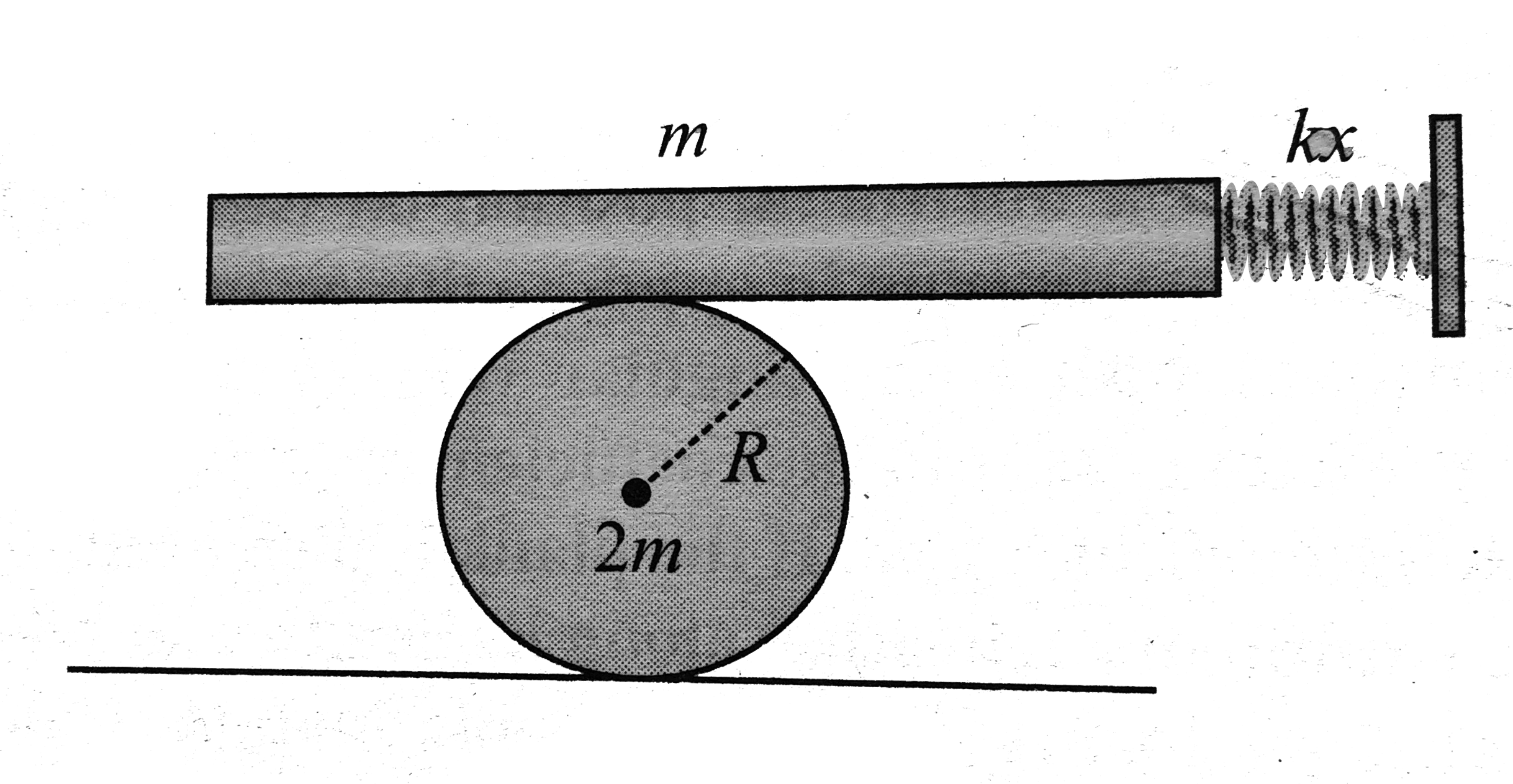
A uniform plank of mass m, free to move in the horizontal direction only , is placed at the top of a solid cylinder of mass 2m and radius R. The plank is attached to a fixed wall by mean of a light spring constant k. There is no slipping between the cylinder and the planck , and between the cylinder and the ground. Find the time period of small oscillation of the system.
 View Solution
View SolutionQuestion 58
A certain of a perfect gas is enclosed in a cylinder of volume V0 fitted with a smooth heavy piostion of mass m and area a. The piston is displaced through a small distance downwards so as to compress the gas isother mally , and then it is left free to go show that it performs SHM and also find its period . Take the atmospheric pressure as Pa→m.View SolutionQuestion 61
One end of an ideal spring is fixed to a wall at origin O and axis of spring is parallel to x-axis. A block of mass m=1kg is attached to free end of the spring and it is performing SHM. Equation of position of the block in co-ordinate system shown in figure is x=10+3sin(10t). Here, t is in second and x in cm. Another block of mass M=3kg, moving towards the origin with velocity 30cm/s collides with the block performing SHM at t=0 and gets stuck to it. Calculate

(a) new amplitude of oscillations,
(b) neweqution for position of the combined body,
( c) loss of energy during collision. Neglect friction.View SolutionQuestion 62
A circular spring of natural length l0 is cut and weided with two beads of masses m1andm2 such that the ratio of the lengths of the springs between the beads is 4:1 if the stiffness of the spring is k. find the frequency of oscillation of the beads in a smooth horizontal rigid tube. Assume m_(1) = m and m_(2) = 3 m.
 View Solution
View SolutionQuestion 64
A 2kg mass is attached to a spring of force constant 600N/m and rests on a smooth horizontal surface. A second mass of 1kg slides along the surface toward the first at 6m/s.
(a) Find the amplitude of oscillation if the masses make a perfectly inelastic collision and remain together on the spring. what is the period of oscillation ?
(b) Find the amplitude and period of oscillation if the collision is perfectly elastic.
( c) For each case , write down the position x as a function of time t for the mass attached to the spring, assuming that the collision occurs at time t=0. What is the impulse given to the 2kg mass in each case ?View SolutionQuestion 66
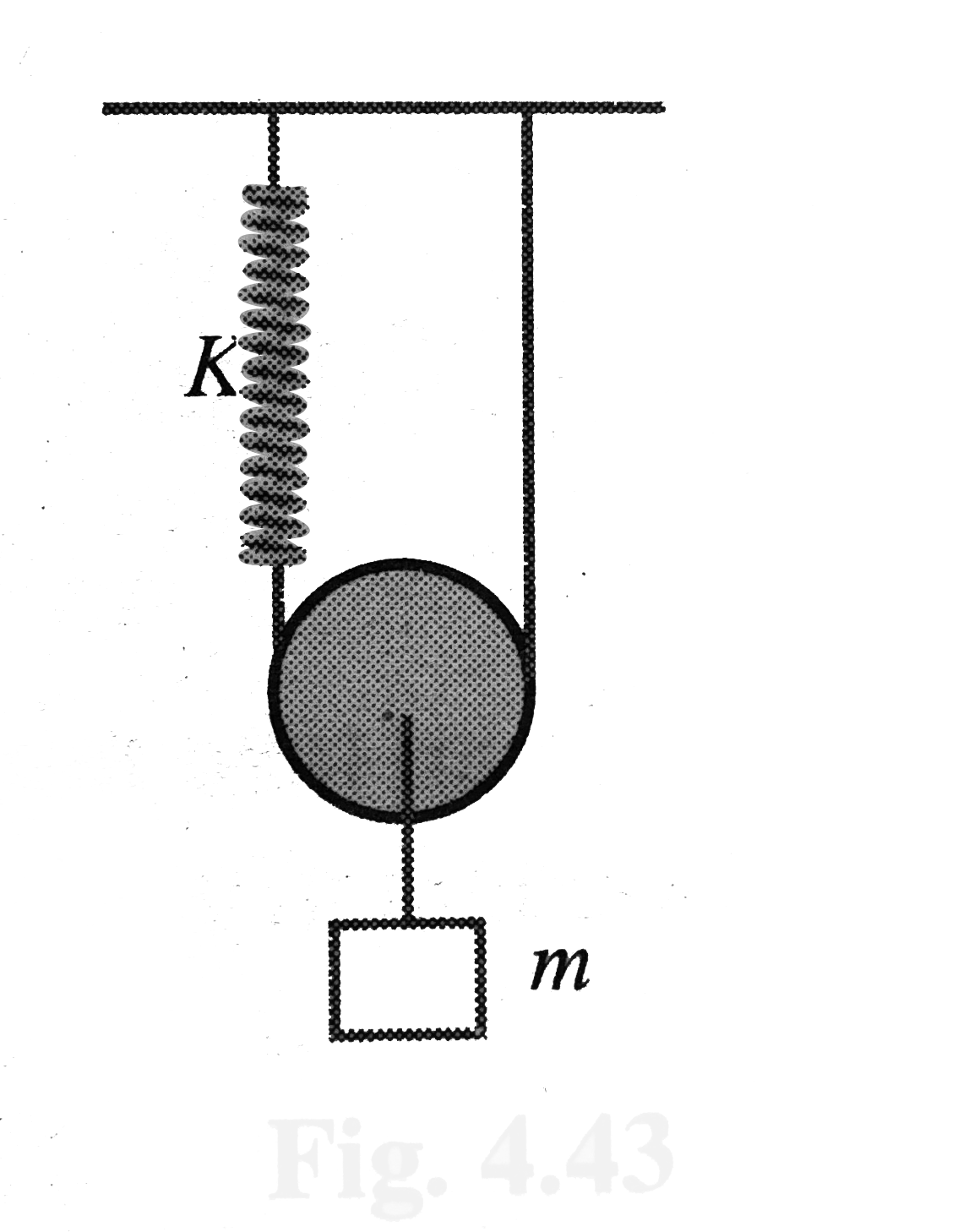
Figure shown a spring block system hanging in equilibrium. The block of system is pulled down by the distance x and imparted a velocity v in downward direction as shown in figure. Find the time it will take to reach its mean position. Also find the maximum distance to which if will move before returning back towards mean position.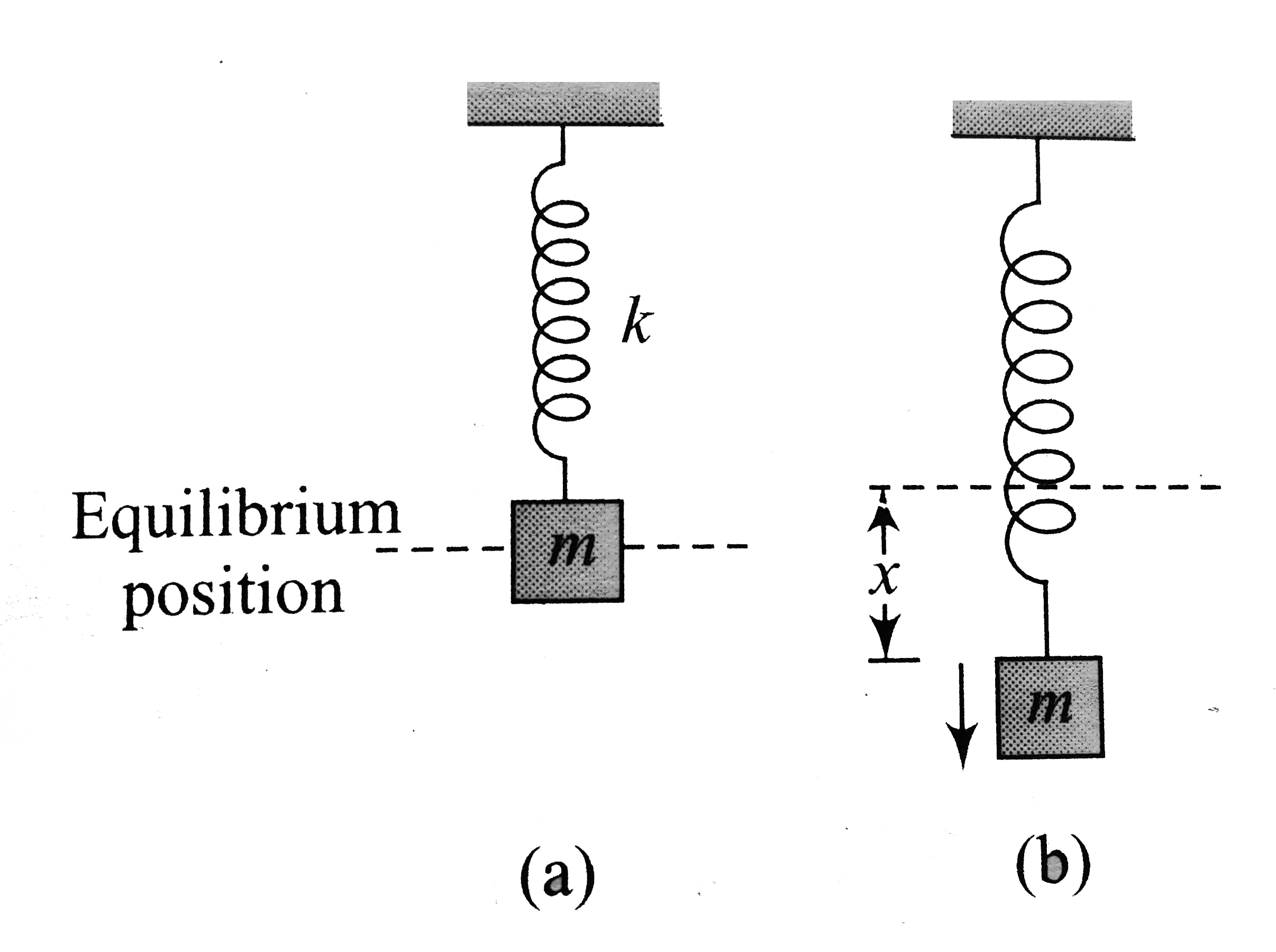 View Solution
View SolutionQuestion 67
Figure shown a block P of mass m resting on a smooth horizontal surface, attached to a spring of force constant k which is rigidly fixed on the wall on left side, shown in the figure . At a distance l to the right of the block there is a rigid wall. If block is pushed towards left so that spring is compressed by a distance 5l/3 and when released, if will starts its oscillations. If collision of block with the wall is considered to be perfectly elastic. Find the time period of oscillation of the block.
 View Solution
View Solution

 .
.