Subjective from CENGAGE PHYSICS Chapter 25 TRAVELLING WAVES for Class 11
| Class 11 | PHYSICS |
| Chapter | TRAVELLING WAVES |
| CENGAGE PHYSICS | Subjective |
| Medium | English |
| Academic Year | 2023-2024 |
Question 1
A 100 Hz sinusoidal wave is travelling in the positive x-direction along a string with a linear mass density of 3.5×103kg/m and a tension of 35 N. time t=0, the point x=0 has maximum displacement in the positive y-direction. Next, when this point has zero displacement the slope (iii) the expression which represents the displacement of string as a function of x (in metres) and t (in seconds). View SolutionQuestion 2
One end of a long string of linear mass density 10−2kgm−1 is connected to an electrically driven tuning fork of frequency 150 Hz. The other end passes over a pulley and is tied to a pan containig a mass of 90 kg. the pulley end absorbs all the incoming energy so that reflected waves from this end have neglidible amplitude , At t =0, the left end (fork end ) of the string is at x=0 has a transverse displacement of 2.5 cm and is moving along positive y-direction. the amplitude of the wave is 5 cm. write down the transverse displacement y (in cetimetres) as function of x(in metres) and t (in seconds ) that describes the wave on the string.
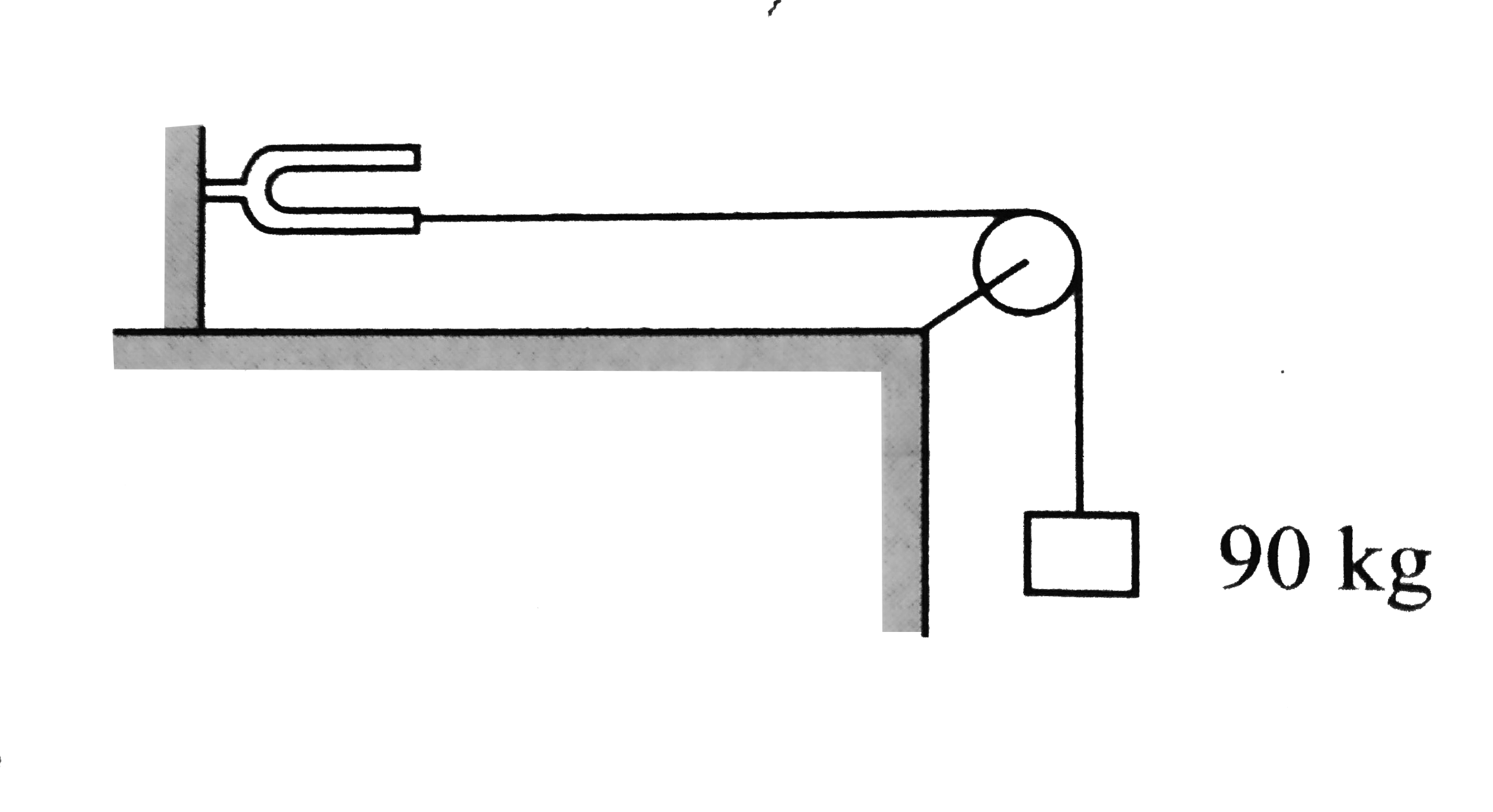View SolutionQuestion 3
An harmonic wave has been set up on a very long string which travels along the length of the string. The wave has a frequency of 50 Hz, amplitude 1 cm and wavelength 0.5 m. find
(a) the time taken by the wave to travel a distance of 8 m along the length of string (b) the time taken by a point on the string to travel a distance of 8 m, once the wave has reached the point and sets it into motion (c ) also. consider the above case when the amplitude gets doubled View SolutionQuestion 6
A steel wire has a mass of 50g/m and is under tension 450N.
(a) Find the maximum average power that can be carried by the transverse wave in the wire if the amplitude not to exceed 20% of the wavelength. (b) The change in maximum average power if the mass per unit length of the wire is doubled. (Useπ2≅10.)View SolutionQuestion 7
A wave is propgting of a long stretched string along its length taken as the positive x-axis. The wave equation is given as
y=y0e−(tT−xλ)^2
where y0=4mm,T=1.0sandλ=4cm. d. Find the velocity of the particle t x=0. c. Find the function g(x) giving the shape of the string t t=0. d. Plot the shape g(x) of the string at t=0. e. Plot of the shape of the string at t=5s.View SolutionQuestion 9
A 4.0 kg block is suspended from the ceiling of an elevator through a string having a linear mass desity of 19.2×10−3kgm−1. Find the speed (with respect to the string) with which a wave pulse can proceed on the string if the elavator accelerates up at the rate of 2.0ms−2.Takeg=10ms−2.View SolutionQuestion 12
A transverse harmonic wave of amplitude 0.01 m is genrated at one end (x=0) of a long horizontal string by a tuning fork of frequency 500 Hz. At a given instant of time the displacement of the particle at x=0.1 m is -0.005 m and that of the particle at x=0.2 m is +0.005 m. calculate the wavelength and the wave velocity. obtain the equetion of the wave assuming that the wave is traveling along the + x-direction and that the end x=0 is at he equilibrium position at t=0. View SolutionQuestion 13
shows the position of a medium particle at t=0, supporting a simple harmonic wave travelling either along or opposite to the positive x-axis.
(a) write down the equation of the curve. (b) find the angle θ made by the tangent at point P with the x-axis. (c ) If the particle at P has a velocity vpm/s, in the negative y-direction, as shown in figure, then determine the speed and direction of the wave. (d) find the frequency of the wave. (e) find the displacement equation of the particle at the origin as a function of time. (f) find the displacement equation of the wave.View SolutionQuestion 15
The equetion of a progressive wave travelling along a string is given by
y=10sinπ(0.01x−2.00t)
where x and y are in centimetres and t in seconds. Find the (a) velocity of a particle at x=2 m and t=5/6 s. (b) acceleration of a particle at x=1 m and t=1/4 s. also find the velocity amplitude and acceleration amplitude for the wave. View Solution
