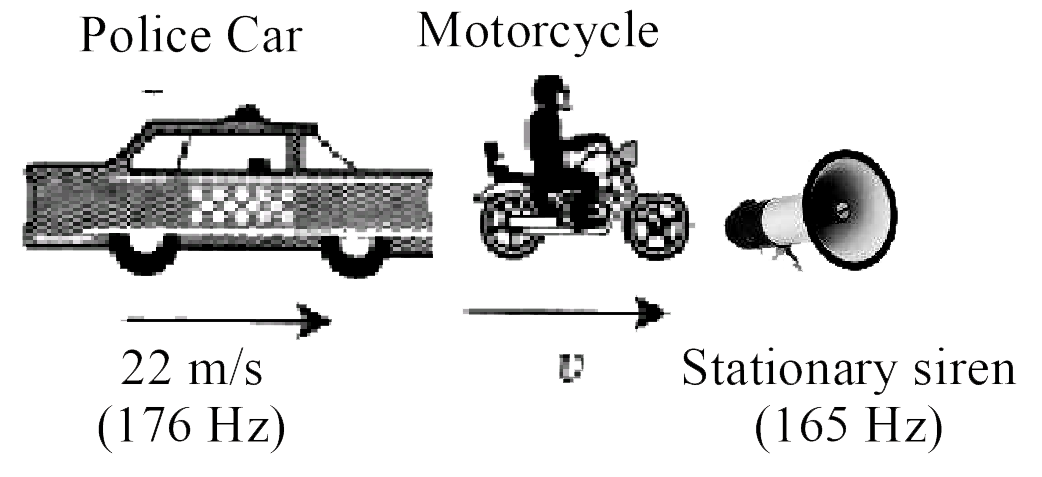All Questions from DHANPAT RAI & CO PHYSICS (HINGLISH) IIT SUPPLEMENT for Class 11
| Class 11 | PHYSICS |
| Chapter | IIT SUPPLEMENT |
| DHANPAT RAI & CO PHYSICS (HINGLISH) | All Questions |
| Medium | English |
| Academic Year | 2023-2024 |
Question 3
On a frictionless horizontal surface , assumed to be the x−y plane , a small trolley A is moving along a straight line parallel to the y−aξs( see figure) with a constant velocity of (√3−1)m/s . At a particular instant , when the line OA makes an angle of 45(∘) with the x−aξs , a ball is thrown along the surface from the origin O. Its velocity makes an angle ϕ with the x−aξsandithitsthetrol≤y.<br>(a)Themotionoftheballisobservedomtheameofthetrol≤y.Calca––tethe∠thetamadebythevelocity→−−→roftheballwiththe x-axis in this frame .
(b) Find the speed of the ball with respect to the surface , if ϕ=(4θ)/(4).
 View Solution
View SolutionQuestion 4
An object A is kept fixed at the point x=3m and y=1.25m on a plank p raised above the ground . At time t=0 the plank starts moving along the +x direction with an acceleration 1.5m/s2. At the same instant a stone is projected from the origin with a velocity →u as shown . A stationary person on the ground observes the stone hitting the object during its downward motion at an angle 45(∘) to the horizontal . All the motions are in the X−Yplane . Find →u and the time after which the stone hits the object . Take g=10m/s
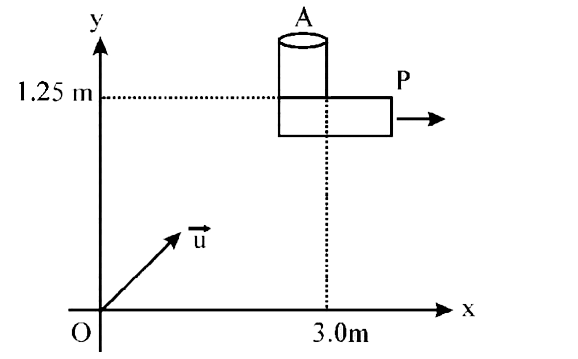 View Solution
View SolutionQuestion 5
A particle of mass m, moving in a cicular path of radius R with a constant speed v2 is located at point (2R,0) at time t=0 and a man starts moving with a velocity v1 along the +ve y-axis from origin at time t=0. Calculate the linear momentum of the particle w.r.t. the man as a function of time.
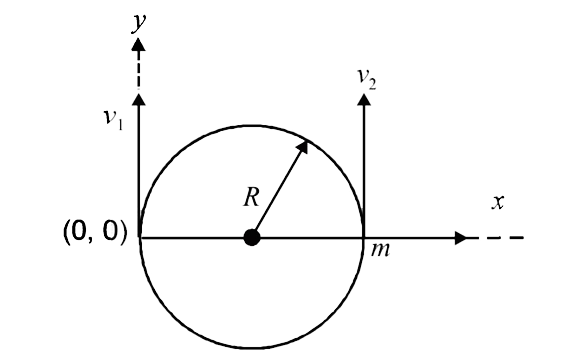 View Solution
View SolutionQuestion 9
An insect crawls up a hemispherical surface very slowly (see the figure). The coefficient of friction between the insect and the surface is 1/3. If the line joining the centre of the hemispherical surface to the insect makes an angle α with the vertical, the maximum possible value of α is given by
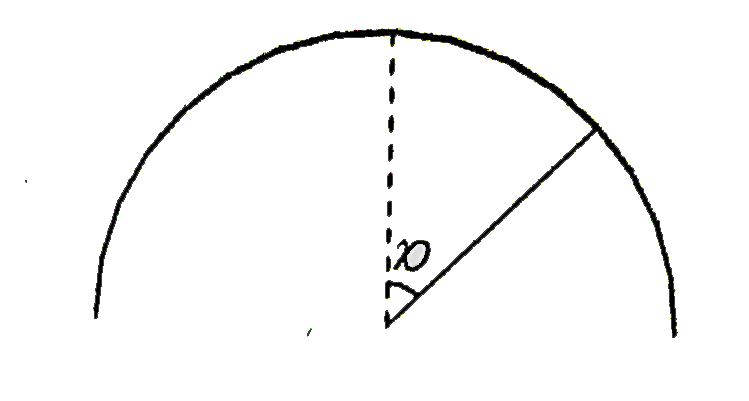 View Solution
View SolutionQuestion 11
In the figure masses m1, m2 and M are 20 kg, 5kg and 50kg respectively. The coefficient of friction between M and ground is zero. The coefficient of friction between m1 and M and that between m2 and ground is 0.3. The pulleys and the strings are massless. The string is perfectly horizontal between P1 and m1 and also between P2 and m2. The string is perfectly vertical between P1 and P2. An external horizontal force F is applied to the mass M. Take g=10m/s2.

(a) Draw a free body diagram for mass M, clearly showing all the forces.
(b) Let the magnitude of the force of friction between m1 and M be f1 and that between m2 and ground be f2. For a particular F it is found that f1=2f2. Find f1 and f2. Write equations of motion of all the masses. Find F, tension in the spring and acceleration of masses.View SolutionQuestion 14
A car P is moving with a uniform speed 5√3m/s towards a carriage of mass 9 kg at rest kept on the rails at a point B as shown in figure. The height AC is 120 m. Cannon balls of 1 kg are fired from the car with an initial velocity 100m/s at an angle 30∘ with the horizontal. The first cannon hall hits the stationary carriage after a timet0 and sticks to it. Determine t0.

At t0, the second cannon ball is fired. Assume that the resistive force between the rails and the carriage is constant and ignore the vertical motion of the carriage throughout. If the second ball also hits and sticks to the carriage, what will be the horizontal velocity of the carriage just after the second impact? View SolutionQuestion 17
A cubical block of side L rests on a rough horizonta surface with coefficient of friction μ. A horizontal force F is applied on the block as shown. If the coefficient of friction is sufficiently high so that the block does not slide before toppling, the minimum force required to topple the block is
 View Solution
View SolutionQuestion 20
A long horizontal rod has a bead which can slide along its length and initially placed at a
distance L from one end A of the rod. The rod is set in angular motion about A with constant angular acceleration α. if the coefficient of friction between the rod and the bead is μ, and gravity is neglected, then the time after which the bead starts slipping is View SolutionQuestion 21
A spherical balll of mass m is the highest point in the space between two fixed , concentic sphere A and B the smaller the two sphere A has a radius R and the space between the two spheres has a width d . The bell has a disneter very dightly less then d . All surface are frictionless . The bell is a given a gentle push (owards the right in the figure ) The upward vertical is denoted by θ (shown ijn the figure)

(a)Express the total normal reaction force exerted by the sphore on the as a finction of angle θ
(b) Let N_(A)andNBdenote in the magnitubes of the normal reaction force on the bell evered by the sphare A and B repectively Skech the variation of NAandN_(B)asfunctionsofcos theta ∈theran≥0 le theta le pi bydraw∈gtwoseparategraph∈youranswerb∞ktak∈gcos theta an the horizental axas. View SolutionQuestion 22
Three particles A, B and C each of mass m, are connected to each other by three massless rigid rods to form a rigid, equilateral triangular body of side l. This body is placed on a horizonta frictionsess table (x-y plane) and is hinged to it at the point A so that it can move without friction about the vertical axis through A . the body is set into rotational motion on the table about A with a constant angular velocity ω.

(a) Find the magnitude of the horizontal force exerted by the hinge on the body.
(b) At time T, when the side BC is parallel to the x-axis, a force F is applied on B along BC (as shown). Obtain the x-component and the y-component of the force exerted by the hinge on the body, immediately after time T.View SolutionQuestion 23
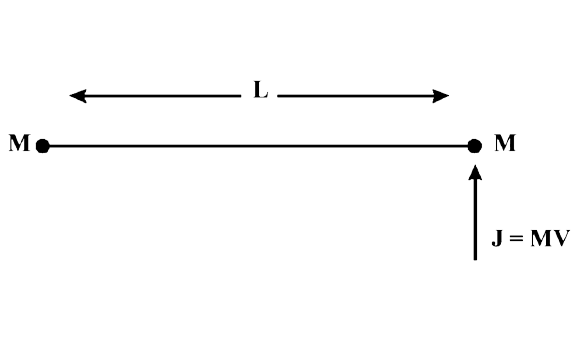
A rod AB of mass M and length L is lying on a horizontal frictionless surface. A particle of mass m travelling along the surface hits the end A of the rod with a velocity v0 in a direction perpendicular to AB. The collision in elastic. After the collision the particle comes to rest
(a). Find the ratio m/M
(b). A point P on the rod is at rest immediately after collision find the distance AP.
(c). Fid the linear speed of the point P a time πL/3v0 after the collision. View SolutionQuestion 24
Two heavy metallic plates are joined together at 90∘ to each other. A laminar sheet of mass 30kg is hinged at the line AB joining the two heavy metallic plates. The hinges are frictionless. The moment of inertia of the laminar sheet about an axis parallel to AB and passing through its center of mass is 1.2 kg m2. Two rubber obstacles P and Q are fixed, one on each metallic plate at a distance 0.5m from the line AB. This distance is chosen so that the reaction due to the hinges on the laminar sheet is zero during the impact. Initially the laminar sheet hits one of the obstacles with an angular velocity 1 rad/s and turns back. If the impulse on the sheet due to each obstacal is 6 N-s,
(a) Find the location of the center of mass of the laminar sheet from AB.
(b) At what angular velocity does the laminar sheet come back after the first impact?
(c) After how many impacts, does the laminar sheet come to rest?
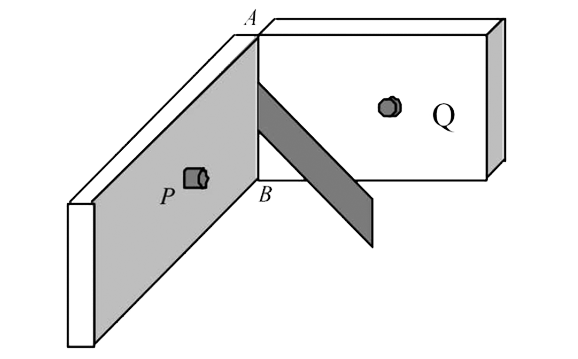 View Solution
View SolutionQuestion 29
A hemispherical portion of radius R is removed from the bottom of a cylinder of radius R. The volume of the remaining cylinder is V and its mass M. It is suspended by a string in a liquid of density ρ where it stays vertical. The upper surface of the cylinder is at a depth h below the liquid surface. The force on the bottom of the cylinder by the liquid is
 View Solution
View SolutionQuestion 30
A large open tank has two holes in the wall. One is a square hole of side L at a depth y from the top and the other is a circular hole of radius R at a depth 4y from the top. When the tank is completely filled with water, the quantities of water flowing out per second from both holes are the same. Then, R is equal to View SolutionQuestion 31
A uniform solid cylinder of density 0.8g/cm3 floats in equilibrium in a combination of two non-mixing liquids A and B with its axis vertical.
The densities of the liquids A and B are 0.7g/cm3 and 1.2g/cm3, respectively. The height of liquid A is hA=1.2cm. The length of the part of the cylinder immersed in liquid B is hB=0.8cm.

(a) Find the total force exerted by liquid A on the cylinder.
(b) Find h, the length of the part of the cylinder in air.
(c) The cylinder is depressed in such a way that its top surface is just below the upper surface of liquid A and is then released. Find the acceleration of the cylinder immediately after it is released.View SolutionQuestion 32
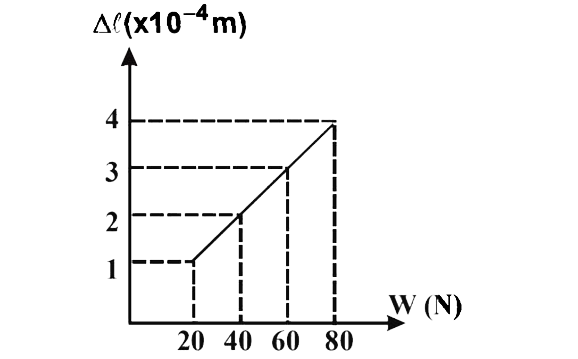
A 5m long cylindrical steel wire with radius 2×10−3m is suspended vertically from a rigid support and carries a bob of mass 100kg at the other end . If the bob gets snapped , calculate the change in temperature of the wire ignoring radiation losses. ( Take g=10m/s2)
( For the steel wire , young's modulus =2.1×1011N/m2 , Density =7860kg/m3, Specific heat =420J/kg∘C ) . View SolutionQuestion 33
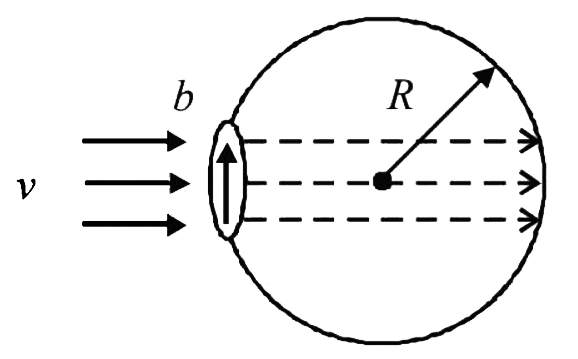
A bubble having surface tension T and radius R is formed on a ring of radius b(b<<R). Air is blown inside the tube with velocity v as shown. The air molecule collides perpendicularly with the wall of the bubble and stops. Calculate the radius at which the bubble separates from the ring.
 View Solution
View SolutionQuestion 34
_E01_290_Q01.png)
Shown in the figure is a container whose top and bottom diameters are D and d respectively At the bottom of the container these is a cappillary tube of outer radius b and inner radius a. the volume flow rate in the capillary is Q. if the capillary is removed the liquid comes out with a velocity of v0. The density of the liquid is given as calculate the coefficient of viscosity η (given πa2=10−6m2 and a2l=2×10−6m]View SolutionQuestion 36
A cubical box of side 1m contains helium gas (atomic weight 4) at a pressure of 100N/m2. During an observation time of 1second, an atom travelling with the root - mean - square speed parallel to one of the edges of the cube, was found to make 500hits with a particular wall, without any collision with other atoms . Take R=253j/mol−Kandk=1.38×10−23J/K.
(a) Evaluate the temperature of the gas.
(b) Evaluate the average kinetic energy per atom.
( c) Evaluate the total mass of helium gas in the box.View SolutionQuestion 37
2kg of ice at 20∘C is mixed with 5kg of water at 20∘C in an insulating vessel having a negligible heat capacity. Calculate the final mass of water remaining in the container. It is given that the specific heats of water & ice are 1kcal/kg/∘C and 0.5
kcal/kg/∘C while the latent heat of fusion of ice is 80kcal/kgView SolutionQuestion 38
Two rods, one of aluminium and other made of steel, having initial lengths l1andl2 are connected together to form a single rod of length (l1+l2). The coefficient of linear expansions for aluminium and steel are αa and αs respectively. If length of each rod increases by same amount when their tempertures are raised by t∘C, then find the ratio l1(l1+l2).View SolutionQuestion 40
When a block of iron in mercury at 0∘C, fraction K1of its volume is submerged, while at the temperature 60∘C, a fraction K2 is seen to be submerged. If the coefficient of volume expansion of iron is γFe and that of mercury is γHg, then the ratio (K1)/(K2) can be expressed as View SolutionQuestion 43
A monoatomic ideal gas, initially at temperature T1, is enclosed in a cylinder fitted with a friction less piston. The gas is allowed to expand adiabatically to a temperature T2 by releasing the piston suddenly. If L1andL2 are the length of the gas column before expansion respectively, then T1T2 is given byView SolutionQuestion 44
An ice cube of mass 0.1 kg at 0∘C is placed in an isolated container which is at 227∘C. The specific heat s of the container varies with temperature T according to the empirical relation s=A+BT, where A=100cal/kg.KandB=2×10−2cal/kg.K2. If the final temperature of the container is 27∘C, determine the mass of the container.
(Latent heat of fusion for water = 8×104cal/kg, specific heat of water =103cal/kg.K).View SolutionQuestion 45
Hot oil is circulated thorugh an insulated container with a wooden lid at the top whose conductivity K=0.149J/(m−∘C−sec), thickness t=5mm,emissivity=0.6 Temperature of the top of the lid is maintaining at Tl=127∘C. If the ambient temperature Ta=27∘C.

Calculate:
(a) rate of heat loss per unit area due to radiation from the lid.
(b) temperature of the oil. (Givenσ=173×10−8Wm−2K−4)View SolutionQuestion 46
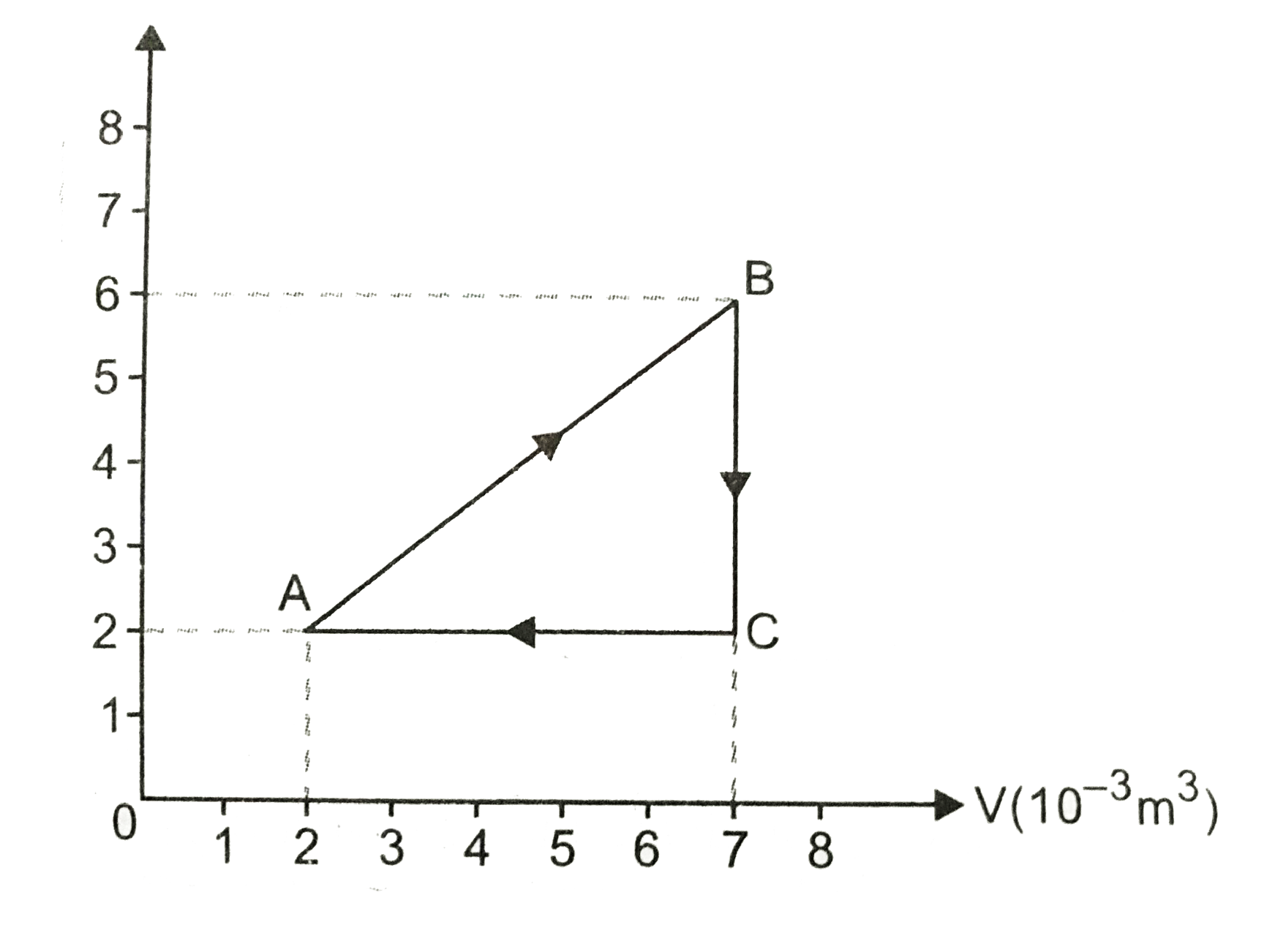
Two moles of an ideal monoatomic gas is taken through a cycle ABCA as shown in the P-T diagram. During the process AB , pressure and temperature of the gas very such that PT=Constant. It T1=300K, calculate
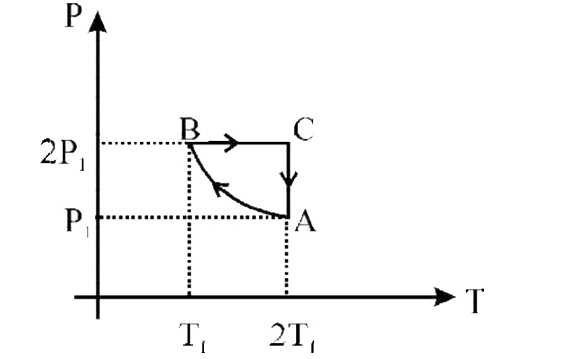
(a) the work done on the gas in the process AB and
(b) the heat absorbed or released by the gas in each of the processes. Give answer in terms of the gas constant R.View SolutionQuestion 47
A monoatomic ideal gas of two moles is taken through a cyclic process starting from A as shown in figure. The volume ratios are VBVA=2andVDVA=4. If the temperature TA at A is 27∘C.
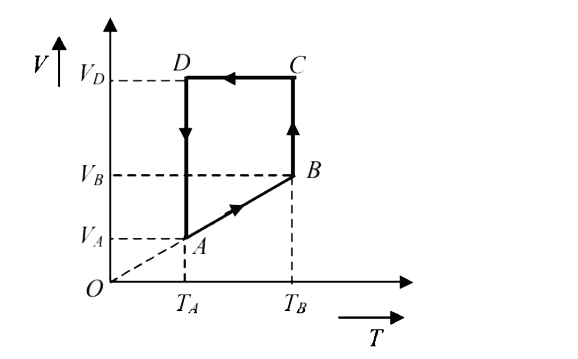
Calculate,
(a) the temperature of the gas at point B,
(b) heat absorbed or released by the gas in each process,
(c) the total work done by the gas during the complete cycle. Express your answer in terms of the gas constant R.View SolutionQuestion 51
Two vibrating strings of the same material but lengths L and 2L have radii 2r and r respectively. They are stretched under the same tension. Both the string vibrate in their fundamental nodes, the one of length L with freuqency v1 and the other with frequency v2. the ratio v1/v2 is given by View SolutionQuestion 53
A sonometer wire resonates with a given tuning fork forming a standing wave with five antinodes between the two bridges when a mass of 9kg is suspended from the wire. When this mass is replaced by a mass 'M' kg, the wire resonates with the same tuning fork forming three antinodes for the same positions of the bridges. Find the value of M.View SolutionQuestion 54
In the experiment for the determination of the speed of sound in air using the resonance column method, the length of the air column that resonates in the fundamental mode, with a tuning fork is 0.1m. When this length is changed to 0.35m, the same tuning fork resonates with the first overtone. Calculate the end correction.View SolutionQuestion 56
A siren placed at a railway platform is emitting sound of frequency 5kHz. A passenger sitting in a moving train A records a frequency of 5.5kHz while the train approaches the siren. During his return journey in a different train B he records a frequency of 6.0kHz while approaching the same siren. the ratio the velocity of train B to that of train A is View SolutionQuestion 60
Two narrow cylindrical pipes AandB have the same length. Pipe A is open at both ends and is filled with a monoatomic gas of molar mass MA. Pipe B is open at one end and closed at the other end, and is filled with a diatomic gas of molar mass MB. Both gases are at the same temperature.
(a) If the frequency of the second harmonic of the fundamental mode in pipe A is equal to the frequency of the third harmonic of the fundamental mode in pipe B, determine the value of MB/MB.
(b) Now the open end of pipe B is also closed (so that the pipe is closed at both ends). Find the ratio of the fundamental frequency in pipe A to that in pipe B. View SolutionQuestion 61
A 3.6m long vertical pipe resonates with a source of frequency 212.5Hz when water level is at certain height in the pipe. Find the height of water level (from the bottom of the pipe) at which resonance occurs. Neglect end correction. Now , the pipe is filled to a height H(≈3.6m). A small hole is drilled very close to its bottom and water is allowed to leak. Obtain an expression for the rate of fall of water level in the pipe as a function of H. If the radii of the pipe and the hole are 2×10−2m and 1×10−3m respectively, Calculate the time interval between the occurance of first two resonances. Speed of sound in air 340m/s and g=10m/s2.View SolutionQuestion 62
A boat is travelling in a river with a speed of 10 m/s along the stream flowing with a speed of 2m/s. From this boat, a sound transmitter is lowered into the river through a rigid support. The wavelength of the sound emitted from the transmitter inside the water is 14.45 mm. Assume that attenuation of sound in water and air is negligible. What will be the frequency detected by a receiver kept inside downstream?View Solution


 .
.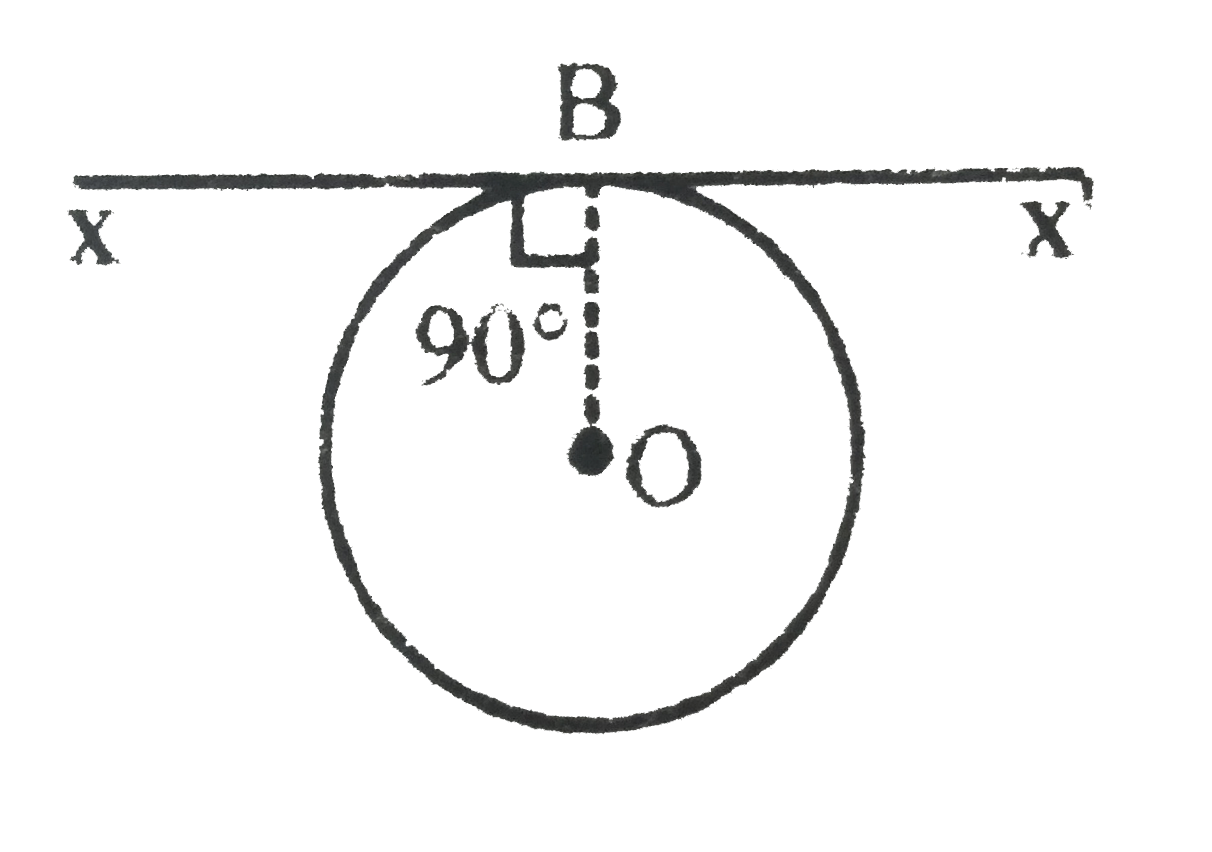 .
.