Worked Out Examples from HC VERMA PHYSICS Chapter 8 HEAT TRANSFER for Class 11

Class 11	PHYSICS
Chapter	HEAT TRANSFER
HC VERMA PHYSICS	Worked Out Examples
Medium	English
Academic Year	2023-2024

Question 1
The lower surface of a slab of stone of face-area 3600cm^(2) and thickness 10cm is exposed to steam at $100^{\circ} C$ . A block of ice at 0^(@)C rests on the upper surface of the slab. 4.8g of ice melts in one hour. Calculate the thermal conductivity of the stone. Latent heat of fusion of ice =3.36xx10^(5) J kg^(-1)View Solution
Question 2
An icebox made of 1.5cm thick stuyrofoam has dimensions $60 c m \times 60 c m \times 30 c m . I t c o n t a \in s i c e a t w h i c h t h e i c e i s m e < \in g . L a t e n t h e a t o f f u s i o n o f i c e$ =3.36xx10^(5)J kg^(-1) $. and t h e r m a l c o n d u c t i v i t y o f s t y r o f o a m$ =0.04Wm^(-1) $^(\circ) C^{- 1}$ .View Solution
Question 3
A closed cubical box is made of perfectly insulating material and the only way for heat to enter or leave the box is through two solid cylindrical metal plugs, each of cross sectional area $12 c m^{2}$ and length 8cm fixed in the opposite walls of the box. The outer surface of one plug is kept at a temperature of $100^{\circ} C$ . while the outer surface of the plug is maintained at a temperature of $4 (\circ) C$ . The thermal conductivity of the material of the plug is $2.0 W m^{- 1}$ ^(@)C^(-1) . A source of energy generating 13W is enclosed inside the box. Find the equilibrium temperature of the inner surface of the box assuming that it is the same at all points on the inner surface.View Solution
Question 4
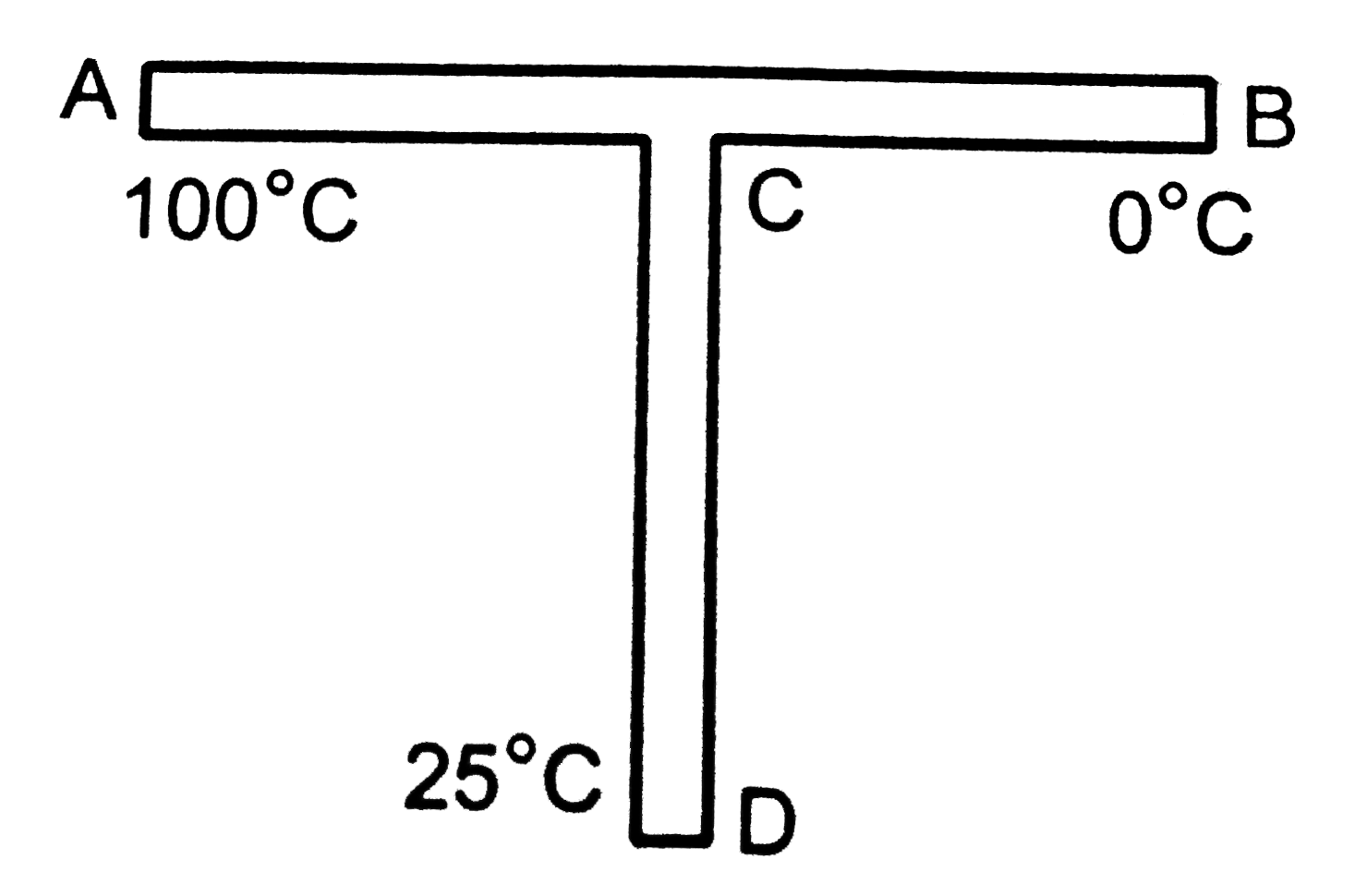
A bar of copper of length 75cm and a abr of steel of length 125cm are joined together end to end. Both are of circular cross section with diameter 2cm. The free ends of the copper and the steel bors are maintained at $100^{\circ} C$ and 0^(@)C $r e s p e c t i v e l y . T h e c u r v e d s u r f a c e o f t h e b or s . a r e t h e r m a l l y \in s a - - t e d . W ˆ i s t h e t e m p e r a t u r e o f t h e c o p p e - s t e e l j u n c t i o n ? W ˆ i s t h e a m o u n t o f h e a t t r a n s m i e d p e r u n i t t i m e a c r o s s t h e j u n c t i o n ? T h e r m a l c o n d u c t i v i t y o f c o p p e r i s$ 386Js^(-1)m^(-1) $^(\circ) C^{- 1}$ and that of steel is 46Js^(-1)m^(-1)(@)C^(-1)View Solution
Question 5
Two parallel plates A and B are joined together to form a compound plate . The thicknesses of the plate are $4.0 c m$ and $2.5 c m$ respectively and the area of cross section is $100 c m^{2}$ for each plate. The thermal conductivities are $K_{A} = 200 W m^{- 1}$ ^(@)C^(-1) $f or t h e p a < e B . T h e o u t e r s u r f a c e o f t h e p l a t e A i s m a \int a \in \neq d a t$ 100^(@)C $and t h e o u t e r s u r f a c e o f t h e p l a t e A i s m a \int a \in e d a t$ 100^(@)C . and the outer surface of the plate B is maintained at 0^(@)C. Find (a) the rate of heat flow through any cross section, (b) the temperature at the interface and (c) the equivalent thermal conductivity of the compound plate.
View Solution
Question 6
A room has a $4 m \times 4 m \times 10 c m$ concrete roof $(K = 1.26 W m^{- 1}$ ^(@)C^(-1) $. A t s o m e \in s tan t, t h e t e m p e r a t u r e o u t s i s$ 40(@)C $and t ˆ \in s i s 32 (\circ) C$ . (a) Neglecting converction, calculate the amount of heat flowing per second into the room through the roof. (b) Bricks $(K = 0.65 W m^{- 1}$ ^(@)C^(-1) of thickness $7.5 c m$ are loid down on the roof. Calculate the new rate of heat flow under the some temperature conditions. View Solution
Question 7
An electric heatet is uesd in a room of total wall area $137 m^{2} \to m a \int a \in a t e m p e r a t u r e o f$ 20^(@)C inside it, when the outside temperature is $- 10^{\circ} C$ .The wall have three different layers of matwerials. The innermost layer is of wood of thickness 2.5cm, the middle layer is of cement of thickness 1.0cm and the outermost layer is of brick of thickness 25.0cm. Find the power of the electric heater. Assume that there is no heat loss through the flooor and the celling. The thrermal conductivities of wood, cement and brick aree $0.125 W m^{- 1}$ ^(@)C^(-1) $, 1.5 W m^{- 1}$ ^(@)C^(-1) $. and 1.0 W m^{- 1}$ ^(@)C^(-1) respectively.
View Solution
Question 8
Three rods of material x and three of material y are connected as shown in figure. All the rods are identical in length and cross sectional area. If the end A is maintained at $60^{\circ} C$ and the junction E at $10^{\circ} C$ , calculate the temperature of the junction B. The thermal conductivity of x is $800 W m^{- 1}$ ^(@)C^(-1) $and t ˆ o f y i s$ 400Wm^(-1) $^(\circ) C^{- 1}$ .
View Solution
Question 9
A rod CD of thermal resistance $5.0 K W_{- 1} i s j o \in e d a t t h e m \leq o f a n n t i c a l r o d A B a s s h o w n \in f i g u r e . T h e e n d s A, B and D a r e m a \int a \in e d a t$ 100^(@)C $,$ 0(@)C and 25(@)C respectively. Find the heat current in CD.
View Solution
Question 10
Two thin metallic spherical shells of radii $r_{1} and r_{2} (r_{1} < r_{2})$ are placed with their centres coinciding. A material of thermal conductivity K is filled in the space between the shells. The inner shells. Is maintained at temperature $θ_{1}$ .and the outer shell at temperature $θ_{2} (θ_{1} < θ_{2})$ . Calculate the rate at which heat flows radially through the material.
View Solution
Question 11
On a cold winter day, the atmospheric temperature is $- θ$ (on Celsius scale) which is below $0^{\circ} C$ . A cylindrical drum of height h made of a bad conductor is completely filled with water at $0^{\circ} C$ and is kept outside without any lid. Calculate the time taken for the whole mass of water to freeze. Thermal conductivity of ice is K and its latent heat of fusion is L. Neglect expansion of water on freezing.
View Solution
Question 12
Figure shows a large tank of water at a constant temperature $θ_{0}$ . and a small vessel containinng a mass m of water at an initial temperature $θ (< θ_{0} . A m η l r o d o f \leq n > h L, a r e a o f c r o s s sec t i o n A and t h e r m a l c o n d u c t i v i t y K c o \cap e c t t h e t w o v e s s e l s . F \in d t h e t i m e t a k e n f or t h e t e m p e r a t u r e o f t h e w a t e r \in t h e s m a l \leq r v e s s e l \to b e c o m e$ theta_(2)(theta_(1)lttheta_(2)lttheta_(0)) . Specific heat capacity of water is s and all other heat capacities are negligible.
View Solution
Question 13
One mode of an ideal monatomic gas is kept in a rigid vessel. The vessel is kept inside a steam chamber whose temperature is $97^{\circ} C$ . Initially, the temperature of the gas is ${5.0}^{\circ} C$ . The walls of the vessel have an inner surface of area $800 c m^{2}$ and thickness $1.0 c m$ If the temperature of the gas increases to ${9.0}^{\circ} C$ in $0.5$ second, find the thermal conductivity of the material of the walls. View Solution
Question 14
monatomic ideal gas is contained in a rigid container of volume V with walls of totsl inner surface area A, thickness x and thermal condctivity K. The gas is at an initial temperature $t_{0}$ and pressure $P_{0}$ . Find tjr pressure of the gas as a function of time if the temperature of the surrounding air is $T_{s}$ . All temperature are in absolute scale. View Solution
Question 15
Conside a cubical vessel of edge a having a small hole in one of its walls is r. At time $t = 0$ , it contains air at atmospheric pressure $p_{a} and t e m p e r a t u r e$ T_(0) $. T h e t e m p e r a t u r e o f t h e s u r r o u d \in g a i r i s$ T_(a)(gtT_(0) $. F \in d t h e a m o u n t o f t h e g a s (\in m o \leq s) \in t h e v e s s e l a t t i m e t . T a k e$ C_(v) $o f a i r \to b e 5 R / 2$ . View Solution
Question 16
A blackbody of surface area $1 c m^{2}$ is placed inside an enclosure. The enclosure has a constant temperature $27 (\circ) C$ and the blackbody is maintained at $327 (\circ) C$ by heating it electrically. What electric power is needed to maintain the temperature? $σ = 6.0 \times 10^{- s} W m^{- 2} K (- 2)$ . View Solution
Question 17
An electric heater emits 100W of thermal radiation. The coil has a surface area of $0.02 m^{2}$ . Assuming that the coil radiates like a blackbody, Find its temperature. Sigma=6.00xx10^(-s)Wm^(-2)K(-4) . View Solution
Question 18
The earth receives solor radiation at a rate of $8.2 J c m^{- 2} - 1 min$ . Assuming that the sun radiates like a blackbody, calculate the surface of the sun. The angle subtended by the sun on the earth is $0.55 (\circ) C$ and the stefan constant $σ = 5.67 \times 10^{- s} W m^{- 2} K^{- 4}$ . View Solution
Question 19
The temperature of a body falls from $40^{\circ} C$ to $36 (\circ) C$ in 5 minutes when placed in a surrouning of constant temperature $16 (\circ) C$ Find the time taken for the temperature of the body to become $32 (\circ) C$ .View Solution
Question 20
A hot fbody placed in air is cooled down according to Newton's law of cooling, the rate of decrease of temperature being k times the temperature difference from the surrounding. Starting from $t = 0$ , find the time in which the body will loss half the maximum heat it can lose.View Solution

All Exercises from HC VERMA PHYSICS Class 11 PHYSICS HEAT TRANSFER

Home
Ask Doubt
Profile