Question

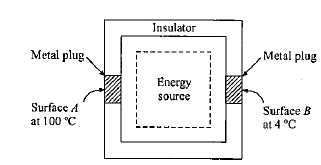
A closed cubical box is made of perfectly insulating material and the only way for heat to enter or leave the box is through two solid cylindrical metal plugs, each of cross sectional area $12c{m}^2$ and length 8cm fixed in the opposite walls of the box. The outer surface of one plug is kept at a temperature of ${100}^{\circ }C$ . while the outer surface of the plug is maintained at a temperature of $4(\circ )C$ . The thermal conductivity of the material of the plug is $2.0W{m}^{-1}$^(@)C^(-1) . A source of energy generating 13W is enclosed inside the box. Find the equilibrium temperature of the inner surface of the box assuming that it is the same at all points on the inner surface.

Explanation

The situation is show in figure. Let the temperature inside the box be (theta). The rate at which heat enters the box through the left plug is
`(DeltaQ_(1))/(Deltat)=(KA(theta_(1)-(theta)))/(x)` . The rate of heat generation in the box `=13W` . The rate at which heat fkows out of the box through the right pluyg is `(DeltaQ_(2))/(Deltat)=(KA(theta-theta_(2)))/(x)` . In the steady state
`(DeltaQ_(1))/(Deltat)+13W=(DeltaQ_(2))/(Deltat)` . or, `(KA)/(x)(theta_(1)-theta)+13W=(KA)/(x)(theta-theta_(2))` . or, `2(KA)/(x)theta=(KA)/(x)(theta_(1)+theta_(2))+13W` . or, `theta=theta_(1)+theta_(2)/(2)+((13W)xx0.08m)/(2xx(2.0Wm^(-1)`^(@)C^(-1)(12xx10^(-4)m^(2))` . `=52^(@)C+216.67^(@)C=269^(@)C` .