Exercises from HC VERMA ROTATIONAL MECHANICS for Class 11
| Class 11 | PHYSICS |
| Chapter | ROTATIONAL MECHANICS |
| HC VERMA | Exercises |
| Medium | English |
| Academic Year | 2023-2024 |
Question 22
A rod of mass m and length L , lying horizontally is free to rotate about a vertical axis through its centre. A horizontal force of constant magnitude F acts on the rod at a distance of L/4 from the centre. The force is always perpendicular to the rod. Find the angle rotated by the rod during the time t after the motion starts.View SolutionQuestion 25
A flywheel of moment of inertia 5.0 kg m^2 is rotated at a speed of 60 rad/s. Because of the friction at the axle, it comes to rest in 5.0 minutes. Find a. The average torque of the friction. B. the total work done by the friction and c. the angular momentum of the wheel 1 minute before it stops rotating.View SolutionQuestion 26
Because of the friction between the water in oceans with the earth's surface the rotational kinetic energy of the earth is continuously decreasing. If earth's angular speed decreases by 0.0016 rad/day in 100 years, find the average torque of the friction on the earth. Radius of the earth is 6400 km and its mass is 6.0×1024kg.View SolutionQuestion 28
A wheel of mass 10 kg and radius 0.2 m is rotating at an angular speed of 100 rpm, when the motion is turned off. Neglecting the friction at the axis. Calculate the force that must be applied tangentially to the wheel to bring it to rest in 10 rev. Assumed wheel to be a disc.View SolutionQuestion 29
A cylinder rotating at an angular speed of 50 rev/s is brought in contact with an identical stationary cylinder. Because of the kinetic friction, torques act on the two cylinders, accelerating the stationary one and decelerating the moving one. If the common magnitude of the acceleration and deceleration be one revolution per second square, how long will it take before the two cylinders have equal angular speed?View SolutionQuestion 33
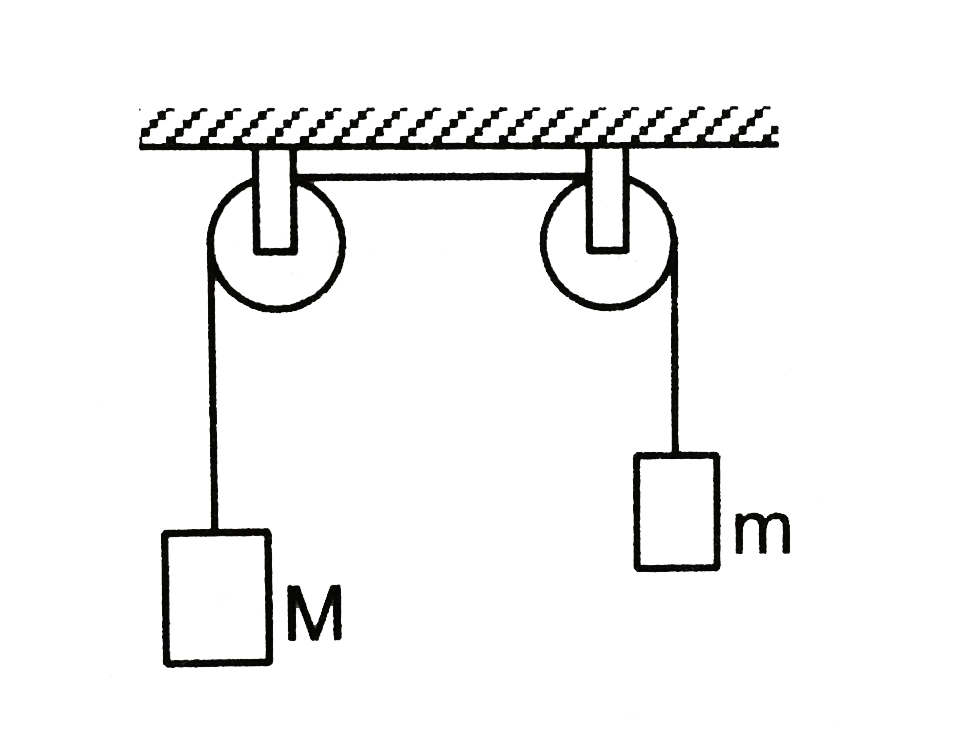
Figure shows two blocks of masses m and M connected by a string passing over a pulley. The horizontal table over which the mass m slides is smooth. The pulley has a radius r and moment of inertia I about its axis and it can freely rotate about this axis. Find the acceleration of the mass M assuming that the string does not slip on the pulley.
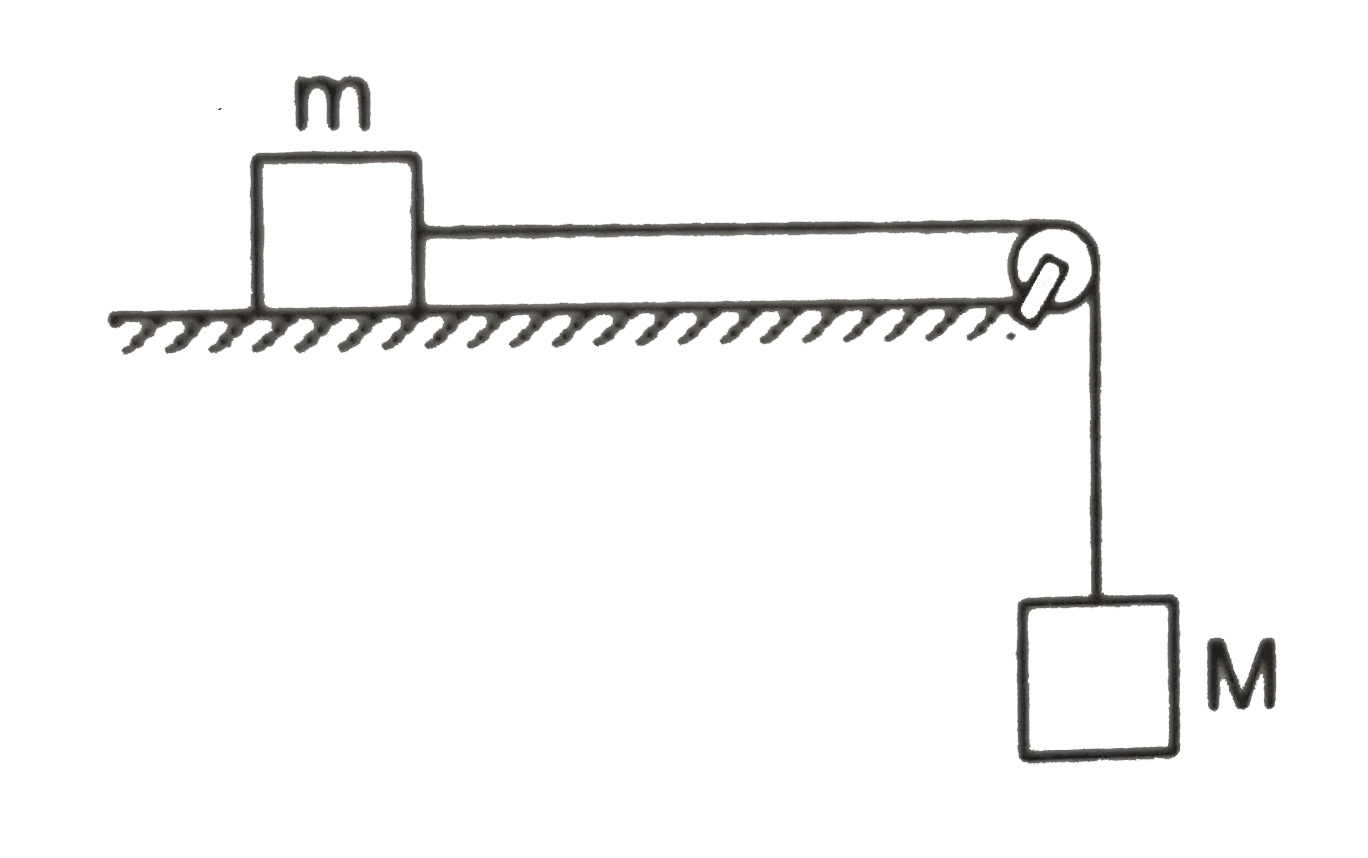 View Solution
View SolutionQuestion 41
A uniform ladder of length 10.0 m and mass 16.0 kg is resting against a vertical smooth wall making an angle of 37∘ with it. An electrian weighing 60.0 kg climbs up the ladder. If the stays on the ladder at a point 8.00 m from the lower end, what will be normal force and the force of friction on the ladder by the ground? What should be the minimum coefficient of friction for the electrician to work safely?View SolutionQuestion 43
A 6.5 m long ladder rests against as vertical wall reaching a height of 6.0 m. A 60 kg man stands hlf way up the ladder. A. Find the torque of the force exerted by the man on the ladder bout the upper end of the ladder. b.Assuming the weight of the ladder of be negligible as compared to the man and assuming the wall to be smooth find the force exerted by the ground on the ladder.View SolutionQuestion 49
Two particles of masses m1andm2 are joined by a light rigid rod of length r. The system rotates at an angular speed ω about an axis through the centre of mass of the system and perpendicular to the rod. Show that the angular momentum of the system is L=μr2ω where μ is the reduced mass of the system defined as μ=m1m2m1+m2View SolutionQuestion 50
A dumb bell consists of two identicasl small balls offmss 1/2 kg each connected to the ends of a 50 cm long light rod. The dumb bell is rotating about a fixed axis through the centre of the rod and perpendicular to it t an angular speed of 10 rad/s. An impulsive force of average magnitude 5.0 N acts on one of the masses in the direction of its velocity for 0.10s. Find the new angular velocity of the system.View SolutionQuestion 53
A boy is seated in a revolving chair revolving at an angular speed of 120 revolutions per minute. Two heavy balls form part of the revolving system and the boy can pull the balls closer to himself or may push them apart. If by pulling the balls closer, the boy decreases the moment of inertia of the system from 6kg−m2→2kg−m2 what will be the new angular speed?View SolutionQuestion 54
A boy is standing on a platform which is free to rotate about its axis. the boys holds an open umbrella in his hand. The axis of the umbrella coincides with tht of the platform. The moment of inertias of the platform plus the boy sytem is 3.0×10−3kg−m and that of the umbrella is 2.0×10−3 kg-m^2. The boy starts spinning the umbrella about the axis at an angular speed of 2 rev s1 with respect to himself . Find the angular velocity imparted to the platform.View SolutionQuestion 55
A wheel of moment of inertia 0.10kg−m2 is rotating about a shaft at an angular speed of 160revmin. A second wheel is set into rotation at 300 rev/minute and is coupled to the same shaft so that both the wheels finally rotate with as common angular speed of 200 rev/minute. Find the moment of inertia of the second wheel.View SolutionQuestion 56
A kid of mass M stands at the edge of a platform of radius R which can be freely rotated about its axis. The moment of inertia of the platform is I . The system is at rest when a friend throws as ball of mass m and the kid catches it. If the velocity of the ball is v horizontally along the tangent to the edge of the platform when it was caught by the kid find the angular speed of the platform after the event.View SolutionQuestion 57
Suppose the platform of the previous problem is brought to rest with the ball in tehhad of the kid standin on the rim. The kid throuws the ball horizontaly to his friend in a direction tangentiasl to the rim with a speed v as seen by his friend. Find the angular velocity wilth which the platform will start rotating.View SolutionQuestion 58
Suppose the platform with the kid in the previous problem is rotting in anticlockwise directioin at an angular speed ω. The kid starts walking along the rim with a speed v relative to the platform also in the anticlockwise direction. Find the new angular speed of the platform.View SolutionQuestion 59
A uniform rod of mass m and length l is struck at an end by a force F perpendicular to the rod for a short time interval t. Calculate
a. the speed of the centre of mass ,b. the angular speed of the rod about centre of mass, c. the kinetic energy of the rod and d. the angular moment of the rod about the centre of mass after the force has stopped to act. Assume that t is so small that the rod does not apreciably change its direction while the force acts.View SolutionQuestion 60
A uniform rod of length L lies on a smooth horizontal table. A particle moving on the table strikes the rod perpendicularly at an end and stops. Find the distance travelled by the centre of the rod by the time it turns through a right angle. Show that if the mass of the rod is four times that of the particle, the collision is elastic View SolutionQuestion 61
Suppose the particle of the previous problem has a mass m and a speed v before the collision and it sticks to the rod after the collision. The rod has a mass M. a. Find the velocity of the particle with respect to C of the system consituting the rod plus the particle. b. Find the velociyt of the particle with respect to C before the collision. c. Find the velocity of the rod with respect to C before the colision. e. find the moment of inertia of the system about the vertical axis through the centre of mass C after the collision. f. Find the velociyt of the centre of mass C and the angular velocity of the system about the centre of mass after the collision.View SolutionQuestion 62
Two small bals A and B, each of mass m, are joined rigidlyl by a light horizontal rol of lengh L. The rod is clasmped at the centre in such a way that it c an rotate freely about a verticl axis through its centre. The systemis rotated with an angualr speed ω about the axis. A particle P of masss m kept at rest sticks to the ball A as the ball collides with it. Find the new angular speed of the rod.View SolutionQuestion 63
Two small balls A and B each of mass m, are joined rigidly to the ends of a light rod of length L figure. The system translates on a frictionless horizontal surface with a velocity v0 in a direction perpendicular to the rod. A particle P of mass kept at rest on the surface sticks to the ball A as the ball collides with it . Find
a. the linear speeds of the balls A and B after the collision, b. the velocity of the centre of mass C of the system A+B+P and c. the angular speed of the system about C after the collision.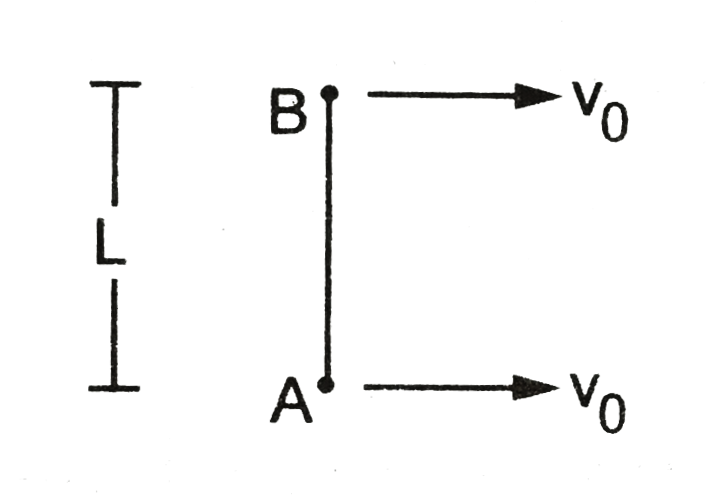 View Solution
View SolutionQuestion 64
Suppose the rod with the balls A and B of theprevious problem is clamped at the centre in such a way that it ca rotate freely about a horizontal axis through the clamp. The system is kept at rest in the horizontal position. A particle P of the same mass m is dropped from a heigh h hon the ball B. The particle collides with B and sticks to it. a. Find the angular momentum and the angular speed of the system just after the collision. b. What should be the minimum value of h so that the system makes a full rotation after the collision.View SolutionQuestion 65
Two blocks of masses 400 g and 200 g are connected through a light string going over a pulley which is free to rotate about its axis. The pulley has as moment of inertia 1.6×10−4kg−m2 and a radius 2.0 cm. Find a. the kinetic energy of the system as the 400 block falls thrug 50 cm b. the speed of the blcok at this instant.View SolutionQuestion 66
The pulley shown in figure has a radius of 20 cm and moment of inertial 0.2 kg-m^2. The string going over it is attached at one end to a vertical sprign of spring constant 50 N/m fixed from below and supports a 1 kg mas at other end. The system is released from rest with the spring at its natural length. Find the speed of the block when it has desceds through 10 cm. Take g=10ms2.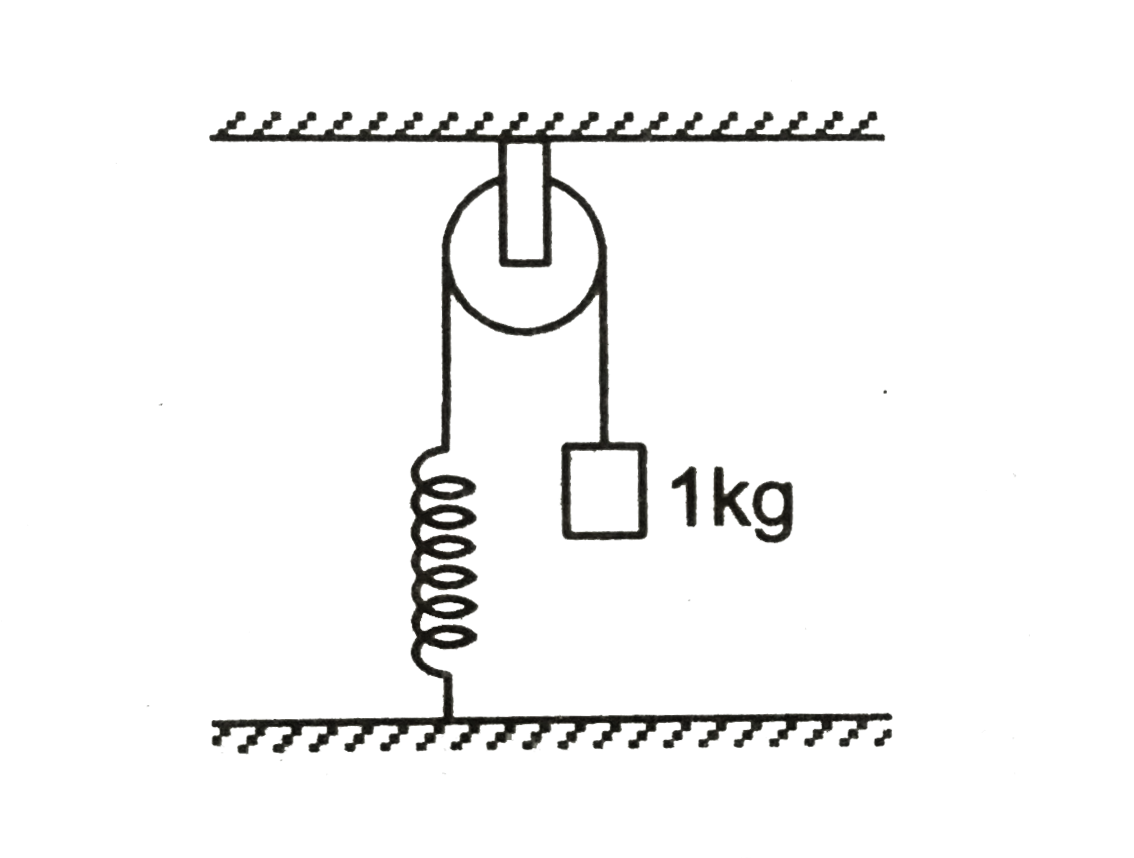 View Solution
View SolutionQuestion 68
A metre stick weighing 240 g is pivoted at its upper end in such a way that it can freely rotate in a vertical plane through this end figure. A particle of mass 100 g is attached to the upper end of the stick through a light sting of length 1 m. Initially the rod is kept veritcal and the string horizontal when the system is released from rest. The particle colides with the lower end of the stick and sticks there. Find the maximum angle through which the stick will rise. View Solution
View SolutionQuestion 76
A hollow sphere is released from the top of an inlcined plane of inclination θ. A. What should be the minimum coefficientof friction between the shphere and the plane to prevent sliding? B. Find the kinetic energy of the ball as it moves down a length l on the incline if the friction coefficient is half the value calculated in part a.View SolutionQuestion 79
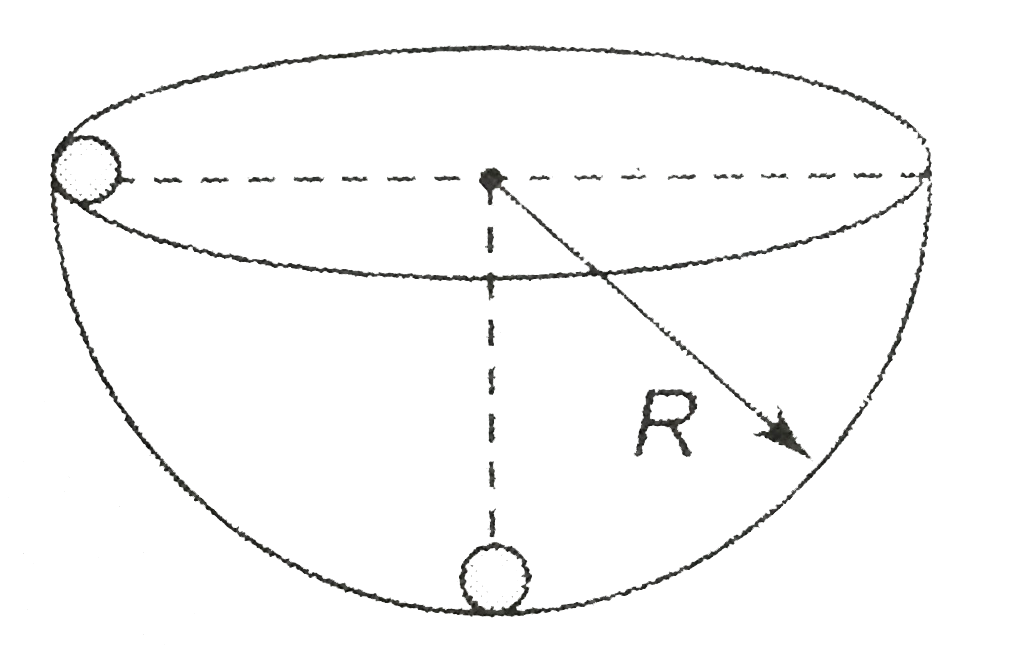
Figure shows a smasll sphereical bal of mass m rolling down the loop track. Thebasll is released on the linear portion at a verticla height H from the lowest point. The circular part show has a radius R.
a. find the kinetic energy of the ball when it is at a point where the radius makes an angle θ with the horizontal.
Find the radial and the tangential accelerations of the cente when the ball is at A. c. find the bnormal force and the frictionasl force acting on the ball if H=60 cm, R=10cm θ=0 and m=70 fg.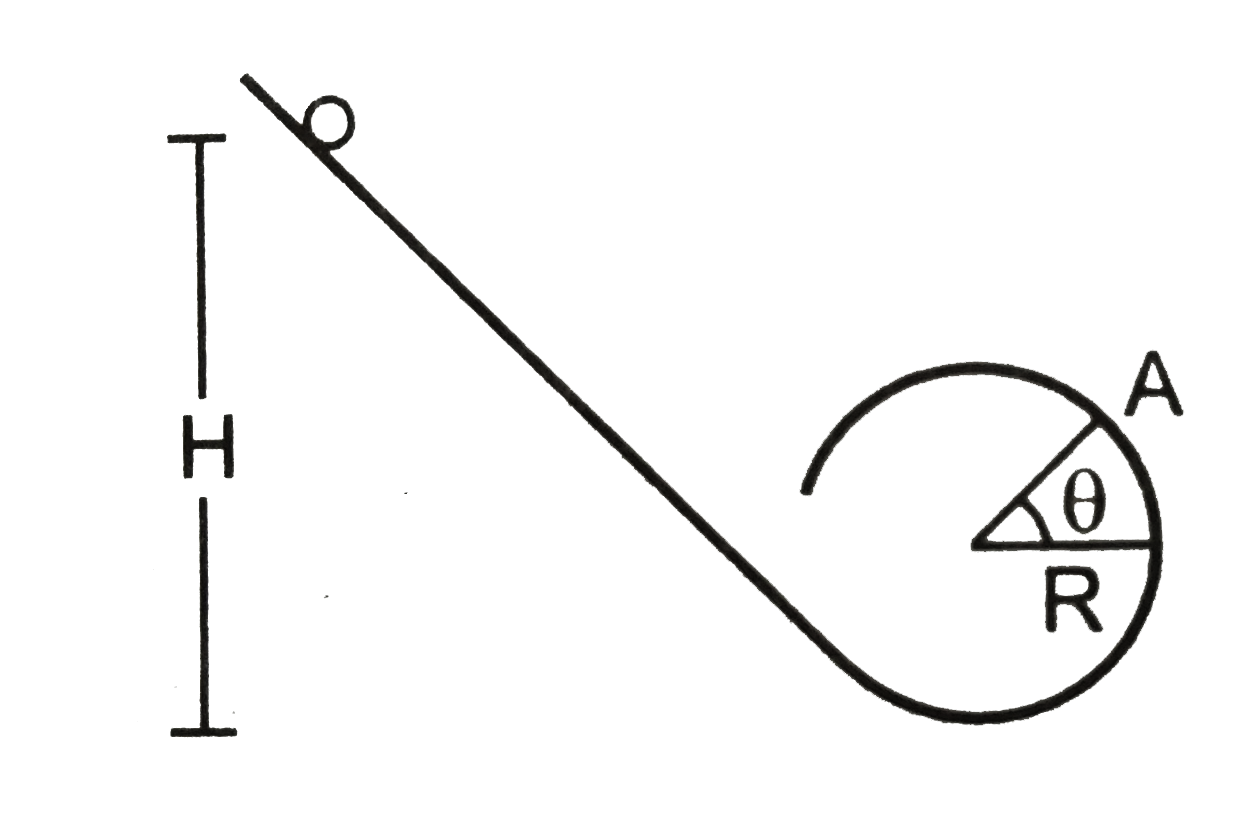 View Solution
View SolutionQuestion 81
A uniform wheel of radius R is set lying on a rough horizontal surface is hit by as cue is such a way that the line of action passes thruogh the centre of the shell. As a result the shelll starts movign with a linear speed v without any initial angular velocity. Find the linear speed of the shell after it starts pure rolling on the surface.View SolutionQuestion 82
A uniform wheel of radius R is set lying on a rough horizontal surface is hit by as cue is such a way that the line of action passes thruogh the centre of the shell. As a result the shelll starts movign with a linear speed v without any initial angular velocity. Find the linear speed of the shell after it starts pure rolling on the surface.View SolutionQuestion 85
A solid sphere is set into motion on a rough horizontal surfce with a linar speed v in the forward direction and an angular speed v/R in the anticlockwise direction as shown infigure . Find the linear speed of the sphere a. where it stops rotating and b. when slipping finally ceases sand pure rolling starts. View Solution
View Solution
All Exercises from HC VERMA Class 11 PHYSICS ROTATIONAL MECHANICS
- EXERCISES
- EXERCISES
- EXERCISES
- EXERCISES
- EXERCISES
- EXERCISES
- EXERCISES
- EXERCISES
- EXERCISES
- EXAMPLES
- EXAMPLES
- EXAMPLE
- EXAMPLES
- EXAMPLES
- EXAMPLE
- EXAMPLES
- EXAMPLES
- EXAMPLE
- OBJECTIVE 1
- OBJECTIVE 1
- OBJECTIVE -1
- OBJECTIVE 1
- OBJECTIVE 1
- OBJECTIVE -1
- OBJECTIVE 1
- OBJECTIVE 1
- OBJECTIVE -1
- OBJECTIVE 2
- OBJECTIVE 2
- OBJECTIVE -2
- OBJECTIVE 2
- OBJECTIVE 2
- OBJECTIVE -2
- OBJECTIVE 2
- OBJECTIVE 2
- OBJECTIVE -2
- SHORT ANSWER
- SHORT ANSWER
- QUESTIONS FOR SHORT ANSWER
- SHORT ANSWER
- SHORT ANSWER
- QUESTIONS FOR SHORT ANSWER
- SHORT ANSWER
- SHORT ANSWER
- QUESTIONS FOR SHORT ANSWER
- WORKED OUT EXAMPLES
- WORKED OUT EXAMPLES
- WORKED OUT EXAMPLES
- WORKED OUT EXAMPLES
- WORKED OUT EXAMPLES
- WORKED OUT EXAMPLES
- WORKED OUT EXAMPLES
- WORKED OUT EXAMPLES
- WORKED OUT EXAMPLES