EXERCISE from NCERT PHYSICS Chapter 10 SYSTEMS OF PARTICLES AND ROTATIONAL MOTION for Class 11

Class 11	PHYSICS
Chapter	SYSTEMS OF PARTICLES AND ROTATIONAL MOTION
NCERT PHYSICS	EXERCISE
Medium	English
Academic Year	2023-2024

Question 1
Given the location of the centre of mass of a (i) sphere, (ii) cylinder, (iii) ring, and (iv) cube, each of uniform mass density. Does the centre of mass of a body necessarily lie on the body ?View Solution
Question 2
In the $H C I$ molecule, the separation between the nuclei of the two atoms is about $1.27 Å (1 Å = 10^{- 10} m)$ . Find the approximate location of the c.m of the molecule, given that a chlorine atom is about $35.5$ times as massive as a hydrogen atom and nearly all the mass of an atom is concentrated in its nucleus ?View Solution
Question 3
A child is standing at one end of a long trolley moving with a speed v on a smooth horizontal track. If the child starts running towards the other end of the trolley with a speed u, the centre of mass of the system (trolley + child) will move with a speed :View Solution
Question 4
Show that the area of the triangle contained between the vector $\to a and \to b$ is one half of the magnitude of $\to a \times \to b$ View Solution
Question 5
Show that $\to a . (\to b \times \to c)$ is equal in magnitude to the volume of the parallelpiped formed by the vectors $\to a, \to b and \to c$ View Solution
Question 6
Find the components along the $x, y, z$ axes of the angular momentum $\to L$ of a particle, whose position vector is $\to r$ with components $x, y, z$ and momentum is $\to p$ with components $p_{x}, p_{y} and p_{z}$ . Show that if the particle moves only in the $x - y$ plane, the angular momentum has only a z-component.View Solution
Question 7
Two particles each of mass $m$ and speed $v$ , travel in opposite direction along parallel lines separated by a distance d. Show that the vector angular momentum of this system of particles is the same about any point taken as origin.View Solution
Question 8
A non-uniform bar of weight $W$ is suspended at rest by two strings of negligible weight as shown in Fig. The angles made by the strings with the vertical are ${36.9}^{\circ} and {53.1}^{\circ}$ respectively. The bar is $2 m$ long. Calculate the distance $d$ of the centre of gravity of the bar from its left end.
View Solution
Question 9
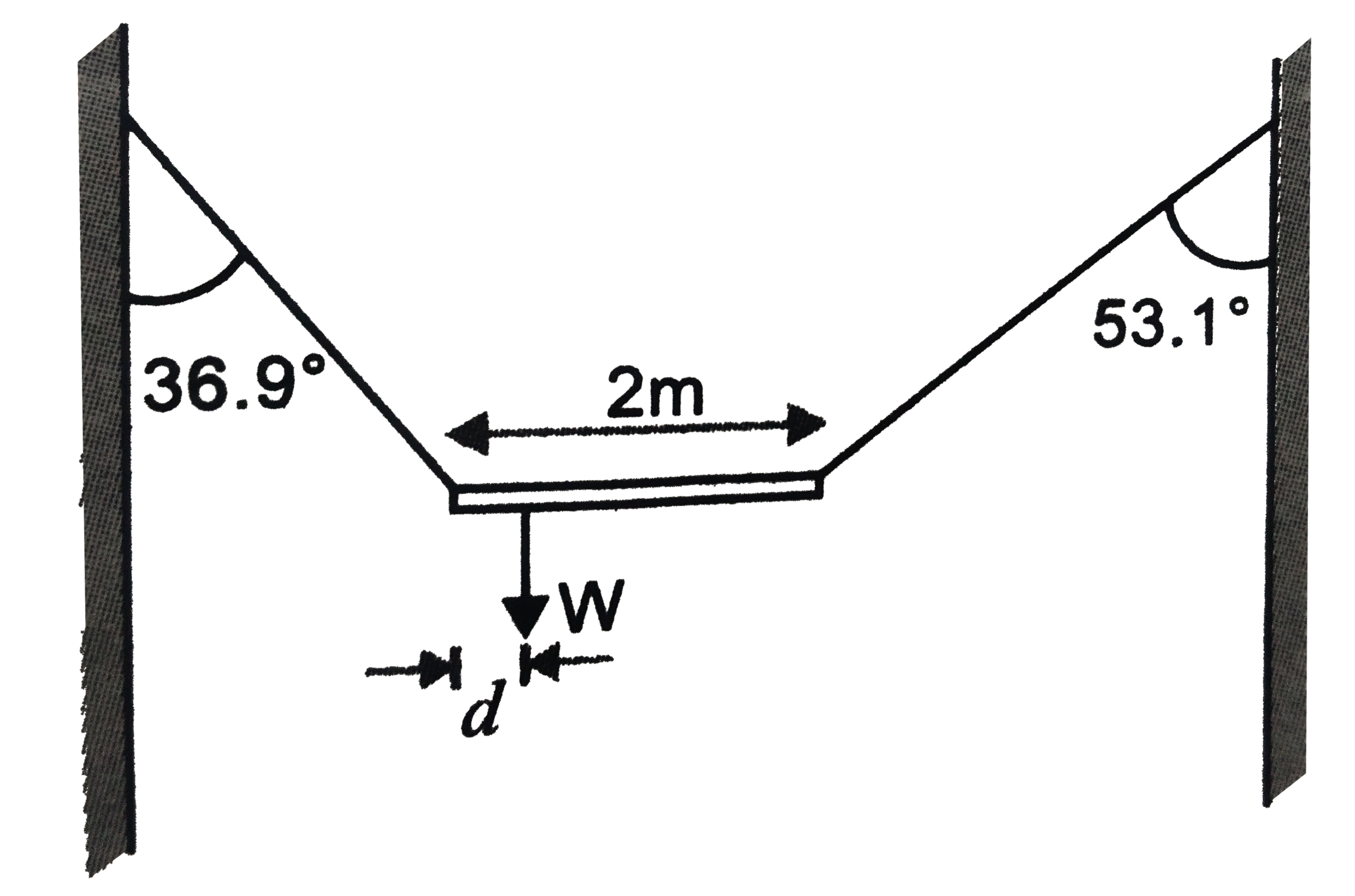A car weighs $1800 k g$ . The distance between its front and back axles is $1.8 m$ . Its centre of gravity is $1.05 m$ behind the front axle. Determine the force exerted by the level ground on each front wheel and each back wheel. View Solution
Question 10
(a) Find the moment of inertia of a sphere about a tangent to the sphere, given the moment of inertia of the sphere about any of its diameters to be $2 M R^{2} / 5, w h e r e M$ is the mass of the sphere and $R$ is the radius of the sphere.
(b) Given the moment of inertia of a disc of mass $M$ and radius $R$ about any of its diameters to be $\frac{1}{4} M R^{2}$ , find the moment of inertia about an axis normal to the disc passing through a point on its edge.View Solution
Question 11
Torques of equal magnitude are applied to hollow cylinder and a solid sphere, both having the same mass and same radius. The cylinder is free to rotate about its standard axis of symmetry, and the sphere is free to rotate about an axis passing through its centre. which of the two will acquire a greater angular speed after a given time ?View Solution
Question 12
A solid cylinder of mass $20 k g$ rotates about its axis with angular speed $100 s^{- 1}$ . The radius of the cylinder is $0.25 m$ . What is the kinetic energy associated with the rotation of the cylinder ? What is the magnitude of angular momentum of the cylinder about its axis ?View Solution
Question 13
A child stands at the centre of a turn table with his two arms outstretched. The turn table is set rotating with an angular speed of $40$ rpm. How much is the angular speed of the child, if he folds his hands back reducing the moment of inertia to $(2 / 5)$ time the initial value ? Assume that the turn table rotates without friction.
(b) Show that the child's new $K . E .$ of rotation is more than the initial $K . E .$ of rotation. How do you account for this increase in $K . E .$ ?View Solution
Question 14
A rope of negligible mass is wound around a hollow cylinder of mass $3 k g$ and radius $40 c m$ . What is the angular acceleration of the cylinder, if the rope is pulled with a force of $30 N$ ? What is the linear acceleration of the rope ? Assume that there is no slipping.View Solution
Question 15
To maintain a rotor at a uniform angular speed of $200 {rad s}^{- 1}$ , an engine needs to transmit a torque of 180 Nm. What is the power of the engine required ?View Solution
Question 16
From a uniform disc of radius $R$ , a circular section of radius $R / 2$ is cut out. The centre of the hole is at $R / 2$ from the centre of the original disc. Locate the centre of mass of the resulting flat body.View Solution
Question 17
A metre stick is balanced on a knife edge at its centre. When two coins, each of mass $5 g$ are put one on of the other at the $12 c m$ mark, the stick is found to balanced at $45 c m$ . The mass of the metre stick is.View Solution
Question 18
A solid wooden sphere rolls down two different inclined planes of the same height but of different inclinations. (a) Will it reach the bottom with same speed in each case ?
(b) Will it take longer to roll down one inclined plane than other ? Explain.View Solution
Question 19
A hoop of radius $2 m$ weight $100 k g$ .It rolls along a horizontal floor so that its centre of mass has a speed of $20 c m s^{- 1}$ . How much work has to be done to stop it ?View Solution
Question 20
The oxygen molecule has a mass of $5.30 \times 10^{- 26} k g$ and a moment of inertia of $1.94 \times 10^{- 46} k g m^{2}$ about an axis through its centre perpendicular to the line joining the two atoms. Suppose the mean speed of such a molecule in a gas is $500 m / s$ and that its kinetic energy of rotation is two thirds of its kinetic energy of translation. Find the average angular velocity of the molecule.View Solution
Question 21
A solid cylinder rolls up an inclined plane of angle of inclination $30^{\circ}$ . At the bottom of the inclined plane, the centre of mass of the cylinder has a speed of $5 m / s$ .
(a) How far will the cylinder go up the plane ? (B) How long will it take to return to the bottom ?View Solution
Question 22
As shown in Fig. the two sides of a step ladder $B A$ and $C A$ are $1.6 m$ long and hinged at $A$ . A rope $D E, 0.5 m$ is tied half way up. A weight $40 k g$ is suspended from a point $F, 1.2 m$ from B along the ladder $B A$ . Assuming the floor to be fricionless and neglecting the weight of the ladder, find the tension in the rope and forces exerted by the floor on the ladder. (Take $g = 9.8 m / s^{2})$
(Hint. Consider the eqilibrium of each side of the ladder separately.)
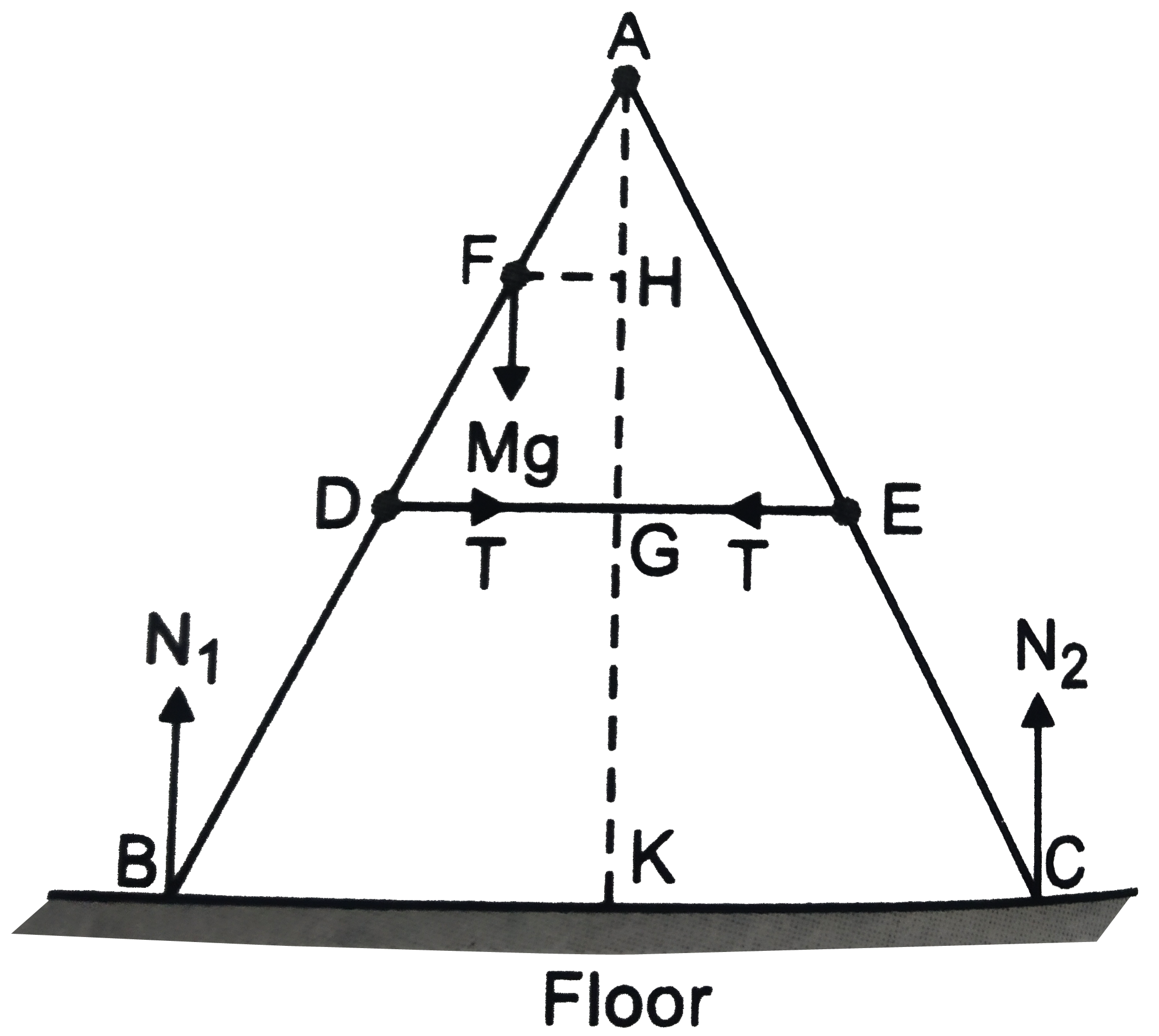View Solution
Question 23
A man stands on a rotating platform, with his arms stretched horizontal holding a $5 k g$ weight in each hand. The angular speed of the platform is $30$ revolutions per minute. The man then brings his arms close to his body with the distance of each weight from the axis changing from $90 c m$ to $20 c m$ . moment of inertia of the man together with the platform may be taken to be constant and equal t $7.6 k g m^{2}$ . (a) What is the his new angular speed ? (Neglect friction.)
(b) Is kinetic energy conserved in the process ? If not, from where does the change come about ?View Solution
Question 24
A bullet of mass $10 g$ and speed $500 m / s$ is fired into a door and gets embedded exactly at the centre of the door. The door is $1.0 m$ wide and weight $12 k g$ . It is hinged at one end and rotates about a vertical axis practically without friction. Find the angular speed of the door just after the bullet embeds into it.(Hint. The moment of inertia of the door about the vertical axis at one end is $M L^{2} / 3)$ View Solution
Question 25
Two discs of moments of inertia $I_{1} and I_{2}$ about their respective axes (normal to the disc and passing through the centre), and rotating with angular speed $ω_{1} and ω_{2}$ are brought into contact face to face with their axes of rotation coincident . What is the angular speed of the two-disc system ? View Solution
Question 26
(a) Prove the theorem of perpendicular axes.
(Hint : Square of the distance of a point (x, y) in the x-y plane from an axis through the origin and perpendicular to the plane is $^(x 2) + y^{2})$ .
(b) Prove the theorem of parallel axes.
(Hint : If the centre of mass of a system of n particles is chosen to be the origin $\sum m_{i} r_{i} = 0$ ).View Solution
Question 27
Prove the result that the velocity $v$ of translation of a rolling body (like a ring, disc, cylinder or sphere) at the bottom of an inclined plane of a height h is given by $v^{2} = \frac{2 g h}{(1 + k^{2} / R^{2})}$ using dynamical consideration (i.e. by consideration of forces and torque). Note k is the radius of gyration of the body about its symmetry axis, and $R$ is the radius of the body. The body starts from rest at the top of the plane.View Solution
Question 28
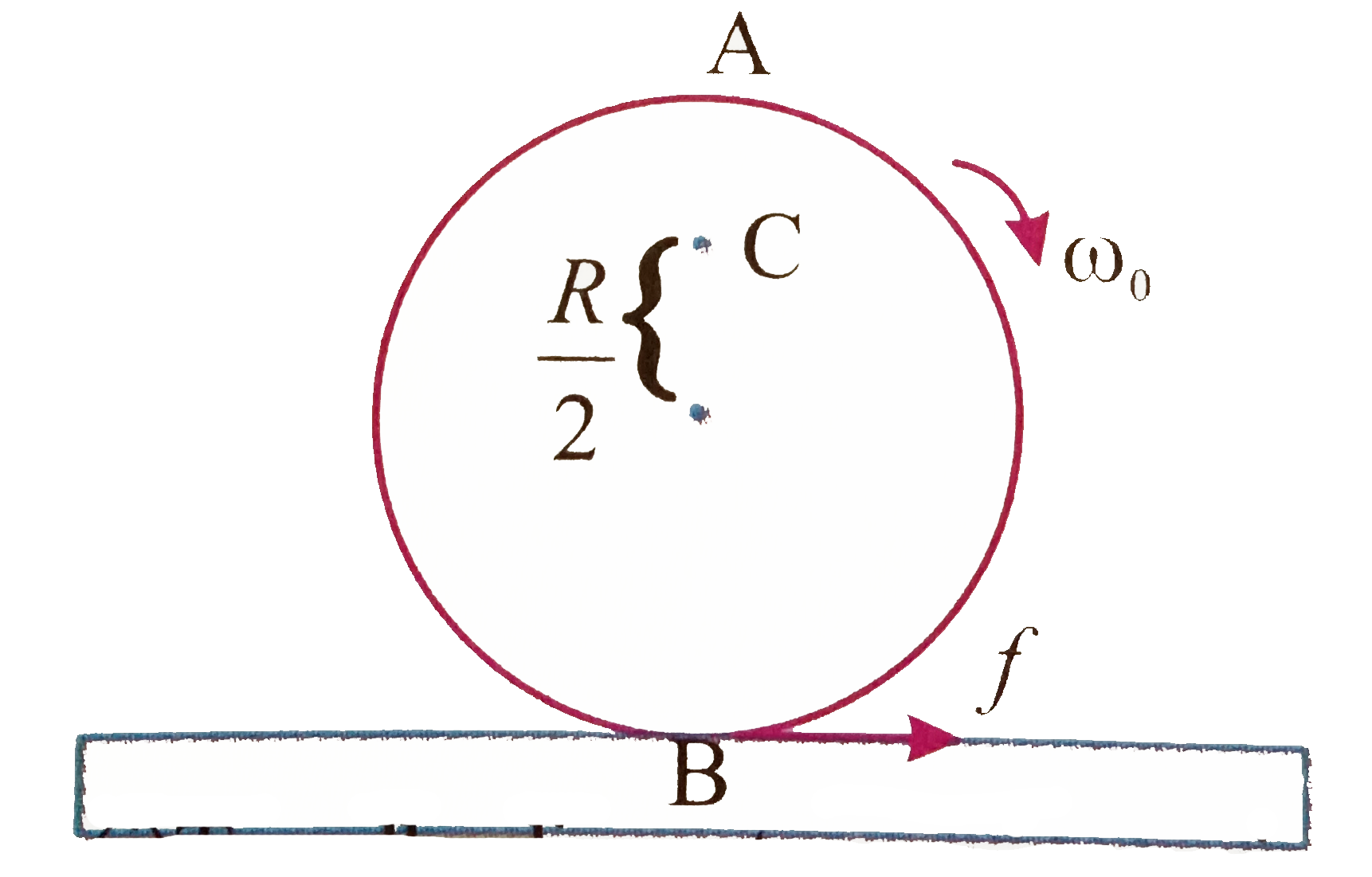
A disc rotating about its axis with angular speed $ω_{0}$ is placed lightly (without any translational pull) on a perfectly frictionless table. The radius of the disc is $R$ . What are the linear velocities of the points $A, B and C$ on the disc shown in Fig. Will the disc roll in the direction indicated ?
View Solution
Question 29
(i) Explain why friction is necessary to make the disc to roll in the direction indicated. (ii) Give the direction of frictional force at $B$ , and the sense of frictional torque, before perfect rolling begins. (iii) What is the force of friction after perfect rolling begins?
View Solution
Question 30
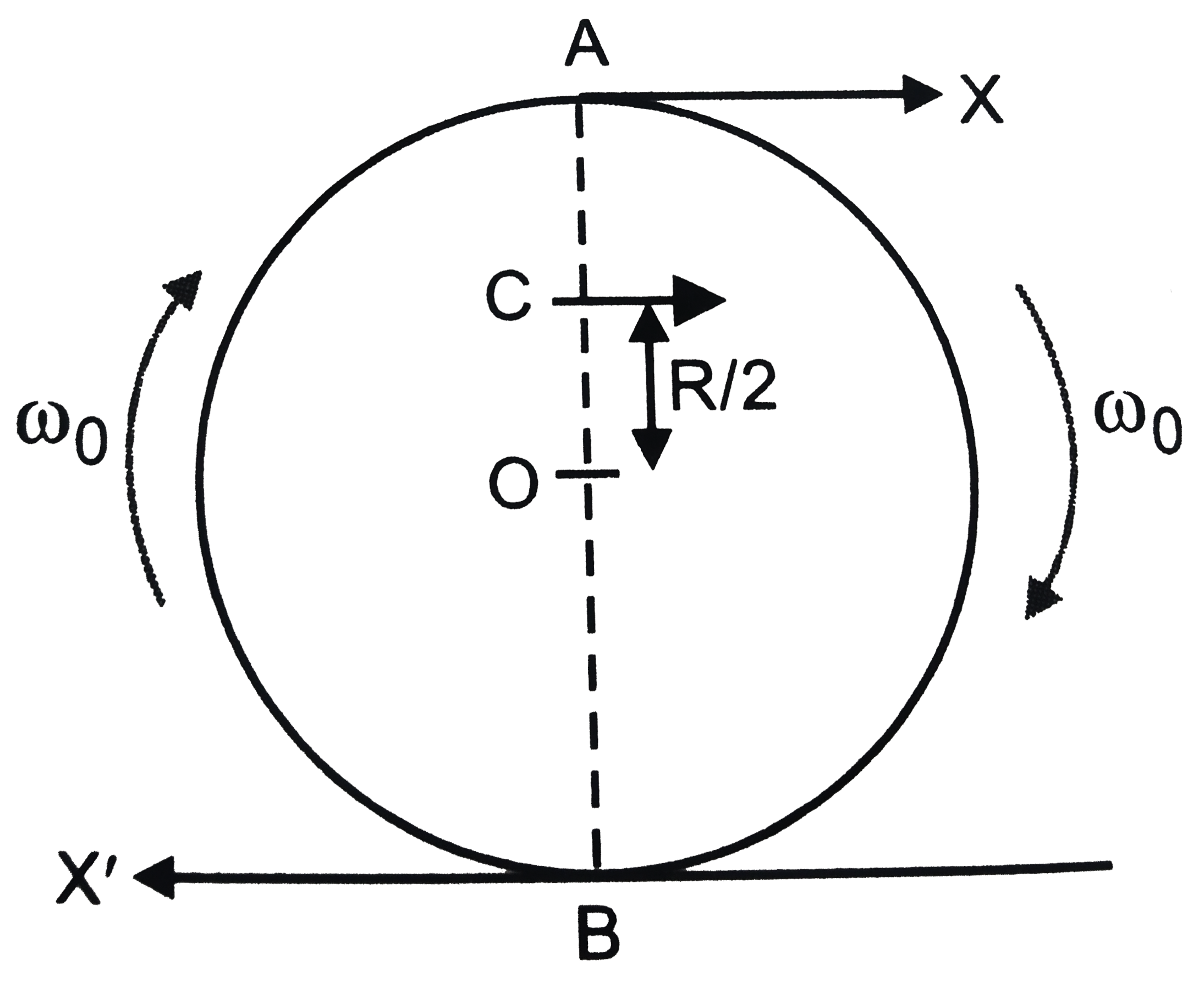A solid disc and a ring, both of radius $10 c m$ are placed on a horizontal table simultaneously, with initial angular speed equal to $10 π r a d / s$ . Which of the two will start to roll earlier ? The coefficient of kinetic friction is $μ_{k} = 0.2$ .View Solution
Question 31
A cylinder of mass $10 k g$ and radius $15 c m$ is rolling perfectly on a plane of inclination $30^{\circ}$ . The coefficient of static friction is $μ_{s} = 0.25$ .
(a) How much is the force of friction acting on the cylinder ?
(b) What is the work done against friction during rolling ?
(c ) If the inclination $θ$ of plane is increased, at what value of $θ$ does the cylinder begin to skid and not roll perfectly ?View Solution
Question 32
Read each statement below carefully and state with reasons, if it is true ot false. (a) During rolling the force of friction acts in the same direction as the direction of motion of c.m of the body. (b) The instantaneous speed of the point of contact during rolling is zero. (c ) The instantaneous acceleration of the point of contact during rolling is zero. (d) For perfect rolling motion, work done against friction is zero. (e) A wheel moving down a perfectly frictionless inclined plane will undergo slipping (not rolling motion).View Solution
Question 33
Separation of Motion of a system of particles into motion of the centre of mass and motion about the centre of mass :
(a) Show $P = P_{i} + m_{i} V$
where $p_{i}$ is the momentum of the ith particle (of mass $m_{i})$ and $p_{i} = m_{i} v_{t} Note v_{i}$ is the velocity of the ith particle relative to the centre of mass.
Also, prove using the definition of the centre of mass $\sum p_{t} = 0$
(b) Show $K = K' + 1 / 2 M V^{2}$
where K is the total kinetic energy of the system of particles. K' is the total kinetic energy of the system when the particle velocities are taken with respect to the centre of mass and $M V^{2} / 2$ is the kinetic energy of the translation of the system as a whole (i.e. of the centre of mass motion of the system). The result has been used in Sec. 7.14.
(c ) Show $L = L' + R \times M V$
where $L' = \sum r'_{t} \times p'_{t}$ is the angular momentum of the system about the centre of mass with velocities taken relative to the centre of mass. Remember $r'_{i} = r_{i} - R$ , rest of the notation is the standard notation used in the chapter. Note L' and $M R \times V$ can be said to be angular momenta, respectively, about and of the centre of mass of the system of particles.
(d) Show $\frac{d L'}{d t} = \sum r'_{i} \times \frac{d p'}{d t}$
Further, show that
$\frac{d L'}{d t} = τ'_{ext}$
where $τ_{ext}$ is the sum of all external torques acting on the system about the centre of mass.
(Hint : Use the definition of centre of mass and third law of motion. Assume the internal forces between any two particles act along the line joining the particles.) View Solution

All Exercises from NCERT PHYSICS Class 11 PHYSICS SYSTEMS OF PARTICLES AND ROTATIONAL MOTION

Home
Ask Doubt
Profile