The oxygen molecule has a mass of 5.30×10−26kg and a moment of inertia of 1.94×10−46kgm2 about an axis through its centre perpendicular to the line joining the two atoms. Suppose the mean speed of such a molecule in a gas is 500m/s and that its kinetic energy of rotation is two thirds of its kinetic energy of translation. Find the average angular velocity of the molecule.
Here, m=5.30×10−26kg
l=1.94×10−46kgm2
v=500m/s
If m2 is mass of each atom of oxygen and 2r is distance between the two atom as shown in Fig, then
I=m2r2+m2r2=mr2
r=√lm=√1.94×10−465.30×10−26
=0.61×10−10m
As K.E. or rotationa=23 K.E. of translation
∴12Iω2=23×13mω2
12(mr2)ω2=12mv2
ω=√23vr=√23×5000.61×10−10=6.7×1012rad/s.
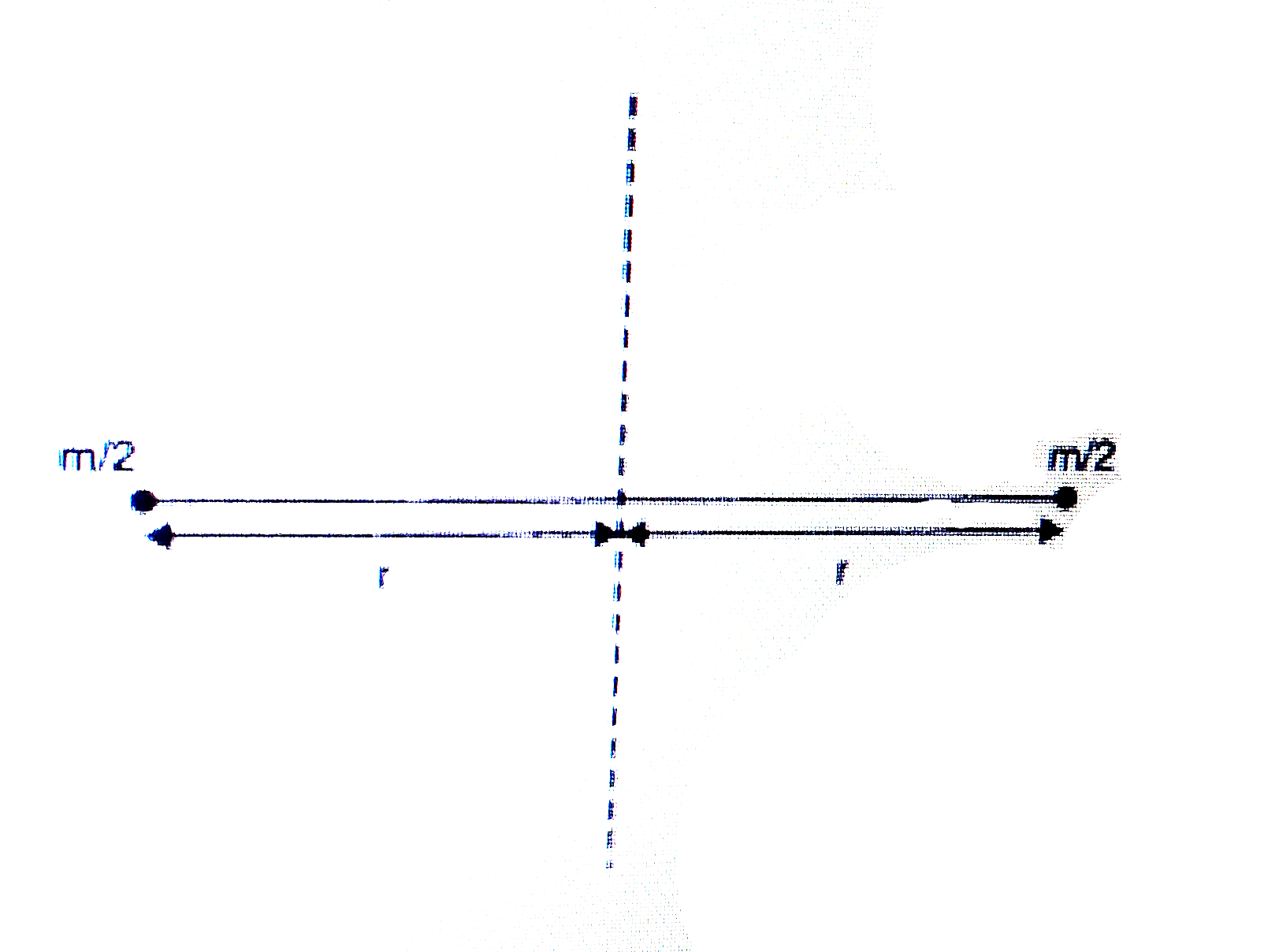
Topper's Solved these Questions
- BOOK - NCERTCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - EXERCISE33videos
SYSTEMS OF PARTICLES AND ROTATIONAL MOTION
- BOOK - NCERTCHAPTER - PHYSICAL WORLD EXERCISE - EXERCISE16videos
PHYSICAL WORLD
- BOOK - NCERTCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - EXERCISE22videos
THERMAL PROPERTIES OF MATTER
Similar Questions
The moment of inertia of a square plate of mass 4kg and side 1m about an axis passing through its centre and perpendicular to its plane is
View SolutionCalculate the moment of inertia of a diatomic molecule about an axis passing through its centre of mass and perpendicular to the line joining the two atoms .
Given : The two masses are m1 and m2 separated by a distance r .View Solution
Knowledge Check
- Question 1 - Select One
A thin ring has mass 0.25 kg and radius 0.5 m. Its moment of inertia about an axis passing through its centre and perpendicular to its plane is ………… .
A0.0625kgm2B0.625kgm2C6.25kgm2D62.5kgm2 - Question 2 - Select One
The moment of inertia of a circular ring of mass 1 kg about an axis passing through its centre and perpendicular to its plane is 4 kg m2. The diameter of the ring is
A2 mB4 mC5 mD6 m - Question 3 - Select One
A ring of mass 10 kg and diameter 0.4m is rotated about an axis passing through its centre and perpendicular to its plane moment of inertia of the ring is
A1.4kgm2B2.4kgm2C0.4kgm2D2kgm2
If a constant torque of 500 Nm turns a wheel of moment of inertia 100kgm2 about an axis through its centre, find the gain in angular velocity in 2s.
View SolutionA rod of mass m spins with an angular speed ω=√gl, Find its a. kinetic energy of rotation. b. kinetic energy of translation c. total kinetic energy.
 View Solution
View SolutionIf a constant torque of 500N−m turns a wheel of moment of inertia 100kgm2 about an axis passing through its centre, find the gain in angular velocity in 2s.
View SolutionTwo particles of masses 2 kg and 3 kg are separated by 5 m. Then moment of inertia of the system about an axis passing through the centre of mass of the system and perpendicular to the line joining them is
View SolutionTwo partcles of masses 1 kg and 2 kg are placed at a distance of 3 m. Moment of inertia of the particles about an axis passing through their centre of mass and perpedicular to the line joining them is (in kg−m2)
View Solution

