EXERCISE from PSEB OSCILLATIONS for Class 11
| Class 11 | PHYSICS |
| Chapter | OSCILLATIONS |
| PSEB | EXERCISE |
| Medium | English |
| Academic Year | 2023-2024 |
Question 20
The motion of a particle executing simple harmonic motion is described by the displacement function, x(t) = A cos (ωt+ϕ). If the initial (t = 0) position of the particle is 1 cm and its initial velocity is ωcm/s, what are its amplitude and initial phase angle ? The angular frequency of the particle is πs−1 s If instead of the cosine function, we choose the sine function to describe the SHM : x= B sin (ωt+α), what are the amplitude and initial phase of the particle with the above initial conditions.View SolutionQuestion 25
Plot the corresponding reference circle for each of the following simple harmonic motions. Indicate the initial (t =0) position of the particle, the radius of the circle, and the angular speed of the rotating particle. For simplicity, the sense of rotation may be fixed to be anticlockwise in every case: (x is in cm and t is in s). x =-2 sin (3t+(π/3))View SolutionQuestion 26
Plot the corresponding reference circle for each of the following simple harmonic motions. Indicate the initial (t =0) position of the particle, the radius of the circle, and the angular speed of the rotating particle. For simplicity, the sense of rotation may be fixed to be anticlockwise in every case: (x is in cm and t is in s). x=cos(π/(6−t))View SolutionQuestion 27
Plot the corresponding reference circle for each of the following simple harmonic motions. Indicate the initial (t =0) position of the particle, the radius of the circle, and the angular speed of the rotating particle. For simplicity, the sense of rotation may be fixed to be anticlockwise in every case: (x is in cm and t is in s). x=3sin(2πt+(π/4))View SolutionQuestion 28
Plot the corresponding reference circle for each of the following simple harmonic motions. Indicate the initial (t =0) position of the particle, the radius of the circle, and the angular speed of the rotating particle. For simplicity, the sense of rotation may be fixed to be anticlockwise in every case: (x is in cm and t is in s). x=2 cosπtView SolutionQuestion 29
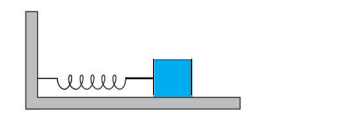
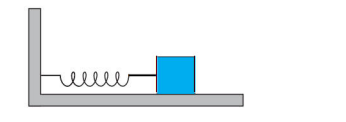
Figure 14.26 (a) shows a spring of force constant k clamped rigidly at one end and a mass m attached to its free end. A force F applied at the free end stretches the spring. Figure 14.26 (b) shows the same spring with both endsfree and attached to a mass m at either end. Each end of the spring in Fig. 14.26(b) is stretched by the same force F What is the maximum extension of the spring in the two cases ?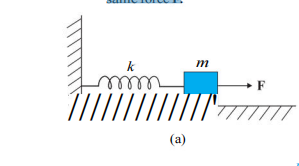
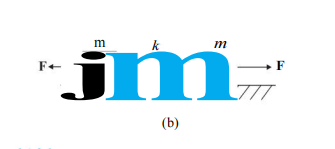View SolutionQuestion 30
Figure 14.26 (a) shows a spring of force constant k clamped rigidly at one end and a mass m attached to its free end. A force F applied at the free end stretches the spring. Figure 14.26 (b) shows the same spring with both endsfree and attached to a mass m at either end. Each end of the spring in Fig. 14.26(b) is stretched by the same force F If the mass in Fig. (a) and the two masses in Fig. (b) are released, what is the period of oscillation in each case ?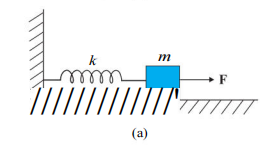
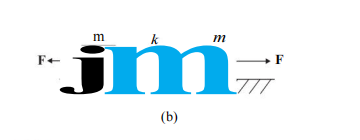View SolutionQuestion 34
Answer the following questions : The motion of a simple pendulum is approximately simple harmonic for small angle oscillations. For larger angles of oscillation, a more involved analysis shows that T is greater than 2π√lg . Think of a qualitative argument to 9 appreciate this resultView SolutionQuestion 37
A simple pendulum of length 1 and having a bob of mass M is suspended in a car. The car is moving on a circular track of radius R with a uniform speed v. If the pendulum makessmall oscillations in a radial direction about its equilibrium position, what will be its time period ?View SolutionQuestion 38
A cylindrical piece of cork of density of base area Aand height h floats in a liquid of density ρl. The cork is depressed slightly and then released. Show that the cork oscillates up and down simple harmonically with a period T=2π√hρρ1g where p is the density of cork. (Ignore damping due to viscosity of the liquid)View SolutionQuestion 39
One end of a U-tube containing mercury is connected to a suction pump and the other end to atmosphere. A small pressure difference is maintained between the two columns. Show that, when the suction pump isremoved, the column of mercury in the U-tube executes simple harmonic motion.View Solution
