CIRCULAR MOTION for Class 11 PHYSICS

INTRODUCTION

Circular motion hai kya? Suppose fan ke blade pr ek particle stuck hai aur fan chal raha hai to wo particle bhi circular motion me move krega. Circular motion me sabhi time pr us particle ki speed constant hogi (agr regulator ko na rotate kiya jae). Pr kya har ek point pr velocity constant hogi? Isse samajhne ke liye hum speed aur velocity ke bich ka difference samjhenge. Speed vector quantity nahi hai (has only magnitude) lekin velocity vector quantity hai (has both magnitude and direction). Jab fan constant speed se chalta hai to har ek point pr velocity ka direction change hota hai. Ager direction change nahi hoga to wo turn nahi lega aur particle straight chala jaega.

Jab koi object circular path me move karta ho ek constant speed me to us object ke motion ko uniform circular motion kahte hai.
In our everyday life, we came across many examples of circular motion for example cars going round the circular track and many more. Also earth and other planets revolve around the sun in roughly circular orbits.
The motion of a body is said to be circular if it moves in such a way that its distance from a certain fixed point always remains the same.

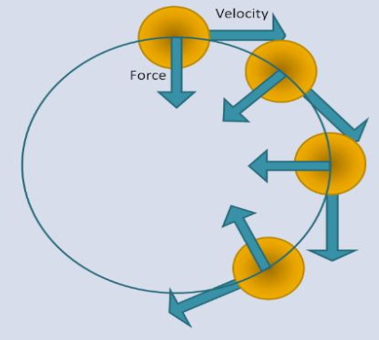
ocr_image

Circular motion uniform ya non-uniform ho sakta hai. Uniform circular motion me, rotation aur speed ka angular rate constant hota hai aur non-uniform motion me, rotation ka rate change hote rehta hai. Isliye, non-uniform acceleration ke liye, angular acceleration zero nahi hota hai.

UNIFORM CIRCULAR MOTION

Jab koi body circular path me constant speed se move krta hai to usse uniform circular motion kehte hai. Particle ka speed constant hoga pr velocity constant nahi hoga. Velocity vector quantity hai aur speed aur direction dono pr depend krta hai. Velocity change ho raha hai matlab acceleration hoga. Isse centripetal acceleration kehte hai. Iska magnitude constant hoga aur ye hmesha axis of rotation ke towards direct krega. Ye acceleration centripetal force produce krta hai.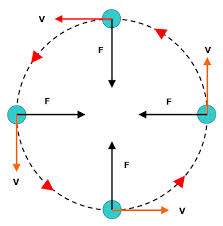

ocr_image

Formula for Uniform Circular Motion:
Tangential speed $= \frac{2 π r}{t}$
Centripetal acceleration, $a = \frac{v^{2}}{r}$

Centripetal acceleration

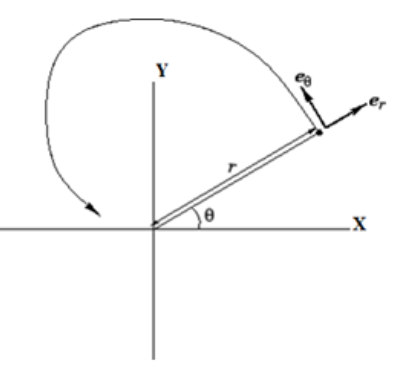
Hum ek particle consider krte hai jo constant speed se circular path me move krta hai. Hum ab normal component of acceleration, particle ke speed aur radius of path ke bich relationship derive krna discuss krenge.
To understand this consider the figure given below

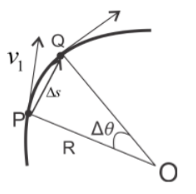
ocr_image

Figure ek particle represent krta hai jo circular path me move kr raha hai, uaka radius

R

aur uska centre

O

pr hai. Yaha vectors

v_{1}

point P pr aur

v_{2}

point Q pr velocities represent krta hai. Niche diye figure me aap dekhenge vector change in velocity (

Δ v

) jab particle time (

Δ t

) me point P se Q move krta hai.

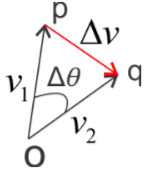
ocr_image

1st figure me triangle OPQ aur 2nd figure me triangle opq dono similar hai kyunki dono hi isosceles triangle hai aur dono triangles me Δθ angles bhi same hai. Hence we have

\frac{Δ v}{v_{1}} = \frac{Δ s}{R}

Δ v = \frac{v_{1}}{R} Δ s

| α_{⊥} |

time Δt me average normal acceleration ka magnitude hai aur ye

\frac{Δ v}{Δ t}

ke equal hai. So from above equation we get

| α_{⊥} | = \frac{Δ v}{Δ t} = \frac{v_{1}}{R} \frac{Δ s}{Δ t}

So the instantaneous acceleration

a_{⊥}

at point P is the limiting value of this expression as we take point Q to point P and

Δ t \to 0

So,

a_{⊥} = lim Δ t \to 0 \frac{v_{1}}{R} \frac{Δ s}{Δ t} = \frac{v_{1}}{R} lim Δ t \to 0 (\frac{Δ s}{Δ t})

But the limiting value of

\frac{Δ s}{Δ t}

is the speed

v_{1}

of the particle at point P. Since P can be any point in the path , we can conveniently drop the subscript from

v_{1}

and let

v

represent the speed of the particle at any point in the circular path. So

a_{⊥} = \frac{v^{2}}{R}

So, from the above equation we can say that
The magnitude of the instantaneous normal acceleration is equal to the square of the speed divided by the radius. Its direction is perpendicular to v and acts along inward along the radius of the circular path towards the center of the circle.

Isliye isse central ya centripetal acceleration kehte hai. Centripetal ka matlab hota hai ‘seeking the center’. Ab tak humne discuss kiya hai circular motion physics with particles moving with constant speed. If the speed varies then above equation for normal acceleration or centripetal acceleration still holds but in case of varying speed you also have a tangential component of acceleration

a_{∥}

, equal of the rate of change of speed. So,

a_{∥} = lim Δ t \to 0 (\frac{Δ v_{∥}}{Δ t})

So if the speed is constant then there is no tangential acceleration. In this case acceleration is purely normal . This normal acceleration is the result of the continuous change in direction of the velocity.

Angular velocity

Consider an object moving in a circle with uniform velocity v as shown below in the figure.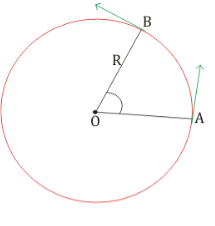

ocr_image

The velocity

v

at any point of the motion is tangential to the circle at that point.Let the particle moves from point A to point Belong the circumference of the circle .The distance along the circumference from A to B is

s = R θ

..........(i)
Where R is the radius of the circle and θ is the angle moved in radians
Magnitude of velocity is

v = \frac{d s}{d t} = R \frac{d θ}{d t}

............(ii)
Since radius of the circle remains constant quantity,

ω = \frac{d θ}{d t}

..........(iii)
is called the angular velocity defined as the rate of change of angle swept by radius with time.
Angular velocity is expressed in radians per second (

r a d s^{- 1}

)
From equation (ii) and (iii),we find the following

v = ω R

............(iv)
Thus for a particle moving in circular motion ,velocity is directly proportional to radius for a given angular velocity.
For uniform circular motion i.e, for motion with constant angular velocity the motion would be periodic which means particle passes through each point of circle at equal intervals of time
Time period of motion is given by

T = 2 \frac{π}{ω}

...........(v)
Since

2 π

radians is the angle θ in one revolution
If angular velocity ω is constant then integrating equation (iii) within limits

θ_{0}

θ

,we find

\int_{θ_{0}}^{θ} d θ = \int_{t_{0}}^{t} ω d t = ω \int_{t_{0}}^{t} d t

or,

θ = θ_{0} + ω (t - t_{0})

…………(vi)
where

θ_{0}

is the angular position at time

t_{0}

and

θ

is the angular position at time

t

.The above equation is similar to rectilinear motion result

x - x_{0} = v (t - t_{0})

Angular acceleration

Angular acceleration is defined as the rate of change of angular velocity moving in circular motion with time.
Thus

α = \frac{d ω}{d t} = \frac{d^{2} θ}{{d t}^{2}}

............(vii)
Unit of angular acceleration is

r a d s^{- 2}

For motion with constant angular acceleration

\int_{θ_{0}}^{θ} d θ = \int_{t_{0}}^{t} ω d t = \int_{t_{0}}^{t} ω_{0} d t + α \int_{t_{0}}^{t} (t - t_{0}) d t

or,

ω = ω_{0} + α (t - t_{0})

...........(viii)
where

ω_{0}

is the angular velocity at time

t_{0}

Again since

ω = \frac{d θ}{d t}

d θ = ω d t

then from equation (viii)
On integrating we get

θ = θ_{0} + ω (t - t_{0}) + \frac{1}{2} α {(t - t_{0})}_{0}^{2}

………….(ix)
If in the beginning

t_{0} = 0 and θ_{0} = 0

the angular position at any time t is given by

θ = ω t + (\frac{1}{2}) α t^{2}

This result is of the form similar to what we find in case of uniformly accelerated motion while studying rectilinear motion.

Linear acceleration is the rate of change of velocity without a change in direction; e.g., when the speed of an aircraft increases while flying a straight pathway.

Relation between linear acceleration and angular acceleration:

v = ω \Rightarrow \frac{d v}{d t} \Rightarrow (\frac{d ω}{d t}) r \Rightarrow a_{l} = a_{r}

This acceleration is along tangent, so it is called tangential acceleration.

ocr_image

Equations of Motion for Uniform Circular Motion

Ek particle jo circular motion perform kr raha hai, usse uske position vector $\to r (t)$ se describe kr sakte hai. Figure me aap dekhenge ek particle counterclockwise direction me circular motion perform kr raha hai.

As the particle moves on the circle, its position vector sweeps out the angle $θ$ with the x-axis. $\to r (t)$ making an angle $θ$ with the x-axis is shown with its components along the x– and y-axes. The magnitude of the position vector is $A = | \to r (t) |$ and is also the radius of the circle, so that in terms of its components, $\to r (t) = A cos ω t ˆ i + A sin ω t ˆ j$ .

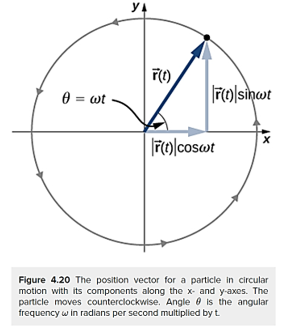
ocr_image

Yaha $ω$ constant hai aur isse particle ka angular frequency kehte hai. The angular frequency has units of radians (rad) per second and is simply the number of radians of angular measure through which the particle passes per second.

The angle $θ$ that the position vector has at any particular time is $ω t$ .
Ager $T$ period of motion hai ya ek revolution complete krne ka time $(2 π r a d)$ hai, to $ω = \frac{2 π}{T}$ .

Velocity and acceleration can be obtained from the position function by differentiation: $\to v (t) = \frac{d \to r (t)}{d t} = - A ω sin ω t ˆ i + A ω cos ω t ˆ j$ .

Figure me aap dekhenge velocity vector particle ke location pr circle ke tangential hai aur uska magnitude $A ω$ hai.

Similarly, the acceleration vector is found by differentiating the velocity: $\to a (t) = \frac{d \to v (t)}{d t} = - A ω^{2} cos ω t ˆ i - A ω^{2} sin ω t ˆ j$ .

Is equation se aap dekhenge acceleration vector ka magnitude $A ω^{2}$ hai aur wo position vector ke opoosite me directed hai, toward the origin, kyunki $\to a (t) = - ω^{2} \to r (t)$ .

Problem solving strategy

Creating an Acceleration of 1 $g$
A jet is flying at

134.1 m / s

along a straight line and makes a turn along a circular path level with the ground. What does the radius of the circle have to be to produce a centripetal acceleration of

1 g

on the pilot and jet toward the center of the circular trajectory?

Strategy
Given the speed of the jet, we can solve for the radius of the circle in the expression for the centripetal acceleration.

Solution
Set the centripetal acceleration equal to the acceleration of gravity:

9.8 m / s^{2} = v^{2} / r

.
Solving for the radius, we find

r = \frac{{(134.1 m / s)}^{2}}{9.8 m / s^{2}} = 1835 m = 1.835 k m

.
Significance
To create a greater acceleration than

g

on the pilot, the jet would either have to decrease the radius of its circular trajectory or increase its speed on its existing trajectory or both.

NON-UNIFORM CIRCULAR MOTION

Non-uniform circular motion me jo particle circular path me move kr raha hai uske speed me change hota hai. Velocity ke vector size me especially change hota hai jo ye batata hai ki velocity ke magnitude me change hua hai.

Non-Uniform circular motion me:

1. Object ka velocity vector hmesha circle ke tangent hoga.
2. Object ka speed aur angular speed constant nahi hoga.
3. Object ka angular acceleration zero nahi hoga.
4. Acceleration vector center of the circle ke towards point nahi krega.

Non-uniform circular motion me, net acceleration (a) Δv ke direction ke along hota hai jo circle ke ander direct krta hai pr centre se pass nahi hota. Net acceleration ko do components me resolve kr sakte hai: tangential acceleration aur normal acceleration jisse centripetal or radial acceleration bhi kehte hai. Centripetal acceleration dono uniform aur non-uniform circular motion me present hota hai.
Jab acceleration vector circle ke centre ke towards point nahi krega to usse do components me break kr sakte hai, $a_{R}$ aur $a_{T}$ . Component $a_{R}$ circle ke centre ke towards hoga (radial) aur component $a_{T}$ circle ke tangent hoga aur radial component ke perpendicular hoga. Radial component velocity ke direction ke change me responsible hota hai.
$a_{R} = \frac{v^{2}}{r}$
$a_{T} = \frac{d v}{d t}$

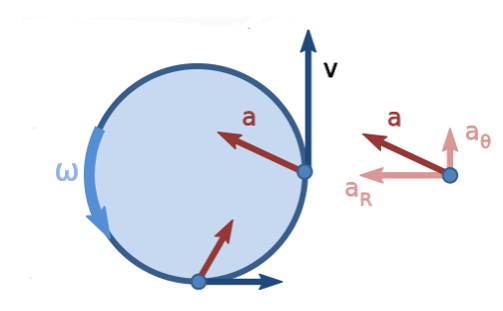
ocr_image

Let us use the vector method to discuss non-uniform circular motion. Niche diye figure me, ${ˆ e}_{r}$ unit vectors along radius hai aur ${ˆ e}_{θ}$ tangent vector hai. $e_{r}$ aur $e_{θ}$ ke terms me, particle ka motion jo circle me clockwise move kr raha hai usse vector equation se describe kr sakte hai.

ocr_image

$\to v = {ˆ e}_{θ} v$
Is case me, sirf ${ˆ e}_{θ}$ hi nahi balki v bhi time ke saath vary krta hai. Hum instantaneous acceleration obtain kr sakte hai,
$\to a = \frac{d \to v}{d t} = {ˆ e}_{θ} (\frac{d θ}{d t}) + v (\frac{d {ˆ e}_{θ}}{d t})$
$\to a = \frac{d \to v}{d t} = \frac{ˆ e θ d θ}{d t} + v (\frac{d ˆ e θ}{d t})$
Again,
$\frac{d {ˆ e}_{θ}}{d t} = \frac{{ˆ e}_{r} v^{2}}{r}$
$\to a = {ˆ e}_{θ} a_{T} - {ˆ e}_{r} (\frac{v^{2}}{r}) = a_{T} {ˆ e}_{θ} - a_{R} {ˆ e}_{r}$
Here, $a_{T} = \frac{d v}{d t}$ and $a_{R} = \frac{v^{2}}{r}$
First term, ${ˆ e}_{θ} a_{T}$ $\to A$ ka vector component hai aur $a_{R}$ centripetal acceleration hai.
The magnitude of $\to A i s | \to a | = \sqrt{a_{T}^{2} + a_{N}^{2}}$

OMR (One Minute Revision)

ω = \frac{v}{r}

Problem Solving Strategy

Total Acceleration during Circular Motion
A particle moves in a circle of radius $r = 2.0 m$ . During the time interval from $t = 1.5 s$ to $t = 4.0 s$ its speed varies with time according to $v (t) = c_{1} - (\frac{c_{2}}{t_{2}}), c_{1} = 4.0 m / s, c_{2} = 6.0 m \cdot s$ .
What is the total acceleration of the particle at $t = 2.0 s$ ?

Strategy
We are given the speed of the particle and the radius of the circle, so we can calculate centripetal acceleration easily. The direction of the centripetal acceleration is toward the center of the circle. We find the magnitude of the tangential acceleration by taking the derivative with respect to time of $| v (t) |$ using and evaluating it at $t = 2.0 s$ . We use this and the magnitude of the centripetal acceleration to find the total acceleration.

Solution
Centripetal acceleration is $v (2.0 s) = (4.0 - \frac{6.0}{{(2.0)}^{2}}) m / s = 2.5 m / s$
$a_{C} = \frac{v^{2}}{r} = \frac{2.5 m / s^{2}}{2.0 m} = 3.1 m / s^{2}$ directed toward the center of the circle.
Tangential acceleration is $a_{T} = ∣ ∣ ∣ \frac{d \to v}{d t} ∣ ∣ ∣ = \frac{2 c_{2}}{t^{3}} = \frac{12.0}{{(2.0)}^{3}} m / s^{2} = 1.5 m / s^{2}$ .
Total acceleration is $| \to a | = \sqrt{{(3.12)}^{2} + {(1.52)}^{2}} m / s^{2} = 3.44 m / s^{2}$ and $θ = {tan}^{-} 1 \frac{3.1}{1.5} = 64 °$ from the tangent to the circle.

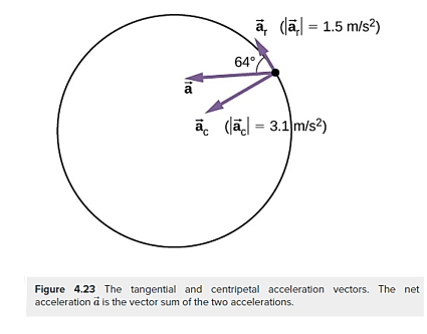
ocr_image

Significance
The directions of centripetal and tangential accelerations can be described more conveniently in terms of a polar coordinate system, with unit vectors in the radial and tangential directions.

POINT

Circular motion Circular motion is described as a movement of an object while rotating along a circular path.

Uniform circular motion Uniform circular motion is a specific type of motion in which an object travels in a circle with a constant speed.

Non uniform circular motion When a motion of an object denotes changes in the speed of the particle moving along the circular path, it is called non-uniform circular motion.

Radial: Moving along a radius.

Centripetal: Directed or moving towards a center.

Angular Velocity:Angular velocity is the time rate at which an object rotates, or revolves, about an axis, or at which the angular displacement between two bodies changes. Denoted by $ω$ .

Angular speed Angular speed is the measure of how fast the central angle of a rotating body changes with respect to time. Denoted by $ω$ . Angular frequency, $ω$ : Rate of change of an angle with which an object that is moving on a circular path.

Centripetal acceleration Component of acceleration of an object moving in a circle that is directed radially inward toward the center of the circle.

Tangential acceleration Magnitude of which is the time rate of change of speed. Its direction is tangent to the circle.

Total acceleration: Vector sum of centripetal and tangential accelerations.

EXAMPLE 1

A cyclist starts from the center O of a circular park of radius 1km, reaches the edge P of the park, then cycles along the PQ circumference and returns to the center along OQ as shown in fig. If the round trip taken ten minute, the (a) net displacement, (b) average velocity and (c) average speed of the cyclists (in kilometer and kinetic per hour) is

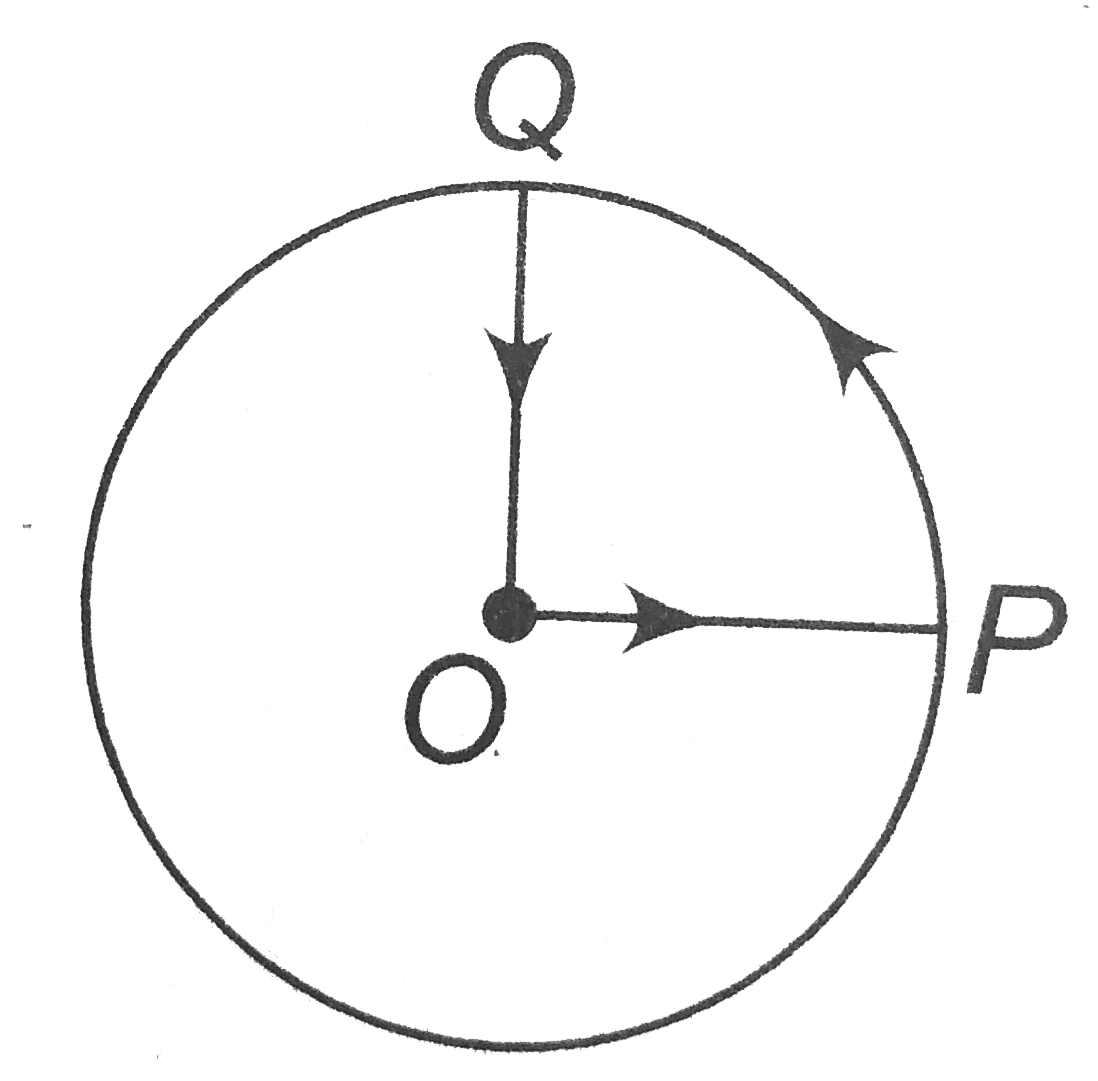
a) Since both the initial and final positions are the same therefore the net displacement is zero.
b) Average velocity is the ratio of net displacement and total time taken. Since the net displacement is zero therefore the average velocity is also zero.
c) Average speed = $\frac{distance covered}{time taken}$
$= (O P + Actual distance PQ + OQ)/(10 min u t e s)$
$\frac{1 k m + \frac{1}{4} \times 2 π \times 1 k m + 1 k m}{10 / 60 h}$
$6 (2 + \frac{22}{14}) k m h^{- 1}$ = $6 \times \frac{50}{14} k m h^{- 1}$
$= 21.43 k m h^{- 1}$

Learn more

EXAMPLE 2

A particle moves on a circular path of radius 8 m. distance traveled by the particle in time t is given by the equation $s = \frac{2}{3} t^{3}$ . Find its speed when tangential and normal accelerations have equal magnitude.

The speed v, tangential acceleration $a_{τ}$ and the normal acceleration $a_{n}$ are expressed bu the following equations.
$v = \frac{d s}{d t}$
Substituting the given expression for s, we have $v = 2 t^{2}$
$a_{τ} = \frac{d^{2} s}{{d t}^{2}}$ …(i)
Substituting the given expression for s, we have $a_{τ} = 4 t$
$a_{n} = \frac{v^{2}}{r}$ ...(ii)
Substituting v from eq. (i) and $r = 8 m$ , we have $a_{n} = \frac{1}{2} t^{4}$ ...(iii)
The instant when the tangential and the normal accelerations have equal magnitude, can be obtained by equating their expressions given in eq. (ii) and (iii).
$a_{n} = a_{T} \to t = 2 s$
Substituting the above value of t in eq. (i), we obtain $v = 8 m / s$

Learn more

EXAMPLE 3

A cyclist is riding with a speed of $27 k m h^{- 1}$ . As he approaches a circular turn on the road of radius 80 m, he applies brakes and reduces his speed at the constant rate $0.5 m s^{- 1}$ . What is the magnitude and direction of the net acceleration of the cyclist on the circular turn ?

Here v= $27 k m / h = 27 \times \frac{5}{18} m / s = 7.5 m / s, r = 80 m$
and tangential acceleration $a_{t} = - 0.50 m / s^{2}$ .
$∴$ Centripetal acceleration $a_{c} = \frac{v^{2}}{r} = \frac{{(7.5)}^{2}}{80} = 0.70 m s^{- 2}$ (radially inwards).
Thus, as shown in fig. above, two acceleration are acting in mutually perpendicular directions. If $\to a$ be the resultant accelerations, then
$| \to a | = \sqrt{a_{1}^{2} + a_{c}^{2}} = \sqrt{{(0.5)}^{2} + {(0.7)}^{2}} = 0.86 m s^{- 2}$
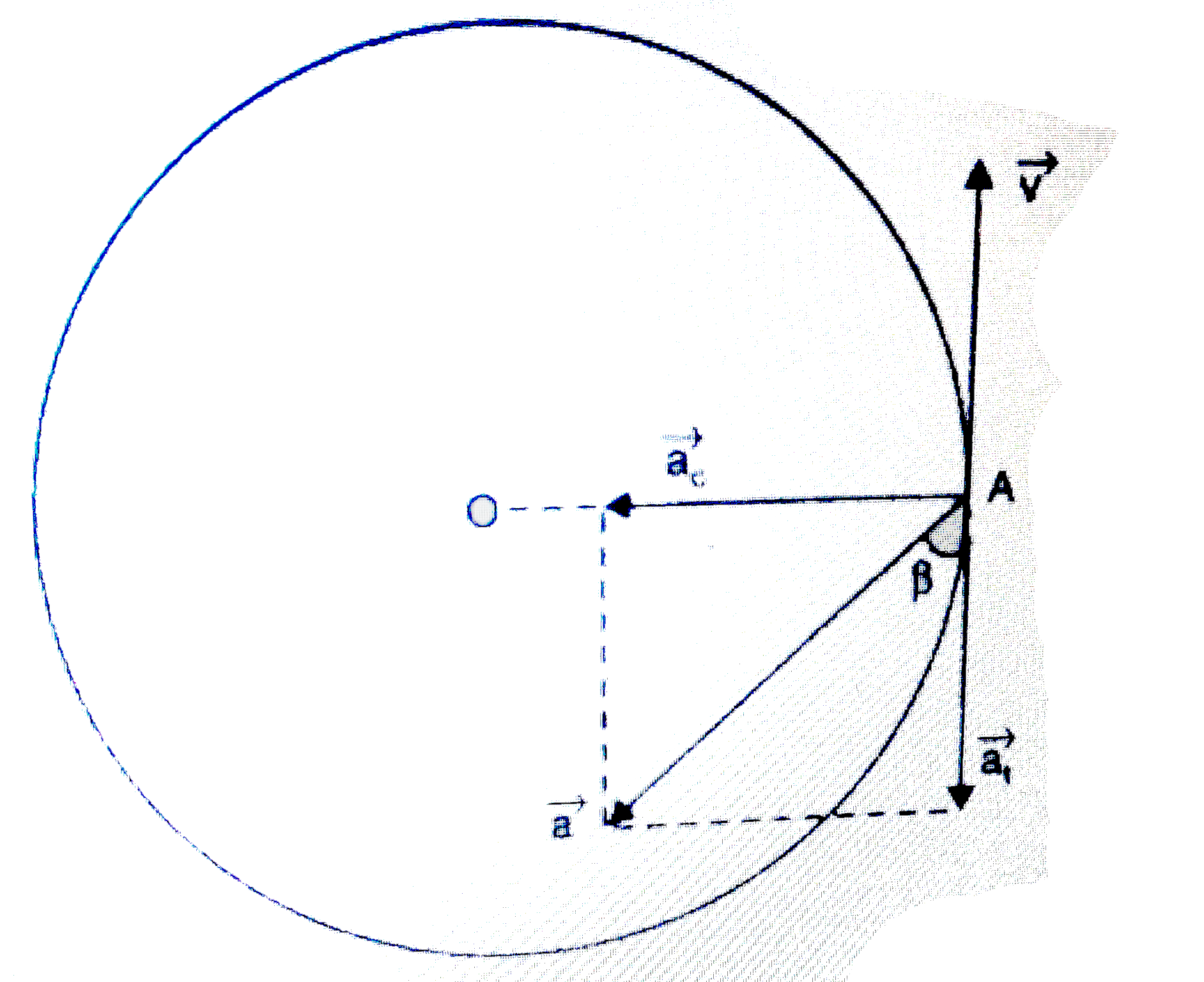
ocr_image
and $tan β = \frac{a_{c}}{a_{t}} = \frac{0.7}{0.5} = 1.4$
$\Rightarrow β = {tan}^{- 1} (1 . $ = {54.5}^{\circ}$ from the direction of negative of the velocity.

Learn more

EXAMPLE 4

(a) Earth can be thought of as a sphere of radius 6400 km. Any object (or a person) is performing circular motion around the axis of the earth due to the earth rotation (period 1 day ). What is acceleration of object on the surface of the earth (at equator) towards its centre ? What is it at latitude $θ$ ? How does these accelerations compare with $g = 9.8 m / s^{2}$ ?
(b) Earth also moves in circular orbit around the sun once every year with an orbital radius of $1.5 \times 10^{11}$ m. What is the acceleration of the earth (or any object on the surface of the earth) towards the centre of the sun? How does this acceleration compare with $g = 9.8 m / s^{2}$ ?

(a) Radius of the earth (R)= $6400 k m = 6.4 \times 10^{6} m$
Time period (T) = 1 day $= 24 \times 60 \times 60 s = 86400 s$
Centripetal acceleration $(a_{c}) = ω^{2} = R = R {(\frac{2 π}{T})}^{2} = \frac{4 π^{2} R}{T}$
$= \frac{4 \times {(22 / 7)}^{2} \times 6.4 \times 10^{6}}{{(24 \times 60 \times 60)}^{2}}$
$= \frac{4 \times 484 \times 64 \times 10^{6}}{49 \times {(24 \times 3600)}^{2}}$
$= 0.034 m / s^{2}$
At equator, latitude $θ = 0^{\circ}$
$∴ \frac{a_{c}}{g} = \frac{0.034}{9.8} = \frac{1}{288}$
(b) Orbital radius of the earth around the sun (R) $= 1.5 \times 10^{11} m$
Time period =1 Yr =365 day
$= 365 \times 24 \times 60 \times 60 s = 3.15 \times 10^{7} s$
Centripetal acceleration $(a_{c}) = R ω^{2} = \frac{4 π^{2} R}{T^{2}}$
$= \frac{4 \times {(22 / 7)}^{2} \times 1.5 \times 10^{11}}{{(3.15 \times 10^{7})}^{2}}$
$= 5.97 \times 10^{- 3} m / s^{2}$
$∴ \frac{a_{c}}{g} = \frac{5.97 \times 10^{- 3}}{9.8} = \frac{1}{1641}$

Learn more

EXAMPLE 5

A particle moves in a circle of radius 20 cm with linear speed of 10 m/s. Find the angular velocity.

The angular velocity is
$ω$ = v / r = (10m/s)/(20cm)=50 rad/s.

Learn more

EXAMPLE 6

Find the magnitude of the linear acceleration of a particle moving in a circle of radius 10 cm with uniform speed completing the circle in 4s.

The distance covered in completing the circle is $2 π r = 2 π \times 10 c m .$ The linear speed is
$v = 2 π \frac{r}{t}$
$= \frac{2 π \times 10 c m}{4 s} = 5 π \frac{c m}{s}$ .
The linear acceleration is
$= \frac{v^{2}}{r} = \frac{{(5 π \frac{c m}{s})}^{2}}{10 c m} = 2.5 π^{2} \frac{c m}{s^{2}}$
This acceleration is directed towards the centre of the circle.

Learn more

EXAMPLE 7

Angular position $θ$ of a particle moving on a curvilinear path varies according to the equation $θ = t^{3} - 3 t^{2} + 4 t - 2$ , where $θ$ is in radians and time t is in seconds. What is its average angular acceleration in the time interval $t = 2 s$ to $t = 4 s$ ?

Like average linear acceleration, the average angular acceleration $α_{a v}$ equals to ratio of change in angular velocity $Δ ω$ to the concerned time interval $Δ t$ .
$α_{a v} = \frac{Δ ω}{Δ t} = \frac{ω_{final} - ω_{initial}}{t_{final} - t_{initial}}$ ...(i)
The angular velocity $ω$ being rate of charge in angular position can be obtained by equation
$ω = \frac{d θ}{d t}$
Substituting the given expression of the angular position $θ$ , we have
$ω = 3 t^{2} - 6 t + 4$ ...(ii)
From the above eq. (ii), angular velocities $o m e h a_{2}$ and $ω_{4}$ at the given instants $t = 2 s$ and $4 s$ are
$ω_{4} = 4 r a d / s$ and $ω_{4} = 28 r a d / s$
Substituting the above values in eq. (1), we have $α_{a v} = 12 r a d / s^{2}$

Learn more

EXAMPLE 8

A particle is moving in a circular orbit when a constant tangential acceleration. After $2 s$ from the beginning of motion, angle between the total acceleration vector and the radius E becomes $45^{\circ}$ . What is the angular acceleration of the particle?

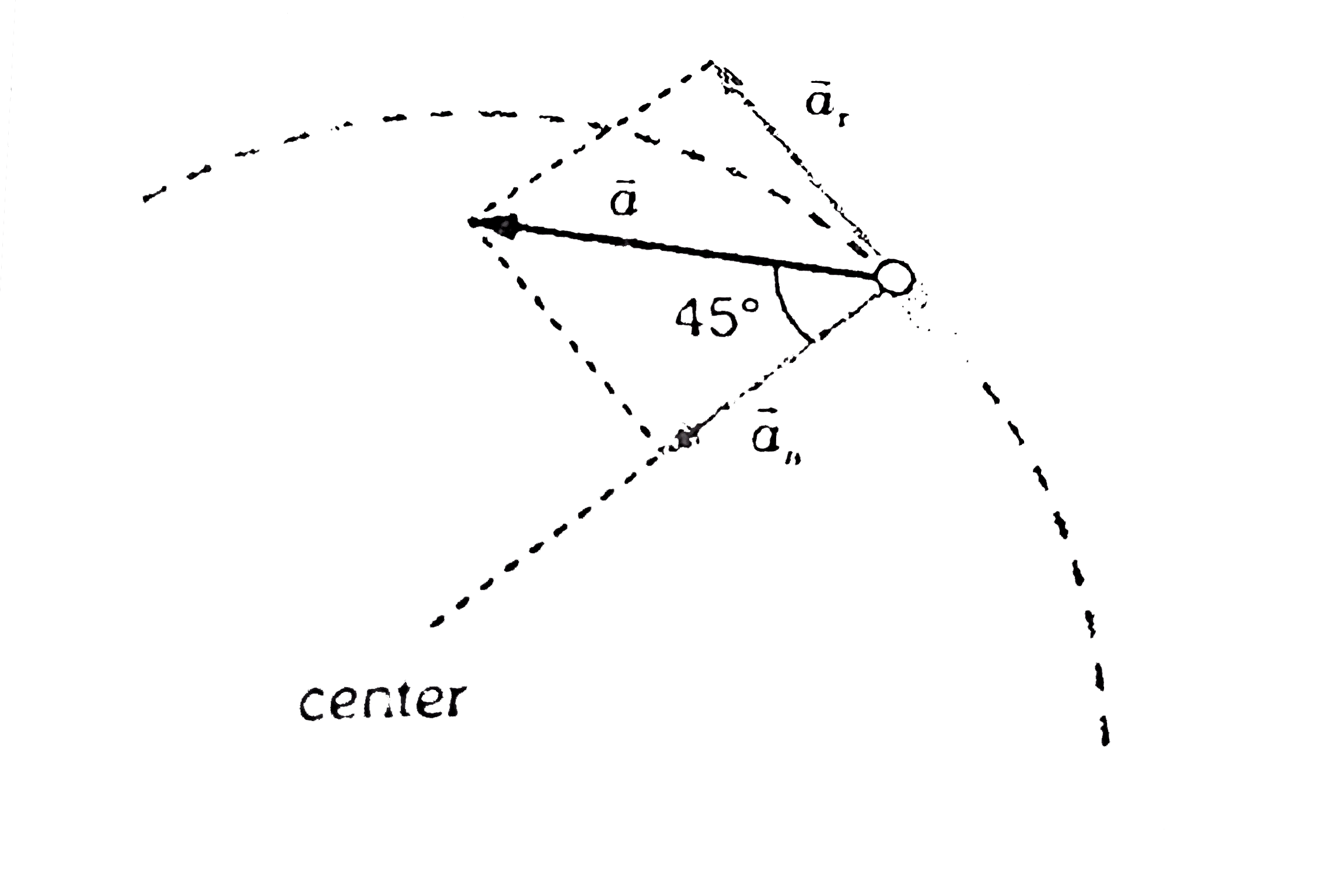
In the adjoining figure are shown the total acceleration vector $\to a$ and its components the tangential accelerations ${\to a}_{τ}$ and normal acceleration ${\to a}_{n}$ are shown. These two components are always mutually perpendicular to each other and act along the tangent to the circle and radius respectively. Therefore, if the total acceleration vector makes an angle of $45^{\circ}$ with the radius, both the tangential and the normal components must be equal in magnitudr.
Now from equation and, we have
$a_{τ} = a_{n} \to α R = ω^{2} R \Rightarrow α = ω^{2}$ ...(i)
Since angular acceleration is uniform, form equation, we have $ω = ω_{o} + α t$
Substituting $ω_{0} = 0$ and $t = 2 s$ , we have $ω = 2 α$ ...(ii)
From equation (i) and (ii), we have $α = 0.25 r a d / s^{2}$

Learn more

EXAMPLE 9

An insect trapped in a circular groove of radius $12 c m$ moves along the groove steadily and completes 7 revolutions in $100 s$ . (a) What is the angular speed, and the linear speed of the motion? (b) Is the acceleration vector a constant vector ? What is its magnitude ?

This is an example of uniform circular motion. Here $R = 12 c m$ . The angular speed $ω$ is given by
$ω = \frac{2 π}{T} = 2 π \times \frac{7}{100} = 0.44 r a d / s$
The linear speed v is :
$v = ω R = 0.44 s^{- 1} \times 12 c m = 5.3 c m s^{- 1}$
The direction of velocity $v$ is along the tangent to the circle at every point. The acceleration is directed towards the centre of the circle. Since this direction changes continuously, acceleration here is not a constant vector. However, the magnitude of acceleration is constant:
$a = ω^{2} R = {(0.44 s^{- 1})}^{2} (12 c m)$
$= 2.3 c m s^{- 2}$

Learn more

SUMMARY

1. Uniform circular motion is motion in a circle at constant speed.

2. Centripetal acceleration ${\to a}_{C}$ is the acceleration a particle must have to follow a circular path. Centripetal acceleration always points toward the center of rotation and has magnitude $a_{C} = \frac{v^{2}}{r}$ .

3. Non uniform circular motion occurs when there is tangential acceleration of an object executing circular motion such that the speed of the object is changing. This acceleration is called tangential acceleration ${\to a}_{T}$ .

4. The magnitude of tangential acceleration is the time rate of change of the magnitude of the velocity. The tangential acceleration vector is tangential to the circle, whereas the centripetal acceleration vector points radially inward toward the center of the circle. The total acceleration is the vector sum of tangential and centripetal accelerations.

5. An object executing uniform circular motion can be described with equations of motion. The position vector of the object is $\to r (t) = A cos ω t ˆ i + A sin ω t ˆ j$ , where $A$ is the magnitude $| \to r (t) |$ , which is also the radius of the circle, and $ω$ is the angular frequency.

Home
Ask Doubt
Profile