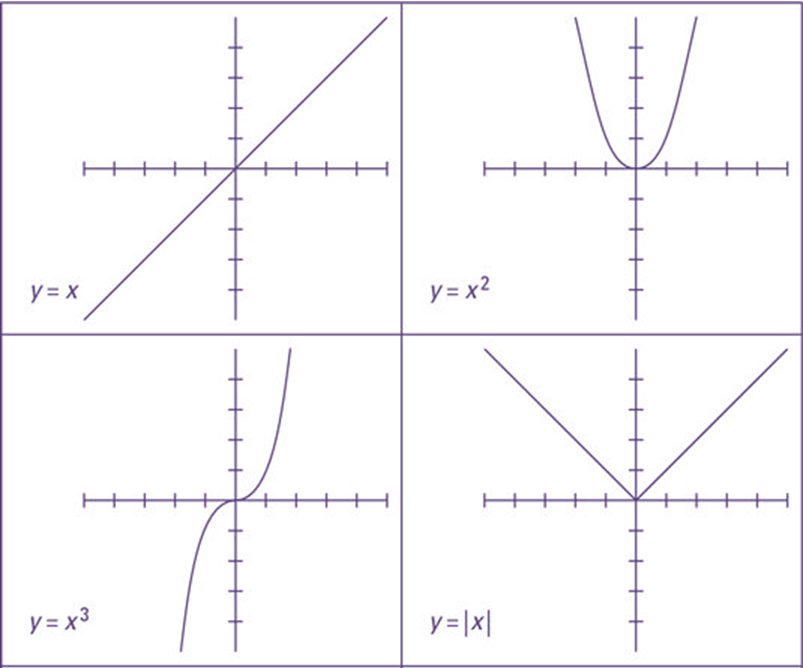
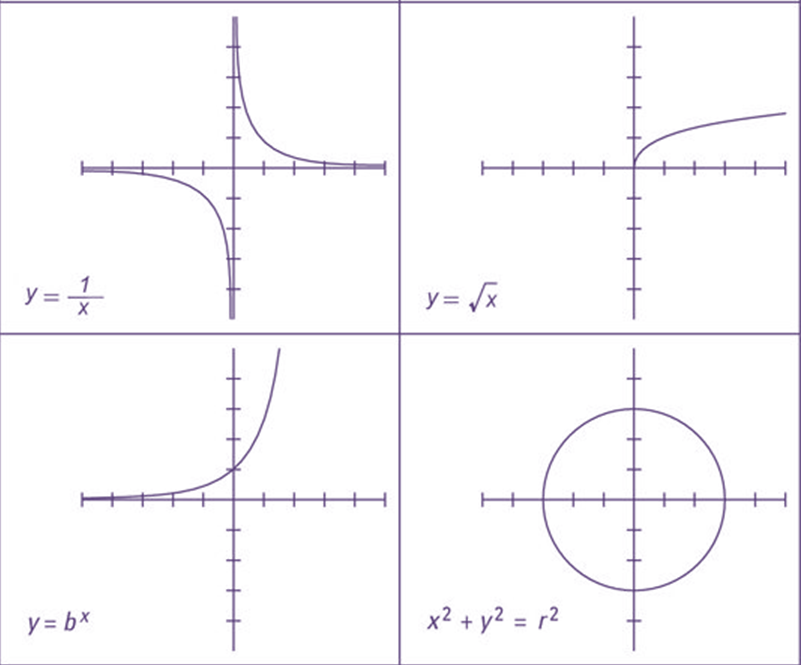
वक्रों के अंतर्गत क्षेत्रफल कक्षा 12 गणित
भूमिका
अभी तक हमने ज्यामिति में त्रिभुजों, आयतों, समलंब चतुर्भुजों एवं वृत्तों सहित विभिन्न ज्यामितीय आकृतियों के क्षेत्रफल सूत्रों की सहायता से ज्ञात किये हैं। प्रारंभिक ज्यामिति के सूत्रों की सहायता से हम अनेक साधारण आकृतियों के क्षेत्रफल ज्ञात कर सकते हैं, लेकिन ये सूत्र वक्रों द्वारा घिरे क्षेत्रफल के परिकलन के लिए पर्याप्त नहीं हैं इसके लिए हमें समाकलन गणित की कुछ संकल्पनाओं की आवश्यकता होगी।
बच्चों यहाँ हम इस अध्याय को प्रतियोगी परीक्षा के अनुसार पढ़ेंगे, साथ ही ऐसे प्रश्नों की चर्चा करेंगे जो प्रतियोगी परीक्षा की दृष्टि से महत्वपूर्ण हों।
यह अध्याय महत्वपूर्ण है तथा प्रतियोगी परीक्षाओं की दृष्टि से भी बहुत उपयोगी है। प्रतिवर्ष समाकलन के अनुप्रयोग ( वक्रों से परिबद्ध क्षेत्रफल ) से JEE Main व अन्य प्रतियोगी परीक्षाओं में एक प्रश्न अवश्य आता है।
इस अध्याय में हम वक्रों के अंतर्गत, सरल रेखाओं एवं वृत्तों, परवलयों, तथा दीघवृत्तों की चापों के बीच घिरे क्षेत्रफल को ज्ञात करने के लिए समाकलनों के एक विशिष्ट अनुप्रयोग का अध्ययन करेंगे।
आप प्रतिदिन Doubtnut की कक्षा देखें साथ ही अधिक से अधिक अभ्यास करें, आपकी इस अध्याय से संबंधित सभी समस्याएं दूर हो जाएगीं।
आइए बच्चों वक्रों के अंतर्गत क्षेत्रफल को समझते है और करीब से...
पिछले अध्याय में हमने, योगफल की सीमा के रूप में निश्चित समाकलन एवं कलन की आधारभूत प्रमेय का उपयोग करते हुए निश्चित समाकलन का परिकलन कैसे किया जाए, का अध्ययन किया है। अब हम वक्र y=f(x),x−अक्ष एवं कोटियाँ x=a तथा x=b से घिरे क्षेत्रफल को ज्ञात करने की आसान विधि की चर्चा करते हैं।
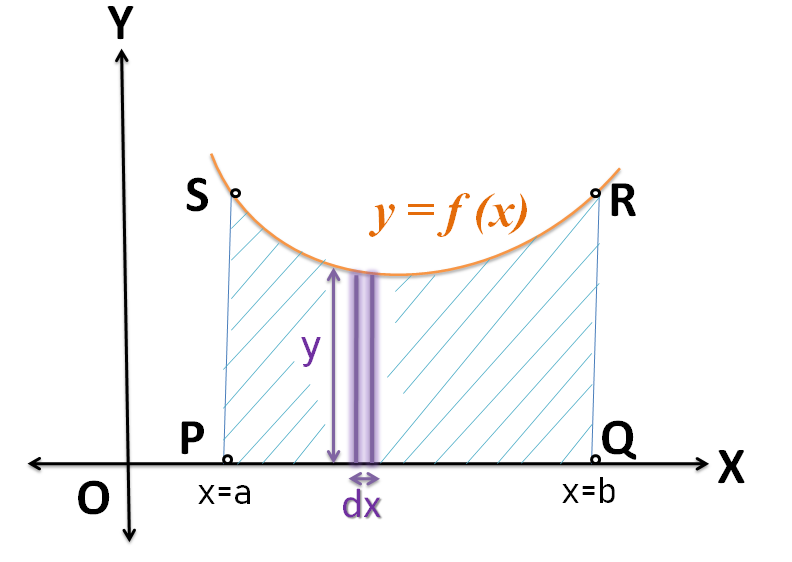
आकृति से हम वक्र के अंतर्गत क्षेत्रफल को बहुत ही पतली एवं उर्ध्वाधर बहुत सी पट्टियों से निर्मित मान सकते हैं। y उँचाई एवं dx चौड़ाई वाली एक स्वेच्छ पट्टी पर विचार कीजिए, इसमें dA (प्रारंभिक पट्टी का क्षेत्रफल) = ydx, जहाँ y=f(x) है।
वक्र y=f(x), कोटियों x=a,x=bएवं x−अक्ष से घिरे क्षेत्र के कुल क्षेत्रफल A को, क्षेत्र PQRSP में सभी पतली पट्टियों के क्षेत्रफलों के योगफल के परिणाम के रूप में देख सकते हैं।
सांकेतिक भाषा में हम इसे इस प्रकार अभिव्यक्त करते हैं:
A=∫badA
=∫baydx
=∫baf(x)dx
वक्रों द्वारा परिभाषित क्षेत्रफल
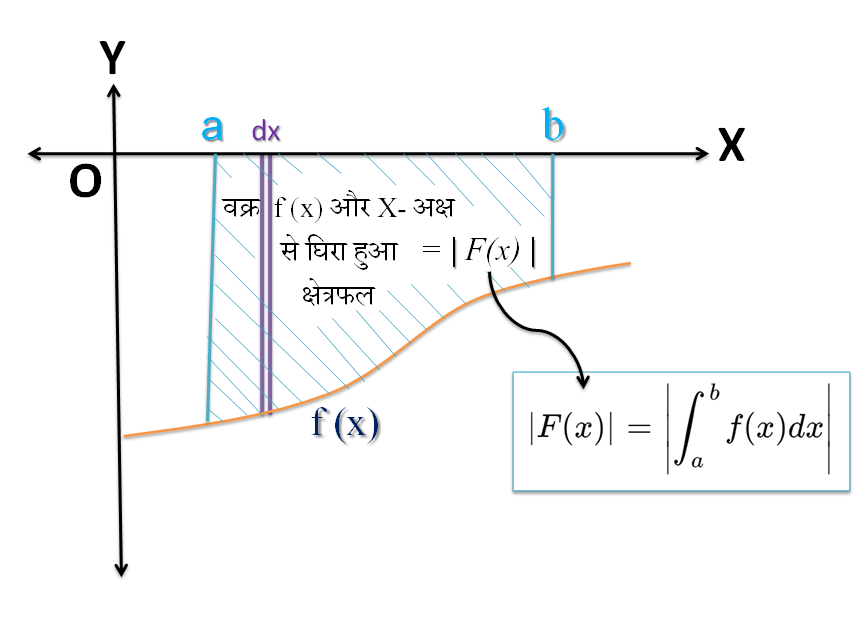
(a) वक्र y=f(x), x−अक्ष तथा कोटियों x=a व x=b के द्वारा परिबद्ध क्षेत्रफल A=∫baydx द्वारा दिया जाता है, जहाँ y=f(x), x−अक्ष के ऊपर स्थित है तथा b>a है। यहाँ x दूरी पर dx चौड़ाई की ऊर्ध्वाधर पट्टी ली जाती है।
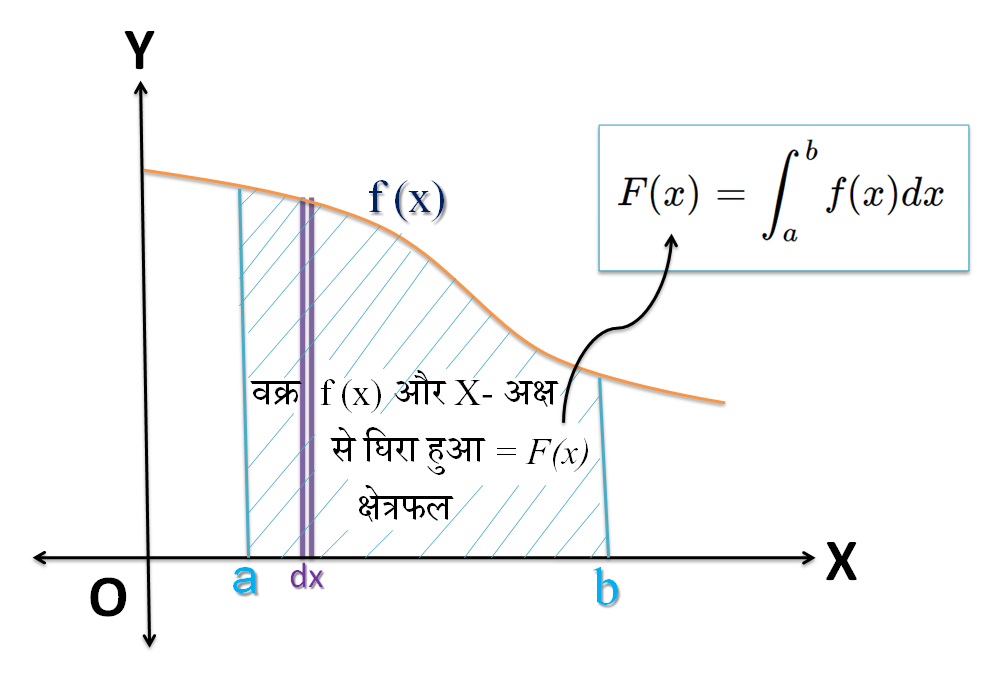
(b) यदि वक्र y=f(x) पूर्णत: x−अक्ष के नीचे स्थित हो, तो A ऋणात्मक होगा तथा हम केवल परिमाण लेंगे, अर्थात् A=∣∣∣∫baydx∣∣∣
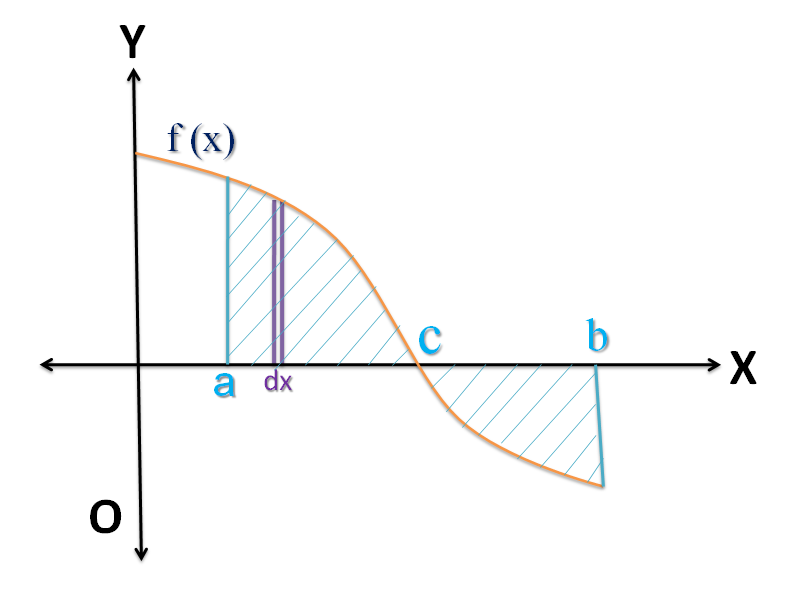
(c) यदि वक्र, x− अक्ष को x=c पर काटता हो, तो A=∫caydx+∣∣∣∫bcydx∣∣∣ होगा।
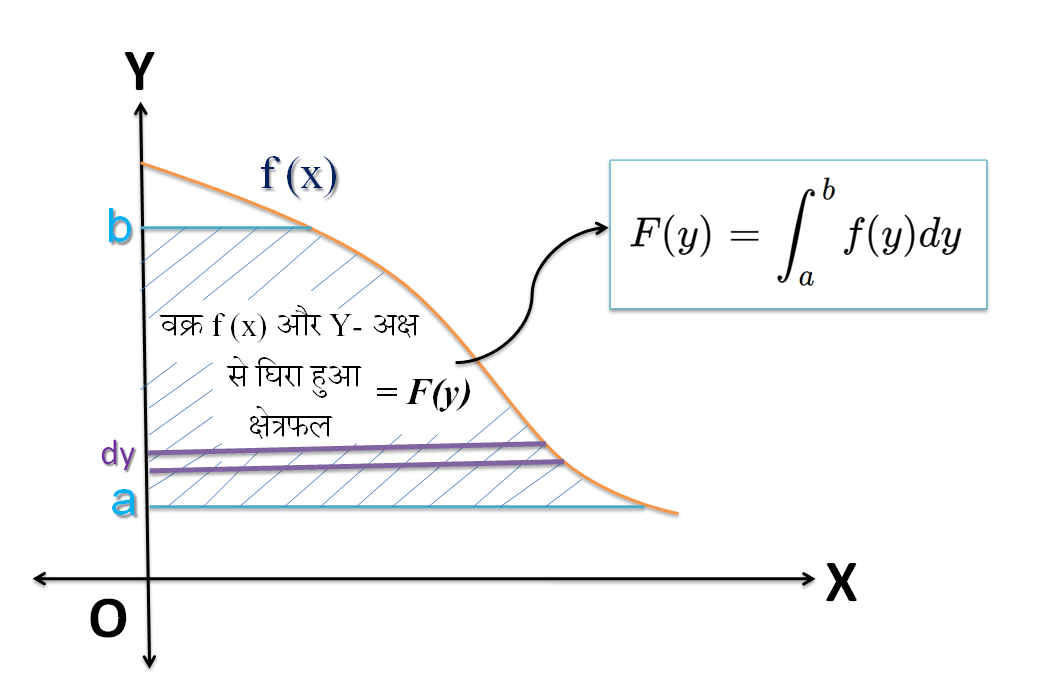
(d) कई बार y के सापेक्ष समाकलन भी उपयोगी होता है। इसमे क्षैतिज पट्टी लेते हैं।
वक्र, y− अक्ष तथा भुजों y=a व y=b द्वारा परिबद्ध क्षेत्रफल
A=∫baxdy द्वारा दिया जाता है, जहाँ X=f(y), y−अक्ष के दायीं ओर स्थित है तथा b>a है। यहाँ y दूरी पर dy चौड़ाई की क्षैतिज पट्टी ली जाती है।
नोट : यदि वक्र सममित हो तथा इसके n सममित भाग हों, तो कुल क्षेत्रफल =n×( किसी एक सममित भाग का क्षेत्रफल )
उदाहरण 1
y=sec2x,x=π6,x=π3 तथा x−अक्ष द्वारा परिबद्ध क्षेत्रफल ज्ञात कीजिए।
अभीष्ट क्षेत्रफल=∫π/3π/6ydx
=∫π/3π/6sec2xdx
=[tanx]π/3π/6
=tanπ3−tanπ6
=√3−1√3=2√3.
उदाहरण 2
प्रथम चतुर्थांश में y=4x2,x=0,y=1 तथा y=4 द्वारा क्षेत्रफल ज्ञात कीजिए।
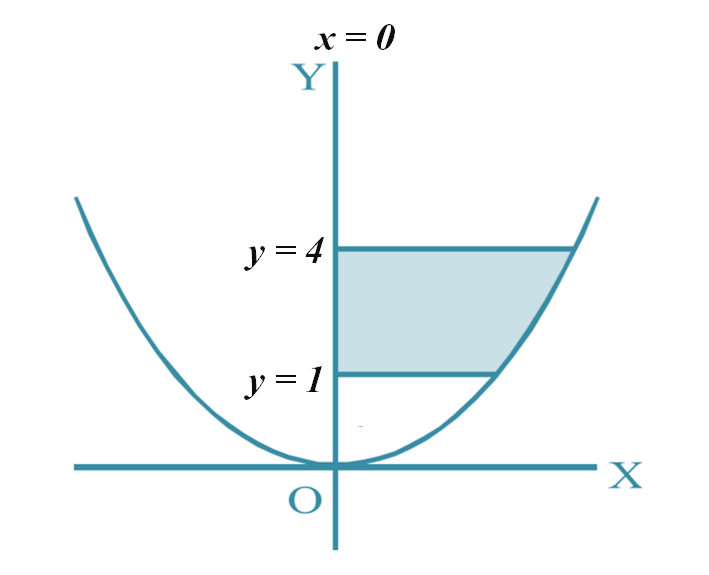
अभीष्ट क्षेत्रफल=∫41xdy
=∫41√y2dy
=12[23y32]41
=13[43/2−1]=13[8−1]
=73=213 वर्ग इकाई
उदाहरण 3
वक्र y=sin2x, x−अक्ष तथा रेखा x=π4 व x=3π4 द्वारा परिबद्ध क्षेत्रफल ज्ञात कीजिए।
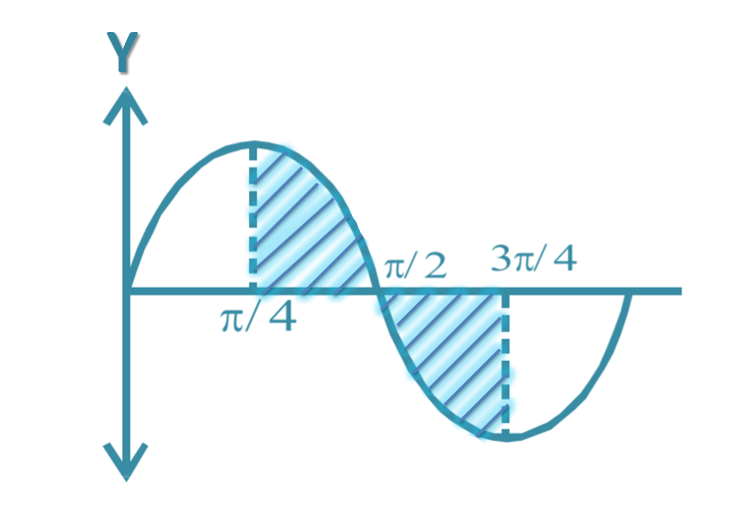
अभीष्ट क्षेत्रफल=∫π2π4sin2xdx
+∣∣∣∫3π/4π/2sin2xdx∣∣∣
=[−cos2x2]π/2π/4
+∣∣ ∣∣[−cos2x2]3π/4π/2∣∣ ∣∣
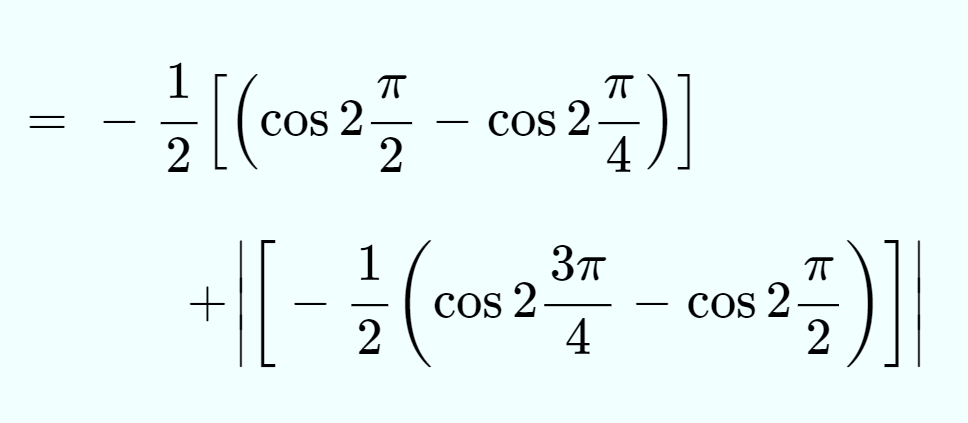
=−12[−1−0]
+∣∣∣−12(0−(−1))∣∣∣
=12+12
=1 वर्ग इकाई
दो वक्रों द्वारा परिबद्ध क्षेत्रफल
(a) दो वक्रों f(x) तथा g(x) द्वारा परिबद्ध क्षेत्रफल,
यदि f(x)>g(x) हो तब क्षेत्रफल A होगा
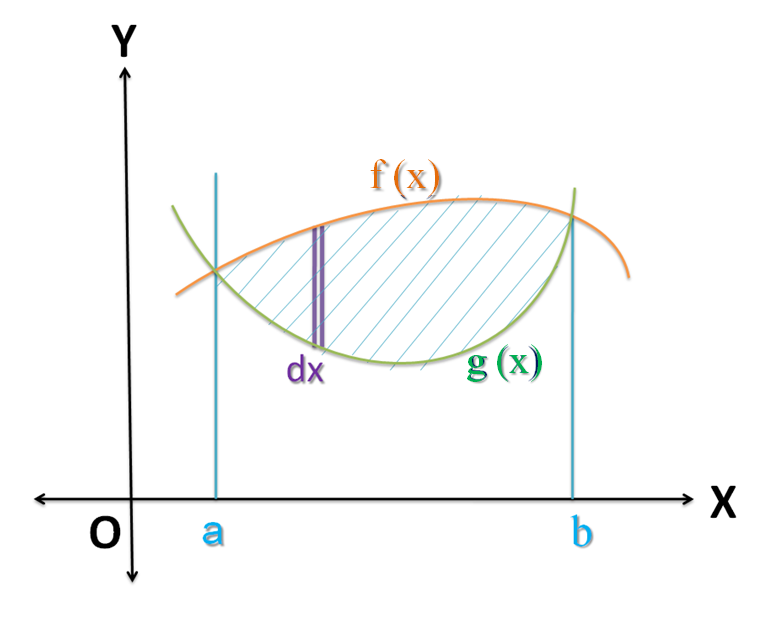
A=∫ba[f(x)−g(x)]dx
(b) यदि क्षैतिज पट्टी ली जाए तो -
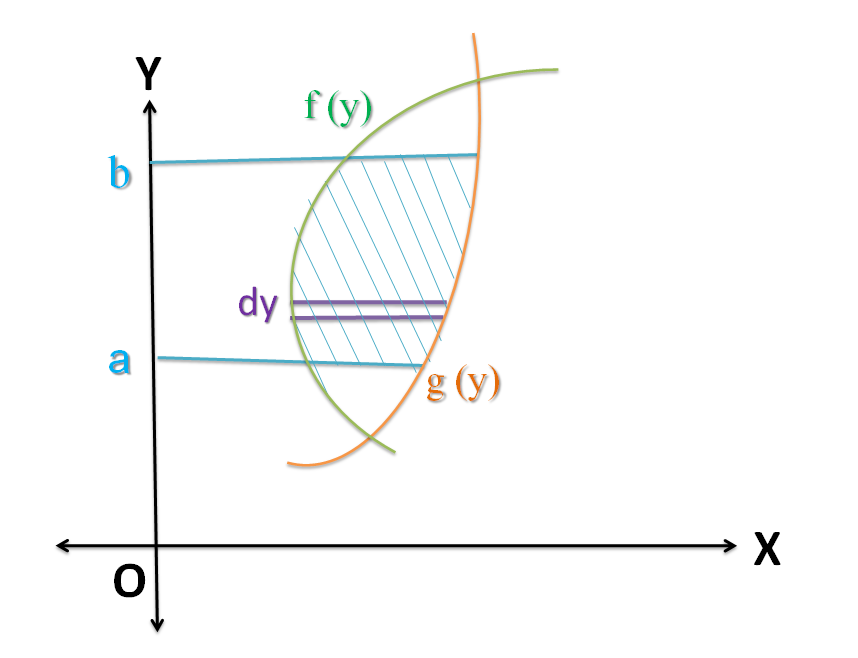
A=∫ba[g(y)−f(y)]dy
(c)यदि f(x) तथा g(x),x=c पर प्रतिच्छेद करते हों, तो अभीष्ट क्षेत्रफल होगा
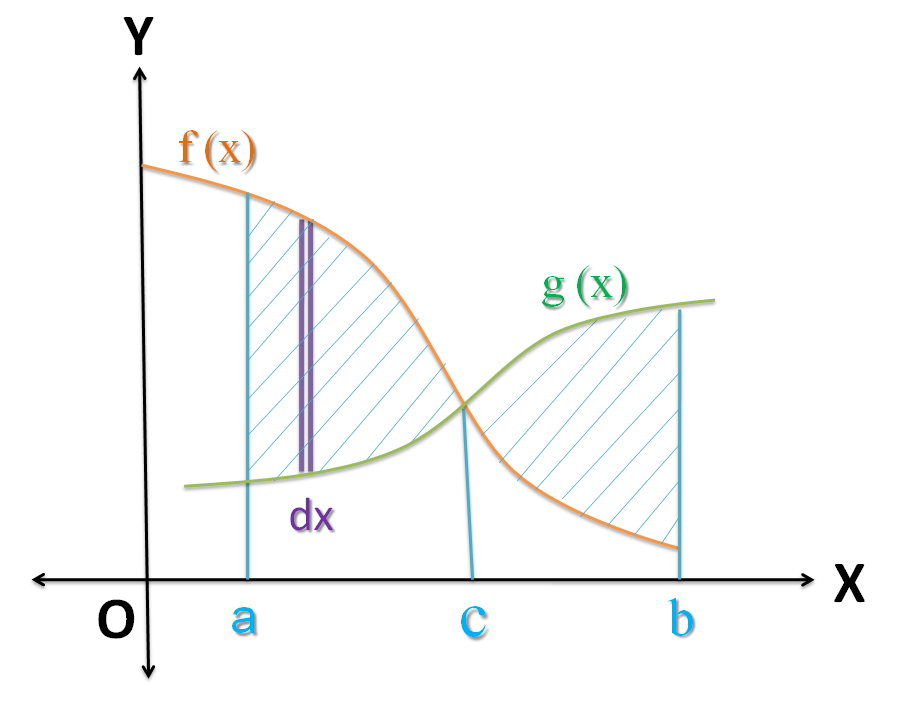
A=∫ca[f(x)−g(x)]dx
+∫bc[g(x)−f(x)]dx
A=∫ba|f(x)−g(x)|dx
उदाहरण 4
वक्र y=(x−1)(x−2)(x−3) जो कोटियों x=0 तथा x=3 के बीच स्थित है तथा x−अक्ष द्वारा परिबद्ध क्षेत्रफल ज्ञात कीजिए।
चिह्न ज्ञात करने के लिए हम सामान्य नियम का पालन करेंगे।
वक्र y=(x−1)(x−2)(x−3)
x>3 के लिए y→+ve
2<x<3 के लिए y→−ve
1<x<2 के लिए y→+ve
x<1 के लिए y→−ve
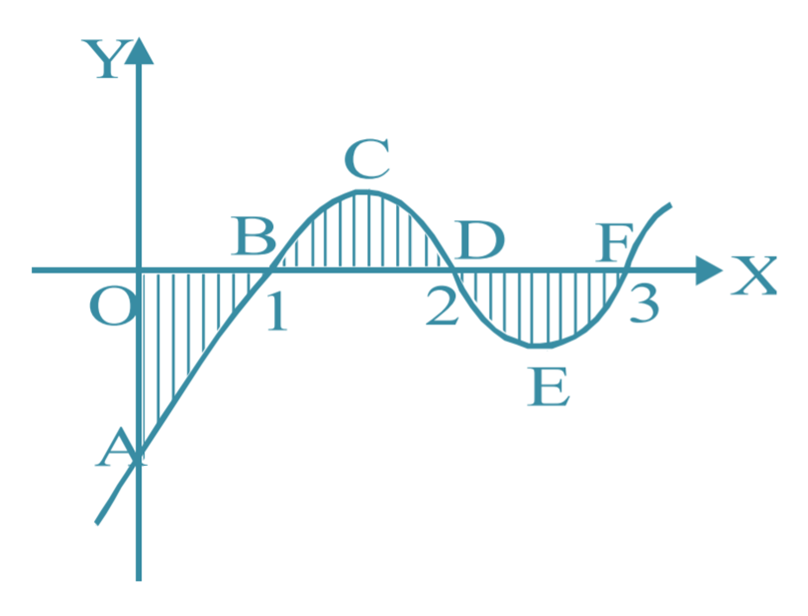
∫30|y|dx=∫10|y|dx+∫21|y|dx+∫32|y|dx
=∫10−ydx+∫21ydx+∫32−ydx
अब माना F(x)=∫(x–1)(x–2)(x–3)dx
=∫(x3–6x2+11x–6)dx
=14x4−2x3+112x2−6x
∴F(0)=0,F(1)=−94,
F(2)=−2,F(3)=−94
अतः अभीष्ट क्षेत्रफल
= −[F(1)−F(0)]
+[F(2)−F(1)]
−[F(3)−F(2)]
=−[−94−0]
+[−2−(−94)]
−[−94−(−2)]
=234वर्ग इकाई
उदाहरण 5
सरल रेखा x=0,x=2 तथा वक्र y=2x,y=2x−x2 द्वारा परिबद्ध क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
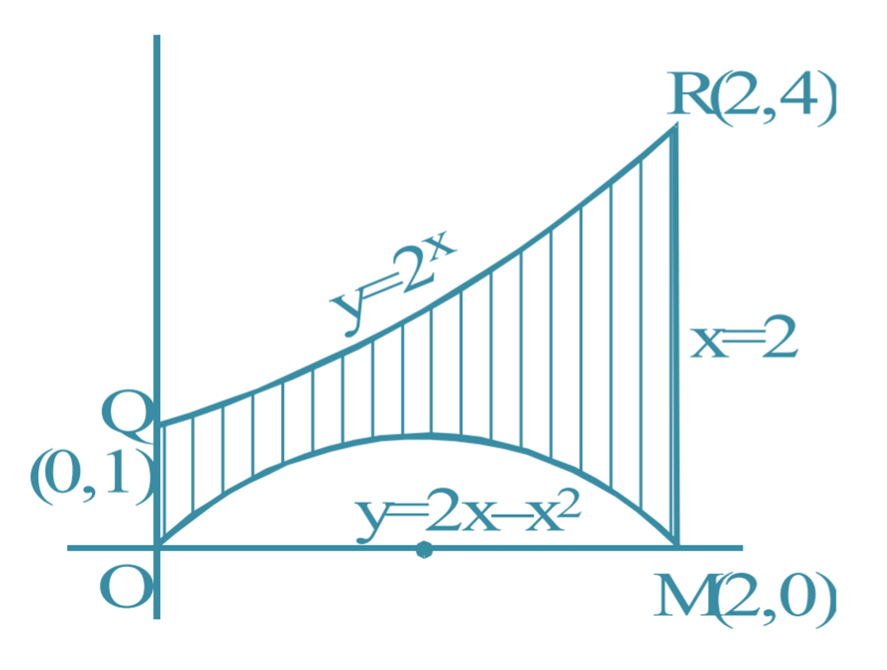
चित्र से हम देख सकते हैं कोटियाँ x1=0,x2=2है।
अभीष्ट क्षेत्रफल
A=∫20(y1−y2)dx
जहाँ y1=2x तथा y2=2x−x2
A=∫20(2x−2x+x2)dx
A=[2xln2−x2+13x3]20
=(4ln2−4+83)−1ln2
=3ln2−43 वर्ग इकाई
उदाहरण 6
परवलयों x=−2y2,x=1−3y2 द्वारा परिबद्ध क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
समीकरण x=−2y2,x=1−3y2 को हल करने पर, दोनों वक्रों की प्रतिच्छेद बिंदुओं की कोटियाँ y1=−1,y2=1 है।
अतः बिन्दु (−2,−1) तथा (−2,1) हैं।
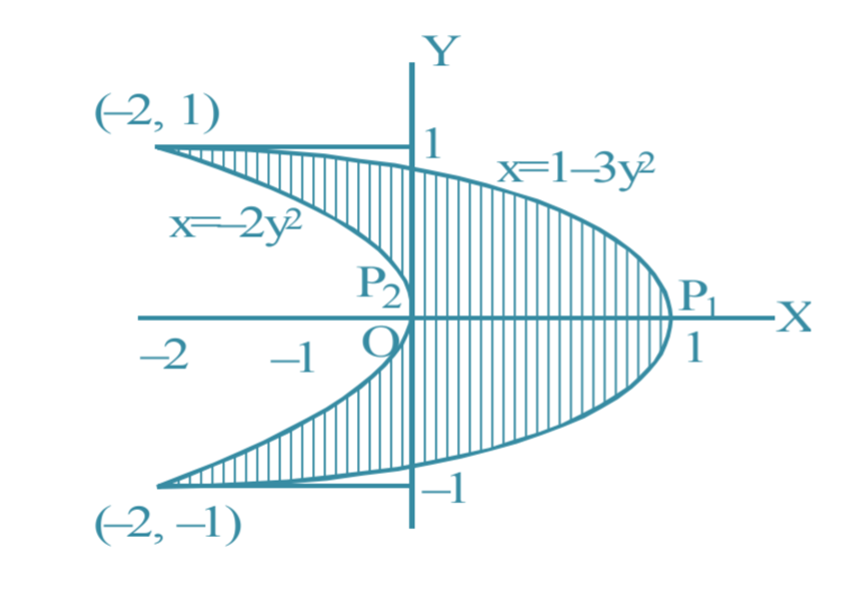
अभीष्ट क्षेत्रफल
=2∫10[(1−3y2)
−(−2y2)]dy
=2∫10(1−y2)dy
=2[y−y33]10
=43 वर्ग इकाई
वक्र अनुरेखण
Curve Tracing
वक्र की अतिसमान आकृति ज्ञात करने के लिए निम्नलिखित प्रणाली निम्न क्रम में उपयोगी है।
(a) सममितता (symmetry):
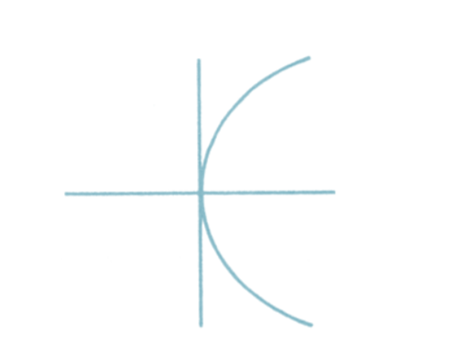
(i) x− अक्ष के सापेक्ष सममित :
यदि समीकरण में 'y' की सभी घातें सम हों, तो वक्र x− अक्ष के सापेक्ष सममित होता है।
उदाहरण - y2=4ax
(ii) y− अक्ष के सापेक्ष सममित :
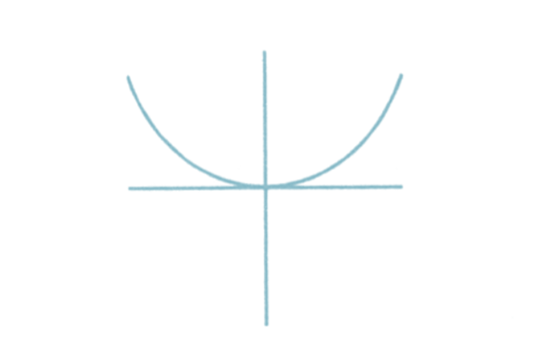
यदि समीकरण में 'x' की घातें सम हो, तो वक्र y− अक्ष के सापेक्ष सममित होता है।
उदाहरण - x2=4ay, a>0
(iii)दोनों आक्षों के सापेक्ष सममित :
यदि समीमकरण में 'x' तथा 'y' की सभी घाते सम हो, तो वक्र x तथा y दोनों अक्षों के सापेक्ष सममित होता है।
उदाहरण - x2+y2=a2

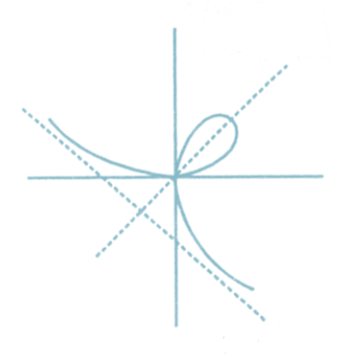
(iv) रेखा y=x के सापेक्ष सममित :
यदि वक्र के समीकरण में x तथा y को आपस में बदलने पर समीकरण अपरिवर्तित रहती हो, तो वक्र रेखा y=x के सापेक्ष सममित होता है।
उदाहरण - x3+y3=3axy
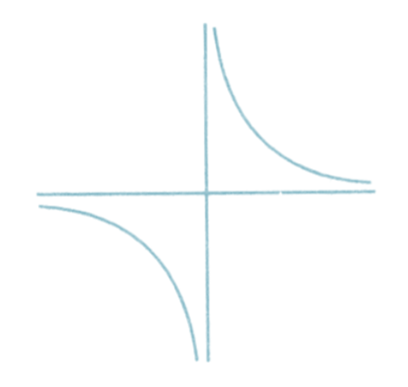
(v) सम्मुख चतुर्थांश में सममित :
यदि x तथा y के स्थान पर क्रमशः −x तथा −y रखने पर वक्र का समीकरण परिवर्तित नहीं हो, तो वह सम्मुख चतुर्थांश में सममित होगा।
(b) उन बिन्दुओं को ज्ञात कीजिए जहाँ वक्र x− अक्ष तथा y− अक्ष को काटता है।
(c) dydx ज्ञात कीजिए तथा वक्र पर उन बिन्दुओं जहाँ वक्र की क्षैतिज स्पर्श रेखाएं स्थित हो, ज्ञात करने के लिए इसकी शून्य से तुलना कीजिए।
(d) यदि संभव हो, तो f(x) वह अन्तराल ज्ञात कीजिए जिसमें वर्द्धमान या ह्रासमान हो।
(e) जब X→∞ या X→−∞ हो, तब y के बारे में परीक्षण कीजिए।
(f) अनन्त स्पर्शियां (Asympotes):
वक्र की अनन्तस्पर्शी उस रेखा को कहते हैं जो उस वक्र को अनन्त पर स्पर्श करती हुई प्रतीत होती है। अर्थात् जैसे-जैसे वक्र तथा वह रेखा अनन्त की ओर अग्रसर होते हैं, वैसे-वैसे उनके बीच की दूरी शून्य की ओर अग्रसर होती है।
कुछ संदर्भों में मोटे तौर पर कह दिया जाता है कि, 'किसी वक्र की अनन्त पर स्पर्शरेखा उस वक्र की अनंतस्पर्शी कहलाती है।'
अनन्तस्पर्शी के ज्ञान से वक्रों के आरेखण में बहुत सहायता मिलती है क्योंकि अनन्तस्पर्शी वक्रों का बहुत दूरी पर स्थिति का संकेत करती है।
- (i)यदि Limx→af(x)=∞ या Limx→af(x)=−∞ हो तब x=a,y=f(x) का अनन्त स्पर्शी है।
(ii) यदि Limx→af(x)=k या Limx→∞f(x)=k हो तब y=k, y=f(x) का अनन्त स्पर्शी है।
उदाहरण 7
वक्र a2y2=x2(a2−x2) के एक लूप का क्षेत्रफल तथा सम्पूर्ण क्षेत्रफल ज्ञात कीजिए।
वक्र दोनों अक्षों के प्रति सममित है। यह x−अक्ष को बिंदुओं (0,0),(−a,0),(a,0) पर काटता है।
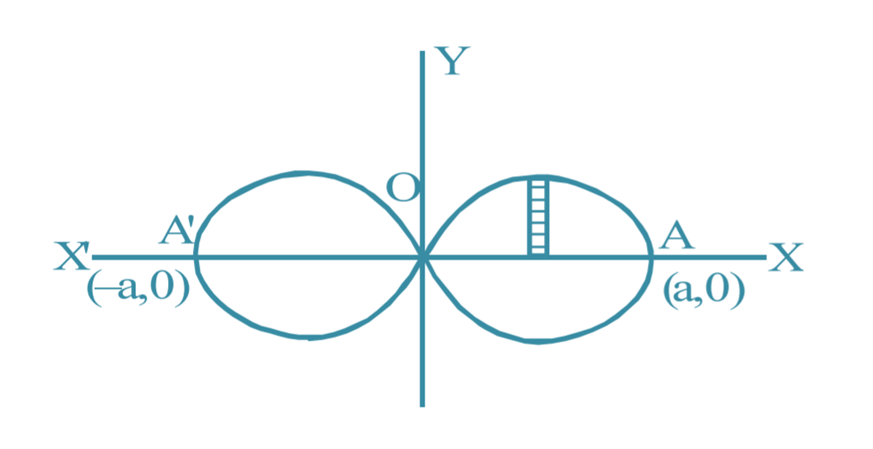
लूप का क्षेत्रफल
=2∫a0ydx
=2∫a0xa√a2−x2dx
=−1a∫a0√a2−x2(−2x)dx
=−1a[23(a2−x2)3/2]a0
=23a2
कुल क्षेत्रफल =2×23a2=43a2
उदाहरण 8
वक्र x2y2=a2(y2−x2) तथा उसकी अनन्त स्पर्शी रेखाओं द्वारा परिबद्ध क्षेत्रफल ज्ञात कीजिए।
वक्र x2y2=a2(y2−x2)
(i) वक्र x− अक्ष व y−अक्ष के सापेक्ष सममित है क्यूंकि x व y की घात सम हैं।
(ii) अनंत स्पर्शी रेखाएं x=±a
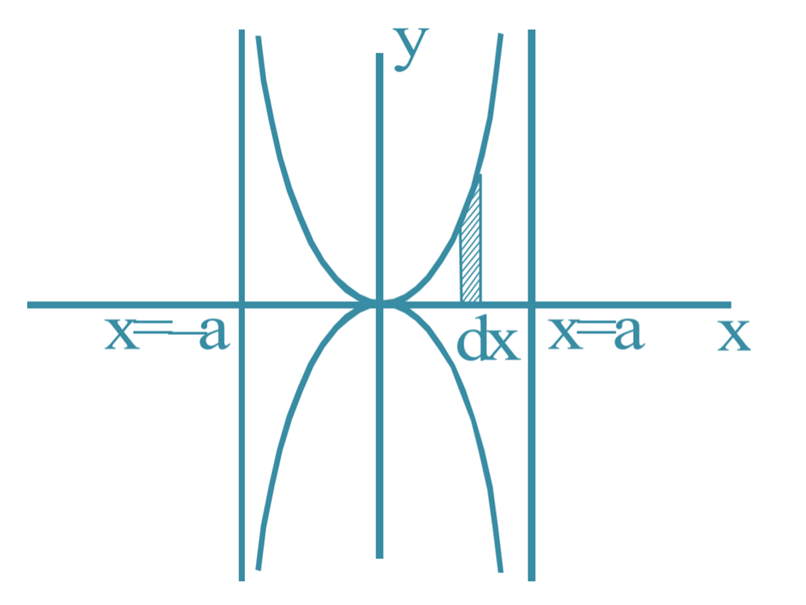
A=4∫a0ydx
=4∫a0ax√a2−x2dx
=4a∣∣−√a2−x2∣∣a0
=4a2
उदाहरण 9
वक्र xy2=4a2(2a−x) व उसकी अनन्त स्पर्शी रेखाओ द्वारा परिबद्ध क्षेत्रफल ज्ञात कीजिए।
xy2=4a2(2a−x)
(i) वक्र x−अक्ष के सापेक्ष सममित होगा क्योंकि y की घात सम है।
(ii) वह (2a,0) से गुजरता है।
(iii) इसकी अनन्त स्पर्शी x=0 अर्थात् y− अक्ष है।
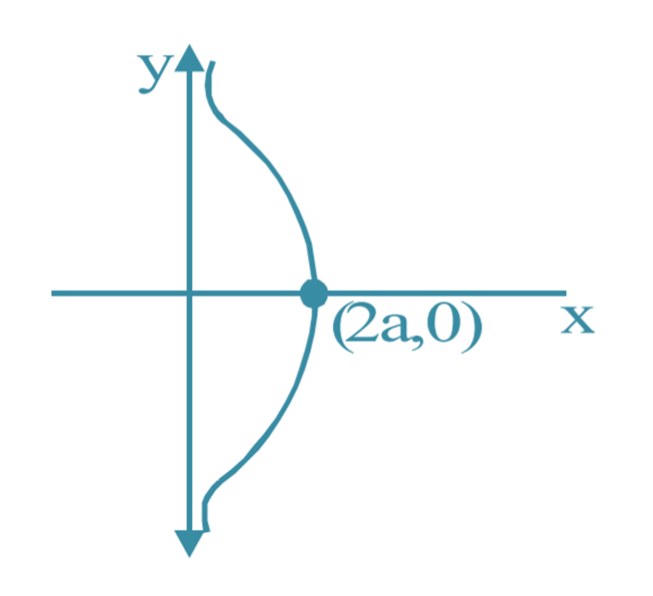
xy2=4a2(2a−x)
y=2a√2a−xx
A=2∫2a0ydx
=2∫2a02a√2a−xxdx
माना x=2asin2θ
A=16a2∫π/20cos2θdθ
=4πa2
महत्वपूर्ण बिन्दु
(a) चूंकि निर्देशी अक्षों के स्थानांतरित होने पर भी क्षेत्रफल अपरिवर्तित रहता है, इसलिए मूल बिन्दु को स्थानांतरित करना कुछ प्रश्नों में सहायक होता है।
उदाहरण 10
|x−1|+|y+1|=1 द्वारा परिबद्ध क्षेत्रफल ज्ञात कीजिए।
मूलबिन्दु को (1,−1) पर स्थानांतरित करते हैं-
X=x−1, Y=y+1
|X|+|Y|=1
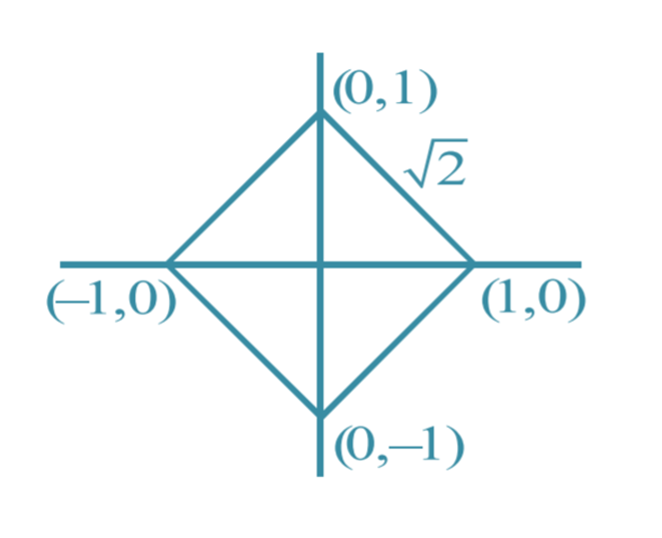
हम यहाँ एक वर्ग देख सकते हैं जिसकी प्रत्येक भुज की लंबाई √(0−1)2+(1−0)2=√2 है।
वक्र का क्षेत्रफल = वर्ग का क्षेत्रफल
=√2×√2=2 वर्ग इकाई
उदाहरण 11
वृत x2+y2+4x+6y−3=0 तथा परवलय x2+4x=6y+14 का उभयनिष्ठ क्षेत्रफल ज्ञात कीजिए।
दिया गया वृत्त
x2+y2+4x+6y–3=0
⇒(x+2)2+(y+3)2=16 मूल बिन्दु को (−2,−3) पर स्थानान्तरित करने पर
X2+Y2=16
दिया गया परवलय
(x+2)2=6(y+3)
X2=6Y
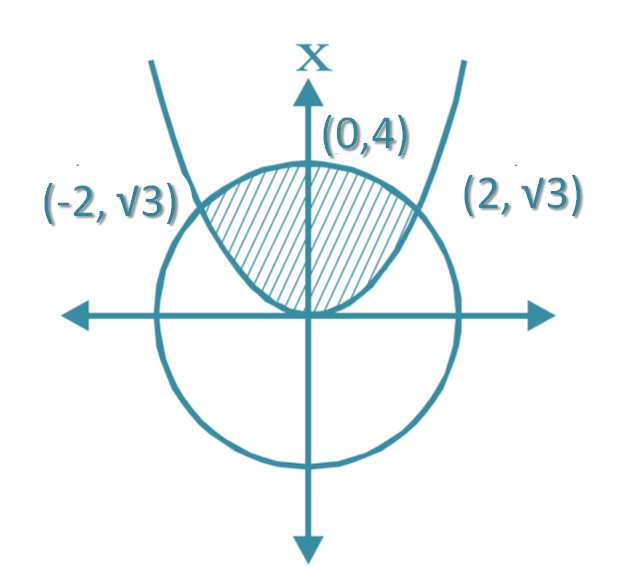
वृत्त तथा परवलय को हल करने पर X=±2√3 अतः वे (−2√3,2) तथा (2√3,2) पर मिलते हैं।
A=2[∫20√6YdY
+∫42√16−Y2dY]
=[23√6[Y3/2]20
+[12Y√16−Y2
+162sin−1Y4]42]
=(4√33+16π3) वर्ग इकाई
उदाहरण 12
वक्र x=asint,y=acost(0≤t≤π) तथा x−अक्ष द्वारा परिबद्ध क्षेत्रफल ज्ञात कीजिए।
दिया है,
x=asint, y=acost (0≤t≤π)
dxdt=acost, dydt=−asint
क्षेत्रफल =∫π0ydx
=∫π0ydxdtdt
=∫π0acost(acost)dt
=a2∫π0cos2tdt
=a22∫π0(1+cos2t)dt
=a22[t+sin2t2]π0dt
=a22[π−0
+12(sin2π−sin0)]
=a22[π+12(0−0)]
=πa22
उदाहरण 13
वक्र x=a(t−sint),y=a(1−cost) के एक चाप तथा x−अक्ष द्वारा परिबद्ध क्षेत्रफल ज्ञात कीजिए।
दिया है,
x=a(t−sint), y=a(1−cost)
यदि एक चाप x− अक्ष को काटेगा तब y=0
अतः y=a(1−cost)=0
1−cost=0
cost=1
अतः t=0,π
dxdt=a(1−cost),
dydt=a(sint)
क्षेत्रफल
=∫π0ydx
=∫π0ydxdtdt
=∫π0a(1−cost)
×(a(1−cost))dt
=a2∫π0(1−cost)2dt
=a2∫π0(1+cos2t−2cost)dt
=a2∫π0(1+12(2cos2t)
−2cost)dt
=a2∫π0(1+12(1+cos2t)
−2cost)dt
=a2∫π0(32+12cos2t
−2cost)dt
=a2[32t+12sin2t2−2sint]π0
=a2[32t+sin2t4−2sint]π0
=a2[32π−0+14(sin2π−sin0)
−2(sinπ−sin0)]=3πa22
उदाहरण 14
'a' का वह मान ज्ञात कीजिए, जिसके लिए x=1,x=2,y=6x2 तथा y=f(a) तथा द्वारा परिबद्ध क्षेत्रफल न्यूनतम हो।
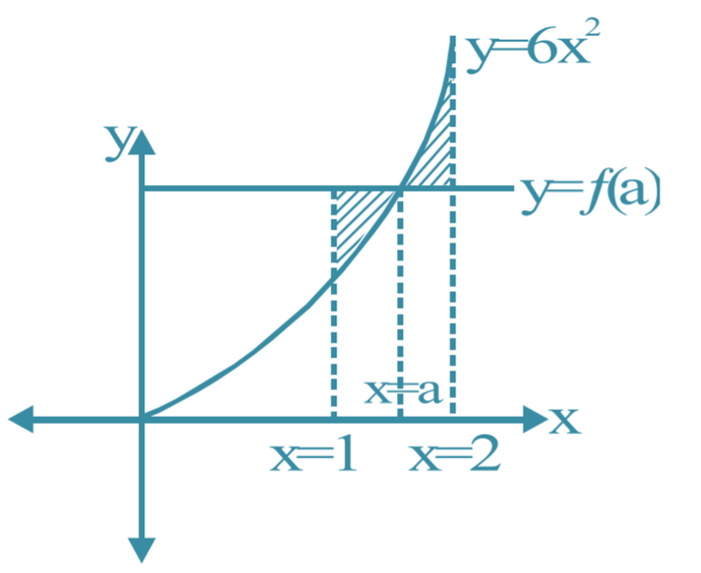
माना,
b=f(a)
क्षेत्रफल
A=∫a1(b−6x2)dx
+∫2a(6x2−b)dx
=[bx−2x3]a1+[2x3−bx]2a
=[ab−b−(2a3−2)]
+[2×23−2×a3
−(2b−ab)]
=ab−b−2a3+2+16
−2a3−2b+ab
=2ab−3b−4a3+18
चूंकि y=b=f(a)
y=6x2=6a2=b
A=2a(6a2)−3(6a2)
−4a3+18
=12a3−18a2−4a3+18
=8a3−18a2+18
न्यूनतम क्षेत्रफल के लिए
dAda=0
dAda=24a2−36a=0
a(24a−36)=0
a=3624
a=1.5
उदाहरण 15
यदि y=g(x) एकैकी आच्छादक फलन f:R→R,f(x)=6x5+4x3+2x का प्रतिलोम हो, तो g(x),x−अक्ष तथा कोटि x=12 द्वारा प्रतिबद्ध क्षेत्रफल ज्ञात कीजिए।
f(x)=6x5+4x3+2x
f(0)=0
f(1)=6+4+2=12
दिया है g(x) प्रतिलोम है f(x)का
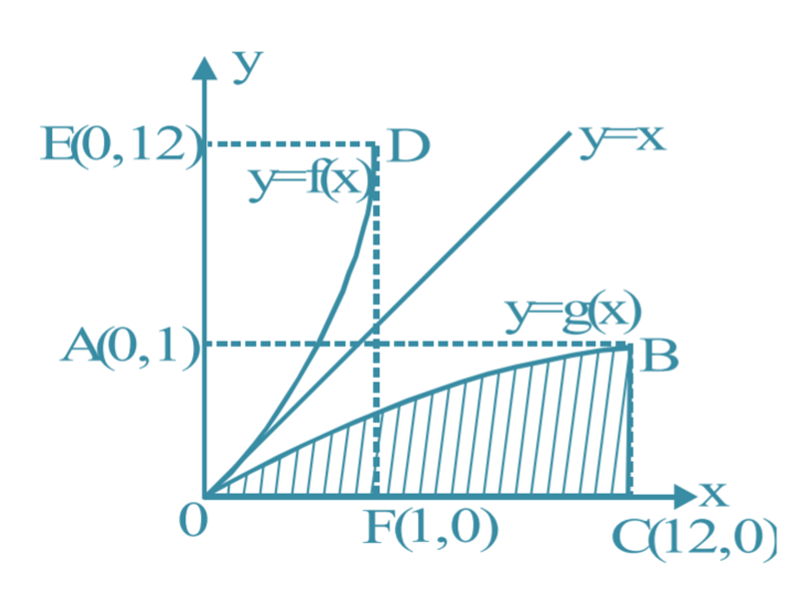
अभीष्ट क्षेत्रफल :
∫120g(x)dx=
आयत OEDF का क्षेत्रफल
−∫10f(x)dx
=1×12
−∫10(6x5+4x3+2x)dx
=12−[x6+x4+x2]10
=12−3
=9 वर्ग इकाई
उपयोगी परिणाम
(a) दीर्घवृत्त x2a2+y2b2=1 का सम्पूर्ण क्षेत्रफल πab होता है।
(b) परवलय y2=4ax तथा x2=4by के मध्य परिबद्ध क्षेत्रफल 16ab/3 होता है।
(c) परवलय y2=4ax तथा रेखा y=mx के मध्य समावेशित क्षेत्रफल 8a2/3m3 होता है।
(d) sinax (या cosax) की एक चाप और x−अक्ष द्वारा परिबद्ध क्षेत्रफल 2a वर्ग इकाई के बराबर होगा।
(e) फलन y=f(x) का अंतराल a≤x≤b पर औसत मान, 1b−a∫baf(x)dx द्वारा परिभाषित किया जाता है।
उदाहरण 16
परवलय 4y2−3x−8y+7=0 तथा दीर्घवृत x2+4y2−2x−8y+1=0 द्वारा परिबद्ध छोटे क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
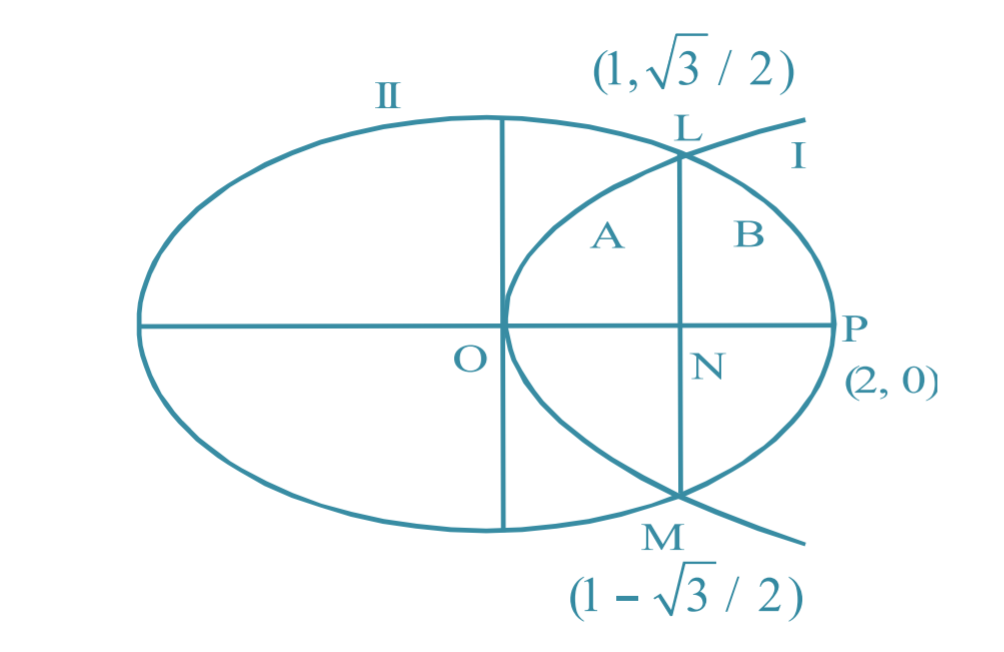
C1:
4(y2−2y)=3x−7 है या
4(y−1)2=3x−3
4(y−1)2=3(x−1)
यह एक परवलय है, जिसका शीर्ष (1, 1) पर है।
C2:
(x2−2x)+4(y2−2y)=−1 है
या (x−1)2+4⋅(y−1)2
=−1+1+4
या (x−1)222+(y−1)212=1
यह एक दीर्घवृत्त है जिसका केंद्र (1,1) पर है। मूल बिन्दु को (1, 1) पर स्थानान्तरित करने पर इसके क्षेत्रफल के परिमाण पर कोई फर्क नहीं पड़ेगा बल्कि गणना सरल हो जाएगी।
अतः दो वक्र 4Y2=3X तथा X222+Y21=1 हैं जो बिंदु (1,±√32) पर मिलते हैं।
अभीष्ट क्षेत्रफल
=2(A+B)
=2[∫Y1dX+∫Y2dX]
=2[√32∫10√XdX
+∫21√4−X22dX]
=√3∫10√XdX
+∫21(√4−X2)dX
=√3[2X3/23]10
+[X2√4−X2
+42sin−1(X2)]21
=2√33+[π−(√32+π3)]
=2√33−√32+π−π3
=[√36+2π3] वर्ग इकाई
उदाहरण 17
क्षेत्र y≥√x, x>−√y तथा वक्र x2+y2=2 द्वारा परिबद्ध क्षेत्रफल ज्ञात कीजिए।
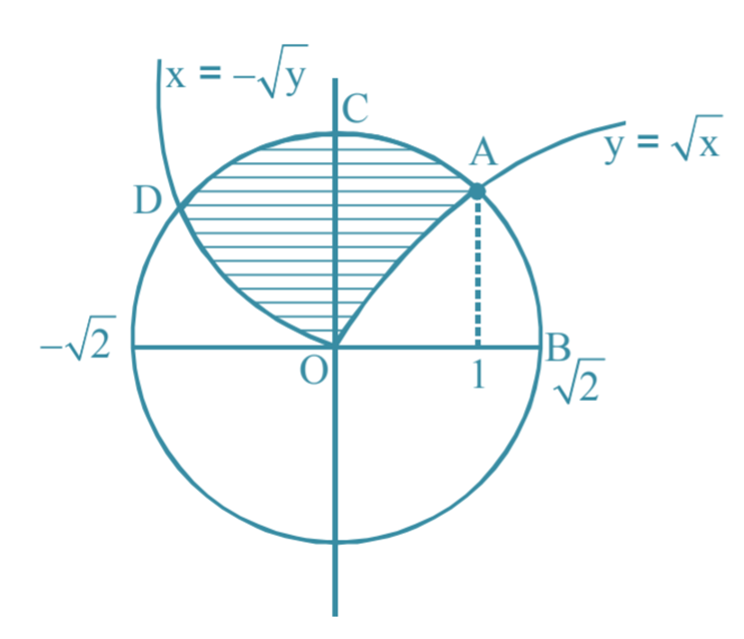
उभयनिष्ठ क्षेत्रफल चित्र द्वारा दिया गया है।
यदि क्षेत्र OAB का क्षेत्रफल =λ
तब क्षेत्र OCD का क्षेत्रफल =λ
क्योंकि y=√x तथा x=−√y
क्रमशः x तथा y-अक्ष से समान क्षेत्रफल परिबद्ध करते है।
y=√x⇒y2=x
x=−√y⇒x2=y
अतः दोनों वक्र रेखा y=x के सापेक्ष सममित है।
प्रथम चतुर्थांश OBC का क्षेत्रफल =πr24=π2(r=√2)
क्षेत्र OCA का क्षेत्रफल =π2−λ
छायांकित भाग का क्षेत्रफल =(π2−λ)+λ=π2 वर्ग इकाई
उदाहरण 18
उस रेखा का समीकरण ज्ञात कीजिए जो मूल बिंदु से गुजरती है तथा वक्रीय त्रिभुज जिसका शीर्ष मूल बिंदु है तथा जो वक्र y=2x−x2,y=0 तथा x=1 द्वारा परिबद्ध है, को सामान क्षेत्रफल के दो भागो में विभाजित करती है।
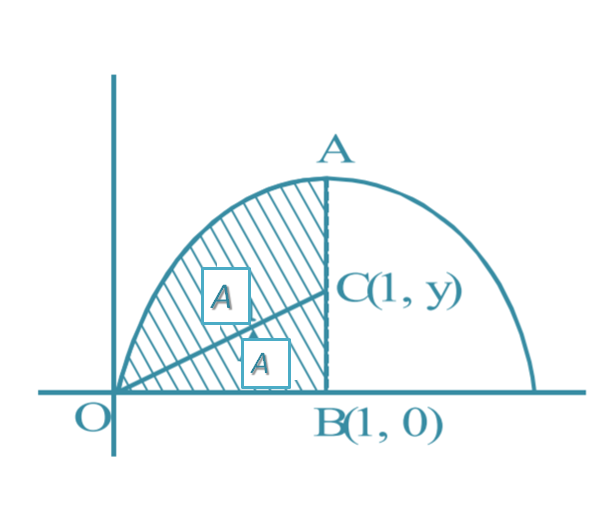
क्षेत्र OBA का क्षेत्रफल
=∫10(2x−x2)dx
=[x2−x33]10
=23
⇒23=A+A=2A
⇒A=13
माना बिन्दु c के निर्देशांक (1,y) हैं
△OCB का क्षेत्रफल =13
⇒12⋅1⋅y=13
⇒y=23
C के निर्देशांक (1,23) है।
रेखा OC की प्रवणता
m=23−01−0=23
रेखा OC की समीकरण y=mx
⇒y=23x
उदाहरण 19
वक्र x2+y2=4 , x2=−√2y तथा रेखा x=y द्वारा x−अक्ष के नीचे परिबद्ध क्षेत्रफल ज्ञात कीजिए।
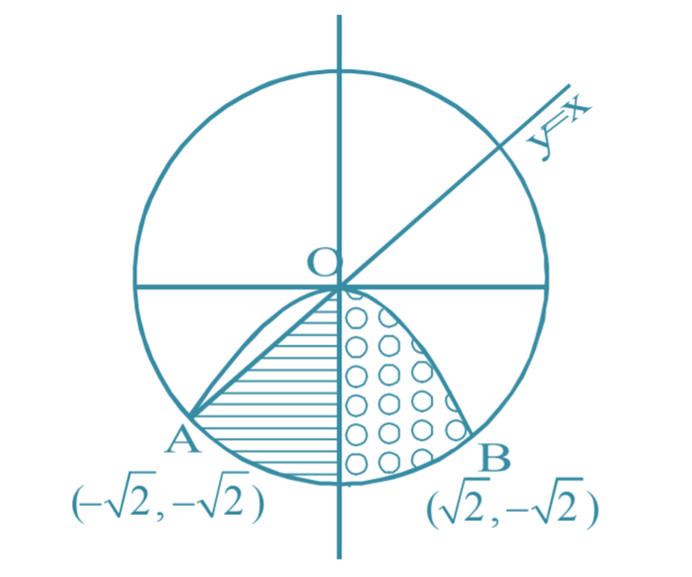
माना वृत्त C: x2+y2=4,
y=√4−x2
परवलय P: y=−x2√2
रेखा L: y=x
हमारे पास उपरोक्त तीन वक्र है।
P व C को हल करने पर निम्न बिन्दु प्राप्त होते है।
A(−√2,−√2), B(√2,−√2)
रेखा y=x, A(−√2,−√2) से गुजरती है।
अभीष्ट क्षेत्रफल A
= छायांकित + बिन्दु अंकित भाग
=∫0−√2(L−C)dx
+∫√20(P−C)dx
=∫0−√2(x−√4−x2)dx
+∫√20(−x2√2−√4−x2)dx
=∫0−√2xdx+∫√20−x2√2dx
−∫0−√2√4−x2dx
−∫√20√4−x2dx
=∫0−√2xdx+∫√20−x2√2dx
−∫√2−√2√4−x2dx
=[x22]0−√2−1√2[x33]√20
−[x2√4−x2+42sin−1(x2)]√2−√2
=1−23−(π2−(−π2))
A=13−π वर्ग इकाई
उदाहरण 20
वक्रो y=x तथा y=x3 के मध्य घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
प्रदत्त वक्र :
y=x ... (1 )
तथा y=x3 ... (2)
समीकरण (1) व (2) से,
x−x3=0
x(1−x)(1+x)=0
∴x=0,x=1
तथा x=−1
समीकरण (1 ) से यदि x=0 तब y=0, यदि x=1 तब y = 1 तथा यदि x=−1 तब y=−1 अतः वक्रों (1 ) व (2 ) के प्रतिच्छेद बिंदु
A(−1,−1),O(0,0) तथा B(1,1) हैं।
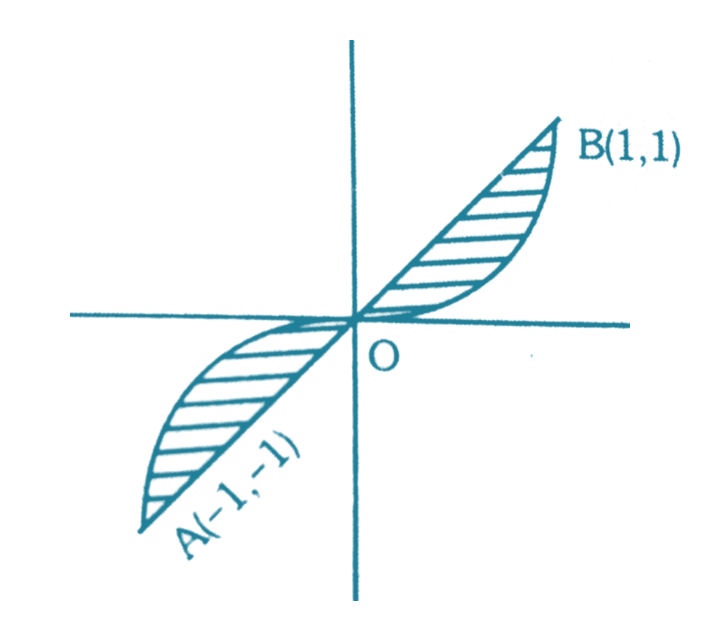
प्रश्नानुसार, हमे छायांकित भाग का क्षेत्रवफल ज्ञात करना है। हम प्रथम चतुर्थांश में स्थित छायांकित भाग का क्षेत्रफल ज्ञात करके उस क्षेत्रफल को '2' से गुणा कर देंगे। हमे अभीष्ट क्षेत्र का क्षेत्रफल ज्ञात हो जाएगा।
प्रथम चतुर्थांश में स्थित क्षेत्र का क्षेत्रफल
=∫10y1dx−∫10y2dx
जबकि y1=x तथा y2=x3
=∫10xdx−∫10x3dx
=[x22]10−[x44]10
=12−14=14
अतः अभीष्ट क्षेत्रफल =2× प्रथम चतुर्थांश में स्थित क्षेत्र का क्षेत्रफल
=2×14=12 वर्ग इकाई
उदाहरण 21
y=x2+1 तथा मूलबिंदु से इस पर खींची गयी स्पर्श रेखाओ द्वारा परिबद्ध क्षेत्रफल है -
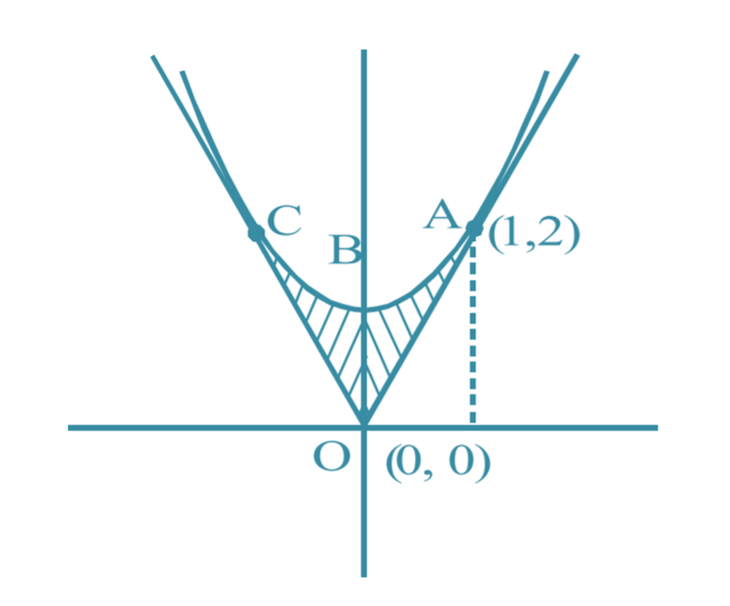
परवलय एक सम फलन होता है तथा माना इसकी स्पर्श रेखा का समीकरण y=mx है। परवलय तथा स्पर्श रेखा का प्रतिच्छेद बिन्दु ज्ञात करते है
mx=x2+1
x2−mx+1=0⇒D=0
⇒m2−4=0
⇒m=±2
अतः दो स्पर्श रेखायें संभव हैं-
y=2x तथा y=−2x
y=x2+1 तथा y=2x का प्रतिच्छेद बिन्दु x=1 तथा y=2 है।
छायांकित क्षेत्र OAB का क्षेत्रफल
=∫10(y2−y1)dx
=∫10[(x2+1)−2x]dx
=[x33+x−x2]10
=13+1−1−0
=13 वर्ग इकाई
संपूर्ण छायांकित भाग का क्षेत्रफल
=2(13)=23 वर्ग इकाई
उदाहरण 22
माना दो वक्र C1:y=1+cosx तथा C2:y=1+cos(x−α) हैं, जहाँ α∈(0,π2),x∈[0,π] है। α का वह मान ज्ञात कीजिए जिसके लिए वक्र C1,C2 तथा x=0 द्वारा परिबद्ध क्षेत्रफल, वक्र C2,y=1 तथा x=π द्वारा परिबद्ध के बराबर हो।
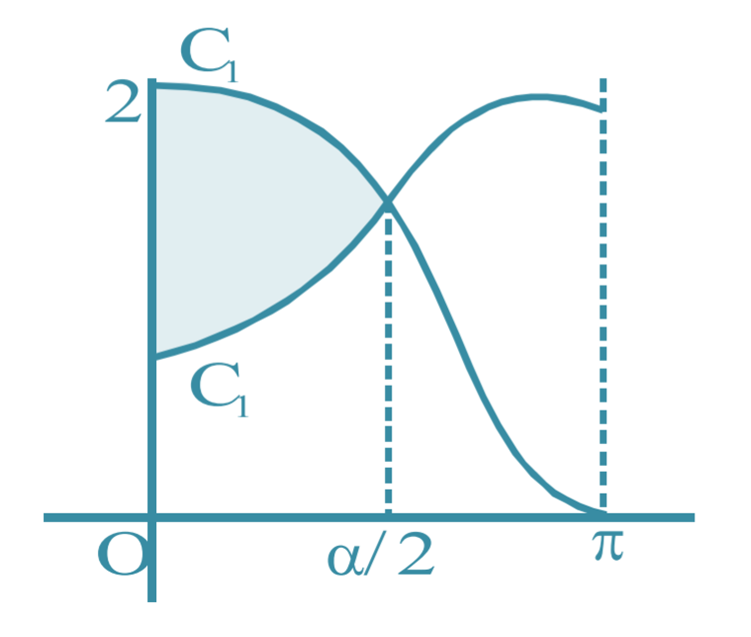
1+cosx=1+cos(x−α)
⇒cosx=cos(x−α)
⇒cosx=cos(α−x)
⇒x=α−x
⇒x=α2
A1=∫α/20(1+cosx)
−(1+cos(x−α))dx
=|sinx−sin(x−α)|α/20
=2sinα2−sinα
1+cos(x−α)=1
⇒x=α+π2
A2=∫πα+π2(1+cos(x−α)−1)dx
=|sin(x−α)|πα+π2
=|sinα−1|=1−sinα
A1=A2
⇒2sinα2−sinα=1−sinα
α=π3
सारांश
(a) यदि वक्र y=f(x) x−अक्ष के ऊपर स्थित हो, तो वक्र y=f(x), x−अक्ष तथा कोटियों x=a व x=b के द्वारा परिबद्ध क्षेत्रफल A=∫baydx द्वारा दिया जाता है

(b) यदि वक्र y=f(x) पूर्णत: x−अक्ष के नीचे स्थित हो, तो A ऋणात्मक होगा तथा हम केवल परिमाण लेंगे, अर्थात् A=∣∣∣∫baydx∣∣∣

(c) यदि वक्र, x− अक्ष को x=c पर काटता हो, तो A=∫caydx+∣∣∣∫bcydx∣∣∣ होगा।

(d) कई बार y के सापेक्ष समाकलन भी उपयोगी होता है। इसमे क्षैतिज पट्टी लेते हैं।
वक्र, y− अक्ष तथा भुजों y=a व y=b द्वारा परिबद्ध क्षेत्रफल
A=∫baf(y)dy=∫baxdy

(e) यदि वक्र सममित हो तथा इसके n सममित भाग हों, तो कुल क्षेत्रफल =n×( किसी एक सममित भाग का क्षेत्रफल )
(f) दो वक्रों f(x) तथा g(x) द्वारा परिबद्ध क्षेत्रफल,
यदि f(x)>g(x) हो तब क्षेत्रफल A होगा

A=∫ba[f(x)−g(x)]dx
(g) दीर्घवृत्त x2a2+y2b2=1 का सम्पूर्ण क्षेत्रफल πab होता है।
(h) परवलय y2=4ax तथा x2=4by के मध्य परिबद्ध क्षेत्रफल 16ab/3 होता है।
(i) परवलय y2=4ax तथा रेखा y=mx के मध्य समावेशित क्षेत्रफल 8a2/3m3 होता है।
(j) sinax या cosax की एक चाप और x−अक्ष द्वारा परिबद्ध क्षेत्रफल 2a वर्ग इकाई के बराबर होगा।
(k) फलन y=f(x) का अंतराल a≤x≤b पर औसत मान, 1b−a∫baf(x)dx द्वारा परिभाषित किया जाता है।
(l) कुछ महत्वपूर्ण वक्रों के आलेख: