LIMITS for Class 12 MATHS
Introduction
There are some functions which have different value over infinitely small intervals means let f(x) be a function dependent on x so for small change in x , a small change in f(x) will be there . We will see some examples to know the difference between limits from trigonometry , sets and other topics .
For example : - Let f(x)=x+2 (As illustrated in given figure).
Here as you see that value of f(x) at points in the neighborhood of x=2 is almost equal to the value at x=2 which means that the limit exists at x=2 . Here we saw some basic concepts . In some cases the function might " not be defined " we will see those also later in chapter.
Index
Limits Definition|Left hand and Right hand rule|Important formulas for limits|Indeterminate forms|L'Hospital's rule|Greatest Integer function|Some tricks to find limits|Rationalization or double rationalization|Trignometric relations in Limits|Series expansion|Sandwich theorem
Limits Definition
Let f(x) be a function which has a limit L at different values near to x but " not necessarily " defined exactly at x . So this limiting behavior of the function in neighborhood of x=a is called "Limit of the function " .
Note :
In the function f(x) = 1x2 , let x assumes a value near to x=0 and clearly function is " undefined " at x=0 that doesn't mean that limit of function doesn't exist . It can have ∞ as it's solution also .
Left Hand and Right hand limit of a function
When value of f(x) approaches to L from Left hand hand side (x→a−)
is called as left hand limit ( LHL ) i.e.
LHL =
Limx→a−f(x)=Limh→0f(a−h)
Similarly when it approaches from Right hand side (x→a+) is called Right hand limit ( RHL ) means
RHL = Limx→a+f(x)=Limh→0f(a+h)
So if limit exists at x→a , than Limx→a+f(x)=Limx→a−f(x)
Important formulas for limits
Let limx→af(x)=l and Limx→ag(x)=m
(a) Sum formula :
Limx→a{f(x)+g(x)}=l+m
(b) Difference formula :
Limx→a{f(x)−g(x)}=l−m
(c) Product formula :
Limx→a[f(x)⋅g(x)]=l⋅m
(d) Quotient formula :
Limx→a[f(x)g(x)]=(lm) , provided m≠0
(e) Natural logarithmic formula :
= Limx→aln(g(x))=ln[Limx→ag(x)]
(f) Constant multiple rule :
limx→ak⋅f(x)=klimx→a ; where k is constant f ( x )
(g) Power rule :
If m and n are integers then limx→a(f(x))mn=lmn provided lmn is a real number
As you will solve more problems, you will get to know some more in detail.
Example 1
Find Limx→2(x3+2x2−6x+1)
So limx→2(x3)+2limx→2(x2)−6limx→2(x)+1
So keeping the limits 23+2⋅22−6⋅2+1=5
Indeterminate forms
00 , ∞∞ , ∞−∞ , 0×∞ , 1∞ , 00 , ∞0
Here are some basic indeterminate forms
Here ∞ does not follow basic algebra rule whether it is addition , subtraction , multiplication , division .
L - Hospital's rule
Let f(x)g(x) is an indeterminate form than we use this rule to find the solution and the general form is f(x)g(x) = f'(x)g'(x)
Example 2
limx→axa−axxx−aa is equal to
We have ,
limx→axa−axxx−aa[00 form ]
limx→aaxa−1−axlogaxx(1+logx)−0 [Using L - Hospital's Rule]
=aa−aalogaaa(1+loga)=1−loga1+loga=log(ea)loge(ae)
Example 3
limx→0tanx−xx2tanx equals
We have ,
limx→0tanx−xx2tanx [00 form]
=limx→0sec2x−12xtanx+x2sec2x [ By L -Hospital's rule ]
=limx→02sec2xtanx2tanx+4xsec2x+2x2sec2xtanx [ By L -Hospital's Rule ]
=limx→02sec4x+4sec2xtan2x6sec2x+12xsec2xtanx+2x2sec4x+4x2sec2xtan2x
= 26=13
Example 4
If limx→0aex−bcosx+ce−xxsinx=2 , than a+b+c=?
We observe that as x→0 , numerator tends to a−b+c whereas the denominator tends to 0 . Therefore , for the limit to exist we must have .
a−b+c=0 .......( i )
Now , if a−b+c=0 , then ,
limx→0aex−bcosx+ce−xxsinx is in the the 00 form .
∴limx→0aex+bsinx−ce−xsinx+cosx=2[ Using L - Hospital's rule ]
Here , the numerator is tending to (a−c) as
(x→0) . Therefore for the limit to exist , we must have
a−c=0 ....... ( ii )
Now , if a−c=0 , then
limx→0aex+bsinx−ce−xsinx+xcosx is in the form 00 .
∴limx→0aex+bcosx+ce−x2cosx−xsinx=2
⇒a+b+c2=2⇒a+b+c=4
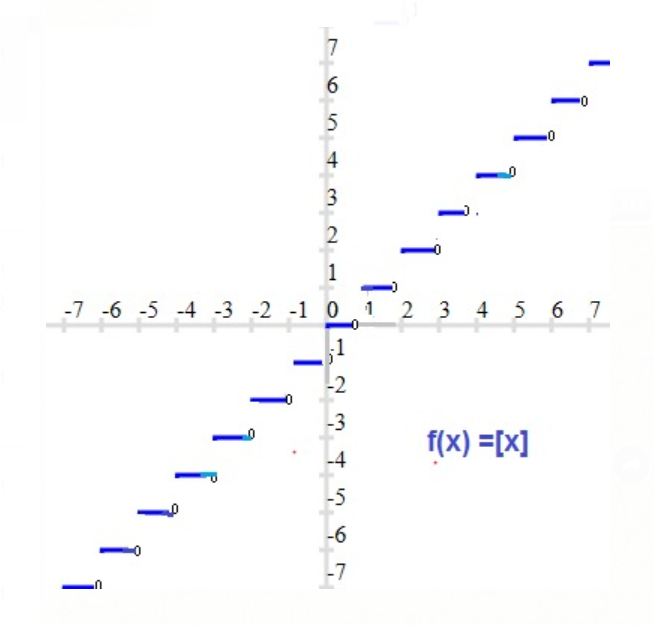
Greatest Integer function
There are some functions which change their value from one integer to another . The function rounds off the number into an integer less than the number called as " Greatest Integer function " .
Example 5
Example 6
If [.] denotes the greatest integer function , then limx→π2[x−π2cosx] is equal to .
We have ,
limx→π2[x−π2cosx]=limθ→0⎡⎢
⎢⎣θcos(π2+θ)⎤⎥
⎥⎦ where x−π2=θ
=limθ→0[−θsinθ]
=−2 [ because limθ→0θsinθ=1 and θ>sinθ for 0<θ<π2]
Example 7
If f ( x ) = {sin[x]x,[x]≠0;[x]=0} , Where[ . ] denotes the greatest integer function, then limx→0f(x) is equal to
We have ,
[x]= {(0 , 0≤x<1) , (−1 , −1≤x<0)}
f(x)= {(sin−1−1 = (sin1, when (−1≤x<0)) , (0 , when (0≤x<1)}
⇒limx→0−f(x)=sin1and,limx→0+f(x)=0
⇒limx→0f(x) does not exist .
Some tricks to find limits
( a ) Factorization : Dividing the equation into its factor so as to remove indeterminate form
( b ) Limit when x→∞
Put x=(1y) and y→0
Example 8
limx→−2(x2−x−6)2(x+2)2=
We have ,
limx→−2(x2−x−6)2(x+2)2
=limx→−2(x−3)2(x+2)2(x+2)2=limx→−2(x−3)2
=(−2−3)2=25
Example 9
limx→axm−amxn−an=(mn)am−n if m>n
We have ,
limx→axm−amxn−an [form00]
limx→a{xm−amx−a×x−axn−an}
limx→a{xm−amx−a÷xn−anx−a}
limx→axm−amx−a÷limx→axn−anx−a
=mn⋅aman=mnam−n
Example 10
limx→1x8−2x+1x4−2x+1 equals
limx→1x8−2x+1x4−2x+1
=limx→1(x−1)(x7+x6+x5+x4+x3+x2+x−1)(x−1)(x3+x2+x−1)
=limx→1x7+x6+x5+x4+x3+x2+x−1x3+x2+x−1
=62=3
Example 11
limx→−∞[√x2+x+1+x]=
We have ,
limx→−∞(√x2+x+1+x)
=limy→∞(√y2−y+1−y)where (y=−x)
=limy→∞(√y2−y+1−y)×√y2−y+1+y√y2−y+1+y
=limy→∞y2−y+1−y2√y2−y+1+y
=limy→∞−y+1√y2−y+1+y
=limy→∞−1+1y√1−1y+1y2+1
=12
Rationalization or double rationalization :
It means multiplying and dividing the same quantity just to make an " irrational " a " rational " number and if you couldn't get it one go then keep on rationalizing it.
Example 12
The value of limx→0√a2−ax+x2−√a2+ax+x2√a+x−√a−x , is
limx→0√a2−ax+x2−√a2+ax+x2√a+x−√a−x
=limx→0−2ax√a+x+√a−x2x(√a2−ax+x2+√a2+ax+x2)
=limx→0−a(√a+x+√a−x)√a2−ax+x2+√a2+ax+x2<br>=−2a322a=−√a
Example 13
The value of limx→2a√x−2a+√x−√2a√x2−4a2 is
We have,
limx→2a√x−2a+√x−√2a√x2−4a2
=limx→2a√x−2a+x−2a√x+2a√x−2a√x+2a
=limx→2a1√x+2a+√x−2a(√x+2a⋅√x+(2a))
=1√4a=12√a
Trignometric relations in Limits
( a )limx→0(sinxx) = limx→0(tanxx) =1
( b ) limx→0(sin−1xx) = limx→0(tan−1xx) = 1
( c ) limx→asin(f(x))f(x)=limx→atan(f(x))f(x)
( d ) limx→asin−1f(x)f(x)=limx→atan−1(f(x))f(x)
Exponential and logarithmic relations in limits
( a )limx→0(1+x)1x=e
( b )limx→0ex−1x=1
( c ) limx→0(ln(1+x)x)=1
( d ) limx→0ax−1x=lna,a∈R+
Example 14
limx→0√1−cos2x2x
limx→0√12(1−cos2x)x=limx→0|sinx|x
Now ,
limx→0+|sinx|x=limx→0sinxx=1
and , limx→0−|sinx|x=limx→0−sinxx=−1
Hence ,limx→0|sinx|x does not exist .
Example 15
limx→π63sinx−√3cosx6x−π
We have ,
limx→π63sinx−√3cosx6x−π
=limx→π62√3(√32sinx−12cosx)6(x−π6)
limx→π61√3sin(x−π6)(x−π6)=1√3
Example 16
The value of limx→0(4x−1)3sinx24⋅log(1+3x) , is
We have ,
limx→0(4x−1)3sinx24⋅log(1+3x)
=limx→0(4x−1x)3sin(x2)4x24×log(1+3x)3x
= 43 (loge4)3
Example 17
limx→0ax−bxex−1 is equal to
We have ,
limx→0ax−bxex−1
=limx→0(ax−1)−(bx−1)ex−1
=limx→0(ax−1x)−(bx−1x)(ex−1x)
=loga−logb1
=loge(ab).
Example 18
The value of limx→0(1+sinx)2cotx , is
We have ,
limx→0(1+sinx)2cotx
=elimx→0sinx×2cotx
=elimx→02cosx
=e2
Series expansion
Here are some trigonometric expansions commonly used
(i) sinx=x−x33!+x55!−x77!+......
( ii ) cosx=1−x22!+x44!−x66!+....( it comes after differentiating sinxexpansion)
( iii ) tanx=x+x33+2x515+.....
( iv ) ex=1+x+x22!+x33!+.....
( v ) (1+x)n = 1+nx + n(n−1)2!x2 + n(n−1)(n−2)3!x3+.....
( vi ) ln(1+x) = x−x22+x33+...... , (-1 < x ≤ 1)
Example 19
The value of limx→0(sin(x)x)1x2, is
We have ,
limx→0(sinxx)x12
=limx→0 ⎛⎜
⎜⎝x−x33ǃ+x55ǃ−x77ǃ+.......x⎞⎟
⎟⎠1x2
=limx→0(1−x23ǃ+x45ǃ−x67ǃ+........)1x2
=elimx→0(1x2)(1−x23ǃ+x45ǃ−x67ǃ+...−1)=e−16 .
Example 20
The value of limx→0(1+x)1x−ex is
"We have , Let y=(1+x)1x ( Taking log both sides )
So logy=1x⋅log(1+x)
(1+x)1x=elog(1+x)x=e1x(x−x22+x33−...)
⇒(1+x)1x=e1−x2+x23−..=e.e−x2+x23.....
limx→0(1+x)1x−ex
limx→0e.e(−x2)+(x23).....−(e)x
elimx→0e(−x2)+(x23)+....−1(−x2+x23+....)×(−x2+x2+....)x
=−12⋅e
"
Example 21
The value of limx→0ex+log(1+x)−(1−x)−2x2 is equal to
We have limx→0ex+log(1+x)−(1−x)−2x2
limx→0(1+x1!+x22!+x33!)+(x−x22+x33−x44+....)−(1+2x+3x2+4x3+....)x2
=limx→0−3x2+x3(13!+13−4)+....x2
=limx→0−3+x(13!+13−4)+....=−3 .
Sandwich theorem
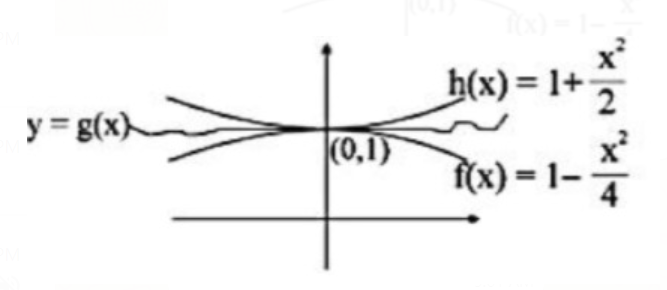
The " Sandwich theorem " also known as " Squeeze play theorem " is used where normal algebraic methods don't work.
Statement : Let f(x) , g(x) and h(x) be three real functions having a common domain D such that f(x) lies in interval
[h(x) , g(x)] , h(x)≤f(x)≤g(x) ∀ x ε D .
If limx→ah(x)=limx→ag(x) , then limx→af(x)=l.
From the figure
Here Limx→0g(x)=1
Example 22
limx→0x2sin(1x) is equal to
LHL : put x=0−h
x→0andh→0 , −1≤siny≤1 where (y=1x)
limh→0−(0−h)2sin(−1h)=0
RHL : put x=0+h
x→0andh→0
limh→0+(0+h)2sin(1h)=0
limx→0(x2)sin(1x)=0